Las cónicas

INTERACTIVO
LAS CÓNICAS
INTERACTIVO
María José García Cebrian
Red Educativa Digital Descartes, España
Fondo Editorial Pascual Bravo
Medellín
Título de la obra
Las cónicas
María José García Cebrian
Primera edición: 2018
Diseño del libro: Juan Guillermo Rivera Berrío
Diseño de cubierta: Diana María Velásquez García
Librería turn.js: Emmanuel García
Herramienta de edición: DescartesJS
Fuente: Amaranth
Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Todos los objetos interactivos y los contenidos de esta obra colectiva están protegidos por la Ley de Propiedad Intelectual.
Tabla de contenido
2.1. Ecuación de la circunferencia3
2.2. Posiciones relativas de un punto o una recta y una circunferencia4
2.3. Potencia de un punto respecto a una circunferencia5
2.4. Posiciones relativas y eje radical de dos circunferencias6
Circunferencias a tu alrededor7
3.1. Ecuación reducida de la elipse9
4.1. Ecuación reducida de la hipérbola13
5.1. Ecuación reducida de la parábola17
5.2. Desplazando el vértice de la parábola18
6. Ecuación general de segundo grado20
7. Ejercicios para practicar22
8. Algunas aplicaciones de las cónicas23
iii
Introducción
Una superficie cónica de revolución es la superficie engendrada por una línea recta que gira
alrededor de un eje manteniendo un punto fijo sobre dicho eje.
Cuando un plano corta a una superficie cónica obtenemos una curva llamada cónica. Según sea la posición del plano respecto al cono obtenemos una curva u otra.
 Un poco de historia1
Un poco de historia1
Aunque fue el matemático griego Menecmo (350 A.C.) quien
las descubrió, debemos a Apolonio de Perga (262-190 A.C.)
el primer estudio detallado de estas curvas en Las Cónicas, un conjunto de ocho libros en
el que también les da nombre.
Posteriormente fue Jan de Witt (1629-1672) quien descubrió que
todas las ecuaciones de segundo grado en dos variables, x e y, representan
secciones cónicas.
v
1. Lugares geométricos
Hemos visto las cónicas como secciones de un cono, sin embargo para estudiar los elementos y propiedades de cada una de ellas en el plano, resulta más conveniente definirlas como lugares geométricos, lo que nos va a permitir obtener una ecuación para cada cónica.
Un lugar geométrico es un conjunto de puntos con una propiedad común, recordemos dos ejemplos de objetos geométricos en el plano que se pueden describir como lugares geométricos.
1
2. La circunferencia
La circunferencia es el lugar geométrico de los puntos del plano que equidistan de uno fijo, el centro. La distancia del centro a uno cualquiera de sus puntos es el radio.
2
2.1. Ecuación de la circunferencia
3
2.2. Posiciones relativas de un punto o una recta y una circunferencia
4
2.3. Potencia de un punto respecto a una circunferencia
5
2.4. Posiciones relativas y eje radical de dos circunferencias
6
Circunferencias a tu alrededor
 |
 |
| Monedas Imagen tomada de |
Cuzco (Perú) Imagen tomada de |
 |
 |
| Un globo se infla antes de sobrevolar Capadocia (Turquía) Imagen tomada de |
Reloj astronómico de Praga (República Checa) Imagen tomada de |
7
3. La elipse
La elipse es el lugar geométrico de los puntos cuya suma de distancias a dos puntos fijos, llamados focos, es constante. La llamaremos 2a.
8
3.1. Ecuación reducida de la elipse
9
3.2. Más elipses
Veamos cómo cambia la ecuación de la elipse cuando los focos o el vértice cambian de posición.
10
Elipses a tu alrededor
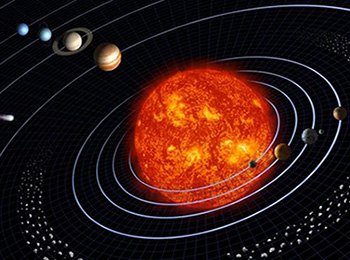 |
 |
| Las órbitas de los planetas Imagen tomada de |
Plaza elíptica en Madrid Imagen tomada de |
 |
 |
| Sala Nacional de las estatuas (Capitolio de Washington) Imagen tomada de |
Anfiteatro de Pompeya Imagen tomada de |
11
4. La hipérbola
La hipérbola es el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos, los focos, es constante. La llamaremos 2a.
12
4.1. Ecuación reducida de la hipérbola
13
4.2. Más hipérbolas
Veamos cómo cambia la ecuación de la hipérbola si los focos o el vértice cambian de posición.
14
Hipérbolas a tu alrededor
 |
 |
| Central nuclear de Trillo (Guadalajara) Imagen tomada de |
Catedral de Brasilia (Brasil) Imagen tomada de |
 |
 |
| Torre del Puerto de Kobe (Japón) Imagen tomada de |
Hipérbolas de luz |
15
5. La parábola
La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo, el foco, y de una recta llamada directriz.
16
5.1. Ecuación reducida de la parábola
17
5.2. El vértice de la parábola se traslada
¿Cómo es la ecuación de la parábola cuando el vértice no es el origen de coordenadas?. Veamoslo.
18
Parábolas a tu alrededor
 |
 |
| Surtidores en los jardines del Generalife (Granada) Imagen tomada de |
En La Pedrera de Gaudí (Barcelona) Imagen tomada de |
 |
 |
| Golden Gate (San Francisco) Imagen tomada de |
Parabólicas en el desierto de Atacama (Chile) Imagen tomada de |
19
6. La ecuación general de segundo grado
Una ecuación de segundo grado con dos incógnitas x e y de la forma Ax2+By2+Cx+Dy+E=0 siempre representa una cónica. El tipo depende de los valores que tomen A, B, C, D y E. Veamos algunos ejemplos:
20
La ecuación general de segundo grado en x e y es de la forma Ax2+Bxy+Cy2+Dx+Ey+F=0, pero la ecuación de las cónicas que hemos visto en este estudio tenían B=0, es decir eran sin término "xy". Esto es debido a que solo hemos estudiado cónicas cuyos ejes eran o bien los ejes de coordenadas o paralelos a ellos.
En la escena1 siguiente puedes observar lo que ocurre cuando los ejes son rectas cualesquiera.
21
7. Ejercicios para practicar
A continuación se presentan más ejercicios para practicar con las cónicas. Puedes elegir en el menú el tipo que prefieras para empezar. De todos ellos se ofrece la solución.
22
8. Algunas aplicaciones de las cónicas
En astronomía, aeronáutica, óptica, comunicaciones y hasta en medicina las aplicaciones de las cónicas son múltiples, veamos algunas.
23
Bibliografía
- Cónicas de Antonio Caro Merchante para Red Descartes (España).
- Secciones cónicas de Elena E. Álvarez Sáiz para Red Descartes (España).
- La elipse: Definición I y Definición II de Ildefonso Fernández Trujillo para Red Descartes (España).
- Las Cónicas (Proyecto MaTEX) de Fco. Javier González Ortiz.
- Cónicas de M. Teresa Pérez y Oscar Arratia.
- Las cónicas y sus aplicaciones de Pedro Alegria.
- Cónicas. Clasificación. de Mª Ángeles Rodríguez Bellido (Universidad de Sevilla).
26
