El Tangram Chino

Veamos si este análisis es correcto:

Despues de hacer el análisis de las figuras propuestas, estamos seguros que todas las figuras que se construyeron tienen igual área, ¿Estamos seguros?, porque fueron compuestas por la misma cantidad y tipo de piezas, pero se sospecha que no pasa lo mismo con el perímetro. ¿Como verificamos que esto es cierto?

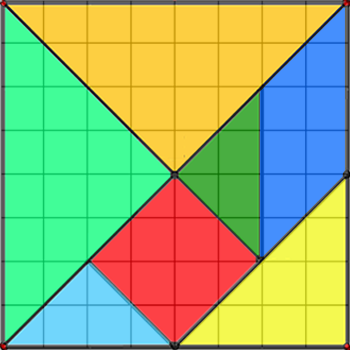Consideremos en la cuadrícula del tangram inicial un cuadrito como unidad de medida (supongamos 1 cm) para medir los lados de las figuras, y aplicar el teorema de pitágoras en los casos que fue necesario. Si deseas puedes imprimir esta plantilla y te ayudas con la regla centimetrada para medir los lados.

Elabora un dibujo de todas piezas del tangram y ubica las medidas tomadas de la longitud de cada lado, por ejemplo:

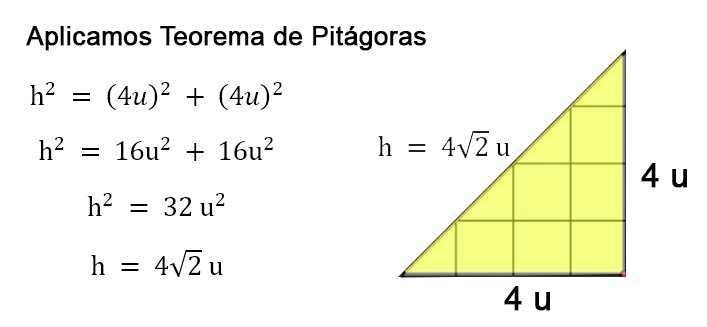
Se observa que:

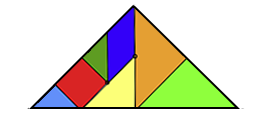1. Los triángulos que se formán son triángulos rectángulos isósceles, por lo tanto uno de sus lados es de mayor longitud (la hipotenusa) que los lados iguales, entonces, si este lado queda en el interior de la figura construida, no es lo mismo que si queda como lado de la construcción (ver figura). es posible encontrar las medidas de los lados del triángulo, ¿Cuánto mide el perímetro del triángulo construido?
2. Con el cuadrado, en cambio, como se trata de un polígono regular, sus lados siempre sumarán la misma longitud en la medida total del contorno de las figuras (su perímetro).

Observando detenidamente las figuras, se encontaron las siguientes relaciones:

1. El área del triángulo amarillo es el doble del área del triángulo naranja.
2. El área del cuadrado es el doble del triángulo verde pequeño.
3. El área de los dos triángulos más grandes es igual al área de todas las otras piezas juntas.
4. El área del cuadrado y el área del paralelogramo, ¿son iguales?

(Si no identificas la fracción, haz clic en cada pieza y observa). $$\frac{1}{8} + \frac{1}{8} = \frac{2}{8} = \frac{1}{4}$$

¿Qué otras relaciones se pueden encontrar?

¿Qué Construcciones tienen mayor perímetro que el Tangram inicial (cuadrado)?, compara los perimetros de las figuras construidas.