Química
Volumen I

Interactivo
Segunda parte

Jorge Wilson Ocampo Vásquez
José Gregorio Doria Andrade
Juan Guillermo Rivera Berrío

Institución Universitaria Pascual Bravo

Obra derivada de Chemistry 2e

Paul Flowers
University of North Carolina at Pembroke
Klaus Theopold (University of Delaware)
Richard Langley and Stephen F. Austin (State University)
William R. Robinson, PhD

Fondo Editorial Pascual Bravo

Medellín

Título de la obra:
Química
Volumen I
Interactivo (Segunda parte)

Autores:
Jorge Wilson Ocampo Vásquez
José Gregorio Doria Andrade
Juan Guillermo Rivera Berrío

Revisoras
Elena Esperanza Alvarez Saiz
María José García Cebrian

Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$

Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co
ISBN: 978-958-56858-9-5

LICENCIA

Tabla de contenido

Introducción

Figura 6.1. La Nebulosa del Cangrejo consiste en restos de una supernova (la explosión de una estrella). El Telescopio Espacial Hubble de la NASA produjo esta imagen compuesta. Las mediciones de las longitudes de onda de la luz emitida permitieron a los astrónomos identificar los elementos en la nebulosa, determinando que contiene iones específicos que incluyen S⁺ (filamentos verdes) y O²⁺ (filamentos rojos). (Crédito: modificación del trabajo de la NASA y la ESA).

En 1054, los astrónomos chinos registraron la aparición de una "estrella invitada" en el cielo, visible incluso durante el día, que luego desapareció lentamente en los próximos dos años. La repentina aparición se debió a una explosión de supernova, que era mucho más brillante que la estrella original. Aunque esta supernova fue observada hace casi un milenio, la Nebulosa del Cangrejo restante (Figura 6.1) continúa liberando energía hoy. Emite no solo luz visible, sino también luz infrarroja, rayos X y otras formas de radiación electromagnética. La nebulosa emite tanto los espectros continuos (el resplandor azul-blanco) como los espectros de emisión atómica (los filamentos coloreados).

En este capítulo, discutiremos la luz y otras formas de radiación electromagnética y cómo se relacionan con la estructura electrónica de los átomos. También veremos cómo esta radiación se puede usar para identificar elementos, incluso a miles de años luz de distancia.

Energía electromagnética

La naturaleza de la luz ha sido objeto de investigación desde la antigüedad. En el siglo XVII, Isaac Newton realizó experimentos con lentes y prismas y pudo demostrar que la luz blanca consiste en los colores individuales del arco iris combinados. Newton explicó sus hallazgos ópticos en términos de una visión "corpuscular" de la luz, en la que la luz estaba compuesta por corrientes de partículas extremadamente pequeñas que viajaban a altas velocidades de acuerdo con las leyes del movimiento de Newton. Otros investigadores en el siglo XVII, como Christiaan Huygens, habían demostrado que fenómenos ópticos como la reflexión y la refracción podrían explicarse igualmente en términos de luz como ondas que viajan a gran velocidad a través de un medio llamado "éter luminífero" que se pensaba que impregnaba todo espacio. A principios del siglo XIX, Thomas Young demostró que la luz que pasaba a través de rendijas estrechas y muy separadas producía patrones de interferencia que no podían explicarse en términos de partículas newtonianas, pero sí podían explicarse fácilmente en términos de ondas. Más tarde, en el siglo XIX, después de que James Clerk Maxwell desarrolló su teoría de la radiación electromagnética y demostró que la luz era la parte visible de un vasto espectro de ondas electromagnéticas, la visión de la luz por las partículas se desacreditó por completo.

A fines del siglo XIX, los científicos consideraban que el universo físico abarcaba aproximadamente dos dominios separados: materia compuesta por partículas que se mueven de acuerdo con las leyes del movimiento de Newton, y radiación electromagnética que consiste en ondas gobernadas por las ecuaciones de Maxwell. Hoy en día, estos dominios se denominan mecánica clásica y electrodinámica clásica (o electromagnetismo clásico). Aunque había algunos fenómenos físicos que no podían explicarse dentro de este marco, los científicos en ese momento estaban tan seguros de la solidez general de este marco que vieron estas aberraciones como paradojas desconcertantes que finalmente se resolverían de alguna manera dentro de este marco. Como veremos, estas paradojas llevaron a un marco contemporáneo que conecta íntimamente partículas y ondas en un nivel fundamental llamado dualidad onda-partícula, que ha superado la visión clásica.

La luz visible y otras formas de radiación electromagnética juegan un papel importante en la química, ya que pueden usarse para inferir las energías de los electrones dentro de los átomos y las moléculas. Gran parte de la tecnología moderna se basa en la radiación electromagnética. Por ejemplo, las ondas de radio de un teléfono móvil, los rayos X utilizados por los dentistas, la energía utilizada para cocinar alimentos en su microondas, el calor radiante de los objetos al rojo vivo y la luz de la pantalla de tu televisor son formas de radiación electromagnética que exhiben un comportamiento en forma de onda.

Ondas

Una onda es una oscilación o movimiento periódico que puede transportar energía de un punto en el espacio a otro. Ejemplos comunes de ondas están a nuestro alrededor.

Sacudir el extremo de una cuerda transfiere energía de tu mano al otro extremo de la cuerda, dejar caer una piedra en un estanque hace que las ondas se ondulen hacia afuera a lo largo de la superficie del agua, y la expansión del aire que acompaña a un rayo genera ondas de sonido (trueno), que puede viajar hacia afuera por varias millas. En cada uno de estos casos, la energía cinética se transfiere a través de la materia (la cuerda, el agua o el aire), mientras que la materia permanece esencialmente en su lugar. Un ejemplo perspicaz de una onda ocurre en los estadios deportivos cuando los fanáticos en una región estrecha de asientos se levantan simultáneamente y permanecen de pie con sus brazos levantados por unos segundos antes de sentarse nuevamente, mientras que los fanáticos en las secciones vecinas también se levantan y se sientan en secuencia. Si bien esta onda puede rodear rápidamente un gran estadio en unos pocos segundos, ninguno de los fanáticos en realidad viaja con la ola, todos permanecen en sus asientos o por encima de ellos.

Las ondas no necesitan estar restringidas para viajar a través de la materia. Como mostró Maxwell, las ondas electromagnéticas consisten en un campo eléctrico que oscila en el paso con un campo magnético perpendicular, los cuales son perpendiculares a la dirección de desplazamiento. Estas ondas pueden viajar a través de un vacío a una velocidad constante de $2.998 \times 10^8 m/s$, la velocidad de la luz (indicada por c).

Todas las ondas, incluidas las formas de radiación electromagnética, se caracterizan por una longitud de onda (indicada por λ, la letra griega minúscula lambda), una frecuencia (indicada por ν, la letra griega minúscula nu) y una amplitud. Como puede verse en la figura 6.2, la longitud de onda es la distancia entre dos picos o depresiones consecutivos en una onda (medida en metros en el sistema SI).

Las ondas electromagnéticas tienen longitudes de onda que caen dentro de un rango enorme de longitudes de onda de kilómetros ($10^3 m$) a picómetros ($10^{-12} m$) que se han observado. La frecuencia es el número de ciclos de onda que pasan un punto específico en el espacio en una cantidad específica de tiempo (en el sistema SI, esto se mide en segundos). Un ciclo corresponde a una longitud de onda completa. La unidad para la frecuencia, expresada en ciclos por segundo [$s^{-1}$], es el hercio o hertz (Hz). Los múltiplos comunes de esta unidad son megahertz, ($1 MHz = 1 \times 10^6 Hz$) y gigahertz ($1 GHz = 1 \times 10^9 Hz$).

La amplitud corresponde a la magnitud del desplazamiento de la onda y, por lo tanto, en la figura 6.2, esto corresponde a la mitad de la altura entre los picos y los valles. La amplitud está relacionada con la intensidad de la onda, que para la luz es el brillo, y para el sonido es la intensidad.

$$c = 2.998 \times 10^8 ms^{-1} = λν$$

Figura 6.2. Las ondas sinusoidales unidimensionales muestran la relación entre la longitud de onda, la frecuencia y la velocidad. La onda con la longitud de onda más corta tiene la frecuencia más alta. La amplitud es la mitad de la altura de la onda desde el pico hasta el canal.

El producto de la longitud de onda de una onda (λ) y su frecuencia (ν), λν, es la velocidad de la onda. Por lo tanto, para la radiación electromagnética en el vacío, la velocidad es igual a la constante fundamental, c. La longitud de onda y la frecuencia son inversamente proporcionales: a medida que aumenta la longitud de onda, la frecuencia disminuye. La proporcionalidad inversa se ilustra en la figura 6.3.

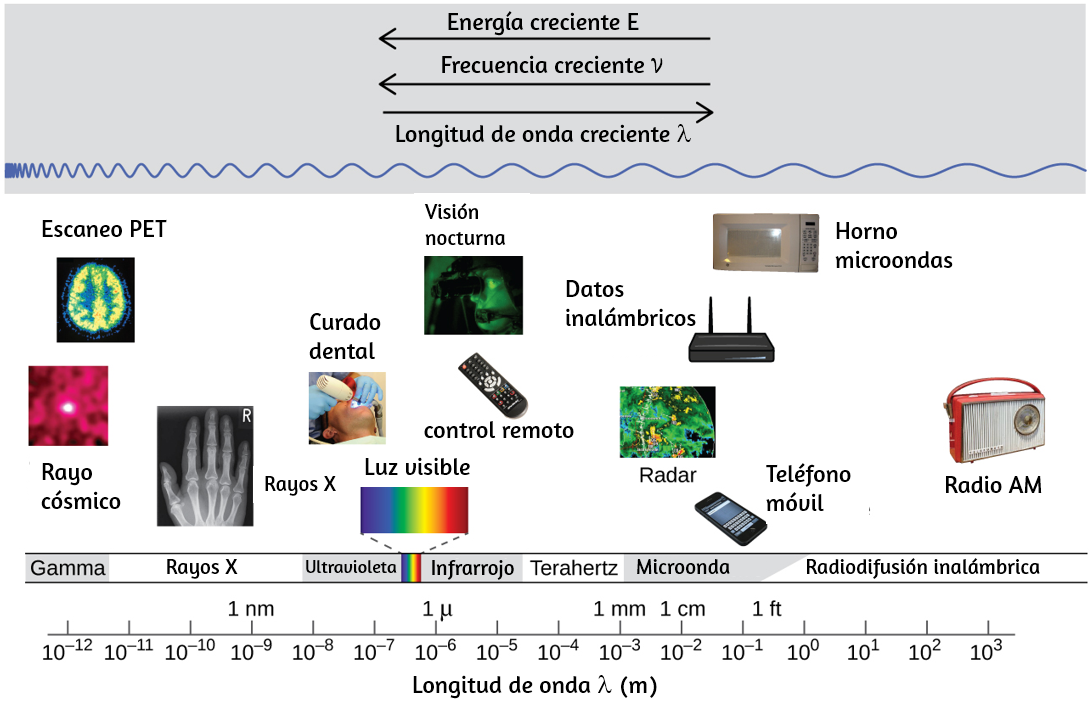
Figura 6.3. Las partes del espectro electromagnético se muestran en orden de frecuencia decreciente y de longitud de onda creciente (Crédito: "Rayo cósmico": modificación del trabajo de la NASA; crédito "PET scan": modificación del trabajo por el Instituto Nacional de la Salud; crédito "Rayos X": modificación del trabajo del Dr. Jochen Lengerke; crédito "Curado dental" : modificación del trabajo por el Departamento de la Marina; crédito "Visión nocturna": modificación del trabajo por el Departamento del Ejército; crédito "Control remoto": modificación del trabajo por Emilian Robert Vicol; crédito "Teléfono celular": modificación del trabajo por Brett Jordan; crédito "Horno de microondas": modificación del trabajo de Billy Mabray; crédito "Ultrasonido": modificación del trabajo de Jane Whitney; crédito "Radio AM": modificación del trabajo de Dave Clausen).

Esta figura también muestra el espectro electromagnético, el rango de todos los tipos de radiación electromagnética. Cada uno de los diversos colores de la luz visible tiene frecuencias y longitudes de onda específicas asociadas, y se puede ver que la luz visible constituye solo una pequeña parte del espectro electromagnético. Debido a que las tecnologías desarrolladas para trabajar en varias partes del espectro electromagnético son diferentes, por razones de conveniencia y legados históricos, las diferentes unidades se usan típicamente para diferentes partes del espectro. Por ejemplo, las ondas de radio se suelen especificar como frecuencias (normalmente en unidades de MHz), mientras que la región visible se suele especificar en longitudes de onda (normalmente en unidades de nm o angstroms).

Ejemplo 6.1

Determinación de la frecuencia y longitud de onda de la radiación

Una farola de sodio emite una luz amarilla que tiene una longitud de onda de $589 \space nm (1 \space nm = 1 \times 10^{-9} \space m$). ¿Cuál es la frecuencia de esta luz?

Solución

Podemos reorganizar la ecuación c = λν para hallar la frecuencia: $ν = \cfrac{c}{λ}$

Como c se expresa en metros por segundo, también debemos convertir 589 nm a metros.

Comprueba tu aprendizaje

Química en la vida cotidiana

Figura 6.4. Las torres de radio y celulares se utilizan normalmente para transmitir radiación electromagnética de longitud de onda larga. Cada vez más, las torres celulares están diseñadas para mezclarse con el paisaje, como con la torre celular de Tucson, Arizona (derecha) disfrazada de una palmera (Crédito extremos: modificación del trabajo por Sir Mildred Pierce; crédito medio: modificación del trabajo por M.O. Stevens).

Muchas tecnologías valiosas operan en la región de frecuencia de radio (3 kHz - 300 GHz) del espectro electromagnético. En el extremo de baja frecuencia (baja energía, longitud de onda larga) de esta región están las señales de radio AM (amplitud modulada) (540-2830 kHz) que pueden viajar largas distancias. Las señales de radio FM (frecuencia modulada) se utilizan en frecuencias más altas (87.5-108.0 MHz). En la radio AM, la información se transmite variando la amplitud de la onda (Figura 6.5). En la radio FM, por el contrario, la amplitud es constante y la frecuencia instantánea varía.

Un fenómeno particularmente característico de las ondas se produce cuando dos o más ondas entran en contacto: interfieren entre sí.

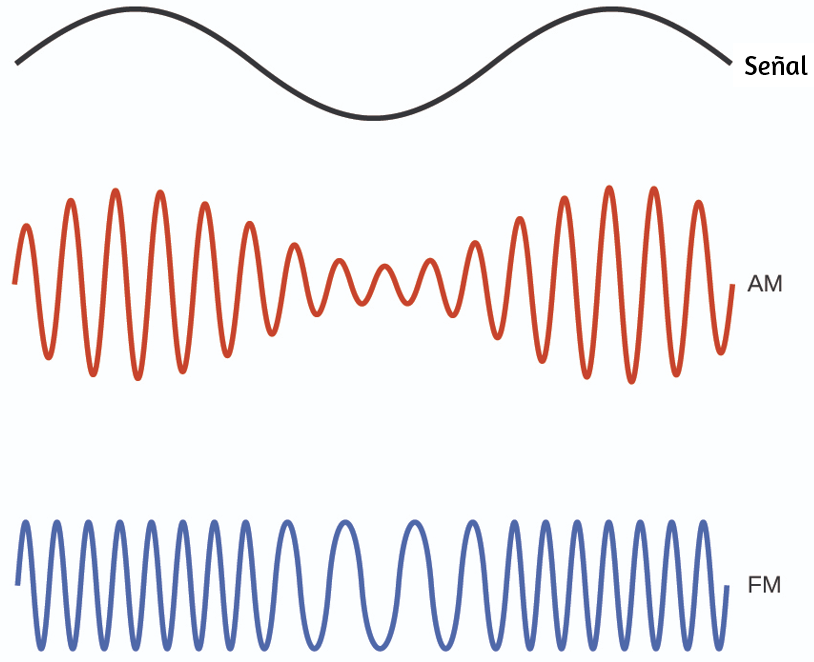
Figura 6.5. Este esquema describe cómo la amplitud modulada (AM) y la frecuencia modulada (FM) se pueden utilizar para transmitir una onda de radio.

La figura 6.6 muestra los patrones de interferencia que surgen cuando la luz pasa a través de rendijas estrechas y espaciadas a una longitud de onda.

Los patrones de flecos producidos dependen de la longitud de onda, con las franjas espaciadas más estrechamente para que la luz de longitud de onda más corta pase a través de un conjunto dado de rendijas. Cuando la luz pasa a través de las dos rendijas, cada rendija actúa efectivamente como una nueva fuente, lo que hace que dos ondas muy próximas entren en contacto con el detector (la cámara en este caso). Las regiones oscuras en la figura 6.6 corresponden a regiones donde los picos para la onda de una rendija coinciden con los depresiones para la onda de la otra rendija (interferencia destructiva), mientras que las regiones más brillantes corresponden a las regiones donde los picos para las dos Las ondas (o sus dos valles) coinciden (interferencia constructiva). Del mismo modo, cuando dos piedras se lanzan juntas en un estanque, los patrones de interferencia son visibles en las interacciones entre las ondas producidas por las piedras. Tales patrones de interferencia no pueden explicarse por las partículas que se mueven de acuerdo con las leyes de la mecánica clásica.

Figura 6.6. Los patrones de franjas de interferencia se muestran para la luz que pasa a través de dos rendijas estrechas y muy separadas. El espaciado de las franjas depende de la longitud de onda, con las franjas más espaciadas para la luz azul de longitud de onda más corta (crédito: PASCO).

En la escena interactiva que presentamos a continuación, tomada de las simulaciones Phet, puedes realizar varias actividades: utilizar múltiples fuentes con un espacio diferente y ver cómo cambia un patrón de interferencia, encontrar puntos de interferencia constructiva y destructiva, poner una barrera para ver cómo las ondas se mueven a través de una o dos rendijas.

En la escena interactiva de la siguiente página, diseñada con ChemDoodle, puedes observar la molécula de la penicilina cuya fórmula es $C_{16}H_{18}N_2O_4S$

No todas las ondas son ondas viajeras. Las ondas estacionarias permanecen limitadas dentro de alguna región del espacio. Como veremos, las ondas estacionarias desempeñan un papel importante en nuestra comprensión de la estructura electrónica de los átomos y las moléculas. El ejemplo más simple de una onda estacionaria es una onda unidimensional asociada con una cuerda vibrante que se mantiene fija en sus dos puntos finales.

La figura 6.7 muestra las cuatro ondas estacionarias de menor energía (la onda fundamental y los tres armónicos más bajos) para una cuerda vibrante a una amplitud particular.

Aunque el movimiento de la cuerda se encuentra principalmente dentro de un plano, se considera que la onda en sí es unidimensional, ya que se encuentra a lo largo de la longitud de la cuerda. El movimiento de los segmentos de cuerda en una dirección perpendicular a la longitud de la cuerda genera las ondas, por lo que la amplitud de las ondas es visible como el desplazamiento máximo de las curvas que se ve en la figura 6.7. La observación clave de la figura es que solo se pueden formar las ondas que tienen un número entero, n, de longitudes de onda medias entre los puntos finales. Un sistema con puntos finales fijos como este restringe el número y el tipo de las posibles formas de onda. Este es un ejemplo de cuantización, en el que solo se observan valores discretos de un conjunto más general de valores continuos de alguna propiedad.

Otra observación importante es que las ondas armónicas (aquellas ondas que muestran más de la mitad de la longitud de onda) tienen una o más puntos entre los dos puntos finales que no están en movimiento. Estos puntos especiales son nodos. Las energías de las ondas estacionarias con una amplitud dada en una cuerda vibrante aumentan con el número de medias longitudes de onda n. Dado que el número de nodos es n - 1, también se puede decir que la energía depende del número de nodos, generalmente aumentando a medida que aumenta el número de nodos.

Figura 6.7. Una cuerda vibrante muestra algunas ondas estacionarias unidimensionales. Dado que los dos puntos finales de la cuerda se mantienen fijos, solo se pueden formar ondas con un número entero de medias longitudes de onda. Los puntos en la cadena entre los puntos finales que no se mueven se denominan nodos.

Un ejemplo de ondas estacionarias bidimensionales se muestra en la figura 6.8, que muestra los patrones de vibración en una superficie plana. Si bien las amplitudes vibracionales no se pueden ver como se podían ver en la cuerda vibrante, los nodos se han hecho visibles rociando la superficie del tambor con un polvo que se acumula en las áreas de la superficie que tienen un desplazamiento mínimo.

Para las ondas estacionarias unidimensionales, los nodos eran puntos en la línea, pero para las ondas estacionarias bidimensionales, los nodos son líneas en la superficie (para las ondas estacionarias tridimensionales, los nodos son superficies bidimensionales dentro de la línea tridimensional).

Figura 6.8. Las ondas estacionarias bidimensionales se pueden visualizar en una superficie vibrante. La superficie ha sido rociada con un polvo que se acumula cerca de las líneas nodales. Hay dos tipos de nodos visibles: nodos radiales (círculos) y nodos angulares (radios).

En la siguiente escena interactiva, diseñada por Andrew Duffy, puedes interactuar con diferentes valores de n, los cuales determinan el número de nodos en la onda estacionaria. Un ejercicio interesante es usar los botones paso adelante y atrás, para obtener una onda estacionaria de amplitud cero.

La radiación del cuerpo negro y la catástrofe ultravioleta

Las últimas décadas del siglo XIX fueron testigos de una intensa actividad de investigación en la comercialización de la iluminación eléctrica recién descubierta.

Esto requería obtener una mejor comprensión de las distribuciones de luz emitidas desde varias fuentes consideradas. La iluminación artificial generalmente está diseñada para imitar la luz solar natural dentro de las limitaciones de la tecnología subyacente. Dicha iluminación consiste en un rango de frecuencias ampliamente distribuidas que forman un espectro continuo.

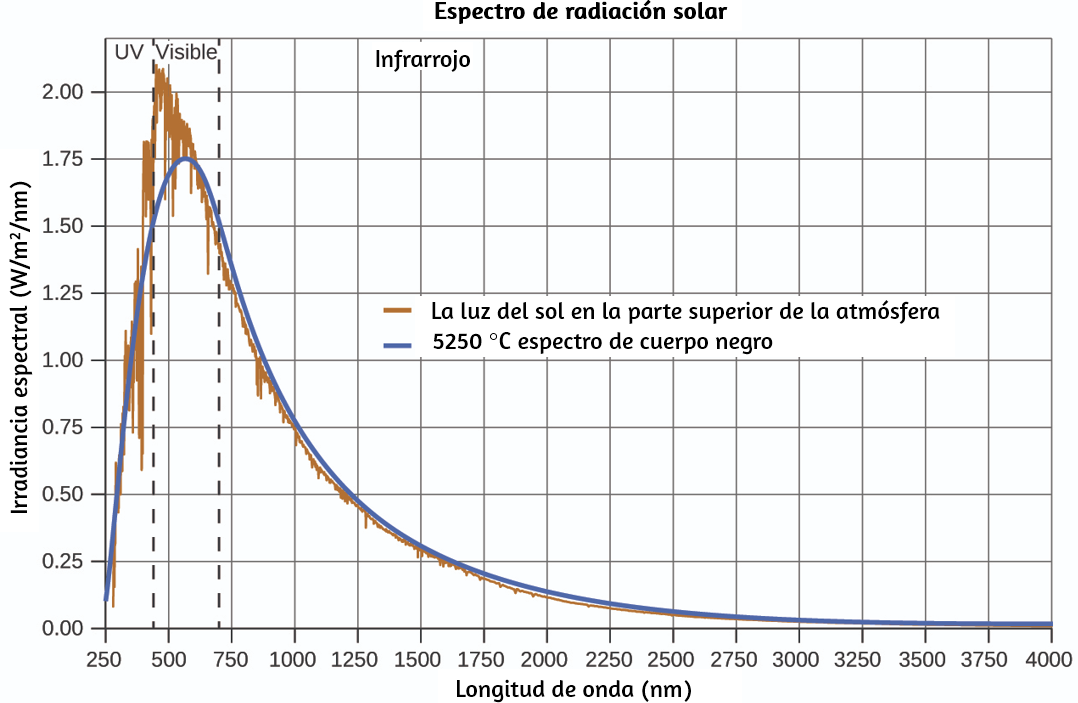
Figura 6.9. La distribución espectral (intensidad de la luz en función de la longitud de onda) de la luz solar alcanza la atmósfera de la Tierra como luz UV, luz visible y luz IR. La luz solar no absorbida en la parte superior de la atmósfera tiene una distribución que coincide aproximadamente con la distribución teórica de un cuerpo negro a 5250 °C, representada por la curva azul (Crédito: modificación del trabajo realizado por la Sociedad Americana de Pruebas y Materiales (ASTM), Espectros de Referencia Terrestres para la Evaluación del Desempeño Fotovoltaico).

En la figura 6.9, la distribución solar se compara con una distribución representativa, llamada espectro de cuerpo negro, que corresponde a una temperatura de 5250 °C.

El espectro del cuerpo negro coincide bastante bien con el espectro solar. Un cuerpo negro. La figura 6.9 muestra la distribución de longitud de onda para la luz solar. La radiación más intensa está en la región visible, con la intensidad disminuyendo rápidamente para la luz ultravioleta (UV) de longitud de onda más corta, y más lentamente para la luz infrarroja (IR) de longitud de onda más larga.

es un emisor ideal que se aproxima al comportamiento de muchos materiales cuando se calienta. Es "ideal" en el mismo sentido que un gas ideal es una representación conveniente y simple de gases reales que funciona bien, siempre que la presión no sea demasiado alta ni la temperatura demasiado baja. Una buena aproximación de un cuerpo negro que se puede usar para observar la radiación del cuerpo negro es un horno de metal que se puede calentar a temperaturas muy altas. El horno tiene un pequeño orificio que permite observar la luz emitida dentro del horno con un espectrómetro para poder medir las longitudes de onda y sus intensidades. La figura 6.10 muestra las curvas resultantes para algunas temperaturas representativas. Cada distribución depende solo de un único parámetro: la temperatura. Los máximos en las curvas del cuerpo negro, λ_max, cambian a longitudes de onda más cortas a medida que aumenta la temperatura, lo que refleja la observación de que los metales que se calientan a altas temperaturas comienzan a brillar de un rojo más oscuro que se vuelve más brillante a medida que aumenta la temperatura, y eventualmente se vuelve blanco caliente a temperaturas muy altas a medida que las intensidades de todas las longitudes de onda visibles se vuelven apreciables. Esta observación común estuvo en el corazón de la primera paradoja que mostró las limitaciones fundamentales de la física clásica que examinaremos.

Los físicos derivaron expresiones matemáticas para las curvas del cuerpo negro usando conceptos bien aceptados de las teorías de la mecánica clásica y el electromagnetismo clásico. Las expresiones teóricas como funciones de la temperatura se ajustan bien a las curvas experimentales del cuerpo negro en longitudes de onda más largas, pero mostraron discrepancias significativas en longitudes de onda más cortas. No solo las curvas teóricas no mostraron un pico, sino que mostraron absurdamente que la intensidad se hizo infinitamente grande a medida que la longitud de onda se hacía más pequeña, lo que implicaría que los objetos cotidianos a temperatura ambiente deberían emitir grandes cantidades de luz UV. Esto se conoció como la "catástrofe ultravioleta" porque nadie pudo encontrar ningún problema con el tratamiento teórico que podría llevar a un comportamiento tan poco realista de onda corta. Finalmente, alrededor de 1900, Max Planck dedujo una expresión teórica para la radiación del cuerpo negro que se ajusta exactamente a las observaciones experimentales (dentro del error experimental). Planck desarrolló su tratamiento teórico extendiendo el trabajo anterior que se había basado en la premisa de que los átomos que componían el horno vibraban a frecuencias crecientes (o longitudes de onda decrecientes) a medida que aumentaba la temperatura, siendo estas vibraciones la fuente de la radiación electromagnética emitida. Pero donde los tratamientos anteriores permitieron que los átomos vibrantes tuvieran valores de energía obtenidos de un conjunto continuo de energías (perfectamente razonable, según la física clásica), Planck descubrió que al restringir las energías vibratorias a valores discretos para cada frecuencia, podía deducir una expresión para la radiación del cuerpo negro que correctamente tuvo la intensidad disminuyendo rápidamente para las longitudes de onda cortas en la región UV.

La cantidad h es una constante ahora conocida como la constante de Planck, en su honor. Si bien Planck estaba satisfecho de haber resuelto la paradoja de la radiación del cuerpo negro, le molestaba que para hacerlo, tenía que asumir que los átomos vibrantes requerían energías cuantificadas, lo que no podía explicar. El valor de la constante de Planck es muy pequeño, 6.626 × 10⁻³⁴ julios segundos (J s), lo que ayuda a explicar por qué la cuantificación de la energía no se había observado previamente en los fenómenos macroscópicos.

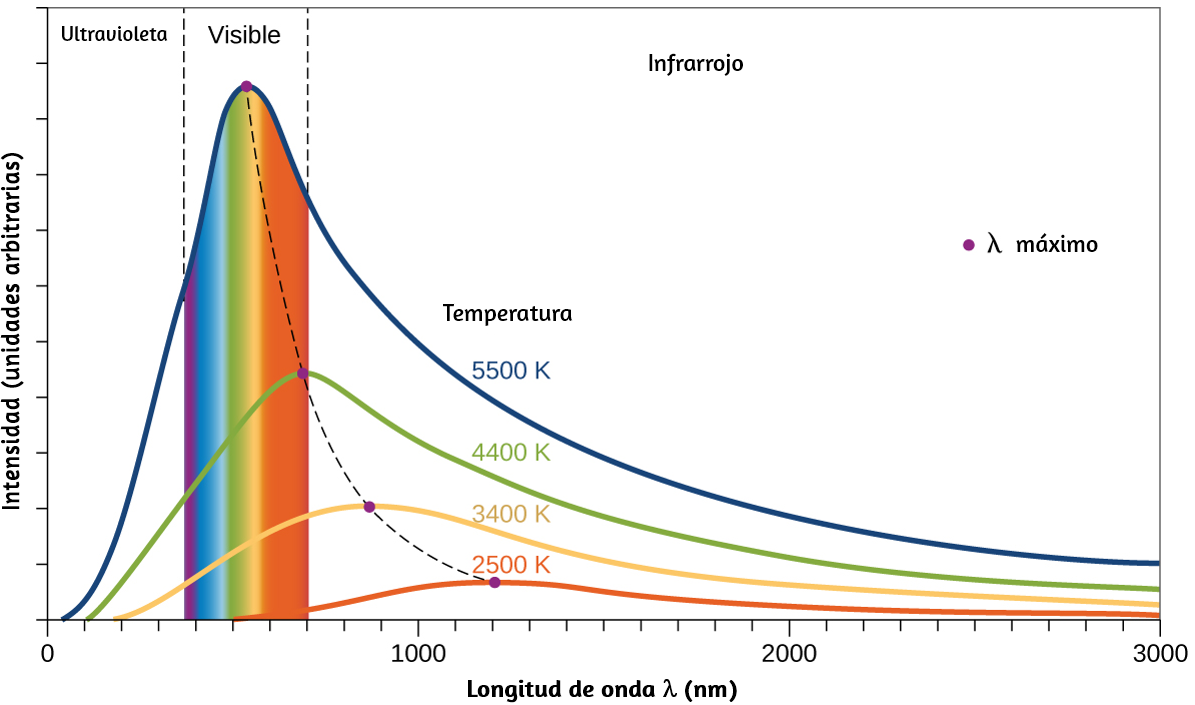
Figura 6.10. Se muestran curvas de distribución espectral de cuerpo negro para algunas temperaturas representativas.

En la siguiente unidad interactiva, diseñada por Victor Hugo García Jarillo, se muestran las diferentes etapas del pensamiento científico para la solución al problema de la radiación de cuerpo negro que fue históricamente el primer fenómeno en ser explicado con un modelo cuántico y más que un fenómeno físico es considerado un concepto matemático que por alguna razón coincidía con los resultados experimentales.

El vídeo de motivación corresponde al capítulo 50 de la serie "Universo Mecánico" del Instituto de Tecnología de California (te sugerimos explorar esta unidad didáctica en una pantalla ampliada).

El efecto fotoeléctrico

La siguiente paradoja en la teoría clásica por resolver se refería al efecto fotoeléctrico (Figura 6.11). Se había observado que los electrones podían ser expulsados ​​de la superficie limpia de un metal cuando la luz que tenía una frecuencia mayor que la de una frecuencia umbral se reflejaba en ella. Sorprendentemente, la energía cinética de los electrones expulsados ​​no dependía del brillo de la luz, sino que aumentaba con el aumento de la frecuencia de la luz.

Ya que los electrones en el metal tenían una cierta cantidad de energía de enlace manteniéndolos allí, la luz incidente necesitaba tener más energía para liberar los electrones. Según la teoría de la onda clásica, la energía de una onda depende de su intensidad (que depende de su amplitud), no de su frecuencia. Una parte de estas observaciones fue que la cantidad de electrones expulsados ​​dentro de un período de tiempo determinado aumentaba a medida que aumentaba el brillo. En 1905, Albert Einstein pudo resolver la paradoja al incorporar los hallazgos de cuantización de Planck en la visión desacreditada de partículas de la luz (Einstein ganó su premio Nobel por este trabajo, y no por sus teorías de la relatividad por las que es más famoso).

Einstein argumentó que las energías cuantificadas que Planck había postulado en su tratamiento de la radiación del cuerpo negro podrían aplicarse a la luz en el efecto fotoeléctrico, de modo que la luz que golpea la superficie del metal no debería verse como una onda, sino como una corriente de partículas (luego llamados fotones) cuya energía dependía de su frecuencia, de acuerdo con la fórmula de Planck, E = hν (o, en términos de longitud de onda usando c = νλ, $E = \cfrac{hc}{λ}$). Los electrones fueron expulsados ​​cuando fueron alcanzados por fotones que tenían suficiente energía (una frecuencia mayor que el umbral). Cuanto mayor sea la frecuencia, mayor será la energía cinética impartida a los electrones que escapan por las colisiones. Einstein también argumentó que la intensidad de la luz no dependía de la amplitud de la onda entrante, sino que correspondía al número de fotones que golpeaban la superficie dentro de un período de tiempo determinado. Esto explica por qué el número de electrones expulsados ​​aumentó con el aumento del brillo, ya que cuanto mayor es el número de fotones entrantes, mayor es la probabilidad de que colisionen con algunos de los electrones.

Con los hallazgos de Einstein, la naturaleza de la luz adquirió un nuevo aire de misterio. Aunque muchos fenómenos de luz podrían explicarse en términos de ondas o partículas, ciertos fenómenos, como los patrones de interferencia obtenidos cuando la luz pasaba a través de una doble rendija, eran completamente contrarios a una vista de la luz como partícula, mientras que otros fenómenos, como el Efecto fotoeléctrico, eran completamente contrarios a una vista de la luz como onda. De alguna manera, en un nivel fundamental profundo que aún no se comprende del todo, la luz es tanto ondulada como de partículas. Esto se conoce como dualidad onda-partícula.

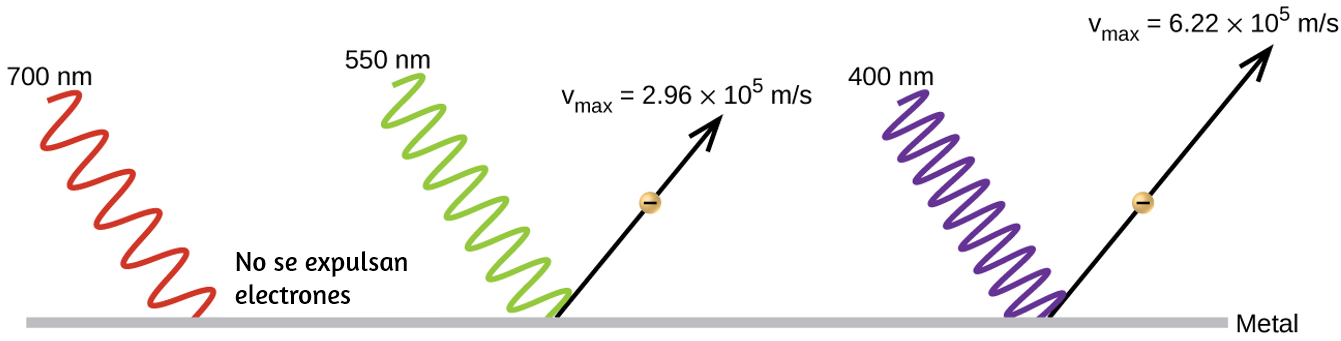
Figura 6.11. Los fotones con bajas frecuencias no tienen suficiente energía para hacer que los electrones sean expulsados a través del efecto fotoeléctrico. Para cualquier frecuencia de luz por encima de la frecuencia umbral, la energía cinética de un electrón expulsado aumentará linealmente con la energía del fotón entrante.

En la siguiente unidad interactiva, diseñada por Tine Stalmans, a través de una conversación con un tutor digital y la observación simultánea de modelos y simulaciones, podrás conocer y entender el efecto fotoeléctrico, así como las aplicaciones tecnológicas que tiene.

Al igual que en la unidad interactiva anterior, te recomendamos ampliar la unidad en una ventana emergente.

Ejemplo 6.2

Calculando la energía de la radiación

Cuando vemos la luz de un aviso de neón, estamos observando la radiación de los átomos de neón excitados. Si esta radiación tiene una longitud de onda de 640 nm.

¿Cuál es la energía del fotón que se está emitiendo?

Solución

Usamos la parte de la ecuación de Planck que incluye la longitud de onda, λ, y convertimos las unidades de nanómetros a metros para que las unidades de λ y c sean las mismas.

Comprueba tu aprendizaje

Ejemplo 6.3

Efecto fotoeléctrico

Identifica cuáles de las siguientes afirmaciones son falsas y, cuando sea necesario, cambia la palabra o frase en cursiva para que sean verdaderas, de acuerdo con la explicación de Einstein del efecto fotoeléctrico.

(a) Aumentar el brillo de la luz entrante aumenta la energía cinética de los electrones expulsados.
(b) Aumentar la longitud de onda de la luz entrante aumenta la energía cinética de los electrones expulsados.
(c) Aumentar el brillo de la luz entrante aumenta el número de electrones expulsados.
(d) Aumentar la frecuencia de la luz entrante puede aumentar el número de electrones expulsados.

Solución

(a) Falso. El aumento del brillo de la luz entrante no tiene ningún efecto sobre la energía cinética de los electrones expulsados. Sólo la energía, no el número o la amplitud, de los fotones influye en la energía cinética de los electrones.
(b) Falso. Aumentar la frecuencia de la luz entrante aumenta la energía cinética de los electrones expulsados. La frecuencia es proporcional a la energía e inversamente proporcional a la longitud de onda. Las frecuencias por encima del valor umbral transfieren el exceso de energía a la energía cinética de los electrones.
(c) Verdadero. Debido a que la cantidad de colisiones con fotones aumenta con una luz más brillante, la cantidad de electrones expulsados ​​aumenta.
(d) Cierto con respecto al umbral de energía que une los electrones al metal. Por debajo de este umbral, los electrones no se emiten y están por encima de ellos. Una vez sobre el valor de umbral, aumentar la frecuencia no aumenta el número de electrones expulsados.

Comprueba tu aprendizaje

Línea espectral

Otra paradoja dentro de la teoría electromagnética clásica con la que lucharon los científicos a fines del siglo XIX se refería a la luz emitida por los átomos y las moléculas. Cuando los sólidos, líquidos o gases condensados ​​se calientan lo suficiente, irradian parte del exceso de energía en forma de luz. Los fotones producidos de esta manera tienen un rango de energías y, por lo tanto, producen un espectro continuo en el que está presente una serie ininterrumpida de longitudes de onda. La mayor parte de la luz generada por las estrellas (incluido nuestro sol) se produce de esta manera. Puedes ver todas las longitudes de onda visibles de la luz presente en la luz solar utilizando un prisma para separarlas. Como puede verse en la figura 6.9, la luz solar también contiene luz UV (longitudes de onda más cortas) y luz IR (longitudes de onda más largas) que se pueden detectar utilizando instrumentos pero que son invisibles para el ojo humano. Los sólidos incandescentes (brillantes) como los filamentos de tungsteno en las luces incandescentes también emiten luz que contiene todas las longitudes de onda de la luz visible.

Estos espectros continuos a menudo se pueden aproximar mediante curvas de radiación del cuerpo negro a una temperatura adecuada, como las que se muestran en la figura 6.10.

A diferencia de los espectros continuos, la luz también puede ocurrir como espectros discretos o lineales con anchos de línea muy estrechos intercalados en todas las regiones espectrales, como las que se muestran en la figura 6.13.

La activación de un gas a baja presión parcial utilizando una corriente eléctrica, o su calentamiento, producirá espectros de línea. Las bombillas fluorescentes y los letreros de neón funcionan de esta manera (Figura 6.12). Cada elemento muestra su propio conjunto característico de líneas, al igual que las moléculas, aunque sus espectros son generalmente mucho más complicados.

Figura 6.12. Los avisos de neón funcionan al excitar un gas a baja presión parcial usando una corriente eléctrica. Este aviso muestra los efectos artísticos muy elaborados que se pueden lograr (crédito: Dave Shaver).

Figura 6.13. Compara los dos tipos de espectros de emisión: espectro continuo de luz blanca (arriba) y los espectros de línea de la luz de los átomos de sodio, hidrógeno, calcio y mercurio excitados.

Cada línea de emisión consiste en una única longitud de onda de luz, lo que implica que la luz emitida por un gas consiste en un conjunto de energías discretas. Por ejemplo, cuando una descarga eléctrica pasa a través de un tubo que contiene gas hidrógeno a baja presión, las moléculas de $H_2$ se dividen en átomos de H separados y vemos un color azul-rosado. Al pasar la luz a través de un prisma se produce un espectro de líneas, lo que indica que esta luz está compuesta de fotones de cuatro longitudes de onda visibles, como se muestra en la figura 6.13.

El origen de los espectros discretos en átomos y moléculas fue extremadamente desconcertante para los científicos a fines del siglo XIX, ya que, según la teoría electromagnética clásica, solo se deberían observar los espectros continuos.

Aún más desconcertante, en 1885, Johann Balmer pudo derivar una ecuación empírica que relacionaba las cuatro longitudes de onda visibles de la luz emitida por los átomos de hidrógeno con enteros. Esa ecuación es la siguiente, en la que k es una constante:

$$\cfrac{1}{λ} = k\bigg(\cfrac{1}{4} - \cfrac{1}{n^2}\bigg), n = 3, 4, 5, 6$$

Otras líneas discretas para el átomo de hidrógeno se encontraron en las regiones UV e IR. Johannes Rydberg generalizó el trabajo de Balmer y desarrolló una fórmula empírica que predijo todas las líneas de emisión de hidrógeno, no solo aquellas restringidas al rango visible, donde n₁ y n₂ son números enteros, n₁ < n₁, y R_∞ es la constante de Rydberg ($1.097 \times 10^7 m^{-1}$).

$$\cfrac{1}{λ} = R_{∞}\bigg(\cfrac{1}{n_1^2} - \cfrac{1}{n_2^2}\bigg)$$

Incluso a fines del siglo XIX, la espectroscopia era una ciencia muy precisa, por lo que las longitudes de onda del hidrógeno se midieron con una precisión muy alta, lo que implicaba que la constante de Rydberg, también podía determinarse con mucha precisión. Que una fórmula tan simple como la fórmula de Rydberg pudiera explicar mediciones tan precisas en aquel momento parecía sorprendente, pero fue la explicación final de los espectros de emisión de Neils Bohr en 1913 lo que finalmente convenció a los científicos a abandonar la física clásica y estimuló el desarrollo de la tecnología de la mecánica cuántica moderna.

El modelo de Bohr

Siguiendo el trabajo de Ernest Rutherford y sus colegas a principios del siglo XX, la imagen de los átomos consistía en pequeños núcleos densos rodeados de electrones más ligeros y aún más pequeños que se movían continuamente alrededor del núcleo. Esta imagen se llamó modelo planetario, ya que representaba al átomo como un "sistema solar" en miniatura con los electrones orbitando el núcleo como planetas orbitando el sol. El átomo más simple es el hidrógeno, que consiste en un único protón como el núcleo sobre el cual se mueve un solo electrón. La fuerza electrostática que atrae el electrón al protón depende solo de la distancia entre las dos partículas. Sin embargo, esta descripción mecánica clásica del átomo es incompleta, ya que un electrón que se mueve en una órbita elíptica se aceleraría (al cambiar de dirección) y, de acuerdo con el electromagnetismo clásico, debería emitir continuamente radiación electromagnética. Esta pérdida de energía orbital debería hacer que la órbita del electrón sea cada vez más pequeña hasta llegar a un espiral en el núcleo, lo que implica que los átomos son inherentemente inestables.

En 1913, Niels Bohr intentó resolver la paradoja atómica ignorando la predicción del electromagnetismo clásico de que el electrón en órbita en el hidrógeno emitiría luz continuamente. En cambio, se incorporó a la descripción de la mecánica clásica de las ideas de cuantización del átomo de Planck y al hallazgo de Einstein de que la luz consiste en fotones cuya energía es proporcional a su frecuencia. Bohr asumió que el electrón que orbita el núcleo normalmente no emitiría ninguna radiación (la hipótesis del estado estacionario), pero emitiría o absorbería un fotón si se moviera a una órbita diferente. La energía absorbida o emitida reflejaría diferencias en las energías orbitales de acuerdo con esta ecuación:

$$|ΔE| = |E_f - E_i| = hν = \cfrac{hc}{λ}$$

En esta ecuación, h es la constante de Planck y $E_i$ y $E_f$ son las energías orbitales inicial y final, respectivamente. Se utiliza el valor absoluto de la diferencia de energía, ya que las frecuencias y las longitudes de onda son siempre positivas. En lugar de permitir valores continuos de energía, Bohr asumió que las energías de estos orbitales electrónicos se cuantificaron:

$$E_n = -\cfrac{k}{n^2}, n = 1, 2, 3, ...$$

En esta expresión, k es una constante que comprende constantes fundamentales como la masa y la carga del electrón y la constante de Planck. Insertando la expresión de las energías de órbita en la ecuación para ΔE, obtenemos:

$$ΔE = k\bigg(\cfrac{1}{n_1^2} - \cfrac{1}{n_2^2}\bigg) = \cfrac{hc}{λ}$$

$$\cfrac{1}{λ} = \cfrac{k}{hc}\bigg(\cfrac{1}{n_1^2} - \cfrac{1}{n_2^2}\bigg)$$

Es idéntica a la ecuación de Rydberg en la que $R_{∞} = \cfrac{k}{hc}$. Cuando Bohr calculó su valor teórico para la constante de Rydberg, $R_{∞}$, y lo comparó con el valor experimentalmente aceptado, obtuvo un excelente acuerdo. Dado que la constante de Rydberg era una de las constantes medidas con mayor precisión en ese momento, este nivel de acuerdo era sorprendente y significaba que el modelo de Bohr se tomaba en serio, a pesar de las muchas suposiciones que Bohr necesitaba para derivarlo.

Los niveles de energía más bajos se muestran en la figura 6.14. Una de las leyes fundamentales de la física es que la materia es más estable con la energía más baja posible. Por lo tanto, el electrón en un átomo de hidrógeno generalmente se mueve en la órbita n = 1, la órbita en la que tiene la energía más baja. Cuando el electrón está en esta órbita de energía más baja, se dice que el átomo está en su estado electrónico básico (o simplemente en el estado fundamental). Si el átomo recibe energía de una fuente externa, es posible que el electrón se mueva a una órbita con un valor n más alto y el átomo se encuentre ahora en un estado electrónico excitado (o simplemente un estado excitado) con una energía más alta. Cuando un electrón pasa de un estado excitado (órbita de mayor energía) a un estado menos excitado, o estado fundamental, la diferencia de energía se emite como un fotón. De manera similar, si un fotón es absorbido por un átomo, la energía del fotón mueve un electrón desde una órbita de energía más baja hasta una más excitada. Podemos relacionar la energía de los electrones en los átomos con lo que aprendimos anteriormente sobre la energía. La ley de conservación de la energía dice que no podemos crear ni destruir energía. Por lo tanto, si se requiere una cierta cantidad de energía externa para excitar un electrón de un nivel de energía a otro, esa misma cantidad de energía se liberará cuando el electrón vuelva a su estado inicial (Figura 6.15).

Dado que el modelo de Bohr involucraba solo un solo electrón, también podría aplicarse a los iones de electrones un solo electrón $He^+$, $Li^{2+}$, $Be^{3+}$, etc., que difieren del hidrógeno solo en sus cargas nucleares, por lo que los átomos e iones de un electrón se denominan colectivamente como átomos parecidos al hidrógeno. La expresión de energía para átomos similares al hidrógeno es una generalización de la energía del átomo de hidrógeno, en la que Z es la carga nuclear (+1 para hidrógeno, +2 para He, +3 para Li, etc.) y k tiene un valor de $2.179 \times 10^{–18} J$.

Figura 6.14. Números cuánticos y niveles de energía en un átomo de hidrógeno. Cuanto más negativo sea el valor calculado, menor será la energía.

Los tamaños de las órbitas circulares para átomos similares al hidrógeno se dan en términos de sus radios mediante la siguiente expresión, en la que $α_0$ es una constante llamada radio de Bohr, con un valor de $5.292 \times 10^{−11} m$:

La ecuación también nos muestra que a medida que aumenta la energía del electrón (a medida que n aumenta), el electrón se encuentra a mayores distancias del núcleo. Esto está implícito en la dependencia inversa de la atracción electrostática en la distancia, ya que, a medida que el electrón se aleja del núcleo, la atracción electrostática entre él y el núcleo disminuye y se mantiene menos apretada en el átomo. Ten en cuenta que a medida que n aumenta de tamaño y las órbitas aumentan de tamaño, sus energías se acercan a cero, por lo que los límites n→∞ y r→∞ implican que E = 0 corresponde al límite de ionización en el que el electrón se elimina completamente del núcleo. Por lo tanto, para el hidrógeno en el estado fundamental n = 1, la energía de ionización sería:

ΔE = E_n→∞ − E₁ = 0 + k = k

Con tres paradojas extremadamente desconcertantes ahora resueltas (radiación de cuerpo negro, el efecto fotoeléctrico y el átomo de hidrógeno), y todas involucrando la constante de Planck de una manera fundamental, quedó claro para la mayoría de los físicos en ese momento que las teorías clásicas que funcionaron tan bien en el mundo macroscópico tenía fallas fundamentales y no podía extenderse hasta el dominio microscópico de los átomos y las moléculas.

Desafortunadamente, a pesar del notable logro de Bohr al derivar una expresión teórica para la constante de Rydberg, no pudo extender su teoría al siguiente átomo más simple, He, que solo tiene dos electrones. El modelo de Bohr tenía fallas severas, ya que todavía se basaba en la noción de mecánica clásica de órbitas precisas, un concepto que luego se descubrió que era insostenible en el dominio microscópico, cuando se desarrolló un modelo adecuado de mecánica cuántica para reemplazar la mecánica clásica.

Ejemplo 6.4

Cálculo de la energía de un electrón en una órbita de Bohr

Los primeros investigadores estaban muy emocionados cuando pudieron predecir la energía de un electrón a una distancia particular del núcleo en un átomo de hidrógeno. Si una chispa promueve el electrón en un átomo de hidrógeno en una órbita con n = 3, ¿cuál es la energía calculada, en julios, del electrón?

Solución

La energía del electrón viene dada por esta ecuación: E = -kZ²/n². El número atómico, Z, de hidrógeno es 1; k = 2.179 × 10^–18 J; y el electrón se caracteriza por un valor n de 3. Así,

Comprueba tu aprendizaje

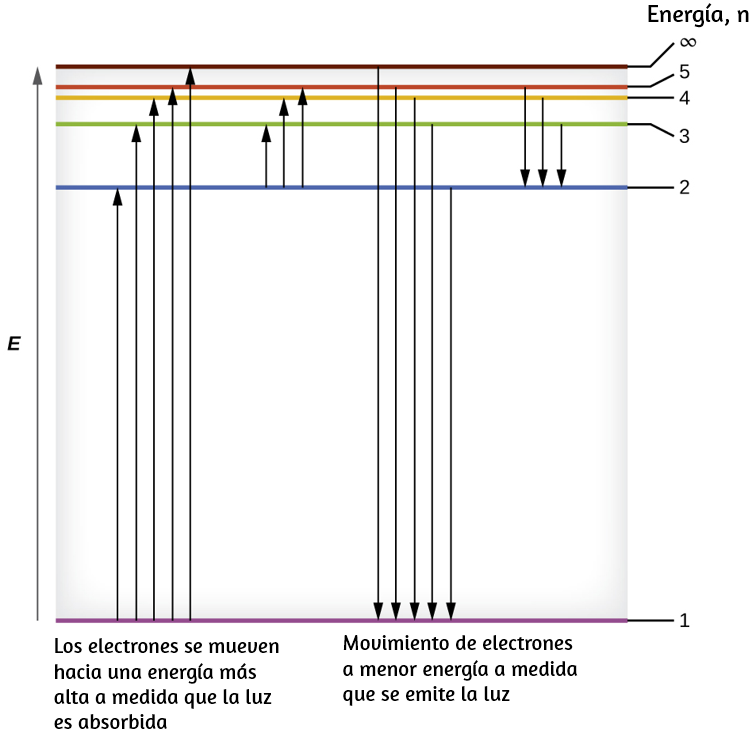
Figura 6.15. Las líneas horizontales muestran la energía relativa de las órbitas en el modelo de Bohr del átomo de hidrógeno, y las flechas verticales la energía de los fotones absorbidos (izquierda) o emitidos (derecha) a medida que los electrones se mueven entre estas órbitas.

Ejemplo 6.5

Cálculo de la energía y la longitud de onda de las transiciones de electrones en un sistema de un electrón (Bohr)

¿Cuál es la energía (en julios) y la longitud de onda (en metros) de la línea en el espectro del hidrógeno que representa el movimiento de un electrón desde la órbita de Bohr con n = 4 a la órbita con n = 6? ¿En qué parte del espectro electromagnético encontramos esta radiación?

Solución

En este caso, el electrón comienza con n = 4, entonces n₁ = 4. Viene a detenerse en la órbita n = 6, entonces n₂ = 6. La diferencia de energía entre los dos estados viene dada por esta expresión:

$$ΔE = E_1 - E_2 = 2.179 \times 10^{-18}\bigg(\cfrac{1}{n_1^2} - \cfrac{1}{n_2^2}\bigg)$$ $$= 2.179 \times 10^{-18}\bigg(\cfrac{1}{4^2} - \cfrac{1}{6^2}\bigg)$$ $$= 2.179 \times 10^{-18}\bigg(\cfrac{1}{16} - \cfrac{1}{36}\bigg) $$ $$= 7.566 \times 10^{-20} J$$

Esta diferencia de energía es positiva, lo que indica que un fotón ingresa al sistema (se absorbe) para excitar el electrón desde la órbita n = 4 hasta la órbita n = 6. La longitud de onda de un fotón con esta energía se encuentra en la expresión E = hc/λ. Con un reordenamiento, obtenemos:

$$λ = \cfrac{hc}{E}$$

$$λ = (6.626 \times 10^{−34} \bcancel{Js}) \times \cfrac{2.998 \times 10^8 m\bcancel{s^{-1}}}{7.566 \times 10^{−20} \bcancel{J}}$$

De la ilustración del espectro electromagnético, podemos ver que esta longitud de onda se encuentra en la porción infrarroja del espectro electromagnético.

Comprueba tu aprendizaje

El modelo de Bohr del átomo de hidrógeno proporciona información sobre el comportamiento de la materia a nivel microscópico, pero no tiene en cuenta las interacciones electrón-electrón en los átomos con más de un electrón. Introduce varias características importantes de todos los modelos utilizados para describir la distribución de electrones en un átomo. Estas características incluyen lo siguiente:

1. Las energías de los electrones (niveles de energía) en un átomo se cuantifican, se describen mediante números cuánticos: números enteros que tienen solo un valor permitido específico y se usan para caracterizar la disposición de los electrones en un átomo.
2. La energía de un electrón aumenta al aumentar la distancia del núcleo.
3. Las energías discretas (líneas) en los espectros de los elementos resultan de energías electrónicas cuantificadas.

De estas características, la más importante es el postulado de los niveles de energía cuantificados para un electrón en un átomo. Como consecuencia, el modelo sentó las bases para el modelo mecánico cuántico del átomo. Bohr ganó un Premio Nobel de Física por sus contribuciones a nuestra comprensión de la estructura de los átomos y cómo esto se relaciona con las emisiones de los espectros de línea.

En el interactivo anterior, presentamos una excelente simulación de David Adam Hernández para todos los elementos de la tabla periódica. Cada elemento presenta las diferentes capas de electrones.

Debes esperar unos segundos para que veas la animación en cada elemento, la cual se construye de abajo hacia arriba o, si lo prefieres, desliza la barra de desplazamiento hacia los últimos elementos. Si haces clic en un elemento, aparecerá la información más relevante del mismo (sólo hemos traducido al español, la información del hidrógeno). Te sugerimos ver la simulación en pantalla ampliada.

Desarrollo de la teoría cuántica

¿Por qué los electrones orbitan a distancias fijas definidas por un solo número cuántico n = 1, 2, 3, etc., pero nunca por el medio? ¿Por qué el modelo funcionó tan bien describiendo hidrógeno e iones de un electrón, pero no pudo predecir correctamente el espectro de emisión para el helio o cualquier otro átomo más grande? Para responder a estas preguntas, los científicos necesitaban revisar completamente la forma en que pensaban sobre la materia.

Comportamiento en el mundo microscópico

Sabemos cómo se comporta la materia en el mundo macroscópico: los objetos que son lo suficientemente grandes para ser vistos a simple vista siguen las reglas de la física clásica. Una bola de billar que se mueve sobre una mesa se comportará como una partícula: continuará en línea recta a menos que colisione con otra bola o con el cojín de la mesa, o sea accionada por alguna otra fuerza (como la fricción). La bola tiene una posición y velocidad bien definidas (o un momento bien definido, p = mv, definido por la masa m y la velocidad v) en cualquier momento dado. En otras palabras, la pelota se mueve en una trayectoria clásica. Este es el comportamiento típico de un objeto clásico.

Cuando las ondas interactúan entre sí, muestran patrones de interferencia que no son mostrados por partículas macroscópicas como la bola de billar. Por ejemplo, las ondas que interactúan en la superficie del agua pueden producir patrones de interferencia similares a los que se muestran en la figura 6.16. Este es un caso de comportamiento de onda en la escala macroscópica, y está claro que las partículas y las ondas son fenómenos muy diferentes en el ámbito macroscópico.

Figura 6.16. Un patrón de interferencia en la superficie del agua está formado por ondas que interactúan. Las ondas son causadas por el reflejo del agua de las rocas (crédito: modificación de obra por Sukanto Debnath).

A medida que las mejoras tecnológicas permitieron a los científicos probar el mundo microscópico con mayor detalle, en la década de 1920 se hizo cada vez más evidente que piezas muy pequeñas de materia siguen un conjunto diferente de reglas de las que observamos para objetos grandes.

La indiscutible separación de ondas y partículas ya no era el caso del mundo microscópico. Una de las primeras personas en prestar atención al comportamiento especial del mundo microscópico fue Louis de Broglie. Él hizo la pregunta: Si la radiación electromagnética puede tener un carácter similar a una partícula, ¿pueden los electrones y otras partículas submicroscópicas exhibir un carácter similar a una onda? En su disertación doctoral de 1925, De Broglie extendió la dualidad onda-partícula de la luz que Einstein usó para resolver la paradoja del efecto fotoeléctrico a las partículas materiales. Predijo que una partícula con masa m y velocidad v (es decir, con momento lineal p) también debe mostrar el comportamiento de una onda con un valor de longitud de onda λ dada por esta expresión familiar, en la que h es la constante de Planck:

$$λ = \cfrac{h}{mv} = \cfrac{h}{p}$$

Esto se llama la longitud de onda de De Broglie. A diferencia de los otros valores de λ descritos en este capítulo, la longitud de onda de De Broglie es una característica de las partículas y otros cuerpos, no de la radiación electromagnética (ten en cuenta que esta ecuación implica la velocidad [v, m/s], no la frecuencia [ν, Hz]. Aunque estos dos símbolos parecen casi idénticos, significan cosas muy diferentes).

Cuando Bohr había postulado que el electrón era una partícula que orbita alrededor del núcleo en órbitas cuantificadas, De Broglie argumentó que la suposición de cuantificación de Bohr puede explicarse si el electrón no se considera como una partícula, sino más bien como una onda estacionaria circular tal que un número entero de longitudes de onda podría caber exactamente dentro de la órbita (Figura 6.17).

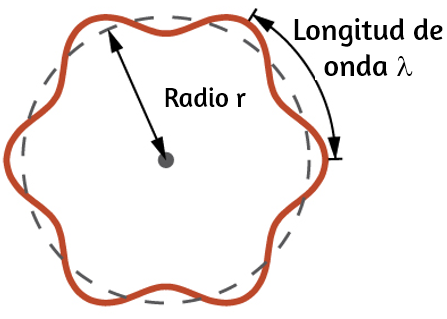
Figura 6.17. Si un electrón se ve como una onda que gira alrededor del núcleo, un número entero de longitudes de onda debe encajar en la órbita para que este comportamiento de onda estacionaria sea posible.

La siguiente escena interactiva, diseñada por Walter Fendt, ilustra un átomo de hidrógeno de acuerdo con el modelo de partículas u ondas. Puedes elegir un número cuántico principal n. La parte derecha de los gráficos representa los niveles de energía del átomo. En la parte inferior, puedes leer el radio orbital r y la energía total E.

Si intentas variar el radio de la órbita con el botón del mouse presionado, esto generalmente conducirá a un estado no estacionario. Puede darse cuenta de que al usar la opción "Modelo de onda": la línea ondulada verde que simboliza la onda de Broglie no se cerrará en la mayoría de los casos. Solo si la circunferencia del círculo es un múltiplo entero de la longitud de onda (azul), obtendrás un estado estacionario.

Para una órbita circular de radio r, la circunferencia es 2πr, por lo que la condición de De Broglie es:

$$2πr = nλ, n = 1, 2, 3, ...$$

Poco después de que De Broglie propusiera la naturaleza ondulatoria de la materia, dos científicos de los Laboratorios Bell, C. J. Davisson y L. H. Germer, demostraron experimentalmente que los electrones pueden mostrar un comportamiento de onda al mostrar un patrón de interferencia para los electrones que viajan a través de un patrón atómico regular en un cristal. Las capas atómicas espaciadas regularmente sirvieron como rendijas, como se usa en otros experimentos de interferencia. Dado que el espaciado entre las capas que sirven como rendijas debe ser similar en tamaño a la longitud de onda de la onda probada para que se forme un patrón de interferencia, Davisson y Germer utilizaron un objetivo de níquel cristalino para sus "rendijas", ya que el espaciado de los átomos dentro de la celosía era aproximadamente la misma que la longitud de onda de Broglie de los electrones que utilizaban. La figura 6.18 muestra un patrón de interferencia. Es sorprendentemente similar a los patrones de interferencia para la luz que se muestra en la Energía electromagnética para la luz que pasa a través de dos rendijas estrechas y muy próximas entre sí. La dualidad onda-partícula de la materia se puede ver en la figura 6.18 observando lo que sucede si las colisiones de electrones se registran durante un largo período de tiempo.

Inicialmente, cuando solo se han registrado unos pocos electrones, muestran un claro comportamiento similar a las partículas, habiendo llegado en pequeños paquetes localizados que parecen ser aleatorios. A medida que más y más electrones llegaron y se registraron, surgió un claro patrón de interferencia que es el sello distintivo del comportamiento de onda. Por lo tanto, parece que si bien los electrones son pequeñas partículas localizadas, su movimiento no sigue las ecuaciones de movimiento implícitas en la mecánica clásica, sino que se rige por algún tipo de ecuación de onda.

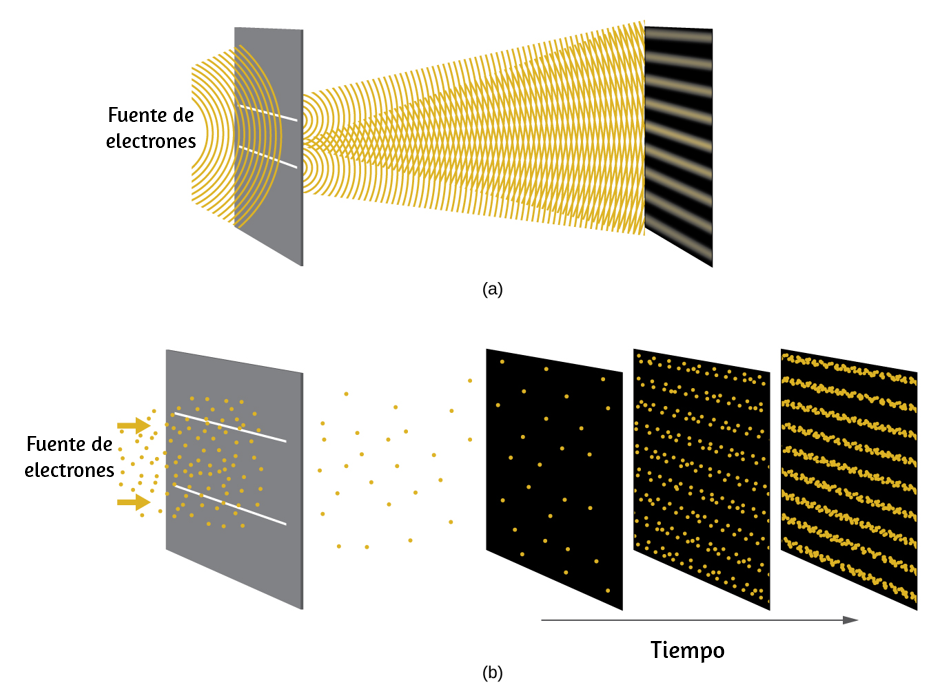
Figura 6.18. a) El patrón de interferencia para los electrones que pasan a través de rendijas muy próximas entre sí demuestra que las partículas cuánticas, como los electrones, pueden exhibir un comportamiento similar a una onda. (b) Los resultados experimentales ilustrados aquí demuestran la dualidad onda-partícula en electrones.

Por lo tanto, la dualidad onda-partícula observada por primera vez con los fotones es en realidad un comportamiento fundamental intrínseco a todas las partículas cuánticas.

Ejemplo 6.6

Cálculo de la longitud de onda de una partícula

Si un electrón viaja a una velocidad de $1.000 \times 10^7\space ms^{-1}$ y tiene una masa de $9.109 \times 10^{-28}\space g$, ¿cuál es su longitud de onda?

Solución

Podemos usar la ecuación de De Broglie para resolver este problema, pero primero debemos hacer una conversión unitaria de la constante de Planck. Ya aprendiste que $1\space J = 1 \space kg m^2/s^2$. Por lo tanto, podemos escribir $h = 6.626 \times 10^{-34} \space Js$ como $6.626 \times 10^{-34} \space kg m^2/s$.

$$λ = \cfrac{h}{mv}$$ $$λ = \cfrac{6.626 \times 10^{-34} \space kg \space m^2/s}{(9.109 \times 10^{-31}\space kg)(1.000 \times 10^{7} \space m/s)}$$ $$λ = 7.274 \times 10^{-11} \space m$$

Este es un valor pequeño, pero es significativamente más grande que el tamaño de un electrón en la vista clásica (partícula). Este tamaño es del mismo orden de magnitud que el tamaño de un átomo. Esto significa que el comportamiento de una onda electrónica se notará en un átomo.

Comprueba tu aprendizaje

Nunca pensamos que una pelota de softball lanzada tenga una longitud de onda, ya que esta longitud de onda es tan pequeña que es imposible que nuestros sentidos o cualquier instrumento conocido la detecte (hablando estrictamente, la longitud de onda de una pelota de béisbol real correspondería a las longitudes de onda de sus átomos y moléculas constituyentes que, aunque es mucho más grande que este valor, aún sería microscópicamente pequeño). La longitud de onda de De Broglie solo es apreciable para la materia que tiene una masa muy pequeña y/o una velocidad muy alta.

Werner Heisenberg consideró los límites de la precisión con la que podemos medir las propiedades de un electrón u otras partículas microscópicas. Determinó que existe un límite fundamental en cuanto a la precisión con la que se puede medir la posición de una partícula y su impulso simultáneamente. Cuanto más exactamente midamos el impulso de una partícula, menos podemos determinar su posición en ese momento y viceversa. Esto se resume en lo que ahora llamamos el principio de incertidumbre de Heisenberg: es fundamentalmente imposible determinar de manera simultánea y exacta tanto el momento como la posición de una partícula.

Para una partícula de masa m que se mueve con la velocidad v_x en la dirección x (o de manera equivalente con el impulso p_x), el producto de la incertidumbre en la posición, Δx, y la incertidumbre en el momento, Δp_x, debe ser mayor o igual a $\cfrac{ℏ}{2}$ (donde $ℏ = \cfrac{h}{2π}$, el valor de la constante de Planck dividido por 2π, $ℏ=1.055\times\:10^{-34}\:Js$).
$$Δx \times Δp_x = (Δx)(mΔv) ≥ \cfrac{ℏ}{2}$$

Esta ecuación nos permite calcular el límite de la precisión con la que podemos conocer la posición simultánea de un objeto y su momento. Por ejemplo, si mejoramos nuestra medición de la posición de un electrón para que la incertidumbre en la posición (Δx) tenga un valor de, por ejemplo, 1 pm (10^–12 m, aproximadamente 1% del diámetro de un átomo de hidrógeno), entonces nuestra determinación de su impulso debe tener una incertidumbre con un valor de al menos

El valor de ℏ no es grande, por lo que la incertidumbre en la posición o el impulso de un objeto macroscópico como una pelota de béisbol es demasiado insignificante para observar. Sin embargo, la masa de un objeto microscópico, como un electrón, es lo suficientemente pequeña como para que la incertidumbre sea grande y significativa.

Cabe señalar que el principio de incertidumbre de Heisenberg no solo se limita a las incertidumbres en la posición y el impulso, sino que también vincula otras variables dinámicas.

Por ejemplo, cuando un átomo absorbe un fotón y realiza una transición de un estado de energía a otro, la incertidumbre en la energía y la incertidumbre en el tiempo requerido para la transición se relacionan de manera similar, como ΔE Δt ≥ 2. El principio de Heisenberg impone límites últimos a lo que es conocible en la ciencia. Se puede demostrar que el principio de incertidumbre es una consecuencia de la dualidad onda-partícula, que se encuentra en el corazón de lo que distingue a la teoría cuántica moderna de la mecánica clásica.

El modelo cuántico-mecánico de un átomo

Poco después, De Broglie publicó sus ideas de que el electrón en un átomo de hidrógeno podría considerarse mejor como una onda estacionaria circular en lugar de una partícula que se mueve en órbitas circulares cuantizadas, Erwin Schrödinger extendió el trabajo de Broglie al derivar lo que hoy se conoce como la ecuación de Schrödinger. Cuando Schrödinger aplicó su ecuación a átomos similares al hidrógeno, fue capaz de reproducir la expresión de Bohr para la energía y la fórmula de Rydberg que rige los espectros de hidrógeno. Schrödinger describió los electrones como ondas estacionarias tridimensionales, o funciones de onda, representadas por la letra griega psi, ψ. Unos años más tarde, Max Born propuso una interpretación de la función de onda que todavía se acepta en la actualidad: los electrones son todavía partículas, por lo que las ondas representadas por ψ no son ondas físicas sino que, en cambio, son amplitudes de probabilidad complejas. El cuadrado de la magnitud de una función de onda |ψ|² describe la probabilidad de que la partícula cuántica esté presente cerca de una cierta ubicación en el espacio. Esto significa que las funciones de onda se pueden usar para determinar la distribución de la densidad del electrón con respecto al núcleo en un átomo. En la forma más general, la ecuación de Schrödinger se puede escribir como:

$$\widehat{H} ψ = Eψ$$

$\widehat{H}$ es el operador hamiltoniano, un conjunto de operaciones matemáticas que representan la energía total de la partícula cuántica (como un electrón en un átomo), ψ es la función de onda de esta partícula que se puede usar para encontrar la distribución especial de la probabilidad de encontrar la partícula, y E es el valor real de la energía total de la partícula.

El trabajo de Schrödinger, así como el de Heisenberg y muchos otros científicos que siguen sus pasos, generalmente se conoce como la mecánica cuántica.

Comprensión de la teoría cuántica de los electrones en los átomos

El objetivo de esta sección es comprender los orbitales electrónicos (ubicación de los electrones en los átomos), sus diferentes energías y otras propiedades. El uso de la teoría cuántica proporciona la mejor comprensión de estos temas. Este conocimiento es un precursor del enlace químico. Como se describió anteriormente, los electrones en los átomos pueden existir solo en niveles de energía discretos pero no entre ellos. Se dice que la energía de un electrón en un átomo se cuantifica, es decir, puede ser igual solo a ciertos valores específicos y puede saltar de un nivel de energía a otro pero no hacer una transición suave o permanecer entre estos niveles.

Los niveles de energía están etiquetados con un valor n, donde n = 1, 2, 3,…. En términos generales, la energía de un electrón en un átomo es mayor para valores mayores de n. Este número, n, se conoce como el número cuántico principal.

El número cuántico principal. define la ubicación del nivel de energía. Es esencialmente el mismo concepto que el n en la descripción del átomo de Bohr. Otro nombre para el número cuántico principal es el número de capa o nivel (shell).

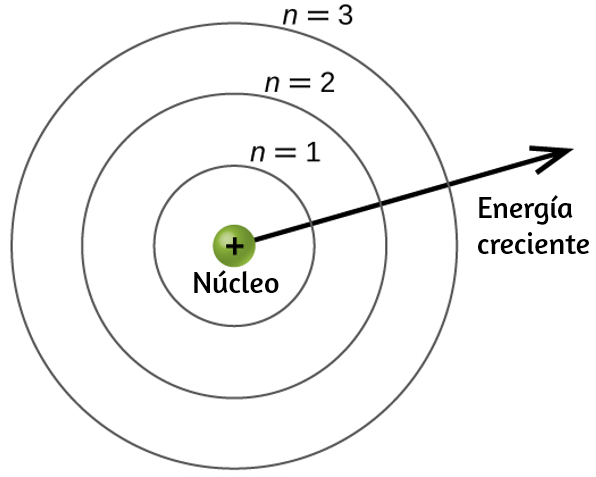
Figura 6.19. Las diferentes capas están numeradas por números cuánticos principales.

Se puede pensar en las capas o niveles de un átomo en círculos concéntricos que irradian desde el núcleo. Los electrones que pertenecen a una capa específica tienen mayor probabilidad de encontrarse dentro del área circular correspondiente. Cuanto más nos alejemos del núcleo, mayor será el número de capa y, por lo tanto, mayor será el nivel de energía (Figura 6.19). Los protones cargados positivamente en el núcleo estabilizan los orbitales electrónicos por atracción electrostática entre las cargas positivas de los protones y las cargas negativas de los electrones. Así que cuanto más lejos esté el electrón del núcleo, mayor será la energía que tiene.

Este modelo mecánico cuántico para el lugar donde residen los electrones en un átomo se puede usar para observar las transiciones electrónicas, los eventos en los que un electrón se mueve de un nivel de energía a otro. Si la transición es a un nivel de energía más alto, la energía se absorbe y el cambio de energía tiene un valor positivo. Para obtener la cantidad de energía necesaria para la transición a un nivel de energía más alto, el fotón es absorbido por el átomo. Una transición a un nivel de energía más bajo implica una liberación de energía, y el cambio de energía es negativo. Este proceso es acompañado por la emisión de un fotón por el átomo. La siguiente ecuación resume estas relaciones y se basa en el átomo de hidrógeno:

$$ΔE = E_{final} − E_{inicial}$$
$$ΔE = −2.18 × 10^{−18} \bigg( \cfrac{1}{n_f^2} - \cfrac{1}{n_i^2} \bigg)\space J$$

Los valores $n_f$ y $n_i$ son los estados de energía final e inicial del electrón. El ejemplo 6.5 en la sección anterior del capítulo muestra los cálculos de dichos cambios de energía. El número cuántico principal es uno de los tres números cuánticos utilizados para caracterizar un orbital. Un orbital atómico es una región general en un átomo dentro del cual es más probable que resida un electrón. El modelo mecánico cuántico especifica la probabilidad de encontrar un electrón en el espacio tridimensional alrededor del núcleo y se basa en soluciones de la ecuación de Schrödinger. Además, el número cuántico principal define la energía de un electrón en un hidrógeno o un átomo similar a hidrógeno o un ion (un átomo o un ion con un solo electrón) y la región general en la que los niveles discretos de energía de los electrones y los iones se encuentran.

Otro número cuántico es l, el número cuántico secundario (momento angular). Es un número entero que puede tomar los valores, l = 0, 1, 2,…, n - 1. Esto significa que un orbital con n = 1 puede tener solo un valor de l, l = 0, mientras que n = 2 permite l = 0 y l = 1, y así sucesivamente. Mientras que el número cuántico principal, n, define el tamaño general y la energía del orbital, el número cuántico secundario l especifica la forma del orbital. Los orbitales con el mismo valor de l definen una subcapa.

Los orbitales con l = 0 se denominan orbitales s y forman las subcapas s. El valor l = 1 corresponde a los orbitales p. Para un n dado, los orbitales p constituyen una subcapa p (por ejemplo, 3p si n = 3). Los orbitales con l = 2 se denominan orbitales d, seguidos de los orbitales f, g y h para l = 3, 4 y 5.

Hay ciertas distancias desde el núcleo a las cuales la densidad de probabilidad de encontrar un electrón ubicado en un orbital particular es cero. En otras palabras, el valor de la función de onda ψ es cero a esta distancia para este orbital. Dicho valor de radio r se denomina nodo radial. El número de nodos radiales en un orbital es
n - l - 1.

Considera los ejemplos en la figura 6.20. Los orbitales representados son del tipo s, por lo tanto, l = 0 para todos ellos. En las gráficas de las densidades de probabilidad se puede ver que hay 1 - 0 - 1 = 0 lugares donde la densidad es cero (nodos) para 1s (n = 1), 2 - 0 - 1 = 1 nodo para 2s, y 3 - 0 - 1 = 2 nodos para los orbitales 3s.

La distribución de la densidad de electrones de la sub-capa s es esférica y la subcapa p tiene una forma de mancuerna. Los orbitales d y f son más complejos. Estas formas representan las regiones tridimensionales dentro de las cuales es probable que se encuentre el electrón.

Figura 6.20. Los gráficos muestran la probabilidad (eje y) de encontrar un electrón para los orbitales 1s, 2s, 3s en función de la distancia desde el núcleo.

El número cuántico magnético, m_l, especifica la orientación espacial relativa de un orbital en particular. En términos generales, m_l puede ser igual a –l, -(l - 1), ..., 0, ..., (l - 1), l. El número total de orbitales posibles con el mismo valor de l (es decir, en la misma subcapa) es 2l + 1. Por lo tanto, hay un s-orbital en una subcapa s (l = 0), hay tres p-orbitales en una subcapa p (l = 1), cinco orbitales d en la subcapa d (l = 2), siete orbitales f en una subcapa f (l = 3), y así sucesivamente. El número cuántico principal define el valor general de la energía electrónica. El número cuántico de momento angular determina la forma del orbital. Y el número cuántico magnético especifica la orientación del orbital en el espacio, como se puede ver en la figura 6.21.

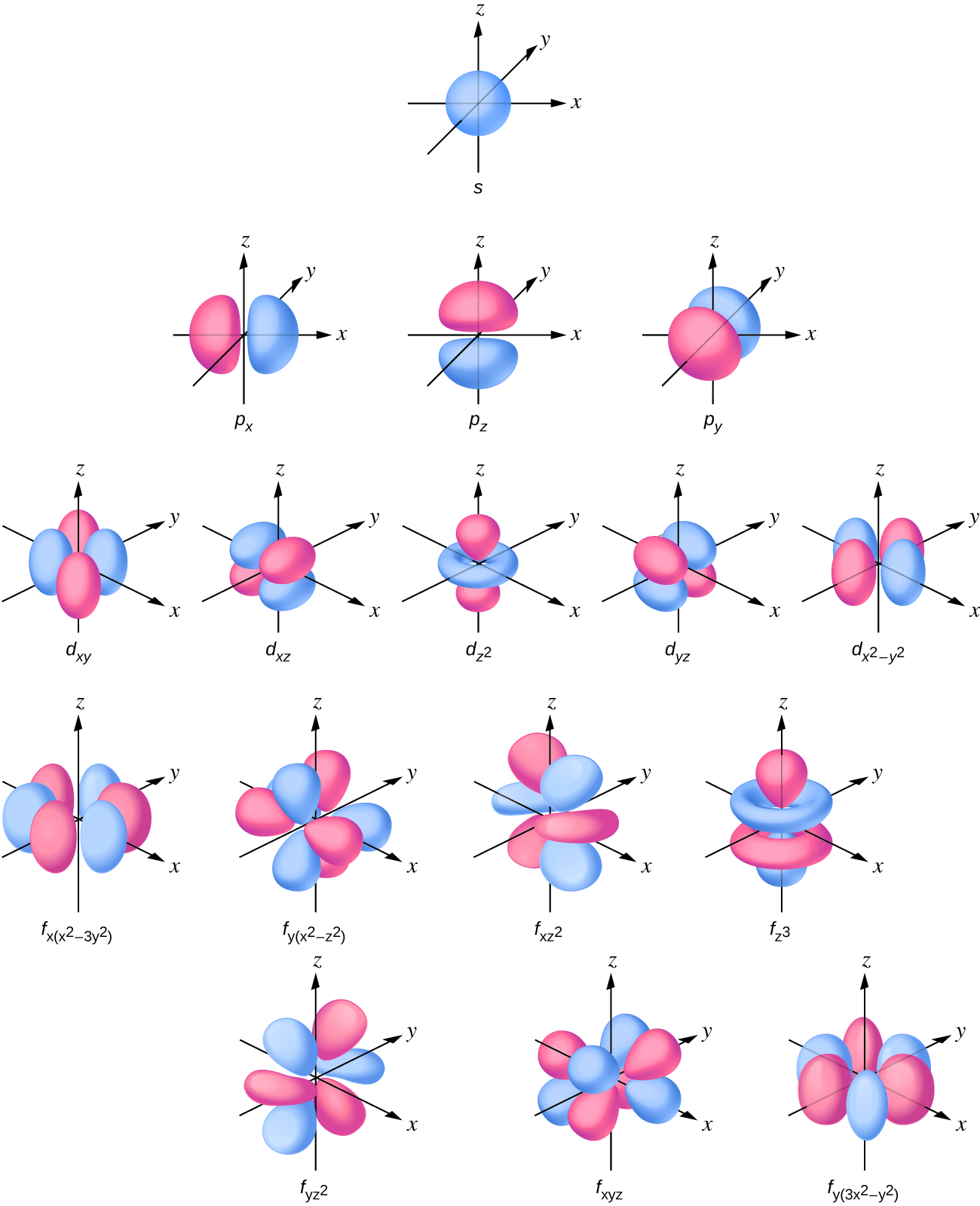
Figura 6.21. Capas de los orbitales s, p, d, y f.

Presentamos una escena interactiva, diseñada por Juan Guillermo Rivera Berrío, que permite interactuar con cinco tipos de orbitales: p_x, p_y, p_z, d_xy y d_z².

La figura 6.22 ilustra los niveles de energía para varios orbitales. El número antes del nombre orbital (como 2s, 3p, etc.) representa el número cuántico principal, n. La letra en el nombre orbital define la subcapa con un número cuántico de momento angular específico l = 0 para s orbitales, 1 para p orbitales, 2 para d orbitales. Finalmente, hay más de un orbital posible para l ≥ 1, cada uno correspondiente a un valor específico de m_l.

En el caso de un átomo de hidrógeno o un ion de un electrón (como He⁺, Li²⁺, etc.), las energías de todos los orbitales con la misma n son iguales. Esto se denomina degeneración, y los niveles de energía para el mismo número cuántico principal, n, se denominan orbitales degenerados. Sin embargo, en los átomos con más de un electrón, esta degeneración es eliminada por las interacciones electrón-electrón, y los orbitales que pertenecen a diferentes sub-capas tienen diferentes energías, como se muestra en la figura 6.22. Los orbitales dentro de la misma subcapa todavía están degenerados y tienen la misma energía.

Figura 6.22. La tabla muestra las energías de los orbitales de electrones en un átomo de múltiples electrones.

Si bien los tres números cuánticos analizados en los párrafos anteriores funcionan bien para describir orbitales de electrones, algunos experimentos demostraron que no eran suficientes para explicar todos los resultados observados. Se demostró en la década de 1920 que cuando los espectros de líneas de hidrógeno se examinan con una resolución extremadamente alta, algunas líneas no son en realidad picos individuales, sino pares de líneas estrechamente espaciadas.

Esta es la llamada estructura fina del espectro, e implica que existen pequeñas diferencias adicionales en las energías de los electrones, incluso cuando se encuentran en el mismo orbital. Estas observaciones llevaron a Samuel Goudsmit y George Uhlenbeck a proponer que los electrones tienen un cuarto número cuántico. Llamaron a esto el número cuántico de espín, o m_s.

Los otros tres números cuánticos, n, l y m_l, son propiedades de orbitales atómicos específicos que también definen en qué parte del espacio es más probable que se ubique un electrón. Los orbitales son el resultado de resolver la ecuación de Schrödinger para los electrones en los átomos. El giro electrónico es un tipo diferente de propiedad. Es un fenómeno completamente cuántico sin análogos en el reino clásico. Además, no se puede deducir al resolver la ecuación de Schrödinger y no está relacionado con las coordenadas espaciales normales (como la cartesiana x, y, z). El giro del electrón describe una "rotación" o "giro" intrínseco del electrón. Cada electrón actúa como un pequeño imán o un pequeño objeto giratorio con un momento angular, o como un bucle con una corriente eléctrica, incluso aunque esta rotación o corriente no se pueda observar en términos de coordenadas espaciales.

La magnitud del espín general de electrones solo puede tener un valor, y un electrón solo puede "girar" en uno de los dos estados cuantificados. Uno se denomina estado α, y la componente z del giro se encuentra en la dirección positiva del eje z. Esto corresponde al número cuántico de espín $m_s = 1/2$. El otro se denomina estado β, con el componente z del giro negativo y $m_s = -1/2$. Cualquier electrón, independientemente del orbital atómico en el que se encuentre, solo puede tener uno de esos dos valores del número cuántico de espín.

Las energías de los electrones que tienen $m_s = -1/2$ y $m_s = 1/2$ son diferentes si se aplica un campo magnético externo. La figura 6.23 ilustra este fenómeno. Un electrón actúa como un pequeño imán. Su momento se dirige hacia arriba (en la dirección positiva del eje z) para el número cuántico de $1/2$ giros y hacia abajo (en la dirección z negativa) para el número cuántico de spin de $-1/2$. Un imán tiene una energía más baja si su momento magnético está alineado con el campo magnético externo (el electrón izquierdo en la figura 6.23) y una energía más alta para el momento magnético es opuesta al campo aplicado.

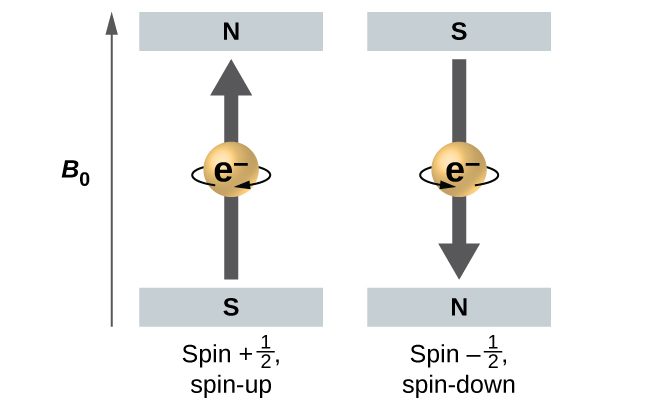
Figura 6.23. Electrones con valores de espín ±1/2 en un campo magnético externo.

Es por esto que un electrón con $m_s=1/2$ tiene una energía ligeramente más baja en un campo externo en la dirección z positiva, y un electrón con $m_s=-1/2$ tiene una energía ligeramente más alta en el mismo campo. Esto es cierto incluso para un electrón que ocupa el mismo orbital en un átomo. Una línea espectral correspondiente a una transición para electrones del mismo orbital pero con diferentes números cuánticos de espín tiene dos valores posibles de energía; por lo tanto, la línea en el espectro mostrará una estructura fina dividida.

El principio de exclusión de Pauli

Un electrón en un átomo se describe completamente mediante cuatro números cuánticos: n, l, m_l y m_s. Los tres primeros números cuánticos definen el orbital y el cuarto número cuántico describe la propiedad electrónica intrínseca llamada espín. Un físico austriaco Wolfgang Pauli formuló un principio general que brinda la última información que necesitamos para comprender el comportamiento general de los electrones en los átomos. El principio de exclusión de Pauli se puede formular de la siguiente manera: no hay dos electrones en el mismo átomo que puedan tener exactamente el mismo conjunto de los cuatro números cuánticos. Lo que esto significa es que dos electrones pueden compartir el mismo orbital (el mismo conjunto de los números cuánticos n, l y m_l) solo si sus números cuánticos de espín tienen valores diferentes. Dado que el número cuántico de espín solo puede tener dos valores $\big(±1/2\big)$, no más de dos electrones pueden ocupar el mismo orbital (y si dos electrones se ubican en el mismo orbital, deben tener espines opuestos). Por lo tanto, cualquier orbital atómico puede ser poblado por solo cero, uno o dos electrones.

Las propiedades y el significado de los números cuánticos de electrones en los átomos se resumen brevemente en la tabla 6.1.

Tabla 6.1 . Números cuánticos, sus propiedades y significado.

Ejemplo 6.7

Trabajando con capas y subcapas

Indica el número de subcapas, el número de orbitales en cada subcapa y los valores de l y m_l para los orbitales en la capa n = 4 de un átomo.

Solución

Para n = 4, l puede tener valores de 0, 1, 2 y 3. Por lo tanto, las subcapas s, p, d y f se encuentran en la capa n = 4 de un átomo. Para l = 0 (la subcapa s), m_l solo puede ser 0. Por lo tanto, solo hay un orbital de 4s. Para l = 1 (orbitales tipo p), m puede tener valores de –1, 0, +1, por lo que encontramos tres orbitales 4p. Para l = 2 (orbitales tipo d), m_l puede tener valores de –2, –1, 0, +1, +2, por lo que tenemos cinco orbitales 4d. Cuando l = 3 (orbitales tipo f), m_l puede tener valores de –3, –2, –1, 0, +1, +2, +3, y podemos tener siete orbitales 4f.

Por lo tanto, encontramos un total de 16 orbitales en la capa n = 4 de un átomo.

Comprueba tu aprendizaje

Ejemplo 6.8

Número máximo de electrones

Calcula el número máximo de electrones que pueden ocupar una capa con (a) n = 2, (b) n = 5 y (c) n como variable. Ten en cuenta que solo estás mirando los orbitales con el valor n especificado, no aquellos con energías más bajas.

Solución

(a) Cuando n = 2, hay cuatro orbitales (un solo orbital 2s, y tres orbitales etiquetados como 2p). Estos cuatro orbitales pueden contener ocho electrones.

(b) Cuando n = 5, hay cinco subcapas de orbitales que necesitamos sumar:

1 orbital etiquetado 5s
3 orbitales etiquetados 5p
5 orbitales etiquetados 5d
7 orbitales etiquetados 5f
+9 orbitales etiquetados 5g
___________________________
25 orbitales totales

Una vez más, cada orbital tiene dos electrones, por lo que 50 electrones pueden caber en esta capa.

(c) El número de orbitales en cualquier capa n será igual a n². Puede haber hasta dos electrones en cada orbital, por lo que el número máximo de electrones será 2 × n².

Comprueba tu aprendizaje

Ejemplo 6.9

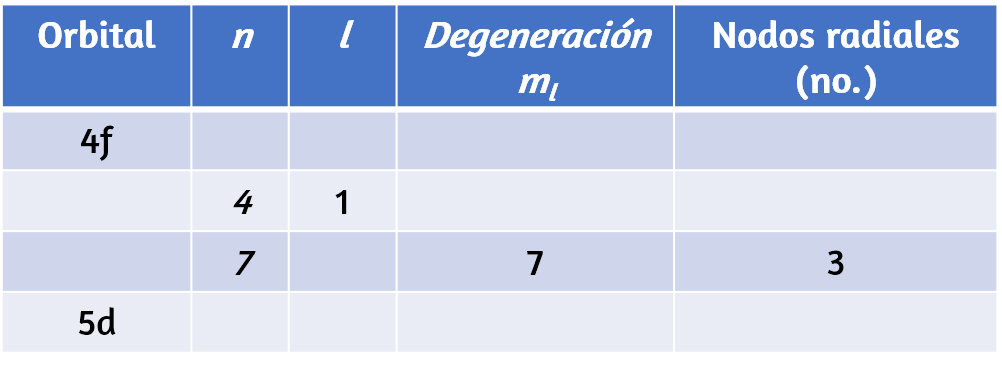
Trabajando con números cuánticos

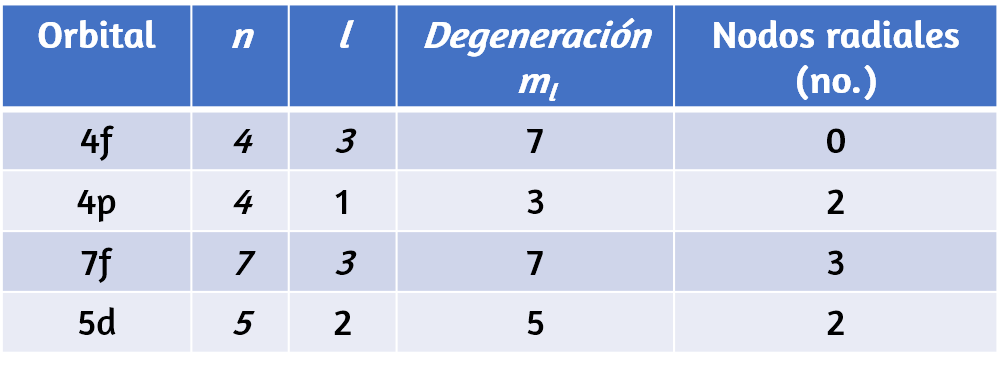
Completa la siguiente tabla para los orbitales atómicos:

Solución

La tabla se puede completar utilizando las siguientes reglas:

• La designación orbital es nl, donde l = 0, 1, 2, 3, 4, 5, ... se asigna a la secuencia de letras s, p, d, f, g, h, ...
• La degeneración de m_l es el número de orbitales dentro de una subcapa, y también lo es 2l + 1 (hay un orbital s, tres orbitales p, cinco orbitales d, siete orbitales f, etc.).
• El número de nodos radiales es igual a n - l - 1.

De acuerdo a estas reglas, la tabla completa sería la siguiente:

Comprueba tu aprendizaje

Estructura electrónica de los átomos (configuraciones electrónicas)

Habiendo introducido los conceptos básicos de la estructura atómica y la mecánica cuántica, podemos utilizar nuestra comprensión de los números cuánticos para determinar cómo se relacionan entre sí los orbitales atómicos. Esto nos permite determinar qué orbitales están ocupados por electrones en cada átomo. La disposición específica de los electrones en los orbitales de un átomo determina muchas de las propiedades químicas de ese átomo.

Energías orbitales y estructura atómica

La energía de los orbitales atómicos aumenta a medida que aumenta el número cuántico principal, n,. En cualquier átomo con dos o más electrones, la repulsión entre los electrones hace que las energías de las subcapas con diferentes valores de l difieran, de modo que la energía de los orbitales aumenta dentro de una capa en el orden s < p < d < f. La figura 6.24 muestra cómo se relacionan estas dos tendencias en el aumento de la energía. El orbital 1s en la parte inferior del diagrama es el orbital con electrones de la energía más baja.

La energía aumenta a medida que avanzamos hacia los orbitales 2s y luego 2p, 3s y 3p, lo que muestra que el valor n creciente tiene más influencia sobre la energía que el valor l creciente para los átomos pequeños. Sin embargo, este patrón no se mantiene para los átomos más grandes. El orbital 3d es más alto en energía que el orbital 4s. Tales superposiciones continúan ocurriendo con frecuencia a medida que avanzamos en el gráfico.

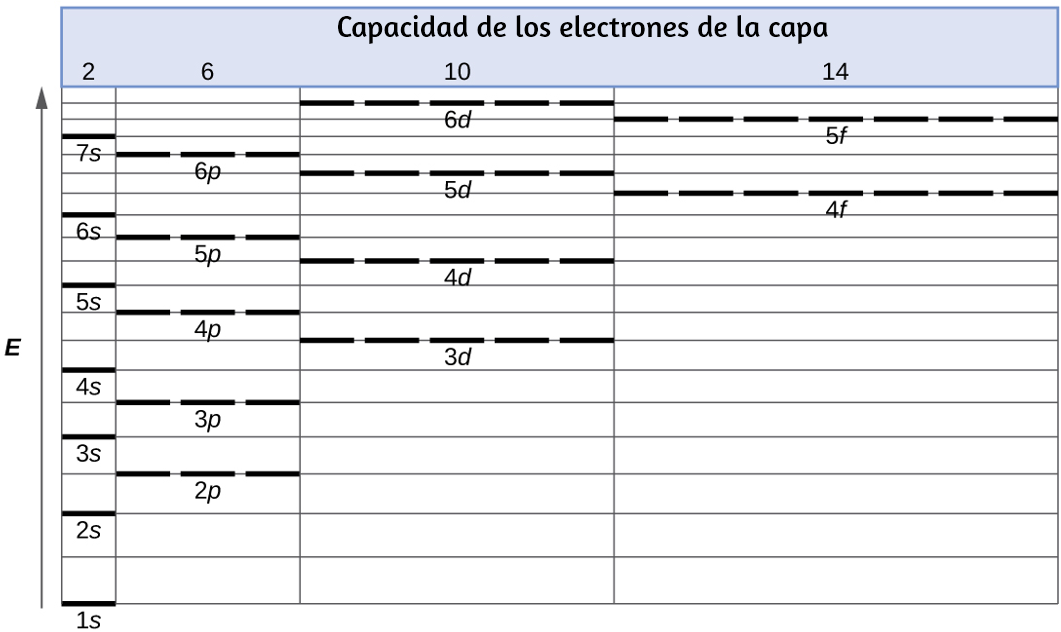
Figura 6.24. Diagrama generalizado de nivel de energía para orbitales atómicos en un átomo con dos o más electrones (no a escala).

Los electrones en los átomos sucesivos en la tabla periódica tienden a llenar los orbitales de baja energía primero. Por lo tanto, a muchos estudiantes les resulta confuso que, por ejemplo, los orbitales 5p se llenen inmediatamente después del 4d, e inmediatamente antes del 6s. El orden de llenado se basa en los resultados experimentales observados y se ha confirmado mediante cálculos teóricos. A medida que aumenta el número cuántico principal, n, aumenta el tamaño de la órbita y los electrones pasan más tiempo lejos del núcleo.

Por lo tanto, la atracción hacia el núcleo es más débil y la energía asociada con el orbital es más alta (menos estabilizada). Pero este no es el único efecto que debemos tener en cuenta. Dentro de cada capa, a medida que aumenta el valor de l, los electrones son menos penetrantes (lo que significa que se encuentra menos densidad de electrones cerca del núcleo), en el orden s > p > d > f. Los electrones que están más cerca del núcleo repelen ligeramente los electrones que están más alejados, compensando ligeramente las atracciones electrón-núcleo más dominantes (recuerda que todos los electrones tienen cargas de -1, pero los núcleos tienen cargas de +Z). Este fenómeno se llama blindaje y se analizará con más detalle en la siguiente sección. Los electrones en los orbitales que experimentan más protección están menos estabilizados y, por lo tanto, tienen mayor energía. Para orbitales pequeños (1s a 3p), el aumento de energía debido a n es más significativo que el aumento debido a l; sin embargo, para orbitales más grandes, las dos tendencias son comparables y no se pueden predecir simplemente. Discutiremos los métodos para recordar el orden observado.

La disposición de los electrones en los orbitales de un átomo se denomina configuración electrónica del átomo. Describimos una configuración electrónica con un símbolo que contiene tres datos (Figura 6.25):

1. El número de la capa cuántica principal (nivel), n,
2. La letra que designa el tipo de órbita (la subcapa, l), y
3. Un número superíndice que designa el número de electrones en esa subcapal en particular.

Por ejemplo, la notación 2p⁴ (lea "dos – p – cuatro") indica cuatro electrones en una subcapa (l = 1) con un número cuántico principal (n) de 2.

La notación 3d⁸ (lee "tres – d - ocho" ) indica ocho electrones en la subcapa d (es decir, l = 2) de la capa principal para la cual n = 3.

Figura 6.25. El diagrama de una configuración electrónica especifica la subcapa (valor n y l, con el símbolo de la letra) y el número superíndice de electrones.

El principio del Aufbau

Para determinar la configuración electrónica de cualquier átomo en particular, podemos "construir" las estructuras en el orden de los números atómicos. Comenzando con el hidrógeno y continuando a través de los períodos de la tabla periódica, agregamos un protón a la vez al núcleo y un electrón a la subcapa apropiada hasta que hayamos descrito las configuraciones electrónicas de todos los elementos. Este procedimiento se denomina principio del Aufbau, de la palabra alemana Aufbau ("construir"). Cada electrón agregado ocupa la subcapa de la energía más baja disponible (en el orden que se muestra en la figura 6.24), sujeto a las limitaciones impuestas por los números cuánticos permitidos de acuerdo con el principio de exclusión de Pauli. Los electrones ingresan a las subcapas de mayor energía solo después de que las subcapas de menor energía se hayan llenado al máximo. La figura 6.26 ilustra la forma tradicional de recordar el orden de llenado de los orbitales atómicos.

Dado que la disposición de la tabla periódica se basa en las configuraciones electrónicas, la figura 6.27 proporciona un método alternativo para determinar la configuración electrónica. El orden de llenado simplemente comienza en el hidrógeno e incluye cada subcapa a medida que avanza en un orden Z creciente. Por ejemplo, después de llenar el bloque 3p hasta el Ar, vemos que el orbital será 4s (K, Ca), seguido de los orbitales 3d.

Figura 6.26. Este diagrama representa el orden de energía para los orbitales atómicos y es útil para derivar configuraciones de electrones en estado fundamental.

Ahora construiremos la configuración electrónica del estado fundamental y el diagrama orbital para una selección de átomos en el primer y segundo período de la tabla periódica. Los diagramas orbitales son representaciones pictóricas de la configuración

Figura 6.27. Esta tabla periódica muestra la configuración electrónica para cada subcapa. Al "construir" a partir del hidrógeno, esta tabla se puede usar para determinar la configuración electrónica de cualquier átomo en la tabla periódica.

electrónica, que muestran los orbitales individuales y la disposición de los electrones. Comenzamos con un solo átomo de hidrógeno (número atómico 1), que consiste en un protón y un electrón. Con referencia a la Figura 6.26 o Figura 6.27, esperaríamos encontrar el electrón en el orbital 1s. Por convención, el valor $m_s = +\cfrac12$ generalmente se llena primero. La configuración electrónica y el diagrama orbital es:

Siguiendo al hidrógeno está el gas noble helio, que tiene un número atómico de 2. El átomo de helio contiene dos protones y dos electrones. El primer electrón tiene los mismos cuatro números cuánticos que el átomo de hidrógeno $(n = 1,$ l = 0, m_l = 0, $m_s = +\cfrac12)$. El segundo electrón también entra en el orbital 1s y lo llena. El segundo electrón tiene los mismos números cuánticos n, l y m_l, pero debe tener el número cuántico de espín opuesto, $m_s = −\cfrac12$. Esto está de acuerdo con el principio de exclusión de Pauli: no hay dos electrones en el mismo átomo que puedan tener el mismo conjunto de cuatro números cuánticos. Para los diagramas orbitales, esto significa que dos flechas van en cada caja (que representan dos electrones en cada orbital) y las flechas deben apuntar en direcciones opuestas (que representan giros pareados).

La configuración electrónica y el diagrama orbital del helio son:

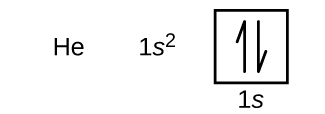
La capa n = 1 está completamente llena en un átomo de helio.

El siguiente átomo es el metal alcalino litio con un número atómico de 3. Los dos primeros electrones en litio llenan el orbital 1s y tienen los mismos conjuntos de cuatro números cuánticos que los dos electrones en helio. El electrón restante debe ocupar el orbital de la siguiente energía más baja, el orbital 2s (Figura 6.26 o Figura 6.27). Así, la configuración electrónica y el diagrama orbital del litio son:

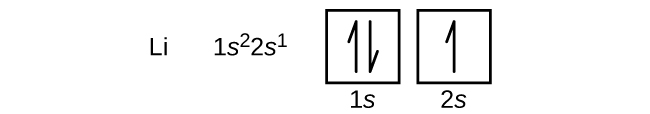
Un átomo del berilio de metal alcalinotérreo, con un número atómico de 4, contiene cuatro protones en el núcleo y cuatro electrones que rodean el núcleo. El cuarto electrón llena el espacio restante en el orbital 2s.

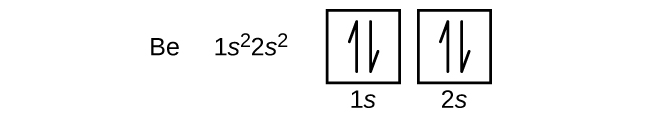
Un átomo de boro (número atómico 5) contiene cinco electrones. La capa n = 1 se llena con dos electrones y tres electrones ocuparán la capa n = 2. Debido a que cualquier subcapa puede contener solo dos electrones, el quinto electrón debe ocupar el siguiente nivel de energía, que será un orbital 2p. Hay tres orbitales 2p degenerados (m_l = −1, 0, +1) y el electrón puede ocupar cualquiera de estos orbitales p. Al dibujar diagramas orbitales, incluimos cuadros vacíos para representar los orbitales vacíos en la misma subcapa que estamos llenando.

El carbono (número atómico 6) tiene seis electrones. Cuatro de ellos llenan los orbitales 1s y 2s.

Los dos electrones restantes ocupan la subcapa 2p. Ahora tenemos la opción de llenar uno de los orbitales 2p y emparejar los electrones o dejar los electrones desparejados en dos orbitales p diferentes, pero degenerados. Los orbitales se llenan según lo descrito por la regla de Hund: la configuración de energía más baja para un átomo con electrones dentro de un conjunto de orbitales degenerados es la que tiene el número máximo de electrones no apareados. Por lo tanto, los dos electrones en los orbitales 2p de carbono tienen números cuánticos n, l y m_s idénticos y difieren en su número cuántico de m_l (de acuerdo con el principio de exclusión de Pauli). La configuración electrónica y el diagrama orbital del carbono son:

El nitrógeno (número atómico 7) llena las subcapas 1s y 2s y tiene un electrón en cada uno de los tres orbitales 2p, de acuerdo con la regla de Hund. Estos electrones tienen espines impares. El oxígeno (número atómico 8) tiene un par de electrones en cualquiera de los orbitales 2p (los electrones tienen espines opuestos) y un solo electrón en cada uno de los otros dos. El flúor (número atómico 9) tiene un orbital 2p que contiene un electrón no pareado. Todos los electrones en el gas neón (número atómico 10) están emparejados, y todos los orbitales en las capas n = 1 y n = 2 están llenos. Las configuraciones electrónicas y los diagramas orbitales son:

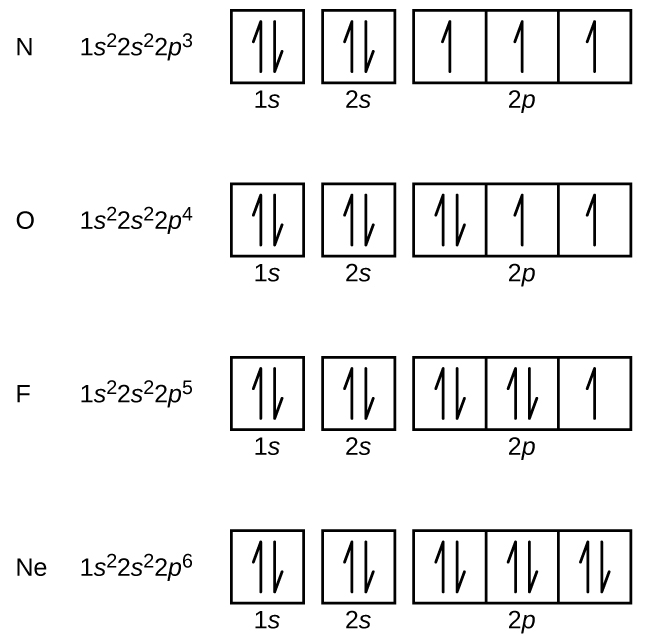
El metal alcalino sodio (número atómico 11) tiene un electrón más que el átomo de neón. Este electrón debe ir a la subcapa de energía más baja disponible, el orbital 3s, dando una configuración de 1s²2s²2p⁶3s¹. Los electrones que ocupan los orbitales de la capa más externa (valor más alto de n) se denominan electrones de valencia, y los que ocupan los orbitales de la capa interna se denominan electrones centrales (Figura 6.28).

Dado que las capas de electrones del núcleo corresponden a configuraciones de electrones de gases nobles, podemos abreviar las configuraciones de electrones al escribir el gas noble que coincide con la configuración de los electrones del núcleo, junto con los electrones de valencia en un formato condensado. Para nuestro ejemplo de sodio, el símbolo [Ne] representa electrones centrales, $(1s^22s^22p^6)$ y nuestra configuración abreviada o condensada es $[Ne] \space3s^1$.

Figura 6.28. Una configuración de electrones abreviada con el núcleo (derecha) reemplaza los electrones del núcleo con el símbolo de gas noble cuya configuración coincide con la configuración electrónica del núcleo del otro elemento.

De manera similar, la configuración abreviada de litio se puede representar como $[He] \space 2s^1$, donde [He] representa la configuración del átomo de helio, que es idéntica a la de la capa interna rellena de litio. Escribir las configuraciones de esta manera enfatiza la similitud de las configuraciones de litio y sodio. Ambos átomos, que se encuentran en la familia de los metales alcalinos, tienen un solo electrón en una subcapa de valencia fuera de un conjunto lleno de envolturas internas.

$$Li: [He]\space 2s^1$$ $$Na: [Ne] \space 3s^1$$

El metal alcalinotérreo magnesio (número atómico 12), con 12 electrones en una configuración $[Ne] \space3s^2$, es análogo al miembro de la familia berilio, $[He] \space 2s^2$.

Ambos átomos tienen una subcapa llena fuera de sus cubiertas internas llenas. El aluminio (número atómico 13), con 13 electrones y la configuración electrónica $[Ne] \space 3s^23p^1$, es análogo al miembro de la familia boro, $[He] \space 2s^22p^1$.

Las configuraciones electrónicas de silicio (14 electrones), fósforo (15 electrones), azufre (16 electrones), cloro (17 electrones) y argón (18 electrones) son análogas en las configuraciones electrónicas de sus capas externas a sus correspondientes miembros de la familia carbono , nitrógeno, oxígeno, flúor y neón, respectivamente, excepto que el número cuántico principal de la cubierta exterior de los elementos más pesados ha aumentado en uno a n = 3. La figura 6.29 muestra la configuración de electrones de la energía más baja, o estado fundamental, para estos elementos así como el de los átomos de cada uno de los elementos conocidos.

Cuando lleguemos al siguiente elemento de la tabla periódica, el metal alcalino potasio (número atómico 19), podríamos esperar que comenzaríamos a agregar electrones a la subcapa 3d. Sin embargo, toda la evidencia química y física disponible indica que el potasio es como el litio y el sodio, y que el próximo electrón no se agrega al nivel 3d sino que, en cambio, se agrega al nivel 4s (Figura 6.29). Como se mencionó anteriormente, el orbital 3d sin nodos radiales tiene mayor energía porque es menos penetrante y está más protegido del núcleo que los 4, que tiene tres nodos radiales. Así, el potasio tiene una configuración electrónica de $[Ar] \space 4s^1$. Por lo tanto, el potasio corresponde a Li y Na en su configuración de capa de valencia. El siguiente electrón se agrega para completar la subcapa 4s y el calcio tiene una configuración electrónica de $[Ar] \space 4s^2$. Esto le da al calcio una configuración electrónica de la capa externa correspondiente a la del berilio y el magnesio.

Comenzando con el metal de transición escandio (número atómico 21), se agregan sucesivamente electrones adicionales a la subcapa 3d. Esta subcapa se llena a su capacidad con 10 electrones (recuerda que para l = 2 [orbitales d], hay 2l + 1 = 5 valores de m_l, lo que significa que hay cinco orbitales d que tienen una capacidad combinada de 10 electrones). La subcapa 4p se llena a continuación. Ten en cuenta que para tres series de elementos, escandio (Sc) hasta el cobre (Cu), itrio (Y) hasta la plata (Ag) y lutecio (Lu) hasta el oro (Au), se agregan sucesivamente 10 electrones a la capa (n - 1) junto a la capa n para llevar esa capa (n - 1) de 8 a 18 electrones.

Figura 6.29. Esta versión de la tabla periódica muestra la configuración electrónica de la capa externa de cada elemento. Ten en cuenta que en cada grupo, la configuración es a menudo similar.

Para dos series, lantano (La) hasta el lutecio (Lu) y el actinio (Ac) hasta el lawrencio (Lr), 14 electrones de f (l = 3, 2l + 1 = valores de 7 m_l; por lo tanto, siete orbitales con una capacidad combinada de 14 se agregan sucesivamente electrones) a la capa (n - 2) para llevar esa capa de 18 electrones a un total de 32 electrones.

Ejemplo 6.10

Números cuánticos y configuraciones electrónicas

¿Cuál es la configuración electrónica y el diagrama orbital de un átomo de fósforo? ¿Cuáles son los cuatro números cuánticos para el último electrón agregado?

Solución

El número atómico del fósforo es 15. Por lo tanto, un átomo de fósforo contiene 15 electrones. El orden de llenado de los niveles de energía es 1s, 2s, 2p, 3s, 3p, 4s,. . . Los 15 electrones del átomo de fósforo se llenarán hasta el orbital 3p, que contendrá tres electrones:

El último electrón agregado es un electrón 3p. Por lo tanto, n = 3 y, para un orbital de tipo p, l = 1. El valor de m_l podría ser –1, 0 o +1. Los tres orbitales p están degenerados, por lo que cualquiera de estos valores de m_l es correcto. Para electrones no apareados, la convención asigna el valor de $+1/2$ para el número cuántico de espín; así, $m_s = +1/2$.

Comprueba tu aprendizaje

La tabla periódica puede ser una herramienta poderosa para predecir la configuración electrónica de un elemento. Sin embargo, sí encontramos excepciones al orden de llenado de los orbitales que se muestran en la figura 6.26 o la figura 6.27. Por ejemplo, las configuraciones electrónicas (mostradas en la figura 6.29) de los metales de transición cromo (Cr; número atómico 24) y cobre (Cu; número atómico 29), entre otros, no son las que cabría esperar. En general, tales excepciones involucran subcapas con energía muy similar, y pequeños efectos pueden llevar a cambios en el orden de llenado.

En el caso del Cr y el Cu, encontramos que las subcapas medio llenas y completamente llenas aparentemente representan condiciones de estabilidad preferidas. Esta estabilidad es tal que un electrón se desplaza de los 4s al orbital 3d para obtener la estabilidad adicional de una subcapa 3d medio llena (en Cr) o una subcapa 3d llena (en Cu). También se producen otras excepciones. Por ejemplo, se predice que el niobio (Nb, número atómico 41) tendrá la configuración electrónica $[Kr] \space 5s^24^3$.

Experimentalmente, observamos que su configuración electrónica del estado fundamental es en realidad $[Kr] \space 5s^14d^4$. Podemos racionalizar esta observación diciendo que las repulsiones electrón-electrón experimentadas al emparejar los electrones en el orbital 5s son mayores que la brecha en la energía entre los orbitales 5s y 4d. No existe un método simple para predecir las excepciones para los átomos en los que la magnitud de las repulsiones entre los electrones es mayor que las pequeñas diferencias en la energía entre las subcapas.

Configuraciones electrónicas y la tabla periódica

Como se describió anteriormente, la tabla periódica organiza los átomos en función del aumento del número atómico para que los elementos con las mismas propiedades químicas se repitan periódicamente. Cuando se agregan sus configuraciones electrónicas a la tabla (Figura 6.29), también vemos una recurrencia periódica de configuraciones electrónicas similares en las capas externas de estos elementos. Debido a que se encuentran en las capas externas de un átomo, los electrones de valencia desempeñan el papel más importante en las reacciones químicas. Los electrones externos tienen la energía más alta de los electrones en un átomo y se pierden o comparten más fácilmente que los electrones centrales.

Los electrones de valencia también son el factor determinante en algunas propiedades físicas de los elementos. Los elementos en cualquier grupo (o columna) tienen el mismo número de electrones de valencia; los metales alcalinos, litio y sodio, cada uno tiene solo un electrón de valencia, los metales alcalinotérreos berilio y magnesio tienen cada uno dos, y los halógenos flúor y cloro tienen cada uno siete electrones de valencia.

La similitud en las propiedades químicas entre elementos del mismo grupo se produce porque tienen el mismo número de electrones de valencia. Es la pérdida, ganancia o intercambio de electrones de valencia lo que define cómo reaccionan los elementos.

Es importante recordar que la tabla periódica se desarrolló sobre la base del comportamiento químico de los elementos, mucho antes de que estuviera disponible la idea de su estructura atómica. Ahora podemos entender por qué la tabla periódica tiene la disposición que tiene: la disposición pone elementos cuyos átomos tienen el mismo número de electrones de valencia en el mismo grupo. Esta disposición se enfatiza en la figura 6.29, que muestra en forma de tabla periódica la configuración electrónica de la última subcapa que se llenará con el principio del Aufbau. Las secciones coloreadas de la figura 6.29 muestran las tres categorías de elementos clasificados por los orbitales que se llenan: grupo principal, transición y elementos de transición interna. Estas clasificaciones determinan qué orbitales se cuentan en la capa de valencia o los orbitales de mayor nivel de energía de un átomo.

1. Los elementos del grupo principal (a veces llamados elementos representativos) son aquellos en los que el último electrón agregado ingresa un orbital s o p en la capa más externa, que se muestra en azul y rojo en la figura 6.29. Esta categoría incluye todos los elementos no metálicos, así como muchos metales y los metaloides. Los electrones de valencia para los elementos del grupo principal son aquellos con el nivel n más alto. Por ejemplo, el galio (Ga, número atómico 31) tiene la configuración electrónica $[Ar] \space 4s^23d^{10}4p^1$, que contiene tres electrones de valencia (subrayados). Los orbitales completamente llenos cuentan como núcleo, no como valencia, los electrones.

2. Elementos de transición o metales de transición. Estos son elementos metálicos en los que el último electrón agregado entra en un orbital. Los electrones de valencia (aquellos agregados después de la última configuración de gas noble) en estos elementos incluyen los electrones n_s y (n - 1) d. La definición oficial de la IUPAC de elementos de transición especifica aquellos con orbitales parcialmente llenos. Por lo tanto, los elementos con orbitales completamente llenos (Zn, Cd, Hg, así como Cu, Ag y Au en la figura 6.29) no son elementos de transición técnicamente. Sin embargo, el término se usa frecuentemente para referirse a todo el bloque d (de color amarillo en la figura 6.29), y adoptaremos este uso en este libro de texto.
3. Los elementos de transición interna son elementos metálicos en los que el último electrón agregado ocupa un orbital. Se muestran en verde en la figura 6.29. Las capas de valencia de los elementos de transición interna consisten en (n - 2)f, la (n - 1)d y las subcapas ns. Hay dos series de transición interna:
   
   
   1. La serie de lantánidos: lantánido (La) hasta el lutecio (Lu)
   2. La serie de actínidos: actínidos (Ac) hasta el lawrencium (Lr)
   El lantano y el actinio, debido a sus similitudes con los otros miembros de la serie, se incluyen y utilizan para nombrar la serie, aunque sean metales de transición sin electrones f.

Configuraciones electrónicas de iones

Los iones se forman cuando los átomos ganan o pierden electrones. Un catión (ion cargado positivamente) se forma cuando uno o más electrones se eliminan de un átomo principal.

Para los elementos del grupo principal, los electrones que se agregaron en último lugar son los primeros electrones eliminados. Sin embargo, para los metales de transición y los metales de transición internos, los electrones en el orbital s son más fáciles de eliminar que los electrones d o f, por lo que los electrones ns más altos se pierden, y luego los (n - 1)d o (n - 2) Se eliminan los electrones f. Un anión (ion cargado negativamente) se forma cuando uno o más electrones se agregan a un átomo principal. Los electrones agregados completan el orden previsto por el principio del Aufbau.

Ejemplo 6.11

Predicción de configuraciones electrónicas de iones

¿Cuál es la configuración electrónica de:

(a) Na⁺
(b) P^3-
(c) Al²⁺
(d) Fe²⁺
(e) Sm³⁺

Solución

Primero, escribe la configuración electrónica para cada átomo padre.

Hemos elegido mostrar las configuraciones completas y no abreviadas para proporcionar más práctica a los estudiantes que lo deseen, pero también es aceptable hacer una lista de las configuraciones electrónicas abreviadas.

A continuación, determina si un electrón se gana o se pierde.

Recuerda que los electrones están cargados negativamente, por lo que los iones con una carga positiva han perdido un electrón. Para los elementos del grupo principal, el último orbital gana o pierde el electrón. Para los metales de transición, el último orbital s pierde un electrón antes de los d orbitales.

$(a) Na: \space 1s^22s^22p^63s^1$. El catión de sodio pierde un electrón, por lo que $Na^+\:=\:1s^22s^22p^6$.
(b) $P: 1s^22s^22p^63s^23p^3$. El trianión de fósforo gana tres electrones, por lo que $P^{3-}: 1s^22s^22p^63s^23p^6$.
(c) $Al: 1s^22s^22p^63s^23p^1$. La dicación de aluminio pierde dos electrones $Al^{2+}: 1s^22s^22p^63s^23p^1 = Al^{2+}: 1s^22s^22p^63s^1$.
(d) $Fe: 1s^22s^22p^63s^23p^64s^23d^6$. El hierro (II) pierde dos electrones y, dado que es un metal de transición, se eliminan del orbital 4s $Fe^{2+}\:=\:1s^22s^22p^63s^23p^63d^6$.
(e) $Sm: 1s^22s^22p^63s^23p^64s^23d^{10}4p^65s^24d^{10}5p^66s^24f^6$. El tricamiento del samario pierde tres electrones. Los dos primeros se perderán del orbital 6s, y el último se eliminará del orbital 4f. $Sm^{3+}\:=\:1s^22s^22p^63s^23p^64s^23d^{10}4p^65s^24d^{10}5p^64f^5$.

Comprueba tu aprendizaje

En la siguiente escena interactiva, diseñada por Juan Guillermo Rivera Berrío (idea original de Jesús Benayas Yepes)Esta escena permite determinar la configuración electrónica de cualquier átomo en particular, podemos "construir" las estructuras en el orden de los números atómicos. Comenzando con el hidrógeno y continuando a través de los períodos de la tabla periódica, agregamos un protón a la vez al núcleo y un electrón a la subcapa apropiada hasta que hayamos descrito las configuraciones electrónicas de todos los elementos. Este procedimiento se denomina principio del Aufbau, de la palabra alemana Aufbau ("construir") (Electronic Structure of Atoms (Electron Configurations)).

La idea original es de Jesús Benayas Yepes.

La escena 3D es el resultado de intervenir el proyecto de Ibis Prevedello., se muestra la configuración electrónica de los elementos de la tabla periódica, también se indican (en rojo) las excepciones al orden de llenado. En la zona de la izquierda y abajo (fondo verde) tenemos la configuración que se obtiene aplicando el orden de llenado teórico siguiendo la regla de Madelung. En la zona de la derecha y arriba (fondo amarillo) tenemos la configuración que se obtiene aplicando métodos de cálculo avanzados que se ajustan mejor a la configuración real.

Variaciones periódicas en las propiedades del elemento

Los elementos en grupos (columnas verticales) de la tabla periódica exhiben un comportamiento químico similar. Esta similitud ocurre porque los miembros de un grupo tienen el mismo número y distribución de electrones en sus capas de valencia. Sin embargo, también hay otros patrones en las propiedades químicas en la tabla periódica. Por ejemplo, a medida que avanzamos hacia abajo en un grupo, aumenta el carácter metálico de los átomos. El oxígeno, en la parte superior del grupo 16 (6A), es un gas incoloro; en la mitad del grupo, el selenio es un sólido semiconductor; y, hacia el fondo, el polonio es un sólido gris plateado que conduce la electricidad.

A medida que atravesamos un período de izquierda a derecha, agregamos un protón al núcleo y un electrón a la capa de valencia con cada elemento sucesivo. A medida que avanzamos en los elementos de un grupo, el número de electrones en la capa de valencia permanece constante, pero el número cuántico principal aumenta en uno cada vez. Una comprensión de la estructura electrónica de los elementos nos permite examinar algunas de las propiedades que rigen su comportamiento químico. Estas propiedades varían periódicamente a medida que cambia la estructura electrónica de los elementos. Son (1) tamaño (radio) de átomos e iones, (2) energías de ionización y (3) afinidades electrónicas.

Variación en el radio covalente

La imagen de la mecánica cuántica hace difícil establecer un tamaño definido de un átomo.

Sin embargo, hay varias formas prácticas de definir el radio de los átomos y, por lo tanto, determinar sus tamaños relativos que dan valores aproximadamente similares. Usaremos el radio covalente (figura 6.30), que se define como la mitad de la distancia entre los núcleos de dos átomos idénticos cuando están unidos por un enlace covalente (esta medida es posible porque los átomos dentro de las moléculas aún conservan gran parte de su atómica identidad). Sabemos que a medida que exploramos un grupo, el número cuántico principal, n, aumenta en uno para cada elemento. Por lo tanto, los electrones se agregan a una región del espacio que está cada vez más alejada del núcleo. En consecuencia, el tamaño del átomo (y su radio covalente) debe aumentar a medida que aumentamos la distancia de los electrones más externos desde el núcleo. Esta tendencia se ilustra para los radios covalentes de los halógenos en la tabla 6.2 y la figura 6.30. Las tendencias para toda la tabla periódica se pueden ver en la figura 6.30.

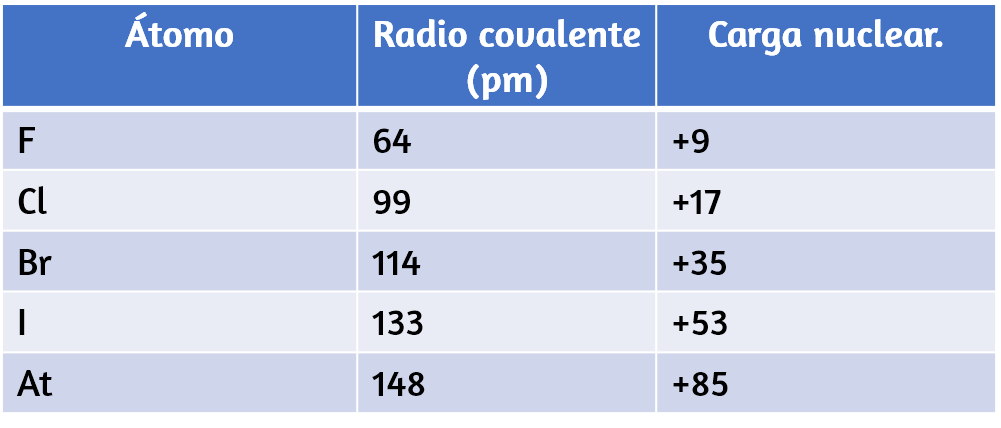
Tabla 6.2 . Radios covalentes de los elementos del grupo halógeno.

Como se muestra en la Figura figura 6.31, a medida que avanzamos en un período de izquierda a derecha, generalmente encontramos que cada elemento tiene un radio covalente más pequeño que el elemento que lo precede. Esto puede parecer contrario a la intuición porque implica que los átomos con más electrones tienen un radio atómico más pequeño.

Esto se puede explicar con el concepto de carga nuclear efectiva, $Z_{eff}$. Esta es la fuerza ejercida sobre un electrón específico por el núcleo, teniendo en cuenta cualquier repulsión electrón-electron. Para el hidrógeno, solo hay un electrón y, por lo tanto, la carga nuclear (Z) y la carga nuclear efectiva (Z_eff) son iguales. Para todos los demás átomos, los electrones internos protegen parcialmente a los electrones externos de la fuerza del núcleo, y por lo tanto:

$$Z_{eff} = Z - blindaje$$

Figura 6.30. (a) El radio de un átomo se define como la mitad de la distancia entre los núcleos en una molécula que consiste en dos átomos idénticos unidos por un enlace covalente. El radio atómico para los halógenos aumenta hacia abajo el grupo a medida que n aumenta. (b) Los radios covalentes de los elementos se muestran a escala. La tendencia general es que los radios aumentan en un grupo y disminuyen a lo largo de un período.

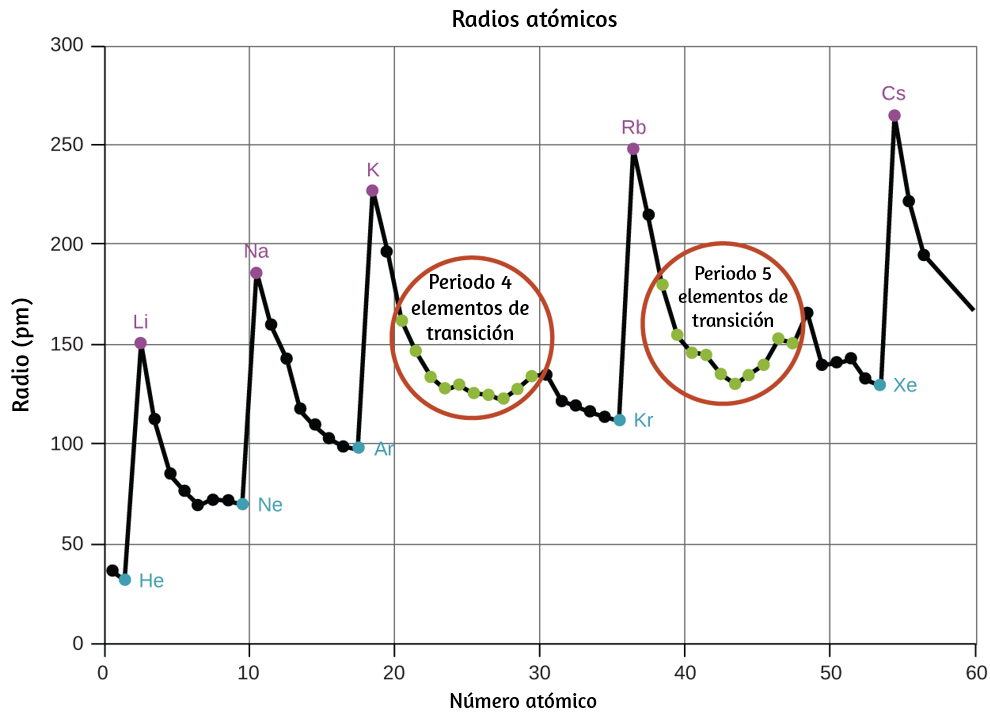
Figura 6.31. (a) El radio de un átomo se define como la mitad de la distancia entre los núcleos en una molécula que consiste en dos átomos idénticos unidos por un enlace covalente. El radio atómico para los halógenos aumenta hacia abajo el grupo a medida que n aumenta. (b) Los radios covalentes de los elementos se muestran a escala. La tendencia general es que los radios aumentan en un grupo y disminuyen a lo largo de un período.

El blindaje o apantallamiento está determinado por la probabilidad de que otro electrón se encuentre entre el electrón de interés y el núcleo, así como por las repulsiones electrón-electrón que encuentra el electrón de interés. Los electrones del núcleo son adeptos al apantallamiento, mientras que los electrones en la misma capa de valencia no bloquean la atracción nuclear experimentada entre sí de manera tan eficiente.

Por lo tanto, cada vez que nos movemos de un elemento a otro a lo largo de un período, Z aumenta en uno, pero el apantallamiento aumenta solo ligeramente. Por lo tanto, Z_eff aumenta a medida que avanzamos de izquierda a derecha a lo largo de un período. El tirón más fuerte (mayor carga nuclear efectiva) experimentado por los electrones en el lado derecho de la tabla periódica los acerca al núcleo, haciendo que los radios covalentes sean más pequeños.

Por lo tanto, como es de esperar, los electrones más externos o de valencia son los más fáciles de eliminar porque tienen las energías más altas, están más protegidos y están más alejados del núcleo. Como regla general, cuando los elementos representativos forman cationes, lo hacen por la pérdida de los electrones ns o np que se agregaron por último en el proceso Aufbau. Los elementos de transición, por otro lado, pierden los electrones ns antes de que empiecen a perder los electrones (n - 1)d, aunque los electrones ns se agregan primero, de acuerdo con el principio del Aufbau.

Ejemplo 6.12

Clasificación de los radios atómicos

Predice el orden al aumentar el radio covalente para Ge, Fl, Br, Kr.

Solución

El radio aumenta a medida que avanzamos hacia abajo en un grupo, por lo que Ge ≤ Fl (Nota: Fl es el símbolo para flerovium, elemento 114, NO flúor). El radio disminuye a medida que nos movemos a través de un período, por lo que Kr ≤ Br ≤ Ge. Juntando las tendencias, obtenemos Kr ≤ Br ≤ Ge ≤ Fl.

Comprueba tu aprendizaje

Variación en los radios iónicos

El radio iónico es la medida utilizada para describir el tamaño de un ion. Un catión siempre tiene menos electrones y la misma cantidad de protones que el átomo original; es más pequeño que el átomo del que se deriva (Figura 6.32). Por ejemplo, el radio covalente de un átomo de aluminio (1s²2s²2p⁶3s²3p¹) es 118 pm, mientras que el radio iónico de un Al³⁺(1s²2s²2p⁶) es 68 pm. A medida que se eliminan los electrones de la capa externa de valencia, los electrones restantes que ocupan capas menores experimentan una mayor carga nuclear efectiva Z_eff (como se comentó antes) y se acercan aún más al núcleo.

Figura 6.32. El radio para un catión es más pequeño que el átomo padre (Al), debido a la pérdida de electrones; el radio para un anión es más grande que el padre (S), debido a los electrones ganados.

Los cationes con cargas más grandes son más pequeños que los cationes con cargas más pequeñas (por ejemplo, V²⁺ tiene un radio iónico de 79 pm, mientras que el de V³⁺ es 64 pm).

Continuando con los grupos de la tabla periódica, encontramos que los cationes de elementos sucesivos con la misma carga generalmente tienen radios más grandes, correspondientes a un aumento en el número cuántico principal, n.

Un anión (ion negativo) se forma mediante la adición de uno o más electrones a la capa de valencia de un átomo. Esto resulta en una mayor repulsión entre los electrones y una disminución de Z_eff por electrón. Ambos efectos (el aumento del número de electrones y la disminución de Z_eff) hacen que el radio de un anión sea mayor que el del átomo principal (Figura 6.32). Por ejemplo, un átomo de azufre ([Ne] 3s²3p⁴) tiene un radio covalente de 104 pm, mientras que el radio iónico del anión sulfuro $([Ne] \space 3s^23p^6)$ es de 170 pm. Para elementos consecutivos que proceden de cualquier grupo, los aniones tienen números cuánticos principales más grandes y, por lo tanto, radios más grandes.

Se dice que los átomos y los iones que tienen la misma configuración electrónica son isoelectrónicos. Ejemplos de especies isoelectrónicas son N^3-, O^2-, F^-, Ne, Na⁺, Mg²⁺ y Al³⁺ (1s²2s²2p⁶). Otra serie isoelectrónica es P3^-, S^2-, Cl^-, Ar, K⁺, Ca²⁺ y Sc³⁺ ([Ne] 3s²3p⁶). Para los átomos o iones que son isoelectrónicos, el número de protones determina el tamaño. Cuanto mayor es la carga nuclear, menor es el radio en una serie de iones y átomos isoelectrónicos.

Variación en las energías de ionización

La cantidad de energía requerida para eliminar el electrón más débilmente unido de un átomo gaseoso en su estado fundamental se denomina su primera energía de ionización (IE₁). La primera energía de ionización para un elemento, X, es la energía requerida para formar un catión con carga +1:

X(g) → X⁺(g) + e^-     IE₁

La energía requerida para eliminar el segundo electrón más débilmente ligado se llama la segunda energía de ionización (IE₂).

X⁺(g) → X²⁺(g) + e^-     IE₂

La energía requerida para eliminar el tercer electrón es la tercera energía de ionización, y así sucesivamente. Siempre se requiere energía para eliminar los electrones de los átomos o iones, por lo que los procesos de ionización son endotérmicos y los valores de IE siempre son positivos. Para los átomos más grandes, el electrón más suelto se encuentra más alejado del núcleo y, por lo tanto, es más fácil de eliminar. Por lo tanto, a medida que aumenta el tamaño (radio atómico), la energía de ionización debería disminuir.

Al relacionar esta lógica con lo que acabamos de aprender sobre los radios, esperaríamos que las energías de ionización primero disminuyan un grupo y aumenten a lo largo de un período.

La figura 6.33 muestra la relación entre la primera energía de ionización y el número atómico de varios elementos. Los valores de la primera energía de ionización para los elementos se dan en la figura 6.34. Dentro de un período, el IE₁ generalmente aumenta con el incremento de Z. En un grupo, el valor de IE₁ generalmente disminuye con el aumento de Z. Sin embargo, hay algunas desviaciones sistemáticas de esta tendencia. Ten en cuenta que la energía de ionización del boro (número atómico 5) es menor que la del berilio (número atómico 4), aunque la carga nuclear del boro es mayor en un protón. Esto se puede explicar porque la energía de las subcapas aumenta a medida que aumenta l, debido a la penetración y el blindaje (como se explicó anteriormente en este capítulo).

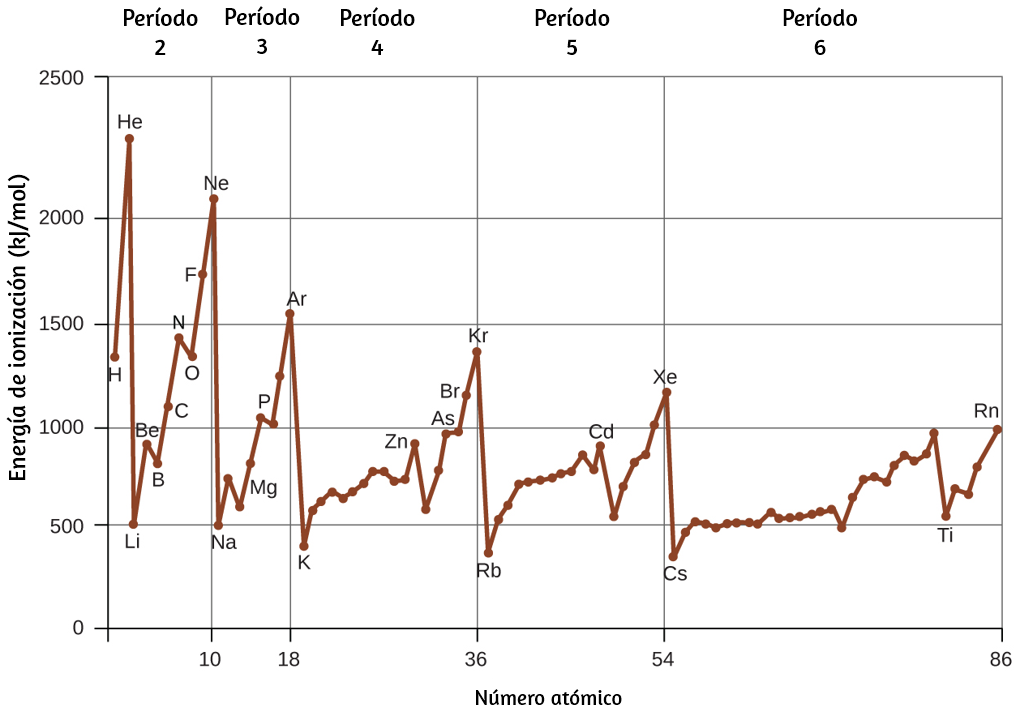
Figura 6.33. La primera energía de ionización de los elementos en los primeros cinco períodos se representa en función de su número atómico.

Dentro de cualquier capa, los electrones s son más bajos en energía que los electrones p. Esto significa que un electrón s es más difícil de eliminar de un átomo que un electrón p en la misma capa. El electrón eliminado durante la ionización del berilio $([He] \space 2s^2)$ es un electrón s, mientras que el electrón eliminado durante la ionización del boro $([He] \space 2s^22p^1)$ es un electrón p; esto da como resultado una primera energía de ionización más baja para el boro, aunque su carga nuclear es mayor en un protón. Por lo tanto, vemos una pequeña desviación de la tendencia predicha que ocurre cada vez que comienza una nueva subcapa.

Otra desviación ocurre cuando los orbitales se llenan más de la mitad.

La primera energía de ionización para el oxígeno es ligeramente menor que la del nitrógeno, a pesar de la tendencia a aumentar los valores de IE₁ a lo largo de un período. Al observar el diagrama orbital del oxígeno, podemos ver que al eliminar un electrón se eliminará la repulsión electrón-electrón causada por el apareamiento de los electrones en el orbital 2p y se obtendrá un orbital medio lleno (que es energéticamente favorable). Se producen cambios análogos en los períodos sucesivos (observa la caída del azufre después del fósforo en la figura 6.34).

Eliminar un electrón de un catión es más difícil que eliminar un electrón de un átomo neutro debido a la mayor atracción electrostática del catión.

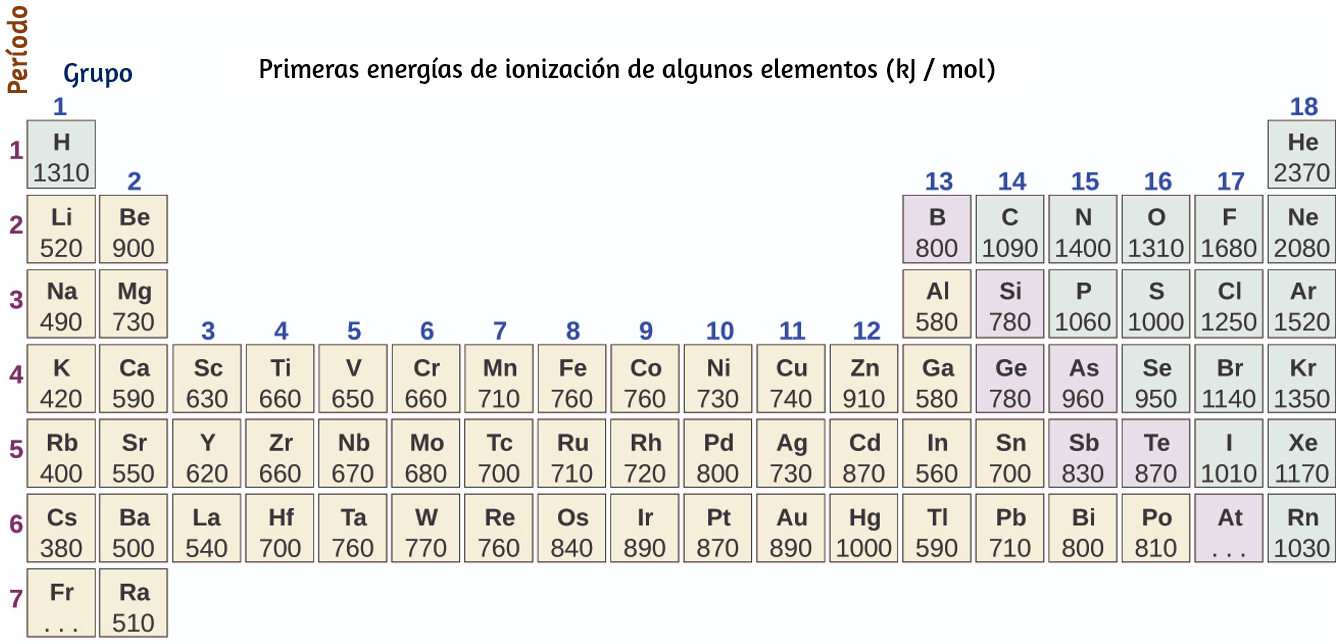
Figura 6.34. Esta versión de la tabla periódica muestra la primera energía de ionización (IE₁), en kJ/mol, de los elementos seleccionados.

Del mismo modo, eliminar un electrón de un catión con una carga positiva más alta es más difícil que eliminar un electrón de un ion con una carga más baja. Así, las energías de ionización sucesivas para un elemento siempre aumentan. Como se ve en la tabla 6.3, hay un gran aumento en las energías de ionización para cada elemento. Este salto corresponde a la eliminación de los electrones centrales, que son más difíciles de eliminar que los electrones de valencia. Por ejemplo, Sc y Ga tienen tres electrones de valencia, por lo que el rápido aumento de la energía de ionización se produce después de la tercera ionización.

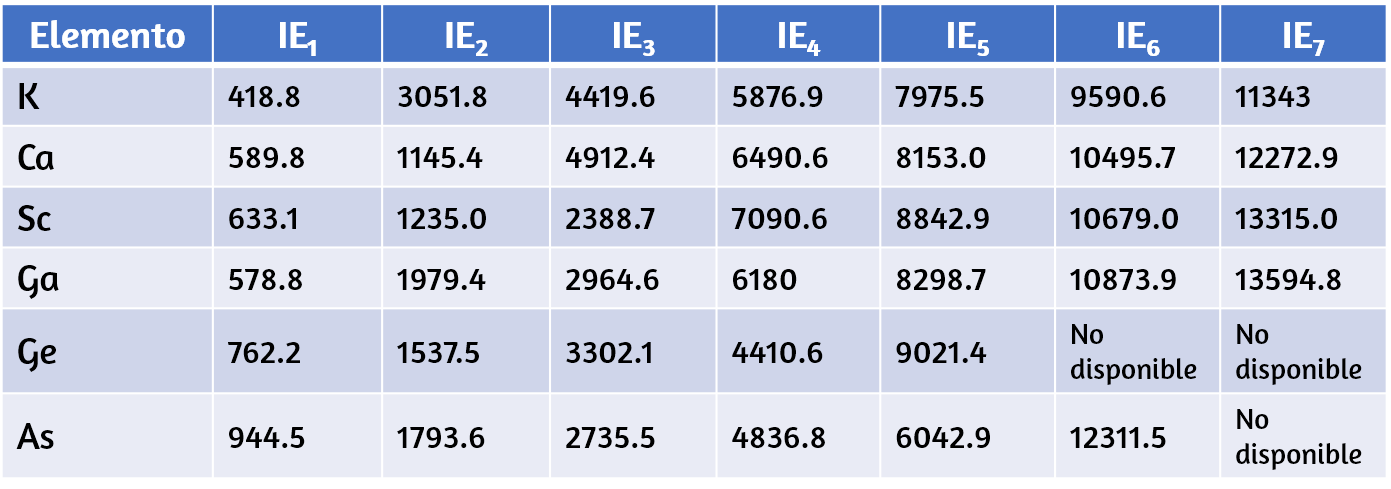
Tabla 6.3 . Energías de ionización sucesivas para elementos seleccionados (kJ/mol).

Ejemplo 6.13

Clasificación de las energías de ionización

Predice el orden de aumentar la energía para los siguientes procesos: IE₁ para Al, IE₁ para Tl, IE₂ para Na, IE₃ para Al.

Solución

Eliminar el electrón $6p^1$ del Tl es más fácil que eliminar el electrón $3p^1$ del Al porque el orbital n más alto está más alejado del núcleo, por lo que IE₁(Tl) ≤ IE₁(Al).

Ionizar el tercer electrón de Al (Al²⁺ → Al³⁺ + e⁻) requiere más energía porque el catión Al²⁺ ejerce una fuerza mayor sobre el electrón que el átomo de Al neutro, por lo que IE₁(Al) ≤ IE₃(Al). La segunda energía de ionización para el sodio elimina un electrón de núcleo, que es un proceso de energía mucho mayor que la eliminación de los electrones de valencia. Juntando todo esto, obtenemos: IE₁(Tl) ≤ IE₁(Al) ≤ IE₃(Al) ≤ IE₂(Na).

Comprueba tu aprendizaje

Variación en las afinidades electrónicas

La afinidad de electrones (AE) es el cambio de energía para el proceso de agregar un electrón a un átomo gaseoso para formar un anión (ion negativo).

X(g) + e⁻ → X⁻(g)          AE₁

Este proceso puede ser endotérmico o exotérmico, dependiendo del elemento. La AE de algunos de los elementos se muestra en la figura 6.35. Puedes ver que muchos de estos elementos tienen valores negativos de AE, lo que significa que la energía se libera cuando el átomo gaseoso acepta un electrón. Sin embargo, para algunos elementos, se requiere energía para que el átomo se cargue negativamente y el valor de su AE es positivo.

Al igual que con la energía de ionización, los valores de AE posteriores se asocian con la formación de iones con más carga. La segunda AE es la energía asociada con la adición de un electrón a un anión para formar un ion -2, y así sucesivamente. Como podríamos predecir, es más fácil agregar un electrón a través de una serie de átomos a medida que aumenta la carga nuclear efectiva de los átomos. A medida que avanzamos de izquierda a derecha a lo largo de un período, las AE tienden a ser más negativas. Las excepciones encontradas entre los elementos del grupo 2 (2A), el grupo 15 (5A) y el grupo 18 (8A) pueden entenderse en base a la estructura electrónica de estos grupos. Los gases nobles, grupo 18 (8A), tienen una capa completamente llena y el electrón entrante debe agregarse a un nivel n más alto, lo que es más difícil de hacer. El grupo 2 (2A) tiene una subcapa ns rellena, por lo que el siguiente electrón agregado entra en la energía np más alta, por lo que, nuevamente, el valor de la AE observada no es como lo predeciría la tendencia. Finalmente, el grupo 15 (5A) tiene una subcapa np medio llena y el siguiente electrón debe emparejarse con un electrón np existente. En todos estos casos, la estabilidad relativa inicial de la configuración electrónica interrumpe la tendencia en la AE.

También podríamos esperar que el átomo en la parte superior de cada grupo tenga la AE más negativa; sus primeros potenciales de ionización sugieren que estos átomos tienen las mayores cargas nucleares efectivas. Sin embargo, a medida que avanzamos hacia abajo en un grupo, vemos que el segundo elemento en el grupo con mayor frecuencia tiene la AE más negativa. Esto puede atribuirse al pequeño tamaño de la capa n = 2 y las grandes repulsiones de electrón-electrón resultantes. Por ejemplo, el cloro, con un valor de AE de –348 kJ/mol, tiene el valor más alto de cualquier elemento en la tabla periódica. La AE del flúor es –322 kJ/mol. Cuando agregamos un electrón a un átomo de flúor para formar un anión fluoruro (F^–),

agregamos un electrón a la capa n = 2. El electrón es atraído hacia el núcleo, pero también hay una repulsión significativa de los otros electrones ya presentes en esta pequeña capa de valencia. El átomo de cloro tiene la misma configuración electrónica en la capa de valencia, pero debido a que el electrón entrante va a la capa n = 3, ocupa una región del espacio considerablemente mayor y las repulsiones electrón-electrón se reducen. El electrón entrante no experimenta tanta repulsión y el átomo de cloro acepta un electrón adicional más fácilmente, lo que resulta en una AE más negativa.

Figura 6.35. Esta versión de la tabla periódica muestra los valores de la afinidad electrónica (en kJ/mol) para los elementos seleccionados.

Las propiedades analizadas en esta sección (tamaño de los átomos e iones, carga nuclear efectiva, energías de ionización y afinidades electrónicas) son fundamentales para comprender la reactividad química. Por ejemplo, debido a que el flúor tiene un AE energéticamente favorable y una gran barrera energética para la ionización (IE), es mucho más fácil formar aniones de flúor que los cationes. Las propiedades metálicas, incluida la conductividad y la maleabilidad (la capacidad de formar láminas) dependen de tener

electrones que se puedan eliminar fácilmente. Por lo tanto, los caracteres metálicos aumentan a medida que avanzamos hacia abajo en un grupo y disminuimos a lo largo de un período en la misma tendencia observada para el tamaño atómico porque es más fácil eliminar un electrón que está más alejado del núcleo.

Preguntas y respuestas - Capítulo VI

Respuestas

Introducción

Figura 7.1 Apodado "buckyballs", las moléculas de buckminsterfullereno (C60) contienen solo átomos de carbono (izquierda) dispuestos para formar un marco geométrico de hexágonos y pentágonos, similar al patrón en un balón de fútbol (centro). Esta estructura molecular lleva el nombre del arquitecto R. Buckminster Fuller, cuyos diseños innovadores combinaron formas geométricas simples para crear estructuras grandes y fuertes como este domo de radar meteorológico cerca de Tucson, Arizona (derecha) (crédito medio: modificación del trabajo por "Petey21"/Wikimedia Commons; derecho de crédito: modificación del trabajo por Bill Morrow).

Desde hace tiempo se sabe que el carbono puro se presenta en diferentes formas (alótropos), incluidos el grafito y los diamantes. Pero no fue sino hasta 1985 que se reconoció una nueva forma de carbono: buckminsterfullereno. Esta molécula lleva el nombre del arquitecto e inventor R. Buckminster Fuller (1895–1983), cuyo diseño arquitectónico característico fue la cúpula geodésica, caracterizada por una estructura reticular que soporta una superficie esférica. La evidencia experimental reveló la fórmula, C60, y luego los científicos determinaron cómo 60 átomos de carbono podrían formar una molécula simétrica y estable. Se guiaron por la teoría de la vinculación, el tema de este capítulo, que explica cómo los átomos individuales se conectan para formar estructuras más complejas.

Enlace iónico

Como has aprendido, los iones son átomos o moléculas que tienen una carga eléctrica. Un catión (un ion positivo) se forma cuando un átomo neutro pierde uno o más electrones de su capa de valencia, y un anión (un ion negativo) se forma cuando un átomo neutro gana uno o más electrones en su capa de valencia.

Los compuestos formados por iones se denominan compuestos iónicos (o sales), y sus iones constituyentes se mantienen unidos por enlaces iónicos: fuerzas electrostáticas de atracción entre cationes y aniones con carga opuesta. Las propiedades de los compuestos iónicos arrojan algo de luz sobre la naturaleza de los enlaces iónicos. Los sólidos iónicos exhiben una estructura cristalina y tienden a ser rígidos y quebradizos; también tienden a tener altos puntos de fusión y ebullición, lo que sugiere que los enlaces iónicos son muy fuertes. Los sólidos iónicos también son malos conductores de la electricidad por la misma razón: la fuerza de los enlaces iónicos evita que los iones se muevan libremente en estado sólido. Sin embargo, la mayoría de los sólidos iónicos se disuelven fácilmente en agua. Una vez disueltos o fundidos, los compuestos iónicos son excelentes conductores de electricidad y calor porque los iones pueden moverse libremente.

Los átomos neutros y sus iones asociados tienen propiedades físicas y químicas muy diferentes. Los átomos de sodio forman metal de sodio, un metal suave de color blanco plateado que arde vigorosamente en el aire y reacciona explosivamente con el agua. Los átomos de cloro forman cloro gaseoso, $Cl_2$, un gas amarillo verdoso que es extremadamente corrosivo para la mayoría de los metales y muy venenoso para los animales y las plantas.

La reacción vigorosa entre los elementos sodio y cloro forma el cloruro de sodio compuesto cristalino blanco, sal de mesa común, que contiene cationes de sodio y aniones de cloruro (Figura 7.2). El compuesto formado por estos iones exhibe propiedades completamente diferentes de las propiedades de los elementos sodio y cloro. El cloro es venenoso, pero el cloruro de sodio es esencial para la vida; los átomos de sodio reaccionan vigorosamente con agua, pero el cloruro de sodio simplemente se disuelve en agua.

Figura 7.2 (a) El sodio es un metal blando que debe almacenarse en aceite mineral para evitar la reacción con el aire o el agua. (b) El cloro es un gas amarillo verdoso pálido. (c) Cuando se combinan, forman cristales blancos de cloruro de sodio (sal de mesa). (crédito a: modificación del trabajo de "Jurii"/Wikimedia Commons).

La formación de compuestos iónicos

Los compuestos iónicos binarios se componen de solo dos elementos: un metal (que forma los cationes) y un no metal (que forma los aniones). Por ejemplo, $NaCl$ es un compuesto iónico binario. Podemos pensar en la formación de tales compuestos en términos de las propiedades periódicas de los elementos. Muchos elementos metálicos tienen potenciales de ionización relativamente bajos y pierden electrones fácilmente.

Estos elementos se encuentran a la izquierda en un período o cerca del final de un grupo en la tabla periódica. Los átomos no metálicos tienen afinidades electrónicas relativamente altas y, por lo tanto, ganan electrones fácilmente perdidos por los átomos metálicos, llenando así sus capas de valencia. Los elementos no metálicos se encuentran en la esquina superior derecha de la tabla periódica.

Como todas las sustancias deben ser eléctricamente neutras, el número total de cargas positivas en los cationes de un compuesto iónico debe ser igual al número total de cargas negativas en sus aniones. La fórmula de un compuesto iónico representa la relación más simple de los números de iones necesarios para dar números idénticos de cargas positivas y negativas. Por ejemplo, la fórmula para el óxido de aluminio, $Al_2O_3$, indica que este compuesto iónico contiene dos cationes de aluminio, $Al^{3+}$, por cada tres aniones de óxido, $O^{2−}$ [por lo tanto, (2 × +3) + (3 × –2) = 0].

Sin embargo, es importante tener en cuenta que la fórmula para un compuesto iónico no representa la disposición física de sus iones. Es incorrecto referirse a una "molécula" de cloruro de sodio ($NaCl$) porque no hay un enlace iónico, per se, entre cualquier par específico de iones de sodio y cloruro. Las fuerzas atractivas entre los iones son isotrópicas, las mismas en todas las direcciones, lo que significa que cualquier ión particular se siente igualmente atraído por todos los iones cercanos de carga opuesta. Esto da como resultado que los iones se organicen en una estructura reticular tridimensional fuertemente unida. El cloruro de sodio, por ejemplo, consiste en una disposición regular de igual número de cationes Na + y aniones $Cl^–$ (Figura 7.3). Puedes apreciar la simulacion del cloruro de sodio en la (Figura 9.39) del cápitulo IX

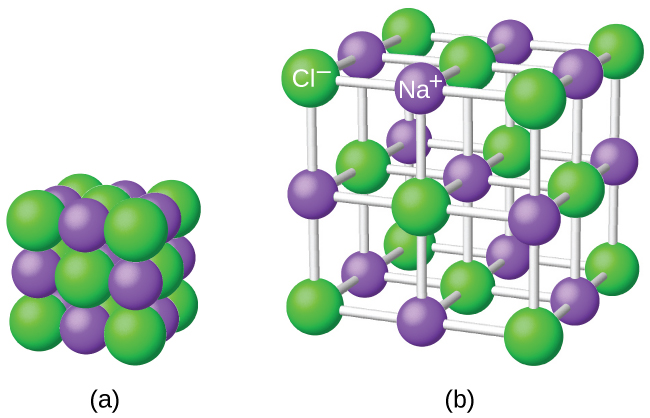
Figura 7.3 Los átomos en el cloruro de sodio (sal de mesa común) están dispuestos para (a) maximizar las cargas opuestas que interactúan. Las esferas más pequeñas representan iones de sodio, las más grandes representan iones de cloruro. En la vista ampliada (b), la geometría se puede ver más claramente. Ten en cuenta que cada ion está "unido" a todos los iones circundantes, seis en este caso.

La fuerte atracción electrostática entre los iones $Na^+$ y $Cl^–$ los mantiene fuertemente unidos en $NaCl$ sólido. Se requieren $769 kJ$ de energía para disociar un mol de $NaCl$ sólido en iones de $Na^+$ y $Cl^–$ gaseosos separados:

Estructuras electrónicas de cationes

Al formar un catión, un átomo de un elemento del grupo principal tiende a perder todos sus electrones de valencia, asumiendo así la estructura electrónica del gas noble que lo precede en la tabla periódica.

Para los grupos 1 (los metales alcalinos) y 2 (los metales alcalinotérreos), los números de grupo son iguales al número de electrones de valencia y, en consecuencia, a las cargas de los cationes formados a partir de los átomos de estos elementos cuando todos los electrones de valencia son removidos. Por ejemplo, el calcio es un elemento del grupo 2 cuyos átomos neutros tienen 20 electrones y una configuración electrónica de estado fundamental de $1s^22s^22p^63s^23p^64s^2$. Cuando un átomo de $Ca$ pierde sus dos electrones de valencia, el resultado es un catión con 18 electrones, una carga 2+ y una configuración electrónica de $1s^22s^22p^63s^23p^6$. El ion $Ca^{2+}$ es por lo tanto isoelectrónico con el gas noble $Ar$.

Para los grupos 13-17, los números de grupo exceden el número de electrones de valencia en 10 (lo que representa la posibilidad de subcapas d completas en átomos de elementos en el cuarto y más períodos). Por lo tanto, la carga de un catión formado por la pérdida de todos los electrones de valencia es igual al número de grupo menos 10. Por ejemplo, el aluminio (en el grupo 13) forma iones 3+ ($Al^{3+}$).

Las excepciones al comportamiento esperado involucran elementos hacia el fondo de los grupos. Además de los iones esperados $Tl^{3+}$, $Sn^{4+}$, $Pb^{4+}$ y $Bi^{5+}$, una pérdida parcial de los electrones de capa de valencia de estos átomos también puede conducir a la formación de iones $Tl^+$, $Sn^{2+}$, $Pb^{2+}$ y $Bi^{3+}$. La formación de estos cationes 1+, 2+ y 3+ se atribuye al efecto del par inerte, que refleja la energía relativamente baja del par de electrones $s$ de valencia para los átomos de los elementos pesados ​​de los grupos 13, 14 y 15.

El mercurio (grupo 12) también exhibe un comportamiento inesperado: forma un ion diatómico, $Hg_2^{2+}$ (un ion formado a partir de dos átomos de mercurio, con un enlace Hg-Hg), además del ion monoatómico esperado $Hg^{2+}$ (formado a partir de un solo átomo de mercurio).

Los elementos metálicos de transición y transición interna se comportan de manera diferente a los elementos del grupo principal. La mayoría de los cationes de metales de transición tienen 2+ o 3+ cargas que resultan primero de la pérdida de su (s) electrón (es) más externo (s), a veces seguido de la pérdida de uno o dos electrones d de la capa más próxima a la más externa. Por ejemplo, el hierro ($1s^22s^22p^63s^23p^63d^64s^2$) forma el ion $Fe^{2+}$ ($1s^22s^22p^63s^23p^63d^6$) por la pérdida de los electrones 4s y el ion $Fe^{3+}$ ($1s^22s^22p^63s^23p^63d^5$) por la pérdida de los electrones 4s y uno de los electrones 3d. Aunque los orbitales d de los elementos de transición son, de acuerdo con el principio de Aufbau, los últimos en llenarse al construir configuraciones de electrones, los electrones s más externos son los primeros en perderse cuando estos átomos se ionizan. Cuando los metales de transición internos forman iones, generalmente tienen una carga de 3+, como resultado de la pérdida de sus electrones s más externos y un electrón d o f.

Ejemplo 7.1

Determinación de las estructuras electrónicas de cationes

Hay al menos 14 elementos categorizados como "oligoelementos esenciales" para el cuerpo humano. Se les llama "esenciales" porque se requieren para funciones corporales saludables, "trazas" porque se requieren solo en pequeñas cantidades y "elementos" a pesar de que realmente son iones.

Se requieren dos de estos oligoelementos esenciales, el cromo y el zinc, como $Cr^{3+}$ y $Zn^{2+}$. Escribe las configuraciones electrónicas de estos cationes.

Solución

Primero, escribe la configuración electrónica para los átomos neutros:

A continuación, elimina los electrones del orbital de mayor energía. Para los metales de transición, los electrones se eliminan del orbital s primero y luego del orbital d. Para los elementos del bloque p, los electrones se eliminan de los orbitales p y luego del orbital s. El zinc es un miembro del grupo 12, por lo que debería tener una carga de 2+, y por lo tanto pierde solo los dos electrones en su órbita. El cromo es un elemento de transición y debería perder sus electrones s y luego sus electrones d al formar un catión. Por lo tanto, encontramos las siguientes configuraciones electrónicas de los iones:

Comprueba tu aprendizaje

Estructuras electrónicas de aniones

La mayoría de los aniones monatómicos se forman cuando un átomo neutro no metálico gana suficientes electrones para llenar completamente sus orbitales s y p externos, alcanzando así la configuración electrónica del siguiente gas noble. Por lo tanto, es simple determinar la carga en un ion tan negativo: la carga es igual al número de electrones que se deben obtener para llenar los orbitales s y p del átomo original. El oxígeno, por ejemplo, tiene la configuración electrónica $1s^22s^22p^4$, mientras que el anión de oxígeno tiene la configuración electrónica del neón de gas noble
($Ne$), $1s^22s^22p^6$. Los dos electrones adicionales necesarios para llenar los orbitales de valencia le dan al ion óxido la carga de 2– ($O_2^{–}$).

Ejemplo 7.2

Determinación de la estructura electrónica de aniones

El selenio y el yodo son dos oligoelementos esenciales que forman aniones. Escribe las configuraciones electrónicas de los aniones.

Solución

$Se^{2–}: [Ar] 3d^{10}4s^24p^6\\ I^–: [Kr] 4d^{10}5s^25p^6$

Comprueba tu aprendizaje

Enlace covalente

El enlace iónico resulta de la atracción electrostática de iones con carga opuesta que normalmente se producen por la transferencia de electrones entre átomos metálicos y no metálicos. Un tipo diferente de enlace resulta de la atracción mutua de átomos para un par de electrones "compartidos". Tales enlaces se llaman enlaces covalentes. Los enlaces covalentes se forman entre dos átomos cuando ambos tienen tendencias similares para atraer electrones hacia sí mismos (es decir, cuando ambos átomos tienen energías de ionización y afinidades de electrones idénticas o bastante similares). Por ejemplo, dos átomos de hidrógeno se unen covalentemente para formar una molécula $H_2$; cada átomo de hidrógeno en la molécula $H_2$ tiene dos electrones que lo estabilizan, dando a cada átomo el mismo número de electrones de valencia que el gas noble $He$.

Los compuestos que contienen enlaces covalentes exhiben diferentes propiedades físicas que los compuestos iónicos.

Debido a que la atracción entre moléculas, que son eléctricamente neutras, es más débil que la existente entre iones cargados eléctricamente, los compuestos covalentes generalmente tienen puntos de fusión y ebullición mucho más bajos que los compuestos iónicos. De hecho, muchos compuestos covalentes son líquidos o gases a temperatura ambiente y, en su estado sólido, suelen ser mucho más suaves que los sólidos iónicos. Además, mientras que los compuestos iónicos son buenos conductores de electricidad cuando se disuelven en agua, la mayoría de los compuestos covalentes son insolubles en agua; Como son eléctricamente neutros, son malos conductores de electricidad en cualquier estado.

Formación de enlaces covalentes

Los átomos no metálicos con frecuencia forman enlaces covalentes con otros átomos no metálicos. Por ejemplo, la molécula de hidrógeno, $H_2$, contiene un enlace covalente entre sus dos átomos de hidrógeno. La figura 7.4 ilustra por qué se forma este enlace. Comenzando en el extremo derecho, tenemos dos átomos de hidrógeno separados con una energía potencial particular, indicada por la línea roja. A lo largo del eje x está la distancia entre los dos átomos. A medida que los dos átomos se acercan entre sí (moviéndose a la izquierda a lo largo del eje x), sus orbitales de valencia (1s) comienzan a superponerse. Los electrones individuales en cada átomo de hidrógeno luego interactúan con ambos núcleos atómicos, ocupando el espacio alrededor de ambos átomos. La fuerte atracción de cada electrón compartido a ambos núcleos estabiliza el sistema, y ​​la energía potencial disminuye a medida que disminuye la distancia del enlace. Si los átomos continúan acercándose, las cargas positivas en los dos núcleos comienzan a repelerse entre sí, y la energía potencial aumenta. La longitud del enlace está determinada por la distancia a la que se alcanza la energía potencial más baja.

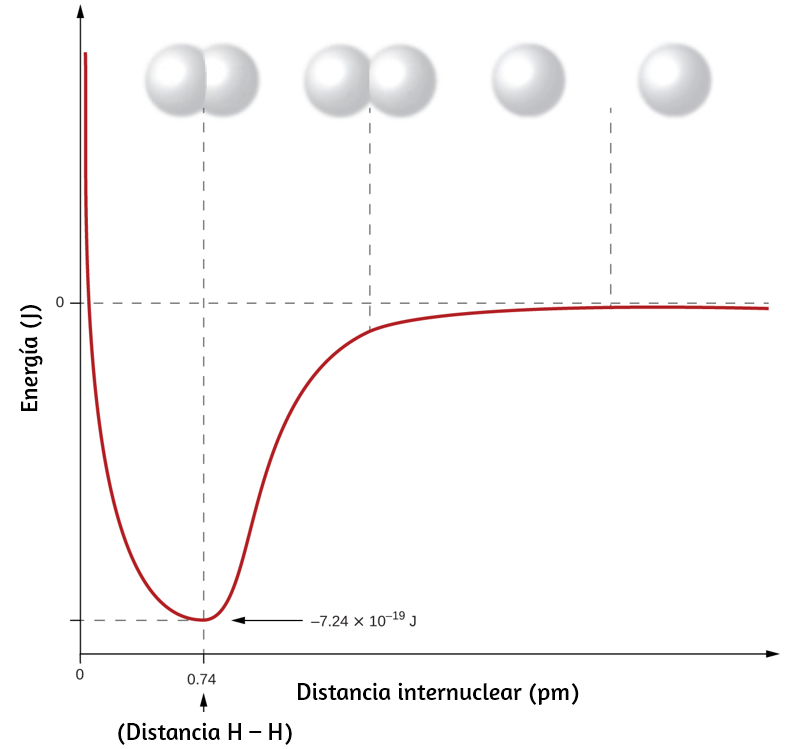
Figura 7.4 La energía potencial de dos átomos de hidrógeno separados (derecha) disminuye a medida que se acercan entre sí, y los electrones individuales en cada átomo se comparten para formar un enlace covalente. La longitud del enlace es la distancia internuclear a la que se alcanza la energía potencial más baja.

Es esencial recordar que se debe agregar energía para romper los enlaces químicos (un proceso endotérmico), mientras que la formación de enlaces químicos libera energía (un proceso exotérmico).

En el caso de $H_2$, el enlace covalente es muy fuerte; Se debe agregar una gran cantidad de energía, 436 kJ, para romper los enlaces en un mol de moléculas de hidrógeno y hacer que los átomos se separen:

Por el contrario, se libera la misma cantidad de energía cuando se forma un mol de moléculas de $H_2$ a partir de dos moles de átomos de H:

Enlaces covalentes puros versus polares

Si los átomos que forman un enlace covalente son idénticos, como en $H_2$, $Cl_2$ y otras moléculas diatómicas, entonces los electrones en el enlace deben compartirse por igual. Nos referimos a esto como un enlace covalente puro. Los electrones compartidos en enlaces covalentes puros tienen la misma probabilidad de estar cerca de cada núcleo.

En el caso de $Cl_2$, cada átomo comienza con siete electrones de valencia, y cada $Cl$ comparte un electrón con el otro, formando un enlace covalente:

El número total de electrones alrededor de cada átomo individual consta de seis electrones no unidos y dos electrones compartidos (es decir, de enlace) para ocho electrones totales, que coinciden con el número de electrones de valencia en el argón de gas noble.

Dado que los átomos de enlace son idénticos, $Cl_2$ también presenta un enlace covalente puro.

Cuando los átomos unidos por un enlace covalente son diferentes, los electrones de enlace se comparten, pero ya no son iguales. En cambio, los electrones de enlace están más atraídos a un átomo que al otro, lo que da lugar a un cambio de densidad de electrones hacia ese átomo. Esta distribución desigual de electrones se conoce como un enlace covalente polar, caracterizado por una carga positiva parcial en un átomo y una carga negativa parcial en el otro. El átomo que atrae a los electrones adquiere más fuertemente la carga negativa parcial y viceversa. Por ejemplo, los electrones en el enlace $\ce{H - Cl}$ de una molécula de cloruro de hidrógeno pasan más tiempo cerca del átomo de cloro que cerca del átomo de hidrógeno. Por lo tanto, en una molécula de $HCl$, el átomo de cloro lleva una carga negativa parcial y el átomo de hidrógeno tiene una carga positiva parcial. La figura 7.5 muestra la distribución de electrones en el enlace $\ce{H – Cl}$. Ten en cuenta que el área sombreada alrededor de $Cl$ es mucho más grande que alrededor de $H$. Compara esto con la figura 7.4, que muestra la distribución uniforme de electrones en el enlace no polar $H_2$.

A veces designamos los átomos positivos y negativos en un enlace covalente polar usando una letra griega minúscula "delta", $\delta$, con un signo más o un signo menos para indicar si el átomo tiene una carga positiva parcial ($\delta +$) o una carga negativa parcial ($\delta -$). Este simbolismo se muestra para la molécula $\ce{H – Cl}$ en la figura 7.5.

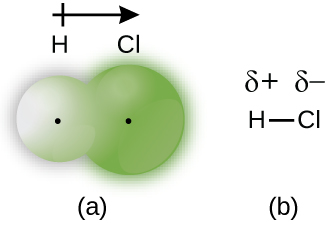
Figura 7.5 (a) La distribución de la densidad de electrones en la molécula de $HCl$ es desigual. La densidad electrónica es mayor alrededor del núcleo de cloro. Los pequeños puntos negros indican la ubicación de los núcleos de hidrógeno y cloro en la molécula. (b) Los símbolos $\delta +$ y $\delta -$ indican la polaridad del enlace $\ce{H – Cl}$.

Electronegatividad

Si un enlace es no polar o covalente polar está determinado por una propiedad de los átomos de enlace llamada electronegatividad. La electronegatividad es una medida de la tendencia de un átomo a atraer electrones (o densidad de electrones) hacia sí mismo. Determina cómo se distribuyen los electrones compartidos entre los dos átomos en un enlace. Cuanto más fuertemente atrae un átomo a los electrones en sus enlaces, mayor es su electronegatividad. Los electrones en un enlace covalente polar se desplazan hacia el átomo más electronegativo; así, el átomo más electronegativo es el que tiene la carga negativa parcial. Cuanto mayor es la diferencia en la electronegatividad, más polarizada está la distribución de electrones y mayores son las cargas parciales de los átomos.

La figura 7.6 muestra los valores de electronegatividad de los elementos propuestos por uno de los químicos más famosos del siglo XX: Linus Pauling (Figura 7.7).

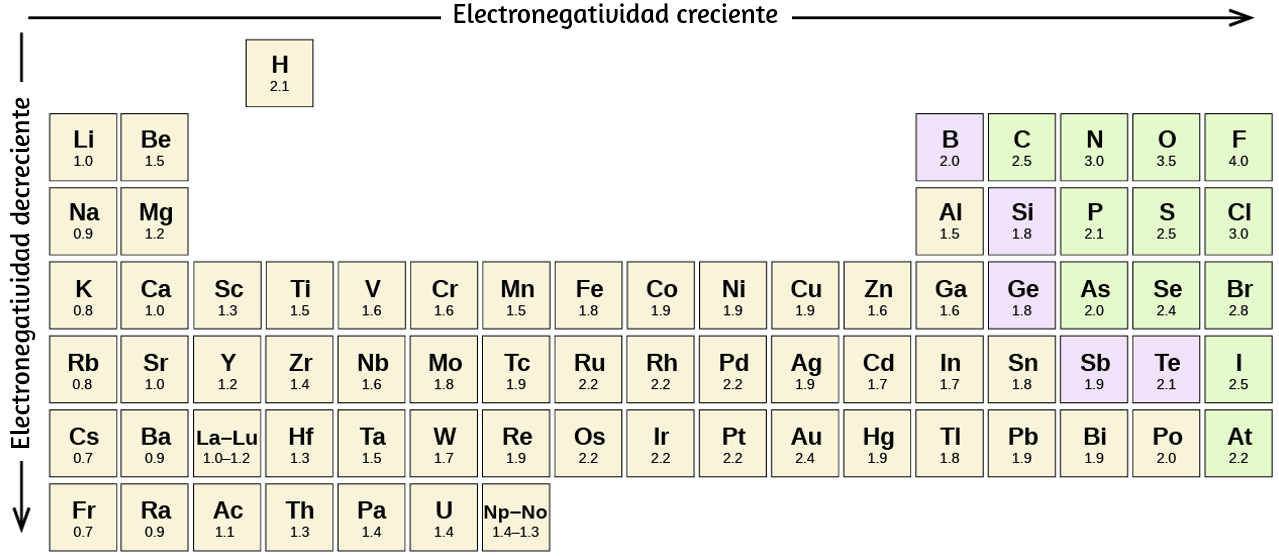
Figura 7.6 Los valores de electronegatividad derivados de Pauling siguen tendencias periódicas predecibles, con las electronegatividades más altas hacia la parte superior derecha de la tabla periódica.

En general, la electronegatividad aumenta de izquierda a derecha en un período de la tabla periódica y disminuye en un grupo. Por lo tanto, los no metales, que se encuentran en la esquina superior derecha, tienden a tener las electronegatividades más altas, siendo el flúor el elemento más electronegativo de todos (EN = 4.0). Los metales tienden a ser elementos menos electronegativos, y los metales del grupo 1 tienen las electronegatividades más bajas. Ten en cuenta que los gases nobles se excluyen de esta figura porque estos átomos generalmente no comparten electrones con otros átomos, ya que tienen una capa de valencia completa (si bien existen compuestos de gases nobles como $XeO_2$, solo se pueden formar en condiciones extremas y, por lo tanto, no encajan perfectamente en el modelo general de electronegatividad).

Electronegatividad versus afinidad electrónica

Debemos tener cuidado de no confundir la electronegatividad y la afinidad electrónica. La afinidad electrónica de un elemento es una cantidad física medible, es decir, la energía liberada o absorbida cuando un átomo de fase gaseosa aislado adquiere un electrón, medido en kJ/mol. La electronegatividad, por otro lado, describe la fuerza con la que un átomo atrae electrones en un enlace. Es una cantidad adimensional que se calcula, no se mide. Pauling obtuvo los primeros valores de electronegatividad al comparar las cantidades de energía requeridas para romper diferentes tipos de enlaces. Eligió una escala relativa arbitraria que va de 0 a 4.

RETRATO DE UN QUÍMICO

Su trabajo también fue fundamental para frenar las pruebas de armas nucleares; demostró que las consecuencias radiactivas de las pruebas nucleares representaban un riesgo para la salud pública.

Figura 7.7. Linus Pauling (1901–1994) hizo muchas contribuciones importantes al campo de la química. También fue un destacado activista, publicitando temas relacionados con la salud y las armas nucleares.

Electronegatividad y tipo de enlace

El valor absoluto de la diferencia en electronegatividad ($\Delta$EN) de dos átomos unidos proporciona una medida aproximada de la polaridad que se espera en el enlace y, por lo tanto, el tipo de enlace.

Cuando la diferencia es muy pequeña o cero, el enlace es covalente y no polar. Cuando es grande, el enlace es polar covalente o iónico. Los valores absolutos de las diferencias de electronegatividad entre los átomos en los enlaces $\ce{H – H}$, $\ce{H – Cl}$ y $\ce{Na – Cl}$ son 0 (no polar), 0.9 (covalente polar) y 2.1 (iónico), respectivamente. El grado en que los electrones se comparten entre los átomos varía de completamente igual (enlace covalente puro) a nada (enlace iónico). La figura 7.8 muestra la relación entre la diferencia de electronegatividad y el tipo de enlace.

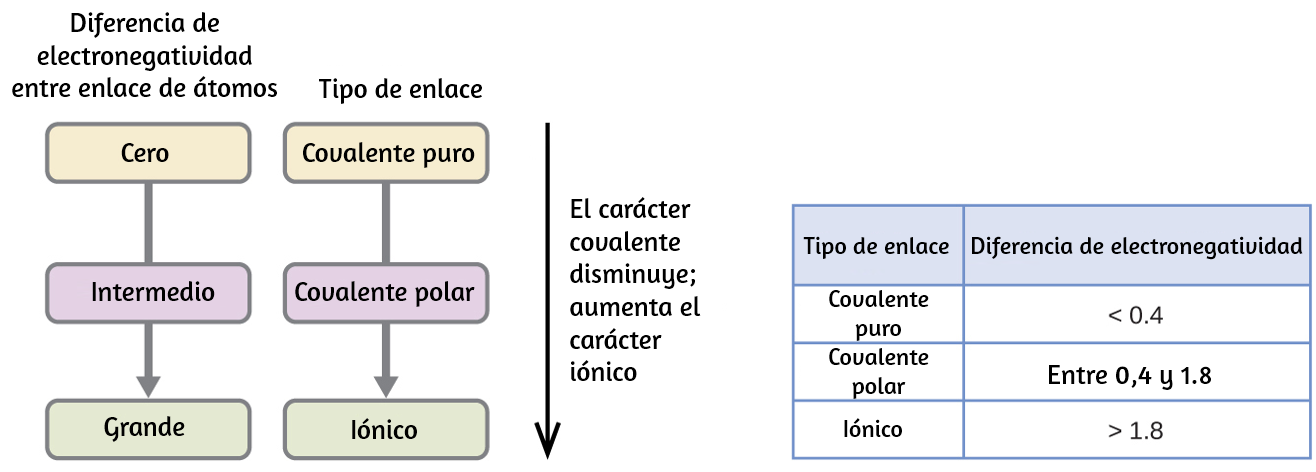
Figura 7.8 . A medida que aumenta la diferencia de electronegatividad entre dos átomos, el enlace se vuelve más iónico.

En la figura 7.8 se muestra una aproximación aproximada de las diferencias de electronegatividad asociadas con enlaces covalentes, covalentes polares e iónicos. Sin embargo, esta tabla es solo una guía general, con muchas excepciones. Por ejemplo, los átomos de $H$ y $F$ en $HF$ tienen una diferencia de electronegatividad de 1.9, y los átomos de $N$ y $H$ en $NH_3$ una diferencia de 0.9, sin embargo, ambos compuestos forman enlaces que se consideran covalentes polares.

Del mismo modo, los átomos de $Na$ y $Cl$ en $NaCl$ tienen una diferencia de electronegatividad de 2.1, y los átomos de $Mn$ e $I$ en $MnI_2$ tienen una diferencia de 1.0, sin embargo, ambas sustancias forman compuestos iónicos.

La mejor guía para el carácter covalente o iónico de un enlace es considerar los tipos de átomos involucrados y sus posiciones relativas en la tabla periódica. Los enlaces entre dos no metales son generalmente covalentes; La unión entre un metal y un no metal es a menudo iónica.

Algunos compuestos contienen enlaces covalentes e iónicos. Los átomos en los iones poliatómicos, como $OH^{–}$, $NO_3^{−}$ y $NH^{4+}$, se mantienen unidos mediante enlaces covalentes polares. Sin embargo, estos iones poliatómicos forman compuestos iónicos al combinarse con iones de carga opuesta. Por ejemplo, el nitrato de potasio, $KNO_3$, contiene el catión $K^{+}$ y el anión poliatómico $NO_3^{−}$. Por lo tanto, la unión en nitrato de potasio es iónica, como resultado de la atracción electrostática entre los iones $K^+$ y $NO_3^{−}$, así como covalente entre los átomos de nitrógeno y oxígeno en $NO_3^{−}$.

Ejemplo 7.3

Electronegatividad y polaridad de enlace

Las polaridades de enlace juegan un papel importante en la determinación de la estructura de las proteínas. Usando los valores de electronegatividad en la figura 7.6, organiza los siguientes enlaces covalentes, todos comúnmente encontrados en aminoácidos, en orden de polaridad creciente. Luego designa los átomos positivos y negativos usando los símbolos $\delta +$ y $\delta -$:

Solución

La polaridad de estos enlaces aumenta a medida que aumenta el valor absoluto de la diferencia de electronegatividad. El átomo con la designación $\delta -$ es el más electronegativo de los dos. La tabla 7.1 muestra estos enlaces en orden de polaridad creciente.

Tabla 71.. Polaridad de enlace y diferencia de electronegatividad

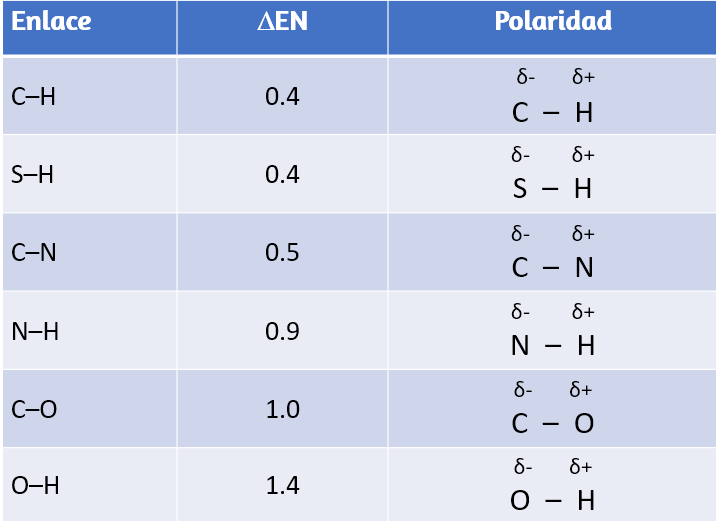
Comprueba tu aprendizaje

En la siguiente escena interactiva Phet de la Universidad de Colorado, podrás observar ¿cuándo es una molécula polar?, puedes cambiar la electronegatividad de los átomos en una molécula para ver cómo afecta a la polaridad. Observa, además, cómo se comporta la molécula en un campo eléctrico. Cambia el ángulo de enlace para ver cómo afecta a la forma de polaridad.

Símbolos y estructuras de Lewis

Hasta ahora en este capítulo, hemos discutido los diversos tipos de enlaces que se forman entre átomos y/o iones. En todos los casos, estos enlaces implican compartir o transferir electrones de capa de valencia entre átomos. En esta sección, exploraremos el método típico para representar electrones de capa de valencia y enlaces químicos, a saber, símbolos de Lewis y estructuras de Lewis.

Símbolos de Lewis

Utilizamos símbolos de Lewis para describir configuraciones electrónicas de valencia de átomos e iones monoatómicos. Un símbolo de Lewis consiste en un símbolo elemental rodeado por un punto para cada uno de sus electrones de valencia:

La figura 7.9 muestra los símbolos de Lewis para los elementos del tercer período de la tabla periódica.

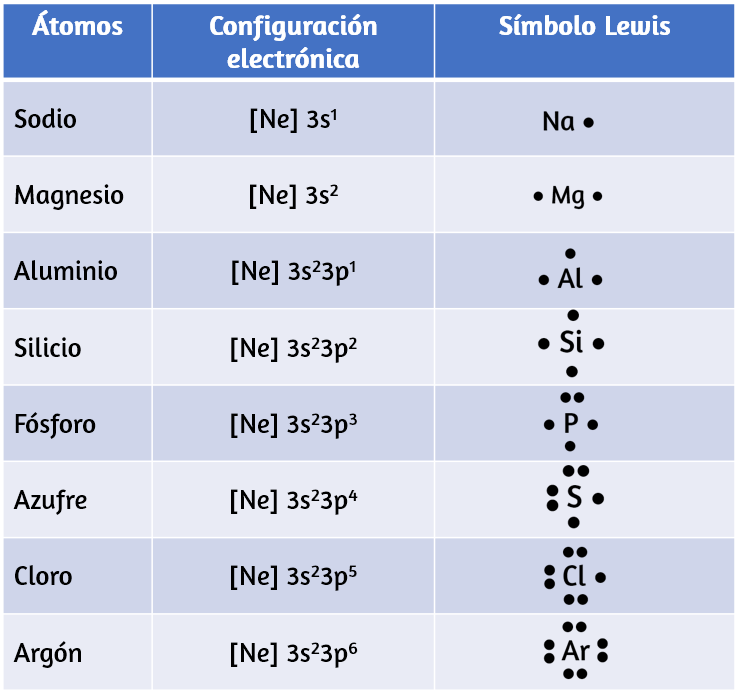
Figura 7.9. Símbolos de Lewis que ilustran el número de electrones de valencia para cada elemento en el tercer período de la tabla periódica.

Los símbolos de Lewis también se pueden usar para ilustrar la formación de cationes a partir de átomos, como se muestra aquí para sodio y calcio:

Del mismo modo, se pueden usar para mostrar la formación de aniones a partir de átomos, como se muestra aquí para el cloro y el azufre:

La figura 7.10 demuestra el uso de los símbolos de Lewis para mostrar la transferencia de electrones durante la formación de compuestos iónicos.

Estructuras de Lewis

También usamos símbolos de Lewis para indicar la formación de enlaces covalentes, que se muestran en las estructuras de Lewis, dibujos que describen la unión en moléculas e iones poliatómicos. Por ejemplo, cuando dos átomos de cloro forman una molécula de cloro, comparten un par de electrones:

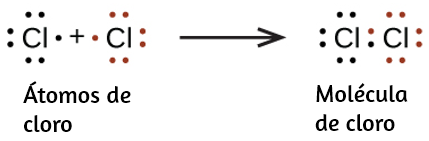
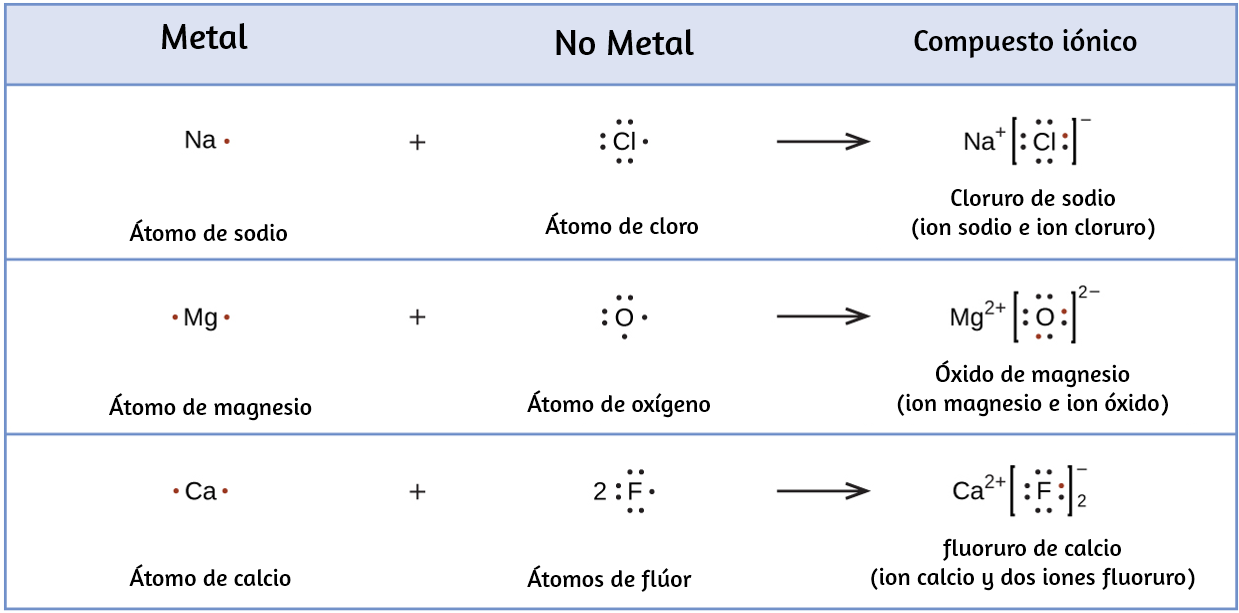
Figura 7.10. Los cationes se forman cuando los átomos pierden electrones, representados por menos puntos de Lewis, mientras que los aniones se forman por átomos que ganan electrones. El número total de electrones no cambia.

La estructura de Lewis indica que cada átomo de Cl tiene tres pares de electrones que no se usan en enlaces (llamados pares solitarios) y un par compartido de electrones (escrito entre los átomos). A veces se usa un guión (o línea) para indicar un par compartido de electrones:

Un solo par compartido de electrones se llama un enlace simple. Cada átomo de Cl interactúa con ocho electrones de valencia: los seis en los pares solitarios y los dos en el enlace único.

La regla del octeto

Las otras moléculas de halógeno ($F_2$, $Br_2$, $I_2$ y $At_2$) forman enlaces como los de la molécula de cloro: un enlace simple entre átomos y tres pares de electrones solitarios por átomo. Esto permite que cada átomo de halógeno tenga una configuración de electrones de gas noble. La tendencia de los átomos del grupo principal a formar suficientes enlaces para obtener ocho electrones de valencia se conoce como la regla del octeto.

El número de enlaces que puede formar un átomo a menudo se puede predecir a partir del número de electrones necesarios para alcanzar un octeto (ocho electrones de valencia). Esto es especialmente cierto para los no metales del segundo período de la tabla periódica (C, N, O y F). Por ejemplo, cada átomo de un elemento del grupo 14 tiene cuatro electrones en su capa más externa y, por lo tanto, requiere cuatro electrones más para alcanzar un octeto. Estos cuatro electrones se pueden obtener formando cuatro enlaces covalentes, como se ilustra aquí para el carbono en $CCl_4$ (tetracloruro de carbono) y el silicio en $SiH_4$ (silano). Debido a que el hidrógeno solo necesita dos electrones para llenar su capa de valencia, es una excepción a la regla del octeto. Los elementos de transición y los elementos de transición internos tampoco siguen la regla del octeto:

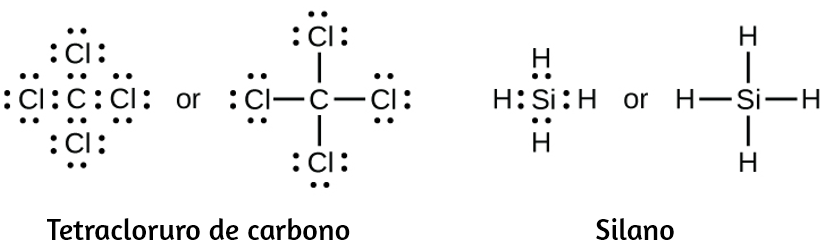
Los elementos del grupo 15, como el nitrógeno, tienen cinco electrones de valencia en el símbolo atómico de Lewis: un par solitario y tres electrones no apareados. Para obtener un octeto, estos átomos forman tres enlaces covalentes, como en el $NH_3$ (amoníaco). El oxígeno y otros átomos en el grupo 16 obtienen un octeto formando dos enlaces covalentes:

Enlaces dobles y triples

Como se mencionó anteriormente, cuando un par de átomos comparte un par de electrones, llamamos a esto un enlace simple.

Sin embargo, un par de átomos puede necesitar compartir más de un par de electrones para lograr el octeto requerido. Se forma un doble enlace cuando dos pares de electrones se comparten entre un par de átomos, como entre los átomos de carbono y oxígeno en $CH_2O$ (formaldehído) y entre los dos átomos de carbono en $C_2H_4$ (etileno):

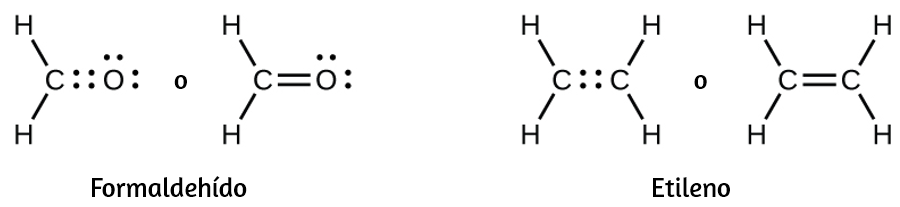
Un triple enlace se forma cuando tres pares de electrones son compartidos por un par de átomos, como en el monóxido de carbono ($CO$) y el ion cianuro ($CN^{–}$):

Escribir estructuras de Lewis con la regla del octeto

Para moléculas e iones moleculares muy simples, podemos escribir las estructuras de Lewis simplemente emparejando los electrones no apareados en los átomos constituyentes. Ver estos ejemplos:

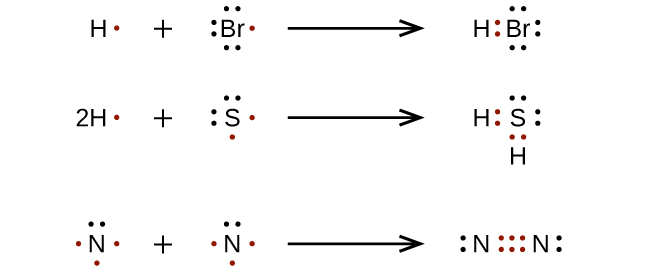
Para moléculas e iones moleculares más complicados, es útil seguir el procedimiento paso a paso descrito aquí:

1. Determina el número total de electrones de valencia (capa externa). Para los cationes, resta un electrón por cada carga positiva. Para aniones, agrega un electrón por cada carga negativa.
2. Dibuja una estructura esquelética de la molécula o ion, ordenando los átomos alrededor de un átomo central (generalmente, el elemento menos electronegativo debe colocarse en el centro). Conecta cada átomo al átomo central con un enlace simple (un par de electrones).

3. Distribuye los electrones restantes como pares solitarios en los átomos terminales (excepto el hidrógeno), completando un octeto alrededor de cada átomo.
4. Coloca todos los electrones restantes en el átomo central.
5. Reorganiza los electrones de los átomos externos para hacer enlaces múltiples con el átomo central para obtener octetos siempre que sea posible.

Determinemos las estructuras de Lewis de $SiH_4$, $CHO_2^{−}$, $NO^+$ y $OF_2$ como ejemplos a seguir este procedimiento:

1. Determina el número total de electrones de valencia (capa externa) en la molécula o ion.
   
   
   Para una molécula, agregamos el número de electrones de valencia en cada átomo en la molécula:
   
   • $SiH_4$ $$\begin{aligned} Si:\text{4 electrones de valencia/átomo x 1 átomo} &= 4\\ + H:\text{1 electrón de valencia/átomo x 4 átomos} &= 4\\ \text{-------------------------------------------------------------}\\ &= 8 \end{aligned}$$
   • Para un ion negativo, como $CHO_2^{−}$, sumamos el número de electrones de valencia en los átomos al número de cargas negativas en el ion (se gana un electrón por cada carga negativa):

• $CHO_2^{-}$ $$\begin{aligned} C:\text{4 electrones de valencia/átomo x 1 átomo} &= 4\\ H:\text{1 electrón de valencia/átomo x 1 átomos} &= 1\\ O:\text{6 electrones de valencia/átomo x 2 átomos} &= 12\\ + \text{1 electrón adicional} &= 1\\ \text{-----------------------------------------------------------------}\\ &= 18 \end{aligned}$$
• Para un ion positivo, como $NO^+$, sumamos el número de electrones de valencia en los átomos en el ion y luego restamos el número de cargas positivas en el ion (se pierde un electrón por cada carga positiva) del número total de valencia electrones:
  
  $NO^+$ $$\begin{aligned} N:\text{5 electrones de valencia/átomo x 1 átomo} &= 5\\ O:\text{6 electrones de valencia/átomo x 1 átomos} &= 6\\ + \text{-1 electrón (carga positiva)} &= -1\\ \text{-----------------------------------------------------------------}\\ &= 10 \end{aligned}$$
• Dado que $OF_2$ es una molécula neutra, simplemente agregamos el número de electrones de valencia:

• $OF_2$ $$\begin{aligned} O:\text{6 electrones de valencia/átomo x 1 átomos} &= 6\\ + F: \text{7 electrones de valencia/átomo x 2 átomos} &= 14\\ \text{-----------------------------------------------------------------}\\ &= 20 \end{aligned}$$

2. Dibuja una estructura esquelética de la molécula o ion, organizando los átomos alrededor de un átomo central y conectando cada átomo al átomo central con un enlace único (un par de electrones). (Ten en cuenta que denotamos iones con corchetes alrededor de la estructura, lo que indica la carga fuera de los corchetes):
   
   

   

   Cuando son posibles varios arreglos de átomos, como para $CHO_2^{−}$, debemos usar evidencia experimental para elegir el correcto. En general, los elementos menos electronegativos tienen más probabilidades de ser átomos centrales. En $CHO_2^{−}$, el átomo de carbono menos electronegativo ocupa la posición central con los átomos de oxígeno e hidrógeno que lo rodean. Otros ejemplos incluyen $P$ en $POCl_3$, $S$ en $SO_2$ y $Cl$ en $ClO_4^{−}$. Una excepción es que el hidrógeno casi nunca es un átomo central. Como el elemento más electronegativo, el flúor tampoco puede ser un átomo central.

3. Distribuye los electrones restantes como pares solitarios en los átomos terminales (excepto el hidrógeno) para completar sus capas de valencia con un octeto de electrones.
   
   
   • No quedan electrones en $SiH_4$, por lo que no cambia:
     
     


4. Coloca todos los electrones restantes en el átomo central.
   
   
   • Para $SiH_4$, $CHO_2^−$ y $NO^+$, no quedan electrones restantes. Ya colocamos todos los electrones determinados en el Paso 1.
   • Para $OF_2$, teníamos 16 electrones restantes en el Paso 3, y colocamos 12, dejando 4 para colocar en el átomo central:

     

5. Reorganiza los electrones de los átomos externos para hacer enlaces múltiples con el átomo central para obtener octetos siempre que sea posible.
   
   
   • $SiH_4$: Si ya tienes un octeto, por lo que no es necesario hacer nada.
   • $CHO_2^{−}$: Hemos distribuido los electrones de valencia como pares solitarios en los átomos de oxígeno, pero el átomo de carbono carece de un octeto:

• $NO^+$: para este ion, agregamos ocho electrones de valencia, pero ninguno de los átomos tiene un octeto. No podemos agregar más electrones ya que ya hemos usado el total que encontramos en el Paso 1, por lo que debemos mover los electrones para formar un enlace múltiple:
  
  

  

  Esto todavía no produce un octeto, por lo que debemos mover otro par, formando un triple enlace:

  

• En $OF_2$, cada átomo tiene un octeto dibujado, por lo que nada cambia.

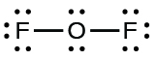
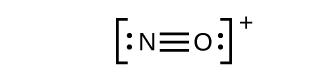
Ejemplo 7.4

Escribir estructuras de Lewis

La misión Cassini-Huygens de la NASA detectó una gran nube de cianuro de hidrógeno tóxico ($HCN$) en Titán (una luna de Saturno).

Titan también contiene etano ($H_3CCH_3$), acetileno ($HCCH$) y amoníaco ($NH_3$). ¿Cuáles son las estructuras de Lewis de estas moléculas?

Solución

Paso 1. Calcula el número de electrones de valencia.

$HCN$: (1 × 1) + (4 × 1) + (5 × 1) = 10
$H_3CCH_3$: (1 × 3) + (2 × 4) + (1 × 3) = 14
$HCCH$: (1 × 1) + (2 × 4) + (1 × 1) = 10
$NH_3$: (5 × 1) + (3 × 1) = 8

Paso 2. Dibuja un esqueleto y conecta los átomos con enlaces simples. Recuerda que H nunca es un átomo central:

Paso 3. Donde sea necesario, distribuye electrones a los átomos terminales:

$HCN$: seis electrones colocados en N
$H_33CCH_3$: no quedan electrones
$HCCH$: no hay átomos terminales capaces de aceptar electrones
$NH_3$: no hay átomos terminales capaces de aceptar electrones

Paso 4. Donde sea necesario, coloca los electrones restantes en el átomo central:

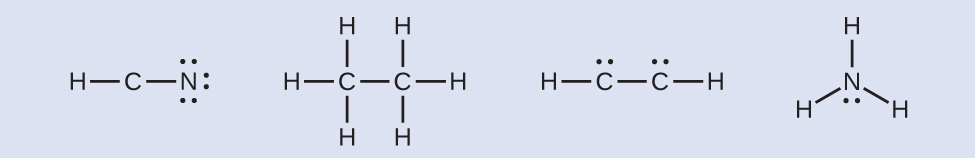
$HCN$: no quedan electrones
$H_3CCH_3$: no quedan electrones
$HCCH$: cuatro electrones colocados en el carbono
$NH_3$: dos electrones colocados en el nitrógeno

Paso 5. Donde sea necesario, reorganiza los electrones para formar enlaces múltiples para obtener un octeto en cada átomo:

$HCN$: forma dos enlaces $\ce{C - N}$ más
$H_3CCH_3$: todos los átomos tienen el número correcto de electrones
$HCCH$: forma un triple enlace entre los dos átomos de carbono
$NH3$: todos los átomos tienen el número correcto de electrones

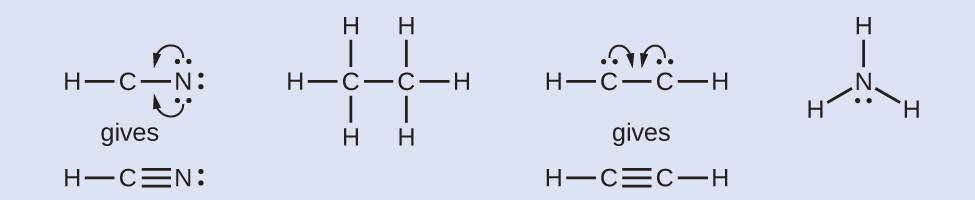
Comprueba tu aprendizaje

Excepciones a la regla del octeto

Muchas moléculas covalentes tienen átomos centrales que no tienen ocho electrones en sus estructuras de Lewis. Estas moléculas se dividen en tres categorías:

• Las moléculas de electrones impares tienen un número impar de electrones de valencia y, por lo tanto, tienen un electrón no apareado.
• Las moléculas deficientes en electrones tienen un átomo central que tiene menos electrones que los necesarios para una configuración de gas noble.
• Las moléculas hipervalentes tienen un átomo central que tiene más electrones de los necesarios para una configuración de gas noble.

Moléculas de electrones impares

Llamamos moléculas que contienen un número impar de electrones: radicales libres. El óxido nítrico, $NO$, es un ejemplo de una molécula de electrones impares; Se produce en motores de combustión interna cuando el oxígeno y el nitrógeno reaccionan a altas temperaturas.

Para dibujar la estructura de Lewis para una molécula de electrones impares como $NO$, seguimos los mismos cinco pasos que seguiríamos para otras moléculas, pero con algunos cambios menores:

1. Determina el número total de electrones de valencia (capa externa). La suma de los electrones de valencia es 5 (de $N$) + 6 (de $O$) = 11. El número impar nos dice de inmediato que tenemos un radical libre, por lo que sabemos que no todos los átomos pueden tener ocho electrones en su capa de valencia.
2. Dibuja una estructura esquelética de la molécula. Podemos dibujar fácilmente un esqueleto con un enlace simple $\ce{N – O}$.
3. Distribuye los electrones restantes como pares solitarios en los átomos terminales. En este caso, no hay un átomo central, por lo que distribuimos los electrones alrededor de ambos átomos. Le damos ocho electrones al átomo más electronegativo en estas situaciones; así el oxígeno tiene la capa de valencia llena:
   

   

4. Coloca todos los electrones restantes en el átomo central. Como no quedan electrones restantes, este paso no se aplica.
5. Reorganiza los electrones para formar enlaces múltiples con el átomo central para obtener octetos siempre que sea posible. Sabemos que una molécula de electrones impares no puede tener un octeto para cada átomo, pero queremos que cada átomo esté lo más cerca posible de un octeto. En este caso, el nitrógeno tiene solo cinco electrones a su alrededor. Para acercarnos a un octeto de nitrógeno, tomamos uno de los pares solitarios del oxígeno y lo usamos para formar un doble enlace $NO$ (No podemos tomar otro par de electrones solitarios en oxígeno y formar un triple enlace porque el nitrógeno tendría nueve electrones):

Moléculas deficientes en electrones

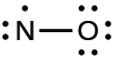
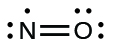
También encontraremos algunas moléculas que contienen átomos centrales que no tienen una capa de valencia llena. En general, se trata de moléculas con átomos centrales de los grupos 2 y 13, átomos externos que son hidrógeno u otros átomos que no forman enlaces múltiples. Por ejemplo, en las estructuras de Lewis del dihidruro de berilio, $BeH_2$ y el trifluoruro de boro, $BF_3$, los átomos de berilio y boro tienen cada uno solo cuatro y seis electrones, respectivamente. Es posible dibujar una estructura con un doble enlace entre un átomo de boro y un átomo de flúor en $BF_3$, satisfaciendo la regla del octeto, pero la evidencia experimental indica que las longitudes de los enlaces están más cerca de lo esperado para los enlaces simples $\ce{B - F}$. Esto sugiere que la mejor estructura de Lewis tiene tres enlaces simples $\ce{B – F}$ y un boro deficiente en electrones. La reactividad del compuesto también es consistente con un boro deficiente en electrones. Sin embargo, los enlaces $\ce{B – F}$ son ligeramente más cortos de lo que se espera realmente para los enlaces simples $\ce{B – F}$, lo que indica que se encuentra algún carácter de doble enlace en la molécula real.

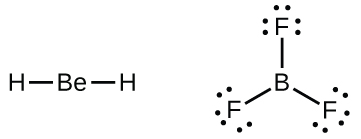
Un átomo como el átomo de boro en $BF_3$, que no tiene ocho electrones, es muy reactivo. Se combina fácilmente con una molécula que contiene un átomo con un par solitario de electrones. Por ejemplo, $NH_3$ reacciona con $BF_3$ porque el único par de nitrógeno se puede compartir con el átomo de boro:

Moléculas Hipervalentes

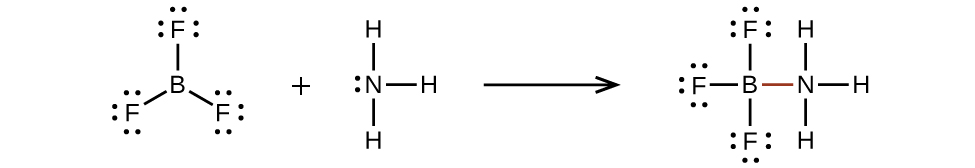
Los elementos en el segundo período de la tabla periódica (n = 2) pueden acomodar solo ocho electrones en sus orbitales de capa de valencia porque tienen solo cuatro orbitales de valencia (un 2s y tres orbitales 2p). Los elementos en el tercer y más períodos (n ≥ 3) tienen más de cuatro orbitales de valencia y pueden compartir más de cuatro pares de electrones con otros átomos porque tienen d orbitales vacíos en la misma capa. Las moléculas formadas a partir de estos elementos a veces se llaman moléculas hipervalentes. La figura 7.12 muestra las estructuras de Lewis para dos moléculas hipervalentes, $PCl_5$ y $SF_6$.

Figura 7.12. En $PCl_5$, el átomo de fósforo central comparte cinco pares de electrones. En $SF_6$, el azufre comparte seis pares de electrones.

Cuando escribimos las estructuras de Lewis para estas moléculas, encontramos que nos sobran electrones después de llenar las capas de valencia de los átomos externos con ocho electrones. Estos electrones adicionales deben asignarse al átomo central.

Usando el aplicativo CheDoodle, presentamos las dos moléculas anteriores:

Ejemplo 7.5

Escribir estructuras de Lewis: violaciones de reglas del octeto

El xenón es un gas noble, pero forma una serie de compuestos estables. Examinamos $XeF_4$ anteriormente. ¿Cuáles son las estructuras de Lewis de $XeF_2$ y $XeF_6$?

Solución

Podemos dibujar la estructura de Lewis de cualquier molécula covalente siguiendo los seis pasos discutidos anteriormente.

En este caso, podemos condensar los últimos pasos, ya que no todos se aplican.

Paso 1. Calcula el número de electrones de valencia:

$XeF_2$: 8 + (2 × 7) = 22
$XeF_6$: 8 + (6 × 7) = 50

Paso 2. Dibuja un esqueleto uniendo los átomos por enlaces simples. El xenón será el átomo central porque el flúor no puede ser un átomo central:

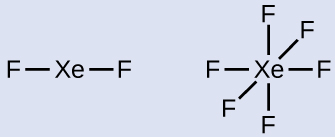
Paso 3. Distribuye los electrones restantes.

$XeF_2$: colocamos tres pares de electrones solitarios alrededor de cada átomo de $F$, contabilizando 12 electrones y dando a cada átomo de $F$ 8 electrones. Por lo tanto, quedan seis electrones (tres pares solitarios). Estos pares solitarios deben colocarse en el átomo $Xe$. Esto es aceptable porque los átomos $Xe$ tienen una capa de valencia d vacía y pueden acomodar más de ocho electrones. La estructura de Lewis de $XeF_2$ muestra dos pares de enlaces y tres pares de electrones solitarios alrededor del átomo de $Xe$:

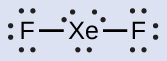
$XeF_6$: colocamos tres pares de electrones solitarios alrededor de cada átomo de $F$, lo que representa 36 electrones. Quedan dos electrones, y este par solitario se coloca en el átomo $Xe$:

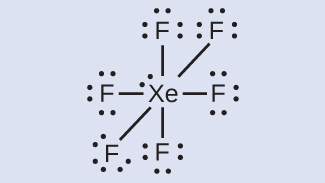
Comprueba tu aprendizaje

Cargas formales y resonancia

En la sección anterior, discutimos cómo escribir estructuras de Lewis para moléculas e iones poliatómicos. Como hemos visto, sin embargo, en algunos casos, aparentemente hay más de una estructura válida para una molécula. Podemos usar el concepto de cargas formales para ayudarnos a predecir la estructura de Lewis más apropiada cuando más de una es razonable.

Cálculo de la carga formal

La carga formal de un átomo en una molécula es la carga hipotética que tendría el átomo si pudiéramos redistribuir los electrones en los enlaces de manera uniforme entre los átomos. Otra forma de decir esto es que la carga formal resulta cuando tomamos la cantidad de electrones de valencia de un átomo neutro, restamos los electrones no enlazantes y luego resta la cantidad de enlaces conectados a ese átomo en la estructura de Lewis.

Por lo tanto, calculamos la carga formal de la siguiente manera:

carga formal = # electrones de capa de valencia (átomo libre) - # electrones de par solitario − 1/2 # electrones de enlace

Podemos verificar los cálculos de cargas formales determinando la suma de las cargas formales para toda la estructura. La suma de las cargas formales de todos los átomos en una molécula debe ser cero; La suma de las cargas formales en un ion debe ser igual a la carga del ion.

Debemos recordar que la carga formal calculada para un átomo no es la carga real del átomo en la molécula.

La carga formal es solo un procedimiento útil de contabilidad; No indica la presencia de cargas reales.

Ejemplo 7.6

Cálculo de la carga formal a partir de estructuras de Lewis

Asigna cargas formales a cada átomo en el ion interhalógeno $ICl_4^{−}$.

Solución

Paso 1. Dividimos los pares de electrones de enlace por igual para todos los enlaces $\ce{I – Cl}$:

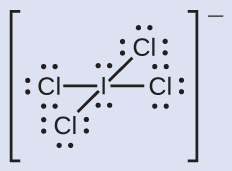
Paso 2. Asignamos pares solitarios de electrones a sus átomos. Cada átomo de $Cl$ ahora tiene siete electrones asignados, y el átomo $I$ tiene ocho.

Paso 3. Resta este número del número de electrones de valencia para el átomo neutro:

$I:$ 7 - 8 = –1
$Cl:$ 7 - 7 = 0

La suma de las cargas formales de todos los átomos es igual a –1, que es idéntica a la carga del ion (–1).

Comprueba tu aprendizaje

Ejemplo 7.7

Cálculo de la carga formal a partir de estructuras de Lewis

Asigna cargas formales a cada átomo en la molécula interhalógena $BrCl_3$.

Solución

Paso 1. Asigna uno de los electrones en cada enlace $\ce{Br – Cl}$ al átomo $Br$ y uno al átomo $Cl$ en ese enlace:

Paso 2. Asigna los pares solitarios a su átomo. Ahora cada átomo de $Cl$ tiene siete electrones y el átomo de $Br$ tiene siete electrones.

Paso 3. Resta este número del número de electrones de valencia para el átomo neutro. Esto te da la carga formal:

$Br:$ 7 - 7 = 0
$Cl:$ 7 - 7 = 0

Comprueba tu aprendizaje

Uso de la carga formal para predecir la estructura molecular

La disposición de los átomos en una molécula o ion se llama estructura molecular. En muchos casos, seguir los pasos para escribir estructuras de Lewis puede conducir a más de una posible estructura molecular: diferentes enlaces múltiples y colocaciones de electrones de par solitario o diferentes disposiciones de átomos, por ejemplo. Algunas pautas relacionadas con la carga formal pueden ser útiles para decidir cuál de las posibles estructuras es más probable para una molécula o ion particular:

1. Una estructura molecular en la que todas las cargas formales son cero es preferible a una en la que algunas cargas formales no son cero.
2. Si la estructura de Lewis debe tener cargas formales distintas de cero, es preferible el arreglo con las cargas formales distintas de cero.
3. Las estructuras de Lewis son preferibles cuando las cargas formales adyacentes son cero o del signo opuesto.
4. Cuando debemos elegir entre varias estructuras de Lewis con distribuciones similares de cargas formales, es preferible la estructura con las cargas formales negativas en los átomos más electronegativos.

Para ver cómo se aplican estas pautas, consideremos algunas estructuras posibles para el dióxido de carbono, $CO_2$. Sabemos por nuestra discusión previa que el átomo menos electronegativo generalmente ocupa la posición central, pero las cargas formales nos permiten entender por qué ocurre esto.

Podemos dibujar tres posibilidades para la estructura: carbono en el centro y enlaces dobles, carbono en el centro con un enlace simple y triple, y oxígeno en el centro con enlaces dobles:

Comparando las tres cargas formales, podemos identificar definitivamente la estructura de la izquierda como preferible porque solo tiene cargas formales de cero (Directriz 1).

Como otro ejemplo, el ion tiocianato, un ion formado a partir de un átomo de carbono, un átomo de nitrógeno y un átomo de azufre, podría tener tres estructuras moleculares diferentes: $NCS^{–}$, $CNS^{–}$ o $CSN^{–}$. Las cargas formales presentes en cada una de estas estructuras moleculares pueden ayudarnos a elegir la disposición más probable de los átomos. Las posibles estructuras de Lewis y las cargas formales para cada una de las tres estructuras posibles para el ion tiocianato se muestran aquí:

Observa que la suma de las cargas formales en cada caso es igual a la carga del ion (–1). Sin embargo, se prefiere la primera disposición de los átomos porque tiene el menor número de átomos con cargas formales distintas de cero (Directriz 2). Además, coloca el átomo menos electronegativo en el centro y la carga negativa en el elemento más electronegativo (Directriz 4).

Ejemplo 7.8

Uso de la carga formal para determinar la estructura molecular

El óxido nitroso, $N_2O$, comúnmente conocido como gas hilarante, se usa como anestésico en cirugías menores, como la extracción rutinaria de muelas del juicio. ¿Cuál es la estructura probable para el óxido nitroso?

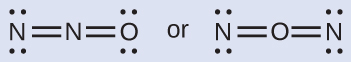
Solución

La determinación de la carga formal produce lo siguiente:

La estructura con un átomo de oxígeno terminal satisface mejor los criterios para la distribución más estable de la carga formal:

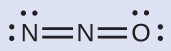
El número de átomos con cargas formales se minimiza (Directriz 2), y no hay carga formal mayor que uno (Directriz 2). Esto es de nuevo consistente con la preferencia por tener el átomo menos electronegativo en la posición central.

Comprueba tu aprendizaje

Resonancia

Es posible que hayas notado que el anión nitrito en el Ejemplo 7.8 puede tener dos estructuras posibles con los átomos en las mismas posiciones. Los electrones involucrados en el doble enlace $\ce{N – O}$, sin embargo, están en diferentes posiciones:

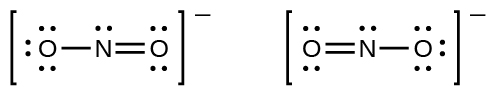
Si los iones nitrito contienen un enlace simple y uno doble, esperaríamos que las dos longitudes de enlace sean diferentes. Un enlace doble entre dos átomos es más corto (y más fuerte) que un enlace simple entre los mismos dos átomos.

Sin embargo, los experimentos muestran que ambos enlaces $\ce{N – O}$ en $NO_2^{−}$ tienen la misma fuerza y ​​longitud, y son idénticos en todas las demás propiedades.

No es posible escribir una sola estructura de Lewis para $NO_2^{−}$ en la que el nitrógeno tenga un octeto y ambos enlaces sean equivalentes. En su lugar, utilizamos el concepto de resonancia: si dos o más estructuras de Lewis con la misma disposición de átomos pueden escribirse para una molécula o ion, la distribución real de electrones es un promedio de la que muestran las diversas estructuras de Lewis. La distribución real de electrones en cada uno de los enlaces nitrógeno-oxígeno en $NO_2^{−}$ es el promedio de un enlace doble y un enlace simple. Llamamos a las estructuras individuales de Lewis formas de resonancia. La estructura electrónica real de la molécula (el promedio de las formas de resonancia) se llama un híbrido de resonancia de las formas de resonancia individuales. Una flecha de dos puntas entre las estructuras de Lewis indica que son formas de resonancia. Por lo tanto, la estructura electrónica del ion $NO_2^{−}$ se muestra como:

Debemos recordar que una molécula descrita como un híbrido de resonancia nunca posee una estructura electrónica descrita por cualquiera de las formas de resonancia. No fluctúa entre las formas de resonancia; más bien, la estructura electrónica real es siempre la media de la que muestran todas las formas de resonancia.

George Wheland, uno de los pioneros de la teoría de la resonancia, utilizó una analogía histórica para describir la relación entre las formas de resonancia y los híbridos de resonancia. Un viajero medieval, que nunca antes había visto un rinoceronte, lo describió como un híbrido de un dragón y un unicornio porque tenía muchas propiedades en común con ambos. Así como un rinoceronte no es un dragón a veces ni un unicornio en otras ocasiones, un híbrido de resonancia no es ninguna de sus formas de resonancia en un momento dado. Como un rinoceronte, es una entidad real que la evidencia experimental ha demostrado que existe. Tiene algunas características en común con sus formas de resonancia, pero las formas de resonancia son imágenes convenientes e imaginarias (como el unicornio y el dragón).

El anión carbonato, $CO_3^{2−}$, proporciona un segundo ejemplo de resonancia:

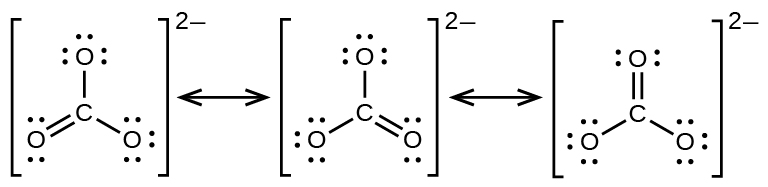
Un átomo de oxígeno debe tener un doble enlace con el carbono para completar el octeto en el átomo central. Sin embargo, todos los átomos de oxígeno son equivalentes, y el doble enlace podría formarse a partir de cualquiera de los tres átomos. Esto da lugar a tres formas de resonancia del ion carbonato. Como podemos escribir tres estructuras de resonancia idénticas, sabemos que la disposición real de los electrones en el ion carbonato es el promedio de las tres estructuras. Una vez más, los experimentos muestran que los tres enlaces $\ce{C – O}$ son exactamente iguales.

Para terminar este apartado, te presentamos la molécula del anión carbonato:

Fortalezas de los enlaces iónicos y covalentes

La fuerza de un enlace describe la fuerza con la que cada átomo se une a otro átomo y, por lo tanto, cuánta energía se requiere para romper el enlace entre los dos átomos. En esta sección, aprenderás sobre la fuerza de enlace de los enlaces covalentes, y luego la compararás con la fuerza de los enlaces iónicos, que está relacionada con la energía reticular de un compuesto.

Fuerza de enlace: enlaces covalentes

Existen moléculas estables porque los enlaces covalentes mantienen unidos a los átomos. Medimos la fuerza de un enlace covalente por la energía requerida para romperlo, es decir, la energía necesaria para separar los átomos unidos. Separar cualquier par de átomos unidos requiere energía (ver figura 7.4). Cuanto más fuerte es un vínculo, mayor es la energía requerida para romperlo.

La energía requerida para romper un enlace covalente específico en un mol de moléculas gaseosas se llama energía de enlace o energía de disociación de enlace. La energía de enlace para una molécula diatómica, $\ce{DX-Y}$, se define como el cambio de la entalpía estándar para la reacción endotérmica:

Por ejemplo, la energía de enlace del enlace $\ce{H - H}$ covalente puro, $\ce{DH - H}$, es 436 kJ por mol de enlaces $\ce{H-H}$ rotos:

Las moléculas con tres o más átomos tienen dos o más enlaces. La suma de todas las energías de enlace en dicha molécula es igual al cambio de la entalpía estándar para la reacción endotérmica que rompe todos los enlaces en la molécula. Por ejemplo, la suma de las cuatro energías de enlace $\ce{C – H}$ en $CH_4$, 1660 kJ, es igual al cambio de la entalpía estándar de la reacción:

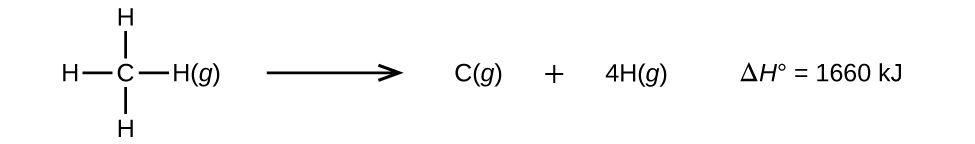
La energía de enlace $\ce{C – H}$ promedio, $\ce{DC – H}$, es $1660/4 = 415\; \pu{kJ//mol}$ porque hay cuatro moles de enlaces $\ce{C – H}$ rotos por mol de la reacción. Aunque los cuatro enlaces $\ce{C – H}$ son equivalentes en la molécula original, no requieren la misma energía para romperse; una vez que se rompe el primer enlace (que requiere $\pu{439 kJ//mol}$), los enlaces restantes son más fáciles de romper. El valor de $\pu{415 kJ//mol}$ es el promedio, no el valor exacto requerido para romper cualquier enlace.

La fuerza de un enlace entre dos átomos aumenta a medida que aumenta el número de pares de electrones en el enlace. Generalmente, a medida que aumenta la resistencia de la unión, la longitud de la unión disminuye. Por lo tanto, encontramos que los enlaces triples son más fuertes y más cortos que los enlaces dobles entre los mismos dos átomos; asimismo, los enlaces dobles son más fuertes y más cortos que los enlaces simples entre los mismos dos átomos. Las energías de enlace promedio para algunos enlaces comunes aparecen en la tabla 7.2, y una comparación de longitudes de enlace y fuerzas de enlace para algunos enlaces comunes aparece en la tabla 7.3.

Cuando un átomo se une a varios átomos en un grupo, la fuerza del enlace generalmente disminuye a medida que avanzamos hacia abajo del grupo. Por ejemplo, $\ce{C – F}$ es $\pu{439 kJ//mol}$, $\ce{C – Cl}$ es $\pu{330 kJ//mol}$ y $\ce{C – Br}$ es $\pu{275 kJ//mol}$.

Tabla 7.2. Energías de enlace

Podemos usar energías de enlace para calcular los cambios aproximados de entalpía para reacciones en las que las entalpías de formación no están disponibles. Los cálculos de este tipo también nos dirán si una reacción es exotérmica o endotérmica. Se produce una reacción exotérmica ($\Delta H$ negativa, producida por calor) cuando los enlaces en los productos son más fuertes que los enlaces en los reactivos. Se produce una reacción endotérmica ($\Delta H$ positiva, absorbida por calor) cuando los enlaces en los productos son más débiles que los de los reactivos.

Tabla 7.3. Promedio de longitudes y energías de enlace para algunos enlaces comunes

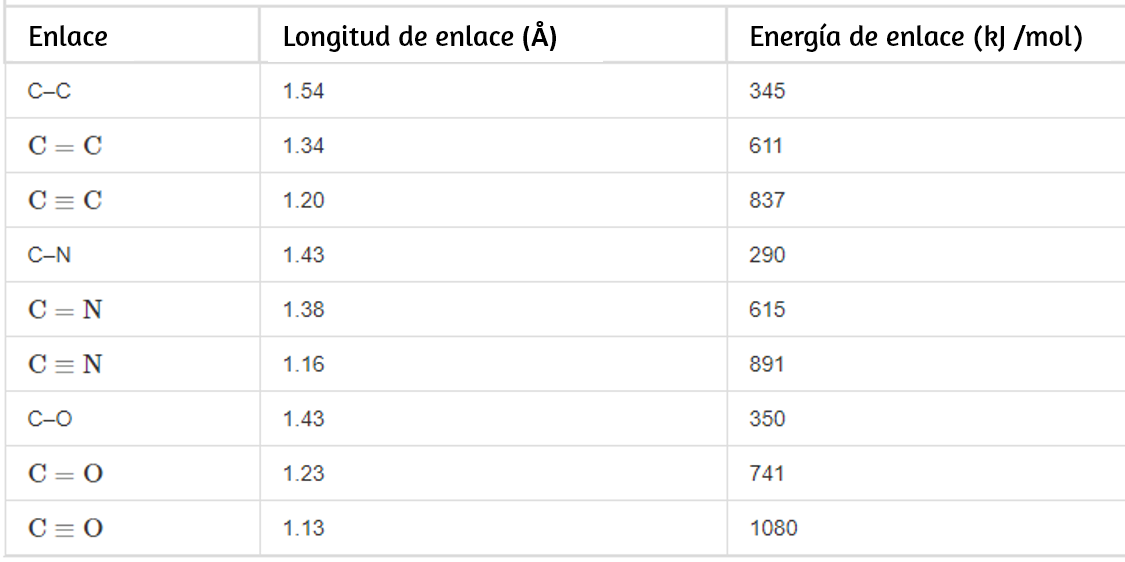
El cambio de entalpía, $\Delta H$, para una reacción química es aproximadamente igual a la suma de la energía requerida para romper todos los enlaces en los reactivos (energía "en", signo positivo) más la energía liberada cuando se forman todos los enlaces en los productos (energía "Fuera", signo negativo). Esto se puede expresar matemáticamente de la siguiente manera:

En esta expresión, el símbolo $\sum$ significa "la suma de" y D representa la energía de enlace en kilojulios por mol, que siempre es un número positivo. La energía del enlace se obtiene de una tabla (como la tabla 7.3) y dependerá de si el enlace particular es un enlace simple, doble o triple. Por lo tanto, al calcular las entalpías de esta manera, es importante que consideremos la unión en todos los reactivos y productos.

Debido a que los valores D suelen ser promedios para un tipo de enlace en muchas moléculas diferentes, este cálculo proporciona una estimación aproximada, no un valor exacto, para la entalpía de reacción.

Considere la siguiente reacción:

o

Para formar dos moles de $HCl$, se deben romper un mol de enlaces $\ce{H – H}$ y un mol de enlaces $\ce{Cl – Cl}$. La energía requerida para romper estos enlaces es la suma de la energía de enlace del enlace $\ce{H – H}$ ($\pu{436 kJ//mol}$) y el enlace $\ce{Cl – Cl}$ ($\pu{243 kJ//mol}$). Durante la reacción, se forman dos moles de enlaces $\ce{H – Cl}$ (energía de enlace = $\pu{432 kJ // mol}$), liberando 2 × 432 kJ; o 864 kJ. Debido a que los enlaces en los productos son más fuertes que los de los reactivos, la reacción libera más energía de la que consume:

Este exceso de energía se libera como calor, por lo que la reacción es exotérmica. El Apéndice B da un valor para la entalpía molar estándar de formación de $HCl (g)$, $\Delta H_f^{\degree}$, de $\pu{–92.307 kJ // mol}$. Dos veces ese valor es –184,6 kJ, lo que concuerda bien con la respuesta obtenida anteriormente para la formación de dos moles de $HCl$.

Ejemplo 7.9

Uso de energías de enlace para calcular los cambios aproximados de la entalpía

El metanol, $CH_3OH$, puede ser un excelente combustible alternativo. La reacción a alta temperatura de vapor y carbono produce una mezcla de los gases monóxido de carbono, $CO$ e hidrógeno, $H_2$, a partir de los cuales se puede producir metanol. Usando las energías de enlace en la tabla 7.3, calcula el cambio de entalpía aproximado, $\Delta H$, para la reacción:

Solución

Primero, necesitamos escribir las estructuras de Lewis de los reactivos y los productos:

A partir de esto, vemos que $\Delta H$ para esta reacción involucra la energía requerida para romper un triple enlace $\ce{C – O}$ y dos enlaces simples $\ce{H – H}$, así como la energía producida por la formación de tres enlaces simples $\ce{C – H}$, un $\ce{C – O}$ enlace sencillo y $\ce{O - H}$ enlace sencillo. Podemos expresar esto de la siguiente manera:

Usando los valores de energía de enlace en la tabla 7.3, obtenemos:

Podemos comparar este valor con el valor calculado en base a los datos $\Delta H^o_f$ del Apéndice B:

Observa que existe una brecha significativa entre los valores calculados utilizando dos métodos diferentes. Esto ocurre porque los valores de D son el promedio de diferentes fuerzas de unión; por lo tanto, a menudo dan un acuerdo aproximado con otros datos.

Comprueba tu aprendizaje

El alcohol etílico, $CH_3CH_2OH$, fue uno de los primeros químicos orgánicos sintetizados deliberadamente por los humanos. Tiene muchos usos en la industria, y es el alcohol contenido en las bebidas alcohólicas. Puede obtenerse por fermentación de azúcar o sintetizarse por hidratación de etileno en la siguiente reacción:

Usando las energías de enlace en la tabla 7.3, calcula un cambio de entalpía aproximado, $\Delta H$, para esta reacción.

Fuerza de enlace iónico y energía reticular

Un compuesto iónico es estable debido a la atracción electrostática entre sus iones positivos y negativos. La energía reticular de un compuesto es una medida de la fuerza de esta atracción. La energía de reticular ($\Delta H_{\text{reticular}}$) de un compuesto iónico se define como la energía requerida para separar un mol del sólido en sus iones gaseosos. Para el $MX$ iónico sólido, la energía reticular es el cambio de entalpía del proceso:

Observa que estamos utilizando la convención donde el sólido iónico se separa en iones, por lo que nuestras energías reticulares serán endotérmicas (valores positivos). Algunos textos usan la convención equivalente pero opuesta, que define la energía reticular como la energía liberada cuando los iones separados se combinan para formar una red y dan valores negativos (exotérmicos). Por lo tanto, si estás buscando energías reticulares en otra referencia, asegúrate de verificar qué definición se está utilizando. En ambos casos, una magnitud mayor para la energía reticular indica un compuesto iónico más estable. Para cloruro de sodio, $\Delta H_{\text{reticular}} = 769 kJ$. Por lo tanto, requiere 769 kJ para separar un mol de $NaCl$ sólido en iones de $Na^+$ y $Cl^{–}$ gaseosos.

Cuando un mol de cada uno de los iones gaseosos de $Na^+$ y $Cl^{–}$ forma $NaCl$ sólido, se liberan 769 kJ de calor.

La energía de la red $\Delta H_{\text{reticular}}$ de un cristal iónico se puede expresar mediante la siguiente ecuación (derivada de la ley de Coulomb, que rige las fuerzas entre las cargas eléctricas):

en el que C es una constante que depende del tipo de estructura cristalina; $Z^+$ y $Z^–$ son las cargas de los iones; y $R_o$ es la distancia interiónica (la suma de los radios de los iones positivos y negativos). Por lo tanto, la energía reticular de un cristal iónico aumenta rápidamente a medida que aumentan las cargas de los iones y disminuyen los tamaños de los iones. Cuando todos los demás parámetros se mantienen constantes, duplicar la carga tanto del catión como del anión cuadruplica la energía de la red. Por ejemplo, la energía reticular de $LiF$ ($Z^+$ y $Z^{–} = 1$) es 1023 kJ/mol, mientras que la de $MgO$ ($Z^+$ y $Z^–$ = 2) es 3900 kJ/mol ($R_o $es casi la misma, alrededor de 200 pm para ambos compuestos).

Diferentes distancias interatómicas producen diferentes energías reticulares. Por ejemplo, podemos comparar la energía de la red de $MgF_2 \;(2957\: kJ/mol)$ con la de $MgI_2\; (2327\; kJ/mol)$ para observar el efecto sobre la energía reticular del tamaño iónico más pequeño de $F^{–}$ en comparación con $I^{–}$.

Ejemplo 7.10

Comparaciones de energía reticular

La preciosa gema rubí es el óxido de aluminio, $Al_2O_3$, que contiene trazas de $Cr^{3+}$. El compuesto $Al_2Se_3$ se usa en la fabricación de algunos dispositivos semiconductores. ¿Cuál tiene la energía reticular más grande, $Al_2O_3$ o $Al_2Se_3$?

Solución

En estos dos compuestos iónicos, las cargas $Z^+$ y $Z^{–}$ son las mismas, por lo que la diferencia en la energía reticular dependerá de $R_o$. El el ion $O_2$ es más pequeño que el ion $Se_2$. Por lo tanto, $Al_2O_3$ tendría una distancia interiónica más corta que $Al_2Se_3$, y $Al_2O_3$ tendría la energía reticular más grande.

Comprueba tu aprendizaje

El ciclo de Born-Haber

No es posible medir las energías reticulares directamente. Sin embargo, la energía reticular se puede calcular usando la ecuación dada en la sección anterior o usando un ciclo termoquímico. El ciclo de Born-Haber es una aplicación de la ley de Hess que descompone la formación de un sólido iónico en una serie de pasos individuales:

• $\Delta H^o_f$, la entalpía estándar de formación del compuesto
• IE, la energía de ionización del metal EA, la afinidad electrónica del no metal
• $\Delta H^o_s$, la entalpía de sublimación del metal D, la energía de disociación de enlace del no metal $\Delta H_{\text{reticular}}$, la energía reticular del compuesto

La figura 7.13 muestra el ciclo de Born-Haber para la formación de fluoruro de cesio sólido.

Comenzamos con los elementos en sus estados más comunes, $Cs (s)$ y $F_2 (g)$. El $\Delta H^o_s$ representa la conversión de cesio sólido en un gas, y luego la energía de ionización convierte los átomos de cesio gaseoso en cationes. En el siguiente paso, tenemos en cuenta la energía requerida para romper el enlace $\ce{F – F}$ para producir átomos de flúor. La conversión de un mol de átomos de flúor en iones fluoruro es un proceso exotérmico, por lo que este paso emite energía (la afinidad electrónica) y se muestra como decreciente a lo largo del eje y. Ahora tenemos un mol de cationes $Cs$ y un mol de aniones $F$. Estos iones se combinan para producir fluoruro de cesio sólido. El cambio de entalpía en este paso es el negativo de la energía reticular, por lo que también es una cantidad exotérmica.

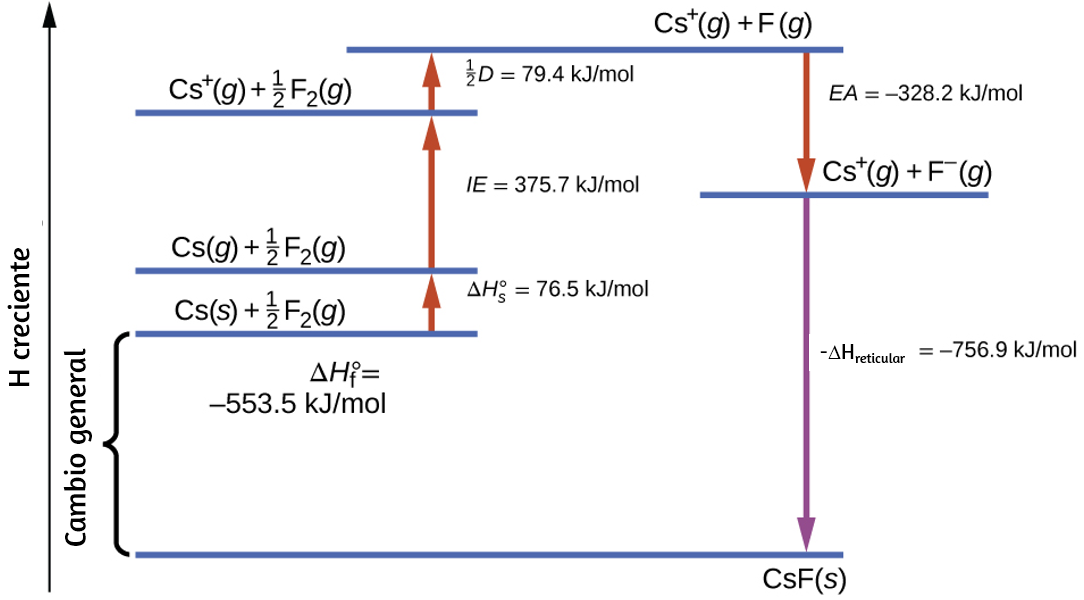
Figura 7.13. El ciclo de Born-Haber muestra las energías relativas de cada paso involucrado en la formación de un sólido iónico a partir de los elementos necesarios en sus estados de referencia.

La energía total involucrada en esta conversión es igual a la entalpía de formación determinada experimentalmente, $\Delta H^o_f$, del compuesto a partir de sus elementos. En este caso, el cambio general es exotérmico.

La ley de Hess también se puede utilizar para mostrar la relación entre las entalpías de los pasos individuales y la entalpía de la formación. La tabla 7.4 muestra esto para fluoruro, $CsF$.

Por lo tanto, la energía reticular se puede calcular a partir de otros valores. Para el fluoruro de cesio, utilizando los datos de la tabla, la energía reticular es:

Tabla 7.4. Relación entre las entalpías de los pasos individuales y la entalpía de formación

El ciclo de Born-Haber también se puede usar para calcular cualquiera de las otras cantidades en la ecuación para la energía reticular, siempre que se conozca el resto. Por ejemplo, si se conoce la entalpía relevante de sublimación $\Delta H^o_s$, la energía de ionización (IE), la entalpía de disociación de enlace (D), la energía reticular $\Delta H_{\text{reticular}}$ y la entalpía estándar de formación $\Delta H^o_f$, se puede utilizar el ciclo de Born-Haber para determinar la afinidad electrónica de un átomo.

Las energías reticulares calculadas para compuestos iónicos son típicamente mucho más altas que las energías de disociación de enlaces medidas para enlaces covalentes. Mientras que las energías reticulares generalmente caen en el rango de 600–4000 kJ/mol (algunas incluso más altas), las energías de disociación de enlaces covalentes están típicamente entre 150–400 kJ/mol para enlaces simples. Sin embargo, ten en cuenta que estos no son valores directamente comparables. Para los compuestos iónicos, las energías reticulares están asociadas con muchas interacciones, ya que los cationes y los aniones se agrupan en una red extendida. Para enlaces covalentes, la energía de disociación de enlaces está asociada con la interacción de solo dos átomos.

Estructura molecular y polaridad

Hasta ahora, hemos utilizado estructuras de Lewis bidimensionales para representar moléculas. Sin embargo, la estructura molecular es en realidad tridimensional, y es importante poder describir los enlaces moleculares en términos de sus distancias, ángulos y disposiciones relativas en el espacio (figura 7.14). Un ángulo de enlace es el ángulo entre dos enlaces que incluyen un átomo común, generalmente medido en grados. Una distancia de enlace (o longitud de enlace) es la distancia entre los núcleos de dos átomos unidos a lo largo de la línea recta que une los núcleos. Las distancias de enlace se miden en Ångstroms ($1 \; \text{\AA} = 10^{–10} \; m$) o picómetros ($1\; pm = 10^{–12}\; m, \;100\; pm = 1\; \text{\AA}$).

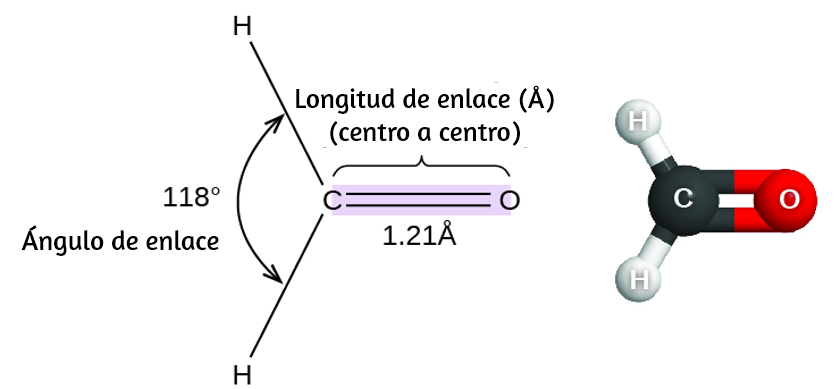
Figura 7.14. Las distancias de enlace (longitudes) y los ángulos se muestran para la molécula de formaldehído, $H_2CO$.

Teoría VSEPR

La teoría de la repulsión del par de electrones de la capa de valencia (teoría VSEPR, por sus siglas en inglés) nos permite predecir la estructura molecular, incluidos los ángulos de enlace aproximados alrededor de un átomo central, de una molécula a partir de un examen del número de enlaces y pares de electrones solitarios en su estructura de Lewis. El modelo VSEPR supone que los pares de electrones en la capa de valencia de un átomo central adoptarán una disposición que minimice las repulsiones entre estos pares de electrones al maximizar la distancia entre ellos. Los electrones en la capa de valencia de un átomo central forman pares de electrones de enlace, ubicados principalmente entre átomos unidos, o pares solitarios. La repulsión electrostática de estos electrones se reduce cuando las diversas regiones de alta densidad electrónica asumen posiciones lo más alejadas posible.

La teoría VSEPR predice la disposición de los pares de electrones alrededor de cada átomo central y, por lo general, la disposición correcta de los átomos en una molécula. Sin embargo, debemos entender que la teoría solo considera las repulsiones de pares de electrones. Otras interacciones, como las repulsiones nuclear-nucleares y las atracciones de electrones nucleares, también están involucradas en la disposición final que los átomos adoptan en una estructura molecular particular.

Como un simple ejemplo de la teoría VSEPR, pronostiquemos la estructura de una molécula gaseosa de $BeF_2$. La estructura de Lewis de $BeF_2$ (Figura 7.15) muestra solo dos pares de electrones alrededor del átomo central de berilio. Con dos enlaces y sin pares solitarios de electrones en el átomo central, los enlaces están lo más separados posible, y la repulsión electrostática entre estas regiones de alta densidad electrónica se reduce al mínimo cuando están en lados opuestos del átomo central. El ángulo de enlace es de 180° (Figura 7.15).

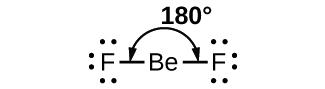
Figura 7.15. La molécula $BeF_2$ adopta una estructura lineal en la que los dos enlaces están lo más separados posible, en lados opuestos del átomo $Be$.

La figura 7.16 ilustra esta y otras geometrías de pares de electrones que minimizan las repulsiones entre regiones de alta densidad de electrones (enlaces y/o pares solitarios).

Dos regiones de densidad electrónica alrededor de un átomo central en una molécula forman una geometría lineal; tres regiones forman una geometría plana trigonal; cuatro regiones forman una geometría tetraédrica; cinco regiones forman una geometría bipiramidal trigonal; y seis regiones forman una geometría octaédrica.

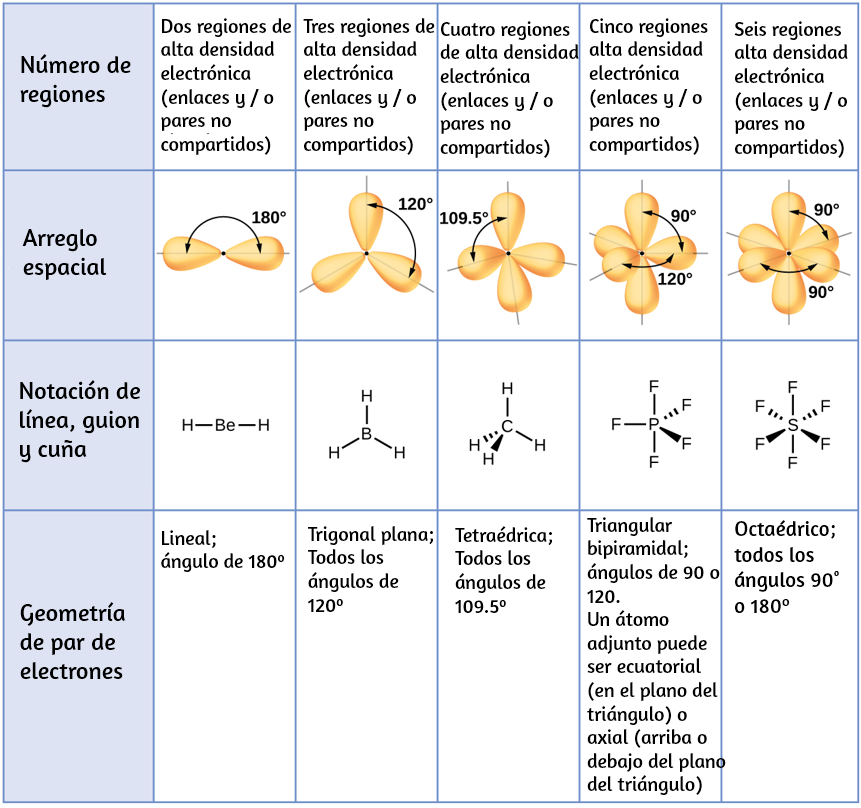
Figura 7.16. Las geometrías básicas de pares de electrones predichas por la teoría VSEPR maximizan el espacio alrededor de cualquier región de densidad de electrones (enlaces o pares solitarios).

Geometría de pares de electrones versus estructura molecular

Es importante tener en cuenta que la geometría de pares de electrones alrededor de un átomo central no es lo mismo que su estructura molecular. Las geometrías de pares de electrones que se muestran en la figura 7.16 describen todas las regiones donde se encuentran los electrones, los enlaces y los pares solitarios. La estructura molecular describe la ubicación de los átomos, no de los electrones.

Diferenciamos entre estas dos situaciones nombrando la geometría que incluye todos los pares de electrones, la geometría de pares de electrones. La estructura que incluye solo la colocación de los átomos en la molécula se llama estructura molecular. Las geometrías de los pares de electrones serán las mismas que las estructuras moleculares cuando no haya pares de electrones solitarios alrededor del átomo central, pero serán diferentes cuando haya pares solitarios presentes en el átomo central.

Por ejemplo, la molécula de metano, $CH_4$, que es el componente principal del gas natural, tiene cuatro pares de electrones de enlace alrededor del átomo de carbono central; La geometría del par de electrones es tetraédrica, al igual que la estructura molecular (Figura 7.17). Por otro lado, la molécula de amoníaco, $NH_3$, también tiene cuatro pares de electrones asociados con el átomo de nitrógeno, y por lo tanto tiene una geometría tetraédrica de pares de electrones. Sin embargo, una de estas regiones es un par solitario, que no está incluido en la estructura molecular, y este par solitario influye en la forma de la molécula (Figura 7.18).

Figura 7.17. La estructura molecular de la molécula de metano, $CH_4$, se muestra con una disposición tetraédrica de los átomos de hidrógeno. Las estructuras VSEPR como esta a menudo se dibujan utilizando la notación de cuña y guión, en la que las líneas continuas representan enlaces en el plano de la página, las cuñas sólidas representan enlaces que salen del plano y las líneas discontinuas representan enlaces que bajan al plano.

Figura 7.18. (a) La geometría del par de electrones para la molécula de amoníaco es tetraédrica con un par solitario y tres enlaces simples. (b) La estructura molecular piramidal trigonal se determina a partir de la geometría del par de electrones. (c) Los ángulos de enlace reales se desvían ligeramente de los ángulos idealizados porque el par solitario ocupa una región de espacio más grande que los enlaces simples, lo que hace que el ángulo $HNH$ sea ligeramente menor que 109.5°.

En la siguiente escena interactiva, diseñada la aplicación Stereo Chem Viewer del proyecto https://threejs.org/, puedes interactuar con la molécula del amoníaco, así:

i) Selecciona dos átomos y luego haz clic en el botón info, para conocer la longitud de enlace en picómetros (pm); ii) selecciona el tercer átomo y conocerás el ángulo de enlace (depende del orden de selección, para identificar el ángulo de 109.5 °).

Como se ve en la figura 7.18, pequeñas distorsiones de los ángulos ideales en la figura 7.16 pueden resultar de diferencias en la repulsión entre varias regiones de densidad de electrones. La teoría VSEPR predice estas distorsiones al establecer un orden de repulsiones y un orden de la cantidad de espacio ocupado por diferentes tipos de pares de electrones. El orden de las repulsiones de pares de electrones de mayor a menor repulsión es:

par solitario-par solitario > par solitario-par de unión > par de unión-par de unión

Este orden de repulsiones determina la cantidad de espacio ocupado por diferentes regiones de electrones. Un par solitario de electrones ocupa una región más grande del espacio que los electrones en un enlace triple; a su vez, los electrones en un enlace triple ocupan más espacio que aquellos en un enlace doble, y así sucesivamente. El orden de tamaños de mayor a menor es:

par solitario > triple enlace > doble enlace > enlace simple

Considera el formaldehído, $H_2CO$, que se usa como conservante para muestras biológicas y anatómicas (Figura 7.14). Esta molécula tiene regiones de alta densidad de electrones que consisten en dos enlaces simples y un enlace doble. La geometría básica es trigonal plana con ángulos de enlace de 120°, pero vemos que el doble enlace causa ángulos ligeramente más grandes (121°), y el ángulo entre los enlaces simples es ligeramente más pequeño (118°).

En la molécula de amoniaco, los tres átomos de hidrógeno unidos al nitrógeno central no están dispuestos en una estructura molecular plana plana trigonal, sino más bien en una pirámide trigonal tridimensional (Figura 7.18) con el átomo de nitrógeno en el ápice y los tres átomos de hidrógeno que forman la base. Los ángulos de enlace ideales en una pirámide trigonal se basan en la geometría del par de electrones tetraédricos. Nuevamente, hay ligeras desviaciones del ideal porque los pares solitarios ocupan regiones más grandes del espacio que los electrones de enlace. Los ángulos de enlace $\ce{H – N – H}$ en $NH_3$ son ligeramente más pequeños que el ángulo de 109.5° en un tetraedro regular (Figura 7.16) porque la repulsión del par de unión de pares solitarios es mayor que la repulsión del par de unión de pares de unión (Figura 7.18).

La figura 7.19 ilustra las estructuras moleculares ideales, que se predicen en base a las geometrías de pares de electrones para diversas combinaciones de pares solitarios y pares de enlace.

Figura 7.19. Las estructuras moleculares son idénticas a las geometrías de pares de electrones cuando no hay pares solitarios presentes (primera columna). Para un número particular de pares de electrones (fila), las estructuras moleculares para uno o más pares solitarios se determinan en función de las modificaciones de la geometría de pares de electrones correspondiente.

De acuerdo con la teoría VSEPR, las ubicaciones de los átomos terminales (X en la figura 7.19) son equivalentes dentro de las geometrías lineal, trigonal plana y tetraédrica de pares de electrones (las primeras tres filas de la tabla). No importa qué X se reemplaza con un par solitario porque las moléculas se pueden rotar para convertir posiciones. Sin embargo, para las geometrías de pares de electrones bipiramidales trigonales, hay dos posiciones X distintas, como se muestra en la figura 7.20: una posición axial (si mantenemos un modelo de una bipirámide trigonal por las dos posiciones axiales, tenemos un eje alrededor del cual podemos rotar el modelo) y una posición ecuatorial (tres posiciones forman un ecuador alrededor del centro de la molécula). Como se muestra en la figura 7.19, la posición axial está rodeada por ángulos de enlace de 90°, mientras que la posición ecuatorial tiene más espacio disponible debido a los ángulos de enlace de 120°. En una geometría de pares de electrones bipiramidales trigonales, los pares solitarios siempre ocupan posiciones ecuatoriales porque estas posiciones más espaciosas pueden acomodar más fácilmente a los pares solitarios más grandes.

Teóricamente, podemos llegar a tres posibles arreglos para los tres enlaces y dos pares solitarios para la molécula de $ClF_3$ (Figura 7.20). La estructura estable es la que coloca los pares solitarios en ubicaciones ecuatoriales, dando una estructura molecular en forma de T.

Cuando un átomo central tiene dos pares de electrones solitarios y cuatro regiones de enlace, tenemos una geometría de pares de electrones octaédricos. Los dos pares solitarios están en lados opuestos del octaedro (separados 180°), dando una estructura molecular plana cuadrada que minimiza las repulsiones par solitario-par solitario (Figura 7.19).

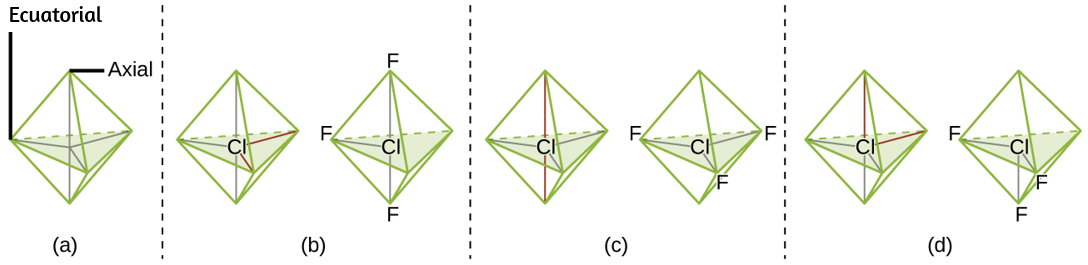
Figura 7.20. (a) En una bipirámide trigonal, las dos posiciones axiales se ubican directamente una frente a la otra, mientras que las tres posiciones ecuatoriales se ubican en una disposición triangular. (b – d) Los dos pares solitarios (líneas rojas) en $ClF_3$ tienen varias disposiciones posibles, pero la estructura molecular en forma de T (b) es la que realmente se observa, consistente con los pares solitarios más grandes que ocupan ambas posiciones ecuatoriales.

Predicción de geometría de pares de electrones y estructura molecular

El siguiente procedimiento utiliza la teoría VSEPR para determinar las geometrías de los pares de electrones y las estructuras moleculares:

1. Escribe la estructura de Lewis de la molécula o ión poliatómico.
2. Cuenta el número de regiones de densidad electrónica (pares y enlaces solitarios) alrededor del átomo central. Un enlace simple, doble o triple cuenta como una región de densidad electrónica.
3. Identifica la geometría del par de electrones en función del número de regiones de densidad de electrones: lineal, trigonal plana, tetraédrica, trigonal bipiramidal u octaédrica (Figura 7.19, primera columna).
4. Usa el número de pares solitarios para determinar la estructura molecular (Figura 7.19).

Si es posible más de un arreglo de pares solitarios y enlaces químicos, elige el que minimice las repulsiones, recordando que los pares solitarios ocupan más espacio que los enlaces múltiples, que ocupan más espacio que los enlaces simples. En arreglos bipiramidales trigonales, la repulsión se minimiza cuando cada par solitario está en una posición ecuatorial. En una disposición octaédrica con dos pares solitarios, la repulsión se minimiza cuando los pares solitarios están en lados opuestos del átomo central.

Los siguientes ejemplos ilustran el uso de la teoría VSEPR para predecir la estructura molecular de moléculas o iones que no tienen pares de electrones solitarios. En este caso, la estructura molecular es idéntica a la geometría del par de electrones.

Ejemplo 7.11

Predicción de geometría de pares de electrones y estructura molecular: $CO_2$ y $BCl_3$

Predecir la geometría de pares de electrones y la estructura molecular para:

(a) dióxido de carbono, $CO_2$, una molécula producida por la combustión de combustibles fósiles

(b) tricloruro de boro, $BCl_3$, un químico industrial importante

Solución

(a) Escribimos la estructura de Lewis del $CO_2$ como:

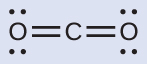
Esto nos muestra dos regiones de alta densidad de electrones alrededor del átomo de carbono: cada doble enlace cuenta como una región, y no hay pares solitarios en el átomo de carbono. Usando la teoría VSEPR, predecimos que las dos regiones de densidad electrónica se disponen en lados opuestos del átomo central con un ángulo de enlace de 180°. La geometría del par de electrones y la estructura molecular son idénticas, y las moléculas de $CO_2$ son lineales.

(b) Escribimos la estructura de Lewis de $BCl_3$ como:

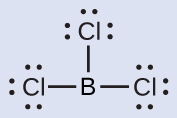
Por lo tanto, vemos que $BCl_3$ contiene tres enlaces, y no hay pares de electrones solitarios en el boro. La disposición de tres regiones de alta densidad de electrones da una geometría de par de electrones plana trigonal. Los enlaces $\ce{B – Cl}$ se encuentran en un plano con ángulos de 120° entre ellos. $BCl_3$ también tiene una estructura molecular plana trigonal (Figura 7.21).

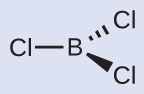
Figura 7.21

La geometría del par de electrones y la estructura molecular de $BCl_3$ son ambas planas trigonales. Observa que la geometría VSEPR indica los ángulos de enlace correctos (120°), a diferencia de la estructura de Lewis que se muestra arriba.

Comprueba tu aprendizaje

Ejemplo 7.12

Predicción de geometría de pares de electrones y estructura molecular: amonio

Dos de los 50 principales químicos producidos en los Estados Unidos, el nitrato de amonio y el sulfato de amonio, ambos utilizados como fertilizantes, contienen el ion amonio. Predecir la geometría del par de electrones y la estructura molecular del catión $NH_4^+$.

Solución

Escribimos la estructura de Lewis de $NH_4^+$ como:

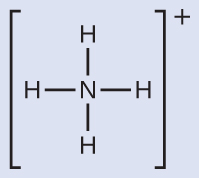
Podemos ver que el $NH_4^+$ contiene cuatro enlaces desde el átomo de nitrógeno a los átomos de hidrógeno y no hay pares solitarios. Esperamos que las cuatro regiones de alta densidad de electrones se organicen de manera que apunten a las esquinas de un tetraedro con el átomo de nitrógeno central en el medio (Figura 7.19). Por lo tanto, la geometría del par de electrones de $NH_4^+$ es tetraédrica, y la estructura molecular también es tetraédrica (Figura 7.22).

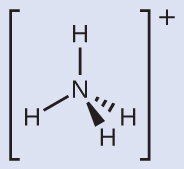
Figura 7.22. El ion amonio muestra una geometría de pares de electrones tetraédricos, así como una estructura molecular tetraédrica.

Comprueba tu aprendizaje

Los siguientes ejemplos ilustran el efecto de pares de electrones solitarios en la estructura molecular.

Ejemplo 7.13

Predicción de la geometría de pares de electrones y estructura molecular: pares solitarios en el átomo central

Predecir la geometría del par de electrones y la estructura molecular de una molécula de agua.

Solución

La estructura de Lewis del $H_2O$ indica que hay cuatro regiones de alta densidad de electrones alrededor del átomo de oxígeno: dos pares solitarios y dos enlaces químicos:

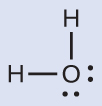
Predecimos que estas cuatro regiones están dispuestas de forma tetraédrica (Figura 7.23), como se indica en la figura 7.19. Por lo tanto, la geometría del par de electrones es tetraédrica y la estructura molecular se dobla con un ángulo ligeramente inferior a 109.5°. De hecho, el ángulo de enlace es 104.5°.

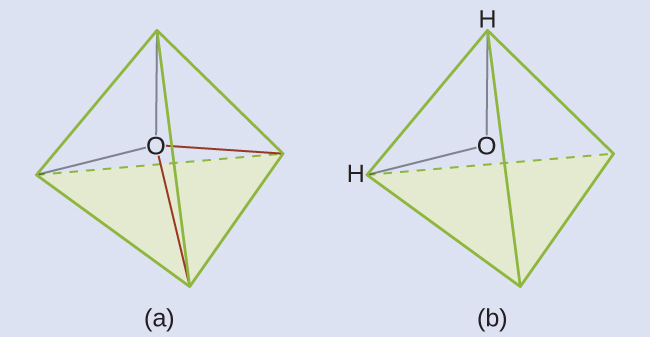
Figura 7.23 El (a) $H_2O$ tiene cuatro regiones de densidad de electrones alrededor del átomo central, por lo que tiene una geometría tetraédrica de pares de electrones. (b) Dos de las regiones de electrones son pares solitarios, por lo que la estructura molecular está doblada.

Comprueba tu aprendizaje

Ejemplo 7.14

Predicción de la geometría de pares de electrones y estructura molecular: $SF_4$

El tetrafluoruro de azufre, $SF_4$, es extremadamente valioso para la preparación de compuestos que contienen flúor usados como herbicidas (es decir, el $SF_4$se usa como agente fluorante). Predecir la geometría del par de electrones y la estructura molecular de una molécula de $SF_4$.

Solución

La estructura de Lewis del $SF_4$ indica cinco regiones de densidad de electrones alrededor del átomo de azufre: un par solitario y cuatro pares de enlace:

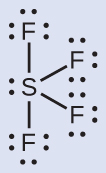
Esperamos que estas regiones adopten una geometría de par de electrones bipiramidal trigonal. Para minimizar las repulsiones del par solitario, el par solitario ocupa una de las posiciones ecuatoriales. La estructura molecular (Figura 7.24) es la de un balancín (Figura 7.19)

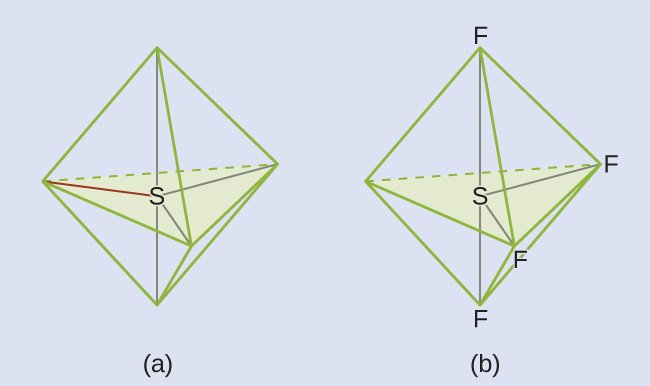
Figura 7.24 (a) El $SF_4$ tiene una disposición bipiramidal trigonal de las cinco regiones de densidad electrónica. (b) Una de las regiones es un par solitario, lo que da como resultado una estructura molecular en forma de balancín.

Comprueba tu aprendizaje

Ejemplo 7.15

Predicción de la geometría de pares de electrones y estructura molecular: $XeF_4$

De todos los gases nobles, el xenón es el más reactivo, reaccionando con frecuencia con elementos como el oxígeno y el flúor. Predecir la geometría del par de electrones y la estructura molecular de la molécula $XeF_4$.

Solución

La estructura de Lewis de $XeF_4$ indica seis regiones de alta densidad de electrones alrededor del átomo de xenón: dos pares solitarios y cuatro enlaces:

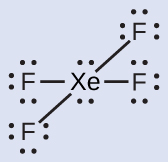
Estas seis regiones adoptan una disposición octaédrica (Figura 7.19), que es la geometría del par de electrones. Para minimizar las repulsiones, los pares solitarios deben estar en lados opuestos del átomo central (Figura 7.25). Los cinco átomos están todos en el mismo plano y tienen una estructura molecular plana cuadrada.

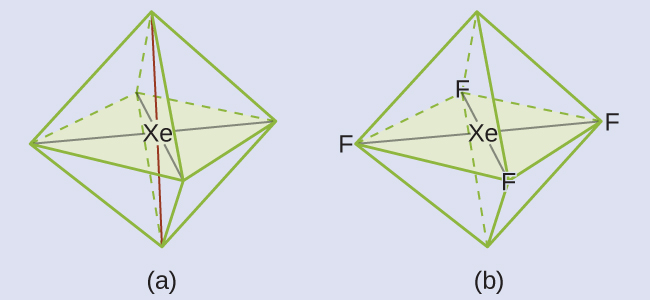
Figura 7.25 (a) El $XeF_4$ adopta una disposición octaédrica con dos pares solitarios (líneas rojas) y cuatro enlaces en la geometría de pares de electrones. (b) La estructura molecular es plana cuadrada con los pares solitarios directamente uno frente al otro.

Comprueba tu aprendizaje

Estructura molecular para moléculas
multicéntricas

Cuando una molécula o ion poliatómico tiene solo un átomo central, la estructura molecular describe completamente la forma de la molécula. Las moléculas más grandes no tienen un solo átomo central, pero están conectadas por una cadena de átomos interiores que poseen una geometría "local". La forma en que estas estructuras locales están orientadas entre sí también influye en la forma molecular, pero tales consideraciones están en gran medida fuera del alcance de esta discusión introductoria. Para nuestros propósitos, solo nos enfocaremos en determinar las estructuras locales.

Ejemplo 7.16

Estructura predictiva en moléculas multicéntricas

Aquí se muestra la estructura de Lewis para el aminoácido más simple, glicina, $H_2NCH_2CO_2H$. Predecir la geometría local para el átomo de nitrógeno, los dos átomos de carbono y el átomo de oxígeno con un átomo de hidrógeno unido:

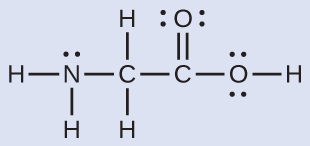
Solución

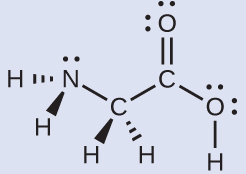
Considera cada átomo central de forma independiente. Las geometrías de pares de electrones:

• nitrógeno –– cuatro regiones de densidad electrónica; tetraédrico
• carbono ($CH_2$) –– cuatro regiones de densidad electrónica; tetraédrico
• carbono ($CO_2$): tres regiones de densidad electrónica; trigonal plana
• oxígeno ($OH$): cuatro regiones de densidad electrónica; tetraédrico

Las estructuras locales:

• nitrógeno –– tres enlaces, un par solitario; piramidal trigonal
• carbono ($CH_2$): cuatro enlaces, sin pares solitarios; tetraédrico
• carbono ($CO_2$): tres enlaces (el doble enlace cuenta como un enlace), sin pares solitarios; trigonal plana
• oxígeno ($OH$): dos enlaces, dos pares solitarios; doblado (109°)

Comprueba tu aprendizaje

Otro aminoácido es la alanina, que tiene la estructura de Lewis que se muestra aquí. Predecir la geometría del par de electrones y la estructura local del átomo de nitrógeno, los tres átomos de carbono y el átomo de oxígeno con hidrógeno unido:

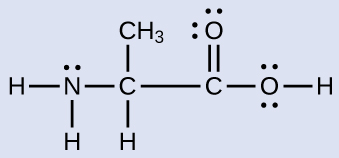
En la siguiente escena interactiva Phet de la Universidad de Colorado, podrás explorar las formas moleculares mediante la construcción de moléculas en 3D, saber cómo cambia la forma molecular con números diferentes de enlaces y pares de electrones; descúbrir mediante la adición de enlaces simples, dobles o triples y pares solitarios al átomo central. Comparar, además, el modelo con moléculas reales.

Ejemplo 7.17

Simulacion Molecular

El uso del simulador de forma molecular nos permite controlar si los ángulos de enlace y/o los pares solitarios se muestran marcando o desmarcando las casillas debajo de "Opciones" a la derecha. También podemos usar las casillas de verificación "Nombre" en la parte inferior izquierda para mostrar u ocultar la geometría del par de electrones (llamada "geometría de electrones" en el simulador) y/o la estructura molecular (llamada "forma molecular" en el simulador).

Construye la molécula $HCN$ en el simulador basándote en la siguiente estructura de Lewis:

Haz clic en cada tipo de enlace o par solitario a la derecha para agregar ese grupo al átomo central. Una vez que tengas la molécula completa, gírala para examinar la estructura molecular pronosticada. ¿Qué estructura molecular es esta?

Solución

La estructura molecular es lineal.

Comprueba tu aprendizaje

Polaridad Molecular y Momento Dipolo

Como se discutió anteriormente, los enlaces covalentes polares conectan dos átomos con diferentes electronegatividades, dejando un átomo con una carga positiva parcial ($\delta +$) y el otro átomo con una carga negativa parcial ($\delta –$), a medida que los electrones son atraídos hacia el átomo más electronegativo.. Esta separación de carga da lugar a un momento dipolar de enlace. La magnitud de un momento dipolar de enlace está representada por la letra griega mu ($\mu$) y está dada por la fórmula que se muestra aquí, donde Q es la magnitud de las cargas parciales (determinada por la diferencia de electronegatividad) y r es la distancia entre las cargas:

Este momento de enlace puede representarse como un vector, una cantidad que tiene dirección y magnitud (Figura 7.26). Los vectores dipolos se muestran como flechas que apuntan a lo largo del enlace desde el átomo menos electronegativo hacia el átomo más electronegativo. Se dibuja un pequeño signo más en el extremo menos electronegativo para indicar el extremo parcialmente positivo del enlace. La longitud de la flecha es proporcional a la magnitud de la diferencia de electronegatividad entre los dos átomos.

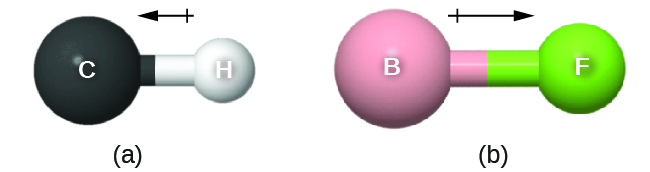
Figura 7.26 Hay una pequeña diferencia en la electronegatividad entre C y H, representada como un vector corto. (b) La diferencia de electronegatividad entre B y F es mucho mayor, por lo que el vector que representa el momento del enlace es mucho más largo.

Una molécula completa también puede tener una separación de carga, dependiendo de su estructura molecular y la polaridad de cada uno de sus enlaces. Si existe tal separación de carga, se dice que la molécula es una molécula polar (o dipolo); de lo contrario, se dice que la molécula es no polar. El momento dipolar mide la extensión de la separación de carga neta en la molécula como un todo. Determinamos el momento dipolar agregando los momentos de enlace en el espacio tridimensional, teniendo en cuenta la estructura molecular.

Para las moléculas diatómicas, solo hay un enlace, por lo que su momento dipolar de enlace determina la polaridad molecular. Las moléculas diatómicas homonucleares como $Br_2$ y $N_2$ no tienen diferencias en la electronegatividad, por lo que su momento dipolar es cero. Para las moléculas heteronucleares como el $CO$, hay un pequeño momento dipolar. Para $HF$, hay un momento dipolar más grande porque hay una mayor diferencia en la electronegatividad.

Cuando una molécula contiene más de un enlace, se debe tener en cuenta la geometría.

Si los enlaces en una molécula están dispuestos de tal manera que sus momentos de enlace se cancelan (la suma del vector es igual a cero), entonces la molécula es no polar. Esta es la situación en $CO_2$ (Figura 7.27). Cada uno de los enlaces es polar, pero la molécula en su conjunto es no polar. A partir de la estructura de Lewis, y utilizando la teoría VSEPR, determinamos que la molécula de $CO_2$ es lineal con enlaces polares $\ce{C = O}$ en lados opuestos del átomo de carbono. Los momentos de enlace se cancelan porque apuntan en direcciones opuestas. En el caso de la molécula de agua (Figura 7.27), la estructura de Lewis muestra nuevamente que hay dos enlaces a un átomo central, y la diferencia de electronegatividad muestra nuevamente que cada uno de estos enlaces tiene un momento de enlace distinto de cero. En este caso, sin embargo, la estructura molecular se dobla debido a los pares solitarios en O, y los dos momentos de enlace no se cancelan. Por lo tanto, el agua tiene un momento dipolar neto y es una molécula polar (dipolo).

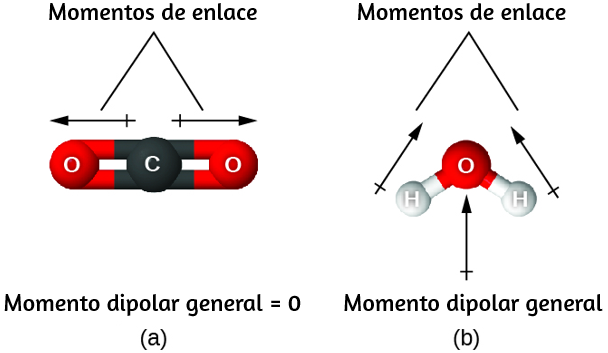
Figura 7.27 El momento dipolar general de una molécula depende de los momentos dipolares de enlace individuales y de cómo están organizados. (a) Cada enlace de $CO$ tiene un momento dipolar de enlace, pero apuntan en direcciones opuestas para que la molécula neta de $CO_2$ sea no polar. (b) En contraste, el agua es polar porque los momentos de enlace $OH$ no se cancelan.

La molécula $OCS$ tiene una estructura similar al $CO_2$, pero un átomo de azufre ha reemplazado a uno de los átomos de oxígeno. Para determinar si esta molécula es polar, dibujamos la estructura molecular. La teoría VSEPR predice una molécula lineal:

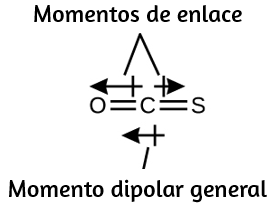
El enlace $\ce{C-O}$ es considerablemente polar. Aunque $C$ y $S$ tienen valores de electronegatividad muy similares, $S$ es ligeramente más electronegativo que $C$, por lo que el enlace $\ce{C-S}$ es ligeramente polar. Como el oxígeno es más electronegativo que el azufre, el extremo de oxígeno de la molécula es el extremo negativo.

El clorometano, $CH_3Cl$, es una molécula tetraédrica con tres enlaces $\ce{C-H}$ ligeramente polares y un enlace $\ce{C-Cl}$ más polar. Las electronegatividades relativas de los átomos unidos son $H$ < $C$ < $Cl$, por lo que todos los momentos de enlace apuntan hacia el extremo $Cl$ de la molécula y suman para producir un momento dipolar considerable (las moléculas son relativamente polares).

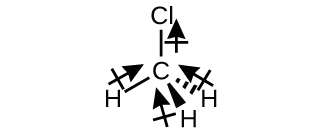
Para las moléculas de alta simetría como $BF_3$ (trigonal planar), $CH_4$ (tetraédrica), $PF_5$ (trigonal bipimidal) y $SF_6$ (octaédrica), todos los enlaces son de polaridad idéntica (mismo momento de enlace) y están orientados en geometrías que producen moléculas no polares (el momento dipolar es cero). Sin embargo, las moléculas de simetría menos geométrica pueden ser polares incluso cuando todos los momentos de enlace son idénticos. Para estas moléculas, las direcciones de los momentos de enlace iguales son tales que suman para dar un momento dipolar distinto de cero y una molécula polar. Ejemplos de tales moléculas incluyen sulfuro de hidrógeno, $H_2S$ (no lineal) y amoníaco, $NH_3$ (piramidal trigonal).

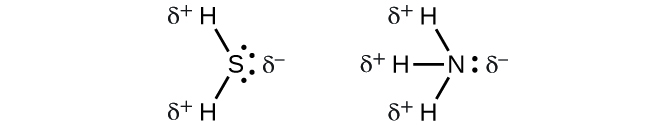
Para resumir, para ser polar, una molécula debe:

1. Contener al menos un enlace covalente polar.
2. Tener una estructura molecular tal que la suma de los vectores de cada momento dipolar de enlace no se cancele.

Propiedades de las moléculas polares

Las moléculas polares tienden a alinearse cuando se colocan en un campo eléctrico con el extremo positivo de la molécula orientado hacia la placa negativa y el extremo negativo hacia la placa positiva (Figura 7.28). Podemos usar un objeto cargado eléctricamente para atraer moléculas polares, pero las moléculas no polares no son atraídas.

Además, los solventes polares son mejores para disolver sustancias polares, y los solventes no polares son mejores para disolver sustancias no polares.

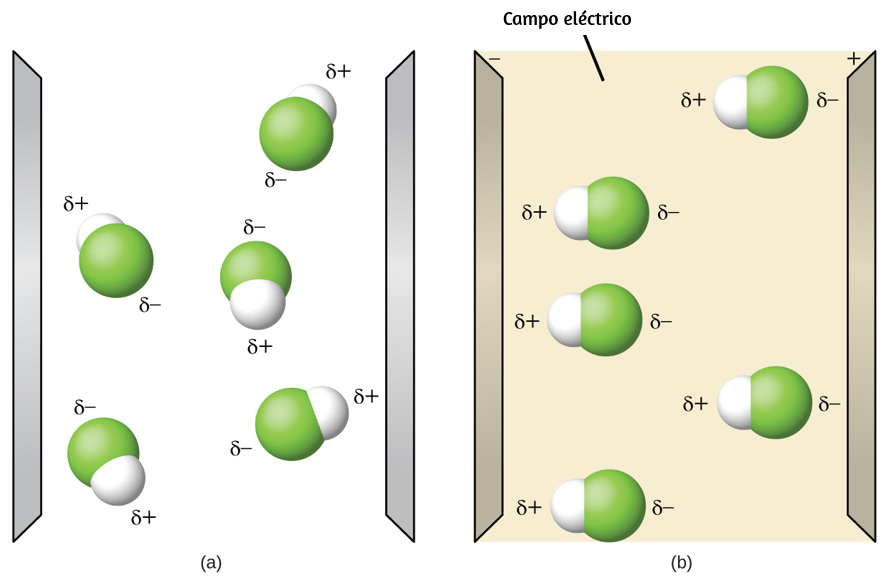
Figura 7.28 (a) Las moléculas siempre se distribuyen aleatoriamente en estado líquido en ausencia de un campo eléctrico. (b) Cuando se aplica un campo eléctrico, las moléculas polares como $HF$ se alinearán con los dipolos con la dirección del campo.

La simulación de polaridad de la molécula, que presentamos en el apartado 7.3, proporciona muchas formas de explorar los momentos dipolares de enlaces y moléculas. A cointinuación, volevemos a presentar este intractivo, de tal forma que puedas estudiar el ejemplo 7.18.

Ejemplo 7.18

Simulaciones de polaridad

Usando la simulación selecciona la pestaña "Tres átomos" en la parte superior. Esto debería mostrar una molécula ABC con tres ajustadores de electronegatividad. Puedes mostrar u ocultar los momentos de enlace, los dipolos moleculares y las cargas parciales a la derecha. Encender el campo eléctrico mostrará si la molécula se mueve cuando se expone a un campo, similar a la figura 7.28.

Usa los controles de electronegatividad para determinar cómo se verá el dipolo molecular para la molécula doblada inicial si:

(a) A y C son muy electronegativos y B está en el medio del rango.
(b) A es muy electronegativo, y B y C no lo son.

Solución

(a) El momento dipolar molecular apunta inmediatamente entre A y C.
(b) El momento dipolar molecular apunta a lo largo del enlace $\ce{A – B}$, hacia A.

Comprueba tu aprendizaje

A continuación, puedes ponerte a prueba con 15 preguntas tipo "falso o verdadero". La preguntas surgen al azar de un total de 50 que hay en el repositoriolas peguntas fueron tomadas del canal TodoFriQuiz. El interactivo fue diseñado por Juan Guillermo Rivera Berrío. de YouTube, puedes ponerte a prueba varias veces.

Preguntas y respuestas - Capítulo VII

Respuestas

Introducción

Figura 8.1 El aire caliente dentro de estos globos es menos denso que el aire frío circundante. Esto da como resultado una fuerza de flotación que hace que los globos se eleven cuando se desatan sus líneas (crédito: modificación del trabajo de Anthony Quintano).

Estamos rodeados por un océano de gas, la atmósfera, y muchas de las propiedades de los gases nos son familiares en nuestras actividades diarias. Los gases calentados se expanden, lo que puede hacer que se eleve un globo de aire caliente (Figura 8.1) o causar una explosión en una llanta de bicicleta que se deja al sol en un día caluroso.

Los gases han jugado un papel importante en el desarrollo de la química. En los siglos XVII y XVIII, muchos científicos investigaron el comportamiento de los gases, proporcionando las primeras descripciones matemáticas del comportamiento de la materia.

En este capítulo, examinaremos las relaciones entre la temperatura, la presión, la cantidad y el volumen del gas.

Estudiaremos un modelo teórico simple y lo usaremos para analizar el comportamiento experimental de los gases. Los resultados de estos análisis nos mostrarán las limitaciones de la teoría y cómo mejorarla.

Presión de gas

La atmósfera de la tierra ejerce una presión, como todo gas. Aunque no notamos la presión atmosférica, somos sensibles a los cambios de presión, por ejemplo, cuando tus oídos "se taponan" durante el despegue y el aterrizaje mientras vuelas, o cuando te sumerges bajo el agua. La presión del gas es causada por la fuerza ejercida por las moléculas de gas que chocan con las superficies de los objetos (figura 8.2). Aunque la fuerza de cada colisión es muy pequeña, cualquier superficie de área apreciable experimenta una gran cantidad de colisiones en poco tiempo, lo que puede provocar una alta presión. De hecho, la presión de aire normal es lo suficientemente fuerte como para aplastar un recipiente de metal cuando no se equilibra con la misma presión desde el interior del recipiente.

Figura 8.2 La atmósfera sobre nosotros ejerce una gran presión sobre los objetos en la superficie de la tierra, aproximadamente igual al peso de una bola de boliche que presiona sobre un área del tamaño de una miniatura humana.

Una ilustración dramática de la presión atmosférica se muestra en el siguiente vídeo, que muestra un vagón cisterna implosionando cuando disminuye su presión interna (vídeo del canal Safety de YouTube):

La presión atmosférica es causada por el peso de la columna de moléculas de aire en la atmósfera sobre un objeto, como el vagón cisterna. Al nivel del mar, esta presión es más o menos la misma que ejerce un elefante africano adulto de pie sobre un felpudo, o una bola de boliche típica que descansa sobre la uña del pulgar. Estas pueden parecer grandes cantidades, y lo son, pero la vida en la Tierra ha evolucionado bajo tanta presión atmosférica. Si realmente posas una bola de boliche en tu uña del pulgar, la presión experimentada es el doble de la presión habitual, y la sensación es desagradable.

En general, la presión se define como la fuerza ejercida sobre un área determinada: $P = \frac{F}{A}$. Observa que la presión es directamente proporcional a la fuerza e inversamente proporcional al área.

Por lo tanto, la presión puede aumentarse aumentando la cantidad de fuerza o disminuyendo el área sobre la que se aplica; la presión puede disminuirse disminuyendo la fuerza o aumentando el área.

Apliquemos este concepto para determinar cuál sería más probable que caiga a través del hielo delgado en la figura 8.3: ¿el elefante o el patinador artístico? Un gran elefante africano puede pesar 7 toneladas, apoyado en cuatro pies, cada uno con un diámetro de aproximadamente 1.5 pies (área de huella de 250 $in^2$), por lo que la presión ejercida por cada pie es de aproximadamente $\pu{14 lb // in2}$:

presión por pie de elefante = $\frac{14,000\; lb}{elefante} \times 1 \frac{elefante}{4\; patas} \times \frac{1\; pata}{\pu{250 in^2}} = \pu{14 lb//in2}$

El patinador pesa aproximadamente 120 libras, apoyado en dos patines, cada uno con un área de aproximadamente 2 $pulgadas^2$, por lo que la presión ejercida por cada hoja es de aproximadamente $\pu{30 libras // pulgada^2}$:

presión por patín = $120\frac{lb}{\text{patín}} \times \frac{1\; patinador}{2\; cuchillas} \times \frac{1\; cuchilla}{2\;in^2} = \pu{30 lb // in^2}$

Aunque el elefante es más de cien veces más pesado que el patinador, ejerce menos de la mitad de la presión y, por lo tanto, es menos probable que caiga a través del hielo delgado. Por otro lado, si la patinadora se quita los patines y se para con los pies descalzos (o calzado normal) sobre el hielo, el área más grande sobre la cual se aplica su peso reduce en gran medida la presión ejercida:

presión por pie humano = $ 120 \frac{lb}{patinador} \times \frac{1\; patinador}{2 pies} \times \frac{1\; pie}{\pu{30 in2}} = \pu{2 lb // in2}$

Figura 8.3 Aunque (a) el peso de un elefante es grande, creando una fuerza muy grande en el suelo, (b) la patinadora artística ejerce una presión mucho mayor sobre el hielo debido a la pequeña superficie de sus patines (crédito a: modificación del trabajo de Guido da Rozze; crédito b: modificación del trabajo de Ryosuke Yagi).

La unidad de presión del SI es el pascal (Pa), con $1 Pa = 1 \;N/m^2$, donde N es el newton, una unidad de fuerza definida como $1 \;kg\; m / s^2$. Un pascal es una pequeña presión; en muchos casos, es más conveniente usar unidades de kilopascal (1 kPa = 1000 Pa) o bar (1 bar = 100,000 Pa). En los Estados Unidos, la presión a menudo se mide en libras de fuerza sobre un área de una pulgada cuadrada (libras por pulgada cuadrada (psi)), por ejemplo, en llantas de automóviles. La presión también se puede medir utilizando la unidad de atmósfera (atm), que originalmente representaba la presión del aire promedio al nivel del mar en la latitud aproximada de París (45°). La tabla 8.1 proporciona información sobre estas y algunas otras unidades comunes para mediciones de presión.

Tabla 8.1. Unidades de presión

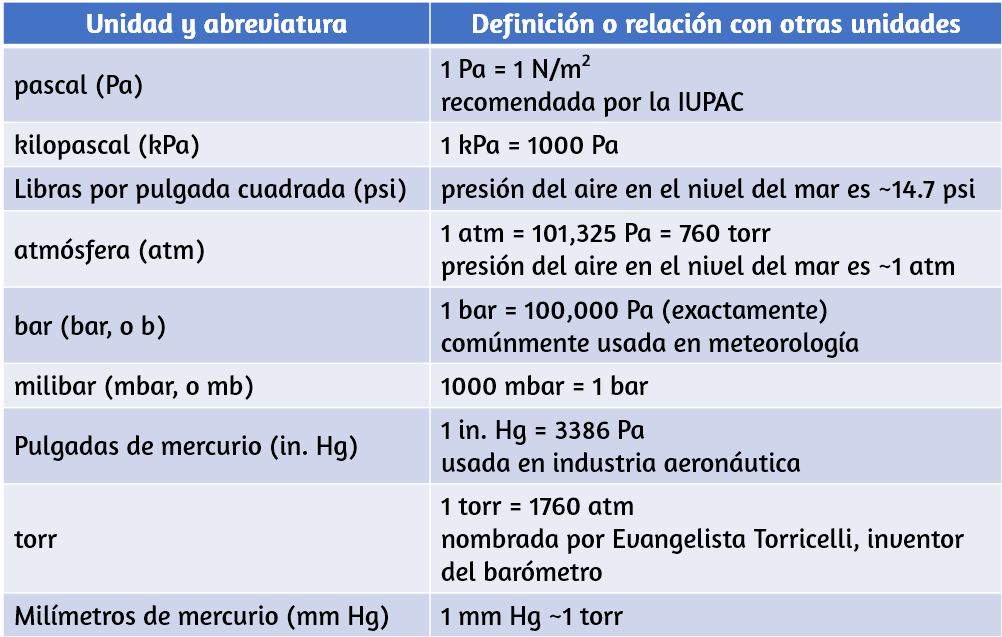
Ejemplo 8.1

Conversión de Unidades de Presión

El Servicio Meteorológico Nacional de los Estados Unidos informa sobre la presión en pulgadas de Hg y milibares. Convierte una presión de 29.2 pulg. Hg en:

(a) torr
(b) atm
(c) kPa
(d) mbar

Solución

Este es un problema de conversión de unidades. Las relaciones entre las distintas unidades de presión se dan en la tabla 8.1.

Comprueba tu aprendizaje

Podemos medir la presión atmosférica, la fuerza ejercida por la atmósfera sobre la superficie de la tierra, con un barómetro (Figura 8.4).

Un barómetro es un tubo de vidrio que se cierra en un extremo, se llena con un líquido no volátil como el mercurio y luego se invierte y se sumerge en un recipiente con ese líquido. La atmósfera ejerce presión sobre el líquido fuera del tubo, la columna de líquido ejerce presión dentro del tubo, y la presión en la superficie del líquido es la misma dentro y fuera del tubo. La altura del líquido en el tubo es, por lo tanto, proporcional a la presión ejercida por la atmósfera.

Figura 8.4 En un barómetro, la altura, h, de la columna de líquido se usa como medida de la presión del aire. El uso de mercurio líquido muy denso (izquierda) permite la construcción de barómetros de tamaño razonable, mientras que el uso de agua (derecha) requeriría un barómetro de más de 30 pies de altura.

Si el líquido es agua, la presión atmosférica normal soportará una columna de agua de más de 10 metros de altura, lo cual es bastante inconveniente para hacer (y leer) un barómetro. Debido a que el mercurio (Hg) es aproximadamente 13.6 veces más denso que el agua, un barómetro de mercurio solo debe tener 113.6 la altura de un barómetro de agua, un tamaño más adecuado. La presión atmosférica estándar de 1 atm al nivel del mar (101,325 Pa) corresponde a una columna de mercurio que tiene aproximadamente 760 mm (29.92 pulg.) de altura. Originalmente, el torr estaba destinado a ser una unidad igual a un milímetro de mercurio, pero ya no corresponde exactamente. La presión ejercida por un fluido debido a la gravedad se conoce como presión hidrostática, p:

aquí $h$ es la altura del fluido, $\rho$ es la densidad del fluido y $g$ es la aceleración debida a la gravedad.

Ejemplo 8.2

Cálculo de la presión barométrica

Muestra el cálculo que respalda la afirmación de que la presión atmosférica cerca del nivel del mar corresponde a la presión ejercida por una columna de mercurio que tiene aproximadamente 760 mm de altura. La densidad del mercurio = $\pu{13,6 g // cm3}$.

Solución

La presión hidrostática viene dada por $p$ = h$\rho$g, con $h$ = 760 mm, $\rho$ = $\pu{13.6 g // cm3}$ y $g$ = $\pu{9.81 m / s2}$. Conectar estos valores a la ecuación y hacer las conversiones de unidades necesarias nos dará el valor que buscamos (Nota: esperamos encontrar una presión de ~ 101,325 Pa).

$p=\bigg(760\; mm \times \frac{1\; m}{1000\; mm} \bigg) \times \bigg(\frac{13.6\; g}{1\;cm^3} \times \frac{1\; kg}{1000\; g} \times \frac{(100 cm)^3}{(1\; m)^3}\bigg) \times \pu{(\frac{9.81\; m}{1\;s2})}$

$= (0.760 \; m)(13,600 \;kg/m^3)(9.81 \;m/s^2) 1.01 \times 10^5\;kg/ms^2 =$
$$= 1.01\times 10^5\;N/m^2$$

Comprueba tu aprendizaje

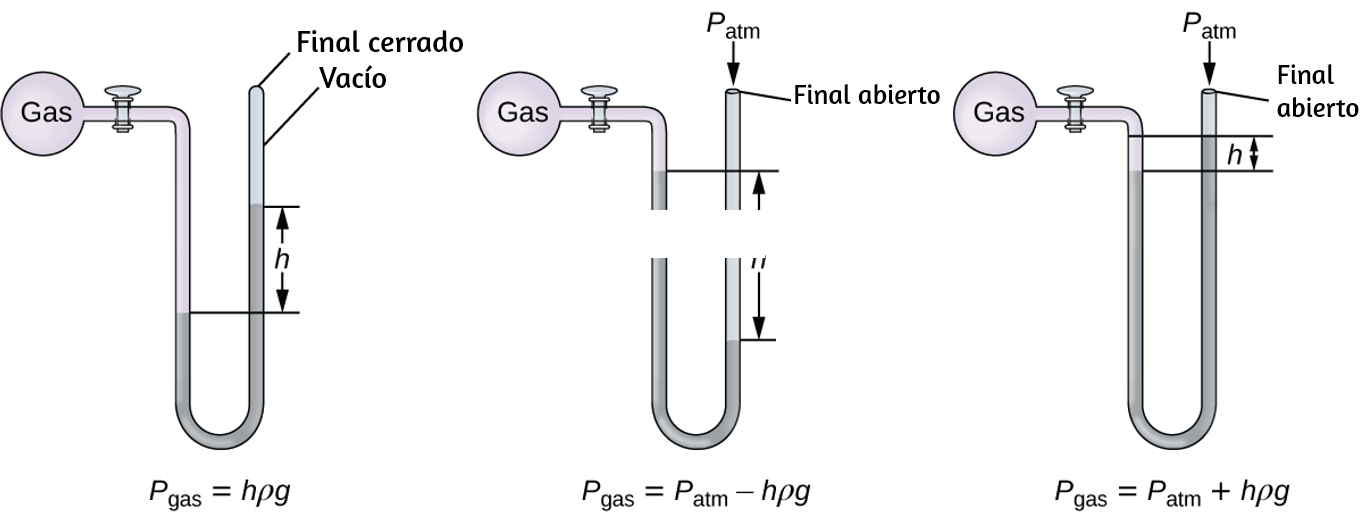
Figura 8.5 Se puede usar un manómetro para medir la presión de un gas. La (diferencia en) altura entre los niveles de líquido (h) es una medida de la presión. El mercurio se usa generalmente debido a su gran densidad.

Ejemplo 8.3

Cálculo de presión usando un manómetro cerrado

La presión de una muestra de gas se mide con un manómetro cerrado, como se muestra a la derecha. El líquido en el manómetro es mercurio. Determina la presión del gas en:

(a) torr (b) Pa (c) bar

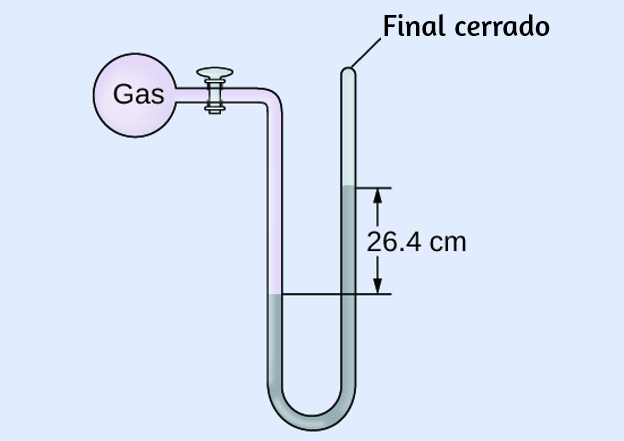Solución

La presión del gas es igual a una columna de mercurio de 26,4 cm de altura (la presión en la línea horizontal inferior es igual en ambos lados del tubo. La presión de la izquierda se debe al gas y la presión de la derecha se debe a 26,4 cm Hg, o mercurio). Podríamos usar la ecuación $p = h\rho g$ como en el ejemplo 8.2, pero es más simple convertir entre unidades usando la tabla 8.1.

Comprueba tu aprendizaje

Como en el ejemplo, determina la presión del gas en:

(a) torr (b) Pa (c) bar

Antes de continuar con otro ejemplo, te presentamos dos escenas interactivas para medir las presiones manométricas.

En la primer escena interactiva, diseñada por Fu-Kwun Hwang, Fremont Teng y Loo Kang Wee, puedes cambiar las alturas y densidades de tres líquidos y observar el cambio en las alturas manométricas.

De los mismos autores, en la segunda escena interactiva puedes interactuar con dos medidores de presión:

Ejemplo 8.4

Cálculo de presión usando un manómetro de extremo abierto

La presión de una muestra de gas se mide al nivel del mar con un manómetro abierto de Hg (mercurio), como se muestra a la derecha. Determina la presión del gas en:

(a) mm Hg
(b) atm
(c) kPa

Solución

La presión del gas es igual a la presión hidrostática debido a una columna de mercurio de 13,7 cm de altura más la presión de la atmósfera al nivel del mar (la presión en la línea horizontal inferior es igual en ambos lados del tubo. La presión de la izquierda se debe al gas y la presión de la derecha se debe a 13,7 cm de Hg más la presión atmosférica).

Comprueba tu aprendizaje

Como en el ejemplo, determina la presión del gas en:

(a) mm Hg (b) atm (c) kPa

Química en la vida cotidiana

Medición de la presión arterial

La presión arterial se mide usando un dispositivo llamado esfigmomanómetro (sphygmos griego = "pulso"). Consiste en un manguito inflable para restringir el flujo sanguíneo, un manómetro para medir la presión y un método para determinar cuándo comienza el flujo sanguíneo y cuándo se dificulta (Figura 8.6). Desde su invención en 1881, ha sido un dispositivo médico esencial. Hay muchos tipos de esfigmomanómetros: manuales que requieren un estetoscopio y son utilizados por profesionales médicos; los de mercurio, utilizados cuando se requiere la mayor precisión; los mecánicos menos precisos; y digitales que pueden usarse con poca capacitación pero que tienen limitaciones. Cuando se utiliza un esfigmomanómetro, el manguito se coloca alrededor de la parte superior del brazo y se infla hasta que el flujo sanguíneo esté completamente bloqueado, luego se libera lentamente. A medida que el corazón late, la sangre forzada a través de las arterias provoca un aumento de la presión. Este aumento de la presión a la que comienza el flujo sanguíneo es la presión sistólica, la presión máxima en el ciclo cardíaco. Cuando la presión del manguito es igual a la presión sistólica arterial, la sangre fluye más allá del manguito, creando sonidos audibles que se pueden escuchar con un estetoscopio. Esto es seguido por una disminución de la presión a medida que los ventrículos del corazón se preparan para otro latido. A medida que la presión del manguito continúa disminuyendo, eventualmente ya no se escucha el sonido; Esta es la presión diastólica: la presión más baja (fase de reposo) en el ciclo cardíaco. Las unidades de presión arterial de un esfigmomanómetro están expresadas en milímetros de mercurio (mm Hg).

Figura 8.6 (a) Un técnico médico se prepara para medir la presión arterial de un paciente con un esfigmomanómetro. (b) Un esfigmomanómetro típico utiliza un bulbo de goma con válvula para inflar el manguito y un medidor de diafragma para medir la presión (crédito a: modificación del trabajo del Sargento Primero Jeffrey Allen).

Química en la vida cotidiana

Meteorología, Climatología y Ciencia
Atmosférica

A lo largo de los siglos, la gente ha observado nubes, vientos y precipitaciones, tratando de discernir patrones y hacer predicciones: cuándo es mejor plantar y cosechar; si es seguro emprender un viaje por mar; y mucho más. Ahora enfrentamos desafíos complejos relacionados con el clima y la atmósfera que tendrán un gran impacto en nuestra civilización y el ecosistema. Varias disciplinas científicas diferentes utilizan principios químicos para ayudarnos a comprender mejor el clima, la atmósfera y el clima. Estos son meteorología, climatología y ciencia atmosférica. La meteorología es el estudio de la atmósfera, los fenómenos atmosféricos y los efectos atmosféricos sobre el clima de la Tierra. Los meteorólogos buscan comprender y predecir el clima a corto plazo, lo que puede salvar vidas y beneficiar a la economía.

Figura 8.7 Los meteorólogos usan mapas meteorológicos para describir y predecir el clima. Las regiones de presión alta (H) y baja (L) tienen grandes efectos en las condiciones climáticas. Las líneas grises representan ubicaciones de presión constante conocidas como isobaras (crédito: modificación del trabajo por la Administración Nacional Oceánica y Atmosférica).

Los pronósticos del tiempo (Figura 8.7) son el resultado de miles de mediciones de la presión del aire, la temperatura y similares, que se compilan, modelan y analizan en los centros meteorológicos de todo el mundo.. En términos de clima, los sistemas de baja presión ocurren cuando la presión atmosférica de la superficie de la tierra es más baja que el entorno: el aire húmedo se eleva y se condensa, produciendo nubes. El movimiento de la humedad y el aire dentro de varios frentes climáticos instiga la mayoría de los eventos climáticos.

La atmósfera es la capa gaseosa que rodea un planeta. La atmósfera de la Tierra, que tiene un grosor aproximado de 100-125 km, consta de aproximadamente 78.1% de nitrógeno y 21.0% de oxígeno, y puede subdividirse en las regiones que se muestran en la figura 8.8:

la exosfera (más alejada de la tierra, > 700 km sobre el nivel del mar), la termosfera (80–700 km), la mesosfera (50–80 km), la estratosfera (segundo nivel más bajo de nuestra atmósfera, 12–50 km sobre el nivel del mar) y la troposfera (hasta 12 km sobre el nivel del mar, aproximadamente el 80% de la atmósfera de la tierra en masa y la capa donde se originan la mayoría de los eventos climáticos). A medida que asciendes en la troposfera, la densidad del aire y la temperatura disminuyen.

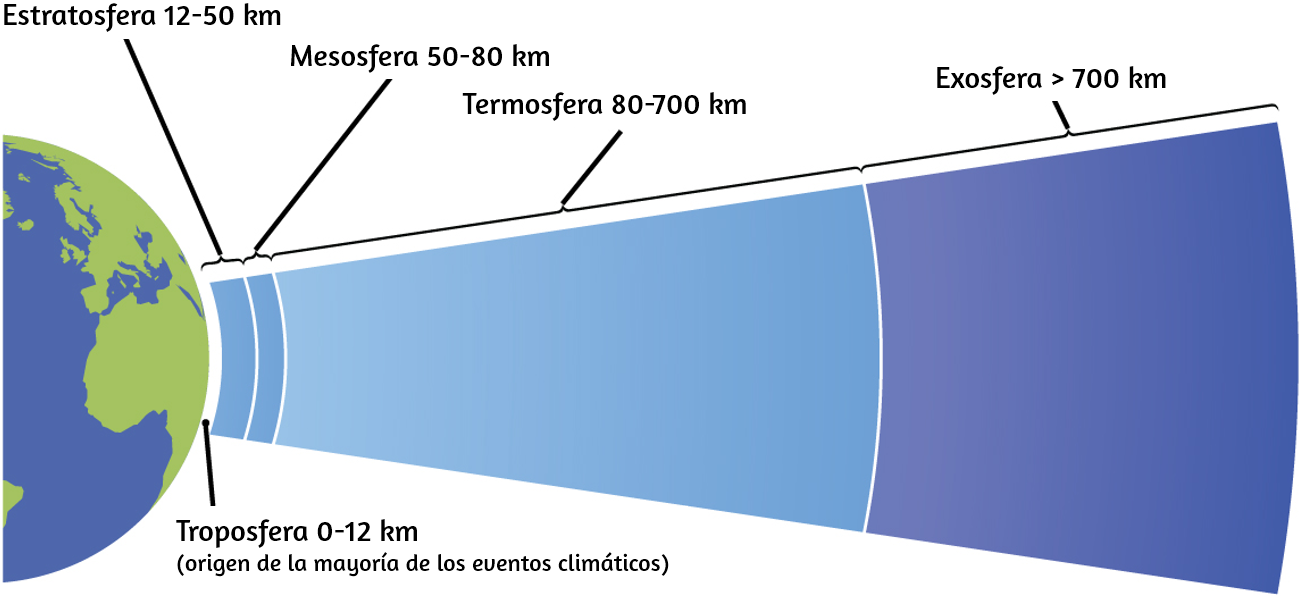
Figura 8.8 La atmósfera de la Tierra tiene cinco capas: la troposfera, la estratosfera, la mesosfera, la termosfera y la exosfera.

La climatología es el estudio del clima, las condiciones climáticas promedio durante largos períodos de tiempo, utilizando datos atmosféricos. Sin embargo, los climatólogos estudian los patrones y los efectos que ocurren durante décadas, siglos y milenios, en lugar de períodos de tiempo, días y semanas más cortos, como los meteorólogos. La ciencia atmosférica es un campo aún más amplio, que combina meteorología, climatología y otras disciplinas científicas que estudian la atmósfera.

Presión, volumen y temperatura: la ley del gas ideal

Durante los siglos XVII y especialmente el XVIII, impulsados ​​tanto por el deseo de comprender la naturaleza como por la búsqueda de hacer globos en los que pudieran volar (Figura 8.9), varios científicos establecieron las relaciones entre las propiedades físicas macroscópicas de los gases, es decir, presión, volumen, temperatura y cantidad de gas. Aunque sus mediciones no eran precisas según los estándares actuales, pudieron determinar las relaciones matemáticas entre pares de estas variables (por ejemplo, presión y temperatura, presión y volumen) que se mantienen para un gas ideal, una construcción hipotética de que los gases reales se aproximan bajo ciertas condiciones. Finalmente, estas leyes individuales se combinaron en una sola ecuación, la ley de los gases ideales, que relaciona las cantidades de gas para gases y es bastante precisa para presiones bajas y temperaturas moderadas. Consideraremos los desarrollos clave en las relaciones individuales (por razones pedagógicas, no del todo en el orden histórico), luego los agruparemos en la ley de los gases ideales.

Figura 8.9 (a) En 1783, se produjo el primer vuelo en globo lleno de hidrógeno, (b) vuelo tripulado en globo aerostático y (c) vuelo en globo tripulado lleno de hidrógeno. Cuando el globo lleno de hidrógeno representado en (a) aterrizó, los aldeanos asustados de Gonesse lo destruyeron con horquillas y cuchillos. El lanzamiento de este último fue visto por 400,000 personas en París.

Presión y temperatura: la ley de Amonton

Imagina llenar un recipiente rígido conectado a un manómetro con gas y luego sellar el recipiente para que no pueda escapar gas. Si el recipiente se enfría, el gas en el interior también se enfría y se observa que su presión disminuye. Dado que el contenedor es rígido y herméticamente cerrado, tanto el volumen como la cantidad de moles de gas permanecen constantes. Si calentamos la esfera, el gas en el interior se calienta (figura 8.10) y la presión aumenta.

Figura 8.10 El efecto de la temperatura sobre la presión del gas: cuando la placa caliente está apagada, la presión del gas en la esfera es relativamente baja. A medida que se calienta el gas, aumenta la presión del gas en la esfera.

Esta relación entre temperatura y presión se observa para cualquier muestra de gas confinada a un volumen constante. En la figura 8.11 se muestra un ejemplo de datos experimentales de presión-temperatura para una muestra de aire en estas condiciones.

Encontramos que la temperatura y la presión están relacionadas linealmente, y si la temperatura está en la escala de Kelvin, entonces P y T son directamente proporcionales (nuevamente, cuando el volumen y los moles de gas se mantienen constantes); Si la temperatura en la escala Kelvin aumenta en un cierto factor, la presión del gas aumenta en el mismo factor.

Figura 8.11 Para un volumen y una cantidad de aire constantes, la presión y la temperatura son directamente proporcionales, siempre que la temperatura esté en grados Kelvin (las mediciones no pueden realizarse a temperaturas más bajas debido a la condensación del gas). Cuando esta línea se extrapola a presiones más bajas, alcanza una presión de 0 a –273 °C, que es 0 en la escala de Kelvin y la temperatura más baja posible , llamado cero absoluto.

Guillaume Amontons fue el primero en establecer empíricamente la relación entre la presión y la temperatura de un gas (~ 1700), y Joseph Louis Gay-Lussac determinó la relación con mayor precisión (~ 1800). Debido a esto, la relación $P-T$ para gases se conoce como ley de Amonton o ley de Gay-Lussac. Bajo cualquiera de los dos nombres, establece que la presión de una cantidad dada de gas es directamente proporcional a su temperatura en la escala Kelvin cuando el volumen se mantiene constante. Matemáticamente, esto se puede escribir:

donde $\propto$ significa "es proporcional a" y k es una constante de proporcionalidad que depende de la identidad, la cantidad y el volumen del gas.

Para un volumen de gas confinado y constante, la relación $\frac{P}{T}$ es, por lo tanto, constante (es decir, $\frac{P}{T}$ = k). Si el gas está inicialmente en “Condición 1” (con $P = P_1$ y $T = T_1$), y luego cambia a “Condición 2” (con $P = P_2$ y $T = T_2$), tenemos que $\frac{P_1}{T_1} = k$ y $\frac{P_2}{T_2} = k$, que se reduce a $\frac{P_1}{T_1} = \frac{P_2}{T_2}.$ Esta ecuación es útil para los cálculos de presión-temperatura para un gas confinado a volumen constante. Ten en cuenta que las temperaturas deben estar en la escala de Kelvin para cualquier cálculo de la ley de gases (0 en la escala de Kelvin y la temperatura más baja posible se llama cero absoluto). (También ten en cuenta que hay al menos tres formas en que podemos describir cómo cambia la presión de un gas a medida que cambia su temperatura: podemos usar una tabla de valores, un gráfico o una ecuación matemática).

Ejemplo 8.5

Predecir el cambio de presión con la temperatura

Se usa una lata de spray para el cabello hasta que esté vacía, excepto el propulsor, el gas isobutano.

Solución

(a) La lata contiene una cantidad de gas isobutano a un volumen constante, por lo que si la temperatura aumenta por calentamiento, la presión aumentará proporcionalmente. La alta temperatura puede conducir a una alta presión, haciendo que la lata explote (además, el isobutano es combustible, por lo que la incineración podría hacer que la lata explote).

(b) Estamos buscando un cambio de presión debido a un cambio de temperatura a volumen constante, por lo que utilizaremos la ley de Amontons/Gay-Lussac. Tomando $P_1$ y $T_1$ como los valores iniciales, $T_2$ como la temperatura donde se desconoce la presión y $P_2$ como la presión desconocida, y convirtiendo °C a K, tenemos:

Resolviendo, obtenemos: $P_2 = \cfrac{360\; kPa \times 323\cancel{\;K}}{297\;\cancel{K}} = 390\;kPa$

Comprueba tu aprendizaje

Volumen y temperatura: la ley de Charles

Si llenamos un globo con aire y lo sellamos, el globo contiene una cantidad específica de aire a presión atmosférica, digamos 1 atm. Si colocamos el globo en un refrigerador, el gas en el interior se enfría y el globo se encoge (aunque tanto la cantidad de gas como su presión permanecen constantes). Si hacemos que el globo esté muy frío, se encogerá mucho y se expandirá nuevamente cuando se caliente.

El siguiente vídeo muestra la relación entre el volumen y la temperatura a medida que un globo se enfría en nitrógeno líquido Vídeo creado por la Escuela de Ciencias y Matemáticas de Carolina del Norte, licenciado bajo Creative Commons CC-BY (https://www.youtube.com/watch?v=Gi5wPnkBEYI).

Estos ejemplos del efecto de la temperatura sobre el volumen de una cantidad dada de un gas confinado a presión constante son ciertos en general: el volumen aumenta a medida que aumenta la temperatura y disminuye a medida que disminuye la temperatura. Los datos de temperatura de volumen para una muestra de 1 mol de gas metano a 1 atm se enumeran y grafican en la figura 8.12.

Figura 8.12 El volumen y la temperatura están linealmente relacionados para 1 mol de gas metano a una presión constante de 1 atm. Si la temperatura está en grados Kelvin, el volumen y la temperatura son directamente proporcionales. La línea se detiene a 111 K porque el metano se licua a esta temperatura; cuando se extrapola, se cruza con el origen del gráfico, representando una temperatura de cero absoluto.

La relación entre el volumen y la temperatura de una cantidad dada de gas a presión constante se conoce como la ley de Charles en reconocimiento del científico francés y pionero del vuelo en globo Jacques Alexandre César Charles. La ley de Charles establece que el volumen de una cantidad dada de gas es directamente proporcional a su temperatura en la escala Kelvin cuando la presión se mantiene constante.

Matemáticamente, esto se puede escribir como:

siendo k una constante de proporcionalidad que depende de la cantidad y presión del gas.

Para una muestra de gas a presión constante y confinada, $frac{V}{T}$ es constante (es decir, la relación = k), y como se ve con la relación P-T, esto lleva a otra forma de la ley de Charles: $\frac{V_1}{T_1} = \frac{V_2}{T_2}$.

Ejemplo 8.6

Predecir cambios en el volumen con la temperatura

Una muestra de dióxido de carbono, $CO_2$, ocupa 0.300 L a 10 °C y 750 torr. ¿Qué volumen tendrá el gas a 30 °C y 750 torr?

Solución

Debido a que estamos buscando el cambio de volumen causado por un cambio de temperatura a presión constante, este es un trabajo para la ley de Charles. Tomando $V_1$ y $T_1$ como los valores iniciales, $T_2$ como la temperatura a la que se desconoce el volumen y $V_2$ como el volumen desconocido, y convirtiendo °C en K tenemos:

Resolviendo, obtenemos: $V_2 = \cfrac{0.300\; L \times 303\;\cancel{K}}{283\; \cancel{K}} = 0.321\; L$

Esta respuesta respalda nuestras expectativas de la ley de Charles, a saber, que elevar la temperatura del gas (de 283 K a 303 K) a una presión constante producirá un aumento en su volumen (de 0.300 L a 0.321 L).

Comprueba tu aprendizaje

Ejemplo 8.7

Medición de la temperatura con un cambio de volumen

La temperatura a veces se mide con un termómetro de gas observando el cambio en el volumen del gas a medida que la temperatura cambia a presión constante. El hidrógeno en un termómetro de gas de hidrógeno particular tiene un volumen de $150.0 \;cm^3$ cuando se sumerge en una mezcla de hielo y agua (0.00 °C). Cuando se sumerge en amoníaco líquido hirviendo, el volumen del hidrógeno, a la misma presión, es de $131.7 \; cm^3$. Encuentra la temperatura del amoníaco hirviendo en las escalas Kelvin y Celsius.

Solución

Un cambio de volumen causado por un cambio de temperatura a presión constante significa que debemos usar la ley de Charles.

Tomando $V_1$ y $T_1$ como los valores iniciales, $T_2$ como la temperatura a la que se desconoce el volumen y $V_2$ como el volumen desconocido, y convirtiendo &DEG;C en K tenemos:

Despejando, obtenemos: $T_2 = \cfrac{131.7\;\cancel{cm3} \times 273.15\;K}{150.0\;\cancel{cm3}} = 239.8\; K$

Restando 273.15 de 239.8 K, encontramos que la temperatura del amoníaco hirviendo en la escala Celsius es –33.4 °C.

Comprueba tu aprendizaje

Volumen y presión: la ley de Boyle

Si llenamos parcialmente una jeringa hermética con aire, la jeringa contiene una cantidad específica de aire a temperatura constante, digamos 25 °C. Si empujamos lentamente el émbolo mientras mantenemos la temperatura constante, el gas en la jeringa se comprime en un volumen más pequeño y su presión aumenta; Si sacamos el émbolo, el volumen aumenta y la presión disminuye.

Este ejemplo del efecto del volumen sobre la presión de una cantidad dada de un gas confinado es cierto en general. Disminuir el volumen de un gas contenido aumentará su presión, y aumentar su volumen disminuirá su presión. De hecho, si el volumen aumenta en cierto factor, la presión disminuye en el mismo factor, y viceversa. Los datos de presión de volumen para una muestra de aire a temperatura ambiente se grafican en la figura 8.13.

Figura 8.13 Cuando un gas ocupa un volumen más pequeño, ejerce una presión más alta; cuando ocupa un volumen mayor, ejerce una presión menor (suponiendo que la cantidad de gas y la temperatura no cambien). Como P y V son inversamente proporcionales, una gráfica de $frac{1}{P}$ vs. V es lineal.

A diferencia de las relaciones P-T y V-T, la presión y el volumen no son directamente proporcionales entre sí. En cambio, P y V exhiben proporcionalidad inversa: el aumento de la presión da como resultado una disminución del volumen del gas. Matemáticamente esto se puede escribir:

con k siendo una constante. Gráficamente, esta relación se muestra mediante la línea recta que resulta al trazar la inversa de la presión ($\frac{1}{P}$) versus el volumen ($V$), o la inversa del volumen ($\frac{1}{V}$) versus la presión ($P$). Los gráficos con líneas curvas son difíciles de leer con precisión a valores bajos o altos de las variables, y son más difíciles de usar para ajustar ecuaciones teóricas y parámetros a datos experimentales. Por esas razones, los científicos a menudo intentan encontrar una manera de "linealizar" sus datos. Si graficamos $P$ versus $V$, obtenemos una hipérbola (ver figura 8.14).

Figura 8.14 La relación entre presión y volumen es inversamente proporcional. (a) La gráfica de P vs. V es una hipérbola, mientras que (b) la gráfica de (1/P) vs. V es lineal.

La relación entre el volumen y la presión de una cantidad dada de gas a temperatura constante fue publicada por primera vez por el filósofo natural inglés Robert Boyle hace más de 300 años. Se resume en la declaración ahora conocida como la ley de Boyle: el volumen de una cantidad dada de gas mantenida a temperatura constante es inversamente proporcional a la presión bajo la cual se mide.

Ejemplo 8.8

Volumen de una muestra de gas

La muestra de gas en la figura 8.13 tiene un volumen de 15.0 mL a una presión de 13.0 psi. Determina la presión del gas a un volumen de 7.5 ml, usando:

(a) el gráfico P-V de la figura 8.13
(b) el gráfico $\frac{1}{P}$ vs. V de la figura 8.13
(c) la ecuación de la ley de Boyle

Comenta sobre la precisión probable de cada método.

Solución

(a) La estimación del gráfico P-V da un valor para P en algún lugar alrededor de 27 psi.

(b) La estimación del gráfico $\frac{1}{P}$ versus V da un valor de aproximadamente 26 psi.

(c) Por la ley de Boyle, sabemos que el producto de presión y volumen ($PV$) para una muestra dada de gas a una temperatura constante siempre es igual al mismo valor. Por lo tanto, tenemos $P_1V_1 = k$ y $P_2V_2 = k$, lo que significa que $P_1V_1 = P_2V_2$.

Usando $P_1$ y $V_1$ como los valores conocidos de 13.0 psi y 15.0 mL, $P_2$ como la presión a la que se desconoce el volumen y $V_2$ como el volumen desconocido, tenemos:

Resolviendo:

Fue más difícil estimar bien a partir del gráfico P-V, por lo que (a) es probablemente más impreciso que (b) o (c). El cálculo será tan preciso como lo permitan la ecuación y las mediciones.

Comprueba tu aprendizaje

Química en la vida cotidiana

La Respiración y la Ley de Boyle

¿Qué haces unas 20 veces por minuto durante toda tu vida, sin descanso y, a menudo, sin siquiera darte cuenta? La respuesta, por supuesto, es la respiración. ¿Como funciona? Resulta que las leyes de gases se aplican aquí. Tus pulmones absorben el gas que tu cuerpo necesita (oxígeno) y eliminan el gas residual (dióxido de carbono). Los pulmones están hechos de tejido esponjoso y elástico que se expande y contrae mientras respiras. Cuando inhalas, el diafragma y los músculos intercostales (los músculos entre las costillas) se contraen, lo que expande la cavidad torácica y aumenta el volumen de los pulmones. El aumento en el volumen conduce a una disminución en la presión (ley de Boyle). Esto hace que el aire fluya hacia los pulmones (de alta presión a baja presión). Cuando exhalas, el proceso se invierte: el diafragma y los músculos de las costillas se relajan, la cavidad toráxica se contrae y el volumen de los pulmones disminuye, lo que aumenta la presión (la ley de Boyle nuevamente) y el aire sale de los pulmones (de alta a baja presión). Luego inhalas y exhalas una y otra vez, repitiendo este ciclo de ley de Boyle por el resto de tu vida (figura 8.15).

Figura 8.15 La respiración se produce porque la expansión y contracción del volumen pulmonar crea pequeñas diferencias de presión entre los pulmones y los alrededores, lo que hace que el aire ingrese y salga de los pulmones.

Moles de Gas y Volumen: Ley de Avogadro

El científico italiano Amedeo Avogadro presentó una hipótesis en 1811 para explicar el comportamiento de los gases, afirmando que volúmenes iguales de todos los gases, medidos en las mismas condiciones de temperatura y presión, contienen el mismo número de moléculas.

Con el tiempo, esta relación fue respaldada por muchas observaciones experimentales según lo expresado por la ley de Avogadro: para un gas confinado, el volumen ($V$) y el número de moles (n) son directamente proporcionales si la presión y la temperatura permanecen constantes.

En forma de ecuación, esto se escribe como:

Las relaciones matemáticas también se pueden determinar para los otros pares de variables, como $P $ versus n y n versus $T$.

La siguiente simulación de PhET te permite bombear moléculas de gas en una caja y analizar qué sucede a medida que cambias el volumen, añades o eliminas el calor, cambias la gravedad, y mucho más. Puedes, además, medir la temperatura y la presión, y descubrir cómo las propiedades del gas varían en relación con lo demás.

La ley del gas ideal

Hasta este punto, se han discutido cuatro leyes separadas que relacionan la presión, el volumen, la temperatura y la cantidad de moles del gas:

• Ley de Boyle: PV = constante, constantes T y n
• Ley de Amonton: $\frac{P}{T}$ = constante, constantes V y n
• Ley de Charles: $\frac{V}{T}$ = constante, constantes P y n
• Ley de Avogadro: $\frac{V}{n}$ = constante, constantes P y T

La combinación de estas cuatro leyes produce la ley del gas ideal, una relación entre la presión, el volumen, la temperatura y el número de moles de un gas:

donde $P$ es la presión de un gas, $V$ es su volumen, $n$ es el número de moles del gas, $T$ es su temperatura en la escala de Kelvin, y R es una constante llamada la constante de gas ideal o la constante de gas universal. Las unidades utilizadas para expresar la presión, el volumen y la temperatura determinarán la forma adecuada de la constante de gas según lo requiera el análisis dimensional, siendo los valores más comúnmente encontrados $0.08206\; L \;atm\; mol^{–1}\; K^{–1}$ y $8.314\; kPa \;L\; mol^{–1}\; K^{–1}$

Se dice que los gases cuyas propiedades de $P$, $V$ y $T$ se describen con precisión por la ley del gas ideal (u otras leyes de los gases) exhiben un comportamiento ideal o se aproximan a los rasgos de un gas ideal.

Un gas ideal es una construcción hipotética que puede usarse junto con la teoría cinética molecular para explicar de manera efectiva las leyes de los gases como se describirá en un módulo posterior de este capítulo. Aunque todos los cálculos presentados en este módulo asumen un comportamiento ideal, esta suposición solo es razonable para gases en condiciones de presión relativamente baja y temperatura alta. En el módulo final de este capítulo, se introducirá una ley de gases modificada que explica el comportamiento no ideal observado para muchos gases a presiones relativamente altas y bajas temperaturas.

La ecuación del gas ideal contiene cinco términos, la constante de gas $R$ y las propiedades variables $P$, $V$, $n$ y $T$. La especificación de cualquiera de estos cuatro términos permitirá el uso de la ley del gas ideal para calcular el quinto término como se demuestra en el siguiente ejemplo.

Ejemplo 8.9

Usando la Ley del Gas Ideal

El metano, $CH_4$, está siendo considerado como un combustible alternativo para automóviles para reemplazar la gasolina. Un galón de gasolina podría ser reemplazado por 655 g de $CH_4$. ¿Cuál es el volumen de esta cantidad de metano a 25 °C y 745 torr?

Solución

Debemos reorganizar $PV = nRT$ para resolver $V$: $V = \frac{nRT}{P}$

Si elegimos usar $0.08206\; L \;atm\; mol^{–1}\; K^{–1}$, entonces la cantidad debe estar en moles, la temperatura debe estar en kelvin y la presión debe estar en atm.

Se necesitarían 1020 L (269 galones) de metano gaseoso a aproximadamente 1 atm de presión para reemplazar 1 galón de gasolina. Requieres un recipiente grande para contener suficiente metano a 1 atm para reemplazar varios galones de gasolina.

Comprueba tu aprendizaje

Si el número de moles de un gas ideal se mantiene constante bajo dos conjuntos diferentes de condiciones, se obtiene una relación matemática útil llamada ley de los gases combinados: $\frac{P_1V_1}{T_1} = \frac{P_2V2}{T_2}$ utilizando unidades de $atm$, $L$ y $K$. Ambos conjuntos de condiciones son iguales al producto de $n \times R$ (donde $n$ = el número de moles del gas y $R$ es la constante ideal de la ley del gas).

Ejemplo 8.10

Usando la Ley de Gas Combinado

Cuando se llena con aire, un tanque de buceo típico con un volumen de 13.2 L tiene una presión de 153 atm (Figura 8.16). Si la temperatura del agua es de 27 °C, ¿cuántos litros de aire proporcionará dicho tanque a los pulmones de un buzo a una profundidad de aproximadamente 70 pies en el océano donde la presión es de 3.13 atm?

Figura 8.16 Los buceadores usan aire comprimido para respirar bajo el agua (crédito: modificación del trabajo de Mark Goodchild).

Dejando que 1 represente el aire en el tanque de buceo y 2 represente el aire en los pulmones, y observando que la temperatura corporal (la temperatura que el aire estará en los pulmones) es de 37 °C, tenemos:

Resolviendo para $V_2$

(Nota: ten en cuenta que este ejemplo particular es uno en el que la suposición del comportamiento ideal del gas no es muy razonable, ya que involucra gases a presiones relativamente altas y bajas temperaturas. A pesar de esta limitación, el volumen calculado puede verse como una buena "estimación" aproximada).

Comprueba tu aprendizaje 6.10

Química en la vida cotidiana

La interdependencia entre la profundidad del océano y la presión en el buceo

Ya sea buceando en la Gran Barrera de Coral en Australia (que se muestra en la Figura 8.17) o en el Caribe, los buzos deben comprender cómo la presión afecta una serie de cuestiones relacionadas con su comodidad y seguridad.

Figura 8.17 Los buzos, ya sea en la Gran Barrera de Coral o en el Caribe, deben ser conscientes de la flotabilidad, la igualación de presión y la cantidad de tiempo que pasan bajo el agua, para evitar los riesgos asociados con los gases presurizados en el cuerpo (crédito: Kyle Taylor).

La presión aumenta con la profundidad del océano, y la presión cambia más rápidamente a medida que los buzos llegan a la superficie.

La presión que experimenta un buzo es la suma de todas las presiones sobre el buzo (del agua y del aire). La mayoría de las mediciones de presión se dan en unidades de atmósferas, expresadas como "atmósferas absolutas" o ATA en la comunidad de buceo: cada 33 pies de agua salada representa 1 ATA de presión además de 1 ATA de presión de la atmósfera al nivel del mar. A medida que un buzo desciende, el aumento de la presión hace que las bolsas de aire del cuerpo en los oídos y los pulmones se compriman; En el ascenso, la disminución de la presión hace que estas bolsas de aire se expandan, lo que podría romper los tímpanos o reventar los pulmones. Por lo tanto, los buzos deben someterse a la ecualización agregando aire a los espacios aéreos del cuerpo en el descenso respirando normalmente y agregando aire a la máscara respirando por la nariz o agregando aire a los oídos y los senos nasales mediante técnicas de ecualización; El corolario también es cierto en el ascenso, los buzos deben liberar aire del cuerpo para mantener la ecualización. La flotabilidad, o la capacidad de controlar si un buzo se hunde o flota, es controlada por el compensador de flotabilidad (BCD).

Si un buzo está ascendiendo, el aire en su BCD se expande debido a una presión más baja de acuerdo con la ley de Boyle (al disminuir la presión de los gases aumenta el volumen). El aire en expansión aumenta la flotabilidad del buzo, y él o ella comienza a ascender. El buzo debe ventilar el aire del BCD o arriesgarse a un ascenso incontrolado que podría romper los pulmones. Al descender, el aumento de la presión hace que el aire en el BCD se comprima y el buzo se hunde mucho más rápidamente; el buzo debe agregar aire al BCD o arriesgarse a un descenso descontrolado, enfrentando presiones mucho más altas cerca del fondo del océano. La presión también afecta cuánto tiempo puede permanecer un buzo bajo el agua antes de ascender.

Cuanto más se sumerge un buzo, más se comprime el aire que se respira debido al aumento de la presión: si un buzo se zambulle $33\,pies$, la presión es de $2\,Atm$ y el aire se comprimiría a la mitad de su volumen original. El buzo utiliza el aire disponible dos veces más rápido que en la superficie.

Condiciones estándar de temperatura y presión

Hemos visto que el volumen de una cantidad dada de gas y el número de moléculas (moles) en un volumen dado de gas varían con los cambios en la presión y la temperatura. Los químicos a veces hacen comparaciones con una temperatura y presión estándar (STP) para informar las propiedades de los gases: $273.15\,K$ y $1\,atm$ ($101.325\,kPa$)La definición IUPAC de presión estándar se cambió de $1\,atm$ a $1\,bar$ ($100\,kPa$) en 1982, pero la definición anterior sigue en uso en muchos recursos de la literatura y se utilizará en este texto.. En STP, un mol de un gas ideal tiene un volumen de aproximadamente $22.4\,L$, esto se refiere como el volumen molar estándar (Figura 8.18).

Figura 8.18 Independientemente de su identidad química, un mol de gas que se comporta idealmente ocupa un volumen de $~22.4\,L$ en STP.

Estequiometría de sustancias gaseosas, mezclas y reacciones

El estudio del comportamiento químico de los gases fue parte de la base de quizás la revolución química más fundamental de la historia. El noble francés Antoine Lavoisier, ampliamente considerado como el "padre de la química moderna", cambió la química de una ciencia cualitativa a una cuantitativa a través de su trabajo con gases. Descubrió la ley de conservación de la materia, descubrió el papel del oxígeno en las reacciones de combustión, determinó la composición del aire, explicó la respiración en términos de reacciones químicas y más. Fue víctima de la Revolución Francesa, guillotinado en 1794. De su muerte, el matemático y astrónomo Joseph-Louis Lagrange dijo: “A la mafia le tomó solo un momento quitarle la cabeza; un siglo no bastará para reproducirlo”"Citas de Joseph-Louis Lagrange", última modificación en febrero de 2006, consultado el 10 de febrero de 2015, http://www-history.mcs.st-andrews.ac.uk/ .

Como se describió en un capítulo anterior de este texto, podemos recurrir a la estequiometría química para obtener respuestas a muchas de las preguntas que preguntan "¿Cuánto?" La propiedad esencial involucrada en dicho uso de la estequiometría es la cantidad de sustancia, típicamente medida en moles ( $n$). Para los gases, la cantidad molar puede derivarse de convenientes mediciones experimentales de presión, temperatura y volumen. Por lo tanto, estas mediciones son útiles para evaluar la estequiometría de gases puros, mezclas de gases y reacciones químicas que involucran gases. Esta sección no presentará ningún material o ideas nuevos, pero proporcionará ejemplos de aplicaciones y formas de integrar conceptos ya discutidos.

Densidad del gas y masa molar

La ley de los gases ideales descrita anteriormente en este capítulo relaciona las propiedades de presión $P$, volumen $V$, temperatura $T$ y cantidad molar $n$. Esta ley es universal y relaciona estas propiedades de manera idéntica independientemente de la identidad química del gas:

La densidad $d$ de un gas, por otro lado, está determinada por su identidad. Como se describe en otro capítulo de este texto, la densidad de una sustancia es una propiedad característica que puede usarse para identificar la sustancia.

Reorganizando la ecuación del gas ideal para aislar $V$ y sustituyendo en la ecuación de densidad se obtiene

La relación m/n es la definición de masa molar:

La ecuación de densidad se puede escribir:

Esta relación puede usarse para calcular las densidades de gases de identidades conocidas a valores específicos de presión y temperatura como se demuestra en el Ejemplo 8.11.

Ejemplo 8.11

Medición de la densidad del gas

¿Cuál es la densidad del gas nitrógeno molecular en STP?

Solución

La masa molar de nitrógeno molecular, $N_2$, es $28.01\,g/mol$. Sustituyendo este valor junto con la temperatura y presión estándar en los resultados de la ecuación de densidad de gas:

Comprueba tu aprendizaje

Cuando se desconoce la identidad de un gas, las mediciones de la masa, la presión, el volumen y la temperatura de una muestra se pueden utilizar para calcular la masa molar del gas (una propiedad útil para fines de identificación). Combinando la ecuación de gas ideal

y la definción de molaridad

resulta la siguiente ecuación

La determinación de la masa molar de un gas mediante este enfoque se demuestra en el Ejemplo 9.12.

Ejemplo 8.12

Determinación de la fórmula molecular de un gas a partir de su masa molar y la fórmula empírica

El ciclopropano, un gas que alguna vez se usó con oxígeno como anestésico general, está compuesto por 85.7% de carbono y 14.3% de hidrógeno en masa. Encuentra la fórmula empírica. Si 1.56 g de ciclopropano ocupan un volumen de 1.00 L a 0.984 atm y 50 °C, ¿cuál es la fórmula molecular para el ciclopropano?

Solución

Primero determina la fórmula empírica del gas.

Supón 100 g y convierte el porcentaje de cada elemento en gramos. Determina la cantidad de moles de carbono e hidrógeno en la muestra de 100 g de ciclopropano. Dividir por el menor número de moles para relacionar el número de moles de carbono con el número de moles de hidrógeno. En el último paso, ten en cuenta que la razón de números enteros más pequeña es la fórmula empírica:

La fórmula empírica es $CH_2$ [masa empírica (EM) de 14.03 g/unidad empírica].

Luego, usa los valores proporcionados para masa, presión, temperatura y volumen para calcular la masa molar del gas:

$\mathscr{M} = \cfrac{mRT}{PV} = \cfrac{(1.56\;g)(0.0821\;L\cdot atm\cdot mol^{−1}K^{−1})(323\;K)}{(0.984\;atm)(1.00\;L)}$

La comparación de la masa molar con la masa de la fórmula empírica muestra cuántas unidades de la fórmula empírica forman una molécula:

La fórmula molecular se deriva de la fórmula empírica multiplicando cada uno de sus subíndices por tres:

Comprueba tu aprendizaje

Ejemplo 8.13

Determinación de la masa molar de un líquido volátil

La masa molar aproximada de un líquido volátil se puede determinar mediante:

1. Calentar una muestra del líquido en un matraz con un pequeño orificio en la parte superior, que convierte el líquido en gas que puede escapar a través del orificio


2. Retirar el matraz del calor en el instante en que el último bit de líquido se convierte en gas, momento en el cual el matraz se llenará solo con una muestra gaseosa a presión ambiente.

3. Sellar el matraz y permitir que la muestra gaseosa se condense en líquido, y luego pesar el matraz para determinar la masa de la muestra (ver Figura 8.19)

Figura 8.19 Cuando el líquido volátil en el matraz se calienta más allá de su punto de ebullición, se convierte en gas y expulsa el aire del matraz. En $\ce{t_{l -> g}}$, el matraz se llena con gas líquido volátil a la misma presión que la atmósfera. Si el matraz se enfría a temperatura ambiente, el gas se condensa y se puede medir la masa del gas que llenó el matraz y ahora es líquido (crédito: modificación del trabajo de Mark Ott).

Mediante este procedimiento, se recoge una muestra de gas cloroformo que pesa 0,494 g en un matraz con un volumen de $129\; cm^3$ a 99,6 &de;C cuando la presión atmosférica es de 742,1 mm Hg. ¿Cuál es la masa molar aproximada de cloroformo?

Solución

Como $\mathscr{M} = \frac{m}{n}$ y $n = \frac{PV}{RT}$, la sustitución y la reorganización dan $\mathscr{M} = \frac{mRT}{PV}$, entonces

Comprueba tu aprendizaje

La presión de una mezcla de gases: la ley de Dalton

A menos que reaccionen químicamente entre sí, los gases individuales en una mezcla de gases no afectan la presión del otro. Cada gas individual en una mezcla ejerce la misma presión que ejercería si estuviera presente solo en el recipiente (Figura 8.20). La presión ejercida por cada gas individual en una mezcla se llama presión parcial. Esta observación se resume en la ley de Dalton de presiones parciales: la presión total de una mezcla de gases ideales es igual a la suma de las presiones parciales de los gases componentes:

En la ecuación $P_{Total}$ es la presión total de una mezcla de gases, $P_A$ es la presión parcial del gas $A$; $P_B$ es la presión parcial del gas $B$; $P_C$ es la presión parcial del gas $C$; y así sucesivamente.

Figura 8.20 Si los cilindros de igual volumen que contienen gas A a una presión de 300 kPa, el gas B a una presión de 600 kPa y el gas C a una presión de 450 kPa se combinan en el cilindro del mismo tamaño, la presión total de la mezcla es 1350 kPa.

La presión parcial del gas $A$ está relacionada con la presión total de la mezcla de gases a través de su fracción molar (X), una unidad de concentración definida como el número de moles de un componente de una solución dividido por el número total de moles de todos los componentes:

donde $P_A$, $X_A$ y $n_A$ son la presión parcial, la fracción molar y el número de moles de gas $A$, respectivamente, y $n_{Total}$ es el número de moles de todos los componentes de la mezcla.

Ejemplo 8.14

La presión de una mezcla de gases

Un recipiente de 10.0 L contiene $2.50 \times 10^{−3}$ mol de $H_2$, $1.00 \times 10^{−3}$ mol de $He$ y $3.00 \times 10^{−4}$ mol de $Ne$ a 35 °C.

(a) ¿Cuáles son las presiones parciales de cada uno de los gases?
(b) ¿Cuál es la presión total en atmósferas?

Solución

Los gases se comportan de manera independiente, por lo que la presión parcial de cada gas se puede determinar a partir de la ecuación del gas ideal, utilizando $P = \frac{nRT}{V}$:

La presión total viene dada por la suma de las presiones parciales:

Comprueba tu aprendizaje

Ejemplo 8.15

La presión de una mezcla de gases

Una mezcla de gases utilizada para la anestesia contiene 2,83 moles de oxígeno, $O_2$ y 8,41 moles de óxido nitroso, $N_2O$. La presión total de la mezcla es de 192 kPa.

(a) ¿Cuáles son las fracciones molares de $O_2$ y $N_2O$?
(b) ¿Cuáles son las presiones parciales de $O_2$ y $N_2O$?

Solución

La fracción molar viene dada por $X_A = \frac{n_A}{n_{Total}}$ y la presión parcial es $P_A = X_A \times P_{Total}$.

Para $O_2$,

y $P_{O_2} = X_{O_2} \times P_{Total} = 0.252 \times 192\; kPa = 48.4\; kPa$

Para $N_2O$,

y $P_{N_2} = X_{N_2} \times P_{Total} = 0.748 \times 192\; kPa = 143.6\; kPa$

Comprueba tu aprendizaje

Recolección de gases sobre el agua

Una manera simple de recolectar gases que no reaccionan con el agua es capturarlos en una botella que se ha llenado con agua y se ha invertido en un plato lleno de agua. La presión del gas dentro de la botella se puede igualar a la presión del aire exterior al subir o bajar la botella. Cuando el nivel del agua es el mismo dentro y fuera de la botella (Figura 8.21), la presión del gas es igual a la presión atmosférica, que se puede medir con un barómetro.

Figura 8.21 Cuando una reacción produce un gas que se recoge sobre el agua, el gas atrapado es una mezcla del gas producido por la reacción y el vapor de agua. Si el matraz de recolección se coloca adecuadamente para igualar los niveles de agua tanto dentro como fuera del matraz, la presión de la mezcla de gases atrapados será igual a la presión atmosférica fuera del matraz (lee la discusión anterior sobre los manómetros).

Sin embargo, hay otro factor que debemos considerar cuando medimos la presión del gas por este método. El agua se evapora y siempre hay agua gaseosa (vapor de agua) sobre una muestra de agua líquida. Cuando un gas se recoge sobre el agua, se satura con vapor de agua y la presión total de la mezcla es igual a la presión parcial del gas más la presión parcial del vapor de agua. Por lo tanto, la presión del gas puro es igual a la presión total menos la presión del vapor de agua; esto se conoce como presión de gas "seco", es decir, la presión del gas solamente, sin vapor de agua.

La presión de vapor del agua, que es la presión ejercida por el vapor de agua en equilibrio con agua líquida en un recipiente cerrado, depende de la temperatura (Figura 8.22). Se puede encontrar información más detallada sobre la dependencia de la temperatura del vapor de agua en la Tabla 8.2, y la presión del vapor se discutirá con más detalle en el próximo capítulo sobre líquidos.

Figura 8.22 Este gráfico muestra la presión de vapor del agua al nivel del mar en función de la temperatura.

Tabla 8.2. Presión de vapor de hielo y agua a diversas temperaturas al nivel del mar

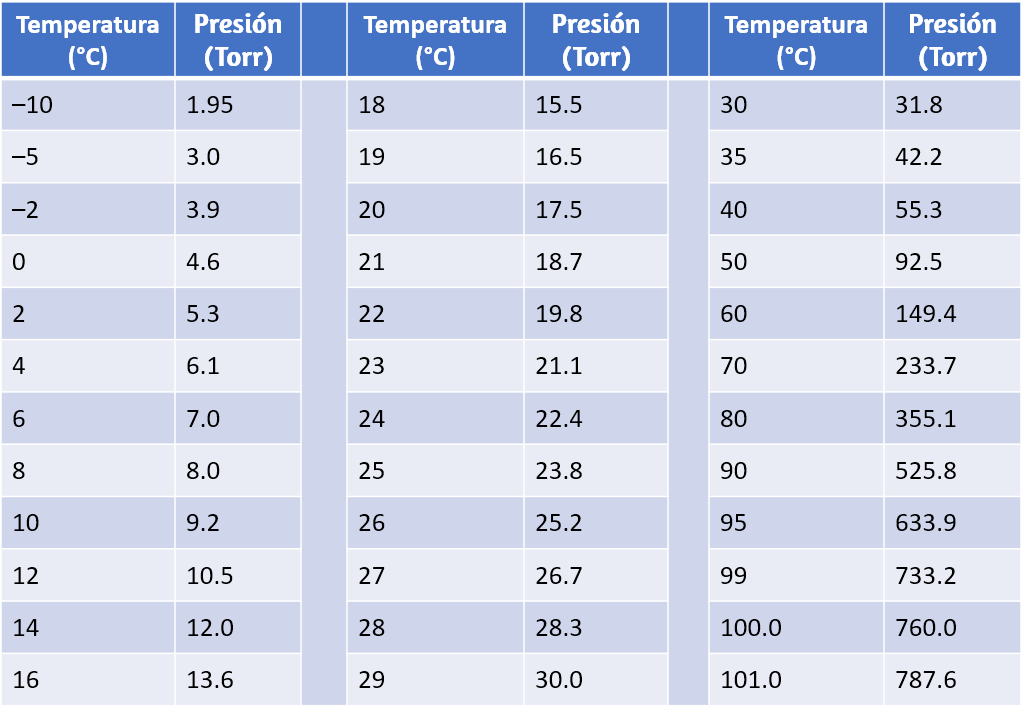
Ejemplo 8.16

Presión de un gas recogido sobre el agua

Si se recogen 0.200 L de argón sobre el agua a una temperatura de 26 °C y una presión de 750 torr en un sistema como el que se muestra en la figura 8.21, ¿cuál es la presión parcial de argón?

Solución

Según la ley de Dalton, la presión total en la botella (750 torr) es la suma de la presión parcial de argón y la presión parcial del agua gaseosa:

Al reorganizar esta ecuación para resolver la presión del argón se obtiene:

La presión del vapor de agua por encima de una muestra de agua líquida a 26 $deg;C es de 25.2 torr, entonces:

Comprueba tu aprendizaje

Estequiometría química y Gases

La estequiometría química describe las relaciones cuantitativas entre reactivos y productos en reacciones químicas.

Anteriormente hemos medido cantidades de reactivos y productos utilizando masas para sólidos y volúmenes junto con la molaridad para soluciones; ahora también podemos usar volúmenes de gas para indicar cantidades. Si conocemos el volumen, la presión y la temperatura de un gas, podemos usar la ecuación de gas ideal para calcular cuántos moles de gas hay presentes. Si sabemos cuántos moles de un gas están involucrados, podemos calcular el volumen de un gas a cualquier temperatura y presión.

Ley de Avogadro revisitada

A veces podemos aprovechar una característica simplificadora de la estequiometría de gases que los sólidos y las soluciones no exhiben: todos los gases que muestran un comportamiento ideal contienen el mismo número de moléculas en el mismo volumen (a la misma temperatura y presión). Por lo tanto, las proporciones de los volúmenes de gases involucrados en una reacción química están dados por los coeficientes en la ecuación para la reacción, siempre que los volúmenes de gas se midan a la misma temperatura y presión.

Podemos extender la ley de Avogadro (que el volumen de un gas es directamente proporcional a la cantidad de moles del gas) a reacciones químicas con gases: los gases se combinan o reaccionan, en proporciones definidas y simples por volumen, siempre que todos los volúmenes de gas sean medido a la misma temperatura y presión. Por ejemplo, dado que los gases de nitrógeno e hidrógeno reaccionan para producir gas amoniaco de acuerdo con $\ce{N_2 \; (g) + 3H_2 \;(g) -> 2NH_3\; (g)}$, un volumen dado de gas nitrógeno reacciona con tres veces ese volumen de gas hidrógeno para producir dos veces el volumen de gas amoniaco, si la presión y la temperatura permanecen constantes.

La explicación de esto se ilustra en la figura 8.23. Según la ley de Avogadro, volúmenes iguales de $N_2$, $H_2$ y $NH_3$ gaseosos, a la misma temperatura y presión, contienen la misma cantidad de moléculas. Debido a que una molécula de $N_2$ reacciona con tres moléculas de $H_2$ para producir dos moléculas de $NH_3$, el volumen de $H_2$ requerido es tres veces el volumen de $N_2$, y el volumen de $NH_3$ producido es dos veces el volumen de $N_2$.

Figura 8.23 Un volumen de $N_2$ se combina con tres volúmenes de $H_2$ para formar dos volúmenes de $NH_3$.

Ejemplo 8.17

Reacción de gases

El propano, $C_3H_8\; (g)$, se usa en parrillas de gas para proporcionar el calor para cocinar. ¿Qué volumen de $O_2\; (g)$ medido a 25 °C y 760 torr se requiere para reaccionar con 2.7 L de propano medido en las mismas condiciones de temperatura y presión? Supón que el propano sufre una combustión completa.

Solución

La relación de los volúmenes de $C_3H_8$ y $O_2$ será igual a la relación de sus coeficientes en la ecuación balanceada para la reacción:

De la ecuación, vemos que un volumen de $C_3H_8$ reaccionará con cinco volúmenes de $O_2$:

Se requerirá un volumen de 13.5 L de $O_2$ para reaccionar con 2.7 L de $C_3H_8$.

Comprueba tu aprendizaje

Ejemplo 8.18

Volúmenes de gases reactivos

El amoniaco es un importante fertilizante y químico industrial. Supón que se fabricó un volumen de 683 mil millones de pies cúbicos de amoníaco gaseoso, medido a 25 °C y 1 atm. ¿Qué volumen de $H_2\; (g)$, medido en las mismas condiciones, se requirió para preparar esta cantidad de amoníaco por reacción con $N_2$?

Solución

Debido a que volúmenes iguales de $H_2$ y $NH_3$ contienen cantidades iguales de moléculas y cada tres moléculas de $H_2$ que reaccionan producen dos moléculas de $NH_3$, la proporción de los volúmenes de $H_2$ y $NH_3$ será igual a 3:2. Se formarán dos volúmenes de $NH_3$, en este caso en unidades de mil millones de pies³, a partir de tres volúmenes de $H_2$:

La fabricación de 683 mil millones de pies³ de $NH_3$ requirió 1020 mil millones de pies³ de $H_2$ (a 25 °C y 1 atm, este es el volumen de un cubo con una longitud de borde de aproximadamente 1.9 millas).

Comprueba tu aprendizaje

Ejemplo 8.19

Volumen de producto gaseoso

¿Qué volumen de hidrógeno a 27 °C y 723 torr puede prepararse mediante la reacción de 8,88 g de galio con un exceso de ácido clorhídrico?

Solución

Convierte la masa proporcionada del reactivo limitante, $Ga$, en moles de hidrógeno producido:

Convierte los valores de temperatura y presión proporcionados en unidades apropiadas (K y atm, respectivamente), y luego usa la cantidad molar de gas hidrógeno y la ecuación de gas ideal para calcular el volumen de gas:

Comprueba tu aprendizaje

Química en la vida cotidiana

Gases de efecto invernadero y cambio climático

La delgada piel de nuestra atmósfera evita que la tierra sea un planeta helado y la hace habitable. De hecho, esto se debe a menos del 0.5% de las moléculas de aire.

De la energía del sol que llega a la tierra, casi 13 se reflejan nuevamente en el espacio, y el resto es absorbido por la atmósfera y la superficie de la tierra. Parte de la energía que absorbe la Tierra es reemitida como radiación infrarroja (IR), una parte de la cual regresa a través de la atmósfera al espacio. La mayoría de esta radiación IR, sin embargo, es absorbida por ciertos gases atmosféricos, atrapando efectivamente el calor dentro de la atmósfera en un fenómeno conocido como efecto invernadero. Este efecto mantiene las temperaturas globales dentro del rango necesario para mantener la vida en la tierra. Sin nuestra atmósfera, la temperatura promedio de la Tierra sería más baja en más de 30 °C (casi 60 °F). Los principales gases de efecto invernadero (GEI) son vapor de agua, dióxido de carbono, metano y ozono.

Figura 8.24 Los gases de efecto invernadero atrapan suficiente energía del sol para hacer habitable el planeta; esto se conoce como efecto invernadero. Las actividades humanas están aumentando los niveles de gases de efecto invernadero, calentando el planeta y causando eventos climáticos más extremos.

Desde la Revolución Industrial, la actividad humana ha aumentado las concentraciones de GEI, lo que ha cambiado el equilibrio energético y está alterando significativamente el clima de la Tierra (Figura 8.24).

Existe una fuerte evidencia de múltiples fuentes de que los niveles más altos de $CO_2$ en la atmósfera son causados por la actividad humana, y la quema de combustibles fósiles representa aproximadamente 34 del reciente aumento en $CO_2$. Los datos confiables de los núcleos de hielo revelan que la concentración de $CO_2$ en la atmósfera está en el nivel más alto en los últimos 800,000 años; otra evidencia indica que puede estar en su nivel más alto en 20 millones de años. En los últimos años, la concentración de $CO_2$ ha aumentado los niveles preindustriales de ~280 ppm a más de 400 ppm en la actualidad (Figura 8.25).

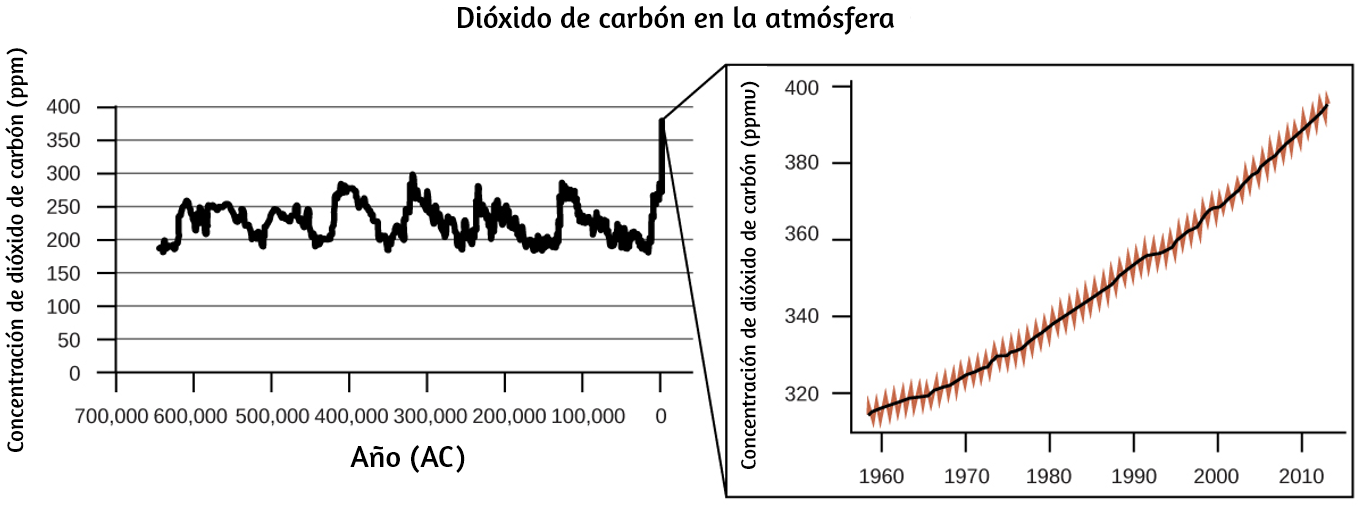
Figura 8.25 Los niveles de $CO_2$ en los últimos 700,000 años fueron típicamente de 200 a 300 ppm, con un fuerte aumento sin precedentes en los últimos 50 años.

Presentamos, en la página siguiente, una unidad interactiva "¿Por qué se dice que la Tierra se está sobrecalentando?", que hace parte de la serie @prende.mx, publicada en la Red Educativa Digital Descartes.

Difusión y efusión de gases

Si alguna vez has estado en una habitación cuando se te entregó una pizza caliente, has advertido el hecho de que las moléculas gaseosas pueden extenderse rápidamente por toda la habitación, como lo demuestra el agradable aroma que pronto llega a tu nariz. Aunque las moléculas gaseosas viajan a velocidades tremendas (cientos de metros por segundo), chocan con otras moléculas gaseosas y viajan en muchas direcciones diferentes antes de alcanzar el objetivo deseado. A temperatura ambiente, una molécula gaseosa experimentará miles de millones de colisiones por segundo. La ruta libre media es la distancia promedio que recorre una molécula entre colisiones. El camino libre medio aumenta con la disminución de la presión; en general, el camino libre medio para una molécula gaseosa será cientos de veces el diámetro de la molécula.

En general, sabemos que cuando se introduce una muestra de gas en una parte de un recipiente cerrado, sus moléculas se dispersan muy rápidamente por todo el recipiente; Este proceso por el cual las moléculas se dispersan en el espacio en respuesta a las diferencias de concentración se llama difusión (se muestra en la figura 8.27). Los átomos o moléculas gaseosas, por supuesto, desconocen cualquier gradiente de concentración, simplemente se mueven al azar: las regiones de mayor concentración tienen más partículas que las regiones de concentraciones más bajas, por lo que se produce un movimiento neto de especies de áreas de alta a baja concentración. En un ambiente cerrado, la difusión en última instancia dará como resultado concentraciones iguales de gas, como se muestra en la figura 8.27. Los átomos y las moléculas gaseosas continúan moviéndose, pero dado que sus concentraciones son las mismas en ambas bombillas, las tasas de transferencia entre las bombillas son iguales (no se produce una transferencia neta de moléculas).

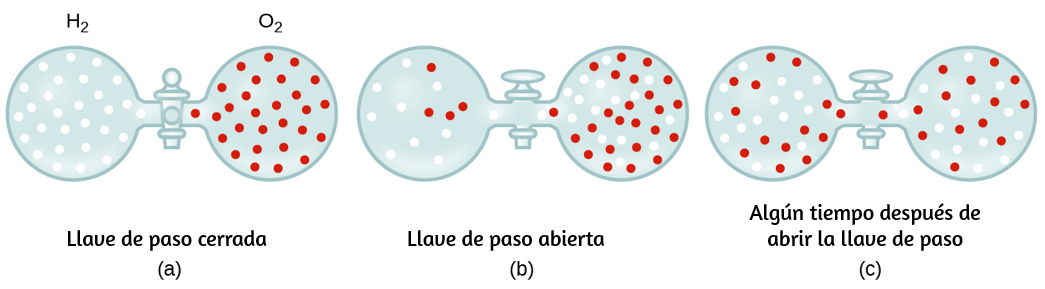
Figura 8.27 (a) Dos gases, $H_2$ y $O_2$, se separan inicialmente. (b) Cuando se abre la llave de paso, se mezclan. El gas más ligero, $H_2$, pasa a través de la abertura más rápido que el $O_2$, por lo que justo después de abrir la llave de paso, más moléculas de $H_2$ se mueven hacia el lado $O_2$ que las moléculas de $O_2$ hacia el lado $H_2$. (c) Después de un corto tiempo, tanto las moléculas de $O_2$ que se mueven más lentamente como las moléculas de $H_2$ que se mueven más rápido se han distribuido uniformemente en ambos lados del recipiente.

A menudo nos interesa la tasa de difusión, la cantidad de gas que pasa por un área por unidad de tiempo:

$\text{tasa de difusión} = \cfrac{\text{cantidad de gas que pasa a través de un área}}{\text{unidad de tiempo}}$

La tasa de difusión depende de varios factores: el gradiente de concentración (el aumento o disminución de la concentración de un punto a otro); la cantidad de superficie disponible para la difusión; y la distancia que deben recorrer las partículas de gas. Ten en cuenta también que el tiempo requerido para que se produzca la difusión es inversamente proporcional a la tasa de difusión, como se muestra en la ecuación de tasa de difusión.

Un proceso que implica el movimiento de especies gaseosas similar a la difusión es el derrame o efusión, el escape de las moléculas de gas a través de un pequeño agujero como un agujero en un globo hacia el vacío (figura 8.28).

Aunque las tasas de difusión y efusión dependen de la masa molar del gas involucrado, sus tasas no son iguales; sin embargo, las proporciones de sus tasas son las mismas.

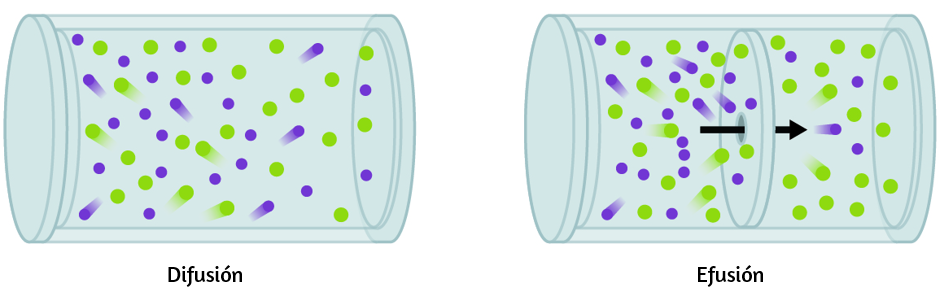
Figura 8.28 La difusión implica la dispersión irrestricta de moléculas por el espacio debido a su movimiento aleatorio. Cuando este proceso se restringe al paso de moléculas a través de aberturas muy pequeñas en una barrera física, el proceso se llama derrame o efusión.

Si se coloca una mezcla de gases en un recipiente con paredes porosas, los gases fluyen a través de las pequeñas aberturas en las paredes. Los gases más ligeros pasan a través de las pequeñas aberturas más rápidamente (a una tasa mayor) que los más pesados (Figura 8.29). En 1832, Thomas Graham estudió las tasas de efusión de diferentes gases y formuló la ley de efusión de Graham: la tasa de efusión de un gas es inversamente proporcional a la raíz cuadrada de la masa de sus partículas:

Esto significa que si dos gases A y B están a la misma temperatura y presión, la proporción de sus tasas de efusión es inversamente proporcional a la proporción de las raíces cuadradas de las masas de sus partículas:

Figura 8.29 La fotografía de la izquierda muestra dos globos inflados con diferentes gases, helio (naranja) y argón (azul). La fotografía del lado derecho muestra los globos aproximadamente 12 horas después de haberse llenado, momento en el cual el globo de helio se ha desinflado notablemente más que el globo con argón, debido a la mayor tasa de efusión del gas helio es más ligero (crédito: modificación del trabajo de Paul Flowers).

Ejemplo 8.20

Aplicación de la ley de Graham a las tasas de efusión

Calcula la relación de la tasa de efusión de hidrógeno a la tasa de efusión de oxígeno.

Solución

De la ley de Graham, tenemos:

Comprueba tu aprendizaje

Ejemplo 8.21

Cálculos del tiempo de efusión

Se necesitan 243 s para que $4.46 \times 10^{−5} mol\,de\,Xe$ se derramen a través de un pequeño agujero. En las mismas condiciones, ¿cuánto tiempo demorará $4.46 \times 10^{−5} mol\,de\,Ne$?

Solución

Es importante resistir la tentación de usar los tiempos directamente y recordar cómo la tasa se relaciona con el tiempo y cómo se relaciona con la masa. Recordemos la definición de tasa de derrame:

y combinarlo con la ley de Graham:

Llegamos a

Observando que cantidad de A = cantidad de B, y resolviendo el tiempo para Ne:

Sustituyendo valores:

Finalmente, halla la cantidad deseada:

Ten en cuenta que esta respuesta es razonable: dado que $Ne$ es más liviano que $Xe$, la tasa de efusión para $Ne$ será mayor que la de $Xe$, lo que significa que el tiempo de efusión para $Ne$ será menor que para $Xe$.

Comprueba tu aprendizaje

Ejemplo 8.22

Determinación de la masa molar usando la ley de Graham

Un gas desconocido se vierte 1,66 veces más rápido que el $CO_2$. ¿Cuál es la masa molar del gas desconocido? ¿Puedes hacer una suposición razonable sobre su identidad?

Solución

De la ley de Graham, tenemos:

Reemplazando datos conocidos:

Resolviendo:

El gas bien podría ser $CH_4$, el único gas con esta masa molar.

Comprueba tu aprendizaje 6.10

Química en la vida cotidiana

Uso de la difusión para aplicaciones de energía nuclear: enriquecimiento de uranio

La difusión gaseosa se ha utilizado para producir uranio enriquecido para su uso en plantas de energía nuclear y armas. El uranio natural contiene solo el 0,72% de $^{235}U$, el tipo de uranio que es "fisible", es decir, capaz de mantener una reacción en cadena de fisión nuclear. Los reactores nucleares requieren un combustible que es de 2 a 5% de $^{235}U$, y las bombas nucleares necesitan concentraciones aún mayores.

Una forma de enriquecer uranio a los niveles deseados es aprovechar la ley de Graham. En una planta de enriquecimiento por difusión gaseosa, el hexafluoruro de uranio ($UF_6$, el único compuesto de uranio que es lo suficientemente volátil para funcionar) se bombea lentamente a través de grandes vasos cilíndricos llamados difusores, que contienen barreras porosas con aberturas microscópicas. El proceso es de difusión porque el otro lado de la barrera no se evacua. Las moléculas de $^{235}UF_6$ tienen una velocidad promedio más alta y se difunden a través de la barrera un poco más rápido que las moléculas de $^{238}UF_6$ más pesadas. El gas que ha pasado a través de la barrera está ligeramente enriquecido en $^{235}UF_6$ y el gas residual está ligeramente agotado. La pequeña diferencia en los pesos moleculares entre $^{235}UF_6$ y $^{238}UF_6$ solo alrededor del 0,4% de enriquecimiento, se logra en un difusor (Figura 8.30). Pero al conectar muchos difusores en una secuencia de etapas (llamada cascada), se puede alcanzar el nivel deseado de enriquecimiento.

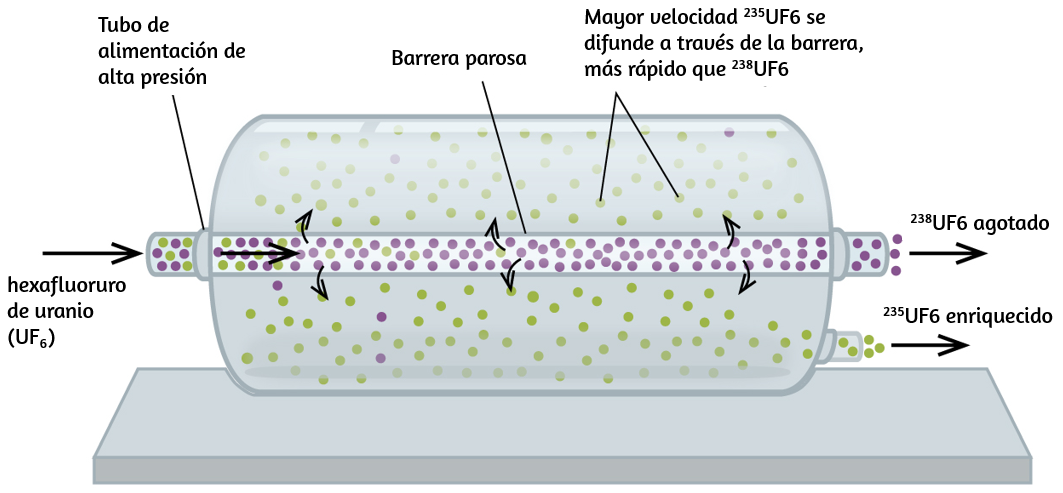
Figura 8.30 En un difusor, el $UF_6$ gaseoso se bombea a través de una barrera porosa, que separa parcialmente $^{235}UF_6$ de $^{238}UF_6$. El $UF_6$ debe pasar a través de muchas unidades difusoras grandes para lograr un enriquecimiento suficiente en $^{235}U$.

La separación a gran escala del $^{235}UF_6$ gaseoso del $^{238}UF_6$ se realizó por primera vez durante la Segunda Guerra Mundial, en la instalación de energía atómica en Oak Ridge, Tennessee, como parte del Proyecto Manhattan (el desarrollo de la primera bomba atómica). Aunque la teoría es simple, esto requirió superar muchos desafíos técnicos desalentadores para que funcione en la práctica. La barrera debe tener agujeros pequeños y uniformes (de unos 10 a 6 cm de diámetro) y ser lo suficientemente porosa como para producir altos caudales. Todos los materiales (barrera, tubería, recubrimientos de superficie, lubricantes y juntas) deben poder contener, pero no reaccionar, con el $UF_6$ altamente reactivo y corrosivo.

Debido a que las plantas de difusión gaseosa requieren grandes cantidades de energía (para comprimir el gas a las altas presiones requeridas y conducirlo a través de la cascada del difusor, para eliminar el calor producido durante la compresión, etc.), ahora está siendo reemplazado por tecnología de centrífuga de gas , que requiere mucha menos energía. Un tema político candente actual es cómo negar esta tecnología a Irán, para evitar que produzca suficiente uranio enriquecido para que puedan usarlo para fabricar armas nucleares.

La teoría cinética-molecular

Las leyes de los gases que hemos visto hasta este momento, así como la ecuación de los gases ideales, son empíricas, es decir, se han derivado de observaciones experimentales. Las formas matemáticas de estas leyes describen de cerca el comportamiento macroscópico de la mayoría de los gases a presiones inferiores a 1 o 2 atm. Aunque las leyes de gases describen relaciones que han sido verificadas por muchos experimentos, no nos dicen por qué los gases siguen estas relaciones.

La teoría cinética molecular (KMT, por sus siglas en inglés) es un modelo microscópico simple que explica de manera efectiva las leyes de gases descritas en módulos anteriores de este capítulo. Esta teoría se basa en los siguientes cinco postulados descritos aquí (Nota: el término "molécula" se utilizará para referirse a las especies químicas individuales que componen el gas, aunque algunos gases están compuestos de especies atómicas, por ejemplo, los gases nobles).

1. Los gases están compuestos de moléculas que están en movimiento continuo, viajan en línea recta y cambian de dirección solo cuando chocan con otras moléculas o con las paredes de un recipiente.
2. Las moléculas que componen el gas son insignificantemente pequeñas en comparación con las distancias entre ellas.
3. La presión ejercida por un gas en un contenedor resulta de colisiones entre las moléculas de gas y las paredes del contenedor.
4. Las moléculas de gas no ejercen fuerzas atractivas o repulsivas entre sí o las paredes del recipiente; por lo tanto, sus colisiones son elásticas (no implican una pérdida de energía).
5. La energía cinética promedio de las moléculas del gas es proporcional a la temperatura del gas en Kelvin.

La prueba del KMT y sus postulados es su capacidad para explicar y describir el comportamiento de un gas. Las diversas leyes de los gases pueden derivarse de los supuestos del KMT, que han llevado a los químicos a creer que los supuestos de la teoría representan con precisión las propiedades de las moléculas de los gases. Primero veremos las leyes individuales del gas (las leyes de Boyle, Charles, Amonton, Avogadro y Dalton) conceptualmente para ver cómo el KMT las explica.

Luego, consideraremos más cuidadosamente las relaciones entre las masas moleculares, las velocidades y las energías cinéticas con la temperatura, y explicaremos la ley de Graham.

La teoría cinética-molecular explica el
comportamiento de los gases, parte I

Recordando que la presión del gas se ejerce al mover rápidamente las moléculas del gas y depende directamente del número de moléculas que golpean un área unitaria de la pared por unidad de tiempo, vemos que el KMT explica conceptualmente el comportamiento de un gas de la siguiente manera:

• La ley de Amonton. Si se aumenta la temperatura, aumentan la velocidad media y la energía cinética de las moléculas del gas. Si el volumen se mantiene constante, el aumento de la velocidad de las moléculas del gas resulta en colisiones más frecuentes y más contundentes con las paredes del contenedor, lo que aumenta la presión (Figura 8.31).
• La ley de Charles. Si aumenta la temperatura de un gas, se puede mantener una presión constante solo si aumenta el volumen ocupado por el gas. Esto dará como resultado mayores distancias promedio recorridas por las moléculas para llegar a las paredes del contenedor, así como un área de superficie de pared incrementada. Estas condiciones disminuirán tanto la frecuencia de las colisiones de la pared de la molécula como el número de colisiones por unidad de área, cuyos efectos combinados equilibran el efecto del aumento de las fuerzas de colisión debido a la mayor energía cinética a la temperatura más alta.

• Ley de Boyle. Si el volumen de gas disminuye, el área de la pared del recipiente disminuye y la frecuencia de colisión de la pared de la molécula aumenta, lo que aumenta la presión ejercida por el gas (Figura 8.31).
• Ley de Avogadro. A presión y temperatura constantes, la frecuencia y la fuerza de las colisiones de la pared de la molécula son constantes. En tales condiciones, el aumento del número de moléculas gaseosas requerirá un aumento proporcional en el volumen del contenedor para producir una disminución en el número de colisiones por unidad de área para compensar la mayor frecuencia de colisiones (Figura 8.31).

Figura 8.31 (a) Cuando la temperatura del gas aumenta, la presión del gas aumenta debido al aumento de la fuerza y la frecuencia de las colisiones moleculares. (b) Cuando el volumen disminuye, la presión del gas aumenta debido a la mayor frecuencia de colisiones moleculares. (c) Cuando la cantidad de gas aumenta, a una presión constante, el volumen aumenta para producir un número constante de colisiones por unidad de área de pared por unidad de tiempo.

• Ley de Dalton. Debido a las grandes distancias entre ellos, las moléculas de un gas en una mezcla bombardean las paredes del recipiente con la misma frecuencia, ya sea que haya otros gases presentes o no, y la presión total de una mezcla de gases es igual a la suma de las presiones (parciales) de los gases individuales.

Velocidades moleculares y energía cinética

La discusión previa mostró que el KMT explica cualitativamente los comportamientos descritos por las diversas leyes de los gases. Los postulados de esta teoría pueden aplicarse de manera más cuantitativa para deducir estas leyes individuales. Para hacer esto, primero debemos observar las velocidades y las energías cinéticas de las moléculas del gas, y la temperatura de una muestra de gas.

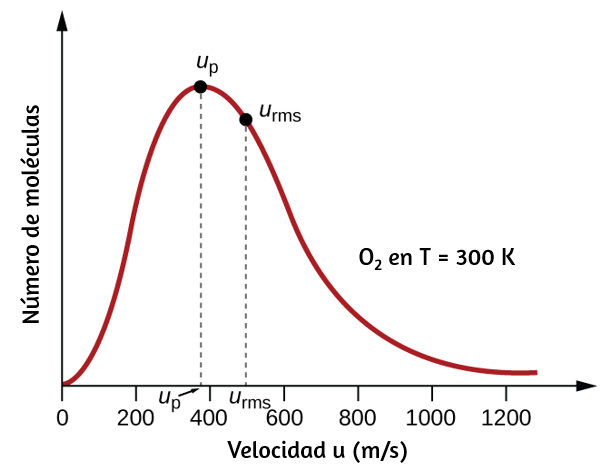
Figura 8.32 La distribución de la velocidad molecular para el gas oxígeno a 300 K se muestra aquí. Muy pocas moléculas se mueven a velocidades muy bajas o muy altas. El número de moléculas con velocidades intermedias aumenta rápidamente hasta un máximo, que es la velocidad más probable, luego disminuye rápidamente. Ten en cuenta que la velocidad más probable, $\nu_p$, es un poco menor que 400 m/s, mientras que la velocidad cuadrática media raíz, $u_{rms}$, está más cerca de 500 m/s.

En una muestra de gas, las moléculas individuales tienen velocidades muy variables; sin embargo, debido a la gran cantidad de moléculas y colisiones involucradas, la distribución de la velocidad molecular y la velocidad promedio son constantes. Esta distribución de velocidad molecular se conoce como distribución de Maxwell-Boltzmann, y representa los números relativos de moléculas en una muestra de gas a granel que posee una velocidad dada (Figura 8.32).

La energía cinética (KE) de una partícula de masa (m) y velocidad (u) viene dada por:

Expresar masa en kilogramos y velocidad en metros por segundo producirá valores de energía en unidades de julios ($J = kg\; m^2\; s^{–2}$). Para lidiar con una gran cantidad de moléculas de gas, utilizamos promedios tanto para la velocidad como para la energía cinética. En el KMT, la velocidad cuadrática media de la raíz de una partícula, $u_{rms}$, se define como la raíz cuadrada del promedio de los cuadrados de las velocidades con n = al número de partículas:

La energía cinética promedio para un mol de partículas, $KE_{prom}$, es entonces igual a:

donde M es la masa molar expresada en unidades de kg/mol.

La $KE_{prom}$ de un mol de moléculas del gas también es directamente proporcional a la temperatura del gas y puede describirse mediante la ecuación:

donde R es la constante del gas y T es la temperatura en Kelvin. Cuando se usa en esta ecuación, la forma apropiada de la constante de gas es $8.314\; J/mol\cdot K$ ($8.314\; kg\; m^2\; s^{–2}\; mol^{–1}\;K^{–1}$). Estas dos ecuaciones separadas para KE_{prom} se pueden combinar y reorganizar para producir una relación entre la velocidad molecular y la temperatura:

Ejemplo 8.23

Cálculo de $u_{rms}$

Calcula la velocidad media cuadrática de la raíz de una molécula de nitrógeno a 30 °C.

Solución

Convierte la temperatura a Kelvin:

Determina la masa molar de nitrógeno en kilogramos:

Reemplaza las variables y constantes en la ecuación de velocidad cuadrática media de la raíz, reemplazando Joules con el equivalente $kg\; m^2\; s^{–2}$:

Comprueba tu aprendizaje

Si la temperatura de un gas aumenta, su $KE_{prom}$ aumenta, más moléculas tienen velocidades más altas y menos moléculas tienen velocidades más bajas, y la distribución cambia hacia velocidades más altas en general, es decir, hacia la derecha. Si la temperatura disminuye, $KE_{prom}$ disminuye, más moléculas tienen velocidades más bajas y menos moléculas tienen velocidades más altas, y la distribución cambia hacia velocidades más bajas en general, es decir, hacia la izquierda. Este comportamiento se ilustra para el gas nitrógeno en la figura 8.33.

Figura 8.33 La distribución de la velocidad molecular del gas nitrógeno ($N_2$) se desplaza hacia la derecha y se aplana a medida que aumenta la temperatura; Se desplaza hacia la izquierda y aumenta a medida que disminuye la temperatura.

A una temperatura dada, todos los gases tienen el mismo $KE_{prom}$ para sus moléculas. Los gases compuestos de moléculas más ligeras tienen más partículas de alta velocidad y u_rms más altos, con una distribución de velocidad que alcanza su punto máximo a velocidades relativamente más altas. Los gases que consisten en moléculas más pesadas tienen más partículas de baja velocidad, u_rms más bajos y una distribución de velocidad que alcanza su punto máximo a velocidades relativamente más bajas. Los datos de una serie de gases nobles que se muestran en la figura 8.34 demuestran esta tendencia.

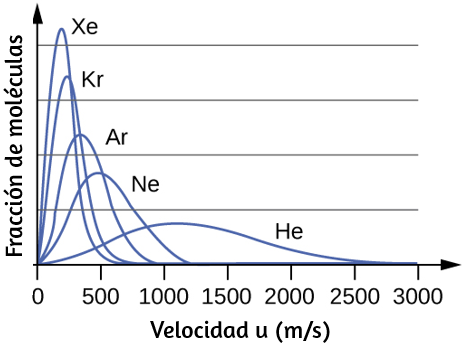
Figura 8.34 La velocidad molecular está directamente relacionada con la masa molecular. A una temperatura dada, las moléculas más ligeras se mueven más rápido en promedio que las moléculas más pesadas.

La simulación de PhET, que presentamos nuevamente, puede usarse para examinar el efecto de la temperatura en las velocidades moleculares.

Examina los "histogramas de energía" del simulador (distribuciones de velocidad molecular) y la "información de especies" (que proporciona valores de velocidad promedio) para moléculas de diferentes masas a varias temperaturas.

La teoría cinética-molecular explica el comportamiento de los gases, parte II

Según la ley de Graham, las moléculas de un gas se mueven rápidamente y las moléculas en sí mismas son pequeñas. La distancia promedio entre las moléculas de un gas es grande en comparación con el tamaño de las moléculas.

Como consecuencia, las moléculas de gas pueden pasar fácilmente entre sí y difundirse a velocidades relativamente rápidas.

La tasa de efusión de un gas depende directamente de la velocidad (promedio) de sus moléculas:

Usando esta relación, y la ecuación que relaciona la velocidad molecular con la masa, la ley de Graham puede derivarse fácilmente como se muestra aquí:

La relación de las tasas de efusión se deduce, por lo tanto, inversamente proporcional a la relación de las raíces cuadradas de sus masas. Esta es la misma relación observada experimentalmente y expresada como la ley de Graham.

Comportamiento del gas no ideal

Hasta ahora, la ley del gas ideal, $PV = nRT$, se ha aplicado a una variedad de diferentes tipos de problemas, que van desde la estequiometría de reacción y los problemas de fórmulas empíricas y moleculares hasta la determinación de la densidad y la masa molar de un gas. Sin embargo, como se mencionó en los módulos anteriores de este capítulo, el comportamiento de un gas a menudo no es ideal, lo que significa que las leyes observadas no describen con precisión las relaciones observadas entre su presión, volumen y temperatura. En esta sección, se consideran las razones de estas desviaciones del comportamiento ideal del gas.

Una forma de juzgar la precisión de $PV = nRT$ es comparando el volumen real de 1 mol de gas (su volumen molar, $V_m$) con el volumen molar de un gas ideal a la misma temperatura y presión. Esta relación se llama factor de compresibilidad (Z) con:

Por lo tanto, el comportamiento del gas ideal se indica cuando esta relación es igual a 1, y cualquier desviación de 1 es una indicación de un comportamiento no ideal. La figura 8.35 muestra gráficos de Z en un amplio rango de presión para varios gases comunes.

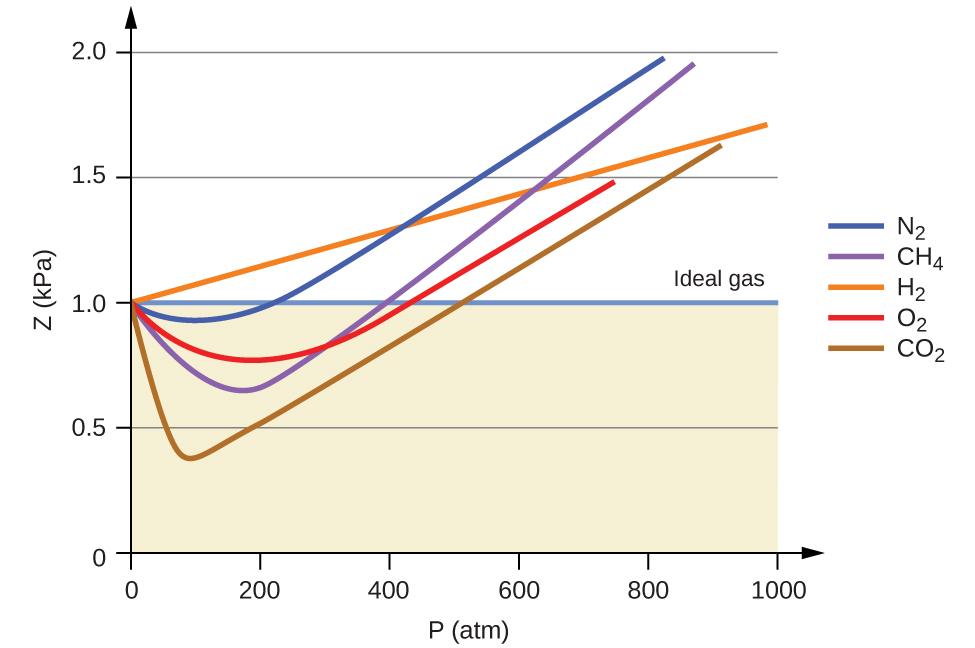
Figura 8.35 Un gráfico del factor de compresibilidad (Z) frente a la presión muestra que los gases pueden exhibir desviaciones significativas del comportamiento predicho por la ley de los gases ideales.

Como se desprende de la figura 8.35, la ley del gas ideal no describe bien el comportamiento del gas a presiones relativamente altas. Para determinar por qué es esto, considera las diferencias entre las propiedades del gas real y lo que se espera de un gas ideal hipotético.

Las partículas de un gas ideal hipotético no tienen un volumen significativo y no se atraen ni se repelen entre sí. En general, los gases reales se aproximan a este comportamiento a presiones relativamente bajas y altas temperaturas. Sin embargo, a altas presiones, las moléculas de un gas se apiñan más juntas y se reduce la cantidad de espacio vacío entre las moléculas.

A estas presiones más altas, el volumen de las propias moléculas de gas se vuelve apreciable en relación con el volumen total ocupado por el gas. Por lo tanto, el gas se vuelve menos compresible a estas altas presiones, y aunque su volumen continúa disminuyendo con el aumento de la presión, esta disminución no es proporcional como lo predice la ley de Boyle.

A presiones relativamente bajas, las moléculas de gas prácticamente no se atraen entre sí porque están (en promedio) muy separadas, y se comportan casi como partículas de un gas ideal. Sin embargo, a presiones más altas, la fuerza de atracción ya no es insignificante. Esta fuerza atrae las moléculas un poco más juntas, disminuyendo ligeramente la presión (si el volumen es constante) o disminuyendo el volumen (a presión constante) (figura 8.36).

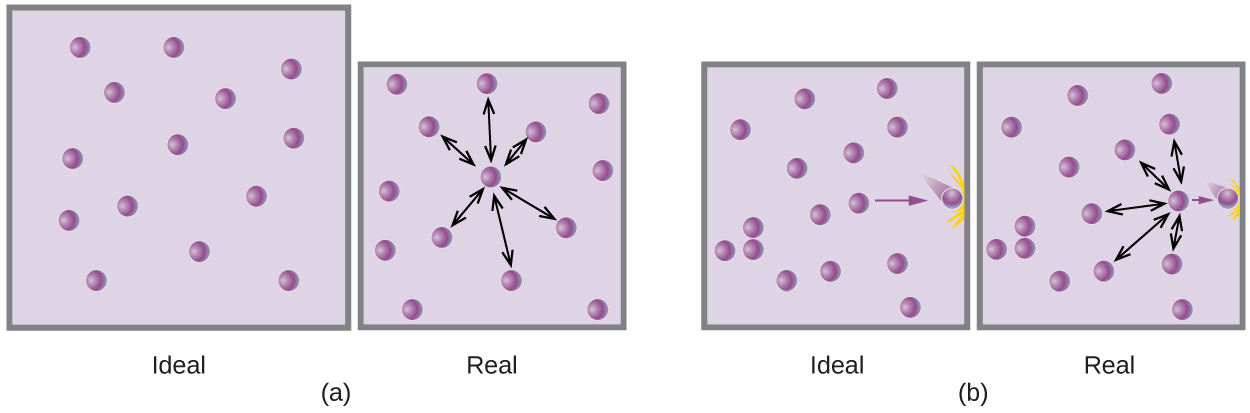
Figura 8.36 a) Las atracciones entre las moléculas de gas sirven para disminuir el volumen de gas a presión constante en comparación con un gas ideal cuyas moléculas no experimentan fuerzas atractivas. (b) Estas fuerzas atractivas disminuirán la fuerza de las colisiones entre las moléculas y las paredes del recipiente, reduciendo así la presión ejercida a un volumen constante en comparación con un gas ideal.

Este cambio es más pronunciado a bajas temperaturas porque las moléculas tienen un KE más bajo en relación con las fuerzas de atracción, por lo que son menos efectivas para superar estas atracciones después de chocar entre sí.

Existen varias ecuaciones diferentes que se aproximan mejor al comportamiento del gas que la ley de los gases ideales. El primero, y el más simple, fue desarrollado por el científico holandés Johannes van der Waals en 1879. La ecuación de van der Waals mejora la ley del gas ideal al agregar dos términos: uno para dar cuenta del volumen de las moléculas de gas y otro para Las fuerzas atractivas entre ellos.

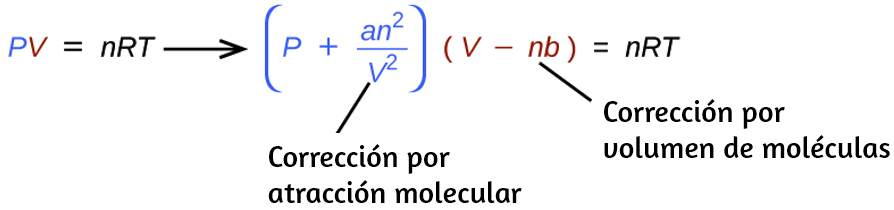
La constante a corresponde a la fuerza de la atracción entre moléculas de un gas particular, y la constante b corresponde al tamaño de las moléculas de un gas particular. La "corrección" del término de presión en la ley de los gases ideales es $\frac{n_2a}{V_2}$, y la "corrección" del volumen es $nb$. Observa que cuando $V$ es relativamente grande y $n$ es relativamente pequeño, ambos términos de corrección se vuelven insignificantes, y la ecuación de van der Waals se reduce a la ley del gas ideal, $PV = nRT$. Tal condición corresponde a un gas en el que un número relativamente bajo de moléculas está ocupando un volumen relativamente grande, es decir, un gas a una presión relativamente baja. Los valores experimentales para las constantes de van der Waals de algunos gases comunes se dan en la tabla 8.3.

A bajas presiones, la corrección de la atracción intermolecular, $a$, es más importante que la del volumen molecular, $b$.

Tabla 8.3. Valores de las constantes de van der Waals para algunos gases comunes

A altas presiones y pequeños volúmenes, la corrección del volumen de las moléculas se vuelve importante porque las moléculas mismas son incompresibles y constituyen una fracción apreciable del volumen total. A alguna presión intermedia, las dos correcciones tienen influencias opuestas y el gas parece seguir la relación dada por $PV = nRT$ en un pequeño rango de presiones. Este comportamiento se refleja en las "caídas" en varias de las curvas de compresibilidad que se muestran en la figura 8.35. La fuerza de atracción entre las moléculas inicialmente hace que el gas sea más compresible que un gas ideal, a medida que aumenta la presión (Z disminuye al aumentar P). A presiones muy altas, el gas se vuelve menos compresible (Z aumenta con P), a medida que las moléculas de gas comienzan a ocupar una fracción cada vez más significativa del volumen total de gas.

Estrictamente hablando, la ecuación de gas ideal funciona bien cuando las atracciones intermoleculares entre las moléculas de gas son insignificantes y las moléculas de gas en sí mismas no ocupan una parte apreciable de todo el volumen. Estos criterios se cumplen en condiciones de baja presión y alta temperatura. Bajo tales condiciones, se dice que el gas se comporta de manera ideal, y las desviaciones de las leyes de gas son lo suficientemente pequeñas como para que puedan ignorarse; sin embargo, esto no suele ser el caso.

Ejemplo 8.24

Comparación de la ley del gas ideal y la ecuación de van der Waals

Un matraz de 4.25 L contiene 3.46 moles de $CO_2$ a 229 °C. Calcula la presión de esta muestra de $CO_2$:

(a) de la ley del gas ideal
(b) de la ecuación de van der Waals
(c) Explica los motivos de la diferencia.

Solución

(a) De la ley del gas ideal:

(b) De la ecuación de van der Waals:

Esto finalmente produce P = 32.4 atm.

(c) Esto no es muy diferente del valor de la ley de los gases ideales porque la presión no es muy alta y la temperatura no es muy baja. El valor es algo diferente porque las moléculas de $CO_2$ tienen cierto volumen y atracciones entre las moléculas, y la ley de gases ideal supone que no tienen volumen o atracciones.

Comprueba tu aprendizaje

En el siguiente objeto interactivo, diseñado en la Universidad de Texas, podrás interactuar con un simulador de gas. Puedes controlar las cantidades relativas de dos gases, A y B con el mango de la bomba. Puedes liberar gas con la válvula de liberación. La temperatura la puedes subir y bajar, además puedes tener volumen bloqueado o cambiar. Juega con él y observa las relaciones de P, V, n y T.

Preguntas y respuestas - Capítulo VIII

Respuestas

Introducción

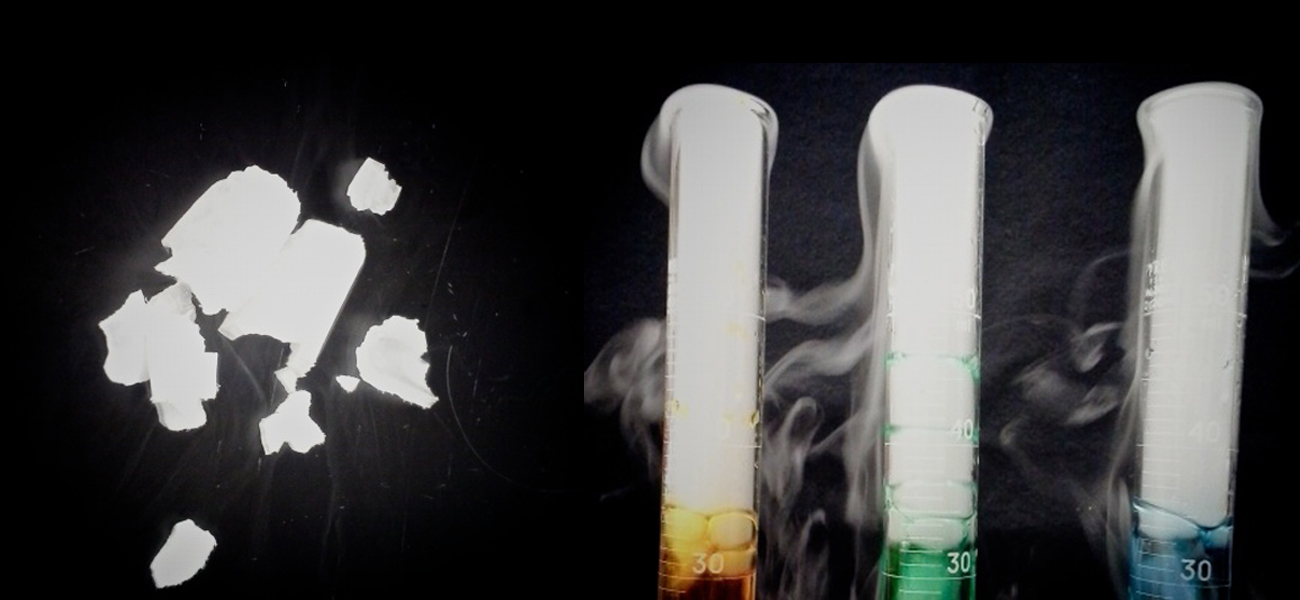
Figura 9.1. El dióxido de carbono sólido ("hielo seco", izquierda) se sublima vigorosamente cuando se coloca en un líquido (derecha), enfría el líquido y genera una densa neblina de agua sobre el cilindro. (crédito: modificación del trabajo de Paul Flowers).

Las grandes distancias entre átomos y moléculas en una fase gaseosa, y la ausencia correspondiente de interacciones significativas entre ellos, permiten descripciones simples de muchas propiedades físicas que son las mismas para todos los gases, independientemente de sus identidades químicas. Como se describe en el módulo final del capítulo sobre gases, esta situación cambia a altas presiones y bajas temperaturas, condiciones que permiten que los átomos y las moléculas interactúen en mayor medida. En los estados líquido y sólido, estas interacciones tienen una fuerza considerable y juegan un papel importante en la determinación de una serie de propiedades físicas que dependen de la identidad química de la sustancia. En este capítulo, examinarás la naturaleza de estas interacciones y sus efectos sobre diversas propiedades físicas de las fases líquida y sólida.

Fuerzas intermoleculares

Como fue el caso de las sustancias gaseosas, la teoría cinética molecular puede usarse para explicar el comportamiento de los sólidos y los líquidos. En la siguiente descripción, el término partícula se usará para referirse a un átomo, molécula o ion. Ten en cuenta que utilizaremos la frase popular "atracción intermolecular" para referirnos a las fuerzas de atracción entre las partículas de una sustancia, independientemente de si estas partículas son moléculas, átomos o iones.

Considera estos dos aspectos de los entornos de nivel molecular en materia sólida, líquida y gaseosa:

• Las partículas en un sólido están compactas y a menudo dispuestas en un patrón regular; en un líquido, están muy juntos sin disposición regular; en un gas, están muy separados sin un arreglo regular.
• Las partículas en un sólido vibran sobre posiciones fijas y generalmente no se mueven en relación entre sí; en un líquido, se mueven entre sí pero permanecen en contacto esencialmente constante; en un gas, se mueven independientemente uno del otro, excepto cuando chocan.

Las diferencias en las propiedades de un sólido, líquido o gas reflejan La fuerza entre las fuerzas de atracción entre los átomos, las moléculas o los iones que forman cada fase. La fase en la que existe una sustancia depende de la extensión relativa de sus fuerzas intermoleculares (FIM) y de las energías cinéticas ($K_E$) de sus moléculas. Los FIM son las diversas fuerzas de atracción que pueden existir entre los átomos y las moléculas de una sustancia debido a fenómenos electrostáticos, como se detallará en este módulo.

Estas fuerzas sirven para mantener las partículas juntas, mientras que el $K_E$ de las partículas proporciona la energía necesaria para superar las fuerzas de atracción y, por lo tanto, aumentar la distancia entre las partículas. La Figura 9.2 ilustra cómo pueden inducirse cambios en el estado físico al cambiar la temperatura, por lo tanto, el $K_E$ promedio de una sustancia dada.

Figura 9.2. Las transiciones entre los estados sólido, líquido y gaseoso de una sustancia ocurren cuando las condiciones de temperatura o presión favorecen los cambios asociados en las fuerzas intermoleculares. (Nota: el espacio entre las partículas en la fase gaseosa es mucho mayor de lo que se muestra).

Como ejemplo de los procesos representados en esta figura, considera una muestra de agua. Cuando el agua gaseosa se enfría lo suficiente, las atracciones entre las moléculas de $\ce{H2O}$ serán capaces de mantenerlas juntas cuando entren en contacto entre sí; el gas se condensa, formando $\ce{H2O}$ líquido. Por ejemplo, se forma agua líquida en el exterior de un vidrio frío a medida que el vapor de agua en el aire es enfriado por el vidrio frío, como se ve en la Figura 9.3.

Figura 9.3. La condensación se forma cuando el vapor de agua en el aire se enfría lo suficiente como para formar agua líquida, como (a) en el exterior de un vaso de bebida fría o (b) en forma de niebla. (crédito a: modificación del trabajo de Jenny Downing; crédito b: modificación del trabajo de Cory Zanker)

También podemos licuar muchos gases comprimiéndolos, si la temperatura no es demasiado alta. El aumento de la presión acerca las moléculas de un gas, de modo que las atracciones entre las moléculas se vuelven fuertes en relación con su $K_E$. En consecuencia, forman líquidos. El butano, $\ce{C4H10}$, es el combustible utilizado en los encendedores desechables y es un gas a temperatura y presión estándar. Dentro del compartimiento de combustible del encendedor, el butano se comprime a una presión que resulta en su condensación al estado líquido, como se muestra en la Figura 9.4 .

Finalmente, si la temperatura de un líquido se vuelve suficientemente baja, o la presión sobre el líquido se vuelve lo suficientemente alta, las moléculas del líquido ya no tienen suficiente $K_E$ para superar el FIM entre ellas, y se forma un sólido. En un módulo posterior de este capítulo se proporciona una discusión más exhaustiva de estos y otros cambios de estado o transiciones de fase.

Enlace a aprendizaje

Accede a esta simulación interactiva sobre estados de la materia, transiciones de fase y fuerzas intermoleculares. Esta simulación es útil para visualizar conceptos introducidos a lo largo de este capítulo.La escena interactiva fue descargada de Phet de Colorado, en la cual puedes construir un átomo con protones, neutrones y electrones, y observar cómo cambia el elemento, la carga y la masa. Además, también puedes probar tus ideas... ¡jugando!.

Figura 9.4. El butano gaseoso se comprime dentro del compartimiento de almacenamiento de un encendedor desechable, lo que resulta en su condensación al estado líquido. (crédito: modificación del trabajo de "Sam-Cat" / Flickr)

Fuerzas entre moléculas

En condiciones apropiadas, las atracciones entre todas las moléculas de gas harán que formen líquidos o sólidos. Esto se debe a fuerzas intermoleculares, no a fuerzas intramoleculares. Las fuerzas intramoleculares son aquellas dentro de la molécula que mantienen la molécula unida, por ejemplo, los enlaces entre los átomos. Las fuerzas intermoleculares son las atracciones entre las moléculas, que determinan muchas de las propiedades físicas de una sustancia. La Figura 9.5 ilustra estas diferentes fuerzas moleculares. Las fuerzas de estas fuerzas atractivas varían ampliamente, aunque generalmente los FIM entre moléculas pequeñas son débiles en comparación con las fuerzas intramoleculares que unen átomos dentro de una molécula. Por ejemplo, para superar los FIM en un mol de $\ce{HCl}$ líquido y convertirlo en $\ce{HCl}$ gaseoso, solo se necesitan unos $17\, kilojulios$. Sin embargo, romper los enlaces covalentes entre los átomos de hidrógeno y cloro en un mol de $\ce{HCl}$ requiere aproximadamente $25$ veces más energía: $430\,kilojulios$.

Figura 9.5. Las fuerzas intramoleculares mantienen una molécula intacta. Las fuerzas intermoleculares mantienen múltiples moléculas juntas y determinan muchas de las propiedades de una sustancia.

Todas las fuerzas atractivas entre los átomos neutros y las moléculas se conocen como fuerzas de van der Waals, aunque generalmente se las conoce de manera más informal como atracción intermolecular. Consideraremos los diversos tipos de FIM en las próximas tres secciones de este módulo.

Fuerzas de dispersion

Una de las tres fuerzas de van der Waals está presente en todas las fases condensadas, independientemente de la naturaleza de los átomos o moléculas que componen la sustancia. Esta fuerza atractiva se llama la fuerza de dispersión de London en honor del físico estadounidense de origen alemán Fritz London, quien, en 1928, lo explicó por primera vez. Esta fuerza a menudo se conoce simplemente como la fuerza de dispersión. Debido a que los electrones de un átomo o molécula están en constante movimiento (o, alternativamente, la ubicación del electrón está sujeta a la variabilidad mecáno cuántica), en cualquier momento, un átomo o molécula puede desarrollar en forma temporal un dipolo instantáneo si sus electrones están distribuido asimétricamente. La presencia de este dipolo puede, a su vez, distorsionar los electrones de un átomo o molécula vecina, produciendo un dipolo inducido.

Estos dos dipolos temporales que fluctúan rápidamente, dan como resultado una atracción electrostática relativamente débil entre las especies, una llamada fuerza de dispersión como la ilustrada en la Figura 9.6.

Figura 9.6. Las fuerzas de dispersión resultan de la formación de dipolos temporales, como se ilustra aquí para dos moléculas diatómicas no polares.

Las fuerzas de dispersión que se desarrollan entre los átomos en diferentes moléculas pueden atraer las dos moléculas entre sí. Sin embargo, las fuerzas son relativamente débiles y se vuelven significativas solo cuando las moléculas están muy cerca. Los átomos y moléculas más grandes y pesados exhiben fuerzas de dispersión más fuertes que los átomos y moléculas más pequeños y livianos. $\ce{F2}$ y $\ce{Cl2}$ son gases a temperatura ambiente (que reflejan fuerzas de atracción más débiles); $\ce{Br2}$ es un líquido e $\ce{I2}$ es un sólido (que refleja fuerzas de atracción más fuertes). Las tendencias en los puntos de fusión y ebullición observados para los halógenos demuestran claramente este efecto, como se ve en la Tabla 9.1.

Tabla 9.1Puntos de fusión y ebullición de los halógenos

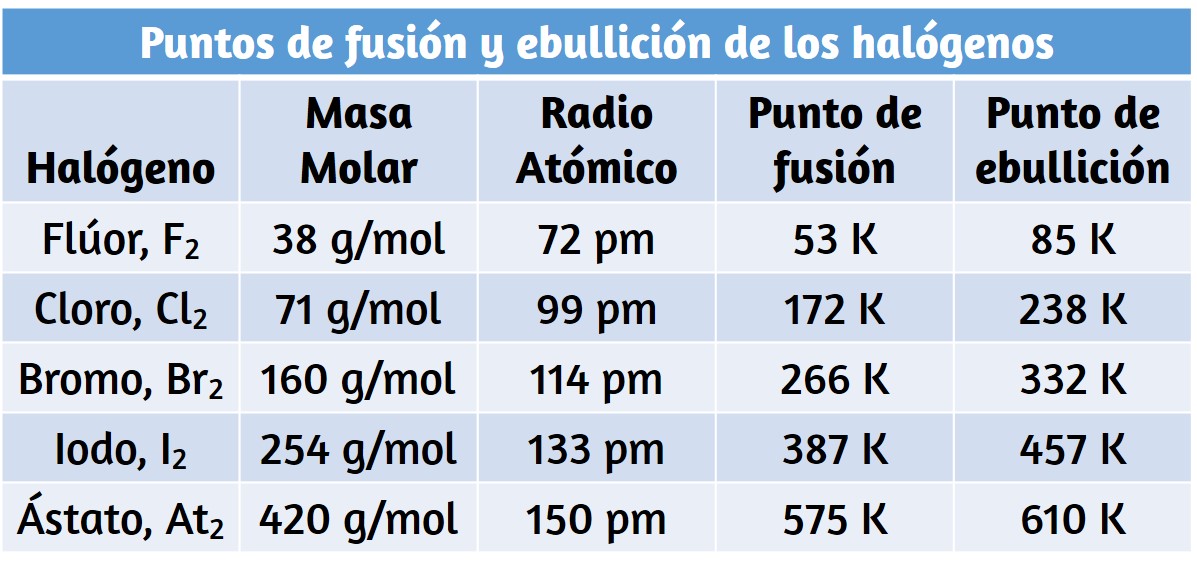
El aumento en los puntos de fusión y ebullición con el aumento del tamaño atómico / molecular puede racionalizarse considerando que la fuerza entre las fuerzas de dispersión se ven afectadas por la estructura electrónica de los átomos o moléculas en la sustancia. En un átomo más grande, los electrones de valencia están, en promedio, más alejados del núcleo que en un átomo más pequeño. Por lo tanto, están menos apretados y pueden formar más fácilmente los dipolos temporales que producen la atracción. La medida de cuán fácil o difícil es para otra carga electrostática (por ejemplo, un ion cercano o una molécula polar) distorsionar la distribución de carga de una molécula (su nube de electrones) se conoce como polarización. Se dice que una molécula que tiene una nube de carga que se distorsiona fácilmente es muy polarizable y tendrá grandes fuerzas de dispersión; uno con una nube de carga que es difícil de distorsionar no es muy polarizable y tendrá pequeñas fuerzas de dispersión.

Ejemplo 9.1

Fuerzas de London y sus efectos

Ordene los siguientes compuestos de un elemento del grupo $14$ e hidrógeno del punto de ebullición más bajo al más alto:

$\ce{CH4, SiH4, GeH4}$ y $\ce{SnH4}$. Explica tu razonamiento.

Solución

Aplicando las habilidades adquiridas en el capítulo sobre enlace químico y geometría molecular, se predice que todos estos compuestos son no polares, por lo que pueden experimentar solo fuerzas de dispersión: cuanto más pequeña es la molécula, menos polarizable y más débiles son las fuerzas de dispersión; cuanto mayor es la molécula, mayor es la fuerza de dispersión. Las masas molares de $\ce{CH4, SiH4, GeH4}$ y $\ce{SnH4}$ son aproximadamente $16\, \frac{g}{mol}$, $32\, \frac{g}{mol}$, $77\, \frac{g}{mol}$ y $123\, \frac{g}{mol}$, respectivamente. Por lo tanto, se espera que $\ce{CH4}$ ten el punto de ebullición más bajo y $\ce{SnH4}$ el punto de ebullición más alto. Se espera que el orden del punto de ebullición más bajo al más alto sea $\ce{CH4 \lt SiH4 \lt GeH4 \lt SnH4}$.

Un gráfico de los puntos de ebullición reales de estos compuestos.

Comprueba tu aprendizaje

Las formas de las moléculas también afectan las magnitudes de las fuerzas de dispersión entre ellas. Por ejemplo, los puntos de ebullición de los isómeros n-pentano, isopentano y neopentano (que se muestran en la Figura 9.7) son $36\,\degree C$, $27\,\degree C$ y $9.5\,\degree C$, respectivamente. Aunque estos compuestos están compuestos por moléculas con la misma fórmula química, $\ce{C5H12}$, la diferencia en los puntos de ebullición sugiere que las fuerzas de dispersión en la fase líquida son diferentes, siendo mayores para el n-pentano y menores para el neopentano. La forma alargada de n-pentano proporciona una mayor área de superficie disponible para el contacto entre moléculas, lo que resulta en fuerzas de dispersión correspondientemente más fuertes.

La forma más compacta del isopentano ofrece un área superficial más pequeña disponible para el contacto intermolecular y, por lo tanto, fuerzas de dispersión más débiles. Las moléculas de neopentano son las más compactas de las tres y ofrecen el área de superficie menos disponible para el contacto intermolecular y, por lo tanto, las fuerzas de dispersión más débiles. Este comportamiento es análogo a las conexiones que se pueden formar entre las tiras de los sujetadores de la marca VELCRO: cuanto mayor es el área de contacto de la tira, más fuerte es la conexión.

Figura 9.7La fuerza entre las fuerzas de dispersión aumenta con el área de contacto entre las moléculas, como lo demuestran los puntos de ebullición de estos isómeros de pentano.

Con el siguiente interactivo puedes visualizar mejor la Figura 9.7 interactuando con las moleculas puedes lograr el mejor área de contacto entre la inferior y la superior

Química en la vida cotidiana

Geckos y Fuerzas Intermoleculares

Los geckos (un lagarto nocturno.) tienen una sorprendente capacidad de adherirse a la mayoría de las superficies. Pueden atravesar rápidamente paredes lisas y techos que no tienen topes, y lo hacen sin tener ventosas o una sustancia pegajosa en sus dedos.

Y si bien un gecko puede levantar sus pies fácilmente mientras camina a lo largo de una superficie, si intenta levantarlo, se adhiere a la superficie. ¿Cómo pueden hacer esto los gecos (así como las arañas y algunos otros insectos)? Aunque este fenómeno ha sido investigado durante cientos de años, los científicos descubrieron recientemente los detalles del proceso que permite que las patas de los geckos se comporten de esta manera.

Los dedos de los geckos están cubiertos con cientos de miles de pequeños pelos conocidos como setas, y cada seta, a su vez, se ramifica en cientos de pequeñas puntas triangulares planas llamadas espátulas. El gran número de espátulas en sus setas proporciona un gecko, que se muestra en la Figura 9.8, con una gran área de superficie total para adherirse a una superficie. En 2000, Kellar Autumn, quien lidera un equipo de investigación de geckos multi-institucional, descubrió que los geckos se adhirieron igualmente bien tanto al dióxido de silicio polar como al arseniuro de galio no polar. Esto demostró que los geckos se adhieren a las superficies debido a las fuerzas de dispersión: atracciones intermoleculares débiles que surgen de distribuciones temporales y sincronizadas de carga entre moléculas adyacentes. Aunque las fuerzas de dispersión son muy débiles, la atracción total sobre millones de espátulas es lo suficientemente grande como para soportar muchas veces el peso del gecko.

En 2014, dos científicos desarrollaron un modelo para explicar cómo los geckos pueden pasar rápidamente de “pegajosos” a “no pegajosos”. Alex Greaney y Congcong Hu de la Oregon State University describieron cómo los geckos pueden lograr esto cambiando el ángulo entre sus espátulas y superficie. Las patas de los geckos, que normalmente no son pegajosas, se vuelven pegajosas cuando se aplica una pequeña fuerza de corte.

Al enroscar y desenroscar los dedos de los pies, los geckos pueden alternar entre pegarse y despegarse de una superficie, y así moverse fácilmente a través de ella. Investigaciones adicionales eventualmente pueden conducir al desarrollo de mejores adhesivos y otras aplicaciones.

Figura 9.8Los dedos de los geckos contienen grandes cantidades de pequeños pelos (setas), que se ramifican en muchas puntas triangulares (espátulas). Los geckos se adhieren a las superficies debido a las atracciones de van der Waals entre la superficie y los millones de espátulas de un gecko. Al cambiar la forma en que las espátulas entran en contacto con la superficie, los geckos pueden activar y desactivar su adherencia (foto de crédito: modificación del trabajo por "JC * + A!" / Flickr)

Enlace a aprendizaje

video

Atracciones en Dipolo-Dipolo

Recuerde en el capítulo sobre enlace químico y geometría molecular que las moléculas polares tienen una carga positiva parcial en un lado y una carga negativa parcial en el otro lado de la molécula, una separación de carga llamada dipolo. Considera una molécula polar como el cloruro de hidrógeno, $\ce{HCl}$. En la molécula de $\ce{HCl}$, el átomo de $\ce{Cl}$ más electronegativo tiene la carga negativa parcial, mientras que el átomo de $\ce{H}$ menos electronegativo tiene la carga positiva parcial. Una fuerza atractiva entre las moléculas de $\ce{HCl}$ resulta de la atracción entre el extremo positivo de una molécula de $\ce{HCl}$ y el extremo negativo de otra. Esta fuerza atractiva se llama atracción dipolo-dipolo: la fuerza electrostática entre el extremo parcialmente positivo de una molécula polar y el extremo parcialmente negativo de otra, como se ilustra en la Figura 9.9.

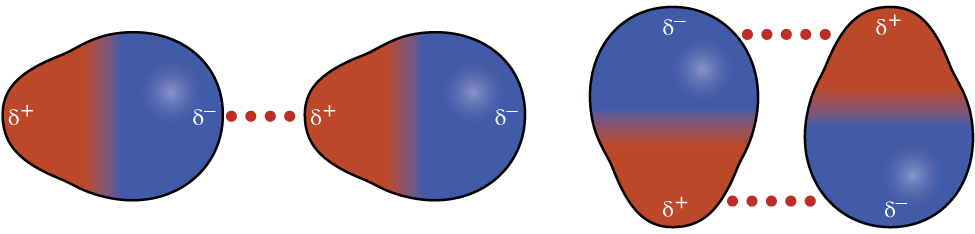
Figura 9.9Esta imagen muestra dos disposiciones de moléculas polares, como $\ce{HCl}$, que permiten una atracción entre el extremo negativo parcial de una molécula y el extremo positivo parcial de otra.

El efecto de una atracción dipolo-dipolo es evidente cuando comparamos las propiedades de las moléculas de $\ce{HCl}$ con las moléculas no polares de $\ce{F2}$. Tanto $\ce{HCl}$ como $\ce{F2}$ consisten en el mismo número de átomos y tienen aproximadamente la misma masa molecular. A una temperatura de $150\,K$, las moléculas de ambas sustancias tendrían el mismo $K_E$ promedio.

Sin embargo, las atracciones dipolo-dipolo entre las moléculas de $\ce{HCl}$ son suficientes para hacer que se "peguen" para formar un líquido, mientras que las fuerzas de dispersión relativamente más débiles entre las moléculas $\ce{F2}$ no polares no lo son, por lo que esta sustancia es gaseosa a esta temperatura. El punto de ebullición normal más alto del $\ce{HCl}$ ($188\,K$) en comparación con $\ce{F2}$ ($85\,K$) es un reflejo de la mayor fuerza de las atracciones dipolo-dipolo entre las moléculas de $\ce{HCl}$, en comparación con las atracciones entre las moléculas no polares de $\ce{F2}$. A menudo usaremos valores como puntos de ebullición o congelación, o entalpías de vaporización o fusión, como indicadores de las fuerzas relativas de los FIM de atracción presentes en diferentes sustancias.

Ejemplo 9.2

Fuerzas dipolo-dipolo y sus efectos

Predice cuál tendrá el punto de ebullición más alto: $\ce{N2}$ o $\ce{CO}$. Explica tu razonamiento.

Solución

$\ce{CO}$ y $\ce{N2}$ son moléculas diatómicas con masas de aproximadamente $28\,uma$, por lo que experimentan fuerzas de dispersión similares en London. Debido a que el $\ce{CO}$ es una molécula polar, experimenta atracciones dipolo-dipolo. Debido a que $\ce{N2}$ es no polar, sus moléculas no pueden exhibir atracciones dipolo-dipolo. Las atracciones dipolo-dipolo entre las moléculas de $\ce{CO}$ son comparativamente más fuertes que las fuerzas de dispersión entre las moléculas de $\ce{N2}$ no polares, por lo que se espera que el $\ce{CO}$ ten el punto de ebullición más alto.

Comprueba tu aprendizaje

Enlaces de hidrógeno

El fluoruro de nitrosilo ($\ce{ONF}$, masa molecular $49\,uma$) es un gas a temperatura ambiente. El agua ($\ce{H2O}$, masa molecular $18\,uma$) es un líquido, a pesar de que tiene una masa molecular más baja. Claramente no podemos atribuir esta diferencia entre los dos compuestos a las fuerzas de dispersión. Ambas moléculas tienen aproximadamente la misma forma y ONF es la molécula más pesada y más grande. Por lo tanto, se espera que experimente fuerzas de dispersión más significativas.

Además, no podemos atribuir esta diferencia en los puntos de ebullición a las diferencias en los momentos dipolares de las moléculas. Ambas moléculas son polares y exhiben momentos dipolares comparables. La gran diferencia entre los puntos de ebullición se debe a una atracción dipolo-dipolo particularmente fuerte que puede ocurrir cuando una molécula contiene un átomo de hidrógeno unido a un átomo de flúor, oxígeno o nitrógeno (los tres elementos más electronegativos). La gran diferencia en la electronegatividad entre el átomo de $\ce{H}\,(2.1)$ y el átomo al que está unido ($4.0$ para un átomo de $\ce{F}\,3.5$ para un átomo de $\ce{O}$, o $3.0$ para un átomo de $\ce{N}$), combinado con el tamaño muy pequeño de un El átomo de $\ce{H}$ y los tamaños relativamente pequeños de los átomos de $\ce{F}$, $\ce{O}$ o $\ce{N}$, conducen a cargas parciales altamente concentradas con estos átomos. Las moléculas con restos $\ce{F-H}$, $\ce{O-H}$ o $\ce{N-H}$ se sienten muy atraídas por restos similares en moléculas cercanas, un tipo particularmente fuerte de atracción dipolo-dipolo llamado enlace de hidrógeno. Los ejemplos de enlaces de hidrógeno incluyen $\ce{HF \cdots HF}$, $\ce{H2O \cdots HOH}$ y $\ce{H3N \cdots HNH2}$, en los que los enlaces de hidrógeno se denotan por puntos. La Figura 9.10 ilustra los enlaces de hidrógeno entre las moléculas de agua.

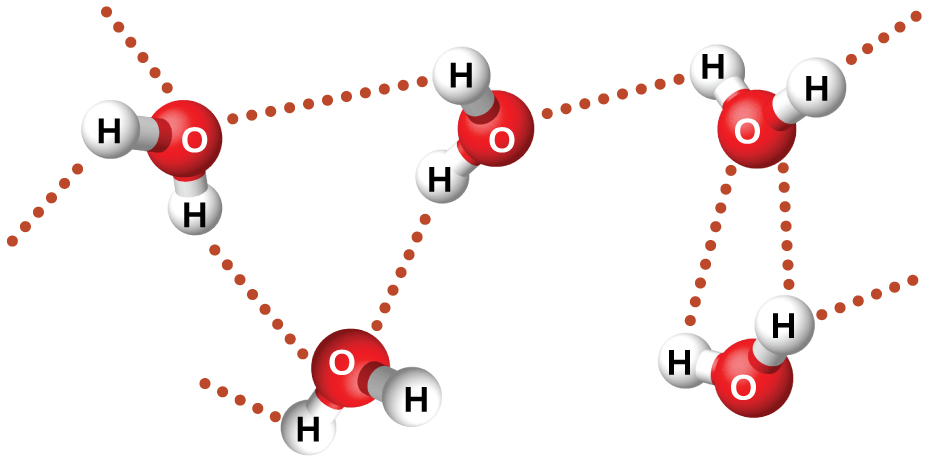
Figura 9.10. Las moléculas de agua participan en múltiples interacciones de enlace de hidrógeno con moléculas de agua cercanas.

A pesar del uso de la palabra "enlace", ten en cuenta que los enlaces de hidrógeno son fuerzas de atracción intermoleculares, no fuerzas de atracción intramoleculares (enlaces covalentes). Los enlaces de hidrógeno son mucho más débiles que los enlaces covalentes, solo de $5$ a $10\%$ más fuertes, pero generalmente son mucho más fuertes que otras atracciones dipolo-dipolo y fuerzas de dispersión.

Los enlaces de hidrógeno tienen un efecto pronunciado sobre las propiedades de las fases condensadas (líquidos y sólidos). Por ejemplo, considera las tendencias en los puntos de ebullición para los hidruros binarios del grupo $15$ ($\ce{NH3}$, $\ce{PH3}$, $\ce{AsH3}$ y $\ce{SbH3}$), los hidruros del grupo $16$ ($\ce{H2O}$, $\ce{H2S}$, $\ce{H2Se}$ y $\ce{H2Te}$) y los hidruros del grupo $17$ ($\ce{HF}$, $\ce{HCl}$, $\ce{HBr}$ y $\ce{HI}$). Los puntos de ebullición de los tres hidruros más pesados ​​para cada grupo se representan en la Figura 9.11.

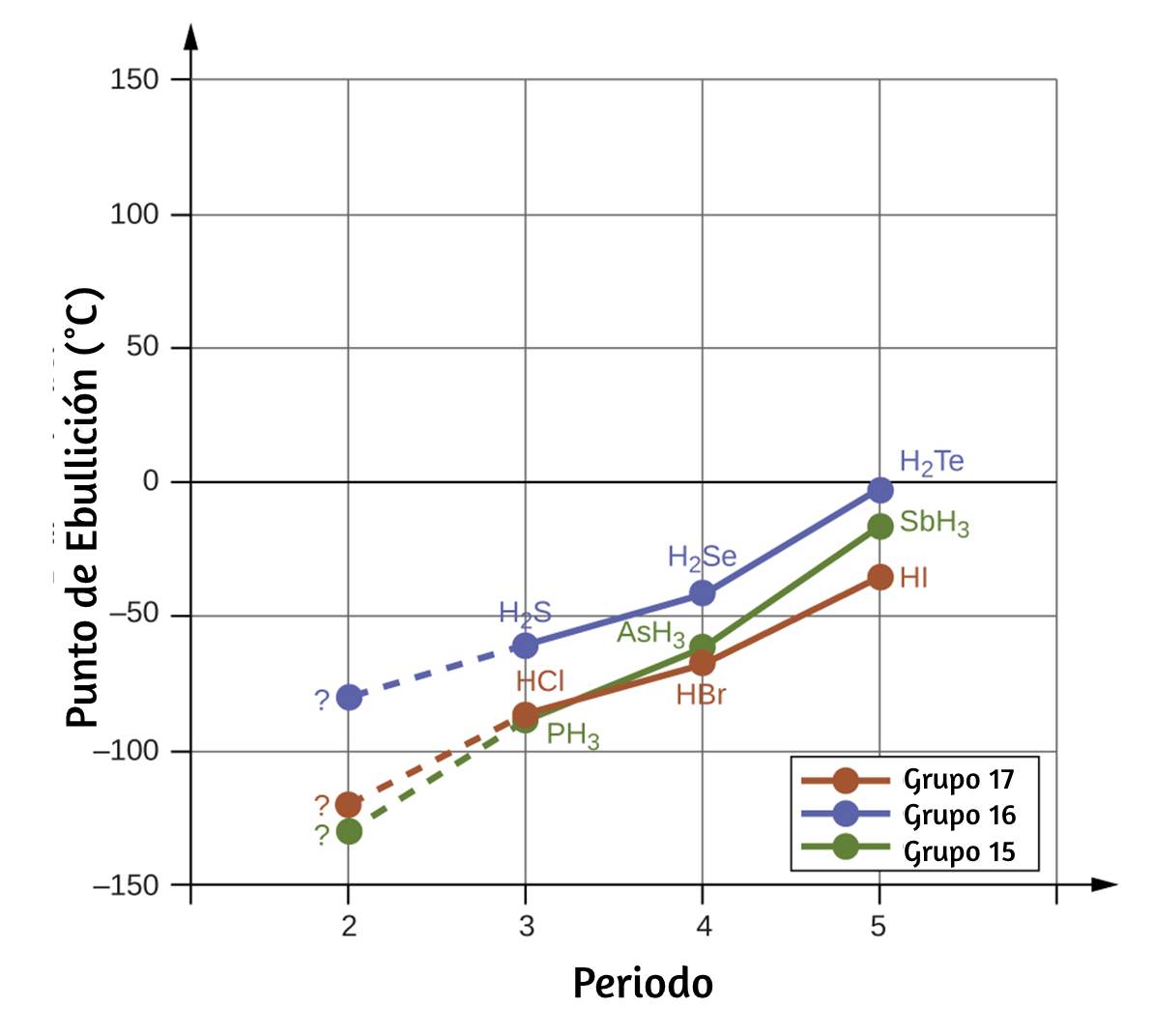
Figura 9.11. Para los hidruros del grupo $15$, $16$ y $17$, los puntos de ebullición para cada clase de compuestos aumentan al aumentar la masa molecular de los elementos en los períodos $3$, $4$ y $5$.

A medida que avanzamos hacia abajo en cualquiera de estos grupos, las polaridades de las moléculas disminuyen ligeramente, mientras que los tamaños de las moléculas aumentan sustancialmente. El efecto de fuerzas de dispersión cada vez más fuertes domina el de atracciones dipolo-dipolo cada vez más débiles, y se observa que los puntos de ebullición aumentan constantemente.

Si utilizamos esta tendencia para predecir los puntos de ebullición del hidruro más ligero para cada grupo, esperaríamos que el $\ce{NH3}$ hierva a aproximadamente $−120\,\degree C$, el $\ce{H2O}$ hierva a aproximadamente $−80\,\degree C$ y el $\ce{HF}$ hierva a aproximadamente $−110\,\degree C$. Sin embargo, cuando medimos los puntos de ebullición de estos compuestos, encontramos que son dramáticamente más altos de lo que predecirían las tendencias, como se muestra en la Figura 9.12.

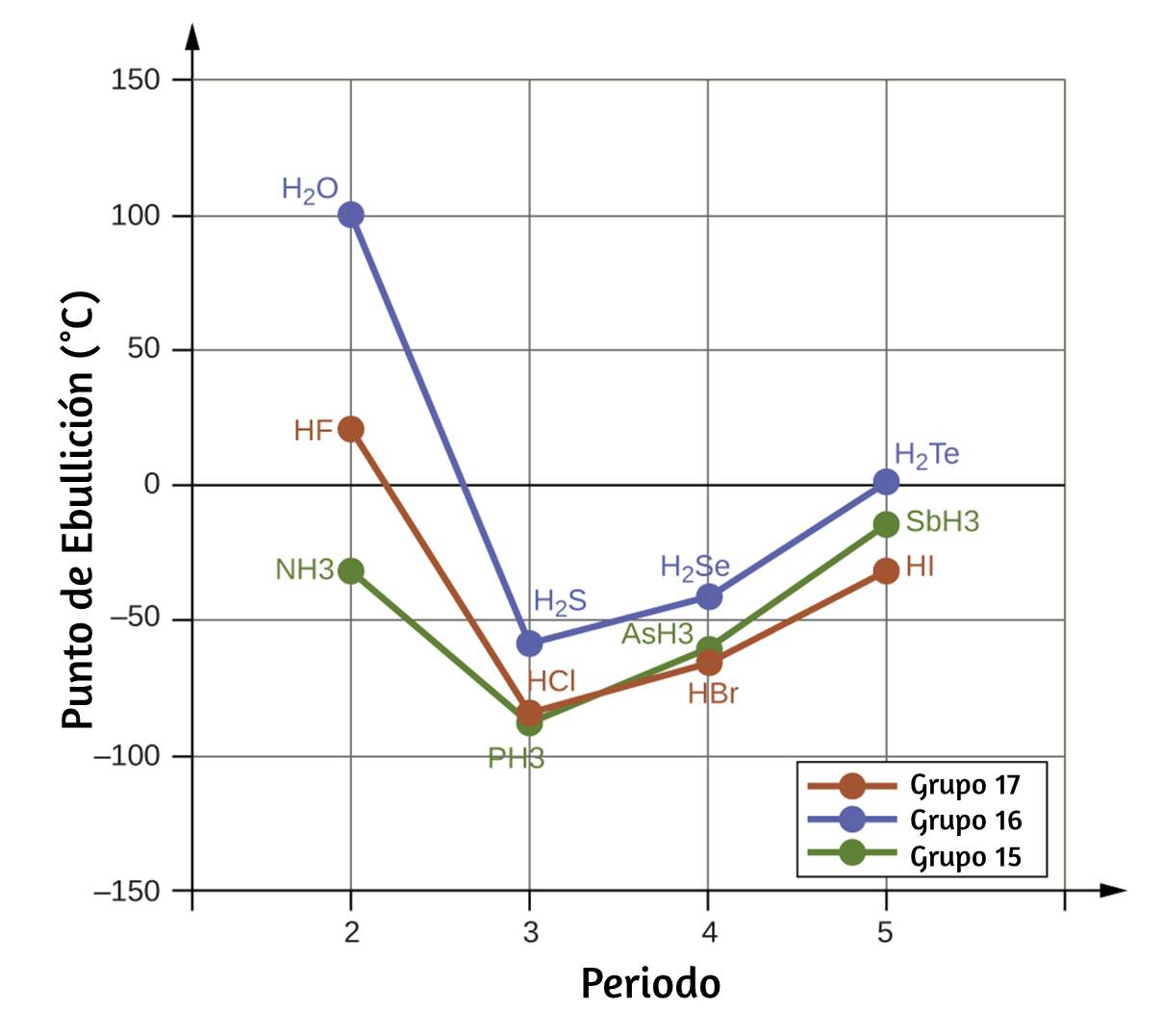
Figura 9.12. En comparación con los períodos $3-5$, los hidruros binarios de los elementos del período $2$ en los grupos $17$, $16$ y $15$ ($\ce{F}$, $\ce{O}$ y $\ce{N}$, respectivamente) exhiben puntos de ebullición anormalmente altos debido al enlace de hidrógeno.

El marcado contraste entre nuestras predicciones ingenuas y la realidad proporciona evidencia convincente de la fuerza del enlace de hidrógeno.

Ejemplo 9.3

Efecto del enlace de hidrógeno en los puntos de ebullición

Considera los compuestos dimetiléter ($\ce{CH3OCH3}$), etanol ($\ce{CH3CH2OH}$) y propano ($\ce{CH3CH2CH3}$). Sus puntos de ebullición, no necesariamente en orden, son $−42.1\,\degree C$, $−24.8\,\degree C$ y $78.4\,\degree C$. Une cada compuesto con su punto de ebullición. Explica tu razonamiento.

Solución

Las formas predichas por VSEPR de $\ce{CH3OCH3}$, $\ce{CH3CH2OH}$ y $\ce{CH3CH2CH3}$ son similares, al igual que sus masas molares ($46\, \frac{g}{mol}$, $46\, \frac{g}{mol}$ y $44\, \frac{g}{mol}$, respectivamente), por lo que exhibirán fuerzas de dispersión similares. Como $\ce{CH3CH2CH3}$ es no polar, puede exhibir solo fuerzas de dispersión. Debido a que $\ce{CH3OCH3}$ es polar, también experimentará atracciones dipolo-dipolo. Finalmente, $\ce{CH3CH2OH}$ tiene un grupo $\ce{−OH}$, por lo que experimentará la atracción dipolo-dipolo excepcionalmente fuerte conocida como enlace de hidrógeno. Entonces, el orden en términos de resistencia de los FIM, y por lo tanto los puntos de ebullición, es $\ce{CH3CH2CH3}\lt\ce{CH3OCH3}\lt \ce{CH3CH2OH}$. El punto de ebullición del propano es $−42.1\,\degree C$, el punto de ebullición del dimetiléter es $−24.8\,\degree C$ y el punto de ebullición del etanol es $78.5\,\degree C$.

Comprueba tu aprendizaje

Cómo se interconectan las ciencias

Enlace de hidrógeno y ADN

El ácido desoxirribonucleico (ADN) se encuentra en todos los organismos vivos y contiene la información genética que determina las características del organismo, proporciona el plan para producir las proteínas necesarias para la vida y sirve como plantilla para transmitir esta información a la descendencia del organismo. Una molécula de ADN consta de dos cadenas (anti-) paralelas de nucleótidos repetidos, que forman su conocida estructura de doble hélice, como se muestra en la Figura 9.13.

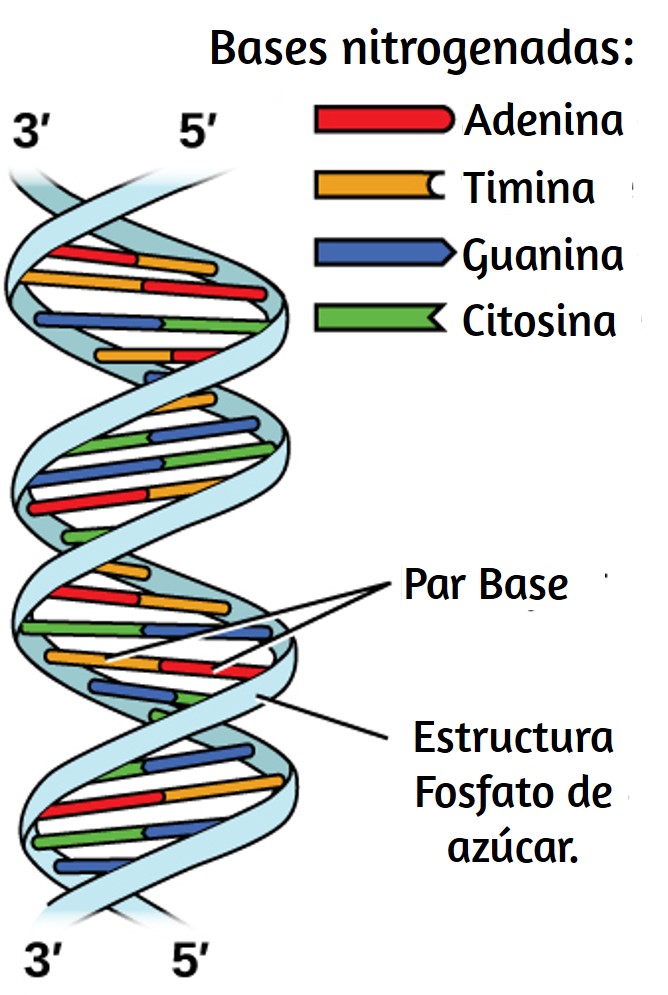
Figura 9.13. Dos moléculas de ADN separadas forman una hélice bicatenaria en la que las moléculas se mantienen juntas mediante enlaces de hidrógeno. (crédito: modificación del trabajo de Jerome Walker, Dennis Myts)

Cada nucleótido contiene un azúcar ($desoxirribosa$) unido a un grupo $fosfato$ en un lado, y una de las cuatro bases nitrogenadas en el otro. Dos de las bases, la $citosina\,(C)$ y la $timina\,(T)$, son estructuras de un solo anillo conocidas como $pirimidinas$. Los otros dos, $adenina\,(A)$ y $guanina\,(G)$, son estructuras de doble anillo llamadas $purinas$. Estas bases forman pares de bases complementarias que consisten en una purina y una pirimidina, con adenina emparejada con timina y citosina con guanina. Cada par de bases se mantiene unido por enlaces de hidrógeno. A y T comparten dos enlaces de hidrógeno, C y G comparten tres, y ambos emparejamientos tienen una forma y estructura similar Figura 9.14.

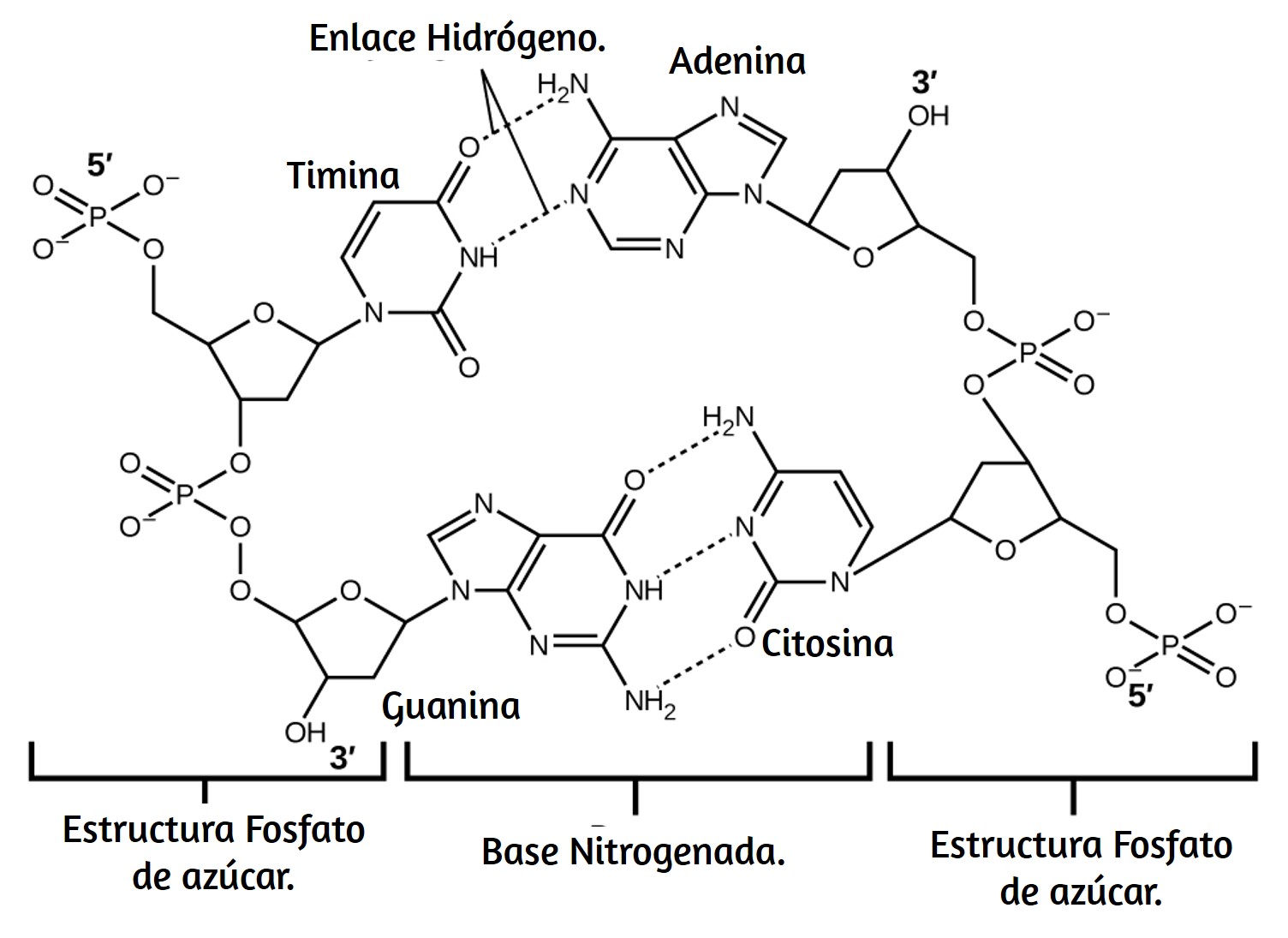
Figura 9.14. Las geometrías de las moléculas base dan como resultado un enlace de hidrógeno máximo entre adenina y timina (AT) y entre guanina y citosina (GC), los llamados "pares de bases complementarias".

El efecto acumulativo de millones de enlaces de hidrógeno mantiene efectivamente unidas las dos cadenas de ADN. Es importante destacar que las dos cadenas de ADN pueden "descomprimirse" relativamente fácilmente en el medio ya que los enlaces de hidrógeno son relativamente débiles en comparación con los enlaces covalentes que mantienen unidos a los átomos de las moléculas de ADN individuales. Esto permite que ambos hilos funcionen como una plantilla para la replicación.

Propiedades de los líquidos

Cuando vierte un vaso de agua o llena un automóvil con gasolina, observa que el agua y la gasolina fluyen libremente. Pero cuando vierte jarabe en panqueques o agrega aceite al motor de un automóvil, observa que el jarabe y el aceite de motor no fluyen tan fácilmente. La viscosidad de un líquido es una medida de su resistencia al flujo. El agua, la gasolina y otros líquidos que fluyen libremente tienen una baja viscosidad. La miel, el jarabe, el aceite de motor y otros líquidos que no fluyen libremente, como los que se muestran en la Figura 9.15, tienen viscosidades más altas.

Figura 9.15. (a) La miel y (b) el aceite de motor son ejemplos de líquidos con altas viscosidades; fluyen lentamente. (crédito a: modificación del trabajo de Scott Bauer; crédito b: modificación del trabajo de David Nagy).

Podemos medir la viscosidad midiendo la velocidad a la que una bola de metal cae a través de un líquido (la bola cae más lentamente a través de un líquido más viscoso) o midiendo la velocidad a la que un líquido fluye a través de un tubo estrecho (los líquidos más viscosos fluyen más lentamente )

Los FIM entre las moléculas de un líquido, el tamaño y la forma de las moléculas y la temperatura determinan la facilidad con la que fluye un líquido. Como muestra la Tabla 9.2, cuanto más estructuralmente complejas son las moléculas en un líquido y cuanto más fuertes son los FIM entre ellas, más difícil es que se muevan entre sí y mayor es la viscosidad del líquido. A medida que aumenta la temperatura, las moléculas se mueven más rápidamente y sus energías cinéticas están en mejores condiciones para superar las fuerzas que las mantienen juntas; así, la viscosidad del líquido disminuye.

Tabla 9.2: Viscosidades de sustancias comunes a $25\,\degree C$

Los diversos FIM entre moléculas idénticas de una sustancia son ejemplos de fuerzas cohesivas. Las moléculas dentro de un líquido están rodeadas por otras moléculas y son atraídas igualmente en todas las direcciones por las fuerzas cohesivas dentro del líquido. Sin embargo, las moléculas en la superficie de un líquido son atraídas solo por aproximadamente la mitad de las moléculas.

Debido a las atracciones moleculares desequilibradas en las moléculas de la superficie, los líquidos se contraen para formar una forma que minimiza el número de moléculas en la superficie, es decir, la forma con el área de superficie mínima. Una pequeña gota de líquido tiende a asumir una forma esférica, como se muestra en la Figura 9.16, porque en una esfera, la relación entre el área de superficie y el volumen es mínima. Las gotas más grandes se ven más afectadas por la gravedad, la resistencia del aire, las interacciones superficiales, etc., y como resultado, son menos esféricas.

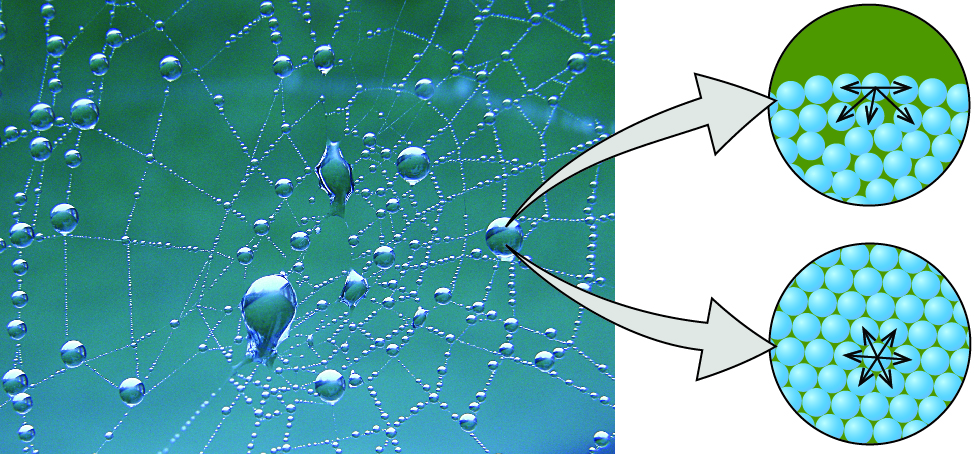
Figura 9.16. Las fuerzas atractivas resultan en una caída de agua esférica que minimiza el área de superficie; fuerzas cohesivas mantienen la esfera unida; Las fuerzas adhesivas mantienen la gota unida a la red. (Foto de crédito: modificación del trabajo de "OliBac" / Flickr)

La tensión superficial se define como la energía requerida para aumentar el área superficial de un líquido, o la fuerza requerida para aumentar la longitud de una superficie líquida en una cantidad dada. Esta propiedad resulta de las fuerzas cohesivas entre las moléculas en la superficie de un líquido, y hace que la superficie de un líquido se comporte como una membrana de goma estirada. Las tensiones superficiales de varios líquidos se presentan en la Tabla 9.3. Entre los líquidos comunes, el agua exhibe una tensión superficial claramente alta debido al fuerte enlace de hidrógeno entre sus moléculas.

Como resultado de esta alta tensión superficial, la superficie del agua representa una "piel relativamente dura" que puede soportar una fuerza considerable sin romperse. Una aguja de acero cuidadosamente colocada sobre el agua flotará. Algunos insectos, como el que se muestra en la Figura 9.17, aunque son más densos que el agua, se mueven sobre su superficie porque están soportados por la tensión superficial.

Figura 9.17. La tensión superficial (derecha) evita que este insecto, un "caminante acuático", se hunda en el agua.

Las FIM de atracción entre dos moléculas diferentes se denominan fuerzas adhesivas. Considere lo que sucede cuando el agua entra en contacto con alguna superficie. Si las fuerzas adhesivas entre las moléculas de agua y las moléculas de la superficie son débiles en comparación con las fuerzas cohesivas entre las moléculas de agua, el agua no "moja" la superficie.

Por ejemplo, el agua no moja las superficies enceradas o muchos plásticos como el polietileno. El agua forma gotas en estas superficies porque las fuerzas cohesivas dentro de las gotas son mayores que las fuerzas adhesivas entre el agua y el plástico. El agua se extiende sobre el vidrio porque la fuerza adhesiva entre el agua y el vidrio es mayor que las fuerzas cohesivas dentro del agua.

Cuando el agua está confinada en un tubo de vidrio, su menisco (superficie) tiene una forma cóncava porque el agua moja el vidrio y se arrastra por el costado del tubo. Por otro lado, las fuerzas cohesivas entre los átomos de mercurio son mucho mayores que las fuerzas adhesivas entre el mercurio y el vidrio. Por lo tanto, el mercurio no humedece el vidrio, y forma un menisco convexo cuando está confinado en un tubo porque las fuerzas cohesivas dentro del mercurio tienden a arrastrarlo hacia una gota (Figura 9.18).

Figura 9.18. Las diferencias en las fuerzas relativas de las fuerzas cohesivas y adhesivas dan como resultado diferentes formas de menisco para mercurio (izquierda) y agua (derecha) en tubos de vidrio. (crédito: Mark Ott)

Si coloca un extremo de una toalla de papel en vino derramado, como se muestra en la Figura 9.19, el líquido absorbe la toalla de papel.

Un proceso similar ocurre en una toalla de tela cuando la usa para secarse después de una ducha. Estos son ejemplos de acción capilar: cuando un líquido fluye dentro de un material poroso debido a la atracción de las moléculas líquidas hacia la superficie del material y hacia otras moléculas líquidas. Las fuerzas adhesivas entre el líquido y el material poroso, combinadas con las fuerzas cohesivas dentro del líquido, pueden ser lo suficientemente fuertes como para mover el líquido hacia arriba contra la gravedad.

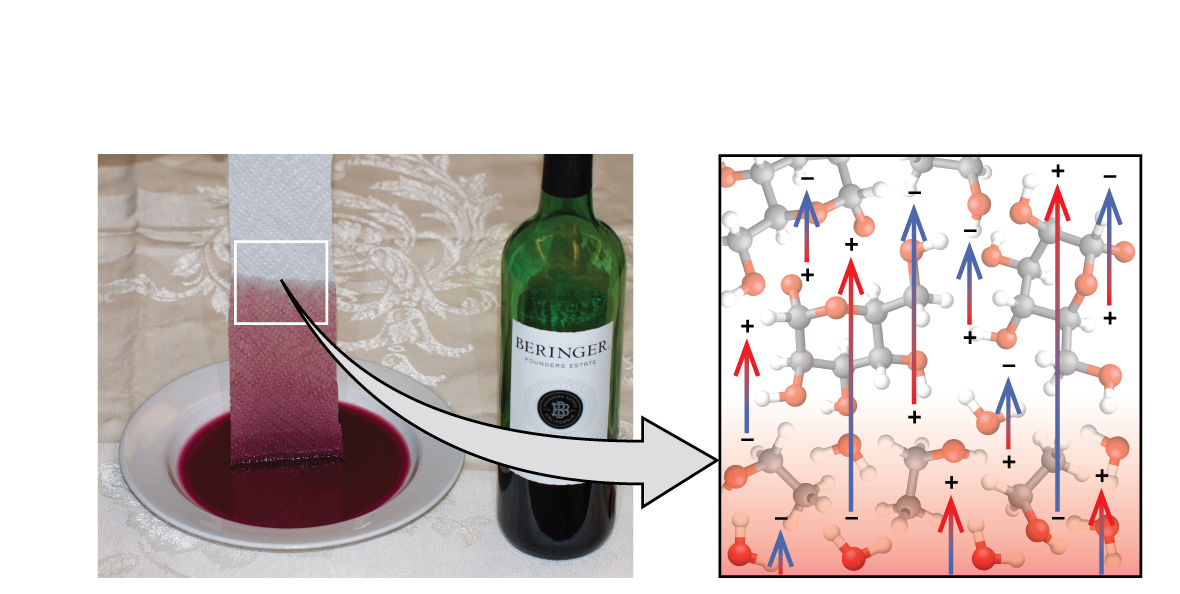
Figura 9.19. El vino se absorbe en una toalla de papel (izquierda) debido a las fuertes atracciones de las moléculas de agua (y etanol) hacia los grupos −OH en las fibras de celulosa de la toalla y las fuertes atracciones de las moléculas de agua hacia otras moléculas de agua (y etanol) (derecha ) (Foto de crédito: modificación del trabajo de Mark Blaser)

Las toallas absorben líquidos como el agua porque las fibras de una toalla están hechas de moléculas que son atraídas por las moléculas de agua. La mayoría de las toallas de tela están hechas de algodón, y las toallas de papel generalmente están hechas de pulpa de papel. Ambos consisten en moléculas largas de celulosa que contienen muchos grupos $\ce{-OH}$. Las moléculas de agua se sienten atraídas por estos grupos $\ce{-OH}$ y forman enlaces de hidrógeno con ellos, lo que atrae las moléculas de $\ce{H2O}$ hacia las moléculas de celulosa. Las moléculas de agua también se atraen entre sí, por lo que se extraen grandes cantidades de agua de las fibras de celulosa.

La acción capilar también puede ocurrir cuando un extremo de un tubo de diámetro pequeño se sumerge en un líquido, como se ilustra en la Figura 9.20. Si las moléculas líquidas son fuertemente atraídas por las moléculas del tubo, el líquido se arrastra por el interior del tubo hasta que el peso del líquido y las fuerzas adhesivas estén en equilibrio. Cuanto más pequeño es el diámetro del tubo, más alto sube el líquido. Es en parte por la acción capilar que ocurre en las células vegetales llamadas xilema que el agua y los nutrientes disueltos son llevados desde el suelo a través de las raíces y dentro de una planta. La acción capilar es la base de la cromatografía en capa fina, una técnica de laboratorio que se usa comúnmente para separar pequeñas cantidades de mezclas. Usted depende de un suministro constante de lágrimas para mantener sus ojos lubricados y de la acción capilar para bombear el líquido lagrimal.

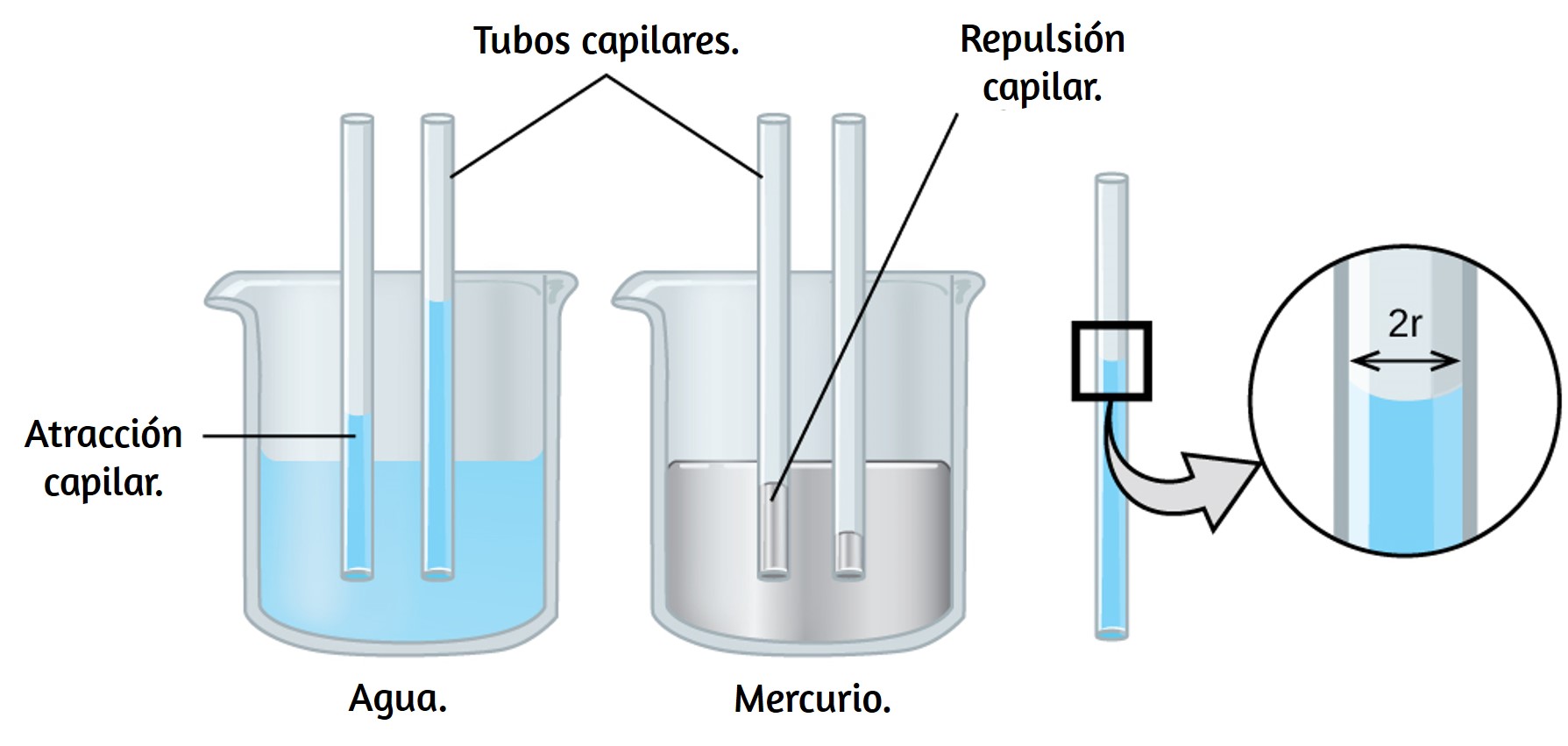
Figura 9.20. Dependiendo de las fuerzas relativas de las fuerzas adhesivas y cohesivas, un líquido puede subir (como el agua) o caer (como el mercurio) en un tubo capilar de vidrio. La extensión del aumento (o caída) es directamente proporcional a la tensión superficial del líquido e inversamente proporcional a la densidad del líquido y al radio del tubo.

La altura a la que se elevará un líquido en un tubo capilar está determinada por varios factores, como se muestra en la siguiente ecuación:

En esta ecuación, $h$ es la altura del líquido dentro del tubo capilar en relación con la superficie del líquido fuera del tubo, $T$ es la tensión superficial del líquido, $\theta$ es el ángulo de contacto entre el líquido y el tubo, $r$ es el radio del tubo, $\rho$ es la densidad del líquido, y $g$ es la aceleración debida a la gravedad, $9.8\, \frac{m}{s^2}$. Cuando el tubo está hecho de un material al que las moléculas líquidas son fuertemente atraídas, se extenderán completamente en la superficie, lo que corresponde a un ángulo de contacto de $0\degree$. Esta es la situación del agua que sube en un tubo de vidrio.

Ejemplo 9.4

Aumento capilar

A $25\,\degree C$, ¿qué tan alto se elevará el agua en un tubo capilar de vidrio con un diámetro interno de $0.25\,mm$?

Para el agua, $T = 71.99 \, \frac{mN}{m}$ y $\rho = 1.0 \frac{g}{cm^3}.$

Solución

El líquido se elevará a una altura $h$ dada por: $h=\frac {2T\cos \theta }{r\rho g}$

El Newton se define como un $\frac{kg \cdot m}{s^2}$, por lo que la tensión superficial proporcionada es equivalente a $0.07199\, \frac{kg}{s^2}$. La densidad proporcionada debe convertirse en unidades que se cancelarán de manera adecuada: $ \rho = 1000 \, \frac{kg}{m^3}$. El diámetro del tubo en metros es de $0.00025 \,m$, por lo que el radio es de $0.000125 \,m$.

Para un tubo de vidrio sumergido en agua, el ángulo de contacto es $ \theta = 0\degree$, entonces $\cos \theta = 1$. Finalmente, la aceleración debida a la gravedad en la tierra es $g = 9.8\, \frac{m}{s^2}$. Sustituyendo estos valores en la ecuación y cancelando unidades, tenemos:

Comprueba tu aprendizaje

Química en la vida cotidiana

Aplicaciones biomédicas de la acción capilar.

Muchas pruebas médicas requieren extraer una pequeña cantidad de sangre, por ejemplo, para determinar la cantidad de glucosa en alguien con diabetes o el nivel de hematocrito en un atleta. Este procedimiento se puede realizar fácilmente debido a la acción capilar, la capacidad de un líquido para fluir por un tubo pequeño contra la gravedad, como se muestra en la Figura 9.21. Cuando se pincha el dedo, se forma una gota de sangre que se mantiene unida debido a la tensión superficial: las atracciones intermoleculares desequilibradas en la superficie de la gota.

Luego, cuando el extremo abierto de un tubo de vidrio de diámetro estrecho toca la gota de sangre, las fuerzas adhesivas entre las moléculas en la sangre y las de la superficie del vidrio llevan la sangre hacia el tubo. La cantidad de sangre que sube por el tubo depende del diámetro del tubo (y del tipo de líquido). Un tubo pequeño tiene un área de superficie relativamente grande para un volumen dado de sangre, lo que da como resultado fuerzas de atracción (relativas) mayores, lo que permite que la sangre se extraiga más arriba del tubo. El líquido mismo se mantiene unido por sus propias fuerzas cohesivas. Cuando el peso del líquido en el tubo genera una fuerza hacia abajo igual a la fuerza hacia arriba asociada con la acción capilar, el líquido deja de elevarse.

Figura 9.21. La sangre se recolecta para análisis médico por acción capilar, que extrae sangre en un tubo de vidrio de diámetro pequeño. (crédito: modificación del trabajo de los Centros para el Control y la Prevención de Enfermedades)

Fases de transición

Somos testigos y utilizamos cambios de estado físico, o fases de transición, de muchas maneras. Como un ejemplo de importancia global, considere la evaporación, condensación, congelación y fusión del agua. Estos cambios de estado son aspectos esenciales del ciclo del agua de nuestra tierra, así como muchos otros fenómenos naturales y procesos tecnológicos de importancia central para nuestras vidas. En este módulo, se exploran los aspectos esenciales de las transiciones de fase.

Vaporización y Condensación

Cuando un líquido se vaporiza en un recipiente cerrado, las moléculas de gas no pueden escapar. A medida que estas moléculas en fase gaseosa se mueven aleatoriamente, ocasionalmente colisionarán con la superficie de la fase condensada y, en algunos casos, estas colisiones harán que las moléculas vuelvan a entrar en la fase condensada. El cambio de la fase gaseosa al líquido se llama condensación. Cuando la velocidad de condensación se vuelve igual a la velocidad de vaporización, no cambia la cantidad de líquido ni la cantidad de vapor en el recipiente. Se dice que el vapor en el recipiente está en $equilibrio$ con el líquido. Tenga en cuenta que esta no es una situación estática, ya que las moléculas se intercambian continuamente entre las fases condensada y gaseosa. Tal es un ejemplo de equilibrio dinámico, el estado de un sistema en el que los procesos recíprocos (por ejemplo, vaporización y condensación) ocurren a velocidades iguales. La presión ejercida por el vapor en equilibrio con un líquido en un recipiente cerrado a una temperatura dada se llama presión de vapor del líquido (o presión de vapor en equilibrio).

El área de la superficie del líquido en contacto con un vapor y el tamaño del recipiente no tienen efecto sobre la presión de vapor, aunque sí afectan el tiempo requerido para alcanzar el equilibrio. Podemos medir la presión de vapor de un líquido colocando una muestra en un recipiente cerrado, como el ilustrado en la Figura 9.22, y usando un manómetro para medir el aumento de presión que se debe al vapor en equilibrio con la fase condensada.

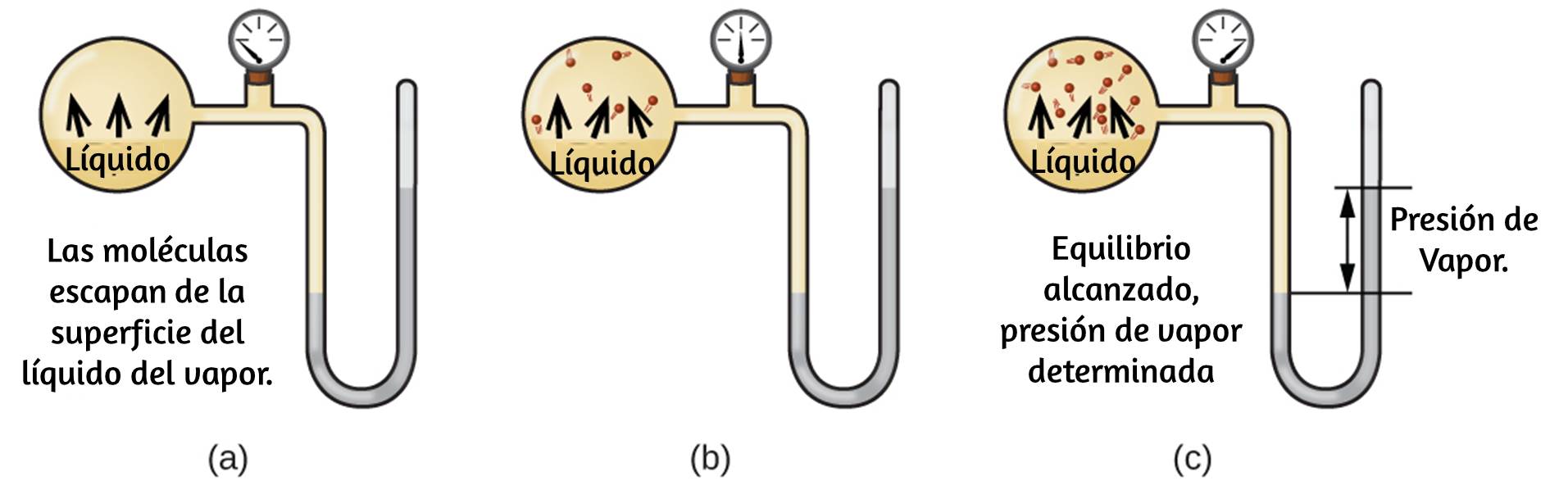
Figura 9.22. En un recipiente cerrado, se alcanza el equilibrio dinámico cuando (a) aumenta la velocidad de las moléculas que escapan del líquido para convertirse en gas (b) y, finalmente, (c) es igual a la velocidad de las moléculas de gas que ingresan al líquido. Cuando se alcanza este equilibrio, la presión de vapor del gas es constante, aunque los procesos de vaporización y condensación continúan.

Las identidades químicas de las moléculas en un líquido determinan los tipos (y fuerzas) posibles de atracciones intermoleculares; en consecuencia, diferentes sustancias exhibirán diferentes presiones de vapor de equilibrio. Las fuerzas de atracción intermoleculares relativamente fuertes servirán para impedir la vaporización y favorecerán la "recaptura" de moléculas de fase gaseosa cuando colisionan con la superficie del líquido, lo que resulta en una presión de vapor relativamente baja. Las atracciones intermoleculares débiles presentan menos barrera para la vaporización y una probabilidad reducida de recaptura de gas, produciendo presiones de vapor relativamente altas. El siguiente ejemplo ilustra esta dependencia de la presión de vapor de las fuerzas de atracción intermoleculares.

Ejemplo 9.5

Explicando la presión de vapor en términos de FIM

Dadas las fórmulas estructurales que se muestran para estos cuatro compuestos, explique sus presiones de vapor relativas en términos de tipos y extensiones de FIM:

las moléculas usadas en este experimento son (a) Etanol, (b) Etilen glicol, (c) éter dietílico y (d) Agua. puedes hacer clic sobre el nombre para interactuar con las moléculas.

Solución

El etilenglicol tiene dos grupos $\ce{-OH}$, por lo que, al igual que el agua, exhibe un enlace de hidrógeno extenso. Es mucho más grande que el agua y, por lo tanto, experimenta fuerzas más grandes de Londres. Sus FIM generales son la mayor de estas cuatro sustancias, lo que significa que su tasa de vaporización será la más lenta y, en consecuencia, su presión de vapor será la más baja.

Comprueba tu aprendizaje

A $20\,\degree C$, las presiones de vapor de varios alcoholes se dan en esta tabla. Explique estas presiones de vapor en términos de tipos y extensiones de FIM para estos alcoholes:

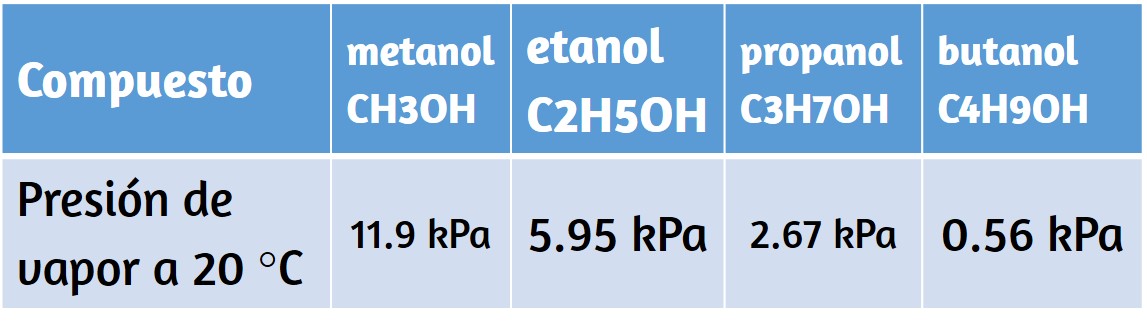
A medida que aumenta la temperatura, la presión de vapor de un líquido también aumenta debido al aumento de $K_E$ promedio de sus moléculas. Recuerde que a cualquier temperatura, las moléculas de una sustancia experimentan un rango de energías cinéticas, con una cierta fracción de moléculas que tienen una energía suficiente para vencer al FIM y escapar del líquido (vaporizarse). A una temperatura más alta, una fracción mayor de moléculas tiene suficiente energía para escapar del líquido, como se muestra en la Figura 9.23. El escape de más moléculas por unidad de tiempo y la mayor velocidad promedio de las moléculas que escapan contribuyen a la mayor presión de vapor.

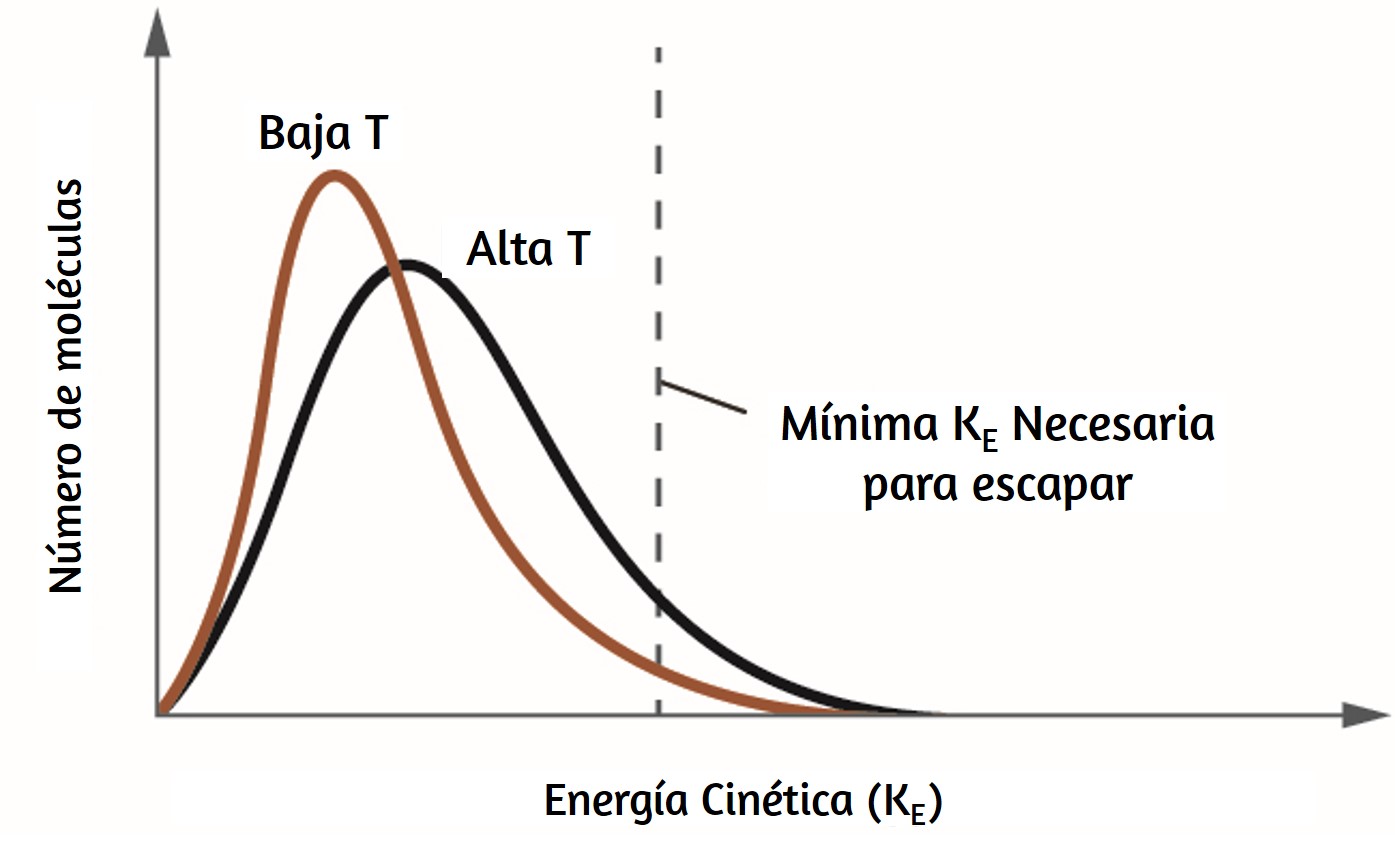
Figura 9.23. La temperatura afecta la distribución de energías cinéticas para las moléculas en un líquido. A la temperatura más alta, más moléculas tienen la energía cinética necesaria, $K_E$, para escapar del líquido a la fase gaseosa.

Puntos de ebullición

Cuando la presión de vapor aumenta lo suficiente como para igualar la presión atmosférica externa, el líquido alcanza su punto de ebullición. El punto de ebullición de un líquido es la temperatura a la cual su presión de vapor de equilibrio es igual a la presión ejercida sobre el líquido por su entorno gaseoso. Para líquidos en recipientes abiertos, esta presión se debe a la atmósfera de la tierra. El punto de ebullición normal de un líquido se define como su punto de ebullición cuando la presión circundante es igual a $1\,atm$ ($101.3\,kPa$). La Figura 9.24 muestra la variación en la presión de vapor con la temperatura para varias sustancias diferentes. Teniendo en cuenta la definición de punto de ebullición, se puede ver que estas curvas representan la dependencia del punto de ebullición de un líquido de la presión circundante.

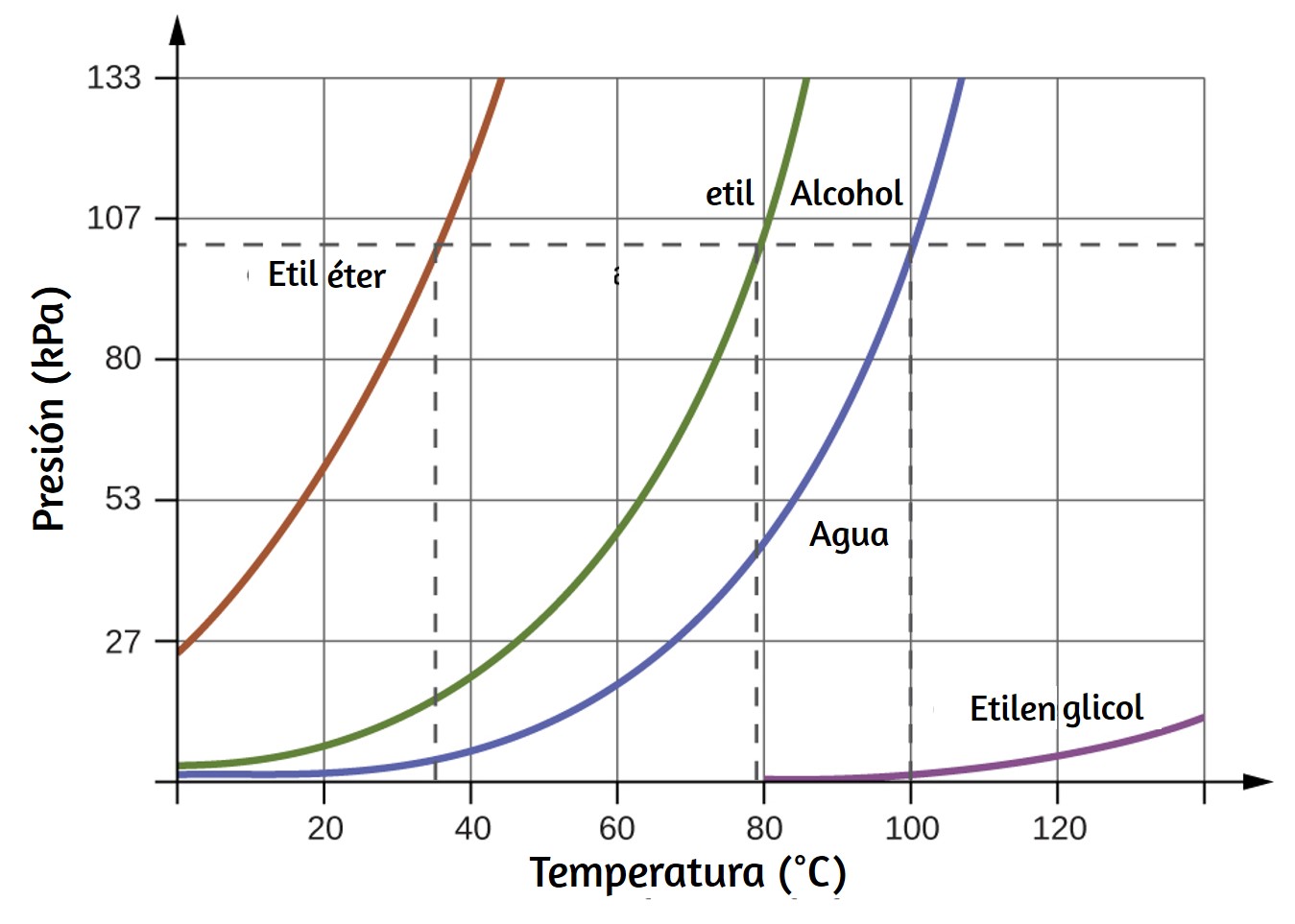
Figura 9.24. Los puntos de ebullición de los líquidos son las temperaturas a las cuales sus presiones de vapor de equilibrio son iguales a la presión de la atmósfera circundante. Los puntos de ebullición normales son los correspondientes a una presión de $1\,atm$ ($101.3\,kPa$).

Ejemplo 9.6

Un punto de ebullición a presión reducida

Una presión atmosférica típica en Leadville, Colorado (elevación $10,200\,pies$) es $68\,kPa$. Use el gráfico de la Figura 9.24 para determinar el punto de ebullición del agua a esta elevación.

Solución

El gráfico de la presión de vapor del agua versus la temperatura en la Figura 9.24 indica que la presión de vapor del agua es de $68\,kPa$ a aproximadamente $90\,\degree C$. Por lo tanto, a aproximadamente $90\,\degree C$, la presión de vapor del agua será igual a la presión atmosférica en Leadville, y el agua hervirá.

Comprueba tu aprendizaje

La ecuación de Clausius-Clapeyron describe la relación cuantitativa entre la presión de vapor de una sustancia y su temperatura:

donde $ΔH_{vap}$ es la entalpía de vaporización del líquido, R es la constante del gas y A es una constante cuyo valor depende de la identidad química de la sustancia. La temperatura T debe estar en Kelvin en esta ecuación. la ecuación a menudo se reorganiza en forma logarítmica para producir la ecuación lineal:

Esta ecuación lineal puede expresarse en un formato de dos puntos que es conveniente para su uso en varios cálculos, como se demuestra en los ejercicios de ejemplo que siguen. Si a la temperatura $T_1$, la presión de vapor es $P_1$, y a la temperatura $T_2$, la presión de vapor es $P_2$, las ecuaciones lineales correspondientes son:

Como la constante, A, es la misma, estas dos ecuaciones se pueden reorganizar para aislar ln A y luego establecerlas iguales entre sí:

Que se puede combinar en:

Ejemplo 9.7

Estimación de la entalpía de la vaporización

El isooctano (2,2,4-trimetilpentano) tiene una clasificación de octano de 100. Se utiliza como uno de los estándares para el sistema de clasificación de octano para gasolina. A 34.0 ° C, la presión de vapor del isooctano es 10.0 kPa, y a 98.8 ° C, su presión de vapor es 100.0 kPa. Use esta información para estimar la entalpía de vaporización para isooctano.

Solución

La entalpía de vaporización, $δH_{vap}$, se puede determinar utilizando la ecuación de Clausius-Clapeyron:

Como tenemos dos valores de presión-temperatura de vapor ($T_1 = 34.0\,\degree C = 307.2\,K$, $P_1 = 10.0\,kPa$ y $T_2 = 98.8\,\degree C = 372.0\,K$, $P_2 = 100\,kPa$), podemos sustituirlos en esta ecuación y resolver $δH_{vap}$ . Reorganizando la ecuación de Clausius-Clapeyron y resolviendo los rendimientos de $δH_{vap}$:

Tenga en cuenta que la presión puede estar en cualquier unidad, siempre que estén de acuerdo con ambos valores de P, pero la temperatura debe estar en kelvin para que la ecuación de Clausius-Clapeyron sea válida.

Comprueba tu aprendizaje

Ejemplo 9.8

Estimación de la temperatura (o presión de vapor)

Para el benceno $\ce{(C6H6)}$, el punto de ebullición normal es $80.1\,\degree C$ y la entalpía de vaporización es $30.8\, \frac{kJ}{mol}$. ¿Cuál es el punto de ebullición del benceno en Denver, donde la presión atmosférica = $83.4 \;kPa$?

Solución

Si la temperatura y la presión de vapor se conocen en un punto, junto con la entalpía de vaporización, $ΔH_{vap}$, entonces la temperatura que corresponde a una presión de vapor diferente (o viceversa) puede determinarse usando el Clausius -La ecuación de Clapeyron:

Dado que el punto de ebullición normal es la temperatura a la cual la presión de vapor es igual a la presión atmosférica a nivel del mar, conocemos un valor de temperatura de presión de vapor ($T_1 = 80.1\,\degree C = 353.3\,K$, $P_1 = 101.3\,kPa$, $ΔH_{vap} = 30.8 \frac{kJ}{mol}$) y desea encontrar la temperatura ($T_2$) que corresponde a la presión de vapor $P_2 = 83.4\,kPa$. Podemos sustituir estos valores en la ecuación de Clausius-Clapeyron y luego resolver $T_2$. Reorganizando la ecuación de Clausius-Clapeyron y resolviendo los rendimientos de $T_2$: $$ T_2 = \Bigg(\frac{-{R \cdot \ln \bigg(\frac {P_2}{P_1}\bigg)}}{ΔH_{vap}} + \frac{1}{T_1} \Bigg)^{-1} $$ $$ T_2 = \Bigg(\frac{-{\bigg(8.314 \frac{J}{mol\,K}\bigg) \cdot \ln \bigg(\frac {83.4\,kPa}{10.0\,kPa}\bigg)}}{30,800 \frac{J}{mol}} + \frac{1}{353\,K} \Bigg)^{-1} $$ $$ T_2 = 346.9\,K\;o\;73.8\,\degree C$$

Comprueba tu aprendizaje

Entalpía de vaporización

La vaporización es un proceso endotérmico. El efecto de enfriamiento puede ser evidente cuando sales de una piscina o una ducha. Cuando el agua de tu piel se evapora, elimina el calor de tu piel y te hace sentir frío. El cambio de energía asociado con el proceso de vaporización es la entalpía de vaporización, $ΔH_{vap}$. Por ejemplo, la vaporización de agua a temperatura estándar está representada por:

Como se describe en el capítulo sobre termoquímica, lo contrario de un proceso endotérmico es exotérmico. Y así, la condensación de un gas libera calor:

Ejemplo 9.9

Usando la entalpía de vaporización

Una forma en que nuestro cuerpo se enfría es mediante la evaporación del agua en el sudor (Figura 9.25). En climas muy calurosos, podemos perder hasta $1.5\,L$ de sudor por día. Aunque el sudor no es agua pura, podemos obtener un valor aproximado de la cantidad de calor eliminada por evaporación suponiendo que lo sea.

¿Cuánto calor se requiere para evaporar $1.5\,L$ de agua ($1.5\,kg$) a $T = 37 \degree C$ (temperatura corporal normal); $ΔH_{vap} = 43.46 \frac{kJ}{mol}$ a $37\degree C$.

Figura 9.25. La evaporación del sudor ayuda a enfriar el cuerpo. (crédito: "Kullez" / Flickr)

Solución

Comenzamos con el volumen conocido de sudor (aproximado como solo agua) y usamos la información dada para convertir a la cantidad de calor necesaria:

Así, $3600\,kJ$ de calor se eliminan por la evaporación de $1.5\,L$ de agua.

Comprueba tu aprendizaje

Derritiendo y Congelando

Cuando calentamos un sólido cristalino, aumentamos la energía promedio de sus átomos, moléculas o iones y el sólido se calienta. En algún momento, la energía añadida se vuelve lo suficientemente grande como para superar parcialmente las fuerzas que mantienen las moléculas o iones del sólido en sus posiciones fijas, y el sólido comienza el proceso de transición al estado líquido, o derretirse o fundirse. En este punto, la temperatura del sólido deja de aumentar, a pesar de la entrada continua de calor, y permanece constante hasta que todo el sólido se derrita. Solo después de que todo el sólido se haya derretido, el calentamiento continuo aumentará la temperatura del líquido (Figura 9.26).

Si dejamos de calentar durante la fusión y colocamos la mezcla de sólido y líquido en un recipiente perfectamente aislado para que no pueda entrar o salir calor, las fases sólida y líquida permanecen en equilibrio.

Figura 9.26. (a) Este vaso de hielo tiene una temperatura de $-12.0\,\degree C$. (b) Después de $10$ minutos, el hielo ha absorbido suficiente calor del aire para calentarse a $0\,\degree C$. Una pequeña cantidad se ha derretido. (c) Treinta minutos después, el hielo ha absorbido más calor, pero su temperatura aún es de $0\,\degree C$. El hielo se derrite sin cambiar su temperatura. (d) Solo después de que todo el hielo se haya derretido, el calor absorbido hace que la temperatura aumente a 2$2.2\,\degree C$. (crédito: modificación del trabajo de Mark Ott)

Esta es casi la situación con una mezcla de hielo y agua en una muy buena botella de termo; casi no entra ni sale calor, y la mezcla de hielo sólido y agua líquida permanece durante horas. En una mezcla de sólido y líquido en equilibrio, los procesos recíprocos de fusión y congelación ocurren a velocidades iguales, y las cantidades de sólido y líquido, por lo tanto, permanecen constantes. La temperatura a la cual las fases sólida y líquida de una sustancia dada están en equilibrio se llama el punto de fusión del sólido o el punto de congelación del líquido. El uso de un término u otro normalmente está dictado por la dirección de la transición de fase que se considera, por ejemplo, de sólido a líquido (fusión) o de líquido a sólido (congelación).

La entalpía de fusión y el punto de fusión de un sólido cristalino dependen de la fuerza de las fuerzas de atracción entre las unidades presentes en el cristal. Las moléculas con fuerzas atractivas débiles forman cristales con puntos de fusión bajos. Los cristales que consisten en partículas con fuerzas atractivas más fuertes se funden a temperaturas más altas.

La cantidad de calor requerida para cambiar un mol de una sustancia del estado sólido al estado líquido es la entalpía de fusión, $ΔH_{fus}$ de la sustancia. La entalpía de fusión del hielo es $6.0\, \frac{kJ}{mol}$ a $0\,\degree C$. La fusión (fusión) es un proceso endotérmico:

El proceso recíproco, congelación, es un proceso exotérmico cuyo cambio de entalpía es −6.0 kJ / mol a 0 \degree C:

Sublimación y deposición

Algunos sólidos pueden pasar directamente al estado gaseoso, evitando el estado líquido, a través de un proceso conocido como sublimación. A temperatura ambiente y presión estándar, se sublima un trozo de hielo seco ($\ce{CO2}$ sólido), que parece desaparecer gradualmente sin formar ningún líquido. La nieve y el hielo sublima a temperaturas por debajo del punto de fusión del agua, un proceso lento que puede ser acelerado por los vientos y las presiones atmosféricas reducidas a gran altura. Cuando el yodo sólido se calienta, el sólido sublima y se forma un vapor púrpura intenso (Figura 9.27). El reverso de la sublimación se llama deposición, un proceso en el cual las sustancias gaseosas se condensan directamente en el estado sólido, evitando el estado líquido. La formación de escarcha es un ejemplo de deposición.

Figura 9.27. La sublimación de yodo sólido en el fondo del tubo produce un gas púrpura que posteriormente se deposita como yodo sólido en la parte más fría del tubo de arriba. (crédito: modificación del trabajo de Mark Ott)

Al igual que la vaporización, el proceso de sublimación requiere un aporte de energía para superar las atracciones intermoleculares. La entalpía de la sublimación, $ΔH_{sub}$, es la energía requerida para convertir un mol de una sustancia del estado sólido al gaseoso. Por ejemplo, la sublimación de dióxido de carbono está representada por:

Del mismo modo, el cambio de entalpía para el proceso inverso de deposición es igual en magnitud pero opuesto en signo al de sublimación:

Considere hasta qué punto se deben superar las atracciones intermoleculares para lograr una transición de fase dada. La conversión de un sólido en un líquido requiere que estas atracciones se superen solo parcialmente; La transición al estado gaseoso requiere que se superen por completo. Como resultado, la entalpía de fusión de una sustancia es menor que la entalpía de vaporización. Esta misma lógica puede usarse para derivar una relación aproximada entre las entalpías de todos los cambios de fase para una sustancia dada. Aunque no es una descripción completamente precisa, la sublimación puede modelarse convenientemente como un proceso secuencial de fusión de dos pasos seguido de vaporización para aplicar la Ley de Hess. Visto de esta manera, la entalpía de sublimación de una sustancia puede estimarse como la suma de sus entalpías de fusión y vaporización, como se ilustra en la Figura 9.28. Por ejemplo:

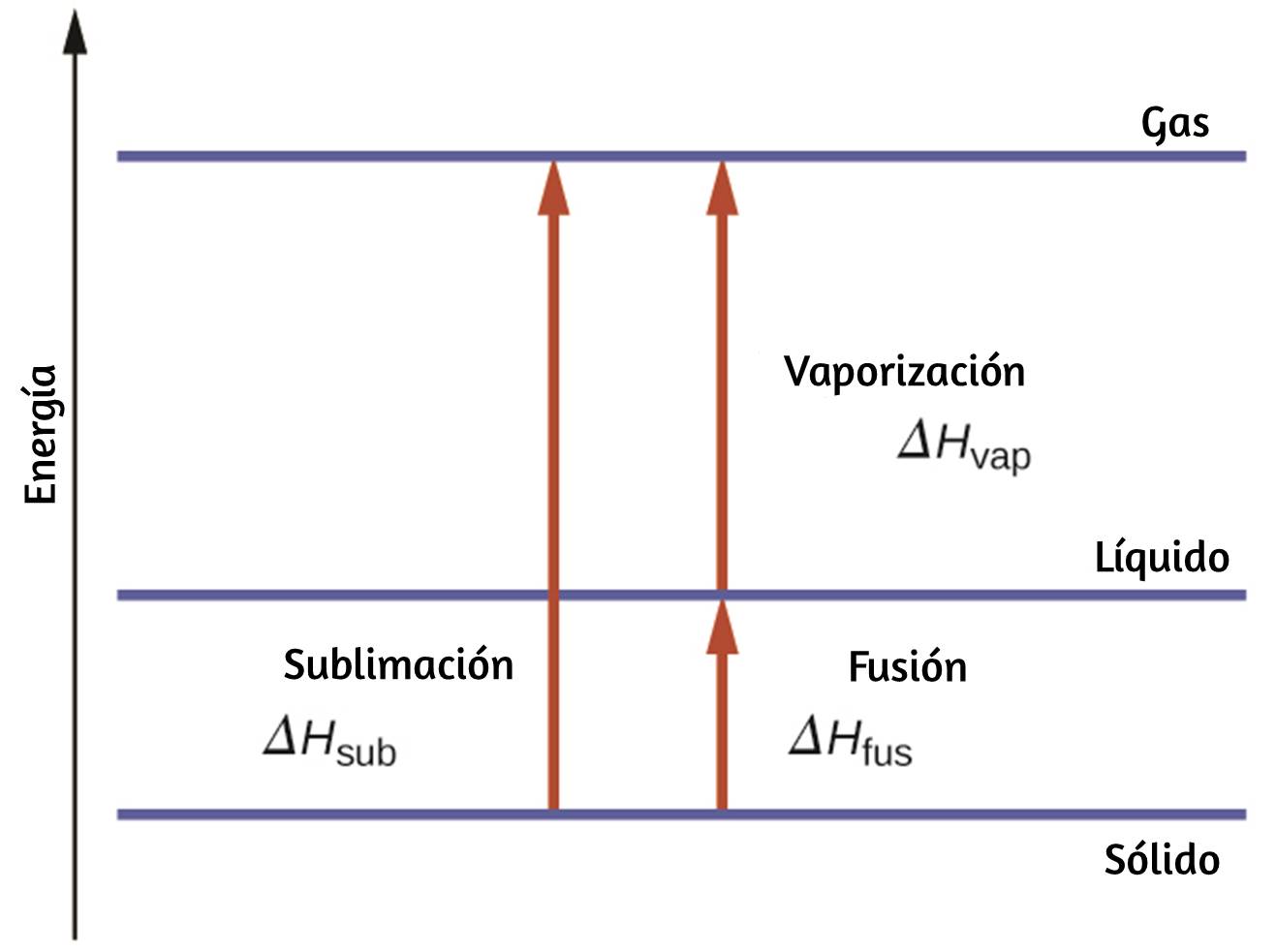
Figura 9.28. Para una sustancia dada, la suma de su entalpía de fusión y entalpía de vaporización es aproximadamente igual a su entalpía de sublimación.

Curvas de calentamiento y enfriamiento

En el capítulo sobre termoquímica, se introdujo la relación entre la cantidad de calor absorbido o liberado por una sustancia, q, y el cambio de temperatura que lo acompaña, $ΔT$:

Donde m es la masa de la sustancia y c es su calor específico. La relación se aplica a la materia que se calienta o enfría, pero que no experimenta un cambio de estado. Cuando una sustancia que se calienta o enfría alcanza una temperatura correspondiente a una de sus transiciones de fase, una mayor ganancia o pérdida de calor es el resultado de disminuir o aumentar las atracciones intermoleculares, en lugar de aumentar o disminuir las energías cinéticas moleculares. Mientras una sustancia está experimentando un cambio de estado, su temperatura permanece constante. La Figura 9.29 muestra una curva de calentamiento típica.

Considere el ejemplo de calentar una olla de agua a ebullición. Un quemador de estufa suministrará calor a una velocidad aproximadamente constante; inicialmente, este calor sirve para aumentar la temperatura del agua. Cuando el agua alcanza su punto de ebullición, la temperatura permanece constante a pesar de la entrada continua de calor del quemador de la estufa. El agua mantiene esta misma temperatura mientras esté hirviendo.

Si se aumenta el ajuste del quemador para proporcionar calor a un ritmo mayor, la temperatura del agua no aumenta, sino que la ebullición se vuelve más vigorosa (rápida). Este comportamiento también se observa para otras transiciones de fase: por ejemplo, la temperatura permanece constante mientras el cambio de estado está en progreso.

Figura 9.29. Una curva de calentamiento típica para una sustancia representa los cambios de temperatura que resultan cuando la sustancia absorbe cantidades crecientes de calor. Las mesetas en la curva (regiones de temperatura constante) se exhiben cuando la sustancia experimenta transiciones de fase.

Ejemplo 9.10

Calor total necesario para cambiar la temperatura y la fase de una sustancia

¿Cuánto calor se requiere para convertir $135\,g$ de hielo a $-15\,\degree C$ en vapor de agua a $120\,\degree C$?

Solución

La transición descrita implica los siguientes pasos:

1. Caliente el hielo de $−15\,\degree C$ a $0\,\degree C$

2. Hielo derretido

3. Calentar agua de $0\,\degree C$ a $100\,\degree C$

4. Agua hervida

5. Calienta el vapor de $100\,\degree C$ a $120\,\degree C$

El calor necesario para cambiar la temperatura de una sustancia determinada (sin cambios en la fase) es: $q = m \times c \times ΔT$ (consulte el capítulo anterior sobre termoquímica). El calor necesario para inducir un cambio de fase dado viene dado por $q = n \times ΔH$.

Usando estas ecuaciones con los valores apropiados para el calor específico de hielo, agua y vapor, y entalpías de fusión y vaporización, tenemos:

$q_{total}=(m \cdot c \cdot ΔT)_{hielo} + n \cdot ΔH_{fus} + (m \cdot c \cdot ΔT)_{Agua} + n \cdot ΔH_{Vap} + (m \cdot c \cdot ΔT)_{Vapor}$

$q_{total}=\bigg(135 \cancel{g} \cdot 2.09 \frac{J}{\cancel{g} \cdot \bcancel{\degree C}} \cdot 15 \bcancel{\degree C} \bigg) + \bigg(135\cancel{g}\cdot\frac{1\bcancel{mol}}{18.02\cancel{g}}\cdot6.01\frac{kJ}{\bcancel{mol}}\bigg) + \bigg(135\cancel{g}\cdot4.18\frac{J}{\cancel{g}\cdot\bcancel{\degree C}}\cdot100\bcancel{\degree C}\bigg) + \bigg(135 \cancel{g} \cdot \frac{1\,\bcancel{mol}}{18.02\,\cancel{g}} \cdot 40.67 \frac{kJ}{\bcancel{mol}}\bigg) + \bigg(135 \cancel{g} \cdot 1.84 \frac{J}{\cancel{g} \cdot \bcancel{\degree C}} \cdot 20 \bcancel{\degree C} \bigg)$

La conversión de las cantidades en $J$ a $kJ$ permite sumarlas, produciendo el calor total requerido:

Comprueba tu aprendizaje

Diagramas de fase

En el módulo anterior, se describió la variación de la presión de vapor de equilibrio de un líquido con la temperatura. Considerando la definición de punto de ebullición, los gráficos de presión de vapor versus temperatura representan cómo el punto de ebullición del líquido varía con la presión. También se describió el uso de curvas de calentamiento y enfriamiento para determinar el punto de fusión (o congelación) de una sustancia. Hacer tales mediciones en un amplio rango de presiones produce datos que pueden presentarse gráficamente como un diagrama de fase. Un diagrama de fases combina gráficos de presión versus temperatura para los equilibrios de transición de fase líquido-gas, sólido-líquido y sólido-gas de una sustancia.

Estos diagramas indican los estados físicos que existen bajo condiciones específicas de presión y temperatura, y también proporcionan la dependencia de la presión de las temperaturas de transición de fase (puntos de fusión, puntos de sublimación, puntos de ebullición). En la Figura 9.30 se muestra un diagrama de fase típico para una sustancia pura.

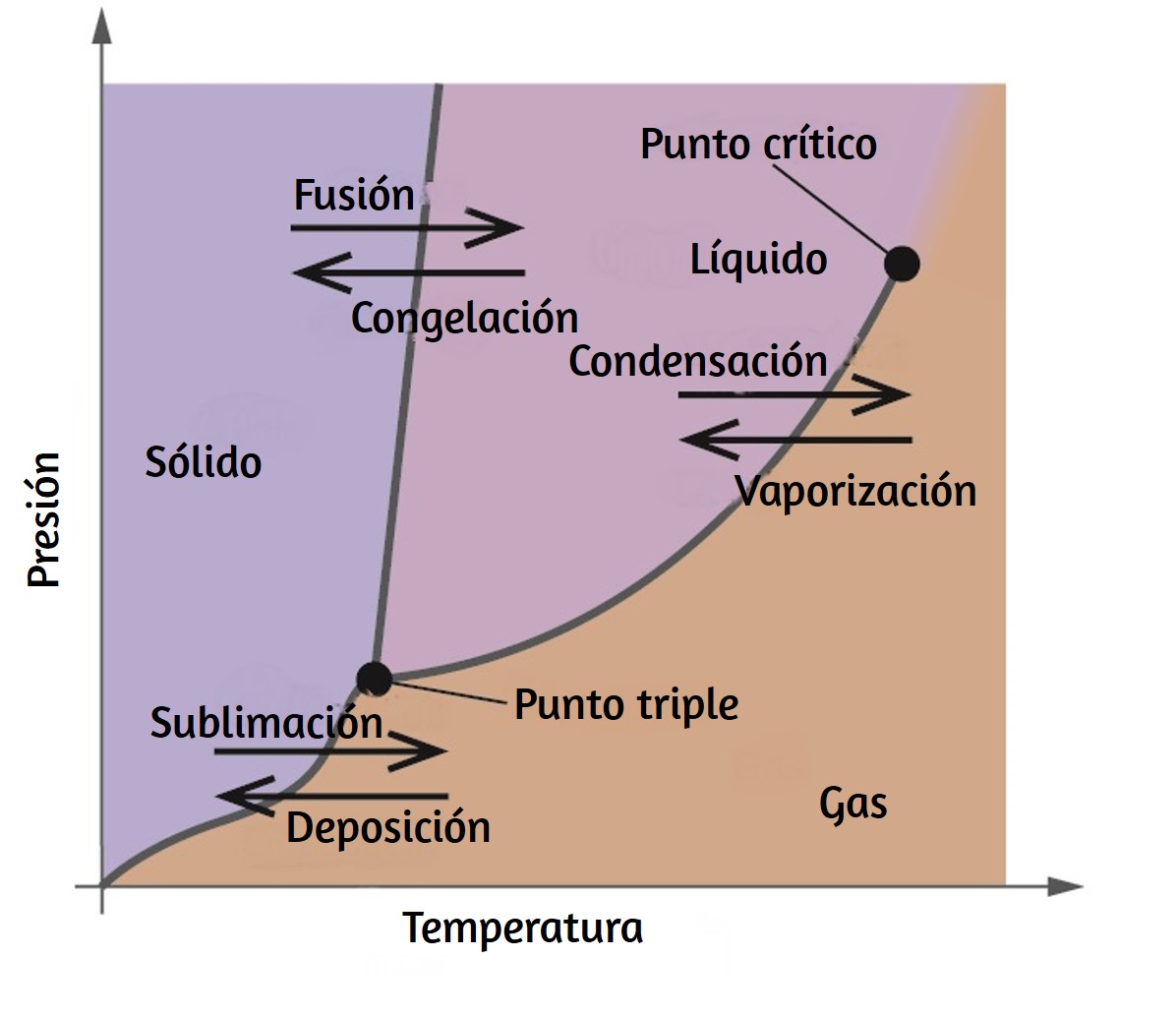
Figura 9.30. El estado físico de una sustancia y sus temperaturas de transición de fase se representan gráficamente en un diagrama de fase.

Para ilustrar la utilidad de estas parcelas, considere el diagrama de fase para el agua que se muestra en la Figura 9.31.

Figura 9.31. Los ejes de presión y temperatura en este diagrama de fase del agua no se dibujan a escala constante para ilustrar varias propiedades importantes.

Podemos usar el diagrama de fases para identificar el estado físico de una muestra de agua en condiciones específicas de presión y temperatura. Por ejemplo, una presión de $50\,kPa$ y una temperatura de $−10\,\degree C$ corresponden a la región del diagrama etiquetada como "hielo". En estas condiciones, el agua existe solo como un sólido (hielo). Una presión de $50\,kPa$ y una temperatura de $50\,\degree C$ corresponden a la región "agua"; aquí, el agua existe solo como un líquido. A $25\,kPa$ y $200\,\degree C$, el agua existe solo en estado gaseoso. Tenga en cuenta que en el diagrama de fase $\ce{H2O}$, los ejes de presión y temperatura no están dibujados a una escala constante para permitir la ilustración de varias características importantes como se describe aquí.

La curva BC en la Figura 9.31 es la gráfica de la presión de vapor versus la temperatura como se describe en el módulo anterior de este capítulo. Esta curva de “líquido-vapor” separa las regiones líquida y gaseosa del diagrama de fases y proporciona el punto de ebullición del agua a cualquier presión. Por ejemplo, a $1\,atm$, el punto de ebullición es de $100'\,\degree C$. Observe que la curva de líquido-vapor termina a una temperatura de $374\,\degree C$ y una presión de $218\,atm$, lo que indica que el agua no puede existir como líquido por encima de esta temperatura, independientemente de la presión. Las propiedades físicas del agua en estas condiciones son intermedias entre las de sus fases líquida y gaseosa. Este estado único de la materia se llama fluido supercrítico, un tema que se describirá en la siguiente sección de este módulo.

La curva de vapor sólido, etiquetada AB en la Figura 9.31, indica las temperaturas y presiones a las que el vapor de hielo y agua están en equilibrio. Estos pares de datos de temperatura-presión corresponden a los puntos de sublimación o deposición del agua. Si pudiéramos acercarnos a la línea de gas sólido en la Figura 9.31, veríamos que el hielo tiene una presión de vapor de aproximadamente $0,20\,kPa$ a $-10\,\degree C$. Por lo tanto, si colocamos una muestra congelada en el vacío con una presión inferior a $0,20\,kPa$, el hielo sublimará. Esta es la base del proceso de "liofilización" que se usa a menudo para conservar alimentos, como el helado que se muestra en la Figura 9.32.

La curva sólido-líquido etiquetada BD muestra las temperaturas y presiones a las que el hielo y el agua líquida están en equilibrio, representando los puntos de fusión/congelación del agua. Tenga en cuenta que esta curva presenta una ligera pendiente negativa (muy exagerada para mayor claridad), lo que indica que el punto de fusión del agua disminuye ligeramente a medida que aumenta la presión.

Figura 9.32. Los alimentos liofilizados, como este helado, se deshidratan por sublimación a presiones por debajo del punto triple para el agua. (crédito: ʺlwaoʺ / Flickr)

El agua es una sustancia inusual a este respecto, ya que la mayoría de las sustancias exhiben un aumento en el punto de fusión al aumentar la presión. Este comportamiento es en parte responsable del movimiento de los glaciares, como el que se muestra en la Figura 9.33. El fondo de un glaciar experimenta una presión inmensa debido a su peso que puede derretir parte del hielo, formando una capa de agua líquida sobre la cual el glaciar puede deslizarse más fácilmente.

Figura 9.33. Las inmensas presiones debajo de los glaciares resultan en una fusión parcial para producir una capa de agua que proporciona lubricación para ayudar al movimiento glacial. Esta fotografía satelital muestra el avance del glaciar Perito Moreno en Argentina. (crédito: NASA)

El punto de intersección de las tres curvas está etiquetado B en la Figura 9.31. A la presión y temperatura representadas por este punto, las tres fases del agua coexisten en equilibrio. Este par de datos de temperatura-presión se llama punto triple. A presiones inferiores al punto triple, el agua no puede existir como líquido, independientemente de la temperatura.

Ejemplo 9.11

Determinando el estado del agua

Usando el diagrama de fase para el agua que figura en la Figura 9.31, determine el estado del agua a las siguientes temperaturas y presiones:

(a) $-10\,\degree C$ y $50\,kPa$
(b) $25\,\degree C$ y $90\,kPa$
(c) $50\,\degree C$ y $40\,kPa$
(d) $80\,\degree C$ y $5\,kPa$
(e) $−10\,\degree C$ y $0.3\,kPa$
(f) $50\,\degree C$ y $0.3\,kPa$

Solución

Usando el diagrama de fase para el agua, podemos determinar que el estado del agua a cada temperatura y presión dada es la siguiente:
(a) sólido
(b) líquido
(c) líquido
(d) gas
(e) sólido
(f) gas.

Comprueba tu aprendizaje

Considere el diagrama de fase para el dióxido de carbono que se muestra en la Figura 9.34 como otro ejemplo. La curva sólido-líquido exhibe una pendiente positiva, lo que indica que el punto de fusión del $\ce{CO2}$ aumenta con la presión como lo hace con la mayoría de las sustancias (el agua es una excepción notable como se describió anteriormente). Observe que el punto triple está muy por encima de $1\,atm$, lo que indica que el dióxido de carbono no puede existir como líquido en condiciones de presión ambiente.

Figura 9.34. Se muestra un diagrama de fase para el dióxido de carbono. El eje de presión se traza en una escala logarítmica para acomodar el amplio rango de valores.

En cambio, enfriar dióxido de carbono gaseoso a $1\,atm$ resulta en su deposición en estado sólido. Del mismo modo, el dióxido de carbono sólido no se funde a una presión de $1\,atm$ sino que se sublima para producir $\ce{CO2}$ gaseoso. Finalmente, observe que el punto crítico para el dióxido de carbono se observa a una temperatura y presión relativamente moderadas en comparación con el agua.

Ejemplo 9.12

Determinación del estado del dióxido de carbono

Usando el diagrama de fase para el dióxido de carbono que se muestra en la Figura 9.34, determine el estado del $\ce{CO2}$ a las siguientes temperaturas y presiones:

(a) $−30\,\degree C$ y $2000\,kPa$
(b) $−60\,\degree C$ y $1000\,kPa$
(c) $−60\,\degree C$ y $100\,kPa$
(d) $−40\,\degree C$ y $1500\,kPa$
(e) $0\,\degree C$ y $100\,kPa$
(f) $20\,\degree C$ y $100\,kPa$

Solución

Usando el diagrama de fase para el dióxido de carbono provisto, podemos determinar que el estado de $\ce{CO2}$ a cada temperatura y presión dada es el siguiente: (a) líquido; (b) sólido; (c) gas; (d) líquido; (e) gas; (f) gas.

Comprueba tu aprendizaje

Fluidos Supercríticos

Si colocamos una muestra de agua en un recipiente sellado a $25\,\degree C$, eliminamos el aire y dejamos que se establezca el equilibrio de vaporización-condensación, nos queda una mezcla de agua líquida y vapor de agua a una presión de $0.03\,atm$. Se observa claramente un límite distintivo entre el líquido más denso y el gas menos denso. A medida que aumentamos la temperatura, aumenta la presión del vapor de agua, como se describe en la curva de líquido-gas en el diagrama de fase para el agua (Figura 9.31), y permanece un equilibrio de dos fases de las fases líquida y gaseosa. A una temperatura de $374\,\degree C$, la presión de vapor ha aumentado a $218\,atm$, y cualquier aumento adicional en la temperatura resulta en la desaparición del límite entre las fases líquida y de vapor. Toda el agua en el recipiente ahora está presente en una sola fase cuyas propiedades físicas son intermedias entre las de los estados gaseoso y líquido.

Esta fase de la materia se llama fluido supercrítico, y la temperatura y la presión por encima de las cuales existe esta fase es el punto crítico (Figura 9.35). Por encima de su temperatura crítica, un gas no puede licuarse sin importar cuánta presión se aplique. La presión requerida para licuar un gas a su temperatura crítica se llama presión crítica. Las temperaturas críticas y las presiones críticas de algunas sustancias comunes se dan en la siguiente tabla.

Tabla 9.5: Las temperaturas y presiones críticas de algunas sustancias comunes

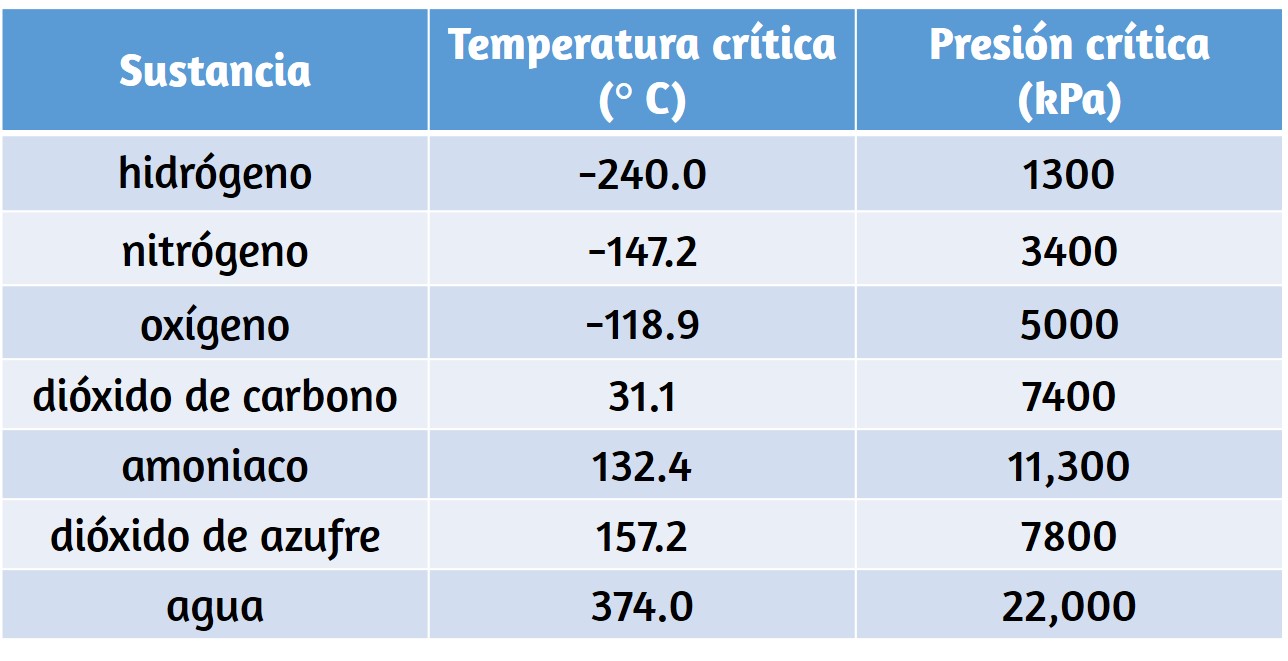
Figura 9.35. (a) Se calienta un recipiente sellado de dióxido de carbono líquido ligeramente por debajo de su punto crítico, lo que resulta en (b) la formación de la fase de fluido supercrítico. El enfriamiento del fluido supercrítico disminuye su temperatura y presión por debajo del punto crítico, lo que resulta en el restablecimiento de fases líquidas y gaseosas separadas (cyd). Los flotadores de colores ilustran las diferencias de densidad entre los estados líquido, gaseoso y fluido supercrítico. (crédito: modificación del trabajo por "mrmrobin" / YouTube)

Enlace a aprendizaje

Al igual que un gas, un fluido supercrítico se expandirá y llenará un contenedor, pero su densidad es mucho mayor que las densidades de gas típicas, típicamente cerca de las de los líquidos. Similar a los líquidos, estos fluidos son capaces de disolver solutos no volátiles. Sin embargo, exhiben esencialmente ninguna tensión superficial y viscosidades muy bajas, por lo que pueden penetrar más eficazmente aberturas muy pequeñas en una mezcla sólida y eliminar componentes solubles. Estas propiedades hacen que los fluidos supercríticos sean disolventes extremadamente útiles para una amplia gama de aplicaciones. Por ejemplo, el dióxido de carbono supercrítico se ha convertido en un solvente muy popular en la industria alimentaria, ya que se utiliza para descafeinar café, eliminar grasas de las papas fritas y extraer compuestos aromatizantes y aromatizantes de los aceites cítricos. No es tóxico, es relativamente económico y no se considera contaminante. Después del uso, el $\ce{CO2}$ puede recuperarse fácilmente reduciendo la presión y recogiendo el gas resultante.

Ejemplo 9.13

La temperatura crítica del dióxido de carbono

Si sacudimos un extintor de dióxido de carbono en un día frío ($18\,\degree C$), podemos escuchar el $\ce{CO2}$ líquido chapoteando dentro del cilindro.

Sin embargo, el mismo cilindro parece no contener líquido en un día caluroso de verano ($35\,\degree C$). Explica estas observaciones.

Solución

En el día frío, la temperatura del $\ce{CO2}$ está por debajo de la temperatura crítica de $\ce{CO2}$, $304\,K$ o $31\,\degree C$ (Ejemplo 9.12), por lo que el $\ce{CO2}$ líquido está presente en el cilindro. En los días calurosos, la temperatura del $\ce{CO2}$ es mayor que su temperatura crítica de $31\,\degree C$. Por encima de esta temperatura, ninguna cantidad de presión puede licuar el $\ce{CO2}$, por lo que no existe $\ce{CO2}$ líquido en el extintor de incendios.

Comprueba tu aprendizaje

Química en la vida cotidiana

Café descafeinado con $\ce{CO2}$ supercrítico

El café es el segundo producto más comercializado del mundo, solo después del petróleo. En todo el mundo, a la gente le encanta el aroma y el sabor del café. Muchos de nosotros también dependemos de un componente del café, la cafeína, para ayudarnos a ponernos en marcha por la mañana o estar alertas por la tarde. Pero al final del día, el efecto estimulante del café puede evitar que duerma, por lo que puede optar por tomar café descafeinado por la noche.

Desde principios de 1900, se han utilizado muchos métodos para descafeinar el café. Todos tienen ventajas y desventajas, y todos dependen de las propiedades físicas y químicas de la cafeína. Debido a que la cafeína es una molécula algo polar, se disuelve bien en agua, un líquido polar. Sin embargo, dado que muchos de los otros 400 compuestos que contribuyen al sabor y aroma del café también se disuelven en $\ce{H2O}$, los procesos de descafeinado con agua caliente también pueden eliminar algunos de estos compuestos, afectando negativamente el olor y el sabor del café descafeinado. El diclorometano ($\ce{CH2Cl2}$) y el acetato de etilo ($\ce{CH3CO2C2H5}$) tienen una polaridad similar a la cafeína y, por lo tanto, son disolventes muy efectivos para la extracción de cafeína, pero ambos también eliminan algunos componentes de sabor y aroma, y su uso requiere largos tiempos de extracción y limpieza. Debido a que ambos solventes son tóxicos, se han planteado problemas de salud con respecto al efecto del solvente residual que queda en el café descafeinado.

La extracción de fluidos supercríticos con dióxido de carbono ahora se está utilizando ampliamente como un método de descafeinación más eficaz y respetuoso con el medio ambiente (Figura 9.36).

A temperaturas superiores a $304,2\,K$ y presiones superiores a $7376\,kPa$, el $\ce{CO2}$ es un fluido supercrítico, con propiedades de gas y líquido. Como un gas, penetra profundamente en los granos de café; Como un líquido, disuelve efectivamente ciertas sustancias. La extracción supercrítica de dióxido de carbono de los granos de café al vapor elimina el $97-99\%$ de la cafeína, dejando intactos los compuestos de aroma y sabor del café. Debido a que el $\ce{CO2}$ es un gas en condiciones estándar, su eliminación de los granos de café extraídos se logra fácilmente, al igual que la recuperación de la cafeína del extracto. La cafeína recuperada de los granos de café a través de este proceso es un producto valioso que se puede utilizar posteriormente como un aditivo para otros alimentos o drogas.

Figura 9.36. (a) Las moléculas de cafeína tienen regiones polares y no polares, lo que las hace solubles en disolventes de polaridades variables. (b) El esquema muestra un proceso típico de descafeinado que involucra dióxido de carbono supercrítico.

El estado sólido de la materia

Cuando la mayoría de los líquidos se enfrían, eventualmente se congelan y forman sólidos cristalinos, sólidos en los que los átomos, iones o moléculas están dispuestos en un patrón repetitivo definido. También es posible que un líquido se congele antes de que sus moléculas se organicen en un patrón ordenado. Los materiales resultantes se denominan sólidos amorfos o sólidos no cristalinos (o, a veces, vidrios). Las partículas de tales sólidos carecen de una estructura interna ordenada y están dispuestas aleatoriamente (Figura 9.37).

Figura 9.37. Las entidades de una fase sólida pueden disponerse en un patrón regular y repetitivo (sólidos cristalinos) o aleatoriamente (amorfo).

Los metales y los compuestos iónicos típicamente forman sólidos cristalinos ordenados. Las sustancias que consisten en moléculas grandes, o una mezcla de moléculas cuyos movimientos son más restringidos, a menudo forman sólidos amorfos. Por ejemplo, las ceras de velas son sólidos amorfos compuestos de grandes moléculas de hidrocarburos. Algunas sustancias, como el dióxido de silicio (que se muestra en la Figura 9.38), pueden formar sólidos cristalinos o amorfos, dependiendo de las condiciones bajo las cuales se produce.

Además, los sólidos amorfos pueden experimentar una transición al estado cristalino en condiciones apropiadas.

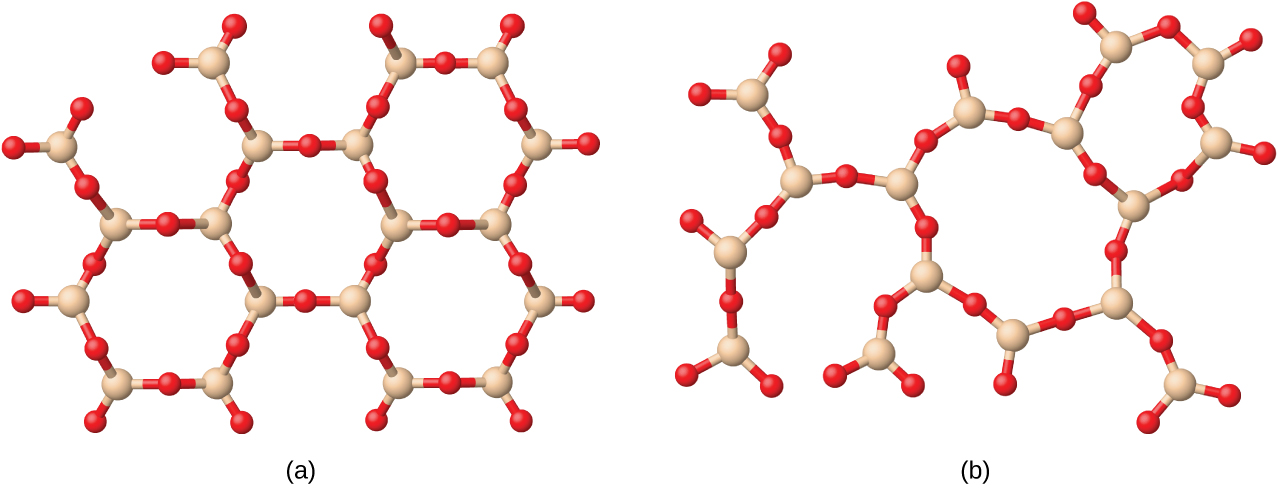
Figura 9.38. (a) El dióxido de silicio, $\ce{SiO2}$, es abundante en la naturaleza como una de varias formas cristalinas del cuarzo mineral. (b) El enfriamiento rápido del $\ce{SiO2}$ fundido produce un sólido amorfo conocido como "sílice fundida".

Los sólidos cristalinos generalmente se clasifican de acuerdo con la naturaleza de las fuerzas que mantienen juntas sus partículas. Estas fuerzas son las principales responsables de las propiedades físicas exhibidas por los sólidos a granel. Las siguientes secciones proporcionan descripciones de los principales tipos de sólidos cristalinos: iónico, metálico, red covalente y molecular.

Sólidos iónicos

Los sólidos iónicos, como el cloruro de sodio y el óxido de níquel, están compuestos de iones positivos y negativos que se mantienen unidos mediante atracciones electrostáticas, que pueden ser bastante fuertes (Figura 9.39). Muchos cristales iónicos también tienen altos puntos de fusión. Esto se debe a las muy fuertes atracciones entre los iones: en los compuestos iónicos, las atracciones entre las cargas completas son (mucho) más grandes que aquellas entre las cargas parciales en los compuestos moleculares polares.

Esto se analizará con más detalle en una discusión posterior de las energías reticulares. Aunque son difíciles, también tienden a ser frágiles y se rompen en lugar de doblarse. Los sólidos iónicos no conducen electricidad; sin embargo, conducen cuando están fundidos o disueltos porque sus iones son libres de moverse. Muchos compuestos simples formados por la reacción de un elemento metálico con un elemento no metálico son iónicos.

Figura 9.39. El cloruro de sodio es un sólido iónico.

Sólidos metálicos

Los sólidos metálicos como los cristales de cobre, aluminio y hierro están formados por átomos metálicos. Figura 9.40. La estructura de los cristales metálicos a menudo se describe como una distribución uniforme de núcleos atómicos dentro de un "mar" de electrones deslocalizados.

Los átomos dentro de tal sólido metálico se mantienen unidos por una fuerza única conocida como enlace metálico que da lugar a muchas propiedades de volumen útiles y variadas. Todos exhiben alta conductividad térmica y eléctrica, brillo metálico y maleabilidad. Muchos son muy duros y bastante fuertes. Debido a su maleabilidad (la capacidad de deformarse bajo presión o martilleo), no se rompen y, por lo tanto, son materiales de construcción útiles. Los puntos de fusión de los metales varían ampliamente. El mercurio es un líquido a temperatura ambiente, y los metales alcalinos se derriten por debajo de $200\,\degree C$. Varios metales posteriores a la transición también tienen puntos de fusión bajos, mientras que los metales de transición se funden a temperaturas superiores a $1000\,\degree C$. Estas diferencias reflejan diferencias en las resistencias de la unión metálica entre los metales.

Figura 9.40. El cobre es un sólido metálico.

Red Covalente Sólida

Los sólidos de red covalente incluyen cristales de diamante, silicio, algunos otros no metales y algunos compuestos covalentes como el dióxido de silicio (arena) y el carburo de silicio (carborundo, el abrasivo sobre papel de lija). Muchos minerales tienen redes de enlaces covalentes. Los átomos en estos sólidos se mantienen unidos por una red de enlaces covalentes, como se muestra en la Figura 9.41. Para romper o derretir una red covalente sólida, los enlaces covalentes deben romperse. Debido a que los enlaces covalentes son relativamente fuertes, los sólidos de la red covalente se caracterizan típicamente por su dureza, resistencia y altos puntos de fusión. Por ejemplo, el diamante es una de las sustancias más duras conocidas y se funde por encima de los $3500\,\degree C$.

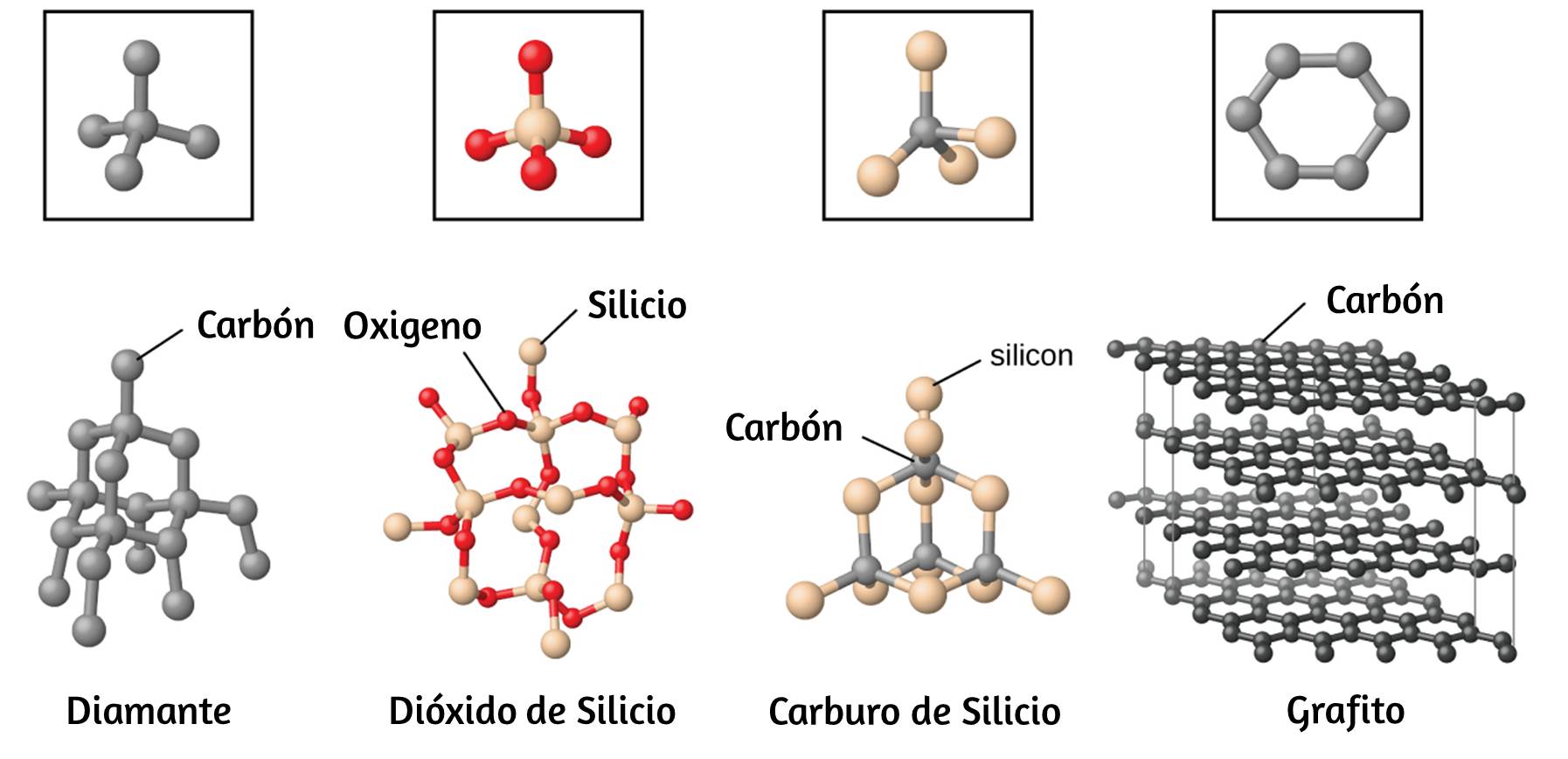
Figura 9.41. Un cristal covalente contiene una red tridimensional de enlaces covalentes, como lo ilustran las estructuras de diamante, dióxido de silicio, carburo de silicio y grafito. El grafito es un ejemplo excepcional, compuesto de láminas planas de cristales covalentes que se mantienen juntas en capas por fuerzas no covalentes. A diferencia de los sólidos covalentes típicos, el grafito es muy blando y eléctricamente conductor.

Sólido molecular

Los sólidos moleculares, como el hielo, la sacarosa (azúcar de mesa) y el yodo, como se muestra en la Figura 9.42, están compuestos de moléculas neutras. Las fuerzas de las fuerzas de atracción entre las unidades presentes en diferentes cristales varían ampliamente, como lo indican los puntos de fusión de los cristales. Las moléculas simétricas pequeñas (moléculas no polares), como $\ce{H2,\,N2,\,O2}$ y $\ce{F2}$, tienen fuerzas de atracción débiles y forman sólidos moleculares con puntos de fusión muy bajos (por debajo de $-200\,\degree C$). Las sustancias que consisten en moléculas no polares más grandes tienen fuerzas atractivas más grandes y se funden a temperaturas más altas. Los sólidos moleculares compuestos de moléculas con momentos dipolares permanentes (moléculas polares) se funden a temperaturas aún más altas. Los ejemplos incluyen hielo (punto de fusión, $0\,\degree C$) y azúcar de mesa (punto de fusión, $185\,\degree C$).

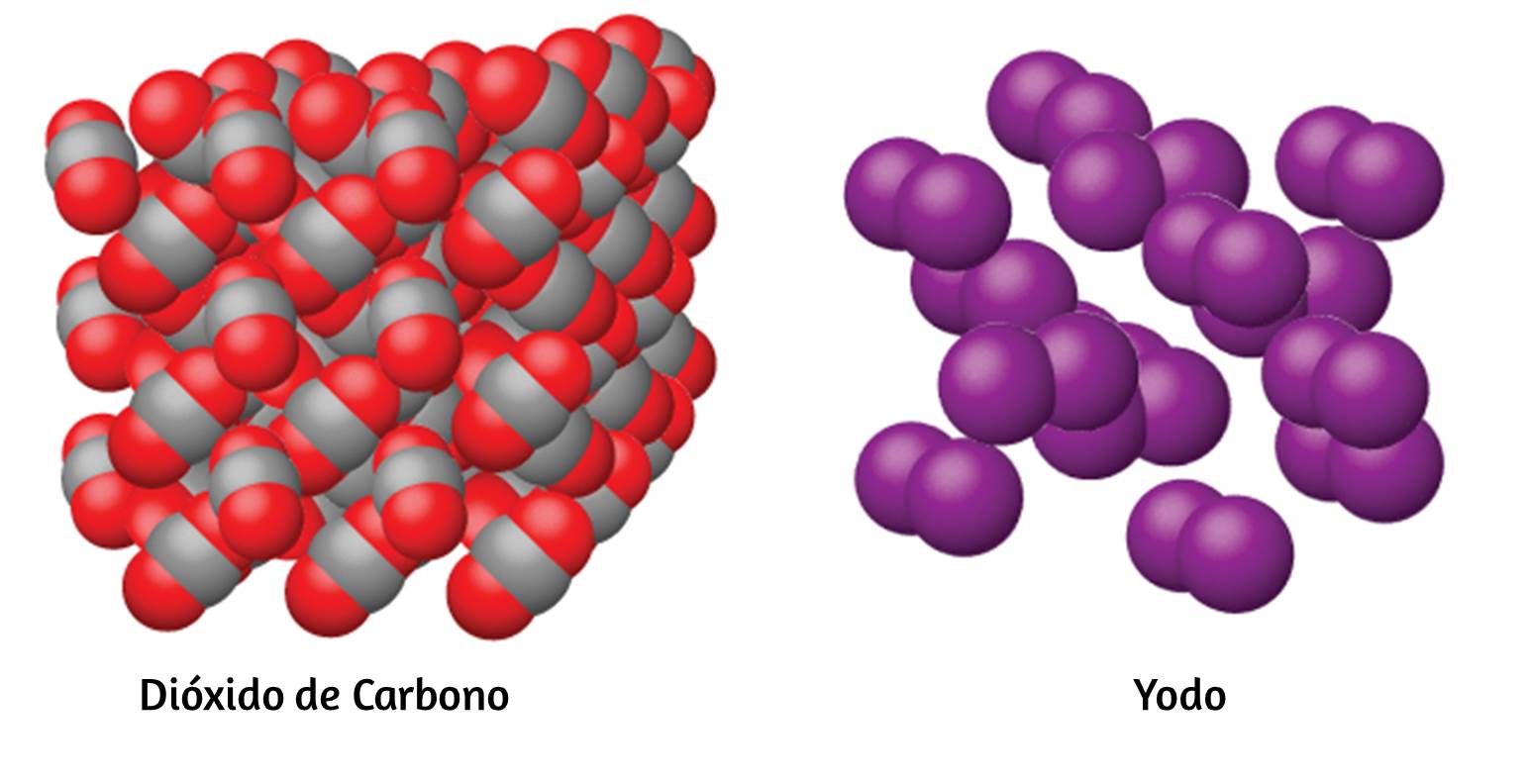
Figura 9.42. El dióxido de carbono ($\ce{CO2}$) consta de pequeñas moléculas no polares y forma un sólido molecular con un punto de fusión de $-78\,\degree C$. El yodo ($\ce{I2}$) consiste en moléculas no polares más grandes y forma un sólido molecular que se funde a $114\,\degree C$.

Propiedades de los sólidos.

Un sólido cristalino, como los enumerados en la Tabla 9.6, tiene una temperatura de fusión precisa porque cada átomo o molécula del mismo tipo se mantiene en su lugar con las mismas fuerzas o energía. Por lo tanto, las atracciones entre las unidades que componen el cristal tienen la misma fuerza y todas requieren la misma cantidad de energía para romperse. El ablandamiento gradual de un material amorfo difiere dramáticamente de la fusión distintiva de un sólido cristalino. Esto resulta de la no equivalencia estructural de las moléculas en el sólido amorfo. Algunas fuerzas son más débiles que otras, y cuando se calienta un material amorfo, las atracciones intermoleculares más débiles se rompen primero. A medida que la temperatura aumenta aún más, se rompen las atracciones más fuertes. Así, los materiales amorfos se ablandan en un rango de temperaturas.

Tabla 9.6. sólido cristalino

Tipos de sólidos cristalinos y sus propiedades

Cómo se interconectan las ciencias

Grafeno: material del futuro

El carbono es un elemento esencial en nuestro mundo. Las propiedades únicas de los átomos de carbono permiten la existencia de formas de vida basadas en el carbono como nosotros. El carbono forma una gran variedad de sustancias que usamos a diario, incluidas las que se muestran en la Figura 9.43. Es posible que esté familiarizado con el diamante y el grafito, los dos alótropos de carbono más comunes. (Los alótropos son diferentes formas estructurales del mismo elemento).

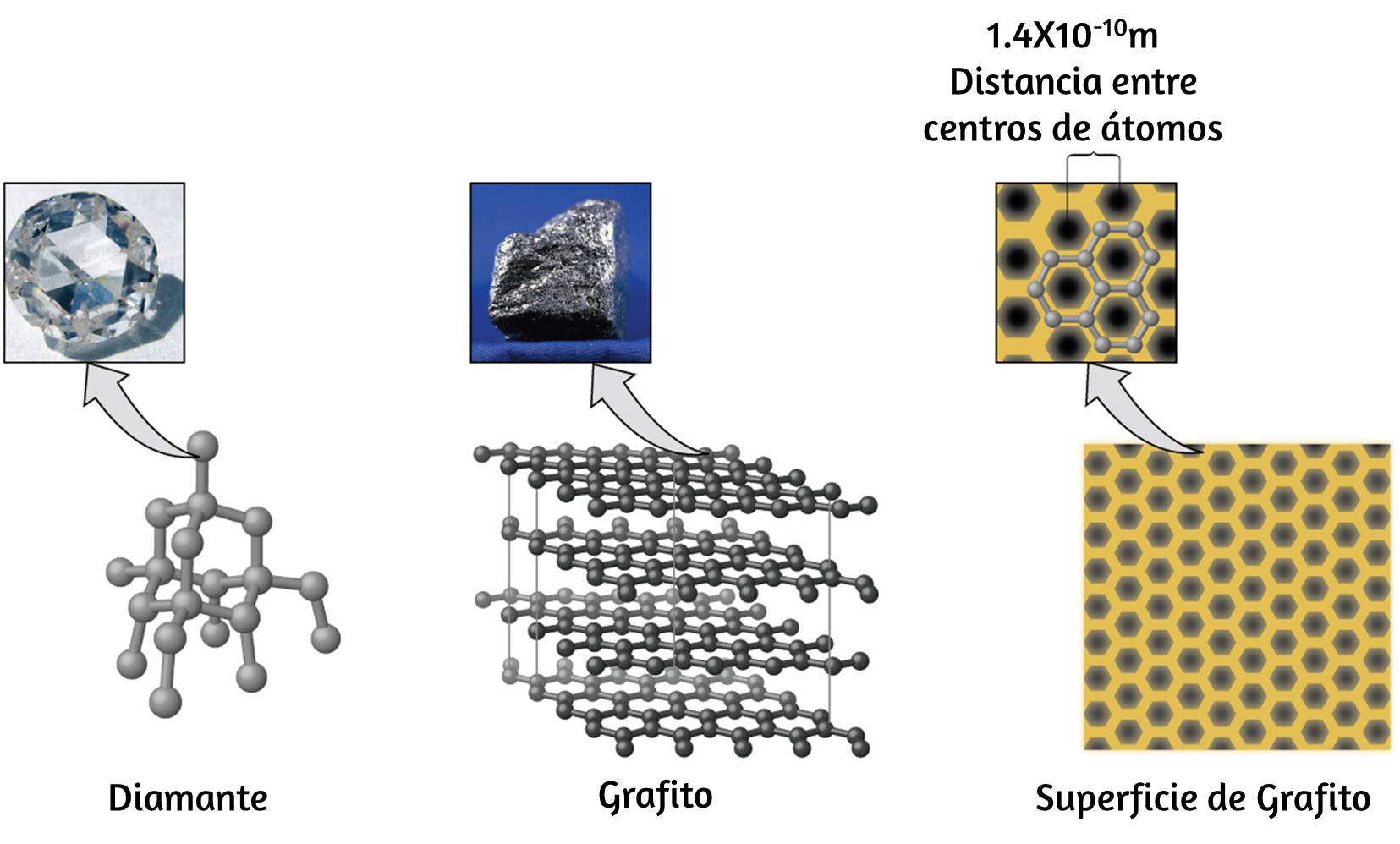
Figura 9.43. El diamante es extremadamente duro debido a la fuerte unión entre los átomos de carbono en todas las direcciones. El grafito (con punta de lápiz) se frota sobre el papel debido a las débiles atracciones entre las capas de carbono. Una imagen de una superficie de grafito muestra la distancia entre los centros de átomos de carbono adyacentes. (Foto de la izquierda del crédito: modificación del trabajo de Steve Jurvetson; foto del medio del crédito: modificación de la obra del Servicio Geológico de los Estados Unidos)

El diamante es una de las sustancias más duras conocidas, mientras que el grafito es lo suficientemente blando como para usarse como plomo para lápiz. Estas propiedades muy diferentes provienen de las diferentes disposiciones de los átomos de carbono en los diferentes alótropos.

Es posible que esté menos familiarizado con una forma de carbono descubierta recientemente: el grafeno. El grafeno se aisló por primera vez en 2004 mediante el uso de cinta para despegar capas más y más delgadas de grafito. Es esencialmente una sola hoja (un átomo de espesor) de grafito. El grafeno, ilustrado en la Figura 9.44, no solo es fuerte y liviano, sino que también es un excelente conductor de electricidad y calor. Estas propiedades pueden resultar muy útiles en una amplia gama de aplicaciones, tales como circuitos y chips de computadora ampliamente mejorados, mejores baterías y celdas solares, y materiales estructurales más fuertes y livianos.

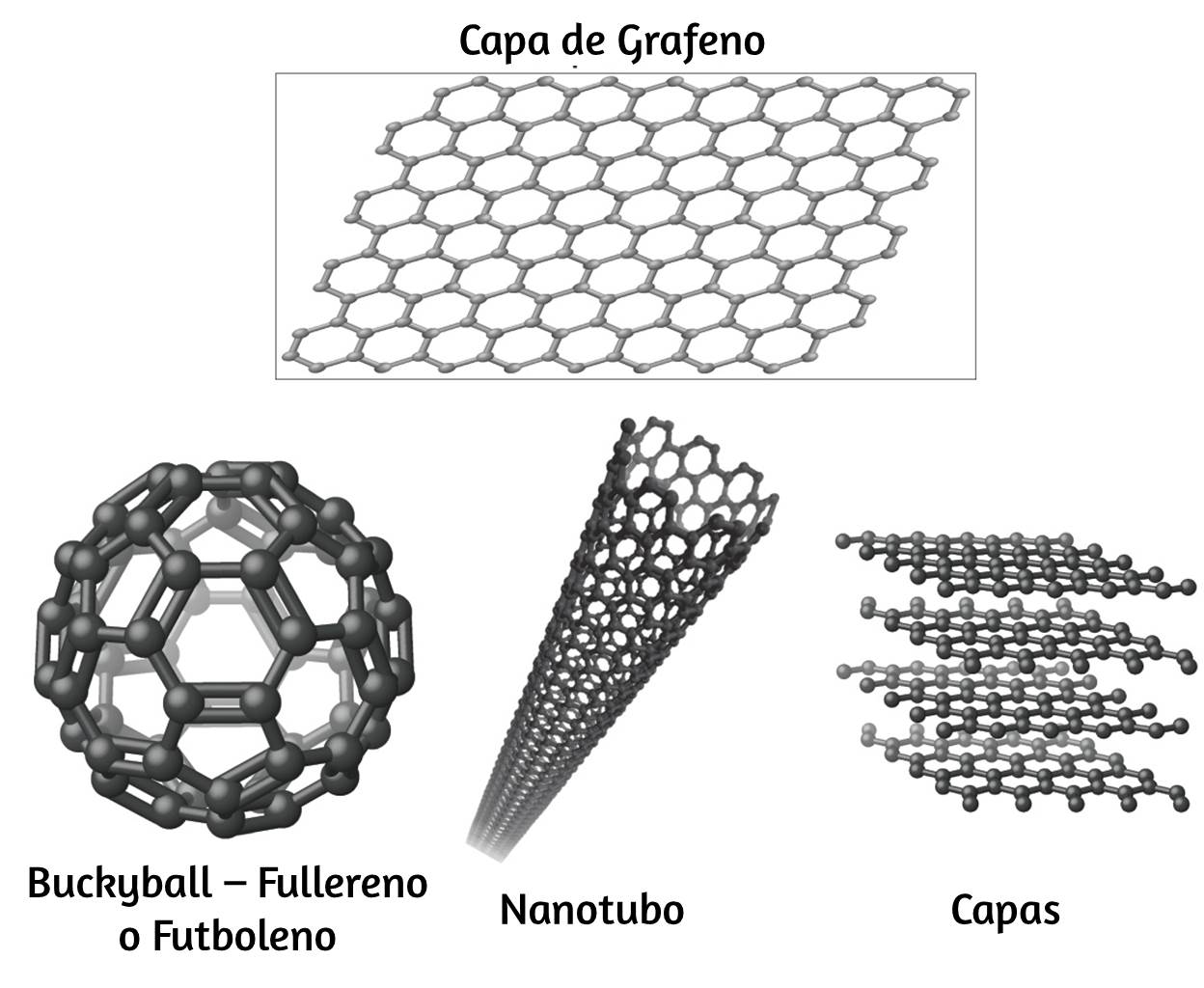
Figura 9.44. Las láminas de grafeno se pueden formar en bolas de bucky, nanotubos y capas apiladas.

El Premio Nobel de Física 2010 fue otorgado a Andre Geim y Konstantin Novoselov por su trabajo pionero con el grafeno.

Defectos de cristal

En un sólido cristalino, los átomos, iones o moléculas están dispuestos en un patrón repetitivo definido, pero pueden producirse defectos ocasionales en el patrón. Se conocen varios tipos de defectos, como se ilustra en la Figura 9.45. Las vacantes son defectos que ocurren cuando las posiciones que deberían contener átomos o iones están vacantes. Con menos frecuencia, algunos átomos o iones en un cristal pueden ocupar posiciones, llamadas sitios intersticiales, ubicadas entre las posiciones regulares de los átomos. Se encuentran otras distorsiones en los cristales impuros, como, por ejemplo, cuando los cationes, aniones o moléculas de la impureza son demasiado grandes para caber en las posiciones normales sin distorsionar la estructura.

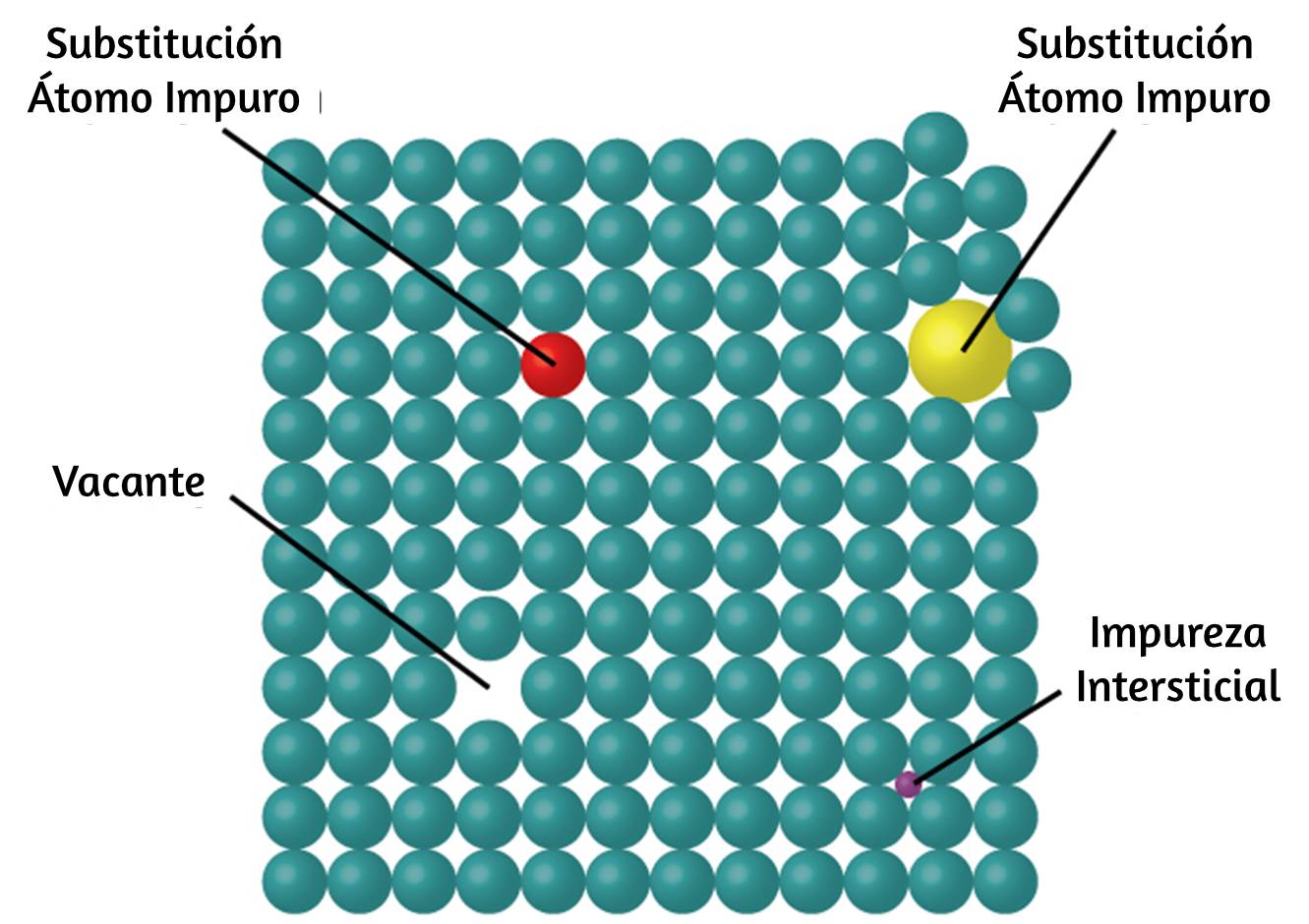
Figura 9.45. Los tipos de defectos de cristal incluyen vacantes, átomos intersticiales e impurezas de sustitución.

Algunas veces se agregan pequeñas cantidades de impurezas a un cristal (un proceso conocido como dopaje) para crear defectos en la estructura que producen cambios deseables en sus propiedades. Por ejemplo, los cristales de silicio se dopan con cantidades variables de diferentes elementos para producir propiedades eléctricas adecuadas para su uso en la fabricación de semiconductores y chips de computadora.

Estructuras de celda en sólidos cristalinos

Más del $90\%$ de los sólidos naturales y artificiales son cristalinos. La mayoría de los sólidos se forman con una disposición regular de sus partículas porque las interacciones atractivas generales entre las partículas se maximizan y la energía intermolecular total se minimiza cuando las partículas se empaquetan de la manera más eficiente. La disposición regular a nivel atómico a menudo se refleja a nivel macroscópico. En este módulo, exploraremos algunos de los detalles sobre las estructuras de los sólidos cristalinos iónicos y metálicos, y aprenderemos cómo estas estructuras se determinan experimentalmente.

Las estructuras de los metales.

Comenzaremos nuestra discusión sobre los sólidos cristalinos considerando los metales elementales, que son relativamente simples porque cada uno contiene solo un tipo de átomo. Un metal puro es un sólido cristalino con átomos metálicos muy juntos en un patrón repetitivo. Algunas de las propiedades de los metales en general, como su maleabilidad y ductilidad, se deben en gran medida a que tienen átomos idénticos dispuestos en un patrón regular.

Las diferentes propiedades de un metal en comparación con otro dependen parcialmente de los tamaños de sus átomos y de los detalles de sus disposiciones espaciales. Exploraremos las similitudes y diferencias de cuatro de las geometrías de cristal metálico más comunes en las siguientes secciones.

Celdas unitarias de metales

La estructura de un sólido cristalino, ya sea un metal o no, se describe mejor considerando su unidad repetitiva más simple, que se denomina celda unitaria. La celda unitaria consiste en puntos reticulares que representan las ubicaciones de átomos o iones. La estructura completa consta de esta celda unitaria que se repite en tres dimensiones, como se ilustra en la Figura 9.46.

Figura 9.46. Una celda unitaria muestra las ubicaciones de los puntos de la red que se repiten en todas las direcciones.

Comencemos nuestra investigación de la estructura reticular de cristal y las celdas unitarias con la estructura más sencilla y la celda unitaria más básica.

Para visualizar esto, imagine tomar una gran cantidad de esferas idénticas, como pelotas de tenis, y colocarlas de manera uniforme en un recipiente. La forma más sencilla de hacer esto sería hacer capas en las que las esferas de una capa estén directamente por encima de las de la capa de abajo, como se ilustra en la Figura 9.47. Esta disposición se llama estructura cúbica simple, y la celda unitaria se llama celda unitaria simple o celda unitaria primitiva.

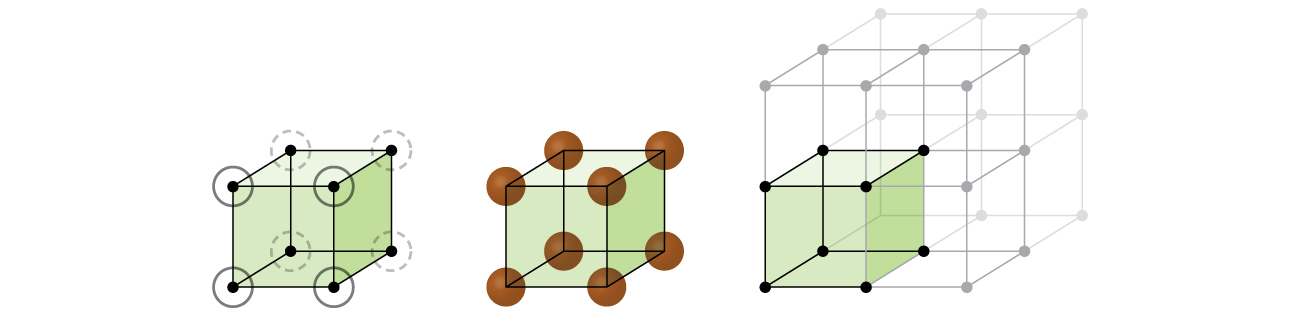
Figura 9.47. Cuando los átomos metálicos se disponen con esferas en una capa directamente encima o debajo de las esferas en otra capa, la estructura reticular se denomina cúbica simple. Tenga en cuenta que las esferas están en contacto.

En una estructura cúbica simple, las esferas no se empaquetan tan estrechamente como podrían, y solo "llenan" aproximadamente el 52% del volumen del contenedor. Esta es una disposición relativamente ineficiente, y solo un metal (polonio, Po) cristaliza en una estructura cúbica simple. Como se muestra en la Figura 9.48, un sólido con este tipo de disposición consiste en planos (o capas) en los que cada átomo contacta solo a los cuatro vecinos más cercanos en su capa; un átomo directamente encima de él en la capa superior; y un átomo directamente debajo de él en la capa de abajo. El número de otras partículas que cada partícula en un sólido cristalino se conoce como su número de coordinación. Para un átomo de polonio en una matriz cúbica simple, el número de coordinación es, por lo tanto, seis.

Figura 9.48. Un átomo en una estructura reticular cúbica simple contacta con otros seis átomos, por lo que tiene un número de coordinación de seis.

En una red cúbica simple, la celda unitaria que se repite en todas las direcciones es un cubo definido por los centros de ocho átomos, como se muestra en la Figura 9.49. Los átomos en las esquinas adyacentes de esta celda unitaria contactan entre sí, por lo que la longitud del borde de esta celda es igual a dos radios atómicos, o un diámetro atómico. Una celda unidad cúbica contiene solo las partes de estos átomos que están dentro de ella. Dado que un átomo en una esquina de una celda unitaria cúbica simple está contenido por un total de ocho celdas unitarias, solo un octavo de ese átomo está dentro de una celda unitaria específica. Y dado que cada celda unitaria cúbica simple tiene un átomo en cada una de sus ocho "esquinas", hay 8 × 18 = 1 átomo dentro de una celda unitaria cúbica simple.

Ejemplo 9.14

Cálculo del radio atómico y la densidad de metales, parte 1

La longitud del borde de la celda unitaria de alfa polonio es 336 pm.

Figura 9.49. Una celda unitaria de celosía cúbica simple contiene un octavo de un átomo en cada una de sus ocho esquinas, por lo que contiene un átomo en total.

(a) Determine el radio de un átomo de polonio.

(b) Determine la densidad del alfa polonio.

Solución

El alfa polonio cristaliza en una celda unitaria cúbica simple:

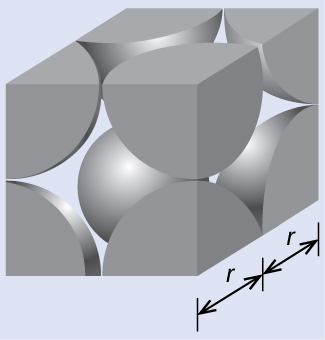
(a) Dos átomos de Po adyacentes contactan entre sí, por lo que la longitud del borde de esta celda es igual a dos radios atómicos de Po: $l = 2r$. Por lo tanto, el radio de Po es $r = \frac{l}{2} = \frac{336\,pm}{2} = 168\,pm$.

(b) La densidad viene dada por $densidad = \frac{masa}{volumen}$. La densidad del polonio se puede encontrar determinando la densidad de su celda unitaria (la masa contenida dentro de una celda unitaria dividida por el volumen de la celda unitaria). Dado que una celda unitaria Po contiene un octavo de un átomo Po en cada una de sus ocho esquinas, una celda unitaria contiene un átomo Po.

La masa de una celda unitaria Po se puede encontrar mediante:

El volumen de una celda unitaria Po se puede encontrar mediante:

(Tenga en cuenta que la longitud del borde se convirtió de pm a cm para obtener las unidades de volumen habituales para la densidad).

Por lo tanto, la densidad de $\ce{Po} = \frac{3.471 \times 10^{−22}g}{3.79 \times 10^{−23}cm^3} = 9.16 \frac{g}{cm^3}$

Comprueba tu aprendizaje

La mayoría de los cristales metálicos son uno de los cuatro tipos principales de celdas unitarias. Por ahora, nos centraremos en las tres celdas de unidades cúbicas: cúbicas simples (que ya hemos visto), celdas de unidades cúbicas centradas en el cuerpo y celdas de unidades cúbicas centradas en la cara, todas las cuales se ilustran en la Figura 9.50. (Tenga en cuenta que en realidad hay siete sistemas de redes diferentes, algunos de los cuales tienen más de un tipo de red, para un total de 14 tipos diferentes de celdas unitarias. Dejamos las geometrías más complicadas para más adelante en este módulo).

Figura 9.50. Las celdas de metales de unidades cúbicas muestran (en las figuras superiores) las ubicaciones de los puntos de la red y (en las figuras inferiores) átomos de metal ubicados en la celda de la unidad.

Algunos metales cristalizan en una disposición que tiene una celda unidad cúbica con átomos en todas las esquinas y un átomo en el centro, como se muestra en la Figura 9.51. Esto se llama un sólido cúbico centrado en el cuerpo ($BCC$). Los átomos en las esquinas de una celda de unidad $BCC$ no se contactan entre sí, sino que se ponen en contacto con el átomo en el centro. Una celda unidad $BCC$ contiene dos átomos: un octavo de un átomo en cada una de las ocho esquinas ($8 \times \frac{1}{8} = 1\, \text{átomo}$ desde las esquinas) más un átomo desde el centro. Cualquier átomo en esta estructura toca cuatro átomos en la capa superior y cuatro átomos en la capa inferior. Por lo tanto, un átomo en una estructura $BCC$ tiene un número de coordinación de ocho.

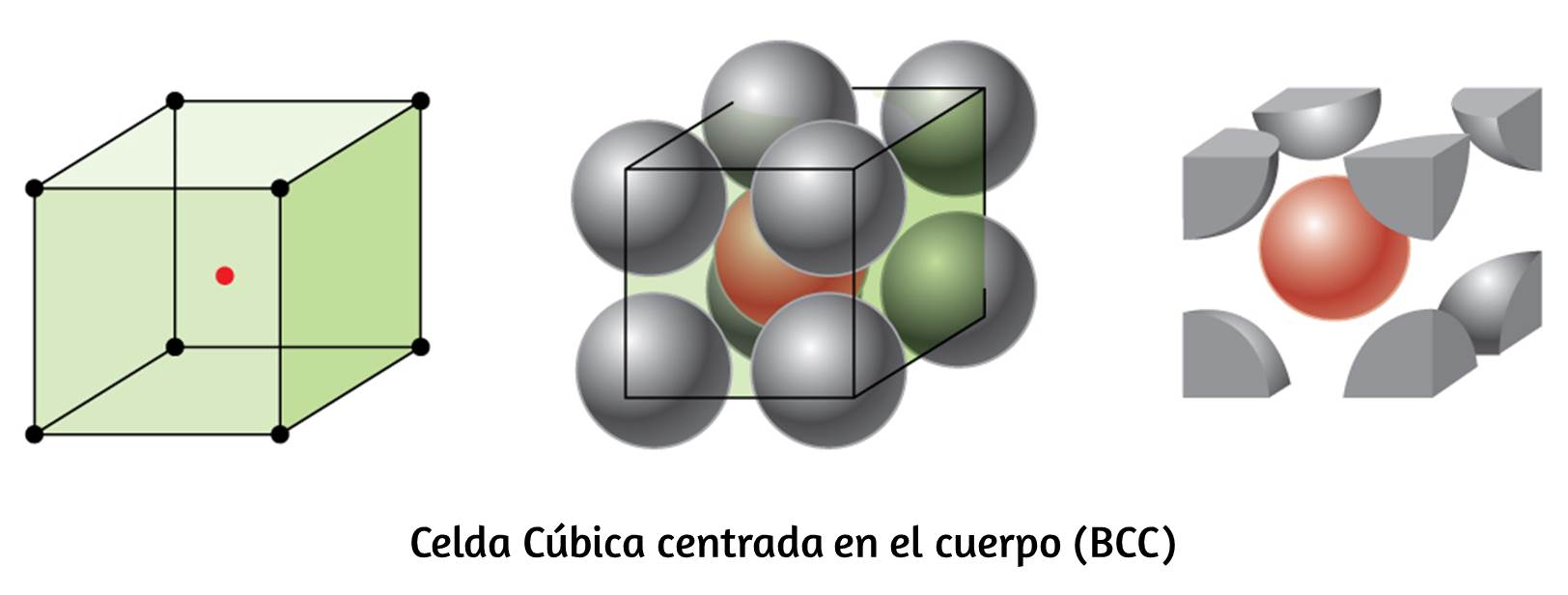
Figura 9.51. En una estructura cúbica centrada en el cuerpo, los átomos en una capa específica no se tocan entre sí. Cada átomo toca cuatro átomos en la capa superior y cuatro átomos en la capa inferior.

Los átomos en los arreglos $BCC$ están empaquetados de manera mucho más eficiente que en una estructura cúbica simple, ocupando aproximadamente el $68\%$ del volumen total. Los metales isomorfos con una estructura $BCC$ incluyen $K$, $Ba$, $Cr$, $Mo$, $W$ y $Fe$ a temperatura ambiente. (Se dice que los elementos o compuestos que cristalizan con la misma estructura son isomorfos).

Muchos otros metales, como el aluminio, el cobre y el plomo, se cristalizan en una disposición que tiene una celda unidad cúbica con átomos en todas las esquinas y en los centros de cada cara, como se ilustra en la Figura 9.52. Este arreglo se llama sólido cúbico centrado en la cara ($FCC$). Una celda unidad $FCC$ contiene cuatro átomos: un octavo de un átomo en cada una de las ocho esquinas ($8 \times \frac{1}{8} = 1\, \text{átomo}$ de las esquinas) y la mitad de un átomo en cada una de las seis caras ($6 \times \frac{1}{2} = 3\, \text{átomos}$ de las caras). Los átomos en las esquinas tocan los átomos en los centros de las caras adyacentes a lo largo de las diagonales de la cara del cubo. Debido a que los átomos están en puntos reticulares idénticos, tienen entornos idénticos.

Los átomos en una disposición de $FCC$ se empaquetan lo más cerca posible, con átomos que ocupan el $74\%$ del volumen.

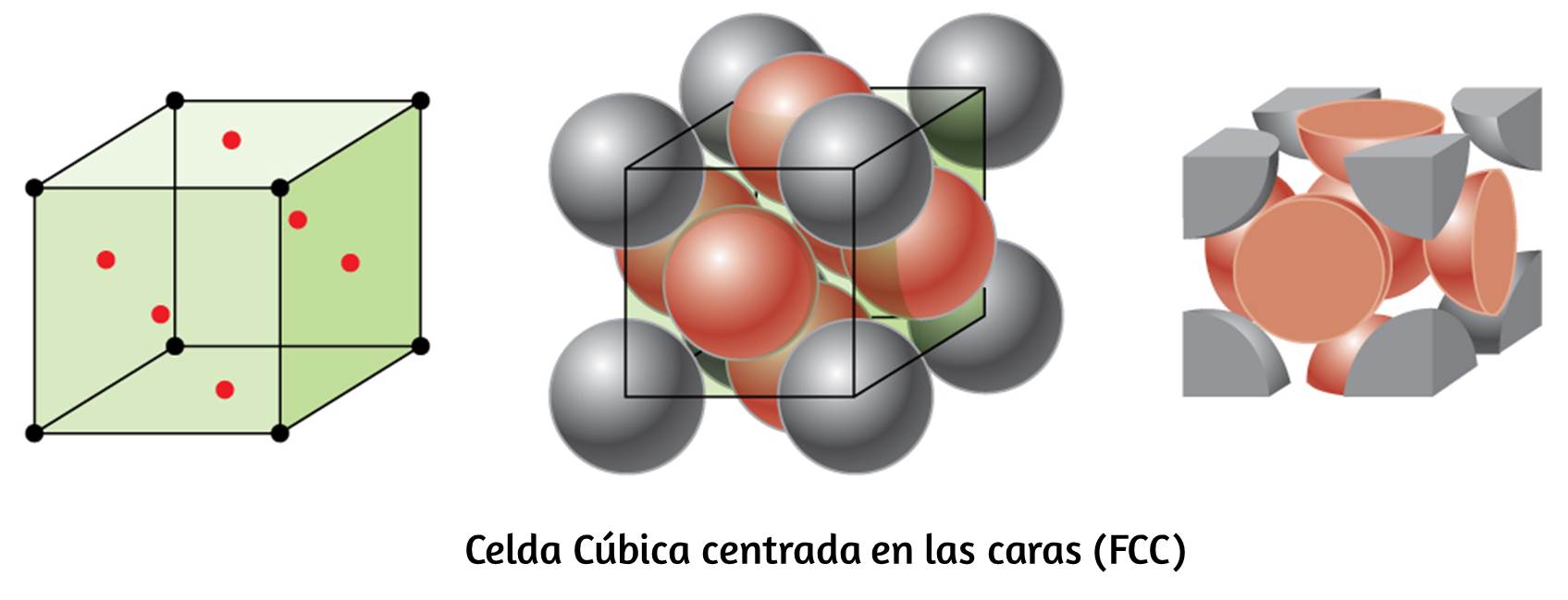
Figura 9.52. Un sólido cúbico centrado en la cara tiene átomos en las esquinas y, como su nombre lo indica, en los centros de las caras de sus celdas unitarias.

Esta estructura también se denomina empaquetamiento cúbico compacto ($PCC$). En $CCP$, hay tres capas repetidas de átomos dispuestos hexagonalmente. Cada átomo contacta seis átomos en su propia capa, tres en la capa superior y tres en la capa inferior. En esta disposición, cada átomo toca a $12$ vecinos cercanos y, por lo tanto, tiene un número de coordinación de $12$. El hecho de que las disposiciones de $FCC$ y $CCP$ sean equivalentes puede no ser obvio de inmediato, pero la Figura 9.53 ilustra por qué en realidad son la misma estructura.

Debido a que el empaquetamiento más cercano maximiza las atracciones generales entre los átomos y minimiza la energía intermolecular total, los átomos en la mayoría de los metales se empaquetan de esta manera. Encontramos dos tipos de empaquetamiento más cercano en estructuras cristalinas metálicas simples: $CCP$, que ya hemos encontrado, y empaquetamiento más cercano hexagonal ($HCP$) que se muestra en la Figura 9.54. Ambos consisten en capas repetitivas de átomos dispuestos hexagonalmente. En ambos tipos, se coloca una segunda capa (B) en la primera capa (A) para que cada átomo en la segunda capa esté en contacto con tres átomos en la primera capa.

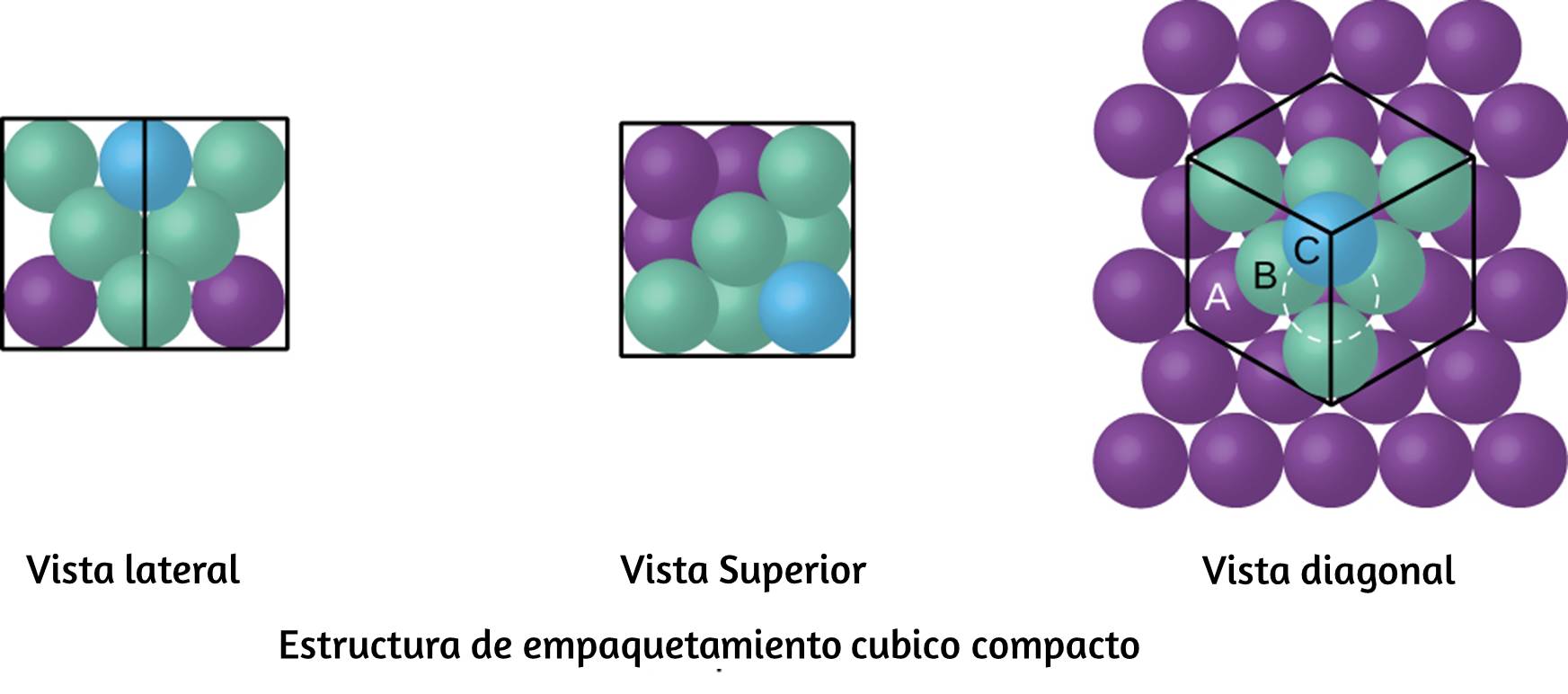
Figura 9.53. Una disposición de $CCP$ consta de tres capas repetitivas (ABCABC ...) de átomos dispuestos hexagonalmente. Los átomos en una estructura $CCP$ tienen un número de coordinación de $12$ porque contactan seis átomos en su capa, más tres átomos en la capa superior y tres átomos en la capa inferior. Al girar nuestra perspectiva, podemos ver que una estructura $CCP$ tiene una celda unitaria con una cara que contiene un átomo de la capa A en una esquina, átomos de la capa B a través de una diagonal (en dos esquinas y en el medio de la cara), y un átomo de la capa C en la esquina restante. Esto es lo mismo que una disposición cúbica centrada en la cara.

La tercera capa se coloca de una de dos maneras. En $HCP$, los átomos en la tercera capa están directamente por encima de los átomos en la primera capa (es decir, la tercera capa también es de tipo A), y el apilamiento consiste en alternar capas compactas de tipo A y tipo B (es decir, ABABAB $\cdots$). En $CCP$, los átomos en la tercera capa no están por encima de los átomos en ninguna de las primeras dos capas (es decir, la tercera capa es del tipo C), y el apilamiento consiste en capas alternas de tipo A, tipo B y tipo C ( es decir, ABCABCABC $\cdots$). Alrededor de dos tercios de todos los metales cristalizan en matrices más cercanas con números de coordinación de $12$. Los metales que cristalizan en una estructura $HCP$ incluyen $\ce{Cd, Co, Li, Mg, Na}$ y $\ce{Zn}$, y los metales que cristalizan en una estructura $CCP$ incluyen $\ce{Ag , Al, Ca, Cu, Ni, Pb}$ y $\ce{Pt}$.

Figura 9.54. En ambos tipos de empaquetamiento más cercano, los átomos se empaquetan de la manera más compacta posible. El empaque hexagonal más cercano consiste en dos capas alternas (ABABAB ...). El empaque cúbico más cercano consta de tres capas alternas (ABCABCABC ...).

Ejemplo 9.15

Cálculo del radio atómico y la densidad de metales, parte 2

El calcio cristaliza en una estructura cúbica centrada en la cara. La longitud del borde de su celda unidad es de $558.8\,pm$.

(a) ¿Cuál es el radio atómico de Ca en esta estructura?

(b) Calcule la densidad de Ca.

Solución

(a) En una estructura $FCC$, los átomos de $Ca$ contactan entre sí a través de la diagonal de la cara, por lo que la longitud de la diagonal es igual a cuatro radios atómicos de $Ca\,(d = 4r)$.

Dos bordes adyacentes y la diagonal de la cara forman un triángulo rectángulo, con la longitud de cada lado igual a $558.8\,pm$ y la longitud de la hipotenusa igual a cuatro radios atómicos de $Ca$:

Resolver esto da $r = \frac {\sqrt{(558.8pm)^2 + (558.5pm)^2}}{16} = 197.6\,pm$ para un radio de $Ca$.

(b) La densidad viene dada por $densidad = \frac{masa}{volumen}$. La densidad del calcio se puede determinar determinando la densidad de su celda unitaria: por ejemplo, la masa contenida dentro de una celda unitaria dividida por el volumen de la celda unitaria. Una celda de unidad de Ca centrada en la cara tiene un octavo de un átomo en cada una de las ocho esquinas ($8 \times \frac{1}{8} = 1\,\text{átomo}$) y la mitad de un átomo en cada una de las seis caras $6 \times \frac{1}{2} = 3\,\text{átomos}$), para un total de cuatro átomos en la celda unitaria (c.u.).

La masa de la celda unitaria (c.u.) se puede encontrar mediante:

El volumen de una celda unitaria de Ca se puede encontrar mediante:

(Tenga en cuenta que la longitud del borde se convirtió de $pm$ a $cm$ para obtener las unidades de volumen habituales para la densidad).

Entonces, la densidad de $Ca = \frac{2.662 \times 10^{−22}g}{1.745 \times 10^{−22}cm^3} = 1.53 \frac{g}{cm^3}$

Comprueba tu aprendizaje

En general, una celda unitaria se define por las longitudes de tres ejes (a, b y c) y los ángulos (\alpha, \beta y \gamma) entre ellos, como se ilustra en la Figura 9.55.

Los ejes se definen como las longitudes entre puntos en la red espacial. En consecuencia, los ejes de la celda unitaria unen puntos con entornos idénticos.

Figura 9.55. Una celda unitaria se define por las longitudes de sus tres ejes (a, byc) y los ángulos (\alpha, \beta y \gamma) entre los ejes.

Hay siete sistemas de red diferentes, algunos de los cuales tienen más de un tipo de red, para un total de catorce celdas unitarias diferentes, que tienen las formas que se muestran en la Figura 9.56.

Figura 9.56. Hay siete sistemas de red diferentes y $14$ celdas unitarias diferentes.

Las estructuras de los cristales iónicos.

Los cristales iónicos consisten en dos o más tipos diferentes de iones que generalmente tienen diferentes tamaños. El empaquetamiento de estos iones en una estructura cristalina es más complejo que el empaquetamiento de átomos metálicos que son del mismo tamaño.

La mayoría de los iones monoatómicos se comportan como esferas cargadas, y su atracción por los iones de carga opuesta es la misma en todas las direcciones. En consecuencia, las estructuras estables para los compuestos iónicos resultan ($1$) cuando los iones de una carga están rodeados por tantos iones como sea posible de la carga opuesta y ($2$) cuando los cationes y aniones están en contacto entre sí. Las estructuras están determinadas por dos factores principales: los tamaños relativos de los iones y la relación de los números de iones positivos y negativos en el compuesto.

En estructuras iónicas simples, generalmente encontramos los aniones, que normalmente son más grandes que los cationes, dispuestos en una matriz compacta más cercana. (Como se vio anteriormente, los electrones adicionales atraídos por el mismo núcleo hacen que los aniones sean más grandes y menos electrones atraídos por el mismo núcleo hacen que los cationes sean más pequeños en comparación con los átomos de los que se forman). Los cationes más pequeños comúnmente ocupan uno de los dos tipos de agujeros ( o intersticios) restantes entre los aniones. El más pequeño de los agujeros se encuentra entre tres aniones en un plano y un anión en un plano adyacente. Los cuatro aniones que rodean este agujero están dispuestos en las esquinas de un tetraedro, por lo que el agujero se llama agujero tetraédrico. El tipo más grande de agujero se encuentra en el centro de seis aniones (tres en una capa y tres en una capa adyacente) ubicados en las esquinas de un octaedro; Esto se llama un agujero octaédrico.

La Figura 9.57 ilustra ambos tipos de agujeros.

Figura 9.57. Los cationes pueden ocupar dos tipos de agujeros entre aniones: agujeros octaédricos u agujeros tetraédricos.

Dependiendo de los tamaños relativos de los cationes y aniones, los cationes de un compuesto iónico pueden ocupar agujeros tetraédricos u octaédricos, como se ilustra en la Figura 9.58. Los cationes relativamente pequeños ocupan agujeros tetraédricos, y los cationes más grandes ocupan agujeros octaédricos. Si los cationes son demasiado grandes para caber en los agujeros octaédricos, los aniones pueden adoptar una estructura más abierta, como una matriz cúbica simple. Los cationes más grandes pueden ocupar los agujeros cúbicos más grandes posibles gracias al espacio más abierto.

Hay dos agujeros tetraédricos para cada anión en un conjunto de aniones $HCP$ o $CCP$. Un compuesto que cristaliza en una matriz de aniones más cercana con cationes en los agujeros tetraédricos puede tener una relación máxima de cationes: aniones de $2$:$1$; Todos los agujeros tetraédricos se llenan en esta proporción.

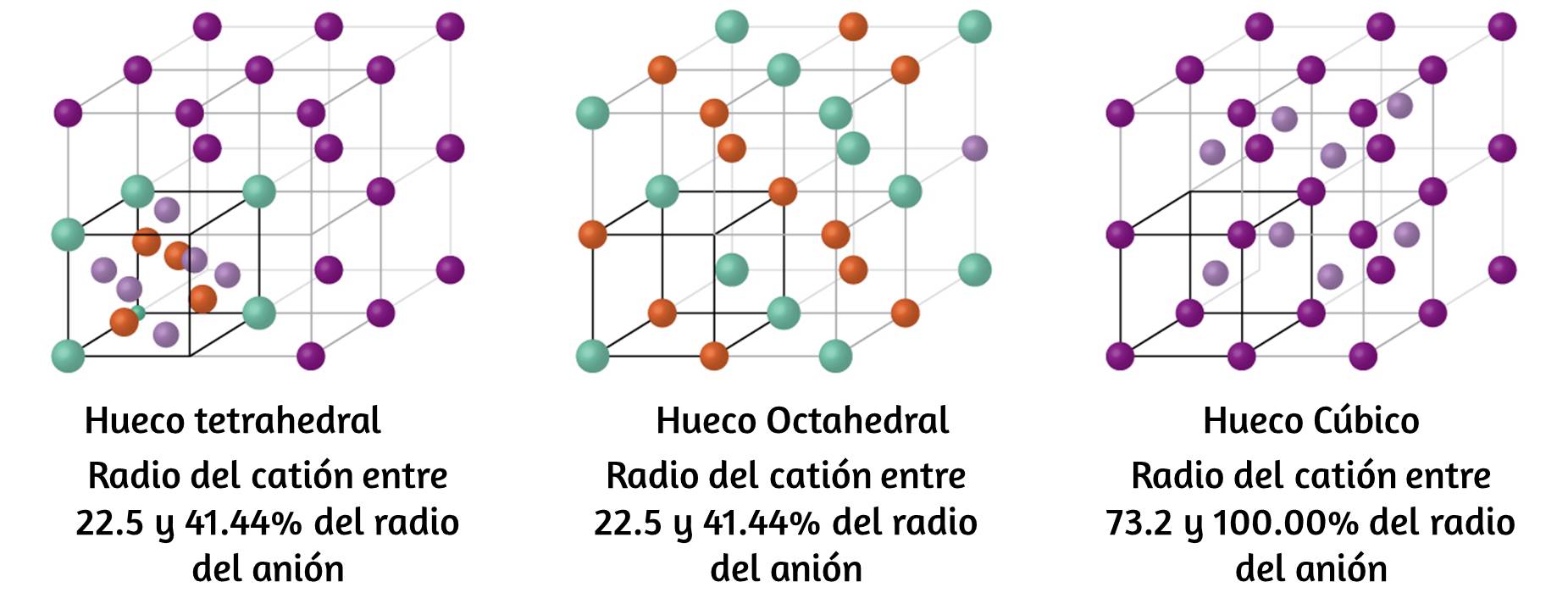
Figura 9.58. El tamaño de un catión y la forma del agujero ocupado por el compuesto están directamente relacionados.

Los ejemplos incluyen $\ce{Li2O}$, $\ce{Na2O}$, $\ce{Li2S}$ y $\ce{Na2S}$. Los compuestos con una relación de menos de $2$:$1$ también pueden cristalizarse en una matriz de aniones más compacta con cationes en los agujeros tetraédricos, si los tamaños iónicos se ajustan. En estos compuestos, sin embargo, algunos de los agujeros tetraédricos permanecen vacantes.

Ejemplo 9.16

Ocupación de agujeros tetraédricos

El sulfuro de zinc es una importante fuente industrial de zinc y también se usa como pigmento blanco en la pintura. El sulfuro de zinc cristaliza con iones de zinc que ocupan la mitad de los agujeros tetraédricos en una matriz de iones de sulfuro más compacta. ¿Cuál es la fórmula del sulfuro de zinc?

Solución

Debido a que hay dos agujeros tetraédricos por anión (ión sulfuro) y la mitad de estos agujeros están ocupados por iones de zinc, debe haber $\frac{2}{2} \times 2,\,o\,1$, ion de zinc por ión sulfuro. Por lo tanto, la fórmula es ZnS.

Comprueba tu aprendizaje

La relación de agujeros octaédricos a aniones en una estructura $HCP$ o $CCP$ es $1$:$1$. Por lo tanto, los compuestos con cationes en agujeros octaédricos en una matriz de aniones más compacta pueden tener una relación catión: anión máxima de $1$:$1$. En $\ce{NiO}$, $\ce{MnS}$, $\ce{NaCl}$ y $\ce{KH}$, por ejemplo, todos los agujeros octaédricos están llenos. Se observan relaciones de menos de $1$:$1$ cuando algunos de los agujeros octaédricos permanecen vacíos.

Ejemplo 9.17

Estequiometría de compuestos iónicos

El zafiro es óxido de aluminio. El óxido de aluminio cristaliza con iones de aluminio en dos tercios de los agujeros octaédricos en una matriz de iones de óxido más compacta. ¿Cuál es la fórmula del óxido de aluminio?

Solución

Debido a que hay un agujero octaédrico por anión (ión óxido) y solo dos tercios de estos agujeros están ocupados.

la proporción de aluminio a oxígeno debe ser $\frac{2}{3}:1$, lo que daría $\ce{Al_{\frac{2}{3}}O}$. La razón de números enteros más simple es $2:3$, por lo que la fórmula es $\ce{Al2O3}$.

Comprueba tu aprendizaje

En una simple matriz cúbica de aniones, hay un agujero cúbico que puede ser ocupado por un catión para cada anión en la matriz. En $\ce{CsCl}$, y en otros compuestos con la misma estructura, todos los agujeros cúbicos están ocupados. La mitad de los agujeros cúbicos están ocupados en $\ce{SrH2, UO2, SrCl2}$ y $\ce{CaF2}$.

Los diferentes tipos de compuestos iónicos a menudo cristalizan en la misma estructura cuando los tamaños relativos de sus iones y sus estequiometrías (las dos características principales que determinan la estructura) son similares.

Celdas unitarias de compuestos iónicos

Muchos compuestos iónicos cristalizan con celdas unitarias cúbicas, y utilizaremos estos compuestos para describir las características generales de las estructuras iónicas.

Cuando un compuesto iónico está compuesto de cationes y aniones de tamaño similar en una proporción $1:1$, generalmente forma una estructura cúbica simple. El cloruro de cesio, $\ce{CsCl}$, (ilustrado en la Figura 9.59) es un ejemplo de esto, con $\ce{Cs^+}$ y $\ce{Cl^{−}}$ con radios de $174\,pm$ y $181\,pm$, respectivamente. Podemos pensar en esto como iones de cloruro que forman una célula unitaria cúbica simple, con un ion de cesio en el centro; o como iones de cesio formando una célula unitaria con un ion cloruro en el centro; o como simples celdas de unidades cúbicas formadas por iones $\ce{Cs^+}$ superponiendo celdas unitarias formadas por iones $\ce{Cl^{−}}$. Los iones de cesio y los iones de cloruro se tocan a lo largo de las diagonales del cuerpo de las celdas unitarias. Un ión de cesio y un ión de cloruro están presentes por celda unidad, dando la estequiometría $1:1$ requerida por la fórmula para el cloruro de cesio.

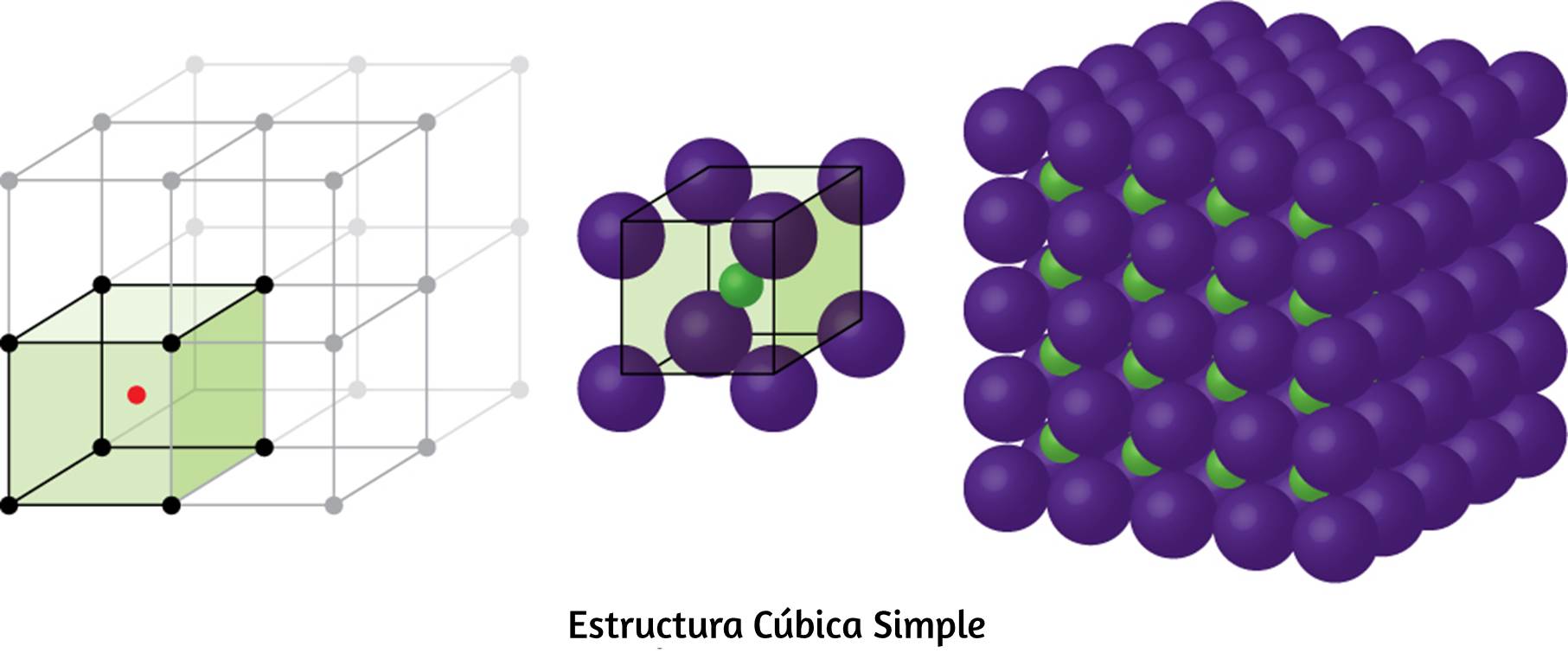
Figura 9.59. Los compuestos iónicos con cationes y aniones de tamaño similar, como CsCl, generalmente forman una estructura cúbica simple. Se pueden describir mediante celdas unitarias con cationes en las esquinas o aniones en las esquinas.

Tenga en cuenta que no hay un punto de red en el centro de la célula, y $\ce{CsCl}$ no es una estructura $BCC$ porque un ion cesio no es idéntico a un ion cloruro.

Hemos dicho que la ubicación de los puntos de la red es arbitraria. Esto se ilustra mediante una descripción alternativa de la estructura de $\ce{CsCl}$ en la que los puntos de la red se encuentran en los centros de los iones de cesio. En esta descripción, los iones de cesio se encuentran en los puntos de la red en las esquinas de la célula, y el ion cloruro se encuentra en el centro de la célula. Las dos celdas unitarias son diferentes, pero describen estructuras idénticas.

Cuando un compuesto iónico se compone de una relación $1:1$ de cationes y aniones que difieren significativamente en tamaño, generalmente se cristaliza con una célula unitaria $FCC$, como la que se muestra en la Figura 9.60. El cloruro de sodio, $\ce{NaCl}$, es un ejemplo de esto, con $Na^+$ y $Cl^{-}$ con radios de $102\,pm$ y $181\,pm$, respectivamente. Podemos pensar en esto como iones de cloruro que forman una célula $FCC$, con iones de sodio ubicados en los agujeros octaédricos en el medio de los bordes de la célula y en el centro de la célula. Los iones de sodio y cloruro se tocan entre sí a lo largo de los bordes de la célula. La celda unitaria contiene cuatro iones de sodio y cuatro iones de cloruro, dando la estequiometría $1:1$ requerida por la fórmula, $\ce{NaCl}$.

La forma cúbica de sulfuro de zinc, zinc blenda, también cristaliza en una celda unitaria $FCC$, como se ilustra en la Figura 9.61. Esta estructura contiene iones de sulfuro en los puntos de la red de una red $FCC$. (La disposición de los iones de sulfuro es idéntica a la disposición de los iones de cloruro en el cloruro de sodio.)

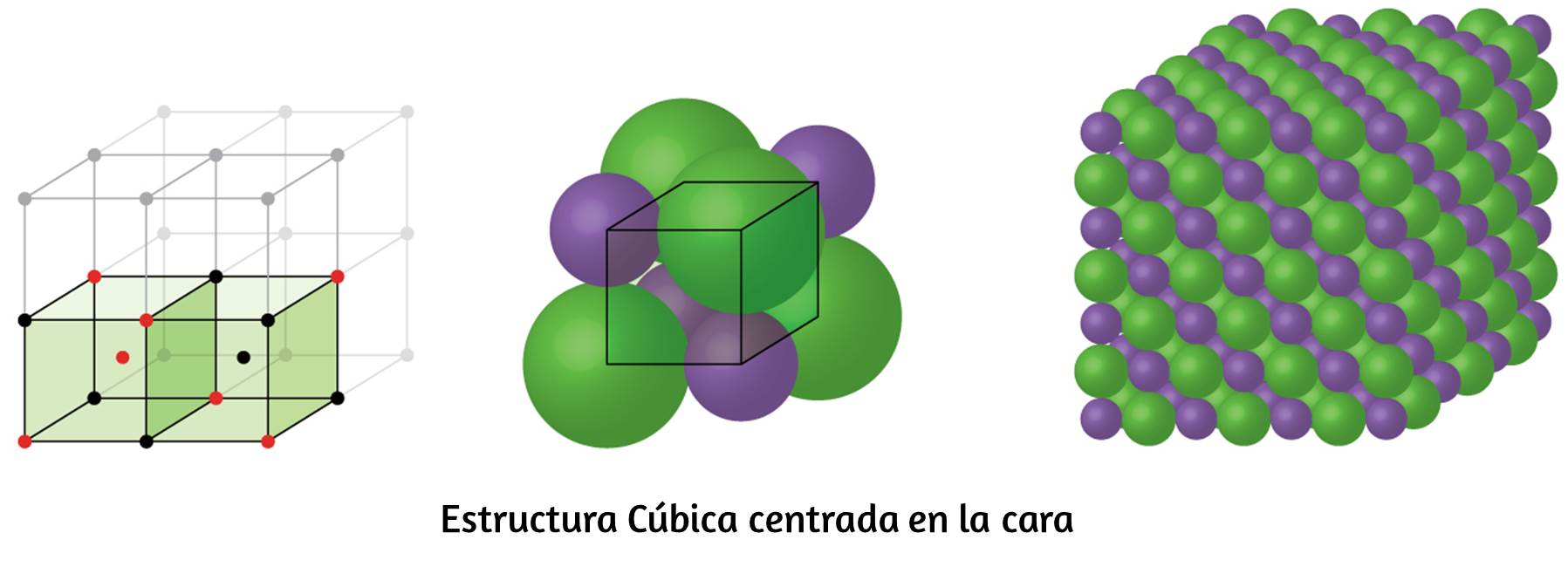
Figura 9.60. Los compuestos iónicos con aniones que son mucho más grandes que los cationes, como el $\ce{NaCl}$, generalmente forman una estructura de $FCC$. Pueden ser descritos por celdas unitarias $FCC$ con cationes en los agujeros octaédricos.

El radio de un ión de zinc es solo alrededor del $40\%$ del radio de un ión de sulfuro, por lo que estos pequeños iones $Zn^{2+}$ están ubicados en agujeros tetraédricos alternos, es decir, en la mitad de los agujeros tetraédricos. Hay cuatro iones de zinc y cuatro iones de sulfuro en la celda unitaria, dando la fórmula empírica $\ce{ZnS}$.

Figura 9.61. $\ce{ZnS}$, el sulfuro de zinc (o mezcla de zinc) forma una celda unidad $FCC$ con iones de sulfuro en los puntos de la red y iones de zinc mucho más pequeños que ocupan la mitad de los agujeros tetraédricos en la estructura.

Una celda unitaria de fluoruro de calcio, como la que se muestra en la Figura 9.62, también es una celda unitaria de $FCC$, pero en este caso, los cationes se encuentran en los puntos de la red; iones de calcio equivalentes se encuentran en los puntos de la red de una red $FCC$. Todos los sitios tetraédricos en la matriz $FCC$ de iones de calcio están ocupados por iones fluoruro. Hay cuatro iones de calcio y ocho iones de flúor en una celda unitaria, lo que da una relación calcio: flúor de $1:2$, como lo requiere la fórmula química, $\ce{CaF2}$. Un examen minucioso de la Figura 9.62 revelará una matriz cúbica simple de iones fluoruro con iones calcio en la mitad de los agujeros cúbicos. La estructura no puede describirse en términos de una red espacial de puntos en los iones fluoruro porque no todos los iones fluoruro tienen entornos idénticos. La orientación de los cuatro iones de calcio sobre los iones de fluoruro difiere.

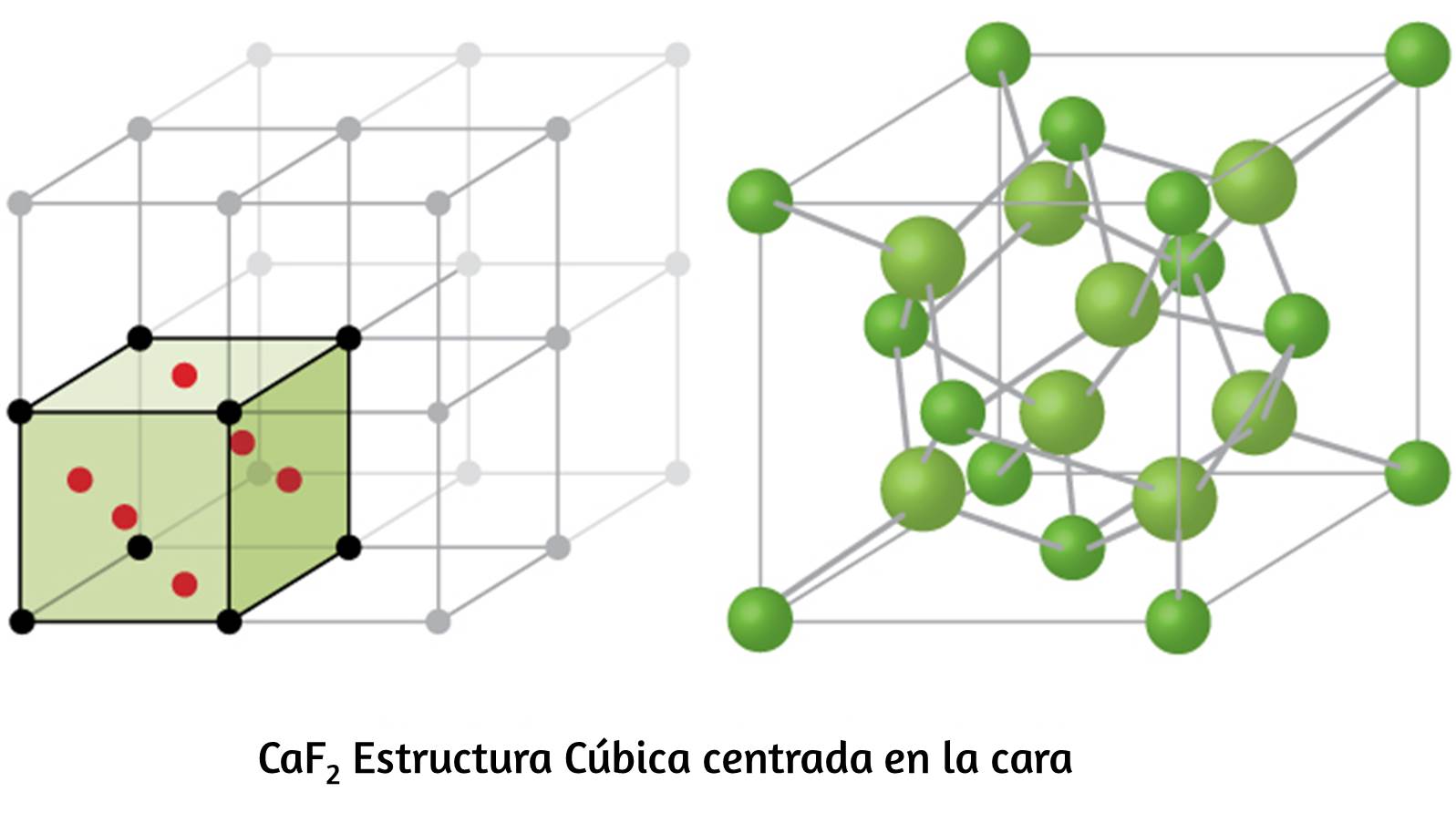
Figura 9.62. El fluoruro de calcio, $\ce{CaF2}$, forma una célula unitaria $FCC$ con iones de calcio (verde) en los puntos reticulares e iones de fluoruro (rojo) que ocupan todos los sitios tetraédricos entre ellos.

Cálculo de radios iónicos

Si conocemos la longitud del borde de una celda unitaria de un compuesto iónico y la posición de los iones en la celda, podemos calcular los radios iónicos para los iones en el compuesto si hacemos suposiciones sobre formas y contactos iónicos individuales.

Ejemplo 9.18

Cálculo de radios iónicos

La longitud del borde de la celda unitaria de $\ce{LiCl}$ (estructura similar a $\ce{NaCl}$, $FCC$) es $0.514\,nm$ o $5.14\,\text{\AA}$. Suponiendo que el ion de litio es lo suficientemente pequeño como para que los iones de cloruro estén en contacto, como en la Figura 9.60, calcule el radio iónico para el ion de cloruro.

Nota: La unidad de longitud angstrom, $\text{\AA}$, se usa a menudo para representar dimensiones de escala atómica y es equivalente a $10^{−10}\,m$.

Solución

En la cara de una celda unitaria de $\ce{LiCl}$, los iones de cloruro se contactan entre sí en la diagonal de la cara:

Al dibujar un triángulo rectángulo en la cara de la celda unitaria, vemos que la longitud de la diagonal es igual a cuatro radios de cloruro (un radio de cada esquina de cloruro y un diámetro, que equivale a dos radios) del ion cloruro en el centro de la cara), entonces $d = 4r$. Del teorema de Pitágoras, tenemos:

cuyos resultados:

Resolver esto da:

$r = \sqrt{\frac{(0.514nm)^2+ (0.514nm)^2)}{16}}=0.182 nm (1.82 \text{\AA})$ para un radio $Cl^{−}$.

Comprueba tu aprendizaje

Es importante darse cuenta de que los valores para los radios iónicos calculados a partir de las longitudes de los bordes de las celdas unitarias dependen de numerosos supuestos, como una forma esférica perfecta para los iones, que en el mejor de los casos son aproximaciones. Por lo tanto, dichos valores calculados son aproximados y las comparaciones no pueden llevarse demasiado lejos. Sin embargo, este método ha resultado útil para calcular radios iónicos a partir de mediciones experimentales, como las determinaciones cristalográficas de rayos X.

Cristalografía de rayos X

El tamaño de la celda unitaria y la disposición de los átomos en un cristal pueden determinarse a partir de mediciones de la difracción de rayos X por el cristal, lo que se denomina cristalografía de rayos X. La difracción es el cambio en la dirección de desplazamiento que experimenta una onda electromagnética cuando encuentra una barrera física cuyas dimensiones son comparables a las de la longitud de onda de la luz. Los rayos X son radiación electromagnética con longitudes de onda aproximadamente tan largas como la distancia entre los átomos vecinos en cristales (del orden de unos pocos $\text{\AA}$).

Cuando un haz de rayos X monocromáticos golpea un cristal, sus rayos se dispersan en todas las direcciones por los átomos dentro del cristal. Cuando las ondas dispersas que viajan en la misma dirección se encuentran entre sí, sufren interferencias, un proceso mediante el cual las ondas se combinan para producir un aumento o una disminución de la amplitud (intensidad) dependiendo de la extensión en que se separan los máximos de las ondas combinadas ( ver Figura 9.63).

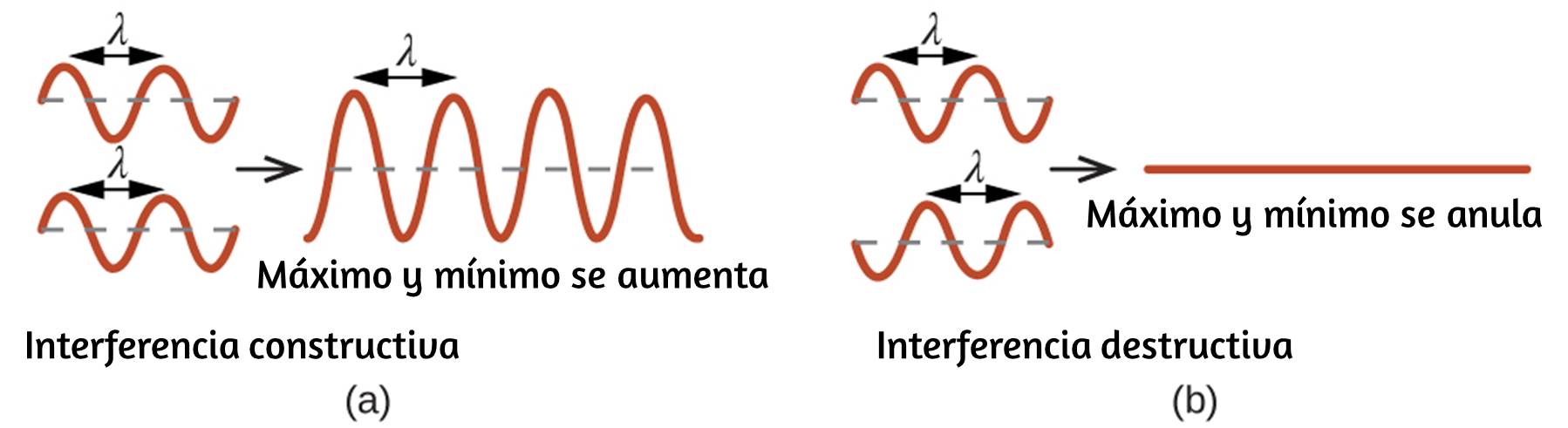
Figura 9.63. Las ondas de luz que ocupan el mismo espacio experimentan interferencia, combinándose para producir ondas de mayor (a) o menor (b) intensidad, dependiendo de la separación de sus máximos y mínimos.

Cuando los rayos X de cierta longitud de onda, $\lambda$, son dispersados por átomos en planos de cristal adyacentes separados por una distancia, $d$, pueden sufrir interferencia constructiva cuando la diferencia entre las distancias recorridas por las dos ondas antes de su combinación es un factor entero , $n$, de la longitud de onda. Esta condición se cumple cuando el ángulo del haz difractado, $\theta$, está relacionado con la longitud de onda y la distancia interatómica por la ecuación:

Esta relación se conoce como la ecuación de Bragg en honor a W. H. Bragg, el físico inglés que primero explicó este fenómeno.

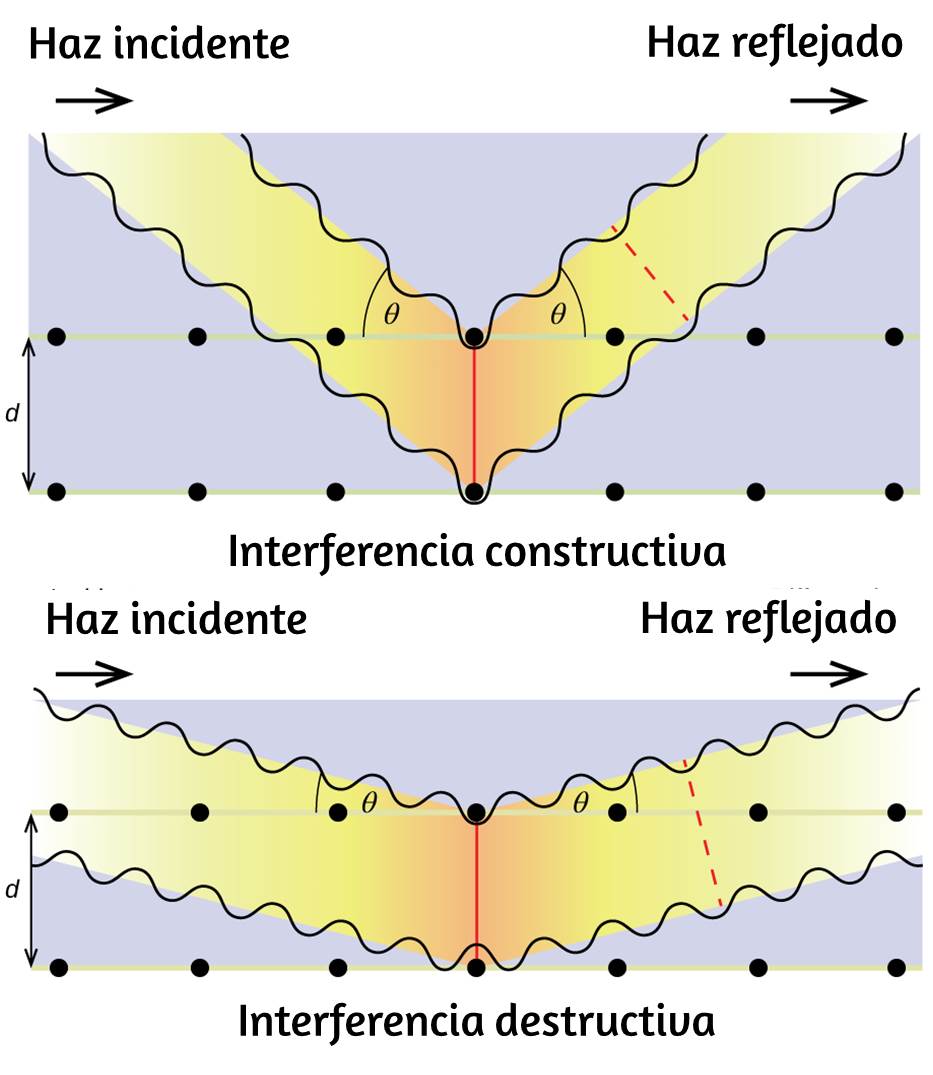
Figura 9.64. La difracción de rayos X dispersos por los átomos dentro de un cristal permite la determinación de la distancia entre los átomos. La imagen superior muestra la interferencia constructiva entre dos ondas dispersas y una onda difractada resultante de alta intensidad. La imagen inferior muestra interferencia destructiva y una onda difractada de baja intensidad.

La Figura 9.64 ilustra dos ejemplos de ondas difractadas de los mismos dos planos de cristal. La figura de la izquierda muestra ondas difractadas en el ángulo de Bragg, lo que resulta en interferencia constructiva, mientras que la de la derecha muestra difracción y un ángulo diferente que no satisface la condición de Bragg, lo que resulta en interferencia destructiva.

Enlace a aprendizaje

Se puede usar un difractómetro de rayos X, como el ilustrado en la Figura 9.65, para medir los ángulos en los que los rayos X se difractan cuando interactúa con un cristal como se describió anteriormente.

Figura 9.65. (a) En un difractómetro, un haz de rayos X golpea un material cristalino, produciendo (b) un patrón de difracción de rayos X que puede analizarse para determinar la estructura cristalina.

A partir de tales mediciones, la ecuación de Bragg puede usarse para calcular distancias entre átomos como se demuestra en el siguiente ejercicio de ejemplo.

Ejemplo 9.19

Usando la ecuación de Bragg

En un difractómetro, se usaron rayos X con una longitud de onda de $0,1315\,nm$ para producir un patrón de difracción para el cobre. La difracción de primer orden ($n = 1$) ocurrió en un ángulo $\theta = 25.25\,\degree$. Determine el espacio entre los planos de difracción en cobre.

Solución

La distancia entre los planos se encuentra resolviendo la ecuación de Bragg, $n\lambda = 2d \sin \theta$, para d.

Esto da: $d = \frac{n\lambda}{2 \sin \theta} = \frac{1 (0.1315\,nm)}{2\sin (25.25\degree)} = 0.154\,nm$

Comprueba tu aprendizaje

Retrato de un químico

Cristalografo de rayos X Rosalind Franklin

El descubrimiento de la estructura del ADN en 1953 por Francis Crick y James Watson es uno de los grandes logros en la historia de la ciencia. Fueron galardonados con el Premio Nobel de Fisiología o Medicina de 1962, junto con Maurice Wilkins, quien proporcionó pruebas experimentales de la estructura del ADN. La química británica Rosalind Franklin hizo contribuciones invaluables a este logro monumental a través de su trabajo en la medición de imágenes de difracción de rayos X del ADN. Al principio de su carrera, la investigación de Franklin sobre la estructura de los carbones resultó útil para el esfuerzo de guerra británico. Después de cambiar su enfoque a los sistemas biológicos a principios de la década de 1950, Franklin y el estudiante de doctorado Raymond Gosling descubrieron que el ADN consta de dos formas: una fibra larga y delgada formada cuando está húmeda (tipo "B") y una fibra corta y ancha formada cuando se seca ( escribe un"). Sus imágenes de ADN de difracción de rayos X (Figura 10.66) proporcionaron la información crucial que permitió a Watson y Crick confirmar que el ADN forma una doble hélice y determinar detalles de su tamaño y estructura. Franklin también realizó una investigación pionera sobre los virus y el ARN que contiene su información genética, descubriendo nueva información que cambió radicalmente el cuerpo de conocimiento en el campo. Después de desarrollar cáncer de ovario, Franklin continuó trabajando hasta su muerte en 1958 a la edad de 37 años.

Entre muchos reconocimientos póstumos de su trabajo, la Facultad de Medicina de Chicago de la Universidad de Ciencias de la Salud de Finch cambió su nombre a Rosalind Franklin University of Medicine and Science en 2004 , y adoptó una imagen de su famosa imagen de difracción de rayos X del ADN como su logotipo oficial de la universidad.

Figura 9.66. Esta ilustración muestra una imagen de difracción de rayos X similar a la que Franklin encontró en su investigación. (crédito: Institutos Nacionales de Salud)

Preguntas y respuestas - Capítulo IX

Respuestas