Título de la obra:
Números enteros (operaciones)

Autores:
Eduardo Barbero Corral
Rita Jiménez Igea
Juan Guillermo Rivera Berrío

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual. Todos los objetos interactivos y los contenidos de esta obra colectiva están protegidos por la Ley de Propiedad Intelectual.

Tabla de contenido

Introducción

Necesidad de los números enteros.

En la vida real hay situaciones en las que los números naturales no son suficientes. Por ejemplo: si tienes 10 pesos y debes 15 pesos ¿De cuánto dispones? Observa en la escena distintas situaciones en las que se necesitan los números enteros.

Ejercicio introductorio

En la siguiente escena puedes practicar lo explicado en la página anterior.

En este libro además se da un repaso de las nociones básicas y se practican con ellos las operaciones multiplicación, división y potencias. Es conveniente que los alumnos ya hayan estudiado los números enteros en la clase tradicional.

Este libro digital interactivo puede servir como repaso para afianzar mejor los conceptos y la realización de operaciones con estos números.

Los números que aparecen en cada escena se generan al azar, lo que permite utilizarla indefinidamente, y sacar de cada una de ellas innumerables actividades diferentes. Además, son números frecuentemente de una sola cifra cuyos cálculos se hacen mentalmente con facilidad.

En las actividades se utilizan cuadrados mágicos aditivos y multiplicativos, pero siempre hay que tener en cuenta que el objetivo es aprender a manejar los números enteros, no se trata de aprender cosas sobre cuadrados mágicos.

Los números naturales

El conjunto $\mathbb{N}$. Entendemos por número la expresión de un valor, la cuantificación de una magnitud.

Los números naturales expresan valores referentes a cosas enteras, no partidas, los números naturales van de uno en uno desde el $0$, no admiten la partición de las unidades, y solamente expresan valores positivos.

Pero ¿Cómo expresar con números la altura y la profundidad, las riquezas y las deudas, las ganancias y las pérdidas, la temperatura por encima o por debajo del punto de congelación del agua?

Los números enteros

En ciertas ocasiones necesitamos expresar valores que están antes o por debajo del valor que consideramos punto de partida o valor cero. Ha sido necesario ampliar el conjunto de los números incluyendo también los negativos, para ello añadimos al número natural un signo $+$ o $-$. De esta manera han surgido los números enteros, que expresan valores que van de uno en uno, pero permiten expresar valores positivos y también valores negativos.

Escritura de un número entero. El conjunto $\mathbb{Z}$

En la expresión escrita de un número entero consideramos dos partes: el signo y el valor absoluto. El conjunto de los números enteros le nombramos con la letra $\mathbb{Z}$.

El conjunto de los números enteros es ilimitado en sentido de los negativos y en sentido de los positivos. Los números naturales están incluidos en los números enteros, son los enteros positivos. Es conveniente buscar la forma más simple de expresar un número, por eso, para escribir un número entero positivo es preferible no poner el signo $+$ y dejarlo en forma de número natural.

Hay otros conjuntos de números más amplios

Seguramente conoces también los números decimales y los racionales, también hay otros más, que estudiarás en los cursos próximos, todos han surgido para poder expresar valores que no se podían poner empleando los números reconocidos hasta entonces. Los conjuntos de números más amplios incluyen dentro de ellos a los anteriores.

A los números enteros los representamos mediante puntos sobre una recta, para ello debemos fijar la posición del punto $0$ y la largura del segmento unidad, que será el segmento que llevaremos sobre la recta sucesivas veces según el valor del número. Los números positivos los colocamos a la derecha y los negativos a la izquierda. Si la recta está en vertical colocamos los positivos arriba y los negativos abajo.

Coloca sobre la recta los puntos de abajo.

En la siguiente escena interactiva, ordena los números de menor a mayor.

Puedes realizar todos los ejercicios que desees, haciendo clic en el botón "Otro ejercicio".

Al sumar juntamos varios valores en uno solo. Como estamos acostumbrados a manejar números naturales tendemos a esperar que el resultado de la suma sea un número mayor que los sumandos, pero con los números enteros no es así, ya que depende de los signos de los sumandos.

En Matemáticas siempre debemos buscar lo más simple, lo que no es necesario estorba y si podemos debemos eliminarlo simplificando esa expresión. El signo positivo de un número solamente lo pondremos cuando sea imprescindible. De esta manera, al sumar números enteros integramos los signos de los números con los signos de sumar, hasta formar algo semejante a una serie de sumas y restas.

Resuelve las sumas de la siguiente página, distribuyendo los números de abajo sobre los círculos correspondientes. Picando sobre los triángulos de la escena puedes ver el paso intermedio para resolverlas, que es prescindir de paréntesis y de signos innecesarios.

En la ventana del control de la siguiente escena marca el resultado de cada suma, sucesivamente de arriba a abajo. Cuando marques el número correcto aparecerá en la escena junto con el paso intermedio. Si el número que marcas no es el correcto no aparecerá.

Desde los círculos puedes mover los nombres de las propiedades y las expresiones numéricas de ejemplo, coloca en la misma línea lo referente a la misma propiedad.

Distribuye los números de abajo en las casillas vacías para completar este cuadrado mágico de números enteros. Debe cumplirse que todas sus líneas horizontales, verticales y las dos diagonales sumen lo mismo. Realiza este ejercicio varias veces.

En los cuadrados mágicos de 4x4 también suman lo mismo los cuatro números del centro del cuadrado, los cuatro números de los vértices del cuadrado y cada grupo de cuatro números que están en vértices de rectángulos concéntricos paralelos al cuadrado.

En este ejercicio debes sumar o restar cada número del cuadrado con el número de fuera. Los resultados son los números de abajo, colócalos en las casillas correspondientes de la derecha.

La suma y la resta quedan englobadas en la misma operación, ya que es lo mismo sumar un número negativo que restar un número natural.

En este ejercicio debes sumar o restar cada número del cuadrado con el número de fuera. Los resultados son los números de abajo, colócalos en las casillas correspondientes de la derecha.

La suma y la resta quedan englobadas en la misma operación, ya que es lo mismo sumar un número negativo que restar un número natural.

Suma los números de las casillas correspondientes de estos cuadrados mágicos. Los resultados son los números de abajo, colócalos en las casillas correspondientes de la derecha. Obtendrás otro cuadrado mágico.

Suma los números de las casillas correspondientes de estos cuadrados mágicos. Los resultados son los números de abajo, colócalos en las casillas correspondientes de la derecha. Obtendrás otro cuadrado mágico.

Sustituye las letras por los valores indicados. Los resultados de las casillas vacías son los números de abajo, colócalos en las casillas correspondientes. Obtendrás un cuadrado mágico de números enteros.

La suma de los tres números que hay en cada segmento es =0. Un número es el opuesto de la suma de los otros dos.

Distribuye los números de abajo colocando junto a cada número su opuesto.

Resuelve estas restas distribuyendo los números de abajo en los círculos correspondientes. Picando sobre los triángulos de la escena puedes ver el paso intermedio para resolverlas.

Escribe el resultado de cada operación, sucesivamente de arriba a abajo. Tras marcar un número debes pulsar intro. Cuando marques el número correcto aparecerá en la escena junto con el paso intermedio, pero si marcas un número incorrecto no aparecerá.

Con números naturales sabemos que la multiplicación es una suma reiterada, sumamos el primer número consigo mismo de forma que interviene de sumando tantas veces como indica el segundo número. Pero con los números enteros también tenemos que considerar el signo. Multiplicar un número por un número negativo es sumar reiteradamente el opuesto del primer número. En la siguiente actividad, practica modificando los valores del primer y segundo factor incluso dando valores negativos entre $+9$ y $-9$. Descubrirás que el signo del producto cumple con una norma, llamada "Ley de los signos", que resumiremos en la siguiente página.

Si analizaste bien los resultados en la actividad anterior, pudiste concluir: el producto de dos números con el mismo signo es un número positivo y, además, que el producto de dos números con distinto signo es un número negativo. Esta conclusión es conocida como la Ley de los signos, tal como se aprecia en la siguiente imagen.

Haz clic sobre la imagen para observar una simpática forma de aprender esta norma.

Aplicando la ley de los signos

Escribe el resultado de cada una de las siguientes multiplicaciones, sucesivamente de arriba a abajo. Tras marcar un número debes pulsar intro.

Cuando marques el número correcto aparecerá en la escena. Si no es correcto no aparecerá.

Los números de abajo son los resultados de estas multiplicaciones. Arrástralos a su puesto.

La multiplicación de enteros cumple con las propiedades que se enuncian en la escena interactiva de abajo.

Haz clic en el botón para que observes otras propiedades.

Ejercicios sobre las propiedades

Desde los círculos puedes mover los nombres de las propiedades y las expresiones numéricas que son ejemplo de ellas. Coloca en la misma línea lo referente a la misma propiedad.

Observa algunos ejemplos de la propiedad distributiva.

En los siguientes ejercicios, debes multiplicar el factor fuera del paréntesis por cada uno de los sumandos, lo escribes en el cuadro de texto y pulsas intro. Si marcas el número correcto aparecerá en la escena, si no es el correcto, no aparecerá.

Multiplica cada número del cuadrado mágico por el número que está afuera.

Los resultados que faltan en la derecha son los números de abajo, arrástralos a las casillas vacías correspondientes.

Multiplicando cuadrados mágicos por un entero

En estos cuadrados mágicos se cumplen con la multiplicación en vez de la suma. El producto de los números de cada una de sus líneas horizontales, verticales y diagonales es el mismo.

Multiplica los números de las casillas correspondientes de los cuadrados mágicos multiplicativos. Los resultados son los números de abajo, arrástralos a las casillas correspondientes. Obtendrás otro cuadrado mágico multiplicativo.

Cuadrados mágicos multiplicativos con fórmulas

Sustituye las letras por los valores indicados. Los resultados que faltan son los números de abajo, colócalos en las casillas correspondientes. Obtendrás un cuadrado mágico multiplicativo de números enteros.

Cuadrado mágico multiplicativo de $4 \times 4$

Completa este cuadrado mágico, también aportan el mismo producto los cuatro números del centro, los cuatro números de los vértices del cuadrado, y cada uno de los grupos de cuatro números que están en vértices de rectángulos concéntricos paralelos al cuadrado.

En la división de números enteros se cumple la misma norma de signos que en la multiplicación.

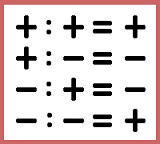
La división no es una operación interna en el conjunto de los números enteros. Es decir, al dividir dos números enteros puede ser que no resulte otro número entero.

¡Nunca se puede dividir por el número $0$!

No obstante, en los ejercicios que aparecen en las siguientes páginas, tendrás siempre divisiones posibles y que dan de resultado números enteros.

Ejercicios de división de números enteros

Distribuye los números de abajo para que se cumplan estas divisiones.

En el cuadro de texto escribe el resultado de cada operación, sucesivamente de arriba a abajo. Tras marcar un número debes pulsar intro o la tecla de tabulación. Cuando marques el número correcto aparecerá en la escena. Si no es correcto no aparecerá.

Ejercicios de división con cuadrados mágicos

Divide cada número del cuadrado mágico de la izquierda por el número de fuera. Los resultados que faltan son los números de abajo, arrástralo a las casillas vacías correspondientes. Obtendrás otro cuadrado mágico de números enteros.

Cada número del cuadrado mágico multiplicativo de la izquierda divídelo por el número de fuera. Los resultados son los números de abajo, colócalos en las casillas correspondientes de la derecha. Obtendrás otro cuadrado mágico multiplicativo.

La potenciación es una multiplicación reiterada, multiplicamos el número base consigo mismo, de forma que interviene de factor tantas veces como indica el exponente. En la escena interactiva puedes variar los números base y exponente y así comprobar el signo de la potencia resultante.

• ¿Qué signo tiene la potencia cuando la base es un número positivo?
• ¿Qué signo tiene la potencia cuando la base es un número negativo y el exponente es un número par?
• ¿Qué signo tiene la potencia cuando la base es un número negativo y el exponente es un número impar?

Ejercicios de potenciación de números enteros

En los cuadros de texto escribe el resultado de cada potencia sucesivamente de arriba a abajo. Tras marcar un número pulsa intro. Si tu respuesta es correcta aparecerá el resultado en la escena junto con su proceso de obtención, pero si marcas un número incorrecto no aparecerá.

Los números de abajo son los resultados de estas potencias, arrastra cada uno a su puesto.

Ejercicios de potenciación con cuadrados mágicos

Eleva al cuadrado o al cubo, según te indique cada número de este cuadrado mágico multiplicativo. Los resultados son los números de abajo, arrástralos cada uno a su casilla correspondiente, habrás obtenido otro cuadrado mágico multiplicativo.

Es una expresión formada por números en operaciones diversas y agrupados mediante paréntesis, corchetes y llaves. Para resolver operaciones combinadas debemos dominar todo lo estudiado anteriormente.

• La misión de los paréntesis es la de unir aquello a lo que afectan.
• Los signos de multiplicar unen más que los de sumar y restar, es decir, cuando dos números están unidos por el signo de multiplicar forman un bloque inseparable, mientras que si los une un signo de sumar o restar están más sueltos.
• Debemos conocer las propiedades de las operaciones para no hacer algo que sea incorrecto.
• Para poder sumar o restar dos números deben estar sueltos, no podemos sumar dos números si uno de ellos está unido por el otro lado a otra expresión mediante un signo de multiplicar.
• Las operaciones combinadas se resuelven en varios pasos, todo lo que no se resuelva en un paso se debe copiar otra vez tal como estaba, sin olvidarlo ni cambiarlo de posición.
• Por eso, antes de comenzar a resolver operaciones combinadas debemos observar la expresión y plantearnos una estrategia a seguir, lo que vamos a hacer antes y después.
• Como norma general es aconsejable comenzar resolviendo lo del interior de paréntesis, seguir luego con las multiplicaciones y terminar realizando las sumas que queden.

En esta última actividad debes escribir el número que sigue al resolver la expresión. Cuando el número marcado sea el correcto aparecerá en la escena, si no es el correcto no aparecerá. Debes hacerlo sucesivamente, paso a paso, para ello debes borrar el número anterior. No se trata de que halles directamente el resultado final.