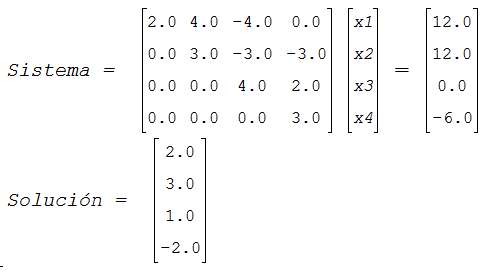MÉTODOS
NUMÉRICOS

INTERACTIVO
MÉTODOS NUMÉRICOS
INTERACTIVO
Juan Guillermo Rivera Berrío
Institución Universitaria Pascual Bravo, Colombia
Elena Esperanza Álvarez Sáiz
Universidad de Cantabria, España
José Román Galo Sánchez
Universidad de Córdoba, España
Héctor Aníbal Tabares Ospina
Institución Universitaria Pascual Bravo, Colombia
Fondo Editorial Pascual Bravo
Medellín - Santander - Córdoba
Título de la obra
Métodos Numéricos Interactivo
Juan Guillermo Rivera Berrío
Elena Esperanza Álvarez Sáiz
José Román Galo Sánchez
Héctor Aníbal Tabares Ospina
Primera edición: 2017
Diseño de cubierta: Diana María Velásquez García
Librería turn.js: Emmanuel García
Herramienta de edición: DescartesJS
Fuente: Amaranth
Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co
ISBN: 978-958-58510-6-1
Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual. Todos los objetos interactivos y los contenidos de esta obra colectiva están protegidos por la Ley de Propiedad Intelectual.
Tabla de contenido
iii
iv
v
vi
vii
Introducción
Los problemas de la ingeniería, matemáticos, estadísticos o, en general, todo problema que se pueda modelar es posible resolverlo por algún método analítico, gráfico o numérico. Los métodos numéricos permiten resolver muchos problemas usando operaciones aritméticas. Un ejemplo introductorio es el problema planteado por Chapra y Canale (2007, pág. 12
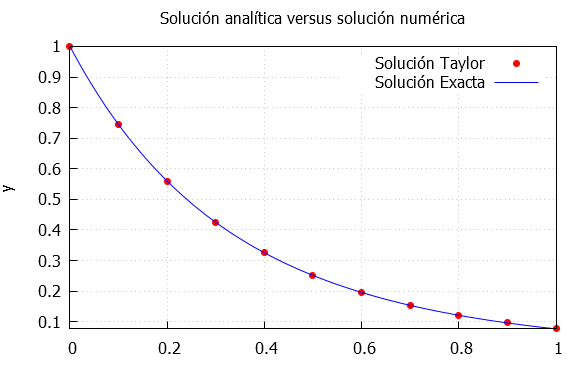
Al hacer clic en el botón Iniciar, observarás la solución analítica del problema y, además, una solución numérica o aproximada conocida como "método de Euler". Este método, que trabajaremos en la última parte de este libro, resuelve una ecuación diferencial utilizando una expansión de la serie de Taylor.
viii
Caminos para llegar a una solución
El problema introductorio nos da una idea de los posibles caminos que podemos seguir para encontrar la solución de un problema. La solución puede ser:
Analítica
Se encuentra una solución exacta.
No siempre se encuentra una solución.
Numérica
Se encuentra una solución aproximada.
Se utiliza el ordenador para hacer los cálculos.
Gráfica
La solución no es muy precisa.
El computador se utiliza como herramienta para graficar.
Sólo se trabaja en dos o tres dimensiones.
Este libro se ha elaborado con un propósito de aprendizaje autodidacta en el que el estudiante es el protagonista, desarrollando la competencia operativa y práctica al comprender y aplicar el funcionamiento de los diferentes algoritmos de cada apartado, su implementación usando el ordenador y su aplicación para la resolución de problemas. Así las cosas, no es objetivo de este libro la fundamentación en aspectos teóricos y demostraciones matemáticas, más allá de lo estrictamente básico.
ix
Es de advertir que esta obra no es un libro más de métodos numéricos, pues su contenido se ha diseñado de tal forma que permita al estudiante interactuar con los objetos de conocimiento que en cada apartado se describen y explican. Al interactuar, el estudiante logra una mayor percepción de estos objetos de conocimiento.
Dicho de otra forma, esta obra es el primer libro digital interactivo de métodos numéricos.
Por otra parte, el libro se ajusta al modelo del aula invertida (flipped classroom), pues el usuario del libro puede obtener información en un tiempo y lugar que no depende de la presencia del profesor, además de poder interactuar tanto en ordenadores como en dispositivos móviles, aumentando su percepción y, en consecuencia, su velocidad de aprendizaje.
Esta primera edición la hemos dividido en seis partes. La primera parte trata sobre la teoría de errores. La segunda, presenta los diferentes métodos numéricos empleados para solucionar ecuaciones no lineales. La tercera estudia los algoritmos que solucionan sistemas de ecuaciones lineales. El tema de interpolación se explica en la cuarta parte. La penúltima parte versa sobre diferenciación e integración numérica. La última parte es acerca de la solución numérica de Ecuaciones Diferenciales, que inician con el modelo simple de Euler (utilizado en la escena introductoria) y termina con los métodos de Runge-Kutta.
Actualmente, existe una gran variedad de libros y textos, algunos de ellos reseñados en la bibliografía, que incluyen algoritmos para ser aplicados en diferentes aplicativos. El más usual de estos aplicativos es el Matlab y, en algunos casos, las macros de Visual Basic de Excel. No osbtante esta tendencia, hemos optado por usar aplicaciones libres, que permitan una mayor accesibilidad de nuestros usuarios, el libro mismo tiene esta naturaleza.
x
El aplicativo que hemos seleccionado para diseñar nuestros algoritmos es el Maxima, el cual es un software libre para la manipulación de expresiones simbólicas y numéricas, incluyendo diferenciación, integración, expansión en series de Taylor, transformadas de Laplace, ecuaciones diferenciales ordinarias, sistemas de ecuaciones lineales, vectores, matrices y tensores. Recomendamos la descarga e instalación de la interface wxMaxima:
Por otra parte, la interactividad del libro se encuentra en los objetos interactivos de aprendizaje diseñados con las herramientas de autor Descartes y el procesador geométrico GeoGebra
Algunas imágenes, especialmente las correspondientes a los algoritmos diseñados en wxMaxima, tienen la opción de ser ampliadas al hacer clic sobre ellas.
Confiamos en que esta obra sea de gran utilidad para el aprendizaje de los métodos numéricos.
xi
parte i
Teoría de errores
Héctor A. Tabares Ospina
Juan Guillermo Rivera Berrío
Introducción
El uso de los ordenadores para resolver problemas por métodos numéricos, pueden generar errores cuyas causas es necesario comprender. Un error puede surgir en la digitación del algoritmo que resuelve un problema, por una mala formulación del modelo, por la elección del modelo (el método de Euler de la introducción) o por problemas propios de la máquina que realiza los cálculos numéricos. De esta última causa nos ocuparemos en esta primera parte del libro, para ello, iniciamos con el siguiente algoritmo escrito en wxMaxima.
14
El algoritmo lo que hace es calcular los siguientes sumatorios:

cuyo resultado debería ser 10, sin embargo, los resultados obtenidos son aproximaciones al número 10, lo que se constituye en un error, muy pequeño... pero, es un error. Se puede observar que el error se reduce cuando el número de ciclos aumenta. Este tipo de error, conocido como de redondeo, se entenderá mejor al conocer cómo trabaja la máquina que calcula, en nuestro caso el ordenador. Pero, antes de ello, nos detendremos, brevemente, para explicar algunos elementos del algoritmo anterior.
Todos los algoritmos de wxMaxima que usaremos en este libro, pueden ser descargados haciendo clic en el símbolo de Maxima. En este primer algoritmo hemos usado tres tipos de bucle, los cuales tienen el mismo funcionamiento lógico. Los dos primeros son del tipo for, cuya única diferencia es el cambio de la palabra thru por while, este bucle genera ciclos desde 1 hasta 1000 en el primero, o hasta 10000 en el segundo. El tercero es del tipo do while que, a diferencia de los otros dos, requiere de un contador (i: i+1), de lo contrario se generaría un error de programación que conduce a ciclos infinitos.
Toda instrucción en un algoritmo de wxMaxima debe terminar con ";" o el signo "$", si se hace con el primero, la instrucción se mostrará en los resultados. Los comentarios irán encerrados entre las expresiones /* y */. Una explicación más amplia de estas y otras instrucciones se encuentra en la ayuda que trae el programa o, si se desea, se puede consultar el texto de Alaminos et al:
15
1. Sistemas numéricos
La humanidad históricamente ha utilizado diferentes sistemas numéricos para representar cantidades, actualmente usamos el sistema decimal que usa 10 dígitos (del cero al nueve). Sin embargo, los ordenadores trabajan con bits (dígitos binarios), conformando grupos denominados palabras, las cuales pueden ir desde ocho bits hasta 64. El manejo de esta gran extensión de bits se facilita al dividirla en grupos de ocho bits, denominados bytes. Internamente, entonces, el ordenador trabaja con bits, no obstante, su interpretación (interface hombre - máquina) se hace tanto en sistemas binarios, como octales y hexadecimales. En este apartado recordaremos algunos aspectos del sistema binario, para los otros sistemas se recomienda consultar la bibliografía.
1.1 Sistema digital (0,1), base 2
Es un sistema de numeración en el que los números se representan utilizando solamente las cifras cero y uno (0 y 1).
Ejemplo
Observa un número binario de varias cifras, haz clic en el botón para observar otros números.
16
1.2 Sistema decimal (0,1,2,3,4,5,6,7,8,9), base 10
En este sistema los números se representan utilizando 10 dígitos, es un sistema de numeración posicional en el que las cantidades se representan utilizando como base aritmética las potencias del número diez.
Ejemplo
Observa un número decimal y su descomposición según la posición de las cifras, haz clic en el botón para observar otros números.
1.3 Conversión de bases
Conversión de decimal a binario
El procedimiento es sencillo, basta dividir el número en base decimal y sus cocientes entre 2, acumulando los residuos que conformarán el número en la nueva base. La lista de ceros y unos leídos de abajo a arriba es el resultado. En la escena que se presenta a continuación, se muestra, paso a paso, cómo hacer la conversión. Este procedimiento es aplicable a cualquier base. En la siguiente escena se incluyen ejemplos con números enteros y con parte fraccionaria, observa el procedimiento para este último caso.
17
Ejemplo
Haz clic en el botón "Siguiente paso" para observar cómo se obtienen los dígitos binarios correspondientes al número decimal dado.
Una vez hayas practicado y comprendido el procedimiento, puedes realizar los ejercicios que desees en la página siguiente, sólo hemos incluido la parte entera.
18
Ejercicios
En el recuadro escribe la respuesta y luego pulsa la tecla "Intro". Puedes realizar varios ejercicios.
19
Conversión de binario a decimal
Para realizar la conversión de binario a decimal sigue los siguientes pasos:
1. Inicia por el lado derecho del número binario, cada cifra multiplícala por 2 elevado a la potencia consecutiva (comenzando por la potencia 0, 1, 2, ....).
2. Después de realizar cada una de las multiplicaciones, súmalas y el número resultante será el equivalente al sistema decimal.
20
2. Aritmética de un ordenador
El ordenador, como lo expresamos antes, trabaja internamente con grupos de bits que, obviamente, por su finitud, no es posible operar con números de una cantidad ilimitada de cifras, tal como las que tendría un número irracional como √3, el ordenador haría una representación aproximada, de tal forma que el cuadrado de este número esté lo bastante cerca de 3. Un ejemplo de estas aproximaciones lo tomamos de una de las escenas anteriores:

Si convertimos el número 10.1110012 a decimal, obtendríamos:
1·21 + 0·20 + 1·2-1 + 1·2-2 + 1·2-3 + 0·2-4 + 0·2-5 + 1·2-6
cuyo resultado es 2.890625, es decir, se genera un error de 0.011575. Este error obedece, obviamente, al número reducido de dígitos empleados. Algo así como la capacidad del ordenador doméstico de 8 bits, Commodore Vic-20, de 1980.
21
2.1 Aritmética del punto flotante
La restricción dada por la cantidad de bits permitidos en un ordenador ha obligado a algunas técnicas de almacenamiento de los números, una de ellas es la representación del punto flotante, que para base binaria y un número x dado, sería:
x = m·2e
En la expresión, e es el exponente o característica y m es conocida como la mantisa, la cual es un número decimal de la forma 0.d1d2d3d4.... Si los primeros decimales valen cero, esto generarían bits innecesarios, por lo que se recurre a correr (flotar) el punto al primer decimal no nulo. Veamos dos ejemplos:
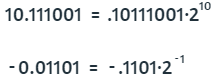
En el primer ejemplo, la coma la desplazamos dos cifras a la izquierda, por ello, el exponente es 10 (dos en decimal). En el segundo ejemplo, eliminamos el cero innecesario en la primera cifra decimal desplazando la coma una cifra a la derecha, por ello, el exponente es -1. Este proceso se conoce como normalización de la mantisa.
Retornando a los años 80 del siglo pasado, supongamos que nuestro ordenador tiene una capacidad de almacenamiento de 16 bits. En la siguiente escena interactiva, observa cómo se almacena un número entero. El primer bit es el signo del número (uno si es negativo y cero si es positivo), el segundo bit es el signo del exponente, los bits 3 a 6 almacenan el valor el exponente y los restantes el valor de la mantisa.
22
Observa que cuando la mantisa tiene 11 dígitos, nuestro ordenador de 16 bits corta o trunca el último dígito. Esto ocurre para números decimales de cuatro dígitos, sin embargo, los procesadores han sido diseñados de tal forma que trabajan con los complementos binarios, por ejemplo, el exponente 1101 tiene como complemento 0010. Esto permite ganar unos bits más para ampliar el número de dígitos permitidos.
Volviendo a nuestra época, los ordenadores actuales tienen una mayor capacidad de almacenamiento. Este libro, por ejemplo, lo estamos diseñando en un ordenador de 64 bits. La siguiente tabla nos da una idea del rango en el cual podemos trabajar.
| Tipo | Tamaño en bits | Rango |
| Entero | 16 | -32768 a 32767 |
| Real | 32 | 3,4x10-38 a 3,4x1038 |
| Real doble | 64 | 1,7x10-308 a 1,7x10308 |
23
2.2 Errores en un ordenador
Presentamos, a continuación, algunos tipos de errores:
2.2.1 Errores inherentes
Son errores inherentes a los datos, a la incertidumbre en las medidas, a los números que se exceden en el tamaño de bits permitidos por el ordenador, al diseño del modelo, a la digitación del algoritmo, entre otros.
2.2.2 Error absoluto
Si p* es una aproximación de p y si p es el valor real, entonces,
Error Absoluto = |p-p*|, o sea el valor absoluto de p menos p*.
El valor absoluto genera sólo errores positivos, lo que se traduce en una suma o acumulación de errores.
El error absoluto se propaga en los cálculos de la siguiente manera:
Producto Ex*y = yEx + xEy
Cociente Ex/y = (Ex/x) + (Ey/y)
Suma Ex+y = Ex + Ey
Resta Ex-y = Ex + Ey
24
2.2.3 Error relativo
El error relativo se define como:
Error relativo = |p-p*|/|p| con la condición de p ≠ 0.
El error relativo es una mejor medida del error, en especial cuando se utilizan sistemas numéricos de punto flotante. Realiza algunos ejercicios en la siguiente escena interactiva:
25
2.2.4 Error de redondeo
Este tipo de error ya lo hemos explicado en la introducción de este apartado, recordemos que las limitaciones de almacenamiento de bits generan cálculos aproximados de los números verdaderos, es decir, los números y errores están sujetos al sistema numérico de punto flotante. Similar al sistema binario, un número real positivo puede ser normalizado para que adquiera la forma:
y = 0.d1d2d3...dkdk+1... x10n
1≤di≤9, con i = 2,3,4,...k
La forma de punto flotante fl(y) se obtiene terminando (recortando) la mantisa de y en k dígitos decimales. Existen dos métodos de terminar:
1. Cortando los dígitos dk+1dk+2... fl(y) = 0.d1d2d3...dk x10n
2. Redondeando el número
Si (dk+1 ≥ 5) Entonces
Se agrega uno a dk para obtener fl(y)
FinSi
Si (dk+1 < 5) Entonces
Se cortan todos excepto los primeros k dígitos.
FinSi
2.2.5 Error de truncamiento
Similar al error de redondeo es originado en un proceso que requiere un número infinito de pasos pero se detiene en un número finito de pasos. Sin embargo, estos errores no son inherentes al ordenador o al sistema numérico utilizado, pues surgen al usar una aproximación en lugar de un procedimiento matemático exacto (Chapra & Canale, 2007, pág. 78
26
Practica con algunos ejercicios de redondeo. En los recuadros escribe el número cortado y redondeado, luego presiona la tecla intro.
Ejercicios
2.2.6 Error por desbordamiento
"Con frecuencia una operación aritmética con dos números válidos da como resultado un número tan grande o tan pequeño que la computadora no puede manejarlo; como consecuencia se produce un overflow o un underflow, respectivamente. Por ejemplo, al multiplicar 0.5·108 por 0.2000·109 se obtiene 0.2000·1017" (Nieves & Domínguez, 2006, pág. 14
27
2.3 Algoritmos y estabilidad
"La condición de un problema matemático relaciona su sensibilidad con los cambios en los datos de entrada. Se dice que un cálculo es numéricamente inestable si la inexactitud de los valores de entrada se aumenta considerablemente por el método numérico" (Chapra & Canale, 2007, pág. 98
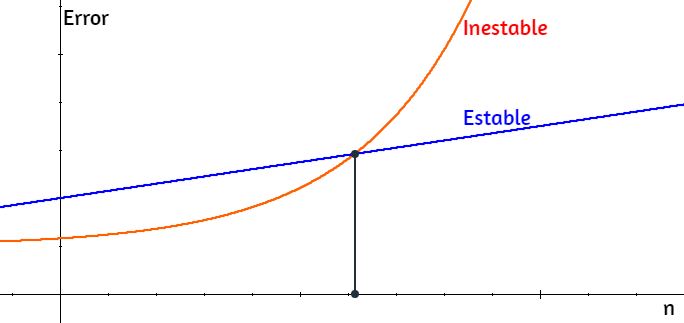
Algunas recomendaciones
Evitar restar números casi iguales.
Evitar la división por un número cercano a cero.
Minimizar la ejecución del número de operaciones en el algoritmo.
Utilizar datos del tipo doble precisión cuando sea necesario.
Realizar escalamiento de los datos si es posible.
28
parte ii
SOLUCIÓN NUMÉRICA DE ECUACIONES NO LINEALES
José R. Galo Sánchez
Juan Guillermo Rivera Berrío
En esta parte del libro estudiaremos los métodos numéricos para determinar las raíces de una Ecuación No Lineal con una variable. Analizaremos los problemas de convergencia y error que puedan presentarse (Burden, 2002, pág. 47
En la mayoría de los casos no es posible determinar las raíces de una función, es decir, los valores x* tal que f(x* ) = 0, aplicando un algoritmo que termine en un número finito de pasos. Para ello, tenemos que usar métodos de aproximación que, en general, son iterativos.
En el tercer capítulo observaremos cómo podemos determinar si una función no lineal tiene raíces, a través de un análisis gráfico y uno análitico. Al final, haremos una introducción a los métodos iterativos
En los dos capítulos siguientes veremos los métodos iterativos usuales: bisección, regula falsi, punto fijo, Newton y el método de la secante.
Incluiremos algunos objetos interactivos diseñados con el editor Descartes, que permitirán un mayor acercamiento a los conceptos, teoremas y métodos iterativos descritos en cada capítulo. No obstante esta ayuda, se recomienda utilizar el cuadernillo de trabajo para realizar algunos ejercicios propuestos
3. Raíces de una ecuación
Para hallar las raíces de una ecuación es necesario saber si la ecuación tiene solución. En caso de la existencia de una solución, convendría identificar en qué intervalo se encuentra, pues ello optimizaría el algoritmo utilizado para hallar la raíz de la ecuación.
32
3.1 Verificación gráfica
Una primera opción es dibujar la gráfica de la función, opción que actualmente no representa problema por la gran cantidad de herramientas digitales disponibles en la red. Observa, por ejemplo, la animación realizada con Descartes
33
En la escena interactiva podrás ver algunas funciones y hallar sus raíces. Puedes escribir tu propia función, pero antes de hacerlo observa cómo se escriben las funciones comparando la expresión que aparece en la parte superior (sintáxis del ordenador) con la expresión de la parte inferior del interactivo (sintáxis matemática).
Haz clic para ampliar la escena
34
3.2 Teorema del valor intermedio
La representación gráfica permite, además de hallar las raíces, la verificación de su existencia. Sin embargo, esta verificación a partir de la gráfica no siempre es el camino más inmediato, una forma analítica de lograrlo es a partir del teorema del valor intermedio, el cual afirma que "Si f es una función continua en un intervalo [a, b], entonces para cada k tal que f(a) ≤ k ≤ f(b), existe al menos un c dentro del intervalo [a, b] tal que f(c) = k". En el siguiente interactivo desplaza el punto c y observa el cumplimiento del teorema, en los ejemplos podrás encontrar su aplicación en la determinación de la existencia de raíces en una ecuación.
35
3.3 Método iterativo
Los métodos numéricos para resolver ecuaciones no lineales son de tipo iterativo, los cuales son modelos de aproximaciones sucesivas. En una forma simple, el método consiste en elegir un valor inicial x0 (semilla), a partir del cual se genera una sucesión de iteraciones x1, x2, x3, ..., hasta que éstas converjan a la solución.
Si una ecuación puede ponerse en la forma f(x) = x, podemos, en principio, empezar con un punto x0 y calcular x1 sustituyendo en la ecuación el valor de x0, el valor obtenido será el nuevo valor a sustituir en la ecuación, y así sucesivamente hasta encontrar un valor de convergencia. Matemáticamente, considerando xn+1 = f(xn) para n ≥ 1, si f es continua y la secuencia {xn} con n ≥ 1 converge, lo hará a la solución x.
Tratemos de resolver la siguiente ecuación x2 - 2x + 1 = 0, cuya solución sabemos que es uno (1), para ello podemos hacer el siguiente despeje: x = √2x - 1. Supongamos que nuestra semilla es x0 = 3, lo que significa que x1 = 2.23607, calculamos x2 reemplazando el valor anterior en la ecuación y obtenemos x2 = 1.86337, en este momento hemos realizado sólo dos iteraciones, si continúas iterando notarás que la convergencia es lenta, lo que justifica el uso de otros métodos que veremos en el siguiente capítulo.
En la escena interactiva de la siguiente página podrás encontrar el número de iteraciones necesarias para hallar la solución en la que, para facilitar el proceso, sólo hemos considerado dos cifras decimales. Observa que la columna xn inicia con el valor semilla, en la columna xn+1 aparecen los cálculos realizados en la ecuación, los cuales se convierten en una nueva semilla, repitiendo (iterando) el proceso hasta que hallamos la solución.
36
En el siguiente interactivo se presenta el método iterativo para hallar la solución de la ecuación dada. Usa el control para generar las iteraciones, si dejas presionado el ratón éstas se generarán más rápido.
37
4. Métodos iterativos abiertos
En el último ejemplo de la escena interactiva anterior, observamos que la convergencia a la solución se realizaba con pocas iteraciones, esto depende del tipo de ecuación y del método iterativo utilizado. En cada ejemplo observamos una convergencia a un punto, el cual se suele llamar “punto fijo atractivo”. Los métodos abiertos utilizan una ecuación similar a la que hemos usado en al apartado anterior para predecir la raíz, la cual puede desarrollarse como una iteración simple de punto fijo (también llamada iteración de un punto o sustitución sucesiva o método de punto fijo). En este capítulo analizaremos los métodos de punto fijo, de Newton y el de la Secante.
4.1 Método de punto fijo
Este método lo explicaremos a través de la unidad didáctica interactiva del proyecto Un_100Métodos de punto fijo, la cual inicia con un método para calcular la raíz cuadrada de un número.
Método de Herón para calcular la raíz cuadrada
Herón de Alejandría (126-51 a.C.) afirmó que si y es una aproximación de la raíz cuadrada de un número positivo a entonces:
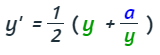
es una aproximación mejor. En base a ello, partiendo de una aproximación inicial y0
38
podemos obtener de manera recurrente una sucesión de valores
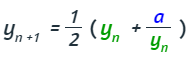
que convergerán a la raíz cuadrada de a.
En la siguiente escena interactiva usa los controles para explorar el método de Herón.
Haz clic para ampliar la escena
39
Formulación general del método iterativo
40
Convergencia y divergencia
42
43
Resolviendo ecuaciones
44
Actividad con GeoGebra
Practica con la siguiente escena creada por Adrian Phelipp Villada
Haz clic para ampliar la escena
46
Programación del método de punto fijo en wxMaxima
El siguiente algoritmo permite calcular la raiz de una función por el método del punto fijo. En wxMaxima puedes cambiar el punto inicial, el número de iteraciones o la función a iterar.

Una ampliación sobre el funcionamiento del algoritmo lo encuentras en el libro de José Ramírez Labrador:
Si tienes instalado wxMaxima en tu ordenador, haz clic en la imagen para descargar el método del punto fijo (lo abres con wxMaxima y lo ejecutas con Control+R):
47
4.2 Método de Newton o de las tangentes
El método de Newton se describe en su libro Method of Fluxions, el cual fue explicado por J. Raphson en 1690, por lo que se suele llamar el método de Newton-Raphson. Es un método cuya convergencia es mucho mejor que la del punto fijo.
Este método lo explicaremos a través de la unidad didáctica interactiva del proyecto Un_100Resolución numérica de ecuaciones, en la cual se describe otros tres métodos que usaremos en este libro.
Considérese una ecuación no lineal de la forma f(x) = 0, donde f es continua y derivable en un intervalo [a, b] con derivada no nula.
Definimos un método iterativo en el que partiendo de un valor inicial x0 construimos una sucesión (xn), donde xn es el punto de intersección de la recta tangente a f(x) en (xn-1, f(xn-1)) con el eje de abscisas. Es decir,
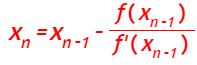
El método de Newton es siempre convergente a una raíz si el valor inicial es lo suficientemente próximo a esa raíz, pero la convergencia es dependiente de ese valor inicial. Por ejemplo, compruebe en la escena interactiva que para f(x) = x2 - 2 si consideramos x0 = 0.5 convergerá a √2 y si consideramos x0 = -0.5 convergerá a -√2.
48
La dificultad de este método radica en la necesidad de calcular los valores de la derivada primera de la función. Para evitar ello hay variantes del método de Newton que obvian ese cálculo, por ejemplo, el método de la Secante y el de “Regula Falsi” o de la falsa posición que combina el de bisección y el de la secante, los cuales veremos más adelante.
No obstante, en programas de cálculo simbólico o de algebra computacional (CAS) como GeoGebra o Maxima, la derivada de la función no es un problema, como veremos a continuación.
En la escena de GeoGebra de la página siguiente hemos usado la misma función de la escena anterior, desplaza uno de los puntos sobre el segmento azul. Puedes observar que a medida que el valor incial esta cerca de una de las dos raíces, el número de iteraciones se reduce. La escala de la gráfica se puede modificar con la rueda del ratón (mouse)".
Ejercicios
1. Obtener la solución única de x3 + 4x2 - 10 = 0 mediante el método de Newton. Compara los resultados obtenidos interactuando con la escena de Descartes.
2. Resuelve las ecuaciones planteadas en el apartado 3.3. Puedes hacerlo con Descartes, GeoGebra o Maxima
3. Usa una calculadora para resolver, paso a paso, la ecuación dada en el ejercicio 1.
50
Actividad con GeoGebra
Practica con la siguiente escena creada por Juan Pablo Serrano
Haz clic para ampliar la escena
51
Programación del método de Newton en wxMaxima
A continuación se presenta el código en wxMaxima para el método de Newton.
/* Definimos en la variable g la función a resolver */
g:x^2-2;
/* Definimos en la variable gd la derivada de la función */
gd:diff(g,x);
/* Para empezar, eliminamos las asignaciones a la variable newton */
kill(newton);
/* Creamos la función de iteración (newton(pn)) con x = pn */
newton(pn):=ev(x-g/gd,x=pn);
/* La primera iteración en pn = 0.2 */
pn:.2;
/* Repetimos el proceso desde 1 hasta 10 iteraciones */
i:0$
while i<10 do (
i:i+1,
print(i,float(pn)),
pn:newton(pn));
/* Dibujamos la función (Paso opcional)*/
plot2d([x^2-2],[x,-2,2]);
Ejecuta el programa combinando las teclas control + R. En la siguiente página se muestran los resultados, observa que en la octava iteración se obtiene la solución. Puedes digitar el código, copiarlo de esta página o hacer clic en la imagen para descargar el archivo.
52
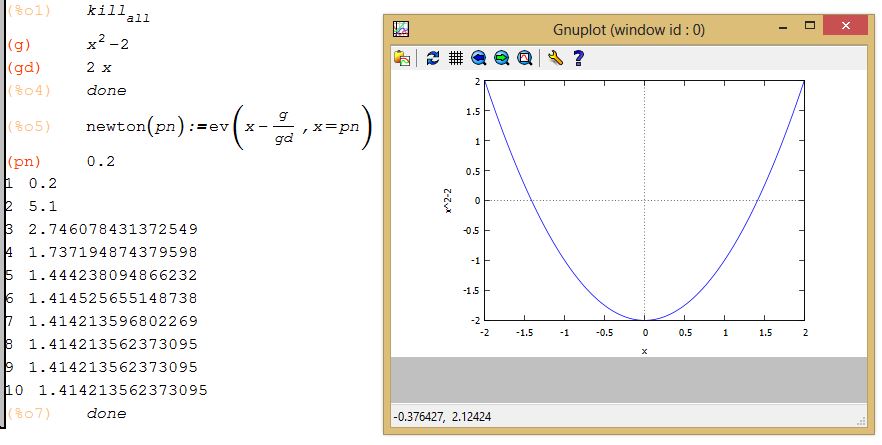
Algunas conclusiones:
El método es altamente eficiente, pues encuentra la raíz en muy pocas iteraciones.
Puede presentar problemas en la derivada si tiende a cero, es muy compleja o no se conoce.
Cuando el algoritmo no converge, es necesario elegir otro punto inicial.
Si la derivada se aproxima a cero el método trabaja demasiado lento.
53
4.3 Método de la Secante
En el método de Newton, para obviar la dificultad de calcular la derivada de la función en cada punto se considera una aproximación
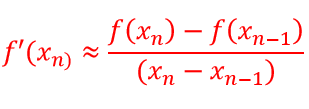
Con lo que el método iterativo quedaría expresado como
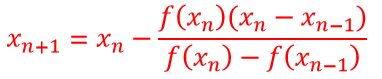
Para poder aplicar el método son necesarias dos aproximaciones iniciales que permitan iniciar el proceso. Hay diversas alternativas como puede ser considerar una aproximación inicial y obtener la segunda aplicando el método de Newton. Aquí consideraremos un intervalo inicial y sus extremos serán esas dos primeras aproximaciones.
El nombre del método es debido a que gráficamente se está sustituyendo la recta tangente del método de Newton por la recta secante.
El método de la Secante puede formularse de manera independiente del método de Newton y como mejora del método de la bisección (ver apartado 5.2) donde en lugar del punto medio del intervalo se selecciona un valor proporcional a los valores de la función en los extremos del intervalo, y de aquí que el método se denomine también “de las partes proporcionales”.
54
El método de la secante como variación del método de Newton busca evitar el cálculo de la derivada de la función, aproximando la pendiente a la recta secante que une los puntos (x1, f(x1)) y (x2, f(x2)) a la recta tangente en el punto de intersección de la función con el eje x.
En la escena de GeoGebra de la página siguiente, aproxima los puntos x1 y x2 a la intersección y observa cómo la solución converge. Desplaza el deslizador para que observes paso a paso la aproximación de la secante a la tangente.
Ejercicios
1. Obtener la solución única de x3 + 4x2 - 10 = 0 mediante el método de la Secante. Compara los resultados obtenidos interactuando con la escena de Descartes.
2. Resuelve las ecuaciones planteadas en el apartado 3.3. Puedes hacerlo con Descartes, GeoGebra o Maxima
3. Halla las raíces de la función f(x) =−11−22x+17x2 −2.5x3
56
Actividad con GeoGebra
Practica con la siguiente escena creada por Kelly Vanessa Peña Rodriguez
Haz clic para ampliar la escena
57
Programación del método de la Secante en wxMaxima
A continuación se presenta el código en wxMaxima para el método de la Secante.
/* Creamos la función de iteración (secante(arg)) */
secante(arg):=block([a:arg[1],b:arg[2],f:arg[3],xsec], xsec:(a*ev(f,x=b)-b*ev(f,x=a))/(ev(f,x=b)-ev(f,x=a)), [b,xsec,f] );
/* La primera iteración en a = 1, b = 2 y f = x^2 - 2 */
ini:[1,2,x^2-2];
/* Repetimos el proceso desde 1 hasta 10 iteraciones */
for i:1 thru 10 do (print(i,float(ini),float(ini:secante(ini))));
/* Dibujamos la función (Paso opcional)*/
plot2d([x^2-2],[x,-2,2]);
En el código hemos empleado la estructura tipo bloque, que permite evaluar varias expresiones y devolver el último resultado. Por ejemplo, la estructura block([a,b],a:2,b:3,a+b); devolvería el valor de 5.
Recuerda de ejecutar el programa con la combinación de las teclas control + R. En la siguiente página se muestran los resultados para dos funciones diferentes, observa que la primera salida es el bloque donde aparece la expresión de la pendiente. Luego aparecen pares de bloque así: [a, b, f(x)] [b, f(b), f(x)].
Puedes digitar el código, copiarlo de esta página o hacer clic en la imagen para descargar el archivo.
58
Estos son dos resultados del método de la Secante ejecutado con wxMaxima

Haz clic para ampliar la imagen

Haz clic para ampliar la imagen
59
5. Métodos iterativos cerrados
Los métodos cerrados están basados en el teorema de Bolzano y la convergencia está garantizada bajo las condiciones del teorema. Los métodos abiertos, anteriormente explicados, no nos garantizan la convergencia, por lo que deberemos definir un número máximo de iteraciones y elegir en el proceso iterativo un buen punto inicial. Los métodos cerrados utilizan intervalos dentro de los que se debe encontrar la raíz de la ecuación, es decir, en ese intervalo la función cambia de signo. El intervalo se determina por medio de la gráfica de la ecuación o del método de búsqueda incremental. En este capítulo trabajaremos con el método de la Bisección y el de Regula Falsi.
5.1 Teorema de Bolzano
Si una función f(x) es continua en un intervalo cerrado [a,b] y f(a) y f(b) son de distinto signo, existe por lo menos un punto entre a y b para el cual f(c)=0.
5.2 Método de la Bisección
También conocido como método de la Bipartición o de la Dicotomía. Para este método presentaremos la programación del código en las herramientas de autor GeoGebra y Descartes, que serán una base conceptual para programar los demás métodos. Igualmente, si ya descargaste este libro a tu ordenador, es posible explorar y analizar los códigos de programación de los métodos anteriores, pues estos se encuentran almacenados en la carpeta interactivos.
60
Considérese una ecuación no lineal de la forma f(x) = 0, donde f es continua en un intervalo [a, b] y tal que f(a) tiene signo contrario a f(b), es decir que f(a)·f(b) < 0. Por el Teorema de Bolzano existirá al menos un punto de este intervalo en el que f(x) se anule.
Nota: El que exista “al menos” un punto en el que se anule f(x) no quiere decir que sólo haya uno. Contando cada raíz de f(x) tantas veces como sea su multiplicidad, si f(a)·f(b) < 0, habrá en general un número impar de raíces y si fuese positivo o no hay ninguna raíz o habrá un número par de ellas.
Una primera aproximación de este punto puede ser el punto medio:
p1 = (a + b)/2
Si f(p1) = 0 ya se tendría calculada una raíz. Pero en general se tendrá que f(p1) ≠ 0. Al ser la función continua, si f(a)·f(p1) < 0 se puede afirmar que en el intervalo [a, p1] habrá al menos una solución de la ecuación. Y si f(a)·f(p1) > 0 se verificará que f(p1)· f(b) < 0 lo que nos indicaría que en el intervalo [p1, b] existirá al menos una raíz. Por tanto, se habrá definido así un nuevo intervalo [a1, b1] en el que existirá una solución. En él puede aplicarse nuevamente el proceso anterior.
En las dos páginas siguientes, presentamos dos escenas, una en Descartes y otra en GeoGebra para que practiques con este método, luego presentamos ejemplos de códigos de programación para Descartes, GeoGebra y Maxima.
61
Actividad con Descartes
Escena creada por José R, Galo, cambia funciones y compara con la escena de GeoGebra.
Haz clic para ampliar la escena
62
Actividad con GeoGebra
Escena creada por K. G Sreekumar. Mueve los puntos del intervalo [a, b]
Haz clic para ampliar la escena
63
Programación del Método de la Bisección con Descartes
En el siguiente vídeo podrás observar cómo se programa una escena de la Bisección con Descartes. Sugerimos verlo en forma ampliada y en el navegador Firefox.
Haz clic para ampliar la escena
64
Programación del Método de la Bisección con GeoGebra
En el siguiente vídeo podrás observar cómo se programa una escena de la Bisección con GeoGebra. Sugerimos verlo en forma ampliada y en el navegador Firefox.
Haz clic para ampliar la escena
65
Programación del método de la Bisección en wxMaxima
A continuación se presenta el código en wxMaxima para el método de la Bisección.
/* Definimos el número de decimales a mostrar */
decimales:4;
prec:10^decimales;
/* Definimos la función f(x) y el intervalo [a, b] */
f(x):=cos(x)-x;
a:0.0;
b:2.0;
/* Usamos un bucle tipo for para las iteraciones */
for i:1 thru 15 do
(
c:(a+b)/2, /* calculamos el punto medio */
if f(a)*f(c)>0 /* ¿Son del mismo signo en [a,c]? */
; ; then a:c /* elegimos [c,b] */
; ; else b:c, /* elegimos [a,c] */
print(i,float(round(a*prec)/prec),float(round(b*prec)/prec)) /* escribimos los resultados con cuatro decimales */
)$
En el código hemos usado el comando round(), el cual trunca los decimales. Recuerda ejecutar el programa con la combinación de las teclas control + R. Puedes digitar el código, copiarlo de esta página o hacer clic en la imagen para descargar el archivo. Recuerda que puedes incluir la gráfica con una expresión como plot2d(f(x),[x,0,2]);
66
5.3 Método del Regula Falsi
Este método es una combinación del método de bisección y del método de la secante.
Partiendo de la situación del método de la bisección, es decir, una ecuación no lineal de la forma f(x) = 0, donde f es continua en un intervalo [a, b] y tal que f(a) tiene signo contrario a f(b), es decir que f(a)·f(b) < 0. Se considera el punto x1 punto de corte con el eje de abscisas de la recta secante que pasa por (a, f(a)), (b, f(b)), es decir al punto
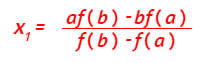
Si f(x1)·f(a) < 0 en el intervalo (a, x1) existirá una solución, y si f(x1)·f(a) > 0 se puede afirmar lo mismo en (x1, b) , habiéndose alcanzado la solución si f(x1) = 0 o bien disponiéndose de un nuevo intervalo en el que aplicar de nuevo el proceso.
En las dos páginas siguientes, presentamos dos escenas, una en Descartes y otra en GeoGebra para que practiques con este método, te queda como tarea programar el método en Maxima.
67
Actividad con Descartes
Escena creada por José R, Galo, cambia funciones y compara con la escena de GeoGebra.
Haz clic para ampliar la escena
68
Actividad con GeoGebra
Escena creada por Andreas Lindner. Mueve los puntos del intervalo [a, b]
Haz clic para ampliar la escena
69
parte iii
SOLUCIóN NUMéRICA DE SISTEMAS DE ECUACIONES LINEALES
Juan Guillermo Rivera Berrío
Héctor A. Tabares Ospina
Introducción
Una ecuación lineal, que denotaremos como E1, con n variables o incógnitas x1,x2,...,xn es de la forma
E1: a1x1 + a2x2 + ... + anxn = b
Tanto los coeficientes (a1,a2,...,an ) como el término independiente b son números reales. La solución de la ecuación lineal es un conjunto de valores para las variables o incógnitas que satisfacen la ecuación. Por otra parte, los sistemas de ecuaciones lineales que surgen al modelar problemas de diferentes áreas del conocimiento, en especial las disciplinas ingenieriles, son un conjunto de m ecuaciones lineales E1,E2,...,Em que se pueden representar así:
E1 : a11x1 + a12x2 + a13x3 + ... + a1nxn = b1
E2 : a21x1 + a22x2 + a23x3 + ... + a2nxn = b2
E3 : a31x1 + a32x2 + a33x3 + ... + a3nxn = b3
Em : am1x1 + am2x2 + am3x3 + ... + amnxn = bm
A este conjunto de ecuaciones se le llama sistema lineal de dimensión m x n. El sistema lineal se puede escribir de la forma Ax = b, donde A es la matriz de coeficientes, b es el vector de términos independientes y x = (x1,x2,...,xn), es la solución.
72
6. Álgebra matricial
En la introducción observamos que el sistema lineal de ecuaciones incorpora una matriz de coeficientes, razón por la cual es importante recordar algunos conceptos trabajados en un curso de álgebra lineal relacionados con el álgebra de matrices o, si se prefiere, el álgebra matricial. Inicialmente, recordemos que una matriz es un arreglo o colección de elementos dispuestos en forma rectangular en filas y columnas.
Una buena opción para repasar las operaciones más simples con matrices es a través del vídeo de Bill Shillito, publicado, inicialmente, en TED-Ed:
Haz clic para ampliar el vídeo
73
6.1 Representación matricial del sistema
El sistema lineal, como vimos antes, se puede escribir de la forma Ax = b. En el siguiente interactivo puedes observar la matriz representativa del sistema.
74
Una matriz, como hemos visto, es una tabla rectangular de datos ordenados en filas y columnas. Todos los elementos de una matriz de dimensión mxn se denotan de la forma aij, el valor de i representa la fila y el valor de j la columna. Demuestra que has entendido esta notación con el siguiente ejercicio:
75
6.2 Tipos de matrices
Existen varios tipos de matrices de acuerdo a su forma y a su contenido. Por ejemplo, la matriz M = [3 2 1 2 4 1], se conoce como matriz fila, por su forma. Otros tipos de matrices las puedes reconocer fácilmente, seleccionando algunas de las opciones que se presentan en el siguiente interactivo. Cuando aparezca el botón "Otro ejemplo", puedes hacer clic varias veces, para observar varias matrices.
76
6.3 Suma de matrices
La suma de matrices la podemos definir así: S = A + B = (aij)+(bij)=(aij + bij)=(sij), donde S, A y B son un matrices de la misma dimensión mxn, similarmente se define la sustracción de matrices: A - B. Practica con el interactivo la suma de matrices.
77
Ejercicio
En este ejercicio practicaremos la suma de matrices a través de colores. El propósito es recordar el procedimiento de la suma.
La suma de A y B da como resultado otra matriz de colores. Recuerda que dos colores iguales dan el mismo color, para colores diferentes, ten en cuenta:
Amarillo + azul = verde, rojo + amarillo = naranja, rojo + blanco = rosa, azul + blanco = turquesa, rojo + azul = magenta y blanco + amarillo = amarillo claro
78
6.4 Producto de un escalar por una matriz
Una matriz se puede multiplicar por un número real llamado escalar. Para ello, se realiza el procedimiento indicado a continuación:
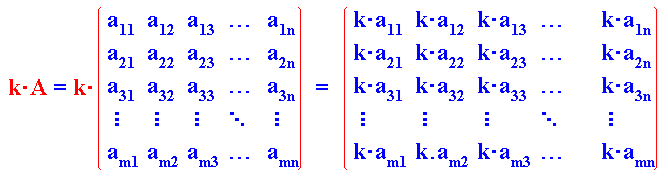
Haz clic en el botón "Multiplicar", para obtener el producto escalar inidcado en la segunda matriz:
79
Ejercicio
En este ejercicio practicaremos la suma de matrices y el producto de un escalar por una matriz. Realiza las operaciones en tu cuaderno y luego haz clic en "Verificar".
Observa que las matrices tienen un contenedor diferente al que veníamos usando (paréntesis en lugar de corchetes), esta representación es usual en algunos textos de métodos numéricos.
80
6.5 Multiplicación de matrices
Es importante que el número de columnas de la primera matriz sea igual al número de filas de la segunda. Observa el procedimiento en matrices cuadradas de orden 3:
El producto de matrices tiene las siguientes propiedades:
A·B ≠ B·A No es conmutativa
(A·B)·C = A·(B·C) Es asociativa
A·I = I·A = A Es modulativa
A·A-1 = A-1·A = I Donde I es la matriz identidad. Aplica sólo si A tiene inversa
81
6.6 Matriz transpuesta
La matriz traspuesta se utiliza con frecuencia en las operaciones entre matrices. Los elementos aij de una matriz A, se cambian por aji y se obtiene la transpuesta de A.
La matriz transpuesta es una de las operaciones más fáciles de realizar, basta con intercambiar las filas por las columnas y las columnas por las filas. Pruébalo con la siguiente escena:
82
La matriz transpuesta permite identificar algunas propiedades de las matrices cuadradas, por ejemplo, si AT = A, significa que A es simétrica, o si A·AT = I, se dice que A es ortogonal. Una característica especial, es que al multiplicar la matriz A por su transpuesta, se obtiene una matriz simétrica.
Verifica la última propiedad con la siguiente escena, trata, además, de realizar manualmente las multiplicaciones y luego haces clic en el botón "Multiplicar", para que verifiques tu respuesta:
83
6.7 Determinante de una matriz
El determinante de una matriz cuadrada A es un número real asignado a ella. Si A es una matriz de orden n, su determinante lo denotaremos por det(A) o también por |A| (no confundir con el valor absoluto). En la escena interactiva se explica, paso a paso, el cálculo del determinante de matrices de orden 2, 3 y 4. El método utilizado se conoce como el desarrollo por cofactores de primera fila. Para ello, se toma la primera fila, multiplicando cada elemento a1i por su cofactor
84
Cálculo matricial con GeoGebra
GeoGebra permite incorporar una ventana para el cálculo simbólico (CAS), que es el que se observa al lado derecho. Puedes analizar algunos cálculos realizados, así: 1. Ingreso de una matriz A de orden 3x3. Observa que se ingresan cada una de las filas agrupadas entre llaves. Practica con el CAS, escribe una sexta instrucción, así: C:=A-3AT o cambia los términos de la matriz A por los de algún ejemplo anterior. |
85
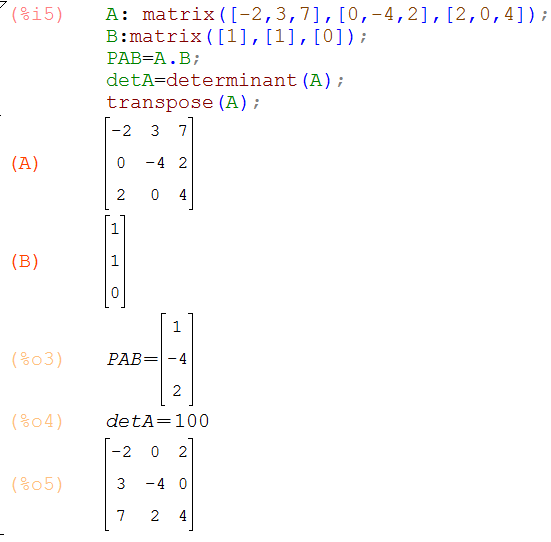
Cálculo matricial con wxMaxima
La sintaxis en Maxima es muy similar a la de GeoGebra, tal como se observa en la imagen, con algunas diferencias, tales como: Maxima exige el uso del punto (.) para el cálculo de productos de matrices, los comándos transpuesta y determinante están en inglés. Observa, además, que GeoGebra usa paréntesis para representar una matriz, mientras que Maxima usa corchetes.
86
7. Resolución por métodos directos
En el conjunto de ecuaciones que hemos llamado sistema lineal de n x n, y representado por AX = B, si la matriz cuadrada de coeficientes A es no singular, es decir, su determinante es no nulo, el sistema tiene una solución única. En este capítulo estudiaremos algunos métodos directos que permiten obtener el vector solución del sistema.
7.1 Sistemas lineales triangulares
En el apartado 6.2 vimos algunos tipos de matrices, entre ellas las matrices triangulares. En general, podemos decir que una matriz A = [aij] de orden nxn es triangular superior cuando sus elementos aij = 0 para todo i > j. Análogamente, una matriz A = [aij] de orden NxN es triangular inferior cuando sus elementos aij = 0 para todo i < j. Observa, en el interactivo, ejemplos de matrices triangulares superiores.
87
Cuando un sistema lineal presenta una matriz de coeficientes de la forma triangular superior, la solución del sistema es inmediata, usando una sustitución regresiva. En el siguiente interactivo puedes generar varios ejemplos de un sistema 4x4, observa lo directa que es su solución. En el siguiente apartado, obtener un sistema triangular es el principal objetivo del método de solución directa.
88
7.2 Método de eliminación de Gauss simple
Sea un sistema AX = B donde A es una matriz cuadrada de orden nxn con | A |≠ 0, el método de Gauss consiste en llevar el sistema a una forma triangular superior, lo que permite realizar la sustitución regresiva que explicamos en el apartado anterior.
Existen tres operaciones elementales de filas que se aplican en el método: intercambiar dos filas entre sí (por ejemplo la fila 3 por la fila 6), multiplicar una fila por un escalar (por ejemplo multiplicar todos los elementos de la fila 2 por el número α, siendo α ≠ 0) y añadir a una fila otra diferente multiplicada por un número cualquiera (por ejemplo sumar a la fila 3 la 5 multiplicada por un escalar β). Se puede demostrar que estas operaciones generan un sistema equivalente, la primera, por ejemplo consiste en cambiar el orden de las ecuaciones, las otras dos son operaciones aritméticas realizadas miembro a miembro en una ecuación.
El procedimiento gaussiano inicia con una matriz ampliada de orden nx(n+1) obtenida al añadir una columna con los elementos del vector B. Luego, realizamos las operaciones elementales de filas para ir obteniendo los sistemas equivalentes: A(1)X = B(1),...,A(k)X = B(k) (k = 1,2,...,n), donde A(k) tiene nulos los elementos por debajo de la diagonal en las k −1 primeras columnas, de esta forma obtendremos en n−1 pasos un sistema A(n)X = B(n) donde A(n) es una matriz triangular superior, que se resolvería por sustitución regresiva.
En la escena interactiva de la siguiente página podrás observar, paso a paso, ejemplos con un sistema 4x4.
89
En la escena de Descartes se puede observar que se elige un elemento de la diagonal principal de la matriz A el cual se llama pivote, pero al figurar en el denominador puede generar errores de división por cero, es recomendable, en estos casos, recurrir a otro pivote ubicado en otra fila y realizar el intercambio de filas (pivote parcial). En la siguiente escena de GeoGebra, prueba cambiando a11 por cero.
Haz clic para ampliar la escena
91
Programación del método de Gauss en wxMaxima
| En estas dos páginas presentamos el código para el método de eliminación de Gauss. Un primer bloque son las declaraciones, en el que se ingresan la matriz de coeficientes A y los vectores B y X, igualmente, hemos declarado el vector X0 en forma simbólica para la presentación de resultados. |
 |
92
El cálculo de la matriz triangular superior, se obtiene con las siguientes instrucciones:

Finalmente, la sustitución regresiva se obtiene con estas instrucciones:

Haz clic en la imagen para descargar el archivo wxMaxima.
93
7.3 Método de Gauss con pivoteo parcial
Cuando un elemento pivote es cero se presentan problemas, pues se origina una división entre cero, igual ocurre cuando el pivote es cercano a cero que pueden introducir errores de redondeo. En el siguiente interactivo haz clic en el botón Triangularizar, luego intenta con el botón Pivote cero y observa los mensajes de error que se presentan.
94
Para evitar el problema de pivote cero, se determina el coeficiente mayor en valor absoluto disponible en la columna debajo del pivote, luego se intercambian las filas de manera que el elemento más grande sea el elemento pivote; este procedimiento se llama pivoteo parcial. Existe otro procedimiento llamado pivoteo total, donde tanto en las columnas como en las filas se busca el elemento más grande y luego se intercambian, pero no es muy utilizado por la complejidad inducida. En la escena interactiva, observa que el primer pivote A(1,1) es cero, toma nota de la fila donde está el coeficiente más grande, luego haz clic en el botón de Triangularizar con pivoteo, observarás que la fila del nuevo pivote es intercambiada a la primera fila.
95
7.4 Método de Gauss-Jordan
Este método es una extensión del método anterior. "La principal diferencia consiste en que cuando una incógnita se elimina en el método de Gauss-Jordan, ésta es eliminada de todas las otras ecuaciones, no sólo de las subsecuentes. Además, todos los renglones se normalizan al dividirlos entre su elemento pivote. De esta forma, el paso de eliminación genera una matriz identidad en vez de una triangular" (Chapra & Canale, 2007, pág. 277
Haz clic para ampliar la escena
96
7.5 Factorización LU de Doolittle
La eliminación gaussiana es la principal herramienta en la solución directa de los sistemas de ecuaciones lineales, no debe sorprendernos que aparezca en otras formas. En la presente sección veremos que los pasos que se siguen para resolver un sistema de la forma AX = B, también pueden servir para factorizar una matriz en un producto matricial. La factorización es muy útil cuando presenta la forma A = LU, donde L es triangular inferior y U es triangular superior. No todas las matrices pueden factorizarse de ese modo, pero es posible hacerlo con un gran número de las que se presentan con frecuencia en las aplicaciones.
Los métodos de factorización LU permiten obtener una matriz equivalente a A para evaluarla con los múltiples vectores del lado derecho B, por ejemplo, en el cálculo de estructuras se suele usar una matriz de rigidez K que depende de las dimensiones y propiedades de los elementos de la edificación, el análisis estructural se realiza con múltiples vectores F que corresponden a las fuerzas externas a las que se somete la estructura.
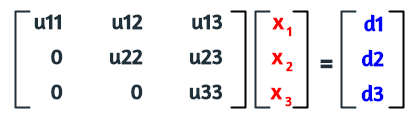
A continuación presentamos una explicación basada en un sistema de tres ecuaciones con tres incognitas. La ecuación AX = B, la podemos expresar como: AX - B = 0. Ahora, supongamos que puede expresar como un sistema triangular superior:
97
El sistema anterior lo podemos expresar en notación matricial, así: UX - D = 0. Ahora, supongamos que existe una matriz diagonal inferior L con la diagonal compuesta de elementos de valor uno:

Se puede demostrar la siguiente igualdad: L(UX - D) = AX - B, lo que nos permite concluir que:
LU = A (Véase la escena de la siguiente página)
LD = B
Para resolver el sistema, se siguen los siguientes pasos:
a) Factorización LU. Se descompone A en las matrices L y U. Donde L, como se dijo antes, es una matriz triangular inferior con los elementos de la diagonal iguales a uno (1), y U es una matriz triangular superior que se obtiene después de la eliminación hacia adelante.
b) Determinación del vector D mediante una sustitución hacia adelante.
c) Determinación del vector X por sustitución regresiva.
98
En la siguiente escena de Descartes puedes observar los pasos anteriormente descritos. Hemos usado el método de factorización que incluye, si es necesario, el pivoteo. Es importante aclarar que si se presenta la necesidad de intercambiar filas (pivoteo), la expresión correcta en la factorización es LU = PA, donde P es una matriz de permutación que se obtiene intercambiando las mismas filas del pivoteo en una matriz identidad.
99
Factorización LU de Doolittle con wxMaxima
Presentamos el algoritmo en wxMaxima para hallar las matrices L y U. Usamos las ecuaciones del primer ejemplo de la escena de Descartes, para efectos de comparación.

Los resultados obtenidos son los siguientes:

100
7.6 Factorización LU de Cholesky
En algunas situaciones problema de la ingeniería, es común encontrar sistemas de ecuaciones cuya matriz de coeficientes es simétrica, es decir, aij = aji para todo ij. Esta propiedad ofrece ventajas para los cálculos computacionales, pues se requeriría la mitad del tiempo para hallar la solución del sistema. Este método de solución directa se fundamenta en un teorema formulado por el matemático André-Louis Cholesky, el cual expresa: "Si A es una mariz simétrica y positiva, entonces existe otra matriz triangular inferior L, invertible, tal que: L LT = A".
En la escena de Descartes de la siguiente página, podrás observar los pasos que conducen a la solución del sistema, usando el método de Cholesky. En la imagen se indican las instrucciones para calcular las matrices L y U de Cholesky en wxMaxima.

101
Método de Cholesky en Descartes
En la siguiente escena se explica, paso a paso, la solución de un sistema lineal con el método de Cholesky. El primer ejercicio presenta una matriz simétrica igual al de la imagen anterior de wxMaxima.
102
7.7 Matriz inversa
Si una matriz A es cuadrada con determinante no nulo, existe otra matriz A–1, conocida como la inversa de A, para la cual se cumple que: AA–1 = A–1A = I. En este apartado explicaremos cómo calcular esta matriz por varios métodos.
Matriz inversa desde la factorización LU
103
Matriz inversa desde la matriz adjunta
Al dividir la matriz adjunta (Adj[A]) de una matriz cuadrada A entre su determinante, se obtiene la matriz inversa.
Es importante aclarar que en los textos de Álgebra Lineal existen dos versiones para calcular la martiz adjunta. La primera versión corresponde a la matriz de cofactores traspuesta; la segunda, se corresponde a la matriz de cofactores. En este libro usaremos la primera versión, más utilizada en los libros clásicos de Álgebra Lineal. En la siguiente escena de Descartes, puedes observar la explicación de esta primera versión.
104
En el siguiente video se muestra, a través de un ejemplo, cómo calcular la matriz adjunta. Es importante que prestes atención al significado de las matrices de menores, cofactores y adjunta que, como advertimos, estas dos últimas no son iguales, tal como se considera en otros textos. La comprensión de estos términos es fundamental para calcular la matriz inversa.
Haz clic para ampliar el vídeo
105
En la siguiente escena puedes observar, paso a paso, el cálculo de la matriz inversa de una matriz A de orden 3. Obviamente, el procedimiento para ecuaciones lineales de grandes dimensiones requiere del diseño de un algoritmo más complejo y la formulación de diferentes modelos, como son los métodos iterativos.
Observa que inicialmente se calcula el determinante de la matriz, pues de ser cero no sería posible calcular la inversa.
106
Matriz inversa con GeoGebra
La siguiente escena, diseñada por José M. Melián, permite calcular la matriz adjunta e inversa de matrices de orden 2, 3 o 4. Observa que la matriz adjunta definida por Melián, corresponde a la segunda versión, es decir, es igual a la matriz de cofactores.
107
7.8 Solución del sistema con la matriz inversa
Con lo aprendido hasta aquí, puedes encontrar los valores de las incógnitas que satisfacen las ecuaciones cuando el sistema es compatible y determinado (o cuando la solución existe y es única). En la escena de abajo, tenemos un sistema de 3x3 (tres ecuaciones y tres incógnitas). Haz clic en el botón para que observes varios ejemplos.
108
Solución con GeoGebra
La siguiente escena, diseñada a partir de una propuesta de Edgar Arana, permite calcular la solución de un sistema de ecuaciones 3x3. Puedes cambiar los valores de la matriz A y del vector B.
109
Resolución del sistema con wxMaxima
En estas dos páginas presentamos el código para la solución de un sistema de ecuaciones lineales usando la matriz inversa. Hemos incluido la matriz adjunta para efectos de comparación con las escenas anteriores, igualmente, se incluye la matriz inversa calculada por el método de la adjunta y por el método de factorización LU. En la página siguiente se muestran los resultados de un ejemplo de un sistema de 3x3. No obstante, es posible modificar el archivo para sistemas de un orden mayor.

110
Observa que Maxima calcula la matriz adjunta de acuerdo a la primera versión, es decir, como la transpuesta de la matriz de cofactores. Para este sistema, no se observan cambios en la matriz inversa calculada por el método de la matriz adjunta, con respecto a la calculada por el método de factorización LU.

111
Ejercicio
Para el ejercicio puedes usar GeoGebra, wxMaxima, una hoja de cálculo como Excel o en forma manual con tu calculadora.
Haz clic para ampliar el vídeo
112
8. Resolución por métodos iterativos
Los métodos iterativos rara vez se usan para resolver sistemas lineales de pequeña dimensión, ya que el tiempo necesario para conseguir una exactitud satisfactoria rebasa el que requieren los métodos directos como el de la eliminación gaussiana. El método iterativo comienza con una aproximación inicial a la solución x. Con este primer vector solución se puede calcular un nuevo vector modificado de la solución. Al repetir estas operaciones muchas veces, se obtiene, si el proceso es convergente, una aproximación cada vez mejor de la solución. Una condición suficiente para que este método sea aplicable es que el sistema lineal sea diagonal estrictamente dominante, es decir, cuando

El método iterativo para resolver un sistema lineal Ax = B sigue el siguiente procedimiento: comienza por una aproximación inicial x(0) de la solución x. Luego, se convierte el sistema Ax = B en otro de la forma x = Mx + N (para convertirlo basta despejar cada xi). A partir de la solución inicial, se genera una sucesión de soluciones
x(k) = Mx(k-1) + N
con k = 1, 2, 3, ..., garantizando que la sucesión x(k) converja a la solución del sistema. A continuación, explicaremos dos métodos iterativos muy utilizados en la solución de sistemas de ecuaciones lineales.
113
8.1 Método de Jacobi
Este método parte de la descomposición de la matriz A en la suma de tres matrices A = L + D + U, donde D es diagonal, L triangular inferior y U triangular superior, formadas con los elementos respectivos de A. Así las cosas, en el método de Jacobi:
M = D y N = L + U
Reemplazando en el sistema Ax = B,
Dx(k+1) = -(L + U)x(k) + B
Cuyos componentes se calculan, así:
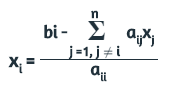
Veamos un ejemplo sencillo con el siguiente sistema:
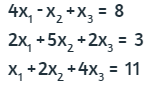
Al cual le hacemos los siguientes despejes de variables:
114
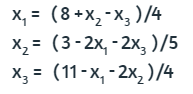
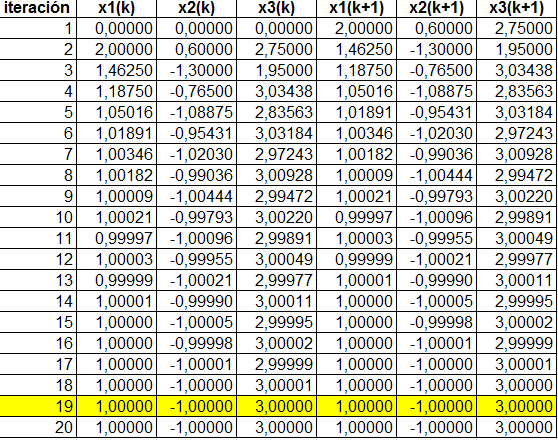
Si suponemos, para k=1, x1 = 0, x2 = 0 y x3 = 0, al reemplazar en las ecuaciones anteriores, obtendríamos, para k=2, x1 = 2, x2 = 0.6 y x3 = 2.75. Si repetimos el proceso con estos nuevos valores, obtendríamos: x1 = 1.4625, x2 = -1.3 y x3 = 1.95. Hemos realizado este proceso 20 veces en una tabla de Excel, obteniendo una convergencia en la iteración 19:
115
En la siguiente escena interactiva de Descartes hemos dejado como primer ejercicio el calculado en Excel, la convergencia se halla en la iteración 12 porque la aproximación utilizada es de tres cifras decimales.
Haz clic para ampliar la escena
116
Método de Jacobi con GeoGebra
Usa el deslizador para verificar si la solución converge, puedes observar varios ejemplos haciendo clic en el botón.
Haz clic para ampliar la escena
117
Método de Jacobi con wxMaxima
En este algoritmo hemos usado el mismo sistema de ecuaciones para efectos de comparación con los resultados obtenidos en Descartes y Excel. Adrede, no hemos cerrado el bloque de instrucciones del bloque jacobi(A,B,n) con el signo $, con el fin de observar en los resultados la expresión general de Jacobi, para ello, hemos invocado el comando sum(), el cual puedes cambiar o reprogramar con un bucle tipo for, en el caso de usar este algoritmo en otra herramienta de programación.

118
La primera salida en wxMaxima es el bloque jacobi(A,B,n), en el cual se aprecian las fórmulas empleadas:

La segunda salida muestra los resultados de las iteraciones, usamos cinco decimales para comparar con los resultados de Excel que, igualmente, presenta solución en la iteración 19.

119
8.1 Método de Gauss-Seidel
Este método es muy semejante al método de Jacobi, pero con una convergencia (si la hay) en menos iteraciones. Recuerda que en Jacobi usamos el valor de las incógnitas calculadas para determinar una nueva aproximación, en el de Gauss-Seidel se van utilizando los valores de las incógnitas recien calculados en la misma iteración, y no en la siguiente. Observa, con un ejemplo, el procedimiento empleado:
Sea el siguiente sistema de ecuaciones:
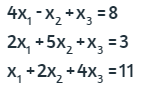
Despejamos la incognita sobre la diagonal, para cada ecuación:
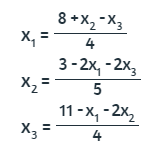
Suponiendo la primera aproximación con x2 = 0 y x3 = 0, obtenemos:
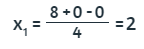
120
Este valor obtenido y con x2 = 0, se sustituye en la segunda ecuación:
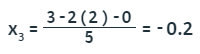
Los valores de x1 y x2 obtenidos hasta aquí, se sustituyen en la tercera ecuación:
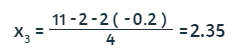
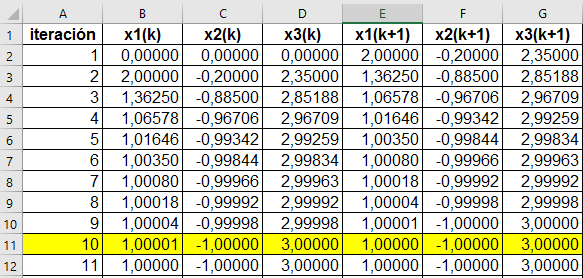
Luego se repite el proceso hasta encontrar la solución. Observa que en Excel, para cinco decimales de tolerancia, sólo se requieren diez iteraciones:
121
En la siguiente escena interactiva de Descartes hemos dejado como primer ejercicio el calculado en Excel, la convergencia se halla en la iteración siete porque la aproximación utilizada es de tres cifras decimales.
Haz clic para ampliar la escena
122
Método de Gauss-Seidel con GeoGebra
Usa el deslizador para verificar si la solución converge (escena diseñada por sridharkrn).
Haz clic para ampliar la escena
123
Método de Gauss-Seidel con wxMaxima
En este algoritmo hemos usado el mismo sistema de ecuaciones para efectos de comparación con los resultados obtenidos en Descartes y Excel. Descarga el archivo y ejecuta el algoritmo.

124
parte iv
INTERPOLACIÓN POLINÓMICA Y AJUSTE DE CURVAS
Elena E. Álvarez Sáiz
José R. Galo Sánchez
Juan Guillermo Rivera Berrío
Introducción
La interpolación se usa para obtener el valor de una función en un punto cuando no se conoce dicha función o, en algunos casos, cuando la función es difícil de evaluar. En otras palabras, si tenemos un conjunto de datos previamente validados, el problema de la interpolación consiste en hallar una función válida para esos datos y fácil de evaluar para el punto que origina el problema. En ingeniería y en algunas ciencias de base empírica es común obtener, por experimentación, un número de puntos que dan respuesta al comportamiento del fenómeno estudiado, a partir de estos datos se procede a construir una función llamada interpolante que los ajuste.
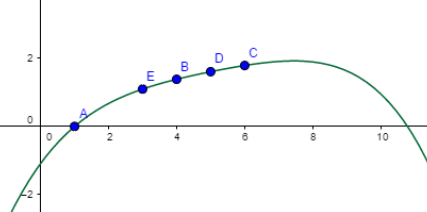
Se trata, entonces, a partir de un conjunto de puntos o nodos (xi,yi), obtener una función f que valide f(xi) = yi, con i = 1, ..., n. Algunas funciones interpolantes se obtienen por interpolación lineal, por interpolación polinómica de Newton o Lagrange (como el caso de la imagen), la interpolación por medio de splines (a trozos) o la interpolación polinómica de Hermite.
128
Existen leyes físicas que determinan que la magnitud entre ciertas variables dependen de ciertos parámetros que se obtienen de forma experimental. Observa los dos vídeos siguientes que muestran ejemplos de fenómenos físicos a los que hay que ajustar alguna función que describa su comportamiento, es decir, una función que de respuesta a la pregunta final en cada vídeo
Haz clic para ampliar la escena
129
9. Polinomios interpolantes
La estimación de valores intermedios entre datos definidos por puntos, se puede lograr con una interpolación polinomial, teniendo en cuenta que la fórmula general para un polinomio de n-ésimo grado es
f(x) = a0 + a1x + a2x2 + ··· + anxn
Si tenemos n + 1 puntos, podemos hallar un polinomio de grado n que contiene esos puntos. Para dos puntos, por ejemplo, la interpolación será lineal (polinomio de primer grado); para tres puntos será una interpolación cuadrática, pues una parábola los une. En este apartado veremos algunos métodos de interpolación polinómica.
9.1 Método de Newton - Diferencias divididas
El polinomio de interpolación de Newton en diferencias divididas, en general, se puede representar por la siguiente expresión (Véase Chapra y Canale, pág 506):
fn(x) = b0 + b1(x - x0) + b2(x - x0)(x - x1)+ ··· + bn(x - x0)(x - x1)···(x - xn)
Para el caso de una interpolación cuadrática f2(x) = b0 + b1(x - x0) + b2(x - x0)(x - x1), que al multiplicar los términos y agrupar términos semejantes, podemos hallar los coeficientes del polinomio, así:
a0 = b0 – b1x0 + b2x0x1
a1 = b1 – b2x0 – b2x1
a2 = b2
130
Ahora, si en f2(x) evaluamos con x = x0, obtenemos:
b0 = f(x0)
Para x = x1:
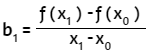
Finalmente, para x = x2:
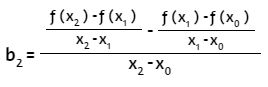
El último término determina el grado del polinomio. Para un polinomio de grado n-ésimo el análisis se puede generalizar, así:
b0 = f(x0)
b1 = f[x1, x0]
b2 = f[x2, x1, x0]
.
.
.
bn = f[xn, xn-1,···, x0]
Al símbolo f[xn, xn-1,···, x0] se le llama diferencia dividida de f
131
La primera diferencia dividida finita, en forma general, se puede representar así:
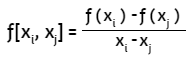
La segunda diferencia dividida finita representa la diferencia de las dos primeras diferencias divididas:
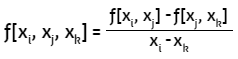
La n-ésima diferencia dividida finita es:
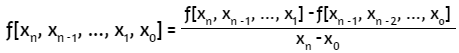
Con estas diferencias divididas obtenemos el polinomio de interpolación de Newton en diferencias divididas:
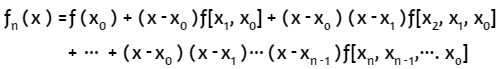
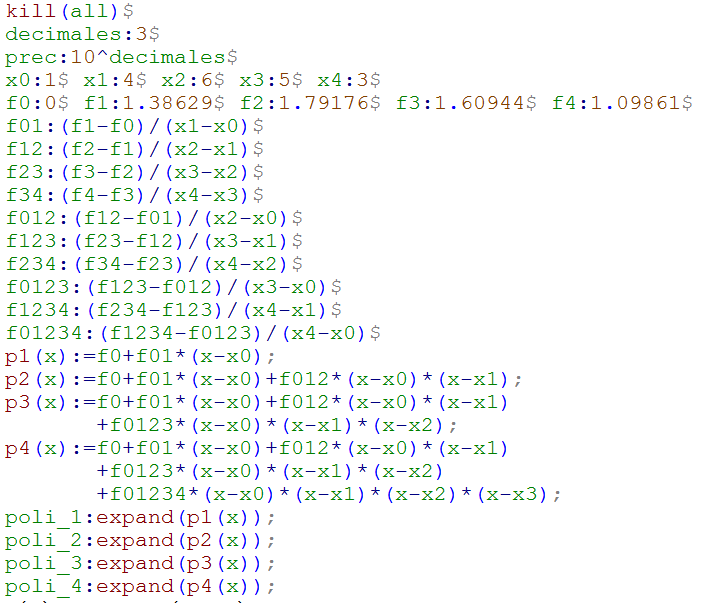
En la página siguiente, hemos diseñado un algoritmo para la determinación de los polinomios de interpolación de grado uno hasta el cuatro en wxMaxima, utilizando datos de la función logaritmo natural. Las diferencias divididas las hemos representado como f012···n, por ejemplo:
f012 = f[x2, x1, x0]. Luego, en Descartes, usamos el mismo algoritmo, permitiendo, además, ingresar un dato a interpolar.
132
Polinomio interpolante de Newton en Descartes
En la siguiente escena puedes observar polinomios desde el grado uno hasta el siete. La función es el logaritmo natural, practica con un valor a interpolar (dos, por ejemplo) y observa que la mejor aproximación es en el polinomio de grado cinco.
134
En la escena anterior se muestra la ecuación del polinomio en el formato general f(x) = a0 + a1x + a2x2 + ··· + anxn. Sin embargo, es posible usar otro algoritmo que permita mostrar los coeficientes del polinomio de Newton (b0, b1, ···, bn), para ello, hemos usado el algoritmo de Chapra y Canale (pág 513):
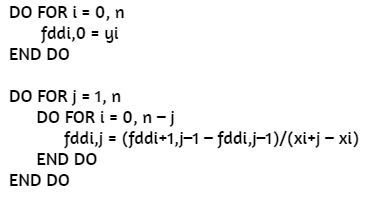
En este algoritmo se hace uso de una matriz fdd, en la cual se almacenan, además de los valores de la función (columna 0), los coeficientes del polinomio interpolante de Newton (fila 0). Por ejemplo, para los datos de la escena y el polinomio de orden 1:

De la fila 1, concluimos: b0 = 0 y b1 = 0.4621, por lo tanto: p(x) = .4621(x-1). Si se desea usar la forma general:
a0 = b1 – b1x0 = 0 - 0.4621*1 = -0.4621
a1 = b1 = 0.4621
p(x) = -0.4621 + 0.4621x
135
Para el polinomio de orden 2, la matriz obtenida es:

De la fila 1, concluimos: b0 = 0, b1 = 0.4621 y b2 = -0.0519 por lo tanto:
p(x) = .4621(x-1) - 0.0519(x-1)(x-4).
En la escena de la siguiente página hemos usado el algoritmo para calcular los coeficientes del polinomio interpolante de Newton (b0, b1, ···, bn) y, en consecuencia, muestra el polinomio por diferencias divididas. Por la extensión del polinomio, sólo mostramos hasta el grado tres.
Se incluyen cuatro ejemplos adicionales. El primero corresponde a los datos de la función f(x) = ln x, que hemos venido trabajando; en el último, con una serie de datos experimentales, podrás notar que los polinomios de orden 1 y 2 son lineales.
¿Qué concluyes con el polinomio de orden 3?
136
137
Polinomios de interpolación con GeoGebra
GeoGebra ofrece el comando Polinomio[ Lista de Puntos ], el cual crea la interpolación polinomial de grado n-1 a través de los n puntos listados. La documentación ofrecida por GeoGebra no explica el método utilizado para calcular el polinomio.
Hemos diseñado una escena utilizando este comando (observa la página siguiente), con los datos de la función f(x) = ln x, los cuales puedes cambiar en la hoja de cálculo de la derecha. Para interactuar con la escena, se han habilitado la barra de entrada y el clic derecho, de tal forma que puedas:
1. Incluir un punto a interpolar, para ello, escribe el valor en la celda A9 de la hoja de cálculo, y en la celda B9: +g(A9), en el caso del polinomio de orden 1, o +h(A9) para el polinomio de orden 2, y así sucesivamente.
2. Selecciona las dos celdas y haz clic derecho, luego escoge la opción Crea Lista de puntos, para que se muestre en la gráfica.
3. En la casilla de entrada, puedes crear más polinomios con el comando polinomio[{A,B,C,D,E,...}].
4. Puedes ampliar el ancho de la hoja de cálculo y con clic derecho abrir la ventana de propiedades para modificar colores, tamaños, etcétera, hazlo, preferiblemente con la escena ampliada. Ahora, si tienes instalado el software de GeoGebra, puedes abrir esta escena desde la carpeta interactivos y el archivo geogebra13.html.
138
Usa el deslizador para aumentar o disminuir el grado del polinomio.
Haz clic para ampliar la escena
139
9.2 Polinomios de interpolación de Lagrange
El polinomio de interpolación de Lagrange es una variante del polinomio de Newton, cuya representación es (Véase Chapra y Canale, pág 516):
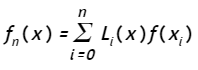
en la cual
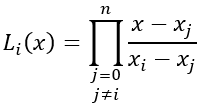
Para el polinomio de primer orden:
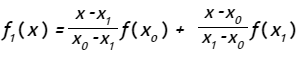
Para el polinomio de segundo orden:
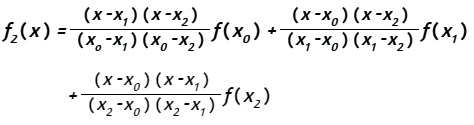
140
Polinomio interpolante de Lagrange en wxMaxima
El siguiente algoritmo fue diseñado por Aureliano M. Robles Pérez, profesor de la Universidad de Granadahttp://www.ugr.es/~arobles/CalInf/Ssn8-1011-v2.pdf:

Observa la sencillez del algoritmo, en el cual Li(x) se corresponde con l(i,x), y f(xi) con yy[i]. La salida de la instrucción pol1(x) := sum(yy[i]*l(i,x),i,1,n);, sería:
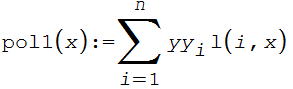
141
La salida de la instrucción pol1(x);,es el polinomio interpolante de Lagrange::
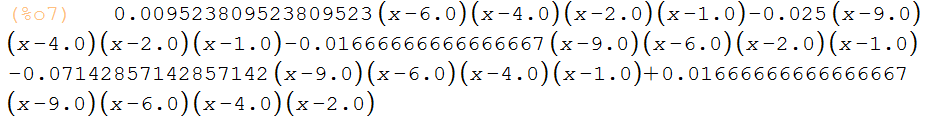
que en forma expandida, sería:

Para los datos dados en el algoritmo, la gráfica del polinomio que muestra wxMaxima es:
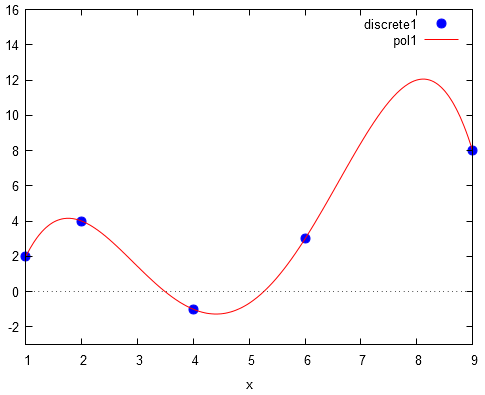
142
Polinomio interpolante de Lagrange en Descartes
En la siguiente escena puedes observar polinomios desde el grado uno hasta el cinco. El primer ejemplo corresponde al presentado en wxMaxima, para efectos de comparación. Observa que para el orden 4, la ecuación del polinomio es igual (salvando los redondeos) a la obtenida con wxMaxima.
143
9.3 Interpolación iterada de Neville
El método de Neville se suele usar cuando nos interesa obtener únicamente el valor numérico en un punto dado. Este método interpola un valor dado con polinomios que crecen hasta que los valores estén suficientemente cercanos, lo que nos permite, por inspección, estimar el valor que presente menor variación.
Tomando la notación de Mora (2013, pág. 36
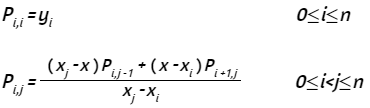
La matriz P es triangular superior, en la cual la diagonal principal contiene los valores de yi, la columna 0 el polinomio P0 (P0,1, P0,1,2, ...), la columna 1 los polinomios P1, ···, la columna 4 los polinomios P4.
Hemos diseñado una escena interactiva de Descartes que muestra la matriz P, en color azul los términos yi y en rojo la mejor aproximación que, en la mayoría de los casos, corresponde a P0,4 o, en la notación de Mora, P0,1,2,3,4. Cuando n es igual a cuatro, mostrará el valor interpolado P(x) calculado por método de Neville y por Lagrange (L(x)). El último ejemplo corresponde a una ecuación cuadrática que se desarrolla con GeoGebra en la siguiente escena interactiva.
144
Método de Neville en Descartes
145
9.4 Funciones splines - suavizando curvas
Las funciones splines o trazadores son funciones construídas a trozos por varios polinomios, que se unen entre sí con ciertas condiciones de continuidad. Recurrir a los splines mejora los resultados de algunas funciones de mayor complejidad, que pueden presentar grandes oscilaciones. En este apartado sólo nos ocuparemos de los splines cúbicos, es decir, la función a trozos estará compuesta de polinomios cúbicos.
La explicación la tomamos del texto de Mora (2013, pág. 52
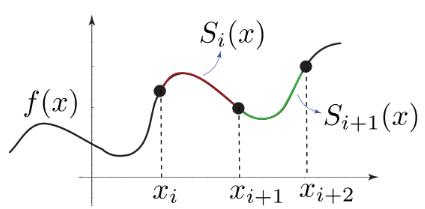
La expresión matemática del trazador cúbico S la definimos a continuación.
147
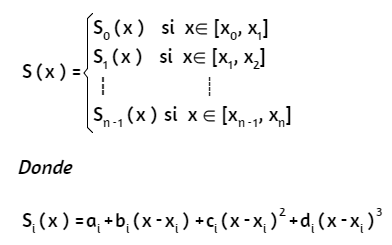
Los polinomios Si−1 y Si interpolan el mismo valor en el punto xi, es decir, se cumple:
Si-1(xi) = yi = Si(xi), para (1 ≤ i ≤ n-1), que garantiza la continuidad de f en todo el intervalo. Suponiendo, además, que S' y S" son continuas, es posible deducir una expresión como:
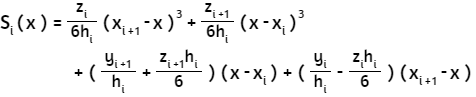
En la cual hi = xi+1 - xi y z0, z1, ···, zn es un vector de incognitas que se debe resolver con alguno de los métodos de resolución de sistemas de ecuaciones lineales. No obstante, Mora presenta el siguiente algoritmo, que permite calcular los coeficientes ai, bi, ci y di de la función splin antes definida.
148
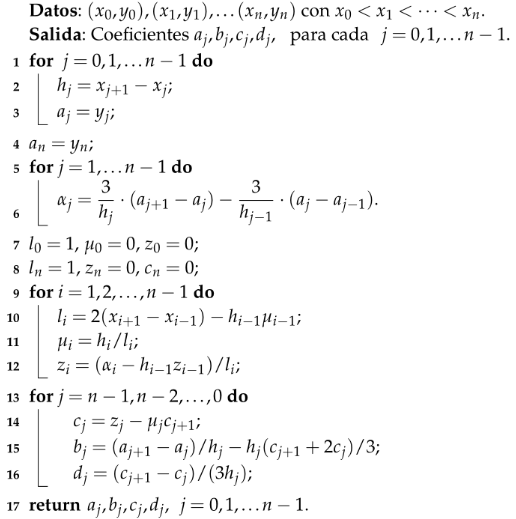
Utilizando este algoritmo, hemos diseñado la siguiente escena interactiva de Descartes, en la cual se puede observar la utilidad de los trazadores cúbicos frente a polinomios interpolantes como el de Lagrange. Observa con atención el primer y último ejemplo, pues en algunos puntos los splines suavizan la curva, permitiendo una mejor aproximación. Por contraste, en los ejemplos dos y tres, el polinomio de Lagrange es la mejor opción.
149
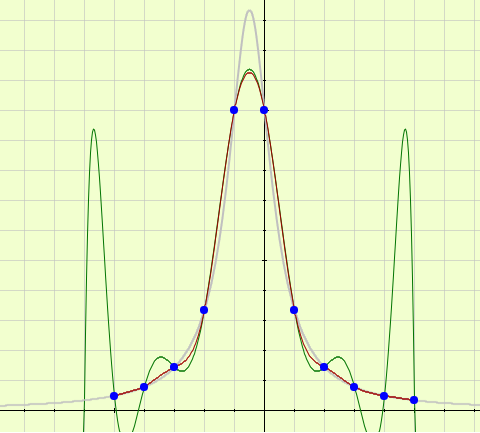
Imagen del primer ejemplo. Observa las oscilaciones de Lagrange (color verde) en los puntos extremos (haz clic sobre la imagen).
Imagen del cuarto ejemplo. Grandes oscilaciones de Lagrange (color verde) en los últimos nodos (haz clic sobre la imagen).
150
Splines cúbicos en Descartes
151
Splines cúbicos en GeoGebra
GeoGebra ofrece un comando para calcular una función splin, dada una nube de puntos; sin embargo, no se sabe qué tipo de trazador o qué método es el que se usa para construirlo, sólo se tiene la siguiente información: "Crea una spline que pase por todos los puntos". Hemos creado una escena con los 10 puntos del primer ejemplo de la escena anterior y usado el comando spline[{A,B,C,D,E,F,G,H,I,L}]. Observa el resultado y concluye (puedes mover los puntos).
152
Splines cúbicos en wxMaxima
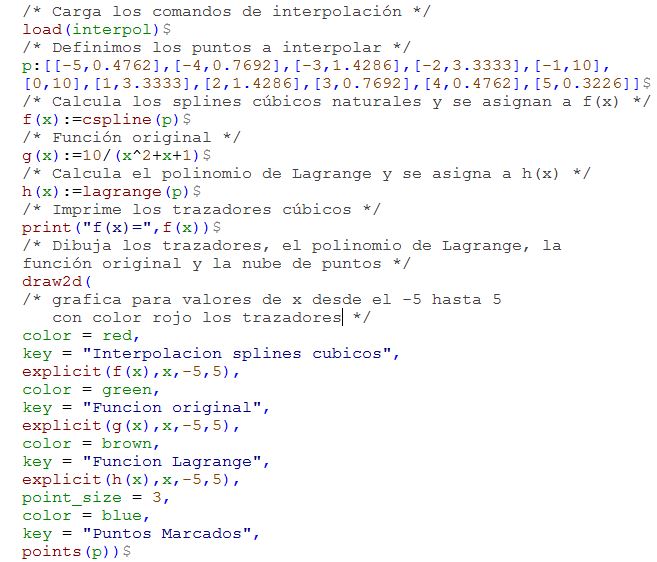
wxMaxima ofrece un paquete de comandos de interpolación, el cual se carga con la instrucción load(interpol). Podemos calcular los splines cúbicos con el comando spline(p), donde p es la matriz donde se almacenan los puntos. En la siguiente imagen observarás las instrucciones para este cálculo (haz clic en la imagen para agrandarla).
153
Tres de los splines calculados son los siguientes:
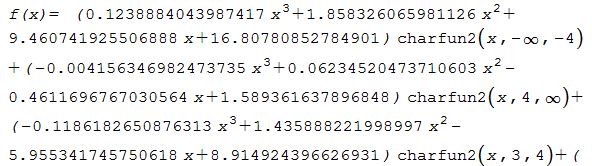
La gráfica muestra los splines, la función original y, para comparar, el polinomio interpolante de Lagrange. Observa las oscilaciones presentadas en este último (haz clic en la imagen para agrandarla).
154
9.5 Ajuste de curvas por mínimos cuadrados
Observa, como introducción, el vídeo de Mª Purificación Galindo Villardón y Purificación Vicente Galindo, que explica el modelo de regresión lineal basado en los mínimos cuadrados (Consulta la unidad Elementos de estadística).
Haz clic para ampliar el vídeo
155
Un resumen del vídeo anterior lo puedes observar en esta presentación:
En la página siguiente, puedes interactuar con una escena diseñada por José Luis Abreu.
156
157
La introducción anterior la hicimos desde la estadística. Ahora, presentamos una explicación desde los métodos numéricos, realizada por Elena Álvarez:
158
En esta escena, la proyección del vector se hace sobre un plano.
159
Proyección de un vector sobre un subespacio
Dado un vector v y un subespacio S, el vector v se puede descomponer de manera única de la forma;
v = v1 + v2 con v1 ∈ S y v2 ortogonal a S
La componente v1 se llama proyección ortogonal de v sobre S, la cual se denota por proyS v
Se calcula de la forma
proySv = proyu1v + ... + proyunv
siendo u1, ..., un una base ortogonal de S.
Teniendo en cuenta como se obtiene la proyección de un vector sobre otro, la proyección se puede obtener de la forma
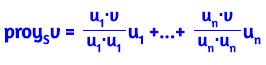
160
161
162
Solución aproximada de sistemas compatibles
Resolver un sistema lineal Ax = b consiste en escribir b como una combinación lineal de los vectores columna de la matriz A
El sistema Ax = b tendrá solución si b pertenece al subespacio S generado por las columnas de la matriz A y el sistema será compatible
Si b no pertenece al subespacio S el sistema será incompatible. En este caso, se puede sustituir b por otro vector c que sí esté en S siempre que c sea la mejor aproximación de b en S.
La idea será resolver Ax = c donde c = proysb, siendo S el subespacio generado por las columnas de la matriz A.
Este método se llama método de mínimos cuadrados ya que hace mínimo el error cuadrático.
A continuación se presentan tres escenas interactivas. La primera, permite generar nubes de puntos y ajustarlos a una recta. Las otras dos dan respuesta a los dos interrogantes planteados en los vídeos de la introducción a esta parte del libro.
163
164
Ejemplo 1. Consideremos que un muelle elástico está sometido a tracción. Aplicando distinto pesos (F), se ha anotado los alargamientos (L). Se sabe por la Ley de Hooke que L = (1/k)F, donde k es una constante característica del muelle, llamada constante elástica del mismo.
Determinemos esta constante por el método de los mínimos cuadrados.
165
Ejemplo 2. Según la primera ley de Kepler, un cometa debe tener una órbita elíptica o hiperbólica. En coordenadas polares, la posición de un cometa, (r, θ), satisface la ecuación r = β + e(r cos φ), donde β es una constante y e la excentricidad de la cónica (si 0 ≤ e ≤ 1 es una elipse, si e=1 es una parábola y si e>1 es una hipérbola).

Suponiendo que las observaciones de un cometa proporcionan los datos que se indican en la escena de la página siguiente,
¿Qué órbita describe el planeta?
166
167
Mínimos cuadrados en wxMaxima
En wxMaxima resolveremos el primer ejemplo relacionado con el muelle o resorte.
Los datos los podemos ingresar como una matriz, sin embargo, se recomienda hacerlo en dos vectores, así:
F : [0.2,0.4,0.5,0.7,0.9,1];
L : [0.06,0.12,0.15,0.21,0.26,0.29];
que corresponden a los del ejemplo. Luego construimos la matriz de esta forma: A : transpose(matrix(F, L));. Finalmente, con la instrucción simple_linear_regression(A);, obtenemos el modelo de regresión, cuyo resultado sería:

168
Observa que la ecuación de regresión lineal sería:
L = 0.2858F +0.0054, que coincide con la calculada en Descartes.
Conocida la ecuación, es posible graficarla, así:
wxdraw2d( points(A), color=red, explicit(.0054 + 0.2858*X, X, 0, 1.2),title="Ejemplo 1",xlabel="Fuerza",ylabel="Alargamiento" )$, cuyo resultado es la siguiente imagen:
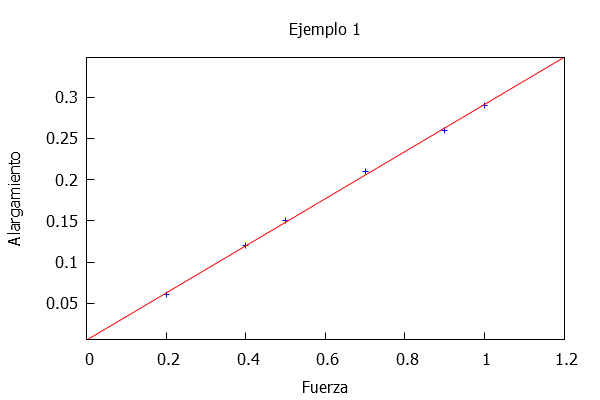
169
En general, wxMaxima estima por mínimos cuadrados modelos no lineales, a través de la expresión: lsquares_estimates(A, [X, Y], Y = a*X^b, [a, b]);, que aplicada al ejemplo anterior, nos daría como resultados a = 0.2895 y b = 0.9515, es decir, un modelo posible para el ejemplo sería: L = 0.2895F0.9515. Si dibujamos esta ecuación, con la expresión: wxdraw2d( points(A), color=red, explicit(0.2895*X^0.9515, X, 0, 1.2),title="Ejemplo 1",xlabel="Fuerza",ylabel="Alargamiento" )$, obtendríamos:
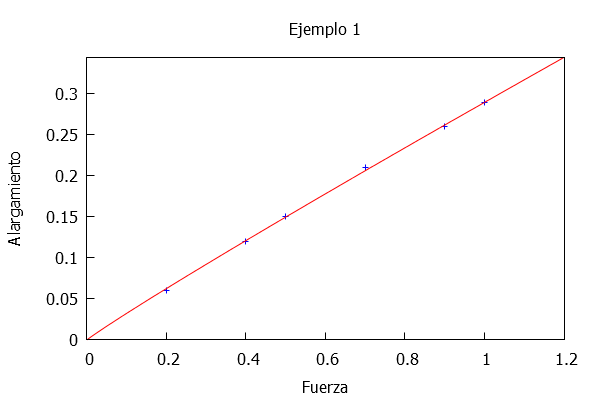
que es muy cercana al modelo de regresión lineal.
170
Mínimos cuadrados en GeoGebra
GeoGebra ofrece dos comandos que permiten realizar regresiones lineales y no lineales, los cuales son AjusteLineal[{A,B,C,D,E,F}] y AjustePotencia[{A,B,C,D,E,F}] respectivamente. En la siguiente escena, hemos diseñado el ejemplo del muelle o resorte.
Observa que hay diferencias con los resultados de wxMaxima para el caso no lineal
171
parte v
DIFERENCIACIÓN E INTEGRACIÓN NUMÉRICAS
Elena E. Álvarez Sáiz
Juan Guillermo Rivera Berrío
Héctor A. Tabares Ospina
Se deduce analíticamente que la fuerza resultante, sobre el tramo de la viga, es igual al área bajo la curva de carga:
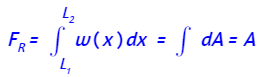
Esta expresión es fácil de utilizar, siempre que conozcamos la función de la curva de carga, tal como se aprecia en la siguiente escena (desplaza el botón):
175
En muchas situaciones nos encontramos con una serie de datos experimentales, que configuran curvas de carga que no tienen una función asociada, como en el ejemplo anterior. En muchos casos se idealiza la curva, con el fin de poder estimar, en forma algo aproximada, el comportamiento de un fenómeno dado. No obstante, en otros casos se requiere de un mayor rigor en los cálculos, pues de ello depende que no fallen los diseños en la ingeniería, los cálculos financieros, cálculo de probabilidades, entre muchos otras situaciones. Nos interesa, entonces, estimar los valores de la derivada o la integral de la función que responde a estos fenómenos, así la función sea difícil de determinar analíticamente y sea conveniente conocer su valor lo más aproximado posible. Es decir, estamos obligados a estimar y a aproximar pero, con un mayor rigor. En los estudios del comportamiento de materiales para estructuras y de las estructuras mismas, por ejemplo, se suelen usar factores de seguridad, pues las aproximaciones generan incertidumbre.
En esta parte del libro conoceremos y aplicaremos fórmulas de integración y derivación numérica, que dan respuesta a las aproximaciones requeridas. Contrario a lo que ocurre en los cursos regulares de Cálculo, iniciaremos con la integración numérica con las fórmulas de Newton-Cotes, las cuales usan como estrategia el reemplazo de una función no determinada o una nube de puntos por un polinomio interpolante. Algunas de estas fórmulas son la regla del trapecio (polinomio de primer grado) y la regla de Simpson (polinomios de segundo y tercer grado) y, para una mejor aproximación, el método de Romberg.
Por otra parte, las fórmulas de diferenciación numérica se utilizan en el desarrollo de algoritmos, para resolver numéricamente problemas de contorno de ecuaciones diferenciales ordinarias y ecuaciones en derivadas parciales. Para este caso, mostraremos diferentes fórmulas de derivación numérica (diferencias progresivas, regresivas y centradas), justificando su validez a partir de desarrollos en series de Taylor.
176
10.1 Integración numérica
Para empezar, observa el siguiente vídeo.
Haz clic para ampliar el vídeo
177
10.2 Fórmula del punto medio
En un curso de cálculo integral utilizamos la suma de Riemann para estimar el área de la región limitada por gráfica de la función f, el eje x y las rectas cuyas ecuaciones son
x = a y x = b.
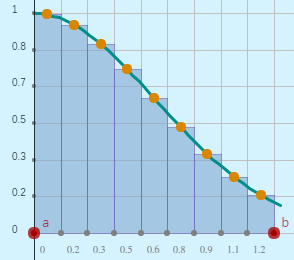
Para encontrar esta área, dividimos el intervalo [a, b] en n subintervalos y, luego, calculamos los n rectángulos de área f(ck)•Δxk. Tras un análisis simple, deducimos la siguiente expresión:
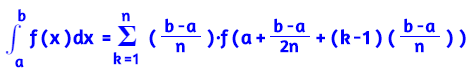
En las siguiente escena interactiva de Descartes, observa cómo se calcula la integral utilizando la fórmula del punto medio; obviamente, con f conocida.
178
Practica la fórmula del punto medio con la siguiente escena. Cambia los valores de n y observa la aproximación en la gráfica.
179
10.3 Fórmula del trapecio
La fórmula de punto medio lo que hace es corregir, en parte, los errores de la suma de Riemann cuando se configuran rectángulos por exceso o por defecto respecto al área delimitada por la curva de la curva. Observa, en la escena de GeoGebra, la suma de rectángulos con extremos izquierdos o derechos
Se podría pensar que bastaría con sumar los valores y promediar, para obtener el mismo resultado de la fórmula del punto medio, pero lo que realmente se obtendría es la fórmula del trapecio.
180
En las dos escenas anteriores (GeoGebra y Descartes), verifica la afirmación anterior. Por ejemplo, para n = 10, ¿Qué resultados se obtienen con el punto medio y promediando las sumas de extremos izquierdos y derechos?, ¿Es cierto que el promedio da como resultado la suma obtenida con la fórmula del trapecio?
181
Fórmula de cuadratura
Ahora, se podría pensar que podríamos sumar los valores obtenidos con las fórmulas del punto medio y del trapecio y luego promediar, para obtener una mejor aproximación. Este razonamiento nos acerca a la fórmula de Simpson.
182
10.4 Fórmula de Simpson
Si se analiza el error que se comete al aplicar la regla del trapecio, éste tiene signo contrario y cerca del doble de magnitud del error que se comete al aplicar la fórmula del punto medio; por ejemplo, para la función f(x) = exp(-x^2) en el intervalo [0, 1] y para un valor de n = 10, el error con la fórmula del trapecio es
0.7468241 - 0.7462108 = 0.0006133
mientras que por la fórmula del punto medio es
0.7468241 - 0.7471309 = -0.0003068.
Sería lógico pensar en un promedio ponderado de las dos fórmulas, con la suma del punto medio ponderada al doble de la suma de la regla del trapecio, pues se tendría un error mucho más pequeño. Este cálculo aproximado se llama Regla de Simpson, fórmula que aproxima la integral definida a partir del uso de parábolas, en lugar de segmentos rectilíneos.
En la siguiente página presentamos una escena interactiva de Descartes con la fórmula compuesta de Simpson, útil cuando el intervalo [a,b] no sea lo suficientemente pequeño, pues el error al calcular la integral puede ser muy grande. En este caso se divide el intervalo [a,b] en n subintervalos iguales (con n par), de manera que xi = a + ih, donde h=(b-a)/n, para i=0,1,...,n.
183
En la siguiente página presentamos el algoritmo en wxMaxima, para este mismo ejemplo. Observa los resultados para las fórmulas del punto intermedio, la del trapecio y la de Simpson.
184
Vamos a practicar con las fórmulas del trapecio y la de Simpson. En las siguiente escena puedes ingresar datos, para realizar cálculos y comparaciones, para ello:
1. Define el conjunto de puntos equidistantes x0, x1, ..., xn, de la forma: xk = x0 + kh, siendo k un número natural desde 0 hasta n.
2. Introduce los valores de las ordenadas correspondientes a los puntos x0, x1, ..., xn. Puedes generar estos datos, a partir de una función, pulsando el botón Generar datos
186
Integración numérica en GeoGebra
En la introducción de la fórmula de Simpson, encontramos que el error en la formúla del punto medio es cerca de la mitad al de la fórmula del trapecio, además de tener signo contario. GeoGebra no tiene un comando que podamos usar para la fórmula de Simpson, sin embargo, con el análisis anterior podemos estimar la fórmula de Simpson como el promedio ponderado del doble del valor obtenido por la fórmula del punto medio más el obtenido por la fórmula trapezoidal. En la siguiente escena de GeoGebra, hemos utilizado los siguientes comandos:
Para el cálculo de la fórmula del punto medio:
msum = SumaRectángulos[f, x(A), x(B), n, 0.5]
En la cual, f es la función, x(A) y x(B) son los extremos del intervalo, n el número de subintervalos y 0.5 es la posición del rectángulo inicial. Lo de la posición inicial hace referencia a la intersección de la curva de la función con la base superior de los rectángulos, si es cero lo hace con los extremos izquierdos, si es uno con los extremos derechos y, si es 0.5 con el punto medio.
Para el cálculo de la fórmula del trapecio:
tsum = SumaTrapezoidal[f, x(A), x(B), n]
Para el cálculo de la fórmula de Simpson, usamos el criterio explicado en la introducción, o sea:
simpsum = (tsum + 2msum) / 3
187
Observa los resultados con las diferentes fórmulas estudiadas en la escena de GeoGebra.
188
10.5 Derivación numérica
Presta atención al siguiente vídeo, en el que recordamos el concepto de derivada como razón de cambio.
Haz clic para ampliar el vídeo
189
10.6 La derivada y la secante
Dada una función de una variable, y = f(x), se define la derivada primera en un punto a de su dominio como:

Se puede obtener una aproximación de la derivada en el punto a mediante el cociente incremental, tomando un valor de h pequeño:
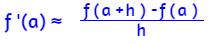
En la escena interactiva de la siguiente página, puedes practicar aproximando el cociente incremental (de color azul) al reducir el tamaño de h. Puedes, también, pulsar el botón Play para ver cómo al hacer h pequeño, se aproxima mejor al valor de la derivada.
Prueba con otras funciones y sus derivadas, ingresándolas en los cuadros de texto correspondientes.
La escena presenta la posibilidad de verse en tamaño ampliado, con el fin de manipular mejor los controles en las opciones gráficas.
190
10.7 Aproximación de la primera derivada
Suponemos conocido el valor de la función en un número de nodos equiespaciados una distancia h>0.
El objetivo es desarrollar fórmulas que permitan aproximar la derivada k-ésima de f(x) en un punto xi, mediante una expresión de la forma:
f(k(xi) ≅ A1f(x1) + ... + Anf(xn)
donde los puntos x1, ..., xn, que se llaman nodos, debe cumplir que están equiespaciados una distancia h>0.
Obtención: Como para la obtención de las distintas aproximaciones de f(k(xi), se utilizará la fórmula de Taylor en el punto (xi), se supondrá que la función cumple las condiciones de regularidad que se precisen.
En la escena interactiva de la siguiente página, comenzamos con la obtención de las fórmulas de aproximación de la primera derivada.
Debes hacer clic sobre uno de los tres números, para ver la información sobre la fórmula.
192
10.8 Analizando el error de la aproximación
Se ha visto que el error de truncamiento es proporcional a una potencia de h. Haciendo h más pequeño se reduce dicho error.
Sin embargo, llega un momento que al disminuir h influye el error de redondeo, haciéndose éste predominante.
Supongamos que la máquina de cálculo tiene una precisión u y consideremos la diferencia central para analizar estos errores.
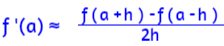
Al evaluar f(a + h) y f(a - h) obtendremos unos valores A(f(a + h)) = f(a + h)·(1 + E1) y A(f(a - h)) = f(a - h)·(1 + E2), siendo E1 y E2, en valor absoluto, menores que u.
El valor estimado de la derivada es:
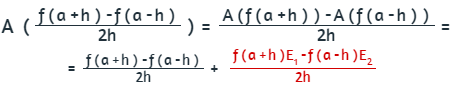
donde el último sumando es el error de redondeo cometido. Como el valor exacto de la fórmula es:
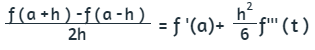
195
de acuerdo a las expresiones anteriores, el resultado numérico puede escribirse, así:
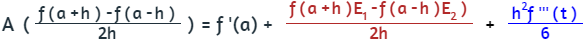
en rojo está marcado el error de redondeo y en azul el de truncamiento.
Para valores pequeños de h se tiene que:
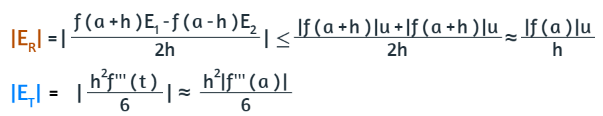
Una acotación aproximada del error total es entonces:
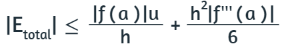
El análisis realizado es teórico, ya que para datos obtenidos, a partir de una tabla, la acotación realizada no es de utilidad (si no se conoce la derivada primera, no se conocerá, tampoco, la tercera).
A continuación, con fines de comparación con la escena interactiva anterior, presentamos el algoritmo en wxMaxima para el cálculo de la derivada primera con las diferencias progresiva, regresiva y central. Posteriormente, presentamos una escena interactiva para el cálculo de la derivada primera con diferencias de orden h2.
196
Derivada primera con wxMaxima
Observa el algoritmo y los resultados, tanto en wxMaxima como en la escena de Descartes. Este algoritmo es fácil de implementar para el resto de apartados que explicaremos sobre derivada numérica.

197
10.9 Derivada primera: otras diferencias de orden h2
Observa e interactúa con las fórmulas de diferencias de segundo orden, con la escena de la siguiente página.
198
10.10 Fórmulas de diferencias para la derivada segunda
Observa e interactúa con las fórmulas de diferencias para la derivada segunda, con la escena de la siguiente página.
200
Practica con las diferencias de orden h2, en la escena de la siguiente página.
202
Derivada segunda con GeoGebra
En las siguientes escenas reproducimos la escena de Descartes para f(x) = sen x + 2
204
205
parte vi
ECUACIONES DIFERENCIALES ORDINARIAS
Juan Guillermo Rivera Berrío
Héctor A. Tabares Ospina
Introducción
En el área de la Tecnología, en especial la Ingeniería, las ecuaciones diferenciales son de gran importancia para modelar y explicar el comportamiento de un fenómeno dado. Igualmente, las leyes físicas, generalmente, se expresan como una razón de cambio, por ejemplo, la caída de un cuerpo, el cambio de temperatura, las variaciones del caudal de una corriente de agua, la deformación de un elemento de hormigón, etcétera.
Las ecuaciones diferenciales ordinarias (EDO) surgen como problemas de valor inicial o problemas con condiciones de frontera. En esta última parte del libro, nos dedicaremos al primer tipo de problemas, los cuales se pueden escribir con la siguiente notación:
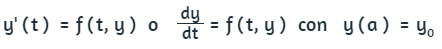
y(a) = y0 es una condición inicial del problema.
Se trata, entonces, de hallar una solución verificando la condición inicial dada. Esta solución es una función y(t) definida en un intervalo, que pase por el punto (a, y0).
Los métodos que vamos a usar para resolver las EDO se suelen llamar métodos o técnicas de Runge-Kutta, entre los cuales se encuentran: el método de Euler, de Heun, métodos de Taylor y los de Runge-Kutta propiamente.
208
11.1 Método de Euler
Este método es el más simple de los que vamos a explicar y, en consecuencia, el que más problemas de aproximación puede presentar.
La solución de ecuaciones diferenciales ordinarias de la forma
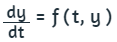
por los métodos de Runge-Kutta, se expresa matemáticamente como:

en la cual la pendiente estimada φ se usa para extrapolar desde una valor anterior yi a un nuevo valor yi+1 en una distancia h. Esta fórmula permite, paso a paso, trazar la trayectoria de la solución (Chapra y Canale, 2007, pág. 719
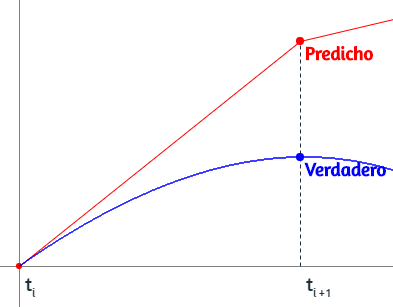
209
El método de Euler inicia con el cálculo de la primera pendiente o derivada:
φ = f(ti, yi+1), donde f(ti, yi+1) es la pendiente de la recta tangente en ti . Esta estimación da origen a la fórmula de punto pendiente o de Euler-Cauchy, conocida como método de Euler:
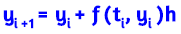
En la escena interactiva de la página siguiente, presentamos el ejemplo de Mora (2013, pág. 192
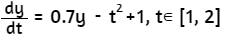
La escena inicia con 11 puntos (n = 10) en el intervalo [1, 2], lo que genera un valor de h de 0.10. Estos valores se pueden variar para observar que a un mayor valor de n la aproximación a la solución (marcada en azul) es mejor. Esta solución es
y(t) = 1.42857t2 + 4.08163t − 4.42583e0.7t + 4.40233. Es de observar que la aproximación depende del tamaño del intervalo y del tipo de ecuación, por ejemplo:
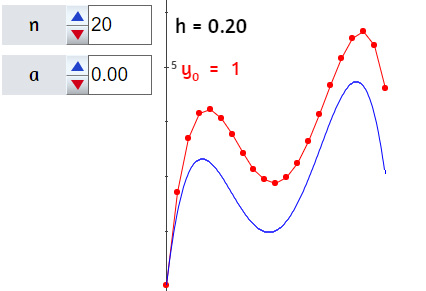
210
En la imagen anterior, pese a no existir una buena aproximación, el cálculo presenta, al menos, la forma de la solución. Veamos, ahora, la escena interactiva para el ejemplo de Mora:
Haz clic para ampliar la escena
211
Método de Euler con wxMaxima
Presentamos el algoritmo para el método de Euler, en el cual hemos incorporado la ecuación diferencial ordinaria presentada en la escena de Descartes. Puedes ampliar la imagen, y descargar y ejecutar el archivo de wxMaxima, para que observes la gráfica comparativa de y(t) aproximada con y(t) exacta.
212
Método de Euler con GeoGebra
En esta escena puedes cambiar la ecuación diferencial y la solución. Hemos hecho una adaptación de la escena diseñada por Juan Carlos Ponce.
Haz clic para ampliar la escena
213
11.2 Mejoras del método de Euler
El error de aproximación en el método de Euler se genera al suponer que la derivada al inicio de un intervalo es la misma a lo largo de todo el intervalo. Existen dos métodos llamados correctivos de Euler: método de Heun y el método del punto medio, en este apartado explicaremos el primero. El método de Euler que predice la pendiente al inicio del intervalo, la podemos expresar así (el superíndice cero significa que la pendiente es una predicción intermedia):
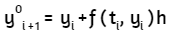
esta ecuación permite estimar la pendiente al final del intervalo:
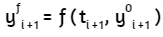
Ahora, combinadas las dos pendientes obtenemos una pendiente promedio que al reemplazar en la fórmula de Euler (predictor) obtenemos el método propuesto por Heun (corrector):
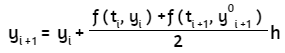
En la siguiente escena de Descartes puedes ver los dos métodos comparados. Puedes cambiar la ecuación y la solución y(t) (si no la conoces, déjala en blanco), para ello, ingresa primero las ecuaciones y luego cambia los valores del intervalo. Usa clic izquierdo sostenido para mover la gráfica y el derecho para zoom.
214
En la escena hemos realizado el ejemplo de Mathews y Fink (2000, pág. 476
y' = (x - y)/2 y desplazando el punto A a las coordenadas (0, 1).
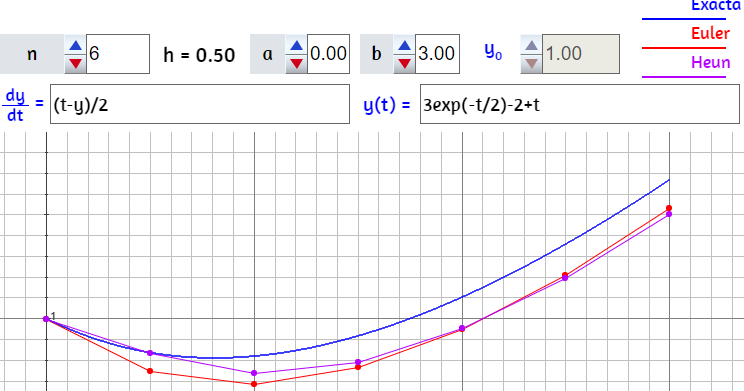
Para h = 0.5, estos fueron los resultados:
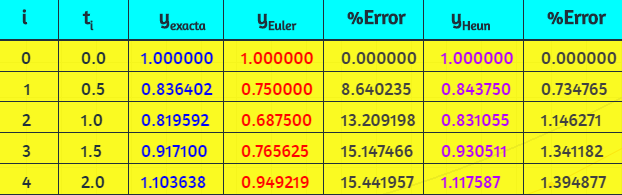
216
Método de Heun con GeoGebra
Es importante tener en cuenta que GeoGebra no admite variables diferentes a x y y, por ello hemos cambiado la variable t por la variable x.
Haz clic para ampliar la escena
217
Método de Heun con wxMaxima
Este es el algoritmo para el método de Heun, en el cual hemos incorporado la ecuación diferencial ordinaria presentada en las escenas enteriores. Puedes ampliar la imagen, y descargar y ejecutar el archivo de wxMaxima, para que observes la gráfica comparativa de y(t) Heun con y(t) exacta.
218
11.3 Métodos de Taylor de orden superior
La expansión de un polinomio de Taylor permite resolver ecuaciones diferenciales con condiciones iniciales. En general, se puede demostrar que para t = ti es posible obtener soluciones numéricas de las ecuaciones diferenciales, calculando las derivadas sucesivas de la ecuación diferencial dada, evaluando las derivadas en el punto inicial y reemplazando el resultado en la serie de Taylor. Esta expansión para un orden cuatro (m = 4) de Taylor, sería:
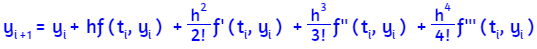
Observa que para orden uno (m=1) se obtiene el método de Euler. Por otra parte, es importante comprender el cálculo de las derivadas sucesivas a partir de y'(t)=f(t, y). Al ser f una función de dos variables, las derivadas sucesivas se obtienen derivando parcialmente con respecto a cada variable, así:
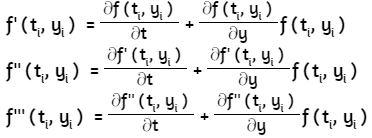
A continuación explicaremos, con más detalle, cómo aplicar este método con wxMaxima y, posteriormente, a través de escenas interactivas de Descartes y GeoGebra podrás practicar con diferentes ecuaciones diferenciales
219
Método de Taylor con wxMaxima
Con el método de Taylor vamos a solucionar la ecuación y′(t) = e-2t – 4y, desde t = 0 hasta t = 1. La condición inicial es t = 0, y(0) = 1.
Inicialmente hacemos las siguientes declaraciones:

Observa que, como en los casos anteriores, hemos incluido la solución que para este problema es y(t) = 0.5e-2t + 0.5e-4t, esto lo hacemos con fines didácticos, para verificar el nivel de aproximación de cada método. Es obvio que recurrimos a una solución numérica cuando la solución análitica es compleja o difícil de evaluar.
A continuación calculamos las derivadas sucesivas y"(t) hasta el máximo orden que queremos evaluar que, para nuestro ejemplo, será cuarto yiv(t)
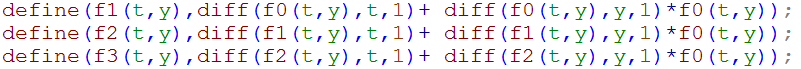
El siguiente paso es crear un ciclo o bucle que calcule los valores de la solución, de acuerdo a la expansión de Taylor descrita anteriormente, estos valores los almacenamos en un vector y[k], donde k toma valores de 0 hasta N
220

Finalmente, realizamos el gráfico que muestre la solución analítica y los puntos encontrados por el método de Taylor.

wxMaxima dispone de varios comándos para graficar, uno de ellos es draw2d que dibuja en una ventana aparte. El prefijo wx permite que la gráfica se presente en la misma ventana de la solución.
221
La imagen de salida muestra que para orden cuatro (m = 4), se obtiene una muy buena solución. Haz clic sobre la imagen para observar el código completo o sobre el ícono de wxMaxima para descargarlo.
En las siguientes escenas de Descartes y GeoGebra, presentamos la solución para la misma ecuación. Para el caso de Descartes, sólo hemos incluido los métodos de Taylor de orden uno (m=1) (Euler) y dos (m=2), con el fin de comparar el nivel de aproximación. Puede observarse que para m=2, la aproximación es superior a la obtenida por el método de Heun.
222
Método de Taylor con GeoGebra
Tanto GeoGebra como wxMaxima, por ser programas de cálculo simbólicos (CAS), permiten calcular las derivadas requeridas para la expansión de Taylor, por ello, se facilita la solución a un orden superior. Es de observar que GeoGebra obliga a usar variables en notación f(x, y). Una ventaja adicional, en las últimas versiones, es la disposición de una hoja de cálculo con funcionamiento similar a una hoja de Excel, lo cual permite la generación sencilla de los puntos de la solución. Por ejemplo, la fórmula de la celda E4 es:

que corresponde a un orden cuatro del método de Taylor.
Otro comando útil es el campo de direcciones, que no hemos incluido en la escena para evitar retardamientos en la interacción, pues dicho comando consume bastantes recursos. El comando para y'(t) que en la escena hemos denotado como f0(x, y), sería:
CampoDirecciones[ f0(x, y), 10]
En la ventana gráfica de la escena sólo hemos habilitado las soluciones hasta el orden tres (m=3), pero en la hoja de cálculo lo hicimos hasta cuarto (m=4).
224
11.4 Método de Runge-Kutta
Como lo enunciamos en la introducción, los métodos anteriores se suelen llamar métodos del tipo Runge-Kutta1 o de un sólo paso (los métodos de varios pasos no serán tratados en este libro), pues su origen surge de la utilización de un número finito de términos de la serie de Taylor, de la forma:
yi+1 = yi + hf(ti, yi) + (h2/2!)f'(ti, yi) + (h3/3!)f"(ti, yi) + ...
Tanto Euler (1745) como Runge (1885), Heun (1900) y Kutta (1901) formulan sus métodos con fundamento en las series de Taylor (1715). Sin entrar en demostraciones o mayores detalles, que sugerimos consultar en algunos de los libros reseñados en la bibliografía, es posible llegar a la siguiente fórmula:
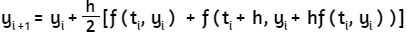
la cual se puede expresar como:
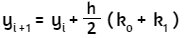
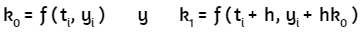
Esta fórmula se conoce como método de Rung-Kutta de segundo orden, que coinciden con los tres primeros términos de la serie de Taylor.
226
El método de Runge-Kutta de cuarto orden se determina por la fórmula:
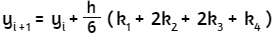
en la cual,
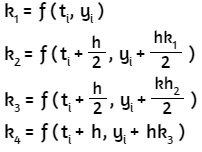
que coincide con los primeros cinco términos de la serie de Taylor, que implica una gran exactitud. Se puede observar que esta alta precisión se logra sin recurrir a las derivadas sucesivas, situación que hace del método de Taylor una opción poco utilizada. La sencillez del método facilita su programación en Descartes, wxMaxima y GeoGebra. Para el diseño de las escenas interactivas utilizaremos esta última fórmula.
En general, los métodos hasta aquí explicados sólo ofrecen información del orden de error, que para Euler es uno O(h), para Heun O(h2) y para Runge-Kutta O(h4). Para determinar el error absoluto se tendría que conocer la solución y(t) exacta, en cuyo caso no tendría sentido usar los métodos.
Para terminar, presentamos un problema resuelto con Descartes, GeoGebra y wxMaxima
227
Método de Runge-Kutta en Descartes
El propósito de este libro no fue explicar como se desarrollan las escenas de Descartes, no obstante, en esta última escena interactiva, presentamos el algoritmo que permite el cálculo del método de Runge-Kutta diseñados en el editor de Descartes.
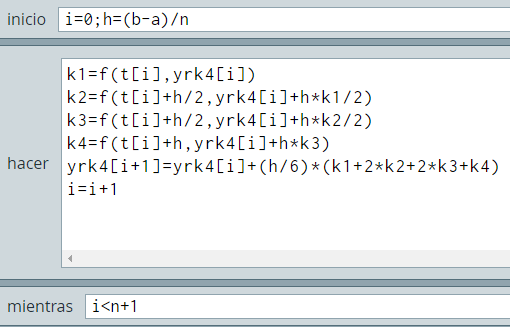
Algoritmo Runge-Kutta
Se puede apreciar la simpleza del algoritmo, el cual incluye los vectores t[i] y yrk4[i], en los que se almacenan los puntos de la solución Runge-Kutta. Descartes permite el diseño de ciclos o bucles tipo do-while.
En la siguiente escena interactiva puedes practicar con el método.
228
229
Método de Runge-Kutta con GeoGebra
GeoGebra, como lo hemos dicho antes, pemite utilizar una hoja de cálculo con funciones similares a las de Excel. Esto posibilita programar, fácilmente, el algoritmo a través de las celdas de la hoja de cálculo.
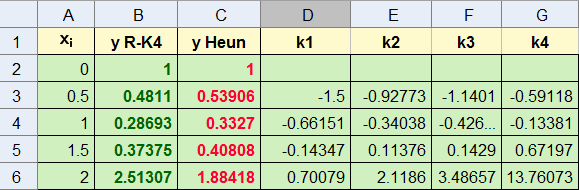
Runge-Kutta y Heun en la hoja de cálculo
En la celda B3, por ejemplo, se incluye la fórmula simplificada de Runge-Kutta.
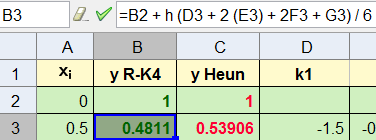
Puedes practicar en la siguiente escena interactiva de GeoGebra.
230
En la escena puedes ampliar la ventana de la hoja de cálculo para ver los resultados de k1, k2, k3 y k4
Haz clic para ampliar la escena
231
Método de Runge-Kutta con wxMaxima
Este es el algoritmo para el método de Runge-Kutta. No se muestran las instrucciones para la gráfica, sin embargo, puedes descargar el archivo y ejecutarlo, para observar los resultados.