Título de la obra:
Matemáticas interactivas
Autor:
Renato Oña Yánez
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS, WebSim y GeoGebra.
Fuentes: Lato y UbuntuMono
Imagen de portada: ilustración generada por Dreamina AI
Red Educativa Digital Descartes
Córdoba (España)
descartes@proyectodescartes.org
https://proyectodescartes.org
Proyecto iCartesiLibri
https://proyectodescartes.org/iCartesiLibri/index.htm
ISBN: 978-84-10368-18-7

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Las matemáticas han sido, desde tiempos inmemoriales, una herramienta esencial para el desarrollo del conocimiento humano. Su influencia se extiende a innumerables campos del saber, desde la ciencia y la ingeniería hasta la economía y la tecnología. Sin embargo, su enseñanza y aprendizaje han sido tradicionalmente percibidos como un desafío, especialmente cuando se presentan de manera estática y teórica.
En este contexto, "Matemáticas Interactivas" surge como una propuesta innovadora que busca transformar la experiencia educativa mediante el uso de recursos interactivos y herramientas digitales. El presente libro ha sido diseñado para que estudiantes y docentes puedan explorar los conceptos matemáticos de forma dinámica, favoreciendo el aprendizaje activo y significativo.
Este libro integra diversos recursos tecnológicos como DescartesJS, WebSim, Generador de Imágenes con AI entre otros, que permiten visualizar y experimentar con los contenidos. De esta manera, se logra no solo comprender la teoría, sino también aplicarla en situaciones reales a través de simulaciones y actividades interactivas.
El enfoque interactivo de esta obra responde a la necesidad de adaptar la enseñanza de las matemáticas a las nuevas generaciones, quienes aprenden mejor cuando se involucran activamente en el proceso.
Esperamos que este libro sea un recurso valioso para la enseñanza y el aprendizaje de las matemáticas, fomentando una comprensión más profunda y accesible para todos.
Los números enteros son números que no tienen decimales. Pueden ser positivos, negativos o cero. Se utilizan para contar cosas, medir temperaturas, y representar ganancias o pérdidas.
Los números enteros son necesarios para representar y operar con cantidades. Permiten expresar deudas, temperaturas bajo cero, cambios de dirección, entre otros conceptos. Además, son fundamentales en matemáticas y en muchas áreas de la vida cotidiana.

Termómetro:
Es un instrumento utilizado para medir la temperatura. Se usa en diversos contextos, como la medicina, la meteorología, la industria y la investigación científica. El termómetro fue desarrollado en el siglo XVII por Galileo Galilei, quien creó un prototipo conocido como termoscopio. Posteriormente, Santorio Santorio ncorporó una escala para medir temperaturas. Daniel Gabriel Fahrenheit introdujo en 1714 el termómetro de mercurio con una escala graduada, mientras que Anders Celsius desarrolló en 1742 la escala centígrada o Celsius.


En la siguiente escena puedes practicar sobre la utilización de los números enteros en la vida cotidiana. .
"Los números positivos son aquellos que tienen un valor mayor que cero, y se encuentran ubicados en la parte derecha de la recta numérica. Los números negativos, por otro lado, son aquellos con valor menor que cero y se encuentran en la parte izquierda de la recta numérica, representando situaciones como pérdidas o descensos." (Sullivan, M., 2012, Precalculus: Concepts Through Functions, p. 74).
Los números positivos y negativos son valores que se utilizan para representar cantidades y direcciones opuestas. Los positivos indican cantidades por encima de un punto de referencia (como 0), mientras que los negativos representan cantidades por debajo de ese mismo punto.
Se escriben con el signo “+” o sin ningún signo. Son los que están a la derecha del cero en la recta numérica (ejemplo: 1, 2, 3…).

Son aquellos que están por debajo de cero y se utilizan para representar situaciones en las que hay una pérdida, una disminución o un movimiento en dirección opuesta a una referencia (como el cero). Los números negativos siempre se escriben con el signo “-” delante, como en −3 o −10. Son los que están a la izquierda del cero en la recta numérica.

La recta numérica es una línea en la que los números se ordenan de menor a mayor, de izquierda a derecha.
Los números negativos están a la izquierda del cero y los positivos a la derecha.
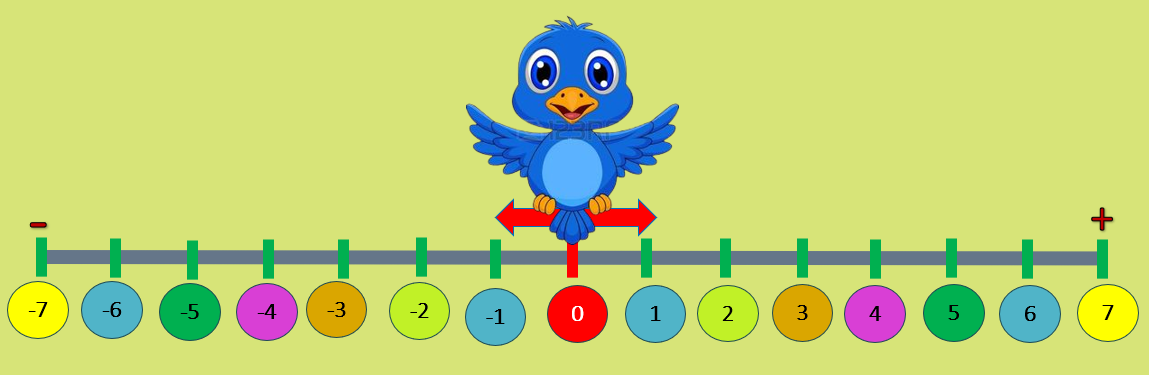


En esta actividad interactiva vamos a ubicar correctamente los números en la recta numérica.
"El plano cartesiano, introducido por René Descartes, consiste en dos ejes perpendiculares que dividen el espacio en cuatro cuadrantes y permiten localizar puntos mediante pares ordenados de números." (Larson & Hostetler, 2007, p. 32).
El Plano Cartesiano es una herramienta matemática clave para representar puntos mediante coordenadas.
Se llaman "ejes coordenados" a las dos rectas perpendiculares que se interconectan en un punto del plano. Estas rectas reciben el nombre de abscisa y ordenada.
Abscisa: El eje de las abscisas está dispuesto de manera horizontal y se identifica con la letra “x”.
Ordenada: El eje de las ordenadas está orientado verticalmente y se representa con la letra “y”.
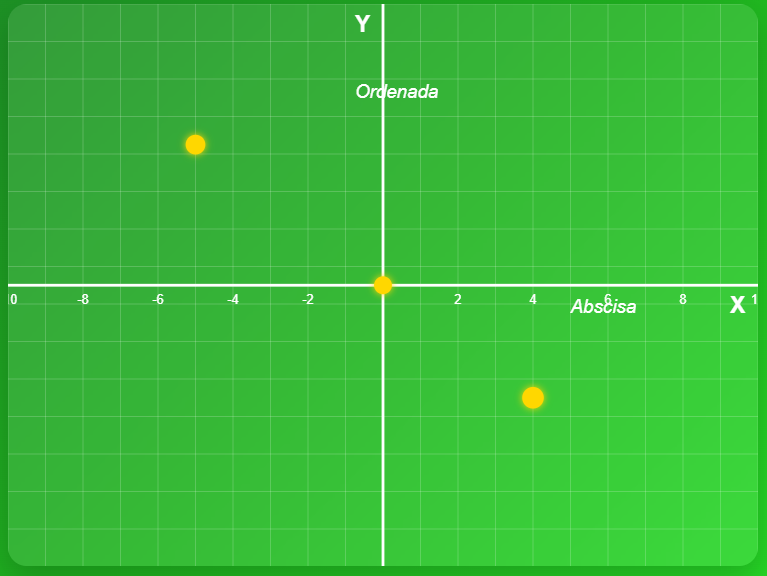

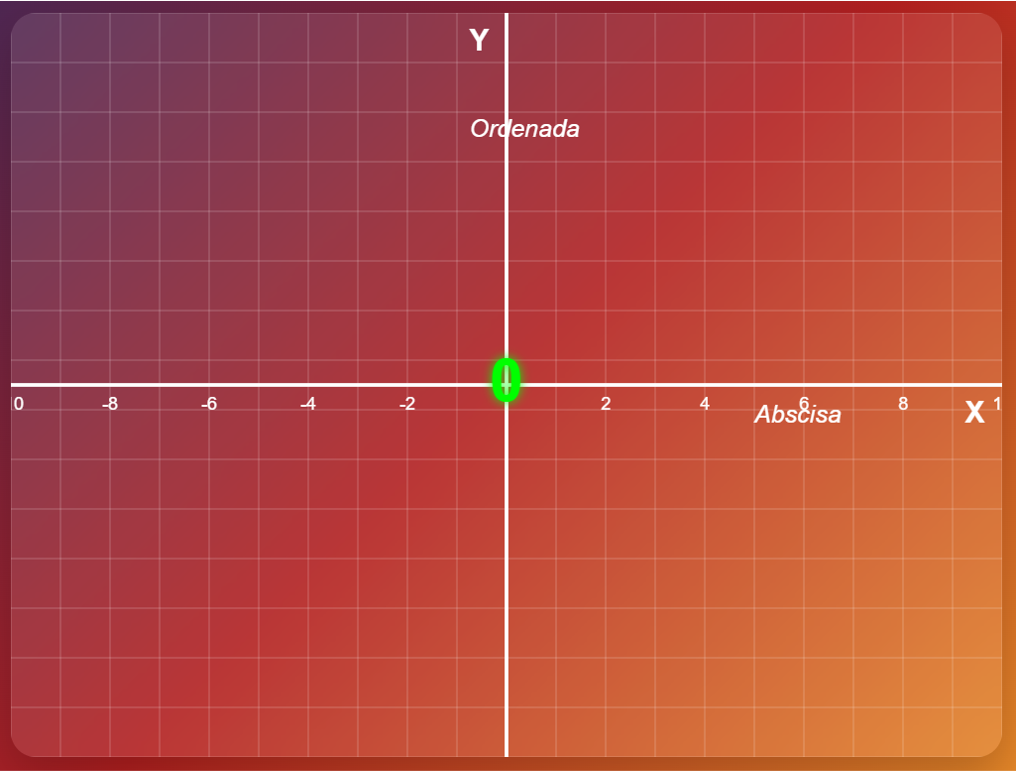
Se llama origen al punto en el que se intersecan los ejes “x” y “y”, punto al cual se le asigna el valor de cero (0).
El segmento derecho del eje “x” es positivo, mientras que el izquierdo es negativo.
Consecuentemente, el segmento ascendente del eje “y” es positivo, mientras que el segmento descendente es negativo.
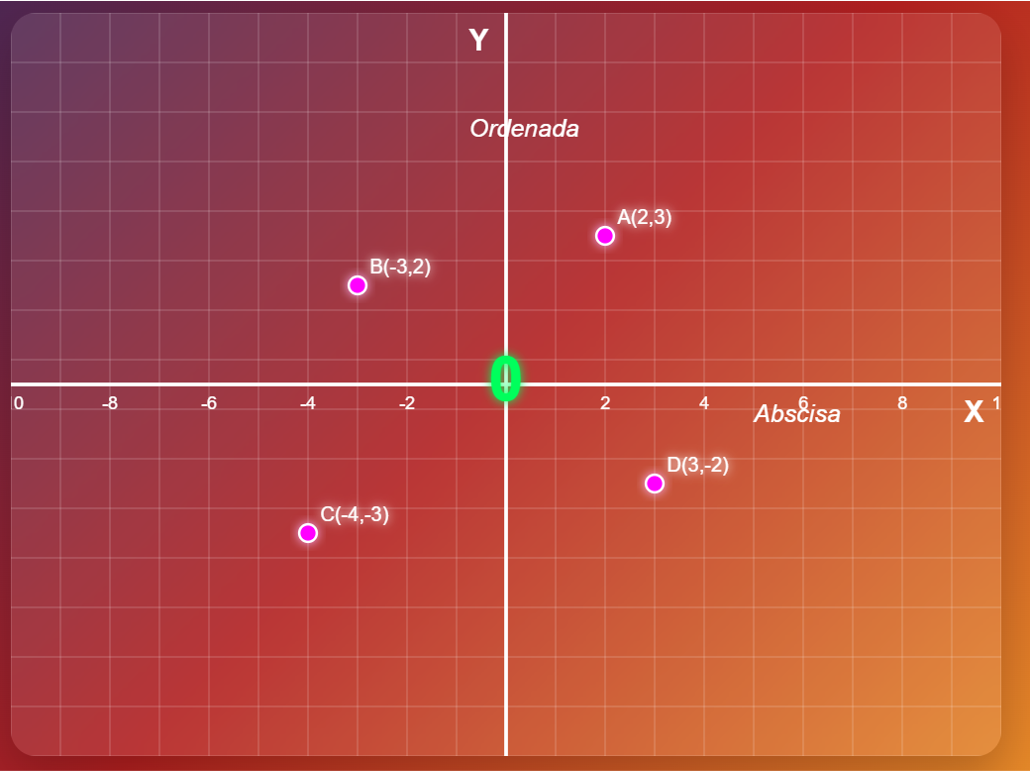
Se llama cuadrantes a las cuatro áreas que se forman por la unión de las dos rectas perpendiculares. Los puntos del plano se describen dentro de estos cuadrantes.
Los cuadrantes se enumeran tradicionalmente con números romanos: I, II, III y IV.
Cuadrante I: la abscisa y la ordenada son positivas.
Cuadrante II: la abscisa es negativa y la ordenada positiva.
Cuadrante III: tanto la abscisa como la ordenada son negativas.
Cuadrante IV: la abscisa es positiva y la ordenada negativa.
Son los números que nos dan la ubicación del punto en el plano. Las coordenadas se forman asignando un determinado valor al eje “x” y otro valor al eje “y”. Esto se representa de la siguiente manera:
P (x, y), donde:
x = eje de la abscisa (horizontal)
y = eje de la ordenada (vertical).
"Los números opuestos son aquellos que, al sumarse, resultan en cero. Se encuentran ubicados a la misma distancia del origen en una recta numérica, pero en direcciones contrarias." (Larson & Hostetler, 2007, Precalculus: A Graphing Approach, p. 45).
En términos matemáticos, si un número es a, su opuesto es −a.
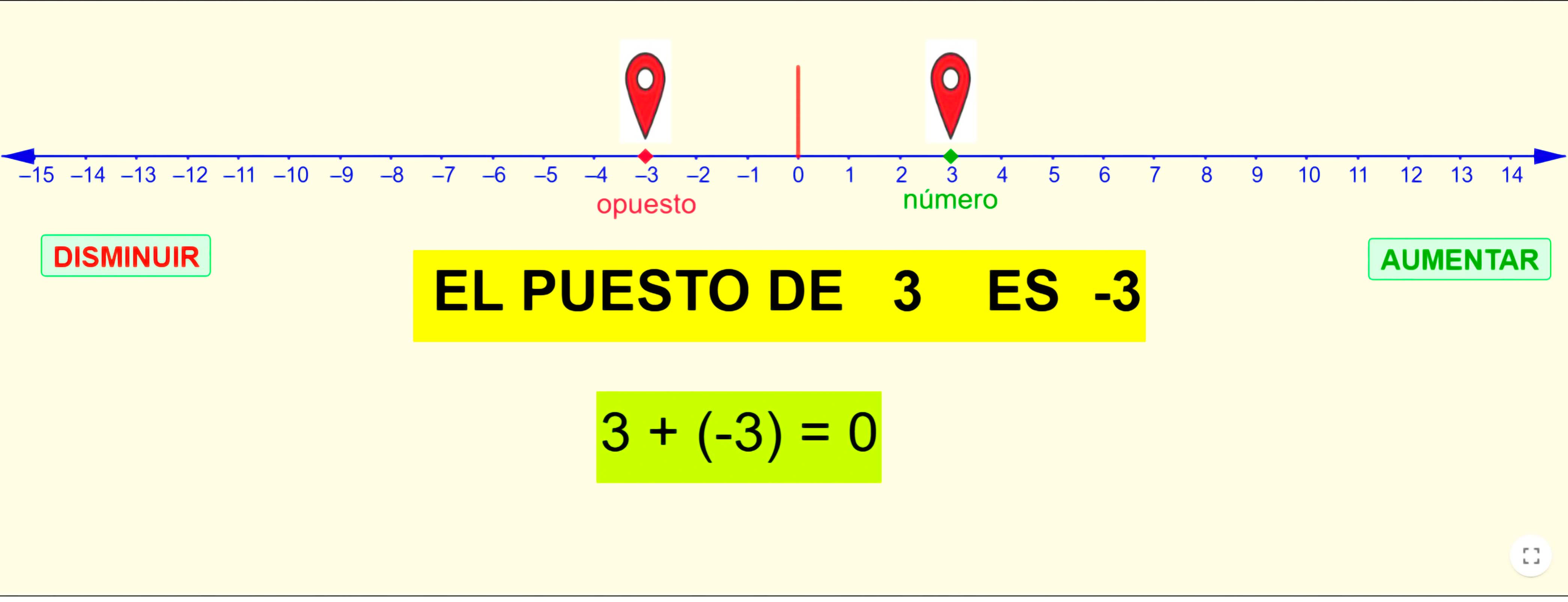
Usos: Los números opuestos son útiles en situaciones como el manejo de deudas y ganancias, temperaturas por encima y por debajo de cero, o movimientos hacia direcciones contrarias.
El orden de los números enteros se establece en una recta numérica, donde los números se ubican de menor a mayor de izquierda a derecha. Esto permite compararlos fácilmente y determinar cuál es mayor o menor.
Son menores que el cero y los números positivos.
Cuanto más lejos está un número negativo del cero, menor es su valor (por ejemplo, −5 es menor que −2).
Son mayores que el cero y todos los números negativos.
Cuanto más lejos están del cero, mayor es su valor (por ejemplo, 5 es mayor que 2).
El mayor es el que tiene un valor numérico más alto.
Ejemplo: 7 > 3
El mayor es el que está más cerca del cero.
Ejemplo: −2 > −5
Siempre un número positivo es mayor que cualquier número negativo.
Ejemplo: 2 > −4
La adición de números enteros consiste en sumar números positivos y negativos siguiendo reglas específicas que dependen de sus signos. Se usa frecuentemente en contextos como ganancias y pérdidas, temperaturas o cambios de nivel.
Signos iguales se suman y conserva el signo común.
Ejemplo:
(+5) + (+3) = +8
(−7) + (−2) = −9
Signos diferentes se restan y se coloca el sino del número mayor
Ejemplo:
(+7) + (−4 )= +3
(−6) + (+2) = −4
La sustracción de números enteros consiste en restar un número de otro, y puede interpretarse como la suma del opuesto del número que se resta. Esto significa que a − b es equivalente a + (−b).
Cambia la sustracción por adición del opuesto:
Luego, aplica las reglas de suma de números enteros.
5 −3 = 5 + (−3) = 2
(Cambia el −3 por su opuesto, −3, y suma).
−4 − 6 = −4 + (−6) = −10
(Suma los valores absolutos y conserva el signo negativo).
7 − (−3) = 7 + 3 = 10
(El opuesto de −3 es +3).
−5 − (−2) = −5 + 2 = −3
(El opuesto de −2 es +2, luego suma con signos diferentes).
La multiplicación de números enteros se realiza siguiendo reglas específicas que dependen de los signos de los números involucrados. Estas reglas determinan si el resultado será positivo o negativo
Resultado positivo.
Ejemplo:
(+3) × (+4) = +12
(−5) × (−2) = +10
Resultado negativo.
Ejemplo:
(+6) × (−3) = −1
(−4) × (+2) = −8
Cualquier número multiplicado por cero es siempre cero.
Ejemplo:
(+5) x 0 = 0
(−7) × 0 = 0

El orden de los factores no altera el producto.
Ejemplo: 3 × (−2) = −6 y (−2) × 3 = −6.
El agrupamiento de los factores no altera el producto.
Ejemplo: (2 × 3) × 4 = 2 × (3 × 4) = 4.
El número 1 es el elemento neutro de la multiplicación.
La multiplicación se distribuye sobre la suma y la resta.
La división de números enteros es una operación matemática que consiste en encontrar el cociente y el resto de la división de un número entero entre otro.
El resultado de dividir dos números enteros con el mismo signo es positivo.
Ejemplo:
(-12) ÷ (+3) = +4
(-12) ÷ (-3) = +4
El resultado de dividir dos números enteros con el mismo signo es positivo.
Ejemplo:
(-12) ÷ (+3) = -4
(12) ÷ (-3) = -4
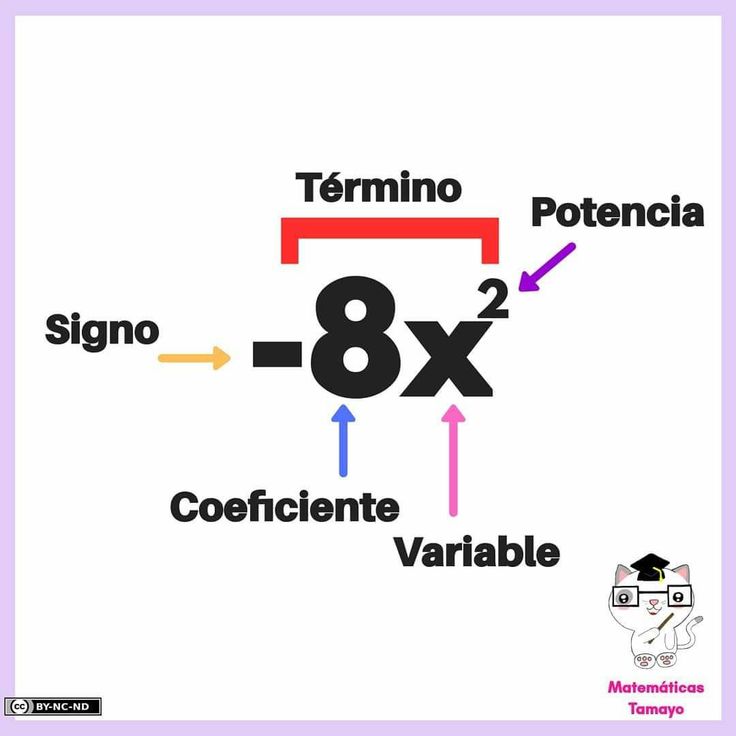
La potenciación de números enteros es una operación matemática que consiste en multiplicar un número entero (la base) por sí mismo tantas veces como indique otro número entero (el exponente). Se representa como:
Ejemplo:
3^4=3×3×3×3=81
Ejemplo:
5^1 = 5.
7^1 = 1.
Ejemplo:
5^0 = 1.
7^0 = 1.
Ejemplo:
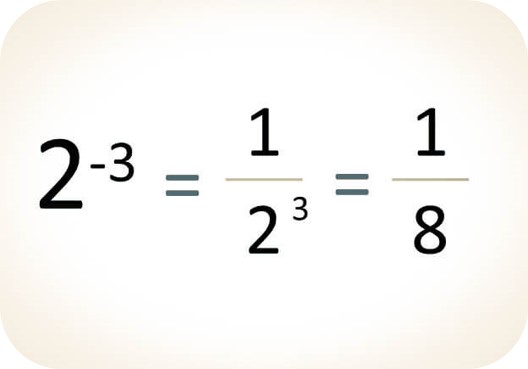

| Propiedades de la potenciación | Esquema | Ejemplo |
|---|---|---|
| Producto de potencias con la misma base | 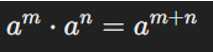 |
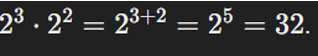 |
| Cociente de potencias con la misma base | 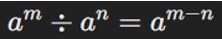 |
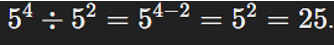 |
| Potencia de una potencia | 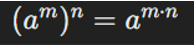 |
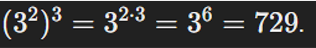 |
| Potencia de un producto | 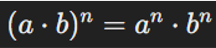 |
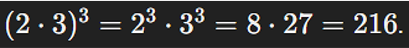 |
| Potencia de un cociente | 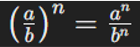 |
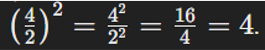 |
Los números fraccionarios son aquellos que representan una parte de un todo o una división entre dos números enteros.
El concepto matemático de fracciones corresponde a la idea de dividir una totalidad en partes iguales. Imagínate una pizza para dividir entre 6 personas.

Las fracciones son una herramienta matemática fundamental que utilizamos para expresar partes de un todo, proporciones o divisiones en cantidades.
Tiempo: Decimos que una actividad dura 1/2 hora (30 minutos) o que una reunión empieza en un cuarto de hora (15 minutos).

Mediciones: Los planos y proyectos de construcción utilizan fracciones para especificar longitudes, como 3/8 de pulgada o 1/2 metro, especialmente en sistemas de medida como el imperial.

Intereses y porcentajes: Los cálculos de intereses fraccionados en préstamos o inversiones son comunes, como tasas de 1/4% o 1/2%.
División de bienes: Las fracciones son esenciales en la división de ganancias, herencias o bienes, especialmente cuando las partes no son iguales.

Cálculos químicos: Las proporciones en reacciones químicas a menudo involucran fracciones para medir cantidades exactas de sustancias.
Dosis de medicamentos: En medicina, las dosis suelen expresarse como fracciones, como 1/2 tableta o 3/4 de una dosis estándar.

Las fracciones se clasifican en propias, impropias y mixtas, según la relación entre el numerador y el denominador:
Son aquellas donde el numerador es menor que el denominador.
Su valor es siempre menor que 1.

Son aquellas donde el numerador es mayor o igual al denominador.
Su valor es igual o mayor que 1.
Ejemplo de fracciones impropias

Son una combinación de un número entero y una fracción propia.
Se utilizan para representar de forma clara cantidades mayores a 1.
Las fracciones mixtas se convierten en impropias multiplicando el entero por el denominador y sumándole el numerador.
Ejemplo de fracciones mixtas

Las fracciones equivalentes son aquellas que representan la misma cantidad o el mismo valor, aunque tengan diferentes numeradores y denominadores.
Las fracciones equivalentes se obtienen al multiplicar o dividir el numerador y el denominador de una fracción por el mismo número (distinto de cero).
Ejemplo de fracciones equivalentes

Las operaciones básicas con fracciones son fundamentales en matemáticas. La suma y resta de fracciones requieren comprender conceptos básicos como denominadores comunes y el orden en que se trabajan numeradores y denominadores.
La suma de dos fracciones con el mismo denominador es otra fracción que tiene: Denominador: el denominador común. Numerador: la suma de los numeradores
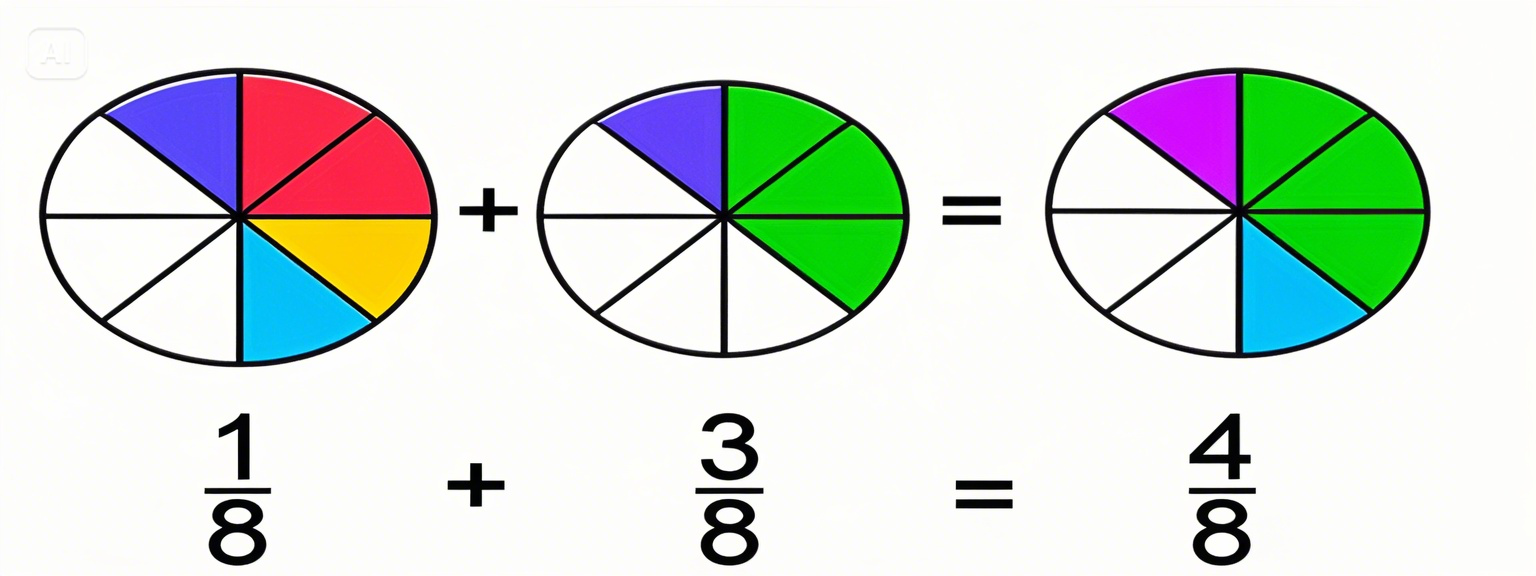

Para sumar o restar fracciones con distinto denominador:
1º Se reducen todas las fracciones a común denominador.
2º Se procede como en el caso anterior.


La multiplicación de fracciones es sencilla. Solo debes seguir estos pasos:

Una división de fracciones se puede convertir en multiplicación, de la siguiente manera:

Mendoza, J. (2018). Matemáticas Básicas para Principiantes. Editorial Trillas.
Redondo, J. (2019). Aprender Matemáticas de Forma Divertida. Editorial SM.
Torres, L. (2020). Matemáticas Elementales. McGraw-Hill Educación.
Baldor, A. (2015). Álgebra de Baldor. Editorial Patria.
Red Educativa Digital Descartes. (2024). Proyecto iCartesiLibri. Recuperado de: https://proyectodescartes.org/iCartesiLibri/index.htm
TDescartesJS. (2024). Recursos interactivos para la enseñanza de las matemáticas. Recuperado de: https://proyectodescartes.org/
WebSim. (2024). Plataforma de simulaciones interactivas. https://websim.ai/
Dreamina AI. (2024). Generador de imágenes con IA. https://dreamina.capcut.com/ai-tool/image/generate
Ideograma IA. (2024). Generación de gráficos y representaciones visuales. https://ideograma.ai/
Polinizaciones AI. (2024). Generación de imágenes educativas. https://pollinations.ai/