Tabla de contenido

Introducción

Este libro interactivo de aprendizaje se constituye en un complemento para la unidad dedicada a la determinación del dominio y rango de una función de la asignatura Cálculo Diferencial. Contiene varios objetos interactivos, que permiten un aprendizaje significativo, en tanto que el estudiante puede interactuar con el objeto de conocimiento propio de esta unidad.

En total son 13 los objetos interactivos, tres de ellos diseñados en GeoGebra y el resto con la herramienta Descartes. Cada objeto es posible abrirlo en una pantalla del navegador más amplia, no obstante, la interacción se puede realizar en la página del libro. Se ha recurrido a la gran cantidad de contenidos digitales de la Red Descartes que, para esta unidad, se encuentran en los Proyectos EDAD y Plantillas. En algunas páginas debes esperar unos segundos a que abra el objeto interactivo.

2

Concepto de función

Haz clic para ampliar la escena

Escena del Proyecto EDAD. Autora:María José García Cebrian

3

Funciones definidas a trozos

Haz clic para ampliar la escena

Escena del Proyecto EDAD. Autora:María José García Cebrian

4

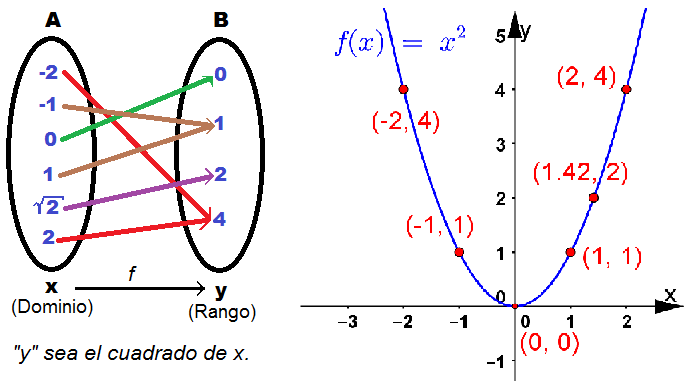
Definición de una función

Una función matemática es la correspondencia o relación f de los elementos de un conjunto A con los elementos de un conjunto B. Una función cumple con la condición de existencia (todos los elementos de A están relacionados con los elementos de B) y con la condición de unicidad (cada elemento de A está relacionado con un único elemento de B)

5

Continuidad de una función

Haz clic para ampliar la escena

Escena del Proyecto EDAD. Autora:María José García Cebrian

6

Dominio y rango con GeoGebra

En las siguientes páginas podrás interactuar con tres escenas diseñadas en GeoGebra. Es importante que entiendas la funcionalidad de algunos elementos presentes en cada escena, tanto de los deslizadores como de los botones.

7

Primera actividad interactiva con GeoGebra

Usa el deslizador para el trazado o, si lo prefieres, haz clic en el botón de animación.

Haz clic para ampliar la construcción

8

Segunda actividad interactiva con GeoGebra

Usa el deslizador para el trazado o, si lo prefieres, haz clic en el botón de animación.

Haz clic para ampliar la construcción

9

Tercera actividad interactiva con GeoGebra

Usa el deslizador para el trazado o, si lo prefieres, haz clic en el botón de animación.

Haz clic para ampliar la construcción

10

Gráficas y ecuaciones que definen funciones

En la siguiente evaluación interactiva practicarás el concepto de función.

En el primer ejercicio, a partir de varias gráficas de relaciones, debes clasificarlas como función teniendo presente la prueba de la recta vertical para examinarlas, que dice:

Una curva en el plano coordenado es la gráfica de una función si y sólo si ninguna línea vertical corta la curva más de una vez.

En el segundo ejercicio, a partir de varias ecuaciones, debes clasificarlas como función o como no función teniendo presente que una ecuación define a la variable dependiente "y " en términos de la variable independiente "x ". Recuerda que Una función f es una regla que asigna a cada valor "x " del dominio exactamente un valor "y " del codominio, llamado imagen de f(x).

11

Evaluación interactiva - Definición de función

En esta evaluación, debes arrastrar las imágenes o ecuaciones al contenedor correspondiente

Haz clic para ampliar la escena

12

Evaluación interactiva - Evalúa una función

Evalúa la función para un el valor real de la variable “x”. Debes asociar las imágenes “valores de y” con la función respectiva

Haz clic para ampliar la escena

13

Ahora tienes la misma evaluación pero con imágenes de la función, que debes asociar a los valores de la segunda columna. Recuerda que en las parejas de la función en un plano cartesiano los valores de la variable “x” los localizamos en el eje horizontal y los variables de la variable “y” los localizamos en el eje vertical.

Haz clic para ampliar la escena

14

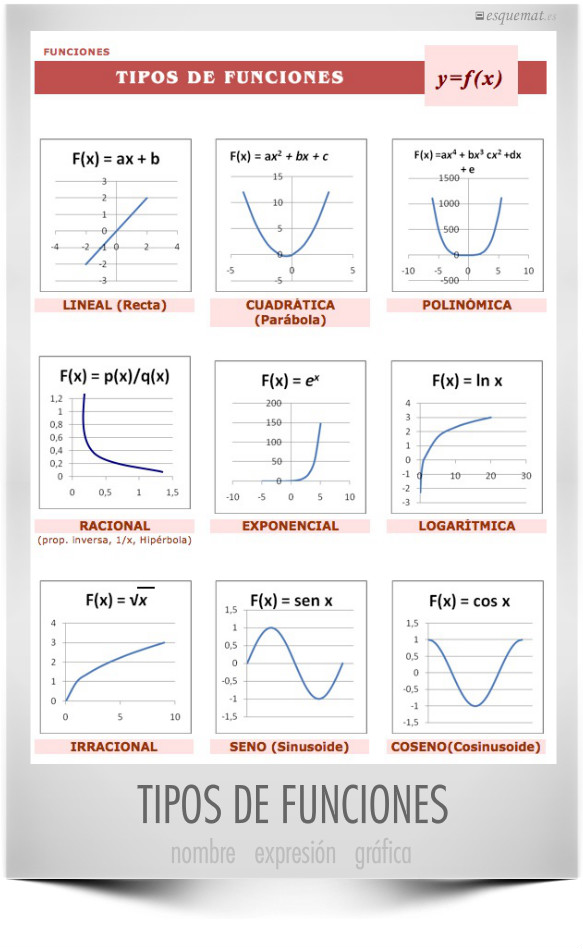
Tipos de funciones - Clasificación analítica

15

Evaluación interactiva - Tipos de funciones

Haz clic en los botones falso o verdadero.

Haz clic para ampliar la escena

16

Evaluación interactiva - Dominio y rango

Asocia gráficas de funciones con su dominio o rango.

Haz clic para ampliar la escena

17

Vídeo interactivo - Determinación del dominio

Para determinar el domino de una función analítica se debe tener en cuenta que no está permitido la división por cero, la raíz de índice par para los números reales negativos y, además, los logaritmos para números negativos y para el número cero no están definidos. Observa con atención el siguiente vídeo:

Haz clic para ampliar el vídeo

18

Evaluación interactiva - Dominio de una función

Teniendo en cuenta las observaciones anteriores, asocia las piezas de la siguiente escena (Haz clic para ampliarla, si lo deseas):

Haz clic para ampliar la escena

19

Créditos y licencia

Créditos

Instituciones y licencia