CÁLCULO DIFERENCIAL
INTERACTIVO

2016
Imagen de portada tomada de https://i.ytimg.com/vi/hJvg9OKdwjo/maxresdefault.jpg
Tabla de contenido
1 |
|
7 | |
11 | |
13 | |
18 | |
20 | |
23 | |
25 | |
30 | |
31 | |
36 | |
39 | |
42 |
i
48 | |
49 | |
51 | |
54 | |
58 | |
62 | |
67 | |
72 | |
77 | |
79 | |
81 | |
82 | |
84 | |
85 |
ii
96 | |
99 | |
104 | |
108 | |
112 | |
116 | |
121 | |
125 | |
133 | |
140 | |
143 | |
151 | |
156 | |
160 | |
164 |
iii
Prólogo

Este libro digital interactivo se ha diseñado utilizando el editor de Descartes para HTML5, de tal forma que se pueda leer en ordenadores y dispositivos móviles sin necesidad de instalar ningún programa o plugin.
El libro se ha elaborado con fundamento en el currículo de la asignatura "Cálculo Diferencial" de la Institución Universitaria Pacual Bravo; no obstante, puede ser utilizado en cualquier Institución que incluya en su desarrollo curricular asignaturas de este tipo. Gran parte de los contenidos del libro se basan en los trabajos del grupo cartesiano del Instituto de Matemáticas de la Universidad Nacional Autónoma de México, liderado por el doctor José Luis Abreu León.
A través de tres capítulos, cerca de 100 objetos interactivos de aprendizaje, animaciones y vídeos, el estudiante puede apropiarse de los objetos de conocimiento necesarios para desarrollar las competencias del Cálculo Diferencial.
1
¿Por qué HTML5?
En 2010 Steve Jobs hizo una fuerte crítica a Flash, en tanto que su desempeño es bueno en ordenadores, pero no es lo mejor para dispositivos móviles. Recomendó, entonces, el uso de HTML5 para la creación de aplicaciones y juegos, además de ser una tecnología sin costo. Con el tiempo, Adobe declaró que iba a dejar de desarrollar la tecnología Flash para dispositivos móviles apoyando a HTML5.
El HTML5 tiene por objetivo la homologación de todos los buscadores y sistemas operativos para que cualquier dispositivo móvil pueda desplegar gráficos, animaciones y videos, entre otras aplicaciones multimedia. Desde 1998 el Consorcio de Internet (World Wide Web Consortium W3C) dejó de evolucionar el protocolo HTML y comenzaron a buscar nuevas maneras de desplegar una red más atractiva desde su base. Tras diversas pruebas y decisiones, en 2007 se formó el grupo actual de trabajo del W3C que revisa la implementación de HTML5.
Su evolución continúa, ya que aún no es estándar, se encuentra en Working Draft (Borrador de Trabajo), pero ya se está aplicando en muchos proyectos Web importantes. Empresas de gran peso en Internet están apoyando HTML5 e impulsando su estandarización y perfeccionamiento, entre ellas podemos nombrar a Google, Mozilla, Adobe y Microsoft y, por qué no, nuestro primer libro digital interactivo.
2
¿Qué es un Objeto Interactivo de Aprendizaje ?
Dado que en este libro el núcleo de desarrollo es el objeto interactivo de aprendizaje, es necesario realizar un inciso en el que se detalle el significado conceptual del mismo, en especial cuando se le está anexando el calificativo de “interactivo”. Existe una amplia gama de definiciones sobre lo que debemos entender por un objeto de aprendizaje (OA). El Comité de Estándares de Tecnologías de Aprendizaje (LTSC: Learning Technology Standards Committee) propone la siguiente definición:
"Un Objeto de Aprendizaje es cualquier entidad, digital o no digital, la cual puede ser usada, reusada o referenciada durante el aprendizaje apoyado por tecnología […] Ejemplos de Objetos de Aprendizaje incluyen una lección, un simple archivo JPEG, contenidos multimedia, un video, simulaciones, cuadros digitales, animaciones…”.
Es común considerar como OA a cualquier recurso digital que pueda ser reutilizado en diferentes ámbitos educativos, teniendo en cuenta que el concepto de reutilización está influido por el contexto en el que puede ser utilizado un OA determinado. Una fotografía sin texto tiene más poder de reutilización que otra que lo incorpore, pues en este último caso se presentan problemas de comprensión del lenguaje.
En general, parece haber consenso en lo referido a que sean recursos digitales que se pueden combinar para construir lecciones, módulos, cursos o, incluso, todo un plan de estudios.
3
Visto de esta manera, el desarrollo de objetos de aprendizaje se configura como un proceso que contempla una secuencia que va desde el diseño, el análisis de herramientas disponibles, la definición de criterios, la reflexión, y a su vez su producción, aplicación y evaluación. La definición más aceptada, desde el contexto de los recursos digitales, establece que el diseño debe contemplar objetivos como: la reutilización, de ahí la posibilidad que brinda para construir unidades más complejas en diferentes contextos; la interoperabilidad, la durabilidad (objetos que no requieren de actualizaciones periódicas) y la accesibilidad (fácilmente identificados y encontrados, bien clasificados por categorías, lo que obliga a almacenarlos en metadatos asociados a él).
Todo lo anterior puede ser válido en el entorno de la web 1.0; sin embargo, en el contexto de los nuevos ambientes virtuales de aprendizaje, el concepto de OA adquiere un nuevo significado o, para ser más precisos, incluye un nuevo componente: la interactividad. Por tanto un OA debe diseñarse a partir de criterios como atemporalidad didáctica, reutilización, interacción y accesibilidad. No en vano, para el caso de las matemáticas, el proyecto ''Definición y selección de competencias clave'', impulsado por la Organización para la Cooperación y el Desarrollo Económico (OCDE), clasifica las destrezas matemáticas como herramientas interactivas, necesarias para resolver múltiples tareas en diversas situaciones; desde esta taxonomía, los OA de la web 1.0 no serían compatibles con estas destrezas, si bien se constituyen en recursos valiosos para los procesos de enseñanza-aprendizaje, ya que no permiten interacción alguna y por tanto podemos considerar que no son más que objetos de información.
4
Pero, ¿Qué es un objeto interactivo? Son objetos de conocimiento que permiten a los usuarios del objeto realizar inferencias. Son dos las condiciones que el objeto tiene que satisfacer para ser interactivo:
La primera condición consiste en que el objeto es utilizado por alguien para representar algo (un volumen de revolución, por ejemplo) y la segunda, que Contessa llama razonamiento subrogatorio, es que el objeto permita que sus usuarios realicen inferencias específicas desde el objeto al fenómeno que representa. Por tanto el objeto no sólo integra la teoría que pretendemos representar, también permite intervenir en su percepción en tanto que interactúa en los procesos cognitivos de los usuarios. La percepción, indudablemente, será de un grado superior. Este objeto de aprendizaje, así comprendido, se constituye en un efectivo mediador (virtual) entre lo que se representa y el usuario que interpreta, o entre la teoría y el usuario, con dos posibles propósitos: que el usuario intervenga sobre lo representado (he ahí la interactividad) y que infiera y deduzca la teoría que sustenta (he ahí la efectividad); es decir, promueve su conocimiento significativo.
Veamos un ejemplo sencillo de objeto de aprendizaje interactivo. En la siguiente página arrastra el punto y observa:
5
Al arrastrar el punto interactúas con la gráfica y, en consecuencia, con el texto que muestra el valor de una función llamada f'(x) en la x donde tienes el punto.
6
1. Introducción al Cálculo
¿Qué es el Cálculo?
Para encontrar el área de una figura rectangular, basta medir dos de sus lados y multiplicar los valores obtenidos. Para encontrar la velocidad de un cuerpo que se mueve con velocidad uniforme, basta medir la distancia que recorre en un tiempo determinado y dividirla entre el tiempo. Esto último equivale a calcular la pendiente de gráfica de la posición del cuerpo con respecto al tiempo, que es una línea recta.
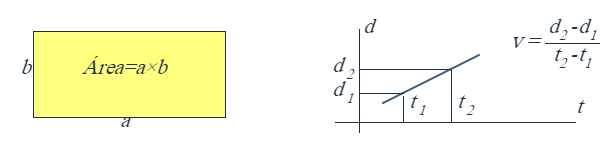
Pero el área de una figura delimitada por curvas o la velocidad instantánea de un cuerpo que se mueve con velocidad variable, no se pueden obtener con procedimientos tan simples
7

Esto requiere de realizar aproximaciones cada vez más parecidas a lo que se quiere calcular, mediante construcciones que podamos manejar, lo cual lleva a considerar no uno sino muchos cálculos, y además algo más complejo que es la obtención de un valor límite, aquel al que se acercan cada vez más los valores aproximados.
Por ejemplo, el área de la figura con frontera curva ilustrada arriba puede aproximarse mediante el área de polígonos de N lados. El área de la figura será el límite de las áreas de esos polígonos. Análogamente, la velocidad en el tiempo t del cuerpo cuya gráfica de movimiento se ilustra arriba, se calcula como el límite de las velocidades medias entre los tiempos t y t+h, cuando h tiende a cero.
8
El Cálculo (llamado también Cálculo diferencial e integral) es la rama de las matemáticas que surge al considerar estos problemas. Para su desarrollo el Cálculo necesita crear los conceptos de límite, integral y derivada, y establecer la profunda relación que existe entre ellos. Dicha relación se conoce como el Teorema fundamental del Cálculo.
La historia del cálculo se remonta a la antigua Grecia con trabajos de los mejores matemáticos griegos como fueron Eudoxo y Arquímedes, y llega a su culminación en el siglo XVIII con los trabajos de Leibniz y Newton. En el siguiente vídeo se describen los conceptos y la teoría creada por Newton y Leibniz.
9
Descubre los personajes
Si deseas saber algo más de los personajes de la página anterior, resuelve el puzle
10
1.1 Coordenadas cartesianas
Para ilustrar la identificación de un punto en el plano a continuación se presenta el plano y un punto que se puede mover libremente con arrastre del ratón y a la vez se pueden observar las coordenadas (x0, y0) del mismo, con una aproximación de hasta dos decimales. Arrastra el punto sobre el plano y observa el valor de sus coordenadas. |
Para identificar un punto de coordenadas (x0,y0) en el plano cartesiano, se procede del siguiente modo: P1. Se localiza el valor x0 en el eje X; P2. Se localiza el valor y0 en el eje Y; P3. Se traza una recta perpendicular al eje X, que pase por x0; P4. Se traza una recta perpendicular al eje Y, que pase por y0; P5. El punto de intersección de ambas rectas es el punto de coordenadas (x0, y0).
11
En el siguiente ejercicio interactivo podrás verificar tu ubicación espacial en el plano cartesiano, determinando la posición de un punto dadas unas coordenadas.
12
1.2 Distancia entre dos puntos
En esta sesión aprenderás cómo calcular la distancia entre dos puntos, dadas las coordenadas de dichos puntos. La sesión incluye un video, conceptos básicos y ejercicios. Te sugerimos realizar las siguientes actividades:
1) Observa el video para comprender cómo se calcula la distancia entre dos puntos.
2) Estudia los conceptos básicos, a través de la interacción en las escenas indicadas.
3) Resuelve los ejercicios propuestos.
13
En la siguiente página practicarás con un ejemplo. Para ello, debes cambiar los valores de las coordenadas de los punto P y Q y observar los cambios en la distancia.
14
Por lo tanto, para calcular la distancia entre P y Q, se sustituyen las coordenadas de cada uno de los puntos en la fórmula (1).
15
A partir del triángulo rectángulo del ejemplo, es sencillo demostrar la fórmula (1). Analiza la demostración que se da a continuación:
16
Finalmente, realiza algunos ejercicios de cálculo de la distancia entre dos puntos.
17
1.3 Coordenadas del punto medio
En este apartado veremos como se encuentra las coordenadas del punto medio de un segmento conocidos sus extremos.
18
En este ejemplo mueve los extremos del segmento y observa cómo se calcula el punto medio.
19
1.4 La pendiente de la recta
La pendiente de una recta la podemos calcular según la información que tengamos de ella, por ejemplo, si conocemos su ángulo de inclinación, la pendiente se calcula como se explica a continuación.
20
21
|
Observa el vídeo e interactúa con el ejemplo. Puedes ver el vídeo en una pantalla más grande, haciendo clic en: |
22
1.5 Ecuación de la recta (y = mx +b)
23
24
1.6 Noción de intervalo
Un subconjunto de números reales de importancia fundamental, tanto en cálculo como en geometría analítica, es aquel formado por aquellos números reales que se encuentran entre dos números fijados de antemano, por ejemplo, todos aquellos números x que satisfacen que 3 ≤ x ≤ 7. Este tipo de conjunto es tan importante que recibe un nombre especial, el de intervalo, y una notación especial, en el ejemplo anterior, el intervalo se denota como [3, 7]. Los corchetes indican que el intervalo contiene a todos los números reales entre 3 y 7, incluyendo a los extremos, es decir, al 3 y al 7.
Los corchetes siempre van asociados con los símbolos ≤ o ≥, sin embargo, también podemos tener al intervalo (3, 7), en cuyo caso los paréntesis indican que este intervalo contiene a todos los números reales entre 3 y 7 sin incluir a los extremos 3 y 7. Los parentesis siempre van asociados a los símbolos < o >
.En la escena de la siguiente página puedes observar distintas gráficas que se encuentran definidas en un intervalo. Observa que éste aparece en forma gráfica, sobre el eje X, como desigualdad y con la notación de intervalo. Utiliza el control gráfico para mover la gráfica.
25
Existen diferentes formas de representar a un intervalo de forma escrita, las cuales tienen su equivalente gráfico. Cuando ponemos un corchete ], queremos indicar que el intervalo incluye al valor que se encuentra en el extremo. Otra forma de escribir esto es usando el símbolo ≥, que en palabras significa mayor o igual que. Por otro lado, si usamos un paréntesis ), queremos decir que el número que se encuentra en el extremo del intervalo se encuentra fuera del intervalo. Esto lo podemos representar con el símbolo >.
26
La forma de representar los intervalos de forma gráfica es poner un punto hueco si no incluye al valor; o un punto relleno, si el valor está incluido en el intervalo. En los siguientes ejemplos, se muestra cada posible intervalo que puede existir, en total cuatro: cerrado, abierto, cerrado por la izquierda y cerrado por la derecha. Para modificar los valores puedes arrastrar los puntos en la gráfica o darle valores en los intervalos.
Tipos de intervalo
Intervalo cerrado
27
Intervalo abierto
Intervalo semiabierto o semicerrado
28
Ejercicios
Selecciona el intervalo que corresponda con la gráfica mostrada
Lo intervalos, entre otras utilidades, permiten expresar la solución de inecuaciones de primer grado
El procedimiento para la solución de inecuaciones de primer grado es similar a como lo hacemos con las ecuaciones; es decir, empleamos las mismas propiedades, excepto que cuando multiplicamos por un número negativo ambos miembros de la inecuación, el sentido de la desigualdad cambia. El resultado será un intervalo.
29
1.7 Inecuaciones de primer grado
Observa, paso a paso, cómo se resuelve la inecuación en el siguiente interactivo:
.La noción de intervalo y la solución de inecuaciones, nos servirán para hallar el dominio y rango de una función, pero, antes de ello, estudiemos el concepto de función.
30
1.8 Noción de función
Como preámbulo a este apartado, observa el siguiente vídeo
Para saber si una gráfica representa a una función, se debe recordar que, para que una relación sea función, debe de tener asignado un solo valor de y para cada x.
31
Una forma de saber si la gráfica representa a una función, es trazando una línea recta vertical en cada valor de x. Si cada recta vertical toca una sola vez a la gráfica, entonces esa gráfica representa una función, en caso contrario, la gráfica no representa a una función. En la siguiente escena, arrastra el control gráfico, punto rojo, a la derecha y observa si la gráfica representa o no una función.
Al observar la gráfica, podemos ver de una forma simple, si representa a una función o no. Basta con trazar líneas rectas verticales (que sean paralelas al eje y). Si la línea corta a la gráfica una sola vez, para cualquier valor de x, entonces la gráfica representa a una función. Si la recta corta a la gráfica más de una vez, para algún valor de x, entonces la gráfica no representa a una función.
32
Ejercicios
Practica lo anterior en la siguiente escena tomada del Proyecto EDAD y diseñada por la profesora María José García Cebrian. Observa la gráfica de la función y haz clic en los botones "SI" o "NO", según el caso.
33
Cuando conocemos la regla de correspondencia que determina a una función, conocemos la manera en que podemos calcular el valor de la ordenada, la cual es la variable dependiente, para cada valor de la abscisa, la variable independiente. Para poder calcular el valor de la ordenada, se debe sustituir el valor de la abscisa en la regla de correspondencia sustituyendo cada x que aparezca en dicha regla por el valor que tenemos de la abscisa. Al realizar todas las operaciones se obtendrá el valor de la ordenada. En la siguiente escena, aparece la regla de correspondencia de una función junto con botones en los que aparecen distintos valores para la abscisa. Oprime estos botones para obtener los correspondientes valores de las ordenadas.
34
Tipos de funciones
En los cursos previos has visto varios tipos de funciones. Algunas de ellas las podrás recordar, a través del siguiente interactivo, en el que puedes modificar algunos de sus parámetros.
35
1.9 Funciones crecientes y decrecientes
Si observas las gráficas de las funciones, te darás cuenta que algunas crecen y/o decrecen a medida que avanzan a lo largo del eje x. Estas variaciones ocurren en los valores que toma la función; es decir, en el cambio de las ordenadas. En esta sesión, aprenderás cuándo una función crece o decrece. Puedes practicar con los ejemplos y los ejercicios que hemos preparado par ti. También puedes observar el video, las veces que desees, hasta que logres el objetivo de esta sesión.
36
Para identificar los intervalos donde una función es creciente a partir de su gráfica, hay que pasar la vista sobre la gráfica de izquierda a derecha. Los intervalos donde la gráfica sube son los intervalos buscados. En otras palabras, buscamos intervalos donde ocurre que, cuando x aumenta f(x) también aumenta.
En términos formales, una función f es creciente en un intervalo si se tiene que:
x1 < x 2 implica que f(x1) < f(x2) para cualesquiera x1, x2 del intervalo.
37
A continuación tendrás cinco ejercicios para verificar lo aprendido, en cada uno de ellos identifica los intervalos donde la función dada sea creciente. Elige la respuesta correcta.
38
1.10 Función continua
De manera informal, decimos que una función es continua en un intervalo, si su gráfica se puede dibujar sin despegar el lápiz del papel en ese intervalo.
Si la función está definida en un sólo intervalo y es continua en éste, entonces se dice que la función es continua.
En términos un poco más formales, una función f es continua en un punto a, si para valores x muy cercanos a a, se tiene que f(x) es casi igual a f(a). Además, una función f es continua en un intervalo si f es continua en cada punto del intervalo.
39
Cuando una función no es continua se dice que presenta alguna discontinuidad. Hay varias razones por las que una función no es continua en un punto: Hay un "agujero" en la gráfica, bien porque la función no está definida en el punto, bien porque su valor queda separado del resto; presenta un salto; o el valor de la función crece (o decrece) indefinidamente cuando nos acercamos al punto.
40
Ejercicios
A continuación se presentan cinco ejercicios para que respondas en qué intervalo es continua la función, debes seleccionar la respuesta correcta para continuar con el siguiente ejercicio.
41
1.11 Dominio y rango de una función
Se llama dominio de una función f al conjunto de valores que toma la variable independiente, x. Se indica como D. El dominio está formado, por tanto, por los valores de x para los que existe la función, es decir, para los que hay un f(x).
El rango, recorrido o imagen es el conjunto de valores que puede tomar la variable dependiente, y, esto es el conjunto de las imágenes. Se representa como R o I.
42
Hallar el dominio de algunas funciones requiere de la determinación de los puntos máximo y mínimo de la función, por ejemplo, para funciones cuadráticas el máximo o mínimo sería el vértice de la parábola. Si bien existen fórmulas para determinar estos puntos extremos, es preferible usar otras técnicas más inmediatas como el concepto de derivada, que estudiaremos más adelante. En otros caso, el procedimiento depende de la ecuación que define la función. A continuación veremos algunos de esos casos.
Un primer caso son funciones del tipo:

Para encontrar el dominio de esta función se siguen los siguientes pasos:
* Igualar a cero el denominador x+b para obtener una ecuación.
* Despejar x de la ecuación.
El dominio de la función serán todos los números reales, excepto el valor de x hallado en el paso 2 que, en general, sería x = -b. Se excluye este valor del dominio porque haría cero el denominador y, en consecuencia, indefinido el valor de f(x).
En la siguiente página puedes practicar con algunos ejercicios.
43
Ejercicios
A continuación se presentan ejercicios, debes seleccionar la respuesta correcta para continuar con el siguiente ejercicio.
En general, para funciones del tipo  el dominio serían todos los reales excepto los valores de la solución de la ecuación Q(x)=0. Veamos algunos ejemplos.
el dominio serían todos los reales excepto los valores de la solución de la ecuación Q(x)=0. Veamos algunos ejemplos.
44
Ejemplos
Haz clic en el botón Continuar para observar paso a paso cómo se halla el dominio.
Ahora, nos ocuparemos de determinar el rango de una función del tipo  con P(x) y Q(x) lineales o cuadráticas.
con P(x) y Q(x) lineales o cuadráticas.
45
En general, para encontrar el rango de una función f(x) debemos buscar los valores y para los cuáles existe x tal que y=f(x). En el caso que nos interesa, cuando f(x) es el cociente de dos polinomios, el problema se traduce en encontrar las yes para las cuales existe x. Si además suponemos que este cociente está reducido, que P(x) y Q(x) no comparten factores comunes, entonces el problema será equivalente a encontrar los valores de y para los cuales la ecuación yQ(x)-P(x)=0 tiene solución.
Como P(x) y Q(x) son lineales o cuadráticos, la ecuación yQ(x) - P(x) = 0 deberá ser lineal o cuadrática en x, lo que vuelve nuestro problema soluble. Pues, debido a las siguientes dos afirmaciones, podemos encontrar las condiciones que debe satisfacer y para que la ecuación yQ(x)-P(x)=0 tenga solcución.
* Ecuaciones lineales. Una ecuación lineal de la forma Bx + C=0 con B distinto de cero siempre tiene solución.
* Ecuaciones cuadráticas. Una ecuación cuadrática de la forma Ax2+Bx+C=0 con A distinto de cero, tiene solución, si y sólo si B2-4*A*C >= 0.
Cabe destacar que las condiciones B≠0, en la primera afirmación; y A≠0, en la segunda, son necesarias, pues de lo contrario la ecuación no sería lineal en el primer caso, o cuadrática en el segundo.
Veamos algunos ejemplos en la página siguiente.
46
Ejemplos
47
2. Límite de una función
El límite de una función es un concepto fundamental del análisis matemático aplicado a las funciones. En particular, el concepto aplica en análisis real al estudio de límites, continuidad y derivabilidad de las funciones reales. Intuitivamente, el hecho que una función f alcance un límite L en un punto c significa que, tomando puntos suficientemente próximos a c, el valor de f puede ser tan cercano a L como se desee. La cercanía de los valores de f y L no depende del valor que adquiere f en dicho punto c.
Aunque implícita en el desarrollo del Cálculo de los siglos XVII y XVIII, la notación moderna del límite de una función se remonta a Bolzano quien, en 1817, introdujo las bases de la técnica épsilon-delta. Sin embargo, su trabajo no fue conocido mientras él estuvo vivo. Cauchy expuso límites en su Cours d'analyse (1821) y parece haber expresado la esencia de la idea, pero no de una manera sistemática. La primera presentación rigurosa de la técnica hecha pública fue dada por Weierstrass en los 1850 y 1860 y desde entonces se ha convertido en el método estándar para trabajar con límites. La notación de escritura usando la abreviatura lim con la flecha debajo es debida a Hardy en su libro A Course of Pure Mathematics en 1908.
https://es.wikipedia.org/wiki/L%C3%ADmite_de_una_funci%C3%B3n
Como un paso previo, haremos una incursión al concepto de límite desde las sucesiones. En las siguientes páginas definimos las sucesiones, sus tipos, algunos ejemplos y, finalmente, el concepto intuitivo de límite.
48
2.1 Sucesiones
Una sucesión es una función que asocia a cada entero positivo un número real. Una sucesión se puede expresar de varias maneras
a) Describiendo en palabras cómo obtener cada uno de sus términos.
b) {an }, es decir, escribiendo entre llaves la expresión de su término general.
c) a1, a2, a3,... , es decir, escribiendo los primeros términos hasta que sea evidente para el
lector cuál es la regla para obtener los siguientes.
En el siguiente vídeo se muestra una de las sucesiones que aparece con frecuencia en la naturaleza: la sucesión de Fibonacci.
49
El siguiente recuadro muestra ejemplos de sucesiones con sus definiciones y sus gráficas. Se puede mover el espacio arrastrándolo a la izquierda y a la derecha, también se puede cambiar la escala con el pulsador que está en la parte inferior derecha.
50
2.2 Límite de una sucesión
Se dice que una sucesión de números reales { an } converge a L si para cualquier número positivo ε, los términos an de la sucesión distan de L menos que ε, para n suficientemente grande. La sucesión: 2.1, 2.01, 2.001, 2.0001, ... converge a 2 y la sucesión {1/n} converge a cero. Éstos son dos ejemplos de sucesiones que convergen.
La sucesión 1, -1, 1, -1, 1, ... no converge. Tampoco converge la sucesión {3n}. Éstos últimos son dos ejemplos de sucesiones que no convergen. Cuando una sucesión {an} converge a un número L, se dice que L es el límite de {an} y se escribe:
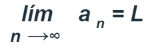
Ejemplos de convergencia
Algunas de las sucesiones que se muestran en el recuadro de la siguiente página convergen y otras no. Estudia cada caso y lee la explicación. Observa que la sucesión converge cuando para cualquier franja de ancho arbitrario ε > 0, la cola de la sucesión queda dentro de ella. En otras palabras, |an-L| < ε para números enteros n suficientemente grandes.
51
Ejemplos
En la siguiente página, hemos incluido un interactivo de la profesora Consolación Ruiz. Puedes hacer todos los ejercicios que desees. Es importante que analices bien cuál es el método empleado para hallar el límite de la sucesión en cada caso.
52
Ejercicios - Cálculo de límites
53
2.3 Límites unilaterales
En este apartado tendremos como objetivos: identificar el valor de límites unilaterales a partir de la observación de la gráfica de una función y, obtener el valor del límite a partir de la observación de la gráfica.
El límite de una función f(x) en un punto x0 es el valor al que se acercan los valores de la función cuando la variable x se acerca a x0. Las funciones no siempre tienen límite en cualquier punto. Inicialmente, observa con detenimiento el siguiente vídeo:
54
Explora los distintos ejemplos que se dan en el interactivo para formarte una idea intuitiva de cuándo una función, en un punto x:
a) tiene límite.
b) tiene límite por la izquierda.
c) tiene límite por la derecha.
d) no tiene límite.
e) tiende a más o menos infinito.
En cada ejemplo, mueve el punto x para buscar los puntos en donde la función no tiene límite.
55
Cuando el límite de una función en un punto x existe y es L, se escribe:

y se lee así: El límite de f cuando x tiende a x0 es L. Cuando los límites laterales por la izquierda y la derecha existen, pero no son iguales, se dice que la función no tiene límite. Así mismo, si la función tiende a ± ∞ en un punto x0, también se dice que no tiene límite; aunque en esos casos está permitido escribir:

Ejercicios
De acuerdo a lo explicado en el vídeo y en los ejemplos anteriores, realiza los jercicios de la siguiente página en la que aparecen las gráficas de unas funciones y un punto. En cada caso, deberás decidir si la función tiene límite en ese punto y cuáles son sus límites laterales.
En cada ejercicio responde si la función tiene límite o no y cuáles son los valores de los límites laterales, en estos últimos puede responder en la caja de texto o, en algunos casos, seleccionando la respuesta en el menú de la derecha.
56
57
2.4 Cálculo de límites no indeterminados
Vamos a obtener el valor del límite de una función f(x) cuando x tiende a un número a y no presenta indeterminación.
Nota: Debido a que es más natural el concepto de continuidad que el concepto de límite, es conveniente estudiar primero las lecciones de continuidad y después las de límite. Si una función es continua en un número a, entonces el valor del límite de ella, cuando x tiende a a, es f(a); es decir,
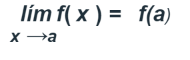
La gran mayoría de las funciones que utilizamos cotidianamente son continuas en todos los números donde están definidas.
● Las funciones polinomiales, f(x)=cnxn + cn-1xn-1 + ... + c1x + c0, son continuas en todos los reales.
● Las funciones racionales, es decir, los cocientes de funciones polinomiales
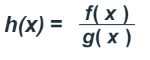
son continuas en todos los números a para los cuales g(a)≠0.
● Las funciones trigonométricas, seno, coseno, tangente, cotangente, secante y cosecante, son continuas en todos los números donde están definidas.
58
● Las funciones logaritmo y exponencial son continuas en todos los números donde están definidas.
59
En el siguiente vídeo podrás observar cómo se aplican las operaciones con límites relacionadas en la página anterior:
60
Para calcular el límite de una función f en un punto a, analizamos si la función es continua en ese número; si lo es, simplemente evaluamos la función en a, y éste es el valor del límite buscado. Los casos en los que la función no está definida en a, o la función no es continua, los estudiaremos en lecciones posteriores. Practica con los siguientes ejemplos:
61
2.5 Cálculo de límites con indeterminación
En esta sesión aprenderás cómo evaluar límites con la indeterminación (0/0). Estudia las explicaciones, observa los ejemplos, practica con los ejercicios y repasa con el video.
Vamos a obtener, por factorizacion, el valor del límite de un cociente de polinomios que dé lugar a una indeterminación del tipo (0/0). Como dijimos antes, es más natural el concepto de continuidad que el concepto de límite. Si una función es continua en un número a, entonces el valor del límite de ella, cuando x tiende a a, es f(a); es decir,
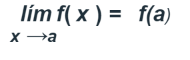
62
Cuando la función no está definida en a porque presenta alguna indeterminación, es necesario buscar un valor L tal que haga continua la función en a. Un caso frecuente es cuando la función es cociente de dos polinomios
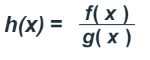
y ambos polinomios valen cero en a, es decir, g(a)=0 y h(a)=0. En este caso no podemos aplicar la regla del cociente de límites.
El siguiente es el procedimiento para calcular este tipo de límites:
• Evaluar el límite en el valor dado de x para comprobar que el resultado es una indeterminacion del tipo (0/0), si esto ocurre, significa que la función no es continua.
• Factorizar el numerador y el denominador de forma que en los dos haya un mismo factor.
• Cancelar este factor que está en el numerador y se repite en el denominador.
• Evaluar la función restante en el valor dado de x, que ahora ya es continua y cuyo resultado ya no es una una indeterminación.
63
Ejemplos
64
Otro caso frecuente de indeterminación es cuando una función racional requiera de un proceso de racionalización. Observa algunos ejemplos.
65
2.6 Límites de funciones trigonométricas
67
El procedimiento para calcular el primer límite es el siguiente:
68
En el siguiente vídeo podrás observar cómo se aplica la propiedad anterior y en la página siguiente un interactivo con ejercicios resueltos que usan los tres tipos de límite.
69
Algunos ejemplos de límites de funciones trigonométricas:
70
En los siguientes ejercicios, escribe las respuestas en los cuadros de texto. Si la respuesta es correcta, se inhabilitará el cuadro y podrás continuar. En estos campos puedes escribir expresiones aritméticas, por ejemplo 3+5, pi/2, etc.
71
2.7 Límites al infinito
El límite de una función f(x) al infinito es el número al que se acercan los valores de la función cuando la variable x tiende a +∞ o a -∞. Las funciones no siempre tienen límite al infinito.
Explora los distintos ejemplos que se dan en el interactivo para formarte una idea intuitiva de los diferentes tipos de límites al infinito:
72
73
Los límites, cuando x → ∞, se pueden sumar, restar, multiplicar y dividir, siempre y cuando no se presente una indeterminación, así, por ejemplo:

Cuando se presenta alguna indeterminación, hay que reescribir la función para eliminar dicha indeterminación. Esto se verá en un apartado posterior.
74
Ejemplos
Veamos algunos ejemplos típicos. En el cuadro de texto escribe un número grande y oprime INTRO para evaluar la función en ese número. A la derecha, puedes arrastrar el plano y hacer zoom para ver el comportamiento de la gráfica.
75
Ejercicios
Para cada función responde si tiene límite en -∞ o en +∞. Si tiene límite, escríbelo y si no, elige la opción correcta entre: tiende a -∞, tiende a +∞ o no tiende a nada.
76
2.8 Límites al infinito con indeterminación
En este apartado vamos a evaluar límites al infinito con indeterminación. Lo haremos con funciones racionales cuyo límite presenta una indeterminación. Inicialmente observa el video para comprender cómo se resuelve la indeterminación en un ejemplo dado.
77
Cuando se presenta alguna indeterminación, hay que reescribir la función para eliminar dicha indeterminación. En el caso del vídeo lo hicimos dividiendo todos los términos por la x de mayor exponente, recordando que en el radical se ingresa elevando al cuadrado la x seleccionada.
En los siguientes ejercicios analiza el límite propuesto, resuélvelo y, finalmente, escribe el resultado en los dos campos de texto que se presentan.
78
2.9 Discontinuidad removible
Una función presenta discontinuidad evitable o removible en un punto a, si tiene límite en un punto, pero la función en ese punto tiene un valor distinto o no existe, por ejemplo:
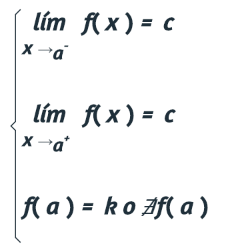
En el caso anterior la función tiene limite en x = a, pero el valor del limite no es el mismo que el valor de la función en ese punto o la función no existe en ese punto.Esta discontinuidad se pueden evitar o remover asignando a la función, en el punto de discontinuidad, el valor del limite en ese punto. Es decir f(a) = c.
En el siguiente interactivo, puedes resolver todos los ejercicios que desees sobre las discontinuidades removibles.
79
2.10 Asíntotas
Informalmente decimos que la recta y=a es una asíntota horizontal de f si el valor de f(x) se acerca tanto como uno quiera al valor de a tomando el valor de x lo suficientemente grande, ya sea positivo o negativo. En otras palabras, la gráfica de la función f se acerca cada vez más a la recta y=a, a medida que x se hace cada vez más grande bien sea hacia la derecha o hacia la izquierda. A continuación se presentan los distintos casos donde se puede identificar una asíntota horizontal en la gráfica de una función f:
81
3. Derivada de funciones
Los problemas que llevaron al Cálculo
Durante el siglo XVII el interés primordial de los científicos de la época se centró en el estudio del movimiento, el movimiento de los objetos en la superficie de la Tierra o cerca de ella y el movimiento de los cuerpos celestes. Naturalmente, en este estudio, era de vital importancia determinar la rapidez y la aceleración de los cuerpos en movimiento, así como la dirección en que se está moviendo un objeto en cualquier punto de su trayectoria. Los movimientos de los objetos no son en línea recta y su rapidez es variable, por lo que la dirección en que se está moviendo un objeto en cualquier punto de su trayectoria es variable de un momento a otro. Entonces su determinación presenta una nueva clase de dificultad. Estos son dos de los problemas que dieron lugar a los procedimientos del Cálculo.
En matemática, la derivada de una función mide la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.
https://es.wikipedia.org/wiki/Derivada
82
El tercer problema que ocupó a los matemáticos y físicos de la época fue encontrar los valores máximo y mínimo de funciones. Cuando se dispara una bala hacia arriba, tal vez se desee saber qué altura alcanzará. Podemos determinar la altura máxima de movimientos simples, pero no es suficiente para analizar el movimiento de los cuerpos que no son próximos a la superficie de la Tierra, por ejemplo, la distancia máximo o mínima de un planeta al Sol. Tampoco lo es para analizar el movimiento de un cohete, en cuyo recorrido se aleja tanto de la Tierra, que debe tomarse en cuenta la variación de la aceleración debida a la gravedad o la aceleración necesaria para despegar.
El cuarto problema fue determinar longitudes, áreas y volumenes. Para encontrar el área de una figura rectangular, basta medir dos de sus lados y multiplicar los valores obtenidos. Pero el área de una figura delimitada por curvas no se pueden obtener con procedimientos tan simples. Por otra parte, los objetos pueden ser tan grandes como la Tierra, o las longitudes a calcular son las de las órbitas de los planetas en un tiempo dado. Todos estos problemas ocuparon la mente de cientos de matemáticos. Fueron Newton y Leibnitz quienes reconocieron claramente la íntima relación entre ellos.
83
3.1 Sobre hombros de gigantes
A mediados del siglo XVII dos grandes científicos sientan las bases del Cálculo diferencial, Newton y Leibnitz. Como introducción a este último capítulo, te invitamos a que observes el siguiente vídeo, que hace parte de la serie Universo matemático, titulado "Sobre hombros de gigantes"
84
3.2 Concepto de derivada
Cambio, razón de cambio y razón de cambio instantánea
Se debe tener cuidado en distinguir cambio, razón de cambio promedio y razón de cambio instantánea. Cuando se arroja una pelota hacia arriba, cambia su altura respecto al suelo. Presiona el botón Animar para que observes este cambio. Pero quizá precisamos saber la velocidad inicial a la que debe ser lanzada para alcanzar determinada altura, o qué velocidad tendrá al momento de tocar tierra.
La velocidad es la razón de cambio de la altura respecto al tiempo. En este caso la flecha representa la velocidad de la pelota durante su trayectoria al ser lanzada hacia arriba desde el punto O.
85
Cambio, razón de cambio y razón de cambio instantánea
Conforme un objeto se mueve transcurre el tiempo, que representamos con t. Cuando un objeto se mueve en línea recta, su velocidad promedio es el cociente (y1-y0)/(t1-t0) donde y1, y0 son las posiciones en los momentos t1, t0 respectivamente. Cabe aclarar que estos momentos son instantes y no intervalos de tiempo. Como a cada tiempo corresponde una posición, podemos hacer una gráfica de posición contra tiempo. Observa, eligiendo un ejemplo y pulsando el botón de animar, el movimiento del punto rojo y la gráfica que genera.
86
La velocidad promedio entre t0 y t1
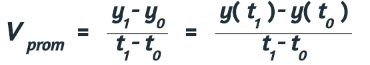
es la pendiente de la secante, es decir, la recta que pasa por los puntos de la gráfica correspondientes a t0 y t1. Mueve los puntos en el eje del tiempo t. Cuando un objeto recorre una distancia d en un lapso de tiempo t, llamamos rapidez promedio al cociente de la distancia recorrida entre tiempo transcurrido d/t.
87
Ejemplos
Observa y analiza los siguientes ejemplos de rapidez o velocidad promedio. Haz clic en los botones inferiores, siempre se presentará un ejemplo diferente
88
Resuelve los problema propuestos de rapidez o velocidad promedio. Haz clic en el botón de Otro ejercicio, siempre se presentará un ejercicio diferente. Haz clic en la imagen de la calculadora si necesitas usarla.
89
En los ejemplos de la sección anterior consideramos el cambio en la posición de un punto sobre la gráfica con respecto al tiempo. Pero no todos los fenómenos estudiados tienen que ver con el tiempo. En general, tomemos los puntos x0 y x1. La razón de cambio promedio de y=f(x) es
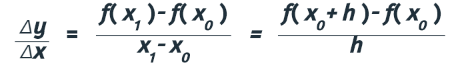
si h = x1 - x0, es decir, la pendiente de la recta secante a la gráfica de la función y=f(x)por los puntos x0 y x1.
90
Fijemos el punto x0. Si h disminuye, es decir, si x1 se aproxima a x0, la recta secante se aproxima a la recta tangente a la gráfica de f(x)en el punto x0. De manera más precisa expresamos esto como

es decir, el límite de f(x0 + h)- f(x0) cuando h tiende a 0. A este límite, lo llamamos la derivada de f(x) en el punto x0 y se denota por f'(x0). f'(x0) nos indica qué tanto y cómo está cambiando la función f(x) en el punto x0.
91
La razón de cambio promedio se calcula en un intervalo, ya sea de tiempo [t0, t1], o en general en el intervalo [x0, x1], si x0 < x1, y si x1 < x0, en [x1, x0].
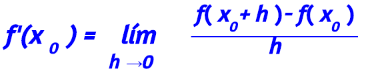
es una razón de cambio instantánea, es decir, en el instante x0, y es la pendiente de la recta tangente a la gráfica en x0. Si estamos considerando un intervalo de tiempo, esta razón de cambio instantánea es la velocidad instantánea de un objeto cuya trayectoria es la gráfica de f(x).
92
De lo expuesto, hemos definido la derivada de la función en un punto (x0, f(x0)) como la pendiente de la recta tangente a ese punto, pendiente que obtenemos al aproximar la pendiente de la secante por un proceso de límite. Así que el problema de encontrar la derivada se resuelve calculando, para cada x = x0 + h, la pendiente de la recta calculando el límite cuando h tiende a 0.
Un procedimiento simple es el siguiente:
1. Calcular el valor f(x0 + h), que aparece en el numerador.
2. Calcular la diferencia f(x0 + h) - f(x0), que aparece en el numerador.
3. Calcular el cociente

y simplificar lo más posible.
4. Calcular el límite del resultado anterior, cuando h tiende a 0.
En la siguiente página puedes observar y analizar algunos ejemplos.
93
Ejemplos
94
Ejercicios
En los siguientes ejercicios, cada vez que escribas un resultado en un campo de texto, oprime intro. Si la respuesta es correcta, se deshabilitará el campo.
95
3.3 La notación de la derivada
La derivada de una función en un punto x indica qué tanto está cambiando la función en ese punto; así, por ejemplo, si la función indica la posición de un móvil en una carretera recta, la derivada indica la velocidad del móvil, es decir, expresa cómo está cambiando la posición en ese momento. Geométricamente, si representamos a la función f mediante su gráfica en un plano, su derivada en un punto x es la pendiente de la recta tangente a la gráfica en el punto (x, f(x)), y ésta indica qué tanto está creciendo o decreciendo la función en ese punto. En el plano del interactivo, arrastra el punto sobre la gráfica y observa el comportamiento de la recta tangente.
96
A lo largo de la historia del cálculo, diferentes autores han ideado diferentes notaciones para la derivada de una función en un punto, algunas de estas notaciones son:
La notación más simple es la de Lagrange, que consiste en poner una prima arriba a la derecha de la función, f'(x), por ejemplo, (x2 -3x + 4)', (sen x)'

97

98
3.4 Fórmulas para funciones algebraicas monómicas
Vamosd obtener por fórmula la derivada de funciones del tipo:
f(x) = c
f(x) = cx
f(x)=xn
f(x)=cxn
cuando c es una constante y n un entero o racional.
99
100
Ejemplos
Selecciona la fórmula que se va a utilizar en el ejemplo y después presiona el botón Continuar.
101
Ejercicios
A continuación se muestra una función para derivar.
- Primero selecciona la fórmula que se debe emplear para resolverlo.
- Después escribe el resultado obtenido después de derivarlo.
102
Aplicación
Este simulador permite comprender la derivada como razón de cambio.
103
3.5 Fórmulas para funciones trigonométricas
Vamos a obtener por fórmula la derivada de funciones del tipo:
f(x) = sen x f(x) = cot x
f(x) = cos x f(x) = sec x
f(x) = tan x f(x) = csc x
104
105
Ejemplos
Selecciona la derivada que quieras practicar y presiona el botón Continuar para ver el procedimiento.
106
Ejercicios
Escribe el resultado que se obtiene al derivar la función planteada. Debes escribir el coeficiente y seleccionar la fórmula adecuada.
107
3.6 Fórmulas para funciones trascendentes
Vamos a obtener obtener por fórmula, la derivada de alguna de las siguientes funciones:
f(x)= ln x f(x) = ex
f(x)= logax f(x)= ax
108
109
Ejemplos
Selecciona la fórmula que deseas observar en el ejemplo y después presiona el botón Continuar para ver el procedimiento de ésta.
110
3.7 Derivada de una suma o resta de funciones
La derivada de la suma de dos funciones es la suma de sus derivadas, y análogamente, la derivada de la diferencia de dos funciones es la diferencia de sus derivadas:
(f+g)'(x) = f'(x) + g'(x) (regla de la suma)
(f-g)'(x) = f'(x) - g'(x) (regla de la diferencia)
de modo que, para derivar una función que es suma (o diferencia) de dos funciones, basta obtener la derivada de cada una de las funciones y después sumar (o restar) las funciones obtenidas.
A continuación se muestra un polinomio con su derivada. Presiona el botón para ver otros ejemplos.
112
113
114
Ejercicios
Resuelve los siguientes ejercicios. Pulsa el botón Ver solución para ver cómo se resuelve el ejercicio.
115
3.8 Derivada de un producto de funciones
116
117
Refuerzo interactivo
Utiliza el siguiente cuadro interactivo para repasar la fórmula de la derivada de un producto de funciones. Arrastra y suelta las expresiones faltantes en el lugar correcto.
118
Ejemplos
A continuación se muestran ejemplos de la derivada del producto de dos funciones.
119
Ejercicios
Resuelve los siguientes ejercicios. Si deseas ver cómo se resuelve el ejercicio, pulsa el botón Ver solución.
120
3.9 Derivada de un cociente de funciones
121
122
Ejemplos
En el siguiente cuadro interactivo se muestran ejemplos de la derivada del producto de dos funciones.
123
Ejercicios
Resuelve los siguientes ejercicios de opción multiple. Pulsa Verificar cuando hayas elegido tu opción.
124
3.10 Regla de la cadena
125
En la siguiente escena puedes observar geométricamente el significado de la composición. Mueve el punto x en la primera gráfica, la flecha roja muestra el valor g(x), en la segunda gráfica se evalúa h en u = g(x) y en la tercera gráfica ese valor, h(u) = h(g(x)) se asocia con x. Con los pulsadores puedes cambiar las funciones g y h.
126
127
128
Ejemplos
Pulsa los botones para ver el procedimiento, paso a paso, aplicado a ejemplos en los cuales las dos funciones son algebraicas.
129
Ejercicios
130
Ejemplos con funciones trascendentes
Pulsa los botones para ver el procedimiento, cada vez que hagas clic en el botón Anterior aparecerá un ejemplo diferente.
131
Ejercicios con diferentes tipos de funciones
Los siguientes ejercicios fueron diseñados por Miguel Ángel Cabezón Ochoa. Selecciona el tipo de derivada a practicar, haciendo clic en una de las opciones de la columna izquierda. La útima opción muestra tipos de funciones aleatoriamente.
Tienes a disposición una gran infinidad de ejercicios. Te sugerimos realizarlos en tu cuaderno y verificarlos con la solución del interactivo
132
3.11 Gráficas de la función derivada
133
En la página anterior se muestran las gráficas de dos funciones y un punto que se mueve sobre cada una de ellas. Conforme el punto se mueve, en cada gráfica inferior se muestra el valor de la pendiente instantánea de la función en ese punto. Es decir, las gráficas inferiores corresponden respectivamente a las derivadas de las gráficas superiores.
A continuación, se describen algunas caracteristicas importantes de la gráfica de la derivada de una función:
1. Si en todos los puntos de un intervalo, la inclinación de la gráfica de una funcion es a la derecha (o lo que es lo mismo, su pendiente es positiva), el valor correspondiente en la gráfica de su derivada será positivo. Conforme mayor sea la inclinación a la derecha en la gráfica original, mayor será el valor correspondiente en la gráfica de su derivada. Si una porción de una gráfica se encuentra inclinada a la derecha, se dice que dicha porción es creciente.
2. Si en todos los puntos de un intervalo, la inclinación de la gráfica de una funcion es a la izquierda (o lo que es lo mismo, su pendiente es negativa), el valor correspondiente en la gráfica de su derivada será negativo. Mientras más inclinada a la izquierda se encuentre la gráfica original en un intervalo, menor será el valor correspondiente en la gráfica de su derivada en ese intervalo. Si una porción de una gráfica se encuentra inclinada a la izquierda, se dice que dicha porción es decreciente.
3. Si para todos los puntos para un intervalo, la gráfica de una funcion es horizontal, el valor correspondiente en la gráfica de su derivada será cero.
134
Ejemplos
Pulsa el botón Generar ejemplo para visualizar la gráfica. Puedes mover el plano arrastrándolo y acercar o alejar la imagen con el pulsador.
135
Cuando se quiere identificar la gráfica de f'(x) a partir de f(x) es útil encontrar los puntos en que cambia f(x) de creciente a decreciente o viceversa. Esos puntos son máximos y mínimos respectivamente en f(x) y corresponden a las raíces de f'(x). Ahora vamos a tomar el camino al revés (ir de f'(x) a f(x)), al localizar raíces en f'(x) encontramos los máximos o mínimos en f(x). Más aún, si f'(x) cruza las abscisas de forma ascendente, podemos deducir que se trata de un mínimo en f(x), mientras que si lo cruza de forma descendente, se trata de un máximo en f(x). Observa los interactivos de la siguiente página. Mueve los puntos en las gráficas superiores (f'(x) y g'(x)) y observa la gráfica inferior.
En los dos planos superiores se muestran las gráficas de las funciones derivadas y en los dos planos inferiores, se muestran respectivamente las gráficas de sus funciones originales. En resumen:
1. Las raíces de las funciones derivadas, que son los valores de x para los que éstas se hacen cero, corresponden a los máximos y mínimos de las funciones originales.
2. Los valores de x que corresponden a máximos locales de las funciones derivadas corresponden a puntos en la gráfica original dónde ésta cambia de ser cóncava hacia arriba a cóncava hacia abajo. De igual forma, los mínimos en la gráfica de las funciones derivadas, corresponden a puntos en la gráfica original dónde ésta pasa de ser cóncava hacia abajo a cóncava hacia arriba. Estos puntos se les conoce como puntos de inflexión y en ellos la segunda derivada es cero. Esto es, si se derivara la función original dos veces y se sustituyera uno de estos puntos en ella, el resultado sería cero.
136
Recuerda mover los puntos de las gráficas superiores, te detienes en los puntos de inflexión (raíces, máximos y mínimos). Las expresiones f''(x) y g''(x) se conocen como segunda derivada de la función, es decir, "la derivada de la derivada", en el próximo apartado veremos este tipo de derivadas sucesivas.
137
Ejemplos
A continuación, se muestran otros ejemplos tanto con funciones algebraicas como trascendentes.
138
Eercicios
Resuelve los siguientes ejercicios para obtener la forma de la función f(x) a partir de la forma de f'(x).
139
3.12 Derivadas sucesivas
140
Ejemplos
141
Ejercicios
Para cada función planteada, calcula la derivada correspondiente.
142
3.13 Puntos críticos de una función
Máximos y mínimos relativos
Un máximo (mínimo) relativo de una función f es un punto de la gráfica de f donde la función cambia de ser creciente (decreciente) a ser decreciente (creciente). Observa la siguiente animación, en ella se muestran algunos máximos y mínimos relativos.
Para encontrar los máximos y mínimos relativos hay que analizar la derivada de la función, tal como lo haremos a continuación.
143
En el siguiente cuadro interactivo mueve el punto rojo y observa la derivada de f en cada punto x (la pendiente de la recta dibujada). Pon especial atención en los casos en que x corresponde a un máximo o a un mínimo relativo.
Los valores de x en donde f'(x) = 0 o f'(x) no está definida son llamados valores críticos. Al punto de la gráfica (x,f(x)) asociado a cada valor crítico se le llama punto crítico. En el cuadro interactivo anterior se pueden notar dos cosas:
- Los máximos y mínimos relativos son puntos críticos.
- No todos los puntos críticos son máximos o mínimos relativos.
144
En el caso de los polinomios, para determinar dónde es creciente o decreciente la función y cuáles son sus máximos y mínimos relativos, se puede proceder de la siguiente manera:
1. Se calcula la derivada de f: f'(x).
2. Se calculan los números críticos. Para lograr esto se encuentran las raíces de f'(x)=0. Cuando el polinomio es de grado dos o tres, se tendrá que f'(x)=0 será una ecuación lineal o cuadrática. Esto permite usar un despeje o la fórmula general para encontrar las raíces.
3. Se especifican intervalos relevantes. Si los numéros críticos encontrados en el paso 2 son p1, p2, entonces los intervalos que será necesario analizar son: (-∞, p1), (p1, p2), (p2, ∞).
4. Determinar si f es creciente o decreciente en cada intervalo. Se determina el signo de f'(x) en cada uno de los intervalos encontrados en el paso 3. Para esto se elige un valor x0 en cada intervalo y se evalúa en la derivada f'(x0):
- Si f'(x0)>0, entonces f es creciente en el intervalo.
- Si f'(x0)<0, entonces f es decreciente en el intervalo.
5. Encontrar los máximos y mínimos relativos. Los máximos relativos serán aquellos puntos críticos donde f cambie de creciente a decreciente; y los mínimos relativos, de decreciente a creciente.
145
Ejemplos
146
Puntos de inflexión y concavidad
Ya estudiaste como determinar los intervalos en los que una función crece o decrece. Ahora determinaremos estos intervalos para la derivada de la función, especialmente cuándo las pendientes de las tangentes de una función crecen o decrecen. Resuelve los siguientes ejercicios en los cuales se pide ordenar cuatro gráficas en orden creciente según su pendiente.
147
Podemos ahora abordar cuándo crece o decrece la derivada de una función. Esto es, cuándo la pendiente de la recta tangente a la gráfica de la función es creciente o decreciente al recorrer la gráfica de izquierda a derecha. Mueve el punto rojo de izquierda a derecha y determina si la pendiente de la recta tangente a la gráfica crece o decrece. Verifica tu respuesta y presiona Siguiente.
148
Como se puede observar en la escena anterior, la forma de la gráfica, cuando la derivada crece, se ve curvada hacia arriba y cuando decrece se ve curvada hacia abajo. Más precisamente, la gráfica es cóncava hacia arriba cuando la derivada crece y cóncava hacia abajo cuando la derivada decrece. Los puntos x, donde la gráfica de f cambia de concavidad, se llaman puntos de inflexión. Es decir, son los puntos en los que la derivada de f cambia de ser creciente a decreciente.
Procedimiento
Como la derivada es la pendiente de la tangente, entonces sólo hay que determinar en qué intervalos f' crece o decrece. Y, por lo tanto, usamos el método visto anteriormente para determinar los intervalos en los que una función crece o decrece:
1. Calcular la derivada de f', esto es f''.
2. Encontrar los números críticos de f', es decir, encontrar las x tales que f''(x)=0,
3. Determinar los intervalos de prueba, es decir, los intervalos en los que los puntos críticos dividen a la recta real.
4. Analizar el signo de f'' en cada uno de los intervalos de prueba. Si f'' es positiva, entonces f es cóncava hacia arriba y si f'' es negativa, entonces f es cóncava hacia abajo.
5. Los valores críticos de f', donde f es cóncava hacia arriba de un lado y hacia abajo del otro, son los puntos de inflexión.
149
Ejercicios
Resuelve cada uno de los siguientes ejercicios.
150
3.14 Teoremas sobre funciones derivables
Para entender los enunciados y las demostraciones de los teoremas sobre funciones derivables que vamos a estudiar, son necesarios los siguientes prerrequisitos:
Definiciones de intervalos abiertos y cerrados de la recta real.
Definiciones de función continua y derivable tanto en un punto como en un intervalo de la recta real.
Teorema de Weierstrass sobre funciones continuas: ''Una función continua en un intervalo cerrado alcanza en él al menos un máximo y un mínimo absolutos''.

Teorema de la anulación de la derivada en un extremo: ''Si una función es derivable en un intervalo abierto (a, b) y alcanza en un punto c del intervalo un máximo o un mínimo, la derivada de la función se anula en c''.
151
Teorema de Rolle
Supongamos que una función f(x) cumple las dos hipótesis de los dos teoremas mencionados, es decir, f(x) es continua en un intervalo cerrado [a, b] de R y derivable en el correspondiente intervalo abierto (a, b). Imaginemos que, además, los valores de f(x) en los extremos coinciden, es decir, f(a)=f(b).
Según el teorema de Weierstrass, f(x) alcanza un máximo y un mínimo en [a, b]. Hay dos posibilidades:
Si alcanza los dos extremos en a o en b, por ser f(a)=f(b), ambos extremos son iguales y la función es constante en [a, b], por lo que su derivada se anula en todos los puntos del intervalo cerrado [a, b].
Si alcanza alguno de los dos extremos en el intervalo abierto (a, b), en virtud del teorema de la anulación de la derivada en un extremo, la derivada de la función se anula en ese punto del intervalo abierto.
En cualquier caso, podemos asegurar que la derivada de f(x) se anula al menos en un punto c del intervalo abierto (a, b). Esa es la tesis del teorema de Rolle y los razonamientos expuestos son las ideas fundamentales de una demostración del teorema basada en los dos teoremas citados en la página anterior. En la siguiente gráfica observa que:
152
1. La función f(x) cumple las siguientes condiciones en el intervalo: f(x) es continua en [0.5, 4.5], f(x) es derivable en (0.5, 4.5) y f(0.5)=f(4.5).
2. Cuánto vale la derivada de f(x) en cada punto (modifica el valor de la abscisa arrastrando el punto o con la barra)
3. Hay puntos en los que la recta tangente a la gráfica es paralela al eje de las x y por tanto la derivada en ellos es nula.
4. Halla dichos puntos y comprueba el resultado analíticamente sabiendo que f(x)=(x-1)(x-2)(x-3)(x-4).
5. Entre 2 raíces consecutivas de la ecuación f(x)=0 existe al menos una de la ecuación f'(x)=0 y que entre 2 raíces consecutivas de la ecuación f'(x)=0 existe como máximo una raíz de la ecuación f(x)=0.
153
Teorema del Valor Medio o de Lagrange
El teorema dice que dada cualquier función f continua en el intervalo [a, b] y derivable en el intervalo abierto (a, b), entonces existe al menos algún punto c en el intervalo (a, b) tal que la tangente a la curva en c es paralela a la recta secante que une los puntos (b, f(b)) y (a, f(a)). Es decir:
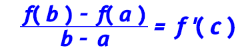
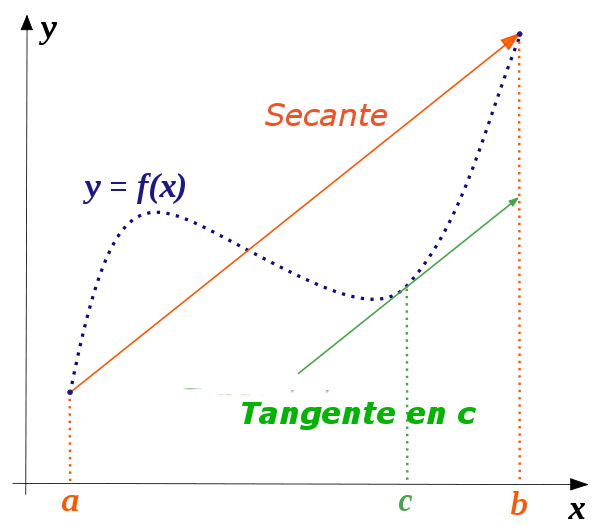
154
El teorema del valor medio de Lagrange, de hecho, es una generalización del teorema de Rolle
https://es.wikipedia.org/wiki/Teorema_del_valor_medio
155
3.15 Ecuación de la recta tangente en un punto
156
157
Ejemplos
Analiza los siguientes ejemplos. Haz clic en el botón Siguiente para otro ejemplo diferente.
158
3.16 Derivación implícita
160
161
Ecuaciones como la de Descartes se denominan ecuaciones paramétricas, puesto que es posible cambiar los valores de los coeficientes o exponentes (parámetros), dando origen a diversas curvas llamadas paramétricas. En el siguiente interactivo podrás observar algunas de estas relaciones y la curvas que se obtienen al variar los parámetros a, b, c y giros.
162
Ejercicios
Resuelve en tu cuaderno los ejercicios planteados y luego haz clic en el botón Solución.
163
3.17 Aplicaciones de la derivada
Las aplicaciones de la derivada son muchas y en varias áreas del conocimiento. En ingeniería sismoresistente, por ejemplo, la ecuación que gobierna el movimiento horizontal de una edificación es: F = m · ü, donde u es el desplazamiento horizontal de la edificación y ü la aceleración, es decir, ü = d2u/dx2 o, si se prefiere u''; esta ecuación es la segunda ley de Newton que, en términos matemáticos, es una ecuación diferencial, no en vano Einstein afirmaba que el mayor aporte que se obtuvo de las derivadas fue la posibilidad de formular diversos problemas de la física mediante ecuaciones diferenciales. La notación para la segunda derivada (ü) fue utilizada por Newton.
En otros casos se aplica la derivada para medir la rapidez con que se produce el cambio de una magnitud o situación, por ello, se constituye en una herramienta de cálculo fundamental para Ingenieros, Físicos, Químicos, Biólogos, Economistas, Sociólogos y un gran etcétera.
En este apartado no resolveremos problemas de estas disciplinas, pues se requiere avanzar en otros estudios avanzados para ello. En el caso del cálculo de la deriva de un edificio, la aparente expresión simple de Newton demanda cálculos complejos que no están al alcance de este libro. No obstante, presentamos dos aplicaciones relacionadas con el movimiento estudiado en un curso de física básica.
164
Rapidez instantánea de un móvil
La velocidad promedio de un objeto que se mueve a lo largo de una línea recta está dada por la expresión:
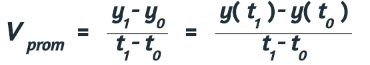
donde y1, y0 son las posiciones en los momentos t1, t0, respectivamente. Puedes observar que como el móvil puede retroceder en un lapso de tiempo ∆t = t1 -t0 positivo, es posible que el desplazamiento y1 - y0 sea negativo y entonces la velocidad promedio también sea negativa.
En ocasiones este cociente es siempre el mismo, entonces decimos que la velocidad es constante, es decir, que el cuerpo se mueve siempre a esa velocidad. Pero no siempre es así. Por ejemplo, los cuerpos que caen recorren una distancia mayor por unidad de tiempo a medida que van cayendo; un automóvil que frena va disminuyendo la distancia recorrida por unidad de tiempo y un objeto colgado de un resorte disminuye su rapidez al acercarse a su máximo desplazamiento, para cambiar de dirección cuando lo alcanza.
En el siguiente interactivo podrás observar con más detalle estos tipos de movimiento.
165
166
Ejemplos
Observa y analiza los siguientes ejemplos.
167
Aceleración instantánea de un móvil
De manera que la aceleración se obtiene derivando dos veces la función posición, una para obtener la velocidad y la segunda para obtener la aceleracion como derivada de la velocidad.
169
Ejemplos
Observa y analiza los siguientes ejemplos.
170
Créditos y licencia
Créditos
|
Adaptación de escenas a JavaScript: |
Juan Guillermo Rivera Berrío |
||
|
Diseño y programación del libro: |
Juan Guillermo Rivera Berrío |
||
|
Revisión: |
José Román Galo Sánchez |
||
|
Librería turn.js: |
Emmanuel García |
||
|
Herramienta de edición: |
DescartesJS |
||
|
Fuente: |
Amaranth |
Instituciones y licencia
Autores
Este libro digital interactivo se realizó gracias a los aportes de profesores dedicados a la producción de contenidos digitales. De las facultades de Ciencias y de Matemáticas de la Universidad Autónoma de México (UNAM), 13 profesores diseñaron gran parte de los interactivos de la obra. Por otra parte, cuatro profesores españoles y uno colombiano completan el grupo de autores.
José Luis Abreu León
José Román Galo Sánchez
Juan Guillermo Rivera Berrío
Héctor de Jesús Argueta Villamar
María Juana Linares Altamirano
Zinnya de Villar Islas
Alberto Bravo García
Fernando René Martínez Ortíz
Carlos Hernández Garciadiego
Norma Patricia Apodaca Álvarez
Valentina Muñoz Porras
Consolación Ruiz Gil
Miguel Ángel Cabezón Ochoa
Octavio Fonseca Ramos
Carlos Alberto Serrato Hernández
María de Lourdes Velasco Arregui
Alejandro Radillo Díaz
Jesús Ángel Sánchez García



