Título de la obra
Los números complejos

María José García Cebrian
Primera edición: 2017

Diseño del libro: Juan Guillermo Rivera Berrío
Diseño de cubierta: Diana María Velásquez García
Librería turn.js: Emmanuel García
Herramienta de edición: DescartesJS
Fuente: Amaranth

Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co
ISBN: 978-958-56476-0-2

Esta obra está bajo una licencia Creative Commons 4.0 internacional: Reconocimiento-No Comercial-Compartir Igual.
Todos los objetos interactivos y los contenidos de esta obra colectiva están protegidos por la Ley de Propiedad Intelectual.

2. Parte real y parte imaginaria

Si consideramos la unidad imaginaria 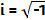 y la representamos en el punto (0,1) del plano, podemos situar de la misma forma los números 2i, 3i, ..., -i, -2i,... en el eje vertical, es decir los números bi que llamaremos imaginarios. Entonces un punto cualquiera del plano (a, b), con a y b números reales, puede escribirse como (a, 0) + (0, b), esto es como la suma de un número real y un número imaginario.

• Los números complejos son de la forma a + bi, donde a es la parte real y b es la parte imaginaria. Cada número complejo z se puede representar en el plano mediante el punto Z(a, b) llamado afijo o bien mediante el vector OZ.

• Dos números complejos son iguales si lo son las partes reales y las partes imaginarias respectivas.

4

3. Operaciones con complejos: sumar y restar

Los números complejos se pueden sumar o restar siguiendo las reglas de las operaciones con números reales.

• Para sumar dos números complejos se suman respectivamente las partes reales y las partes imaginarias. Así dados  z₁ = a₁+ b₁i  y  z₂ = a₂+ b₂i  su suma es:
z₁ + z₂ = (a₁+ a₂) + (b₁+ b₂)i
• Como en los números reales para restar dos complejos hay que sumar al minuendo el opuesto del sustraendo.

6

4. Operaciones con complejos: producto y cociente

Los números complejos se pueden multiplicar siguiendo las reglas de las operaciones con números reales y teniendo en cuenta que i · i = i² = -1.

• z₁ · z₂ = (a₁+b₁i) · (a₂+b₂i) = a₁·a₂ + a₁·b₂i + b₁·a₂i + b₁·b₂i² = (a₁·a₂ - b₁·b₂) + (a₁·b₂ + b₁·a₂)i

8

2. Producto y cociente de complejos en forma polar

La relación entre la forma polar de dos números complejos y la de su producto y cociente, nos permite multiplicar y dividir de forma muy sencilla.

Si expresamos los complejos en forma trigonométrica y operamos:

r_α = r(cos α + i sen α)          r'_β = r'(cos β + i sen β)

• El producto:

Observamos que el módulo del número complejo resultante es el producto de los módulos de los factores y el argumento Recuerda:
cos (α + β) = cos α · cos β - sen α · sen β
sen (α + β) = sen α · cos β + cos α · sen β la suma de los argumentos

• El cociente:

Y el resultado del cociente es un número complejo que tiene por módulo el cociente de los módulos y por argumento Recuerda:
cos (α - β) = cos α · cos β + sen α · sen β
sen (α - β) = sen α · cos β - cos α · sen β la diferencia de los argumentos

            

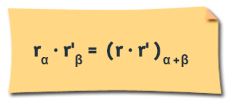
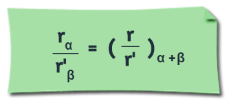
14

3. Potencias de complejos en forma polar

16

4. Raíces de números complejos

Observa que:

• Todo número complejo tiene n raíces n-ésimas. Los afijos de estas n raíces están situados sobre una circunferencia y son los vértices de un polígono regular de n lados.

18

Giro de centro el origen

24