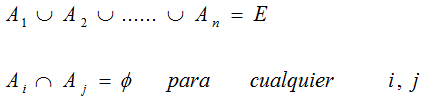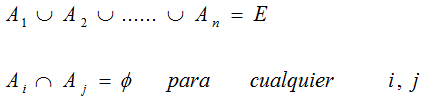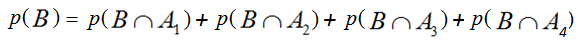En cualquier espacio muestral se pueden observar múltiples sucesos.
Sin embargo, es extraordinariamente importante poder considerar en el
conjunto total del espacio una determinada disposición de sucesos
sencillos de manera que no se solapen unos con otros y tal que la unión
de ellos cubran totalmente y sin ambigüedad a todo el espacio muestral. En este sentido, si por ejemplo pensamos en el espacio muestral de los
resultados posibles del lanzamiento de un dado, los sucesos
elementales: {1} , {2}, {3}, {4}, {5} y {6} cumplen las condiciones anteriores, pero no serían los únicos. Otras formas de
"dividir" el espacio muestral con estas premisas podrían ser:
- {salir par} , {salir impar}
- {salir menor de 3}, {salir mayor o igual de 3}
- {salir primo}, {no salir primo}
¿Qué descomposición utilizar?, obviamente dependerá de lo que se pregunte en cada problema,
pero como veremos más adelante, la disposición de esta manera del
espacio muestral será primordial desde un punto de vista práctico.
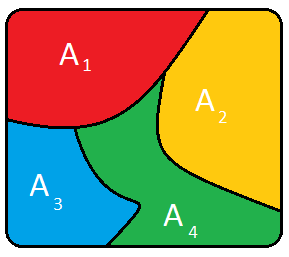
Cuando un conjunto de sucesos cubren totalmente un experimento aleatorio y además estos
sucesos no tienen ningún elemento en común, estamos hablando de un
sistema completo de sucesos. En el lenguaje matemático, se dice que los
sucesos A
1 , A
2 , A
3 , .....A
n
, constituyen un sistema completo de sucesos para un determinado
experimento aleatorio si y solo si la unión de todos ellos es igual a todo el espacio
muestral y además son incompatibles dos a dos; esto es: la intersección
de cualquier pareja de los mismos es vacía.
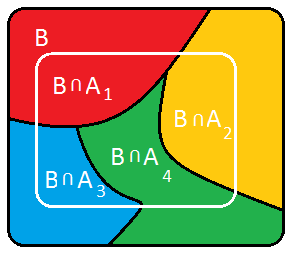
Si se tiene un sistema completo de sucesos, en base a él, cualquier otro suceso se puede descomponer en sucesos independientes, para ello basta intersecar este suceso con cada uno de los del sistema completo.
En la imagen anterior podemos observar cómo se ha realizado una partición del suceso en cuatro sucesos independientes y consecuentemente la probabilidad de ese suceso se puede obtener como la suma de las probabilidades de cada uno de ellos: