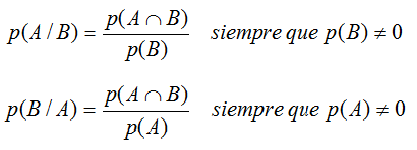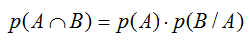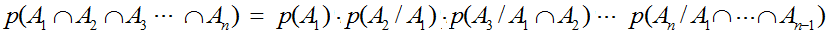6. Probabilidad condicionada
Supongamos que disponemos de una urna en la que hay 4 bolas negras y
una blanca. Si sacamos una bola, la probabilidad de que sea blanca
obviamente sería 1/5. Si la bola extraida la devolvemos a la urna y
realizamos una nueva extracción, la probabilidad de que la bola sea
blanca no ha variado y vuelve a ser la misma. Si por el contrario la
primera bola que extraemos no la devolvemos a la urna, este hecho
influye de forma notable en la probabilidad de que la segunda bola sea
blanca, es decir la probabilidad de que la segunda bola sea blanca
depende o está condicionada por lo que ha ocurrido en la primera
extracción.
Existen muchas situaciones en las que la ocurrencia de un suceso
influye en la ocurrencia o no de otro. Así por ejemplo en medicina, el
hecho de que una mujer sea portadora de cierta enfermedad influye en
que el próximo hijo que tenga adquiera dicha enfermedad, o por ejemplo
si una persona es fumadora el riesgo de padecer hipertensión es mucho
mayor que en un no fumador.
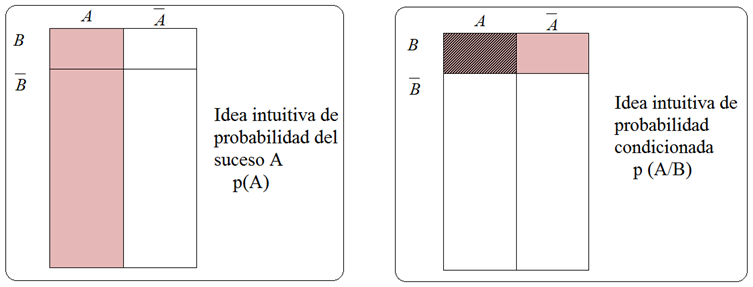
Se denomina probabilidad condicionada del suceso A respecto del suceso
B (probabilidad de A condicionado a B) y se representa p(A/B) al
cociente:
De las definiciones anteriores se obtiene la fórmula general para la probabilidad de la intersección de sucesos.
Esta definición se puede generalizar al caso de la intersección de varios sucesos:
En la siguiente escena puedes comprobar la diferencia entre la
probabilidad de los sucesos cuando se realiza devolución de la carta
extraida y cuando no se hace.
El principal resultado relacionado con la probabilidad condicionada,
especialmente útil desde el punto de vista práctico, es el teorema
conocido con el nombre de probabilidad total que describiremos en un apartado posterior.