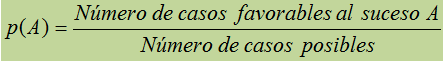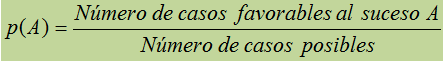5.2. Definición de Laplace
Desde el punto de vista práctico, la
definición que mejor se adapta a la resolución de la mayoría de los
problemas de probabilidad es la de Laplace. Sin embargo desde la óptica
del rigor matemático puede decirse, sin duda, que es la peor.
Para poder aplicarla es necesario contar con un espacio muestral con un número finito de sucesos simples y
todos ellos han de tener la misma posibilidad de suceder, es decir que sean sucesos equiprobables. En este supuesto se
define la probabilidad de cualquier suceso A como:
En el vídeo siguiente podemos ver un ejemplo en el que los sucesos no son equiprobables y por tanto no es aplicable la probabilidad de Laplace.
En el vídeo siguiente podemos ver un ejemplo en el que los sucesos no son equiprobables y por tanto no es aplicable la probabilidad de Laplace.

Vídeo enlazado desde YouTube, licencia de YouTube estándar
En la escena siguiente puedes observar la probabilidad de algunos sucesos;
simplemente tienes que contar los casos favorables y los posibles y efectuar el cociente.
A continuación practica con la siguiente escena donde podrás realizar tanto ejercicios como quieras y necesites, y se corregirán automáticamente tus respuestas.