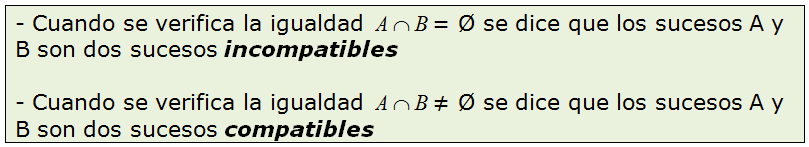3. Operaciones con sucesos
En el conjunto de todos los sucesos asociados a un espacio muestral,
se puede operar con dichos sucesos
para obtener a su vez otros. En este sentido y desde el punto de vista
matemático se puede definir la unión y la intersección de sucesos, y con estas operaciones dicho conjunto adquirirá una
estructura matemática muy importante que se denomina Álgebra de Boole.
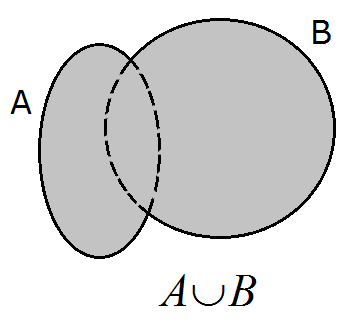
3.1. Unión de sucesos
El suceso unión de A y B es el suceso que ocurre cuando ocurre A,
ocurre B u ocurren ambos. Está formado por todos los elementos de A y
todos los de B. Lo indicamos así:
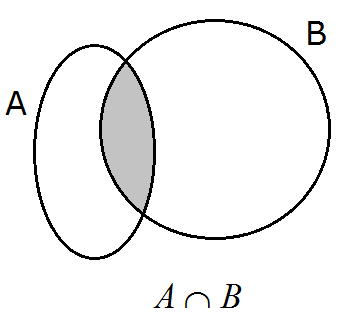
3.2. Intersección de sucesos
El suceso intersección de A y B, es el suceso que ocurre cuando
ocurre A y ocurre B. Está formado por los resultados comunes a los
sucesos A y B. Lo indicamos así:
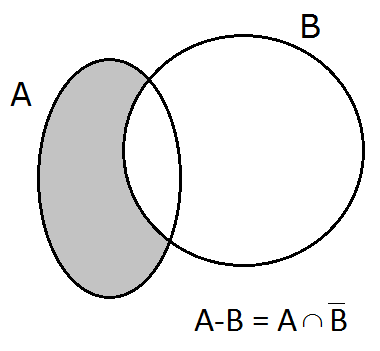
3.3. Diferencia de sucesos
En realidad no se trata de una nueva operación ya que se define a
partir de las dos anteriores. Sin embargo dada la gran asiduidad y el
carácter fundamentalmente práctico con el que aparece en muchas
situaciones merece la pena que hablemos de ella en un apartado
propio.La diferencia de dos sucesos,que se denota A-B o bien A\B, es el suceso que ocurre
cuando ocurre A, pero no ocurre B.
En la siguiente escena pueden observarse algunos ejemplos de sucesos y de operación con ellos.
En la siguiente escena se pueden ver algunos ejemplos de sucesos compatibles e incompatibles.