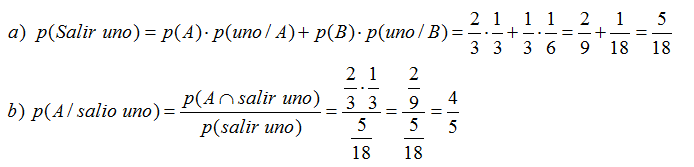11.2. Esquematización en árbol

1. En una autopista, un conductor cambia de carril de forma totalmente aleatoria cada minuto. Si la autopista tiene cuatro carriles, cuál es la probabilidad de que a los cuatro minutos se encuentre en el carril del que partió en un principio? (Estudia los casos de carril interior y exterior)

SOLUCIÓN
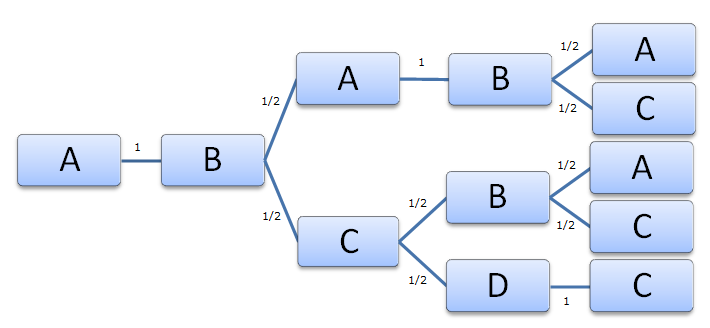
Situación de la autopista:
Primer caso: Supongamos que parte de un carril exterior:

{Acabar en A partiendo de A}
p({Acabar en A partiendo de A})=(1)(1/2)(1)(1/2)+(1)(1/2)(1/2)(1/2) = 1/4 + 1/8 = 3/8
Análogamente desde el otro carril exterior D el resultado sería el mismo.
p({Acabar en D partiendo de D})=(1)(1/2)()1)(1/2)+(1)(1/2)(1/2)(1/2) = 1/4 + 1/8 = 3/8

Segundo caso: Supongamos que parte de un carril interior:

p({Acabar en B partiendo de B}) = (1/2)(1)(1/2)(1) + (1/2)(1/2)(1/2)(1) + (1/2)(1/2)(1/2)(1) +(1/2)(1/2)(1/2)(1/2) + (1/2)(1/2)(1)(1/2) =
1/4 + 1/8 +1/8 +1/16 + 1/8 =
p({Acabar en B partiendo de B}) = 11/16
Análogamente si parte del carril interior C
p({Acabar en C partiendo de C}) =  11/16

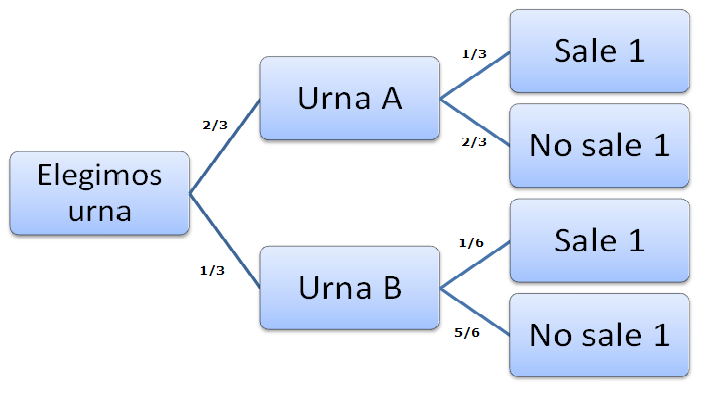
2. Una urna A contiene 3 bolas numeradas del uno al tres y otra urna B contiene 6 bolas numeradas del uno al seis. La urna A tiene el doble de probabilidad de ser elegida que la urna B. Si se elige una urna al azar y se extrae una bola, calcula la probabilidad de que tenga el número uno. Si la bola extraída tenía el número uno, calcula la probabilidad de que proceda de la urna A.

SOLUCIÓN
Dibujamos el diagrama en árbol que esquematiza la situación