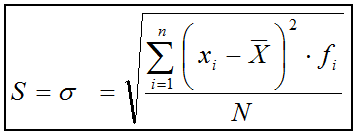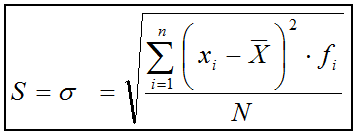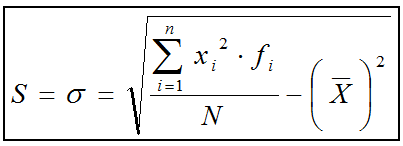6.3. Desviación típica.
La desviación típica se define como la
raíz cuadrada positiva de la varianza. Tiene el mismo cometido que ésta
y además la ventaja de que las unidades en las que se mide son las
mismas que las de los datos de la distribución. Puede considerarse la
medida de dispersión por excelencia y aparece como tecla o función
directa en cualquier calculadora o programa estadístico.
Si tenemos en cuenta excrupulosamente la definición, la fórmula para el cálculo de la desviación típica sería:
De la misma forma que en el apartado
anterior. Si desarrollamos y simplificamos la expresión anterior se
llega a otra mucho más simple que es la que se utiliza en la práctica y
cuya expresión es:
En el apartado cuarto de la escena anterior podemos ver reflejados los datos que están incluidos en el intervalo de centro la media aritmética y radio la desviación típica, y también de radio el doble de la desviación típica. Hay resultados que bajo ciertas circunstacias
(cuando la población es normal) indican que al menos el 68% de los datos están en incluidos en el primer caso y al menos el 95% en el segundo. En otros cursos estudiaremos que es una distribución normal.
En la siguiente escena puedes practicar el cálculo de la media y de la desviación típica.