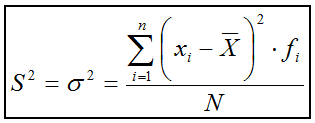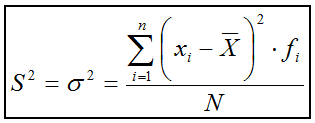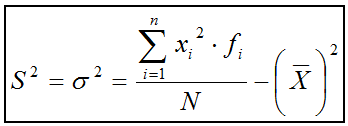La medida de dispersión más popularizada es sin duda la varianza. La filosofía de esta medida es la misma que la de la desviación media, esto es, detectar las variaciones de cada valor respecto a la media aritmética. Sin embargo, como alternativa al valor absoluto cuyo objeto es evitar que se compensen esas variaciones, aquí se elevan esas diferencias al cuadrado y ello además "exagera" estas diferencias. Por último considera el promedio de dichas diferencias al que denomina varianza. Se usa la letra S para variable discreta y la letra griega sigma para variable continua.

A partir de la fórmula anterior y después de desarrollar y simplificar se obtiene otra expresión equivalente para la varianza que permite un cálculo más directo y sencillo ya que en las tablas estadísticas que solemos construir en el cálculo de la media se han calculado los productos xifi y ahora basta multiplicar este valor de nuevo por xi.
Se suele recordar diciendo:

<< La varianza es igual a la media de los cuadrados menos el cuadrado de la media>>

El principal inconveniente que presenta la varianza es que las unidades no son las mismas que las de los datos de la distribución (se ha elevado al cuadrado). Esto se solventa con la definición de un nuevo parámetro que se calculará a partir del anterior que es la desviación típica y que definimos en el siguiente apartado.