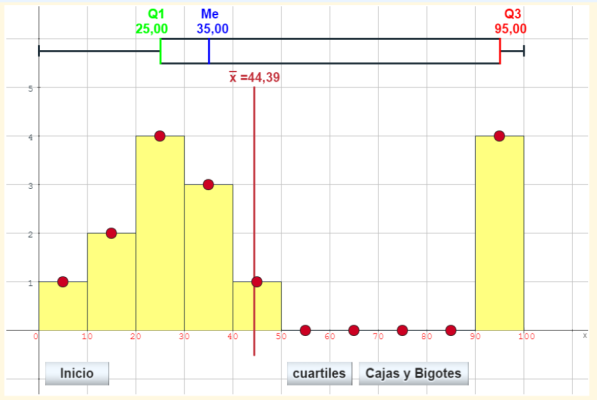
- El primer cuartil Q1 es el valor de la variable que deja por debajo de ella al 25% de los valores de la población.
- El segundo cuartil Q2 que coincide con la Mediana (Me) es el valor de la variable que deja por debajo al 50% de la población.
- El tercer cuartil Q3 es el valor de la variable que deja por debajo de ella al 75% de la población.
Si queremos asociar valores representativos del intervalo a los cuartiles, muchos autores señalan simplemente la marca de clase de dichos intervalos y otros están de acuerdo en utilizar una fórmula que interpola linealmente los valores en los correspondientes intervalos. En los ejercicios prácticos utilizaremos las marcas de clase de los intervalos Q1 y Q3.
El concepto de cuartiles se extiende también al de percentiles como podremos observar en las siguientes escenas. El percentil Pi es el valor de la variable que deja por debajo de ella al i% de los valores de la población, por tanto el primer cuartil coincide con el percentil 25, el segundo con el percentil 50 y el tercero con el 75.
Escena desarrollada por María José García Cebrian(RED Descartes)
A continuación puedes experimentar cómo los valores atípicos influyen sensiblemente en la media y en los cuartiles, y esa influencia es menor para la mediana.
Escena desarrollada por José R. Galo Sánchez