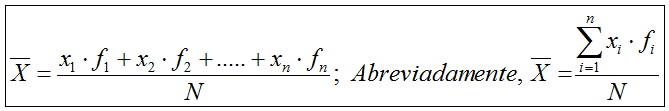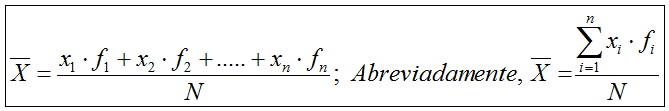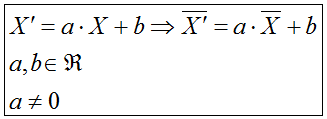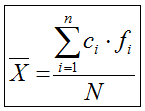Es una medida de centralización aplicable tanto a variables discretas y continuas, pero no para caracteres cualitativos ya que estos no son cuantificables.
La media aritmética se define como la suma de todos los datos dividida entre el número total de los mismos. Como habitualmente dispondremos de una tabla de datos con sus correspondientes frecuencias absolutas, aplicaremos:

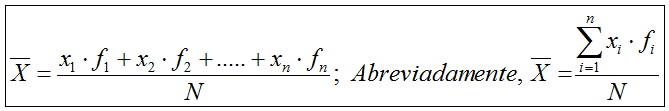
La propia definición de media aritmética da pie a algunas características y comentarios de este parámetro, como por ejemplo:

• La media no tiene porqué ser un  valor propio de la variable.
• Es muy sensible a cambios y valores extremos en los datos.
• Se comporta de forma natural en relación a las operaciones aritméticas suma y producto por un escalar; es decir si a todos los datos de una distribución se les suma una misma cantidad, la media resultante sería la  anterior más dicha cantidad. Si multiplicamos (dividimos) todos los datos de una distribución por una cantidad distinta de cero, la media resultante sería la anterior multiplicada (dividida) por dicha cantidad. Es decir:

Escena desarrollada por Juan Jesús Cañas Escamilla(RED Descartes)

Escena desarrollada por José Ireno Fernández Rubio(RED Descartes)

Para el caso de variable continua, solamente tenemos que  sustituir xi por ci siendo ésta última la marca de clase de cada intervalo; es decir el punto medio o valor central del intervalo. Por abuso de lenguaje se suele utilizar indistintamente también para variables continuas el símbolo xi para las marcas de clase

En la siguiente escena podemos observar cómo influye en la media la inclusión de un nuevo dato o su eliminación:

Escena desarrollada por María José García Cebrian(RED Descartes)