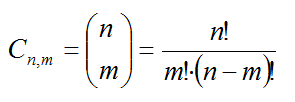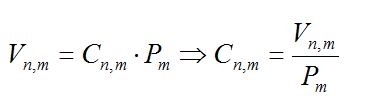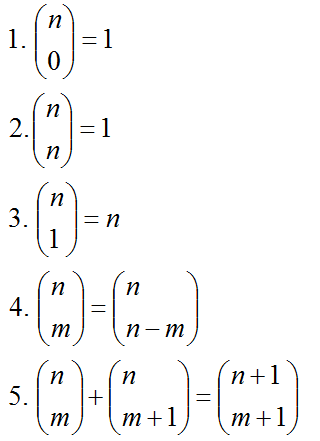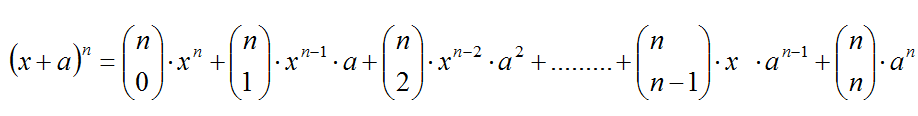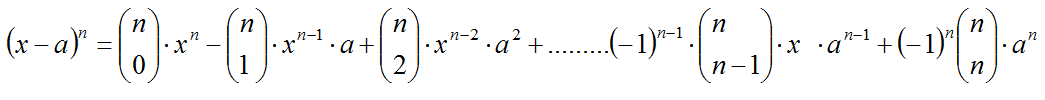7. Combinaciones sin repetición
Y de repente ¡deja de importar el orden!
Todas las semanas Loterías y Apuestas del Estado organiza un sorteo
consistente en la elección de seis números de un total de 49 posibles.
El juego es muy sencillo puesto que se gana premio si la combinación
que tú has elegido coincide con la que públicamente y aleatoriamente se
realiza ante notario mediante un procedimiento consistente en la
extracción sin reemplazamiento de seis bolas de un bombo en el que
están las 49.
Analizando un poco la situación nos damos cuenta que dos personas que
señalen los mismos seis números pero en distinto orden, en realidad
tienen la misma apuesta. es decir las 6!=720 formas distintas en las que se
pueden seleccionar seis números se tendrán que identificar como una
sola.
Por tanto para localizar todas las posibles apuestas, dividiremos V49,6 entre las P6 .
Existen multitud de situaciones parecidas en las que necesitamos
conocer el número de agrupaciones en las que NO IMPORTA EL ORDEN. Por
ejemplo: Seleccionar cuatro alumnos de una clase que irán de excursión
o repartir cinco entradas entre diez amigos para ir a un concierto.

Denominamos combinaciones ordinarias o sin repetición de
n elementos tomados de
m en
m, (siendo m menor o igual que n) a las distintas agrupaciones de
m elementos de manera que:
- En cada grupo entren m elementos distintos.
- Dos grupos son distintos si difieren en algún elemento.
El número de combinaciones ordinarias de
m elementos tomados de
m en
m ,lo denotaremos
Cn,m y se calcula:
Se puede observar fácilmente que:
Las combinaciones sin repetición de n elementos tomados de m en m, podrían formarse a partir de considerar las variaciones sin repetición de n elementos tomados de m en m y posteriormente identificar las posibles reordenaciones de una agrupación, (permutaciones de m elementos), como una única ya que el orden no interviene en la agrupación que estamos considerando; esto es:
Puedes practicar en la siguiente escena:
En el siguiente video podemos observar el planteamiento de un problema que requiere de la combinatoria y su solución.
Vídeo enlazado desde YouTube, licencia de YouTube estándar
Propiedades de los números combinatorios
Los números combinatorios aparecen
muy frecuentemente en multitud de situaciones en Matemáticas, Física,
Biología, etc...Figuran como tecla directa en cualquier calculadora
científica. Como propiedades más interesantes merecen destacarse:
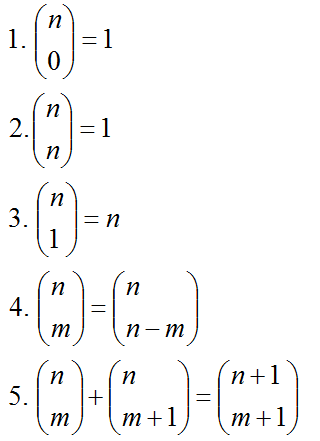
Cuando no existían calculadoras
científicas, el cálculo de números combinatorios requería de un trabajo
complicado. El triángulo de Pascal permitía de una forma recurrente y
muy fácil calcular cualquier número combinatorio, aunque es verdad que
para cantidades elevadas también era bastante engorroso.
En el siguiente video se realiza un análisis del triángulo de Pascal.
Vídeo enlazado desde YouTube, licencia de YouTube estándar
En la siguiente escena puedes ver muchas líneas del triángulo de Pascal y unas propiedades curiosas.
Binomio de Newton
Una de las aplicaciones más interesantes
desde el punto de vista algebraico para los matemáticos, constituye el
desarrollo de las distintas potencias de un binomio. Conocido
como binomio de Newton, utiliza los números combinatorios y sus
propiedades para desarrollar de forma fácil y directa la potencia
natural de cualquier expresión del tipo: