6. Permutaciones con repetición

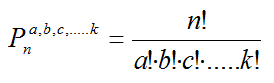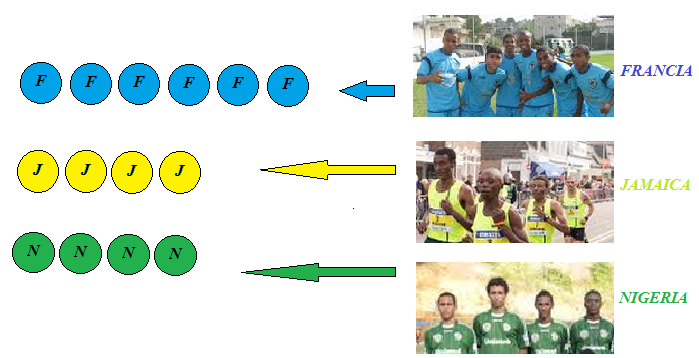
Imaginemos ahora una carrera por equipos. Es decir, una carrera en la que lo importante es el país por el que participas y no el atleta individual.
Si en esta carrera intervienen 6 atletas franceses, 4 atletas jamaicanos y 4 atletas nigerianos. ¿De cuántas maneras diferentes puede acabar la carrera atendiendo solamente a los equipos?
Este caso lo podemos simplificar la situación  identificando los atletas mediante las iniciales de sus respectivos países.
FFFFFF, JJJJ , NNNN.
El problema es por tanto buscar todas las formas posibles de ordenar en la misma fila 6 efes, 4 jotas y 4 enes.

A continuación puedes observar como se irían confeccionando algunas de las ordenaciones. Piensa por un momento que si cerraras los ojos y te cambiaran de lugar dos letras iguales, si los abres no percibirías ningún tipo de cambio.

Por ello necesitamos contar todos los casos en los que no distinguiríamos las ordenaciones si cambiamos de lugar letras iguales

 Denominamos permutaciones con repetición de n elementos en los que uno de ellos se repite "a" veces, otro "b" veces y así hasta el último que se repite "k" veces
(a+b+c+...+k = n) a todas las ordenaciones posibles de estos n elementos. Consideramos dos ordenaciones distintas si difieren en el orden de colocación de algún elemento (distinguible).
  Denotaremos a este tipo de permutación como:

     

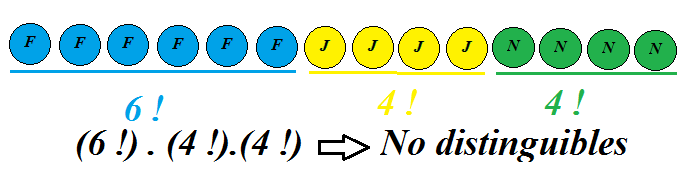
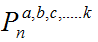
y su cálculo se efectúa como: