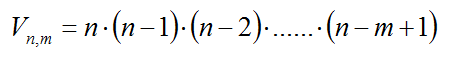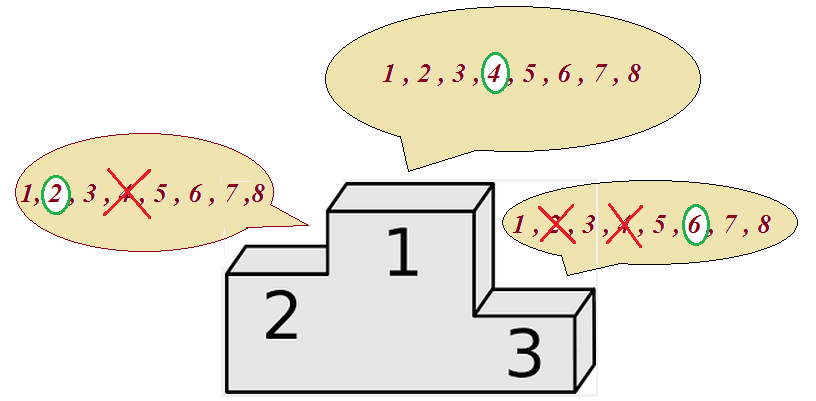
Imaginemos una carrera de 100 metros lisos en las olimpiadas. Nos preguntamos por las distintas formas en las que se pueden obtener las medallas de oro, plata y bronce. Este problema sin duda se puede resolver sin necesidad de conocimientos previos sobre combinatoria. Pensemos que disponemos de tres puestos. Para el primero se puede elegir a cualquiera de los ocho participantes. Para el segundo, no puedo elegir al que ya está elegido para el primero, por tanto solamente podremos elegirlo entre los siete restantes. Para el tercero, siguiendo el mismo razonamiento nos quedarán seis participantes. Ahora aplicando el principio general de recuento al conjunto (O x P x B), el total de resultados posibles para el podium sería 8 x 7 x 6 = 336.