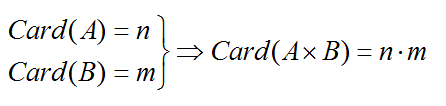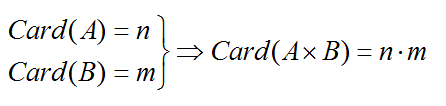2. principio general de recuento

La base sobre la que se apoya el edificio de la teoría combinatoria es el principio general de recuento que no es más que la cardinalidad del producto cartesiano en la teoría de conjuntos.
Si un experimento puede realizarse den formas diferentes y un segundo experimento puede hacerlo de m formas diferentes; entonces los dos experimentos juntos se pueden realizar denm formas diferentes.
En el lenguaje de teoría de conjuntos:

Donde por Card denotamos el cardinal, es decir, número de elementos del conjunto y A x B representa el producto cartesiano.

-Ana tiene en su armario 6 camisetas, 9 pantalones de deporte y 8 pares de zapatillas. Piensa si sería posible no repetir indumentaria duranto todos los días del año. Aplicando el principio general de recuento:
Identificamos indumentaria con (C x P x Z); es decir el producto cartesiano de la terna de conjuntos C (camisetas), P (pantalones), y Z (zapatillas)
El número de indumentarias sería pués 6 x 9 x 8 = 432 indumentarias diferentes.
-Un conocido restaurante afirma que el cliente puede comer durante dos años sin repetir el menú. En la carta aparecen 8 primeros platos, 15 segundos y 8 postres. Analiza si se trata de una propaganda cierta o no.
Identificamos menú con (PP x SP x P); es decir el producto cartesiano de la terna de conjuntos PP (primer plato), SP (segundo plato), y P (postre)
El número de menús diferentes sería pués 8 x 15 x 8 = 960, por tanto mucho más de dos años sin repetir menú

Vídeo enlazado desde YouTube, licencia de YouTube estándar

En el siguiente vídeo podemos ver la importancia de hacer un buen recuento. Se sitúa en Argentina y plantea que las matriculas de los vehículos iban ligadas a un identificador provincial y seis dígitos, pero cuando Buenos Aires se aproximo al vehículo un millón tuvieron que plantear un sistema que permitiera que en el futuro no hubiera que retocar el sistema de nuevo. Al final ¿qué les aconteció?