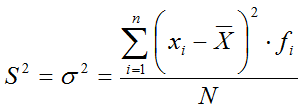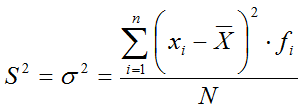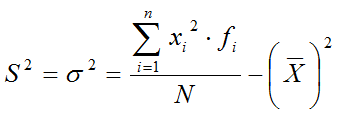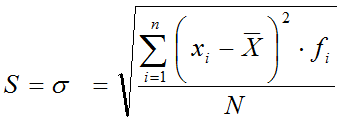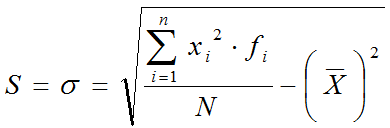6.2. Varianza y desviación típica
Varianza
El objetivo de este parámetro es el mismo que el de la desviación
media, es decir, detectar las variaciones de cada valor
respecto a la media aritmética. Para ello, en lugar de
utilizar el valor absoluto, eleva esas diferencias al cuadrado, con
esto evita posibles compensaciones y además "exagera" estas
diferencias (un número menor que uno al elevarlo al cuadrado se hace menor y uno mayor que uno se hace mayor). Por último, considera el promedio de dichas diferencias
al que denomina varianza. Es junto a la desviación típica la medida de
dispersión más utilizada en estadística.
A partir de la fórmula anterior y
después de desarrollar y simplificar los resultados se obtiene otra
expresión para la varianza que permite un cálculo más directo y
sencillo. Se suele recordar diciendo:
"La varianza es igual a la media de los cuadrados menos el cuadrado de la media"
El principal inconveniente que presenta
la varianza es que las unidades no son las mismas que las de los datos
de la distribución. Esto se solventa con la definición de un nuevo
parámetro que se calculará a partir del anterior.
Desviación típica
La desviación típica se define como la
raíz cuadrada positiva de la varianza. Tiene el mismo cometido que ésta
y además la ventaja de que las unidades en las que se mide son las
mismas que las de los datos de la distribución. Puede considerarse la
medida de dispersión por excelencia y aparece como tecla o función
directa en cualquier calculadora o programa estadístico.
<
De acuerdo a la definición, la fórmula para la obtención de la desviación típica sería:
Si se desarrola la fórmula anterior se
obtiene otra fórmula para la desviación típica bastante más cómoda y
que es la que se utiliza en la práctica.
"Raíz cuadrada de la media de los cuadrados menos el cuadrado de la media"
En la siguiente escena puedes observar
como se calcula la varianza y desviación típica para casos sencillos
con pocos datos, para variable discreta con datos tabulados y para
variable continua con datos agrupados en intervalos. Puedes generar
varias veces datos nuevos y calcular de nuevo los parámetros. También
puedes cambiar la amplitud de los intervalos en el caso del ejemplo de
variable continua y observar qué ocurre con la varianza y desviación
típica. Realiza varias pruebas y extrae tus propias conclusiones.
En la siguiente escena puedes prácticar
con el cálculo de la desviación típica para distintos ejemplos tanto para
variable discreta como para continua, opciones que puedes ir alternando. Es recomendable
que calcules manualmente el parámetro y que después lo introduzcas en
la escena. Realiza varios ejercicios hasta que compruebes que tus
resultados son correctos.