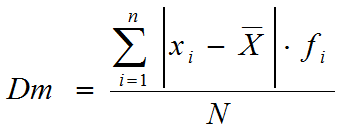Se define el
rango o recorrido
de una variable estadística como la diferencia entre el mayor y
el menor valor de
la variable. El rango indica la longitud del intervalo en el que se
hallan todos
los datos de la distribución. El rango es una medida de
dispersión importante aunque insuficiente para valorar convenientemente
la variabilidad de los datos. Supongamos que el rango en que se mueven
las notas de 6 exámenes es de 9 puntos. Existen muchas y distintas
posibilidades que pueden dar lugar a ese rango, por ejemplo:
- Caso 1: 1, 3, 5, 7, 9, 10.
- Caso 2: 1, 10, 10, 10, 10, 10.
- Caso 3: 1, 1, 10, 1, 1, 1.
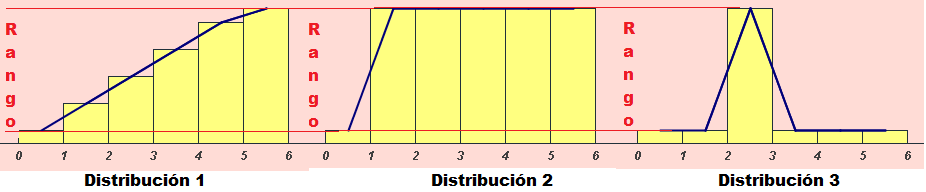
Como puedes observar las posibilidades anteriores son completamente
distintas aunque todas ellas tienen el mismo rango o recorrido.
Este parámetro por tanto presenta bastantes deficiencias en cuanto a
detección de la dispersión de los valores de la población y consecuentemente conviene completarlo con el estudio
de otras medidas.
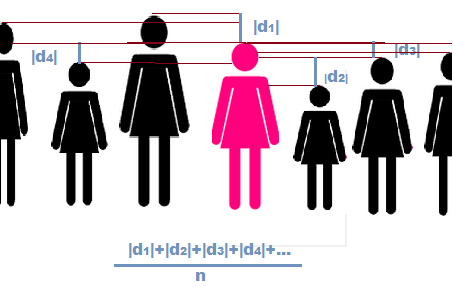
Se define la
desviación media como el parámetro de dispersión que sirve para calcular cuánto se desvían en promedio los datos de la distribución de la
media aritmética. Se calcula como la media de los valores absolutos de
las diferencias entre la media aritmética y los diferentes datos.
En la siguiente escena puedes observar
cómo se calcula esta desviación media en diferentes ejemplos, desde muy
simples con pocos datos a más complejos y con datos agrupados en
intervalos. Puedes generar nuevos datos y calcularla tanto como sea necesario.
Ahora podrás realizar
ejercicios sencillos de cálculo de rango y de desviación media. Puedes
realizarlos de forma manual en tu cuadreno e introducir tus soluciones
en los espacioes correspondientes para así comprobar los resultados.