5.2. Mediana
Los medios de comunicación, las ciencias
naturales y sociales utilizan constantemente referencias al concepto de
mediana. Las ayudas a la pequeña y mediana empresa, el hijo mediano
del matrimonio, la consistencia mediana de una sustancia, etc.
Estamos ante un parámetro que prioriza más la posición que se ocupa en
la distribución que el propio valor en sí mismo. La
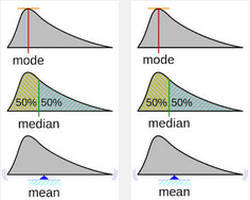
mediana es
aquel valor de la variable estadística que deja el 50% de
observaciones inferiores a él. Así pues, la mediana divide en dos
partes iguales a la distribución estadística.
Propiedades de la mediana:
- Como medida descriptiva no se ve afectada tanto como la media por la presencia de valores extremos.
- Es de cálculo rápido y de fácil interpretación.
- Como inconveniente también hay que decir que tiene propiedades
matemáticas complicadas que hacen que se utilice poco en inferencia
estadística.

|
|
|
En el caso continuo se puede razonar exactamente igual identificando en este caso el intervalo mediana.
Si queremos asociar a la mediana un valor concreto representativo del intervalo,
muchos autores señalan simplemente la marca de clase de dicho intervalo
y otros están de acuerdo en utilizar una fórmula que interpola
linealmente el valor en el intervalo. En los ejercicios prácticos utilizaremos la marca de clase del intervalo mediana.
En la siguiente escena puedes observar como se calcula la mediana en
variable discreta. Puedes elegir entre pocos datos y muchos datos tabulados. También se relaciona la mediana con el polígono de
frecuencias acumuladas. Es aconsejable que realices varios ejemplos
hasta comprender el funcionamiento del cálculo de la mediana
De la misma forma que la mediana divide
en dos partes iguales a la distribución, también podemos hablar de
valores que dividen a la distribución en varias partes iguales. Así se
pueden definir los cuartiles (división en cuatro partes) o los deciles (división en diez partes) o los percentiles (cien partes).
- Se define el primer cuartil Q1, como el valor de la variable estadística que deja el 25% de la población por debajo de él y el 75% por encima.
- Se define el segundo cuartil Q2, como la mediana.
- Se define el tercer cuartil Q3, como el valor de la variable que deja el 75% de la población por debajo de él y el 25% por encima.
En la siguiente escena aparecen ocho
ejemplos para que observes como se calcula la mediana y cuartiles de
una variable. También puedes generar tus propios datos y calcular los
parámetros anteriores. Es aconsejable que como mínimo completes los 8
ejemplos y comprendas cómo se calculan mediana y cuartiles
En la siguiente escena puedes realizar
ejemplos sencillos de cálculo de mediana y cuartiles. Puedes elegir
entre variable discreta y continua. Realiza varios ejercicios y
comprueba los resultados




