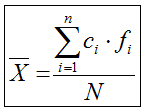La medida de tendencia central más utilizada en Estadísticas y en todos los campos de la vida cotidiana es la media aritmética. Se ha popularizado tanto que el vocablo se ha incorporado al lenguaje habitual sin perder su significado estadístico formal.
La media aritmética se define como la suma de todos los datos dividida entre el número total de los mismos. Como habitualmente dispondremos de una tabla de datos con sus correspondientes frecuencias absolutas, aplicaremos:

• La media aritmética no suele ser un valor propio de la variable. Si la media de un conjunto de exámenes es 6, puede que en ninguno de los exámenes se haya obtenido una nota exacta de 6.
Es muy sensible a cambios y valores extremos en los datos.
• Se comporta de forma natural en relación a las operaciones aritméticas suma y producto por un escalar, es decir, si a todos los datos de una distribución se les suma una misma cantidad, la media resultante sería la anterior más dicha cantidad. Si multiplicamos (o dividimos) todos los datos de una distribución por una cantidad distinta de cero, la media resultante sería la anterior multiplicada (respectivamente dividida) por dicha cantidad.

El hecho de que la media aritmética sea muy sensible, cambie mucho, frente a valore extremos de los datos es algo que constituye un problema en tanto que lo que se pretende en última instancia es que con el valor de la media aritmética se representen de la forma más acertada posible todos los datos de la distribución estadística. En algunas competiciones deportivas y en algunos eventos importantes como por ejemplo la gimnasia artística, rítmica, saltos de trampolín, carreras de coches y motos, para el cálculo de la media aritmética no se utilizan todos los datos sino que algunos se anulan o modifican. Por ejemplo, en las notas que emiten los distintos miembros de un tribunal en un examen de oposición, lo que en realidad se utiliza como nota final del ejercicio del opositor es una especie de media mejorada o recortada. Esta medida consiste en eliminar (recortar) los datos extremos, es decir el valor más alto y el más bajo y calcular después la media aritmética del resto de datos o de los nuevos datos actualizados.

Media o promedio Windsor

Otra variante de la media aritmética que se suele utilizar para evitar el excesivo protagonismo de los datos extremos consiste en sustiruir los datos extremos superior e inferior por sus inmediatos anteriores. Posteriormente se calcula la media aritmética de todos los datos así actualizados.

En el caso anterior se tendría: 7, 6, 6, 5, 10, 8 y 5. La nota más elevada es 10 y se actualiza a 8. La nota más pequeña es 5 y se actualiza a 5.

Calculamos ahora la media aritmética de las notas resultantes: 7, 6, 6, 5, 8, 8 y 5

Calificación final del ejercicio oral es 6,42857.

Para el caso de variable continua, solamente tenemos que sustituir xi por ci siendo ésta última la marca de clase de cada intervalo; es decir el punto medio o valor central del mismo. Por abuso de lenguaje se suele utilizar indistintamente también para variables continuas el símbolo xi para las marcas de clase

En la siguiente escena puedes observar como se calcula la media aritmética para el caso de variable discreta y continua. Es aconsejable que realices varios ejemplos y extraigas conclusiones.

Escena desarrollada por José Ireno Fernández Rubio(RED Descartes)

En la siguiente escena puedes realizar ejercicios sobre utilización y cálculo de la media aritmética.

Escena desarrollada por José Ireno Fernández Rubio(RED Descartes)