
El cálculo de la media aritmética se realiza aplicando la siguiente expresión:
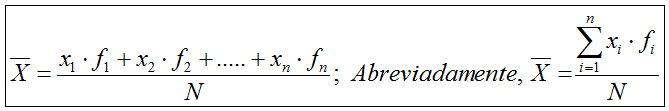
Algunas propiedades sencillas e interesantes de la media aritmética.
- La media no tiene porqué ser un valor propio de la variable.
- Es muy sensible a cambios y valores extremos en los datos.
- Se comporta de forma natural en relación a las operaciones aritméticas suma y producto por un escalar; es decir si a todos los datos de una distribución se les suma una misma cantidad, la media resultante sería la anterior más dicha cantidad. Si multiplicamos o dividimos todos los datos de una distribución por una cantidad distinta de cero, la media resultante sería respectivamente la anterior multiplicada o dividida por dicha cantidad.
El hecho de que la media aritmética sea muy sensible, cambie mucho,
frente a valores extremos de los datos es algo que constituye un
problema en tanto en cuanto que lo que se pretende en última instancia
es que con el valor de la media aritmética se representen de la forma
más acertada posible todos los datos de la distribución estadística. En
algunas competiciones deportivas y en algunos eventos importantes como
por ejemplo la gimnasia artística, rítmica, saltos de trampolín o
las notas que emiten los distintos miembros de un tribunal en un examen
oposición lo que en realidad se utiliza como nota final del ejercicio
del atleta o del opositor es una especie de media mejorada o recortada.
Esta medida consiste en eliminar (recortar) los datos extremos, es
decir el valor más alto y el más bajo y calcular después la media
aritmética del resto de datos.
Veamos un ejemplo de media acotada o recortada:
Veamos un ejemplo de media acotada o recortada:
-
En la exposición oral de un ejercicio de oposición, los 7 miembros del
tribunal calificador deben emitir una nota. Posteriormente se cotejan
las mismas y se calcula la media recortada que será la calificación
definitiva del opositor.
Supongamos que se emiten las siguientes notas: 7, 6, 6, 5, 10, 8 y 5.
-
La nota más elevada es un 10 y la nota más pequeña es un 5. Eliminamos por tanto ese 10 y uno de los dos 5. Calculamos ahora la media aritmética de las notas restantes: 7, 6, 6, 5, 8. Por tanto la calificación final del ejercicio oral es 6,4.
En la siguiente escena puedes observar
como se calcula la media aritmética en distintos ejemplos. Puedes
elegir entre trabajar con pocos datos o con muchos datos agrupadoe en
una tabla. Es conveniente que realices varios ejemplos y extraigas tus
propias conclusiones
Escena desarrollada por Juan Jesús Cañas Escamilla(RED Descartes)
Finalmente en la siguiente escena correspondiente
al proyecto ASIPISA de RED Descartes puedes realizar algunos ejercicios indirectos
relacionados con el concepto de media. Cada vez que pulses el control
inicio, se generará un problema distinto relacionado siempre con el
concepto de media aritmética
Escena desarrollada por Juan Jesús Cañas Escamilla y José R. Galo Sánchez(RED Descartes)