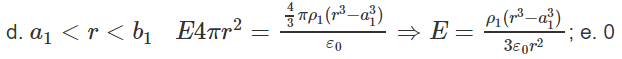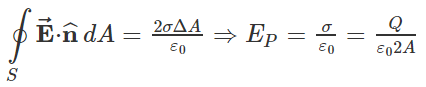Respuestas - Capítulo VI
Excepto por las preguntas de los apartados de Comprueba tu aprendizaje, sólo se dan las respuestas de los numerales impares
Comprueba tu aprendizaje
6.1 Colócalo de modo que su unidad normal sea perpendicular a E→.
6.2 mab2/2
6.3 a. 3,4 × 105 N • m2/C; b. -3.4 × 105 N • m2/C; c. 3,4 × 105 N • m2/C d. 0
6.4 En este caso, solo hay E→ fuera. Entonces, sí.
6.5E→ = λ0/2πε01/dr^; Esto concuerda con el cálculo del Ejemplo 5.5 donde encontramos el campo eléctrico al integrarlo sobre el cable cargado. Observa cuánto más simple es el cálculo de este campo eléctrico con la ley de Gauss.
6.6 Si hay otros objetos cargados alrededor, entonces las cargas en la superficie de la esfera no serán necesariamente esféricas simétricas; habrá más en cierta dirección que en otras direcciones.
Preguntas conceptuales
1. a. Si la superficie plana es perpendicular al vector del campo eléctrico, se obtendría el flujo máximo. b. Si la superficie plana fuera paralela al vector del campo eléctrico, se obtendría el flujo mínimo.
3. Falso. El flujo eléctrico neto que cruza una superficie cerrada es siempre cero si y solo si la carga neta encerrada es cero.
5. Como el vector del campo eléctrico tiene una dependencia 1/r2, los flujos son los mismos desde A = 4πr2.
7. a. no; b. cero
9. Ambos campos varían como 1/r2. Debido a que la constante de gravitación es mucho más pequeña que 1/4πε0, el campo gravitacional es de órdenes de magnitud más débiles que el campo eléctrico. Además, el flujo gravitacional a través de una superficie cerrada es cero o positivo; sin embargo, el flujo eléctrico es positivo, negativo o cero, dependiendo de la definición de flujo para la situación dada.
11. No, es producido por todas las cargas tanto dentro como fuera de la superficie de Gauss.
13. No, ya que la situación no tiene simetría, lo que hace que la ley de Gauss sea un desafío para simplificar.
15. Se puede usar cualquier forma de la superficie Gaussiana. La única restricción es que la integral gaussiana debe ser calculable; por lo tanto, una caja o un cilindro son las formas geométricas más convenientes para la superficie gaussiana.
17. No. Si un metal estuviera en una región de campo eléctrico cero, todos los electrones de conducción se distribuirán uniformemente por todo el metal.
19. Dado que el campo eléctrico es cero dentro de un conductor, se induce una carga de -2.0 μC en la superficie interior de la cavidad. Esto pondrá una carga de + 2.0 μC en la superficie exterior, dejando una carga neta de -3.0 μC en la superficie.
Problemas
21. Φ = E→ • A→ → EAcosθ = 2.2 × 104 N • m2/C, campo eléctrico en la dirección de la unidad normal;
Φ = E→ • A→ → EAcosθ = -2.2 × 104 N • m2/C campo eléctrico opuesto a la unidad normal
23. 3 × 10−5 N • m2/C/(0.05 m)2 = E ⇒ σ = 2.12 × 10-13 C/m2
25. a. Φ = 0.17 N • m2/C;
b. Φ = 0; c. Φ = EAcos0° = 1.0×103 N/C(2.0 × 10−4m)2cos0° = 0.20 N • m2/C
27. Φ = 3.8 × 104 N • m2/C
29. E→(z) = 1/4πε02λ/zk^, ∫E→ • n^dA = λ/ε0l
31. a. Φ = 3.39 × 103 N • m2/C; b. Phi; = 0;
c. Φ = −2.25 × 105 N • m2/C;
d. Φ = 90.4 N • m2/C;
33. Φ = 1.13 × 106 N • m2/C;
35. Haz un cubo con q en el centro, usando el cubo del lado a. Esto tomaría cuatro cubos del lado a para hacer un lado del cubo grande. El lado sombreado del cubo pequeño sería 1/24 del área total del cubo grande; por lo tanto, el flujo a través del área sombreada sería
Φ = 1/24q/ε0.
37. q = 3.54 × 10-7 C
39. Cero.
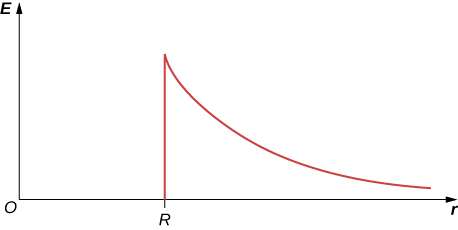
41. r > R, E = Q/4πε0r2; r < R, E = qr/4πε0R3
43. EA = λl/ε0 ⇒ E = 4.50 × 107 N/C
45. a. 0; b. 0; c. E→ = 6.74 × 106 N/C(−r^)
47. a. 0; b. E = 2.70 × 106 N/C
49. a. Sí, la longitud de la varilla es mucho mayor que la distancia al punto en cuestión. b. No, la longitud de la varilla es del mismo orden de magnitud que la distancia al punto en cuestión. c. Sí, la longitud de la varilla es mucho mayor que la distancia al punto en cuestión. d. No. La longitud de la barra es del mismo orden de magnitud que la distancia al punto en cuestión.
51. a. E→ = Rσ0/ε01/rr^ ⇒ σ0 = 5,31 × 10-11 C/m2,
λ = 3,33 × 10-12 C/m;
b. Φ = qenc/ε0 = 3.33 × 10-12 C/m(0.05)/ε0 = 0.019 N • m2/C
53. E2πrl = ρπr2l/ε0 ⇒ E = ρr/2ε0 (r ≤ R);
E2πrl = ρπr2l/ε0 ⇒ E = ρR2/2ε0r (r ≥ R);
55. Φ = qenc/ε0 ⇒ qenc = −4.45 × 10-10 C
57. qenc = 4/5παr5,
E4πr2 = 4παr5/5ε0 ⇒ E = αr3/5ε0 (r ≤ R),
qenc = 4/5παR5, E4πr2 = 4παR5/5ε0 ⇒ E = &aplha;R5/5ε0r2(r ≥ R)
59. Integrando por partes:
qenc = 4πρ0[−e−αr(r2/α 2r/α2 + 2/α3) + 2/α3] ⇒ E = ρ0/r2ε0[−e−αr(r2/α 2r/α2 + 2/α3) + 2/α3]
61.
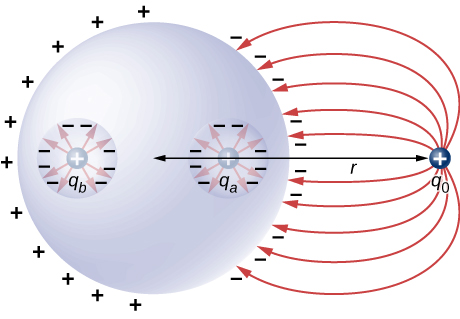
63. a. Exterior: E2πrl = λl/ε0 ⇒ E = 3.0 C/m/2πε0r; Dentro de Ein = 0; b.
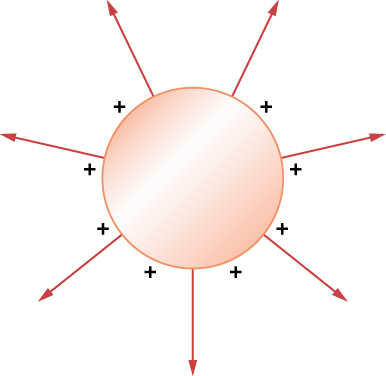
65. a. E2πrl = λl/ε0 ⇒ E = λ/2πε0r r ≥ R, E dentro es igual a 0; b.
69. λ = λl/pi;ε0 ⇒ E = aσ/ε0r, r ≥ a, E = 0 dentro desde qenc = 0
71. a. E = 0; b. E2πrl = Q/ε0 ⇒ E = Q/2πε0rL; c. E = 0 ya que r estaría dentro del segundo caparazón o si está fuera, entonces q encerrado es igual a 0.
Problemas Adicionales
73. ∫E→ • n^dA = a4
75. ∫E→ • n^dA = E0r2π; b. cero, dado que el flujo a través de la mitad superior cancela el flujo a través de la mitad inferior de la esfera.
77. Φ = qencε0; Hay dos contribuciones a la integral de la superficie: una en el lado del rectángulo en x = 0 y la otra en el lado en x = 2.0m;
-E(0) [1.5 m2] + E(2.0m)[1.5m2] = qencε0 = -100 Nm2/C
donde el signo menos indica que en x = 0, el campo eléctrico está a lo largo de x positivo y la unidad normal está a lo largo de x negativo. En x = 2, la unidad normal y el vector de campo eléctrico están en la misma dirección: qenc = ε0Φ = -8.85 × 10-10 C.
79. no mantuvo direcciones consistentes para los vectores de área, o los campos eléctricos
81. a. σ = 3.0 × 10-3 C/m2, + 3 × 10-3 C/m2 en uno y -3 × 10-3 C/m2 en el otro; b. E = 3,39 × 108 N/C
83. Construya un cilindro gaussiano a lo largo del eje z con área de sección transversal A.
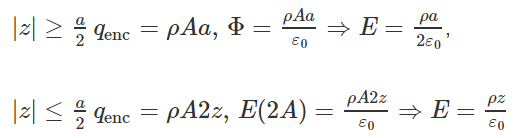
85.
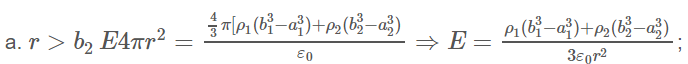
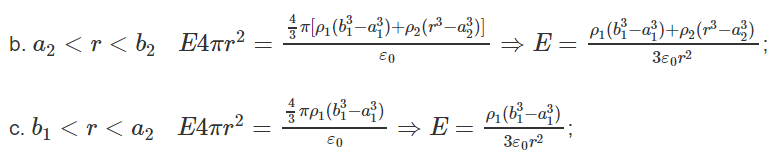
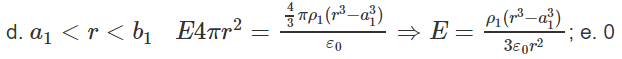
87. Campo eléctrico debido a la placa sin agujero: E = σ/2ε0.
Campo eléctrico del hoyo lleno con -σE = -σ/2ε0(1 - z/√R2 + z2/).
Por lo tanto, Enet = σ/2ε0h/√R2 + h2/.
89. a. E = 0; b. E = q1/4πε0r2; c. E = q1 + q2/4πε0r2; d. 0, q1, -q1, q1 + q2
Problemas Reto
91. Dado el enlace referenciado, usando una distancia a Vega de 237 × 1015 m y un diámetro de 2.4 m para el espejo primario, encontramos que a una longitud de onda de 555.6 nm, Vega está emitiendo 1.1 × 1025 J/s en esa longitud de onda. Ten en cuenta que el flujo a través del espejo es esencialmente constante.
93. La simetría del sistema obliga a E→ a ser perpendicular a la hoja y constante sobre cualquier plano paralelo a la hoja. Para calcular el campo eléctrico, elegimos la superficie Gaussiana cilíndrica que se muestra. El área de la sección transversal y la altura del cilindro son A y 2x, respectivamente, y el cilindro está posicionado de modo que es bisecado por la lámina plana. Como E es perpendicular a cada extremo y paralelo al lateral del cilindro, tenemos EA como flujo a través de cada extremo y no hay flujo a través del costado. La carga encerrada por el cilindro es σA, entonces según la ley de Gauss, 2EA = σA/ε0, y el campo eléctrico de una hoja de carga infinita es E = σ/2ε0, de acuerdo con el cálculo en el texto.
95. Hay Q/2 en cada lado de la placa ya que la carga neta es Q: σ = Q/2A,