Excepto por las preguntas de los apartados de Comprueba tu aprendizaje, sólo se dan las respuestas de los numerales impares
1.1 a. 40.0rev/s = 2π(40.0)rad/s, α_ = ΔwΔt = 2π (40.0)- 0rad/s 20.0 s = 2π (2.0) = 4π rad/s2 b. Dado que la velocidad angular aumenta linealmente, tiene que haber una aceleración constante a lo largo del tiempo indicado. Por lo tanto, la aceleración angular instantánea en cualquier momento es la solución a 4.0πrad /s2.
1.2 a. Usando la ecuación 1.11, wf = w0+ αt, tenemos 7000 rpm = 7000.0 (2πrad) 60.0s = 733.0rad / s
α = ω − ω0t = 7000.0(2πrad)10.0s = 733.0 rad/s,
b. Usando la ecuacion 1.13, wf2 = w02 + 2α(Δθ), tenemos Δθ = wf2 - w022α = 0 - ( 733.0rad/s)22(73.3rad/s2) = 3665.2 rad
1.3. La aceleración angular es α = (5.0 - 0)rad/s20.0s = 0.25rad/s2. Por lo tanto, el ángulo total por el que pasa el niño es:
Δθ = wf2 - w022α = (5.0)2 - 0 2 (0.25) = 50rad. Así, calculamos s = r θ = 5.0m (50.0rad)= 250.0m.
1.4. La energía cinética rotacional inicial de la hélice es Ko=12Iω2 = 12(800.0kg m 2)(4.0×2πrad/s)2 = 2.53×105 J. En 5.0 s la nueva energía cinética rotacional de la hélice es Kf = 2.03×10 2 J, y la nueva velocidad angular es
√x....??????? que es 3.58 rev / s.
1.5. I eje paralelo = Icentro de masa + md2 = mR2 + mR2 = 2mR2
1.6. El ángulo entre el brazo de palanca y el vector de fuerza es de 80°; por lo tanto, r⊥ = 100m (sin 80°) = 98.5m. El producto cruzado τ→ = r→ × F→ da un par negativo o en el sentido de las agujas del reloj. El par es entonces -r⊥F = −98.5m (5.0×105N)= −4.9×107Nm
1.7. a. La aceleración angular es α = 20.0(2π)rad/s − 010.0s = 12.56rad/s2. Resolviendo el par, tenemos ∑iτi = Iα =(30.0kgm2)(12.56rad/s2)= 376.80Nm.
b. α = 020 − 0(2π)rad/s20.0s = −6.28rad/s. Resolviendo el par, tenemos ∑iτi = Iα =(30.0kgm2)(-6.28rad/s2)= −188.50 Nm.
1.8. 3 MW
1. La manecilla de los segundos gira en el sentido de las agujas del reloj, por lo que, según la regla de la mano derecha, el vector de velocidad angular está hacia la pared.
3. Tienen la misma velocidad angular. Los puntos más alejados en el bate tienen mayores velocidades tangenciales.
5. Linea recta, lineal variable de tiempo.
7. Constante .
9. El vector de aceleración centrípeta es perpendicular al vector de velocidad.
11. a. ambos; b. aceleración centrípeta no es cero; c. ambos.
13. La esfera hueca, ya que la masa se distribuye más lejos del eje de rotación.
15. a. Disminuye. b. Los brazos podrían aproximarse con varillas y el disco con un disco. El torso está cerca del eje de rotación, por lo que no contribuye mucho al momento de inercia.
17. Porque el momento de inercia varía según el cuadrado de la distancia al eje de rotación. La masa de la barra ubicada a distancias mayores que L / 2 proporcionaría la mayor contribución para hacer que su momento de inercia sea mayor que la masa puntual en L / 2.
19. Magnitud de la fuerza, longitud del brazo de palanca, el ángulo del brazo de palanca y vector de fuerza.
21.El momento de inercia de las ruedas se reduce, por lo que se necesita un par menor para acelerarlas.
23. Sí.
25. |r→| puede ser igual al brazo de palanca pero nunca menos que el brazo de palanca.
27. Si las fuerzas están a lo largo del eje de rotación, o si tienen el mismo brazo de palanca y se aplican en un punto de la barra.
29. ω = 2πrad45.0s
= 0.14rad/s
31. a. θ = sr=3.0m1.5m = 2.0rad; b. ω = 2.0rad1.0s = 2.0rad/s; c. v2r = (3.0m/s)21.5m = 6.0m/s2
33. La hélice toma solo Δt = Δωα = 0rad / s − 10.0 (2π) rad / s − 2.0rad / s2 = 31.4s para detenerse, cuando la hélice está a 0 rad / s, comenzaría a girar en la dirección opuesta . Esto sería imposible debido a la magnitud de las fuerzas involucradas en hacer que la hélice se detenga y comience a girar en la dirección opuesta.
35. a. ω = 25.0(2.0s)= 50.0rad/s; b. α = dωdt = 25.0rad/s2.
37. a. ω = 54.8rad/s; b. t = 11.0s.
39. a. 0.87rad/s2; b. θ = 12,600rad
41. a. ω = 42.0rad/s; b. θ = 200rad; c. vt = 42m/s, at=4.0m/s2.
43. a. ω = 7.0rad/s; b. θ = 22.5rad; c. at = 0.1m/s.
45. α = 28.6rad/s2.
47. r=0.78m.
49. a. α = −0.314rad/s2, b. ac = 197.4m/s2; c. a = [ a2c+a2t]12 √=197.42+(−6.28)2 = 197.5m/s2; θ = tan-1−6.28197.4 = −1.8° en el sentido de las agujas del reloj desde el vector de aceleración centrípeta
51. ma = 40.0kg(5.1m/s2) = 204.0N. La fuerza máxima de fricción es μsN = 0.6(40.0kg)(9.8m/s2)= 235.2N
La fuerza de fricción máxima es μsN = 0.6 (40.0kg) (9.8m / s2) = 235.2 N para que el niño aún no se caiga.
vt = rω = 1.0(2.0t)m/s
53.ac = vt2r=(2.0t)21.0m= 4.0t2m/s2
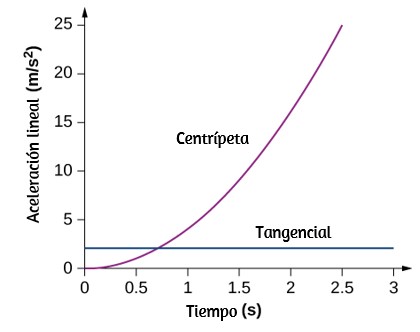
a(t)= rα(t)= rdωdt = 1.0m(2.0) = 2.0m/s2, El la grafica de ambas aceleraciones da

La aceleración tangencial es constante, mientras que la aceleración centrípeta depende del tiempo y aumenta con el tiempo a valores mucho mayores que la aceleración tangencial después de t = 1s. Para tiempos menores a 0.7 sy aproximándose a cero, la aceleración centrípeta es mucho menor que la aceleración tangencial.
55. a. K = 2.56×1029J; b. K=2.68×1033J .
57. K = 434.0J.
59. a. vf = 86.5m/s; b. La velocidad de rotación de la hélice se mantiene igual a 20 rev / s.
61. K = 3.95×1042J .
63. a. I = 0.315 kgm2; b. K = 621.8J .
65. I = 736mL2.
67. v = 7.14m/s.
69. θ = 10.2°.
71. F = 30N.
73. a. 0.85m (55.0N) = 46.75 Nm; b. No importa a qué altura empujes.
75. m2 = 4.9N m9.8(0.3m)= 1.67kg.
77. τnet = −9.0Nm + 3.46Nm + 0 − 3.38Nm = −8.92Nm.
79. τ = 5.66 Nm.
81. ∑τ = 57.82Nm.
83. r→ × F→ = 4.0i^+ 2.0j^ − 16.0k^ Nm.
85. a. τ =(0.280m)(180.0N) = 50.4 Nm; b. α = 17.14rad/s2; c. α = 17.04rad/s2.
87. τ = 8.0 Nm.
89. τ = −43.6 Nm.
91. a. α = 1.4×10 -10rad/s2; b. τ = 1.36×1028Nm; c. F = 2.1×1021N.
93. a = 3.6m/s2.
95. a. a = rα = 14.7m/s2; b. a = L2 α = 34g.
97. τ = Pω = 2.0×106W 2.1rad/s = 9.5×105Nm .
99. a. K = 888.50J; b. Δθ = 294.6rev.
101. a. I = 114.6kgm2; b. P = 104,700W .
103. v = Lω= raiz cuadrada 3Lg.
105. a. a = 5.0m/s2; b. W = 1.25Nm.
107.Δt = 10.0s .
109. a. 0.06rad/s2; b. θ=105.0 rad.
111. s = 405.26m .
113. a. I = 0.363kg m2; b. I = 2.34kg m2.
115. ω = 1.23rad/s.
117. F = 23.3N.
119. α = 190.0N m2.94kg m2 = 64.4rad/s2.
121.a. ω = 2.0t − 1.5t2 ; b. θ = t2−0.5t3; c. θ = −400.0rad; d. el vector está en −0.66(360°)= −237.6°
123. I =25mR2
125. a. ω = 8.2rad/s; b. ω = 8.0rad/s