Física Mecánica
INTERACTIVO
José Ricardo Del Río Quimbayo
Institución Universitaria Pascual Bravo
Título de la obra:
Física Mecánica
Autor:
José Ricardo Del Río Quimbayo
Colaboradores:
Marco Tulio Mesa Cardona
Jaime Humberto Ramírez Rios
Diseño del libro: Juan Guillermo Rivera Berrío
Código JavaScript para el libro: Joel Espinosa Longi, IMATE, UNAM.
Recursos interactivos: DescartesJS
Fuentes: Lato y UbuntuMono
Fórmulas matemáticas: $\KaTeX$
Imagen de portada: Oldtimer Motorcycle Mechanic por forestgreen
Núcleo del libro interactivo: julio 2022
Fondo Editorial Pascual Bravo
Calle 73 73A-226
PBX: (574) 4480520
Apartado 6564
Medellín, Colombia
www.pascualbravo.edu.co
ISBN: 978-958-52963-6-7
En los últimos cuarenta años, el mundo ha experimentado un enorme cambio, a nivel tecnológico, que ha impactado directamente en las últimas generaciones; la generación "millennials", cuyos nativos digitales nacieron entre los años $\hspace{0.1cm} \color{#0000FF} 1980 \ $ y $\hspace{0.1cm} \color{#0000FF} 2000 \ $, los cuales se comunican, preferiblemente, por redes sociales; y la generación "centennials" nacida entre el $\hspace{0.1cm} \color{#0000FF} 2000 \ $ y nuestros días, que son otro tipo de nativos digitales, pues las tecnologías de pantalla representan una extensión de su propio ser.
Los modelos de educación a nivel global y el aprendizaje, no pueden estar ajenos a estos cambios tecnológicos y generacionales, tienen que adaptarse a este nuevo amanecer.
El texto Física Mecánica es creado y diseñado para satisfacer las necesidades de enseñanza-aprendizaje de las nuevas generaciones. Estamos en presencia de un libro interactivo que permite al lector reconocer, entender, simular, crear nuevas situaciones, reflexionar sobre los fenómenos físicos más representativos de la Física mecánica mediante escenas interactivas diseñadas en Descartes JS y GeoGebra.
El texto está escrito en un lenguaje sencillo, ameno que lleva al lector de la mano por los caminos de la Física mostrándole paso a paso el desarrollo de las leyes y principios fundamentales que gobiernan la mecánica clásica.
Al inicio de cada capítulo el lector encontrara un video introductorio de la serie educativa Universo Mecánico que es una colección de $\hspace{0.1cm} \color{#0000FF} 52 \ $ videos creados por el Instituto de Tecnología de California cuyo director y anfitrión es el Dr. David L. Goodtein. Cada video es una presentación contextualizada al tema tratado en dicho capítulo.
El video introductorio hace parte de la serie Universo MecánicoLa serie educativa Universo Mecánico es una colección de 52 videos creados por el Instituto de Tecnología de California cuyo director y anfitrión es el Dr. David L. Goodtein.
Desde la aparición del hombre en la tierra y como mecanismo de supervivencia, el hombre se ha preguntado por el cómo funciona el Universo, cómo comenzó, cómo evoluciona, cómo seguirá evolucionando. Respuesta a estas preguntas estuvieron por muchos siglos en la teología, la mitología. Fue hasta finales del siglo $\color{#0000FF} VII$ y principios del siglo $\color{#0000FF} VI a.c.$ que nace la filosofía y filósofos como Tales De Mileto se cuestionaba sobre el origen de las cosas buscando explicaciones racionales.
Junto con la filosofía nace el termino Physis que en Griego significa Naturaleza, nacer, producir, hacer, significa origen y producción de las cosas. Los primeros filósofos llamados presocráticos se les reconocen como filósofos de la Naturaleza
La física es una ciencia empírica, es por excelencia la ciencia de la naturaleza. La física se basa en la observación para entender el universo.
El hombre siempre se a interesado en saber cómo funciona el universo, porqué los cuerpos cercanos a la tierra caen, porqué cae un rayo, porqué el día, porque la noche, porqué el cielo es azul, y en general el porqué de las cosas.
La Física pretende encontrar las leyes que gobiernan el universo, entre estas leyes tenemos por ejemplo la ley de la gravitación universal que responde al porqué de la atracción entre los cuerpos, la ley de Coulomb que da razón de las fuerzas debidas a cargas eléctricas, las leyes de Newton que nos da la posición, velocidad y aceleración de los cuerpos que son grandes comparados con el tamaño del átomo y que se mueven con velocidades mucho menores a la velocidad de la luz.
Al hombre también le interesa predecir fenómenos de la naturaleza tales como el clima, un temblor, un tsunami, etc. Los más grandes avances de la ciencia han sido posibles gracias a la física.
La física en su experimentación investiga básicamente la materia, la energía, el tiempo y el espacio y evalúa las diferentes interacciones entre ellos.
La física y la física mecánica en especial resultan ser más sencilla de lo que la gran mayoría de las personas creen, es una disposición mental al proceder lógico del funcionamiento de las cosas, es lograr entender conceptos básicos y fundamentales que son los eslabones de esa cadena que mueve ésta hermosa maquina llamada Universo.
La física mecánica es una rama de la física que estudia el movimiento de los cuerpos para dar a conocer esencialmente su posición, velocidad y aceleración. Este estudio lo realiza la física mecánica desde dos frentes, uno de ellos a partir de la geometría del movimiento, es decir, si su movimiento es a lo largo de una línea recta o a lo largo de una curva; el otro frente es estudiar el movimiento de los cuerpos a partir de las fuerzas que actúan sobre el cuerpo.
La Física mecánica considera el estudio de los cuerpos en reposo como un caso especial del movimiento en el cual la velocidad es constante con todas las consecuencias a que ello lleva.
El estudio de la Física mecánica se divide en tres partes fundamentales, la estática, la cinemática y la dinámica o cinética.
Para abordar el estudio de la física mecánica es necesario que al dar a conocer algunos conceptos básicos. También demos a conocer al menos cinco sistemas de unidades: el Sistema Internacional de Unidades S.I., el sistema Técnico S.T., el Sistema Ingles U.S.C.S.(Sistema Consistente de la Unión de Estados), el Sistema F.P.S. y el Sistema cegesimal c.g.s. , de los cuales nos concentraremos en dos de ellos para el desarrollo de este curso, el Sistema Internacional de Unidades y el Sistema F.P.S..
es conveniente que el estudiante se familiarice desde este momento con estos cinco sistemas de unidades ya que serán necesarios para el desarrollo de cursos siguientes a este de física mecánica tales como Mecánica de fluidos, termodinámica entre otros.
Un estudio de los intervalos entre eventos repetitivos dio origen al concepto de tiempo. Haciendo observaciones del paso del día y la noche (el día solar), de la rotación de la tierra sobre su eje, de las estaciones climáticas, el hombre observo como estos fenómenos se repetían así mismos y los fue estandarizando para su provecho como lo es determinar las épocas para cultivar. Pero aun así faltaba determinar el patrón para ese intervalo de repetición de los eventos que fuera permanente.
"Galileo cuando era joven uso el pulso de su muñeca para medir el tiempo de oscilación de un pénduloEugene Hecht, Física en Perspectiva, Editorial Addison-Wesley Iberoamericana, S.A. de E.U.A., 1987, pag.28.".Las vibraciones a nivel molecular en el cristal de cuarzo cuando son estas inducidas eléctricamente, son ejemplos de eventos que se repiten así mismo.
Ya en nuestra época se comenzó a observar fenómenos como las frecuencias de radiación de algunos átomos.
La unidad fundamental para medir el tiempo es el segundo. El segundo es exactamente igual en cualquiera de los sistemas de unidades por lo que no es necesaria ninguna conversión.
"En $\color{#0000FF} 1999$. se adoptó como reloj atómico el cesio $\color{#0000FF} 133$, cuya base fundamental es la frecuencia de radiación de una fuente de átomos de cesio. La variación de este reloj es de menos de un segundos cada $\color{#0000FF} 20$ millones de añosWilson. Buffa. Lou, Física, Editorial Pearson Educación, México, Sexta edición, 2007, pag.5.".Un minuto tiene $\color{#0000FF} 60$ segundos, una hora tiene $\color{#0000FF} 3600$ segundos, un día tiene $\color{#0000FF} 24$ horas.
La longitud hace referencia a la distancia entre puntos.
El hombre en la antigüedad utilizo su cuerpo para medir distancias, el pie, la pulgada, el antebrazo. Los romanos median distancias en pasos que equivalían a la medida de cinco pies. Más adelante en la historia resulto que mil pasos se convirtiera en una milla Británica. La yarda era la medida desde la punta de la nariz a la punta del dedo índice, teniendo el brazo extendido.
En física mecánica se requiere medir distancias, posición de un cuerpo, cambio de posición. En el Sistema Internacional S.I. se utiliza el metro $\color{#0000FF} m$, en el Sistema Técnico S.T. se utiliza el metro $\color{#0000FF} m$, en el sistema Ingles (U.S.C.S.) se utiliza el pie $\color{#0000FF} ft$, en el sistema F.P.S. se utiliza el pie $\color{#0000FF} ft$ y en el sistema Cegesimal se utiliza el centímetro $\color{#0000FF} cm$.
El área es la superficie de un cuerpo; si pasamos suavemente la mano por la parte de arriba de la mesa estamos tocando su superficie, así mismo tocamos la superficie de un globo. En el Sistema Internacional el área se mide en metros cuadrados $\color{#0000FF} m^2$, en el Sistema Técnico S.T. en metros cuadrados $\color{#0000FF} m^2$, en el sistema Ingles U.S.C.S. en pies cuadrados $\color{#0000FF} ft^2$, en el sistema F.P.S. se mide en pies cuadrados $\color{#0000FF} ft^2$, y en el sistema c.g.s. centímetros cuadrados $\color{#0000FF} cm^2$.
El volumen es la capacidad de contenido tridimensional de un cuerpo, como cuando vertimos agua en un vaso. En el Sistema Internacional el volumen se mide en metros cúbicos $\color{#0000FF} m^3$, en el Sistema Técnico en metros cúbicos $\color{#0000FF} m^3$, en el sistema Ingles U.S.C.S. en pies cúbicos $\color{#0000FF} ft^3$, en el sistema F.P.S. se mide en pies cúbicos $\color{#0000FF} ft^3$, y en el sistema Cegesimal en centímetros cúbicos $\color{#0000FF} cm^3$.
La velocidad es el cambio de la posición respecto de un cambio en el tiempo $\color{#0000FF} \overrightarrow {v}=\dfrac {\Delta \overrightarrow {r}}{\Delta t}$. La velocidad tiene dos partes: su valor numérico con unidad y su dirección (para donde va). Sus unidades en el S.I. es
en metros por segundo $\color{#0000FF} \dfrac {m}{s}$, en el sistema S.T. $\color{#0000FF} \dfrac {m}{s}$, en el sistema U.S.C.S.$\color{#0000FF} \dfrac {ft}{s}$, en el sistema F.P.S. $\color{#0000FF} \dfrac {ft}{s}$, en el sistema c.g.s. $\color{#0000FF} \dfrac {cm}{s}$.
Existe aceleración cuando se produce un cambio en la velocidad respecto de un cambio en el tiempo $\color{#0000FF} \overrightarrow {a}=\dfrac {d\overrightarrow {v}}{dt}$. A nivel de unidades será el cambio de $\color{#0000FF} \dfrac {m}{s}$ cada $\color{#0000FF} s$. En el sistema S.I. las unidades de la aceleración es $\color{#0000FF} \dfrac {m}{s^2}$, en el sistema S.T. $\color{#0000FF} \dfrac {m}{s^2}$, en el sistema U.S.C.S. $\color{#0000FF} \dfrac {ft}{s^2}$, en el sistema F.P.S. $\color{#0000FF} \dfrac {ft}{s^2}$, en el sistema c.g.s. $\color{#0000FF} \dfrac {cm}{s^2}$.
Es la cantidad de materia que posee un cuerpo, la materia la constituyen electrones, protones, átomos, moléculas, que son comunes a todos los cuerpos en el universo. La materia no apunta a ninguna parte, ningún lado o sitio.
En el sistema internacional de unidades S.I. la unidad de masa es el kilogramo $\color{#0000FF} Kg$, en el sistema Técnico S.T. es la unidad técnica de
masa U.T.M., en el sistema Ingles U.S.C.S. la libra masa $\color{#0000FF} lbm$, en el sistema F.P.S. el $\color{#0000FF} slug$ y en el sistema Cegesimal c.g.s. el gramo $\color{#0000FF} gr$
La fuerza es la acción de un cuerpo sobre otro, es la acción que intenta o logra cambiar el estado de reposo o movimiento de un cuerpo. En este sentido vemos que las fuerzas no aparecen solas, debe existir la interacción de dos cuerpos.
Podemos decir también que la fuerza es la resistencia que hace un cuerpo a la acción o interacción con otro cuerpo.
Siguiendo a Newton tenemos que el producto de la masa por la aceleración da como resultado una fuerza $\color{#0000FF} F= ma$, así podemos analizar las unidades de la fuerza, entonces, en el sistema S.I. la unidad de fuerza queda $\color{#0000FF} \dfrac {Kg.m}{s^2}=N$ llamado Newton, en el sistema S.T. $\color{#0000FF} \dfrac {utm.m}{s^2}=Kp$ llamada kilopondio, en el sistema U.S.C.S. $\color{#0000FF} \dfrac {lbm.ft}{s^2}$ que por sí sola no tiene un nombre especifico pero cuando se tienen
$\color{#0000FF} \dfrac {32.2lbm.ft}{s^2}=Lb_f$ recibe el nombre de Libra fuerza, en el sistema F.P.S. $\color{#0000FF} \dfrac {slug.ft}{s^2}=Lb$ que se llama libra y en el sistema c.g.s. $\color{#0000FF} \dfrac {gr.cm}{s^2}=dina$.Como todos los cuerpos sobre la tierra tenemos masa, nos vemos sometidos a los efectos producidos por la acción de aceleración de la gravedad terrestre que siempre es hacia el centro de la tierra. De acuerdo con el postulado de Newton $\color{#0000FF} F= ma$ vemos que la unión entre la masa y la aceleración de la gravedad produce una fuerza que por provenir de los efectos de la gravedad terrestre se llama Fuerza de gravedad $\color{#0000FF} Fg=mg$ o peso de un cuerpo $\color{#0000FF}w=mg$.
Bajo este análisis entiéndase que los conceptos de masa y peso de un cuerpo son conceptos diferentes. La masa es la cantidad de materia que posee un cuerpo y esta cantidad no cambia por el lugar donde se encuentre. El peso por ser este el producto entre la masa y la aceleración de la gravedad terrestre puede cambiar su valor pues el valor de la gravedad por ejemplo en la luna es de la sexta parte de la aceleración de la tierra, entonces en la luna una persona pesara la sexta parte de lo que pesa en la tierra.
Ahora pensemos en un lugar en el espacio vacío donde no existe gravedad, no existirá peso; es por ello que los astronautas al encontrarse en el espacio si salen de la nave deben tener un cordón que los ate a la nave para que puedan ser regresados a ella.
Una persona con $\color{#0000FF} 80 Kg$ de masa tendrá en la tierra un peso de:
$\color{#0000FF} F_g=mg= \dfrac {80Kg . 9.81m}{s^2}=784N$.
Si llevamos a esta persona fuera de la tierra al espacio vacío donde
no existe gravedad su peso será: $\color{#0000FF} F_g=mg=\dfrac {80 Kg 0 m}{s^2}=0 N$
Una fuerza que al actuar sobre un cuerpo ayuda a que este se desplace de una posición a otra realiza trabajo $\color{#0000FF} W$ sobre este cuerpo. Pensemos en el ascensor que nos lleva de un primer piso a un quinto piso por ejemplo. También realiza trabajo $\color{#0000FF} W$ aquella fuerza que cuando un cuerpo se desplaza de una posición a otra, esta fuerza se opone a ese desplazamiento, como cuando arrastramos una caja por el suelo y el contacto de la caja con el piso opone resistencia al movimiento.
Por ser el trabajo $\color{#0000FF} W$ una consecuencia de la fuerza y el desplazamiento sus unidades en el Sistema Internacional S.I. es $\color{#0000FF} N.m$, en el Sistema Técnico S.T. $\color{#0000FF} Kp.m$, en el sistema Ingles (U.S.C.S.) $\color{#0000FF} Lbf.ft$, en el sistema F.P.S. $\color{#0000FF} Lb.ft$ y en el sistema Cegesimal $\color{#0000FF} dina.cm.$
Es la capacidad que tienen los cuerpos de producir trabajo. Los conceptos de trabajo y energía se funden en uno solo, cuando hablamos de trabajo $\color{#0000FF} W$, hablamos de energía $\color{#0000FF} E$. y cuando hablamos de Energía $\color{#0000FF} E$, hablamos de trabajo $\color{#0000FF} W$. Existen varios tipos de energía: energía química, energía mecánica, energía nuclear, energía eléctrica entre otras. En este curso hablaremos de energía mecánica.
Las unidades de la energía son las mismas unidades del trabajo, en el Sistema Internacional S.I. es $\color{#0000FF} N.m=J$ llamada julio, en el Sistema Técnico S.T. $\color{#0000FF} Kp.m$, en el sistema Ingles (U.S.C.S.) $\color{#0000FF} Lbf.ft$, en el sistema F.P.S. $\color{#0000FF} Lb.ft$ y en el sistema Cegesimal $\color{#0000FF} dina.cm=erg$ llamada ergio.
Es la rapidez con que se realiza trabajo, es la rapidez con que se entrega energía. Es el cambio en el trabajo respecto de un cambio en el tiempo, es el cambio en la energía respecto del cambio en el tiempo $\color{#0000FF} P= \dfrac {\Delta W}{\Delta t}$, $\color{#0000FF} P=\dfrac {\Delta E}{\Delta t}$. Pensemos en un automóvil que arranca y hace chillar las llantas con el suelo.
La potencia da razón de que tan rápido se transfiere energía o que tan rápido se realiza un trabajo.
El concepto de potencia es muy importante a nivel industrial; una máquina que realice un trabajo de manera más rápida constituye una buena herramienta.
A mediados del siglo $\color{#0000FF} XVIII$ se pretendió tomar una unidad de medida de la potencia y se tomó como referencia el trabajo desarrollado por un caballo. James Watt ingeniero escoses quien trabajo e investigo con motores a vapor, encontró que un caballo al tirar en promedio ejercía una fuerza de $\color{#0000FF} 670N$ caminando a una velocidad de $\color{#0000FF} \dfrac {1m}{s}$, es decir $\color{#0000FF} \dfrac {745.71N.m}{s}$ que equivalen a $\color{#0000FF} \dfrac {550 Lb.ft}{s}$ y a este dato lo conocemos como un caballo fuerza, horsepower ($\color{#0000FF} hp$).
las unidades de la potencia en el sistema internacional S.I. son $\color{#0000FF} \dfrac {N.m}{s}=\dfrac {J}{s}=W$ unidad llamada Watt, en el sistema técnico S.T. $\color{#0000FF} \dfrac {Kp.m}{s}$, en el sistema U.S.C.S. $\color{#0000FF} \dfrac {Lbf.ft}{s}$, en el sistema F.P.S. $\color{#0000FF} \dfrac {Lb.ft}{s}$, en el sistema c.g.s.$\color{#0000FF} \dfrac {dina.cm}{s}=\dfrac {erg}{s}$.
Existe presión cuando una fuerza actúa sobre un área $\color{#0000FF} P= \dfrac {F}{A}$. Como cuando apoyamos verticalmente nuestra palma de la mano sobre una mesa
Sus unidades en el sistema internacional S.I. son $\color{#0000FF} \dfrac {N}{m^2}=Pa$ unidad llamada Pascal, en el sistema técnico S.T. $\color{#0000FF} \dfrac {Kp}{m^2}$, en el sistema U.S.C.S. $\color{#0000FF} \dfrac {Lb_f}{ft^2}$, en el sistema F.P.S. $\color{#0000FF} \dfrac {Lb.}{ft^2}$, en el sistema c.g.s.$\color{#0000FF} \dfrac {dina}{cm^2}=Poisse$.
Se pueden hacer conversiones de unidades para pasar de un sistema de unidades a otro, para ello daremos algunas relaciones que resultan convenientes.
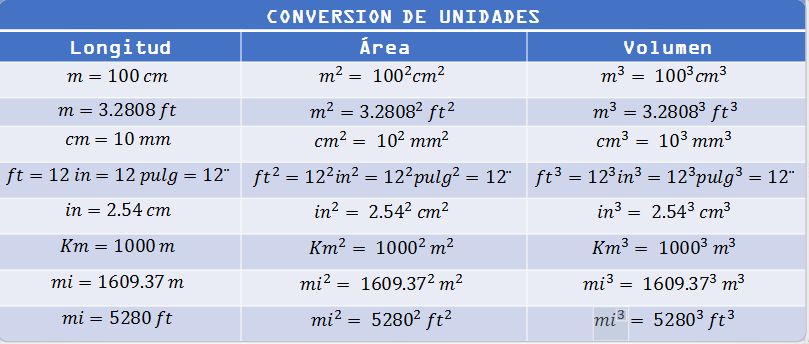
Tabla 1.1: Relaciona unidades de longitud, área y volumen en cinco sistemas de unidades.
En la aplicación de esta tabla debemos tener cuidado del hecho de que cuando una unidad se eleva a una potencia, igualmente se debe elevar su valor numérico correspondiente a la misma potencia.
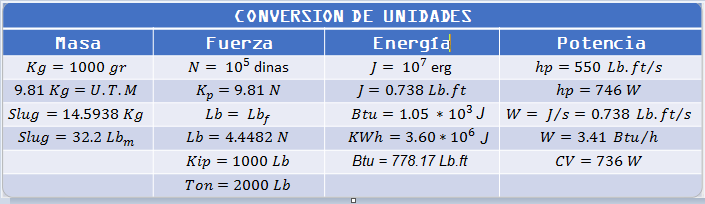
Tabla 1.2: Obsérvese con cuidado en la tabla $\color{#0000FF} 2$ las unidades de masa y peso para distinguir estos dos conceptos a la hora de leer los ejercicios que se desarrollaran durante el curso de Física mecánica.
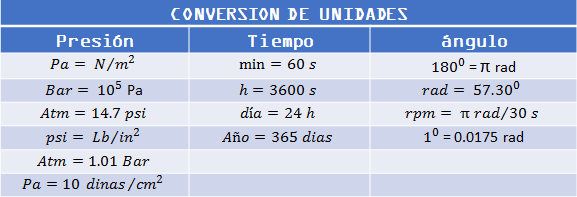
Tabla 1.3: Como complemento anexamos algunas equivalencias entre grados y radianes.
Téngase en cuenta que los conceptos, unidades y factores de conversión que hemos desarrollado en este capítulo son aquellos que vamos a utilizar en este curso de física mecánica.
Solución :
$\color{#0000FF} 14.7 {{\color{Red}\bcancel {{\color{blue}psi}}}}$ $\color{#0000FF} \cdot \dfrac {\dfrac {{{\color{Red}\bcancel {{\color{blue}Lb}}}}}{{{\color{Red}\bcancel {{\color{blue}in^{2}}}}}}}{{{\color{Red}\bcancel {{\color{blue}psi}}}}}\cdot \dfrac {\dfrac {4.4482{{\color{Red}\bcancel {{\color{blue}N}}}}}{{{\color{Red}\bcancel {{\color{blue}Lb}}}}}}{1}\cdot \dfrac {\dfrac {{{\color{Red}\bcancel {{\color{blue}in^{2}}}}}}{{2.54^{2}{{\color{Red}\bcancel {{\color{blue}cm^{2}}}}}}}}{1}\cdot \dfrac {\dfrac {100^{2}{{\color{Red}\bcancel {{\color{blue}cm^{2}}}}}}{{{\color{Red}\bcancel {{\color{blue}m^{2}}}}}}}{1}\cdot$
$\color{#0000FF} \dfrac {{{\color{Red}\bcancel {{\color{blue}P_{a}}}}}}{\dfrac {{{\color{Red}\bcancel {{\color{blue}N}}}}}{{{\color{Red}\bcancel {{\color{blue}m^{2}}}}}}}\cdot \dfrac {Bar}{10^{5}{{\color{Red}\bcancel {{\color{blue}P_{a}}}}}}= \color{#FF0000} 1.01Bar$
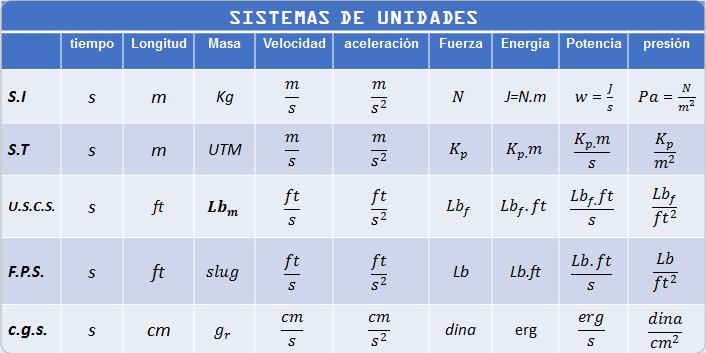
Tabla 1.4: En esta tabla se resumen de los cinco sistemas de unidades.
Para el desarrollo de este curso nos concentraremos en dos sistemas de unidades: Sistema Internacional de Unidades S.I. y Sistema Técnico Ingles F.P.S.
Un número queda descrito en forma de notación científica cuando se escribe con un número entre uno y el número diez multiplicado por una potencia de diez.
Solución:
(a) $\color{#0000FF} 2000 Lb =$ $\color{#FF0000} 2 \cdot 10^3 Lb$
Obsérvese que el número $\color{#0000FF} 2$ esta entre el numero uno y el número diez.
(b) $\color{#0000FF}1609.37 m =$ $\color{#FF0000} 1.61 \cdot 10^3 m$
Obsérvese que el número $\color{#0000FF} 1.61$ esta entre el número uno y el número diez.
(c) $\color{#0000FF}538 ft =$ $\color{#FF0000} 5.38 \cdot 10^2 ft$
Obsérvese que el número $\color{#0000FF} 5.38$ esta entre el numero uno y el número diez.
(d) $\color{#0000FF} 0.2248 ft =$ $\color{#FF0000} 2.22 \cdot 10^{-1} ft$
Obsérvese que el número $\color{#0000FF} 2.2$ esta entre el numero uno y el número diez.
Son una herramienta utilizada por el sistema internacional de unidades que facilita el manejo de las cifras numéricas.
En el estudio de la física mecánica nos encontramos en muchas ocasiones frente a cifras numéricas que son muy grandes o muy pequeñas y su escritura y manejo en la resolución de cálculos matemáticos resultan muy engorrosos. Para hacer más amable estos cálculos matemáticos y además facilitar las expresiones lingüísticas de estas cantidades, el Sistema internacional de Unidades desarrollo una serie de prefijos con nombre, símbolo y valor que permiten dicha finalidad.
La notación de los prefijos se realiza utilizando potencias de $\color{#0000FF} 10$, por ejemplo, el prefijo Mega significa $\color{#0000FF} 1000000$ que se puede escribir como $\color{#0000FF} {10^{6}}$, el prefijo Kilo significa $\color{#0000FF} 1000$ que puede escribirse $\color{#0000FF} {10^{3}}$. Así que si tenemos $\color{#0000FF} 1000$ Julios que son $\color{#0000FF} {10^{3}}$ Julios y se pueden escribir como $\color{#0000FF} 1 \ KJ $.
La utilización de los prefijos es exclusiva del Sistema Internacional, no es válido para ningún otro sistema de unidades.
No es permitido tener dos prefijos para una misma cifra, es decir no valido hablar por ejemplo de $\color{#0000FF} 50$ Mega Giga Newton $\color{#0000FF} 50MGN$, no existe la cifra.
Recordemos que si tenemos $\color{#0000FF} 0.000053m=53.10^{-6}m$.
Ahora, si aplicamos los prefijos métricos la cifra se puede expresar como $\color{#0000FF} 53µm$.
Para facilitar el entendimiento y operatividad de los prefijos hemos elaborado un listado de los más reconocidos y utilizados en el estudio de la física en general.
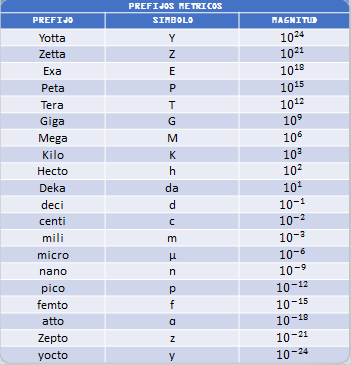
Tabla 1.5: La tabla muestra el nombre del prefijo, el símbolo y su valor en factores de $\color{#0000FF} 10$.
(a) $\color{#0000FF} 4860 \cdot 10^{-12}{\color{Red}\bcancel {{\color{blue}f}}}N\cdot \dfrac {10^{-15}}{{\color{Red}\bcancel {{\color{blue}f}}}}=4860 \cdot 10^{-12} \cdot 10^{-15}N $
$\color{#0000FF} 4860 \cdot 10^{-12}fN$ $\color{#0000FF} = $ $\color{#0000FF} 4860 \cdot 10^{-27}N=\color{#FF0000} 4.86 \cdot 10^{-24}N$
(b) $\color{#0000FF} 0.0019 \cdot 10^{9}{\color{Red}\bcancel {{\color{blue}M}}}J\cdot \dfrac {10^{6}}{{\color{Red}\bcancel {{\color{blue}M}}}}=0.0019 \cdot 10^{9} \cdot 10^{6}J$
$\color{#0000FF} 0.0019 \cdot 10^{9}MJ$ $\color{#0000FF} = $ $\color{#0000FF} 0.0019 \cdot 10^{15}Pa=\color{#FF0000} 1.9 \cdot 10^{12}J$
La siguiente es una escena interactiva, adaptada de Plantillas con descartes_JSLas escenas de Descartes son recursos interactivos que pueden insertarse o embeberse en múltiples soportes y medios como páginas web, blogs, wikispaces, o plataformas de aprendizaje como Moodle, entre otras herramientas., y diseñada por Juan Guillermo Rivera B.
• Convierte $\color{#0000FF} 545 \cdot 10^{9} Mgr$ en $\color{#0000FF} Zgr$ en forma manual.
• Realice la conversión utilizando la escena interactiva y compare los resultados.
• escriba la respuesta en notación científica.
• Convierte $\color{#0000FF} 0.00786 \cdot 10^{3} ngr$ en $\color{#0000FF} Tgr$ en forma manual.
• Realice la conversión utilizando la escena interactiva y compare los resultados.
• escriba la respuesta en notación científica.
• Repita los pasos para convertir:
$\color{#0000FF} 220.45 gr$ en $\color{#0000FF} Ggr$ $\color{#0000FF} \sqrt {458.25} mgr$ en $\color{#0000FF} Tgr$
$\color{#0000FF} \sqrt {Sen 45°} agr$ en $\color{#0000FF} dgr$
Para abordar este curso de física mecánica es necesario entender como mínimo los siguientes conceptos y modelos matemáticos:
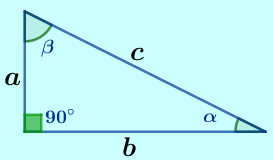 |
$\blacktriangleright\hspace{0.2cm}$ Triángulo Rectángulo Figura geométrica que se caracteriza por tener tres lados, dos de ellos (los lados más cortos) llamados catetos y el otro (el más largo) llamado hipotenusa, un ángulo interno de $\color{#0000FF} 90$ grados: |
La suma de los ángulos internos es de $\color{#0000FF} 180$ grados. Solo para los triángulos rectángulo es válido hablar de la ecuación de Pitágoras, $\color{#0000FF} c^{2}=a^{2}+b^{2}$, donde los lados $\color{#0000FF} a$ y $\color{#0000FF} b$ son los catetos y el lado $c$ es la hipotenusa, Despejando para $\color{#0000FF} c$ : $\color{#0000FF} c=\pm \sqrt {a^{2}+b^{2}}$.
dónde: $\color{#0000FF} c=\sqrt {a^{2}+b^{2}}$
Obsérvese que al despejar $c$ nos queda $\color{#0000FF} \pm$ la raíz cuadrada de $\color{#0000FF} {a^{2}+b^{2}}$ de la cual debemos tomar la raíz positiva en virtud de que los triángulos no tienen lados negativos.
Aplicando el mismo concepto podemos despejar para cada cateto:
$\color{#0000FF} c^{2}=a^{2}+b^{2}$, $\color{#0000FF} a=\pm \sqrt {c^{2}-b^{2}}$, $\color{#0000FF} a=\sqrt {c^{2}-b^{2}}$
$\color{#0000FF} c^{2}=a^{2}+b^{2}$, $\color{#0000FF} b=\pm \sqrt {c^{2}-a^{2}}$, $\color{#0000FF} \color{#0000FF} b=\sqrt {c^{2}-a^{2}}$
$\color{#0000FF} c=\sqrt {4^{2}+3^{2}}$ $\color{#FF0000} c=5m$
Ahora comprobamos para los catetos:
$\color{#0000FF} b=\sqrt {c^{2}-a^{2}}$ $\color{#0000FF} b=\sqrt {5^{2}-3^{2}}$ $ \color{#FF0000} b=4m$
$\color{#0000FF} a=\sqrt {c^{2}-b^{2}}$ $\color{#0000FF} a=\sqrt {5^{2}-4^{2}}$ $\color{#FF0000} a=3m$.
 |
$\blacktriangleright\hspace{0.2cm}$ Funciones Trigonométricas Las funciones trigonométricas son aplicables única y exclusivamente a triángulos rectángulos ya que sus definiciones están basadas en los conceptos de catetos y el concepto de hipotenusa: |
• $\color{#0000FF} Sen \alpha =\dfrac {a}{c}=\dfrac {Cateto Opuesto}{Hipotenusa}$
• $\color{#0000FF} Cos \alpha =\dfrac {b}{c}=\dfrac {Cateto Adyacente}{Hipotenusa}$
• $\color{#0000FF} tg \alpha =\dfrac {a}{b}=\dfrac {Cateto Opuesto}{Cateto Adyacente}$
• $\color{#0000FF} Ctg \alpha =\dfrac {b}{a}=\dfrac {Cateto Adyacente}{Cateto Opuesto}$
• $\color{#0000FF} Sec \alpha =\dfrac {c}{b}=\dfrac {Hipotenusa}{Cateto Adyacente}$
• $\color{#0000FF} Csc \alpha =\dfrac {c}{a}=\dfrac {Hipotenusa}{Cateto Opuesto}$
$\blacktriangleright\hspace{0.2cm}$ Funciones Trigonométricas InversasLas funciones trigonométricas inversas son una herramienta utilizada en la física especialmente para encontrar el valor de un ángulo a partir de una Función Trigonométrica.
• $\color{#0000FF} \alpha =Sen^{-1}\dfrac {a}{c}$ • $\color{#0000FF} \alpha =Ctg^{-1}\dfrac {b}{a}$
• $\color{#0000FF} \alpha =Cos ^{-1}\dfrac {b}{c}$ • $\color{#0000FF} \alpha =Sec ^{-1}\dfrac {c}{b}$
• $\color{#0000FF} \alpha =tag^{-1}\dfrac {a}{b}$ • $\color{#0000FF} \alpha =Csc ^{-1}\dfrac {c}{a}$
En las funciones trigonométricas inversas los símbolos $\color{#0000FF} Sen^{-1}$, $\color{#0000FF} Cos ^{-1}$, $\color{#0000FF} tag^{-1}$, $\color{#0000FF} Ctg^{-1}$, $\color{#0000FF} Sec ^{-1}$, $\color{#0000FF} Csc ^{-1}$, no son sujetos de operaciones algebraicas, son indicativos que hacen alusión a ser la función inversa de la respectiva función.
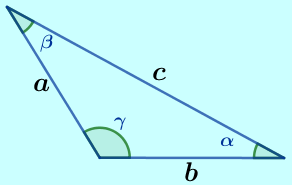 |
$\blacktriangleright\hspace{0.2cm}$ Triángulos que no son Rectángulos. Los triángulos que No son rectángulos No tienen catetos, No tienen hipotenusa y No tienen ángulo de $\color{#0000FF} 90$ grados en su interior. |
Como consecuencia de lo anterior, a los triángulos No rectángulos No se les puede aplicar la ecuación de Pitágoras.
Los triángulos No rectángulos se caracterizan por tener tres lados y No tener en su interior ángulos de $\color{#0000FF} 90$ grados, la suma de sus ángulos internos es de $\color{#0000FF} 180$ grados.
A los triángulos No rectángulos, se les aplica la ley del Coseno y la ley del Seno.
La ley del coseno afirma que si se conocen dos lados de un triángulo y al ángulo entre ellos, se puede conocer el otro lado.
• $\color{#0000FF} c=\sqrt {a^{2}+b^{2}-2ab\cos \gamma }$
• $\color{#0000FF} a=\sqrt {c^{2}+b^{2}-2cb\cos \alpha }$
• $\color{#0000FF} b=\sqrt {c^{2}+a^{2}-2\cos \beta }$
La ley del coseno es una ley que se aplica a todo tipo de triángulos incluyendo a los triángulos rectángulos.
Obsérvese que si $\color{#0000FF} \gamma=90°$, la ecuación para hallar $\color{#0000FF} c$ queda:
$\color{#0000FF} c=\sqrt {a^{2}+b^{2}-2ab\cos 90° }$ y como $\color{#0000FF} cos 90°=0$, esto hace que el termino $\color{#0000FF} -2ab\cos 90°$ desaparezca de la ecuación y quede finalmente que $\color{#0000FF} c=\sqrt {a^{2}+b^{2} }$ que es la ecuación de Pitágoras.
La ley del Seno hace una relación entre el Seno de un ángulo y su respectivo lado opuesto.
• $\color{#0000FF} \color{#0000FF} \dfrac {sen\alpha }{a}=\dfrac {sen\gamma }{c}=\dfrac {sen\beta }{b}$
Por propiedades de los fraccionarios, la ecuación de la ley del seno se puede escribir:
• $\color{#0000FF} \color{#0000FF} \dfrac {a}{sen\alpha }=\dfrac {c}{sen\gamma }=\dfrac {b}{sen_{B}}$
La ley del Seno al igual que la ley del Coseno es aplicable a todo tipo de triángulos incluyendo a los triángulos rectángulos.
Si tomamos las dos primeras relaciones de la ley del seno y hacemos
$\color{#0000FF} \gamma=90°$. $\color{#0000FF} \dfrac {sen\alpha }{a}=\dfrac {sen 90° }{c}$ y despejando para $\color{#0000FF} sen\alpha$ :
$\color{#0000FF} {sen\alpha }=\dfrac {a sen 90° }{c}$ y como $\color{#0000FF} Sen 90°=1$ Queda:
$\color{#0000FF} {sen\alpha }=\dfrac {a}{c}$ Resultado que coresponde a la funcion trigonométrica $\color{#0000FF} sen\alpha$ si el triángulo fuera rectángulo.
 |
Ejercicio 1.7: En el triángulo $\color{#0000FF} a=4m$ $\color{#0000FF} b=3m$ y el ángulo $\color{#0000FF} \gamma=120°$, determinar el valor del lado $\color{#0000FF} c$ y el valor de los ángulos $\color{#0000FF} \alpha$ y $\color{#0000FF} \beta$. |
Solución:
Como conocemos dos lados y el ángulo entre ellos, aplicamos la ley del Coseno para conocer $\color{#0000FF} c$:
$\color{#0000FF} c=\sqrt {a^{2}+b^{2}-2ab\cos \gamma }$
$\color{#0000FF} c=\sqrt {4^{2}+3^{2}-2(4)3\cos 120 }$ $\color{#0000FF} \color{#FF0000} c=6.08m$
Ahora, aplicamos la ley del Seno para hallar $\color{#0000FF} \alpha$:$\color{#0000FF} \dfrac {sen\alpha }{4}=\dfrac {sen 120° }{6.08}$ $\color{#0000FF} {sen\alpha }=\dfrac {4 sen 120° }{6.08}$
$\color{#0000FF} \alpha =Sen^{-1}\dfrac {4 sen 120° }{6.08}$ $\color{#0000FF} \color{#FF0000} \alpha = 34.07°$
Finalmente, como los ángulos internos de un triángulo suman $180°$, entonces:
$\color{#0000FF} \beta=180°-\alpha-\gamma$
$\color{#0000FF} \beta=180°-34.07-120$ $\color{#0000FF} \color{#FF0000} \beta=25.93°$
• En la escena interactiva tomamos el lado de cada cuadro como de $\color{#0000FF} 2 \ m$
• Mueva el vértice $\color{#0000FF} (C)$ del triángulo y logre que el lado $\color{#0000FF} (a)$ mida $\color{#0000FF} 10 \ m$ horizontales
• Mueva el vértice $\color{#0000FF} (A)$ de tal manera que quede localizado a $\color{#0000FF} 6 \ m$ a la derecha del vértice $\color{#0000FF} (C)$ y a $\color{#0000FF} 6m$ arriba. Observe que el ángulo $\color{#0000FF} \gamma$ es de $\color{#0000FF} 135°$
• Determine el valor del lado $\color{#0000FF} (c)$ aplicando la ley del coseno y compárelo con el valor arrojado por la escena interactiva.
• Con la Ley del Seno y con el valor del lado $\color{#0000FF} (C)$ obtenido, encuentre el valor de los ángulos ($\color{#0000FF} \alpha$) y ($\color{#0000FF} \beta$) y compárelos con los valores arrojados por la escena interactiva.
• Mueva el vértice $\color{#0000FF} (A)$ de tal manera que quede localizado a $\color{#0000FF} 6 \ m$ a la izquierda del vértice $\color{#0000FF} (C)$ y a $\color{#0000FF} 6 \ m$ arriba y realice los dos anteriores puntos.
• En la escena interactiva tomamos el lado de cada cuadro como de $\color{#0000FF} 10Lb$
• Mueva los vértices del triángulo y logre que el lado $\color{#0000FF} (a)$ mida $\color{#0000FF} 120Lb$ horizontales
• Logre que el vértice $\color{#0000FF} (A)$ este localizado en la mitad del lado $\color{#0000FF} (a)$ y a $\color{#0000FF} 60$ Lbs arriba.
• Determine el valor del ángulo gamma ($\color{#0000FF} \gamma$) y el valor del lado $\color{#0000FF} (b)$.
• Determine el valor del lado $\color{#0000FF} (c)$ aplicando la ley del coseno y compárelo con el valor arrojado por la escena interactiva.
• Con la Ley del Seno determine el valor de los ángulos alpha ($\color{#0000FF} \alpha$) y Beta ($\color{#0000FF} \beta$).
• Encuentre otras formas de realizar el ejercicio y explique.
• En la escena interactiva recree el siguiente ejercicio.
• Una vía de ferrocarril es horizontal y otra vía de ferrocarril la cruza formando un ángulo de 60° arriba de la horizontal. Por la vía horizontal pasa un tren a una velocidad de $\color{#0000FF} 20\dfrac {Km}{h}$. $\color{#0000FF} 15$ minutos más tarde pasa por el punto de cruce y por la otra vía un tren a una velocidad de $\color{#0000FF} 10\dfrac {Km}{h}$. Determinar la distancia que separa a los dos trenes $\color{#0000FF} 15$ minutos después de pasar el segundo tren por el punto de cruce de las vías. Determine el valor del ángulo entre la distancia recorrida por el tren que viaja horizontalmente con la distancia que los separa.
• Determine primero la distancia que recorre el primer tren multiplicando la velocidad por el tiempo que será de media hora.
• Determine la distancia recorrida por el segundo tren multiplicando su velocidad por el tiempo que será de $\color{#0000FF} \dfrac {1}{4}$ de hora.
• Grafique la distancia recorrida por el primer tren como el lado $\color{#0000FF} (a)$ del triángulo, grafique la distancia recorrida por el segundo tren como el lado $\color{#0000FF} (c)$ y el ángulo entre ellos Beta $\color{#0000FF} \beta = 60°$.
• Aplique la ley del coseno y determine el lado desconocido $\color{#0000FF} (b)$ que será la distancia entre los dos trenes.
• Compare el resultado obtenido con el modelo matemático de la ley del coseno con el valor arrojado por la escena interactiva.
• Para determinar el ángulo entre la distancia recorrida por el tren que viaja horizontalmente con la distancia que los separa se utiliza la Ley del Seno.
El video introductorio hace parte de la serie Universo MecánicoLa serie educativa Universo Mecánico es una colección de 52 videos creados por el Instituto de Tecnología de California cuyo director y anfitrión es el Dr. David L. Goodtein.
Dónde está algo y qué camino sigue, son los interrogantes que tratan de resolver los vectores.
A diario nos encontramos en un mundo definido por vectores, si queremos por ejemplo venir a la universidad desde nuestra casa, seguramente que en nuestra mente tenemos que definir qué camino vamos a recorrer para lograr llegar a la universidad. Seguramente saldremos de nuestra casa, iremos hasta el metro, éste nos llevara hasta una estación donde tomaremos un bus alimentador que nos dejara a unas cuadras de la universidad y así llegaremos. Hemos tenido que realizar varios desplazamientos que sumados logran el objetivo. Hemos sumado vectores.
La siguiente es una escena interactiva, de Plantillas con descartes_JSLas escenas de Descartes son recursos interactivos que pueden insertarse o embeberse en múltiples soportes y medios como páginas web, blogs, wikispaces, o plataformas de aprendizaje como Moodle, entre otras herramientas., y diseñada por Juan Guillermo Rivera B.
En física estudiaremos los vectores porque muchos de los fenómenos de la naturaleza tienen las características propias de los vectores.
$\blacktriangleright\hspace{0.2cm}$ Magnitud: Es lo que mide el vector $\color{#0000FF} (10, 4, 500,...)$. La magnitud de un vector es siempre una cantidad positiva.
$\blacktriangleright\hspace{0.2cm}$ "Unidad": Será, según el sistema de unidades en el que estemos trabajando. Para este curso de física mecánica, será en el sistema internacional S.I. o en el sistema técnico ingles F.P.S.:
$\color{#0000FF} (N, m, Lb, ft$, $\color{#0000FF} \dfrac {m}{s^2}$, $\color{#0000FF} \dfrac {ft}{s^2}$, $\color{#0000FF} \dfrac {m}{s}$, $\color{#0000FF} \dfrac {ft}{s}... ).$
Cuando decimos "unidad" entre comillas, es porque queremos destacar el hecho de que No todos los vectores tienen unidades; más adelante hablaremos de los vectores unitarios que carecen de unidades.
$\blacktriangleright\hspace{0.2cm}$ Dirección: Es el eje que contiene al vector. La dirección de un vector generalmente se indica con el ángulo o ángulos que hace el vector respecto de uno o más ejes de referencia.
$\blacktriangleright\hspace{0.2cm}$ Sentido: Es la punta del vector. Teniendo los conceptos claros podemos decir que una dirección puede tener dos sentidos, pero un vector solo puede tener uno de ellos.
Es muy importante la distinción entre cada uno de los componentes de un vector, pues cada uno de ellos cumple una función específica para describir el vector; sin embargo, cuando leemos a muchos autores, estos hacen referencia a que un vector es una cantidad física determinada por una magnitud y una dirección; esto significa que el autor da por entendido que dentro de la magnitud se puede expresar la unidad y dentro de la dirección se puede expresar el sentido y en ese entendimiento la definición es correcta.
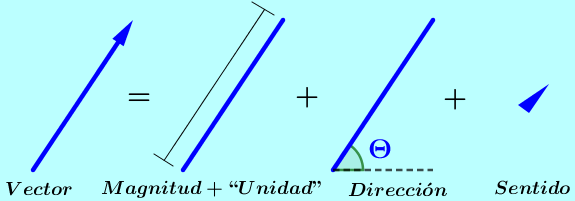
La nomenclatura de un vector se realiza por medio de una flecha, una letra o un símbolo en mayúscula o minúscula y encima de este una flechita pequeña; en algunos textos también se utiliza para indicar que se trata de un vector una letra o símbolo en negrilla:
$\color{#0000FF} \overrightarrow {F}$, $\color{#0000FF} \overrightarrow {T}$, $\color{#0000FF} \overrightarrow {a}$ $\color{#0000FF} \overrightarrow {F}$, $\color{#0000FF} \overrightarrow {v}$, $\color{#0000FF} \overrightarrow {g}$, F, g, r.
La nomenclatura para la magnitud de un vector se realiza por medio de dos barritas que enmarcan la notación de vector, y En el caso de que se utilice la notación para vector de la letra o símbolo en negrilla, simplemente se le quita la negrilla indicando que se trata de la magnitud del vector:
$\color{#0000FF} \left| \overrightarrow {F}\right|=F$, $\color{#0000FF} \left| \overrightarrow {T}\right|=T$, $\color{#0000FF} \left| \overrightarrow {a}\right|=a$, $\color{#0000FF} \left| \overrightarrow {f}\right|=f$,
$\color{#0000FF} \left| \overrightarrow {v}\right|=v$, $\color{#0000FF} \left| \overrightarrow {g}\right|=g$, $\color{#0000FF} F$, $\color{#0000FF} g$, $\color{#0000FF} r$.Dos vectores son iguales cuando tienen la misma magnitud, la misma unidad, la misma dirección, el mismo sentido, así sus orígenes sean diferentes.
El concepto de igualdad de vectores es útil porque facilita las operaciones con vectores como son la suma y resta especialmente cuando utilicemos el método grafico del triángulo o del paralelogramo, métodos que veremos en detalle más adelante.
También el concepto de igualdad de vectores facilita la visualización del ángulo entre ellos.
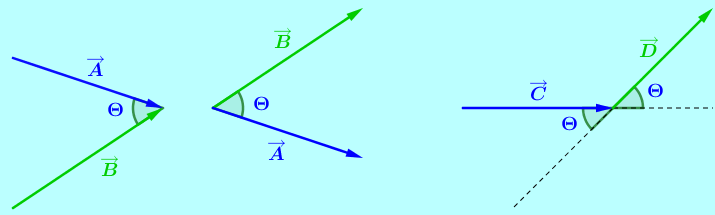
El ángulo entre dos vectores es entre las puntas de los vectores o entre las colas de estos. El principio de igualdad de vectores permite dibujar los vectores y ponerlos en esta condición (entre puntas o entre colas) y así identificar el ángulo entre ellos.
En ocasiones los vectores aparecen alineados punta con cola y no se ve claramente el ángulo entre ellos. En estos casos es aconsejable trazar líneas punteadas en la dirección de los vectores y de manera imaginaria vemos a cada vector desplazarse hacia adelante o hacia atrás y así alineamos los vectores cola con cola o punta con punta como se muestra en la figura.
En la naturaleza existen fenómenos que revisten las características de los vectores (tienen Magnitud, unidad, dirección y sentido), entre ellos el fenómeno de la gravedad que tiene una magnitud de $\color{#0000FF} 9.81$, una unidad de $\color{#0000FF} \dfrac {m}{s^2}$, su dirección vertical a la tierra y su sentido al centro de la tierra. La velocidad que contiene magnitud, unidad, dirección y sentido. La aceleración igualmente con magnitud, unidad, dirección y sentido.
La fuerza que es un fenómeno inherente a la interacción entre los cuerpos. La fuerza eléctrica que aparece de la interacción entre partículas cargadas. El campo eléctrico que aparece cuando una fuerza actúa sobre una carga. El campo magnético y muchos fenómenos más.
Existen también muchos fenómenos en la naturaleza que no son vectores y también le interesan a la física, tales como el tiempo, la energía, el trabajo, la potencia y muchos fenómenos más.
Un escalar es un número o un número acompañado de una unidad. Un escalar puede ser de signo positivo, negativo o ser cero:
$\color{#0000FF} (2, 5, -10, 6m, 500N, 230 Lb.ft ....)$Los escalares pueden alterar o afectar a los vectores
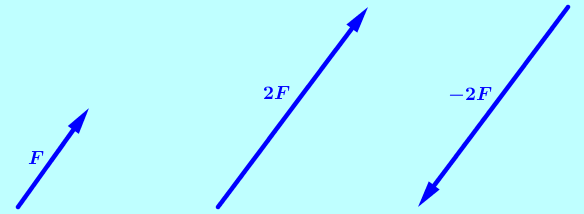
Obsérvese como en este caso el escalar $\color{#0000FF} 2$ duplico al vector fuerza afectando su magnitud. Enseguida el escalar $\color{#0000FF} -2$ cambio el sentido al vector. Téngase claro que si bien es cierto que el signo $\color{#0000FF} (-)$ cambio el sentido al vector, no afecto el signo de la magnitud que sigue siendo positiva, en este caso sigue siendo la magnitud de $\color{#0000FF} 2$.
Todo vector tiene un escalar positivo incluido en su estructura
Los vectores unitarios son aquellos que tienen una magnitud igual a uno $\color{#0000FF} (1)$. Los vectores unitarios no tienen unidades y sirven para indicar la dirección y sentido de un fenómeno físico.
La nomenclatura de un vector unitario es una letra o un símbolo en mayúscula o en minúscula acompañada de un gorrito encima.
$\color{#0000FF} \widehat {i}$, $\color{#0000FF} \widehat {j}$, $\color{#0000FF} \widehat {k}$, $\color{#0000FF} \widehat {r}$, $\color{#0000FF} \widehat {\lambda }$, $\color{#0000FF} \widehat {\theta }$.
Analicemos la dirección y sentido de estos dos vectores:

Observemos el vector velocidad; el ángulo de $\color{#0000FF} 30$ grados hacia arriba de la horizontal indican la dirección y sentido de esa velocidad. Esta dirección y sentido son un claro ejemplo de un vector unitario.
Este vector unitario no puede cambiar ni la magnitud ni la unidad de esta velocidad, de ahí que este vector unitario tiene su propia magnitud que es igual a uno $\color{#0000FF} (1)$ y no puede tener unidades.
$\color{#0000FF} \left| \widehat {i}\right|=1$, $\color{#0000FF} \left| \widehat {j}\right|=1$, $\color{#0000FF} \left| \widehat {k}\right|=1$, $\color{#0000FF} \left| \widehat {r}\right|=1$
Igualmente sucede con la dirección y sentido del vector fuerza, que indica que la fuerza de $\color{#0000FF} 500N$ está dirigida de forma horizontal y a la derecha.
El hecho de indicar para donde va la fuerza no puede afectar la magnitud de la fuerza que es de $\color{#0000FF} 500N$.
Es precisamente el vector unitario el que le da el carácter de vector a la velocidad y a la fuerza si el vector unitario no aparece solo tendríamos la magnitud de la velocidad y la magnitud de la fuerza.
Con lo visto hasta el momento sobre vectores podemos afirmar que:
Un vector es una cantidad física determinada por un escalar positivo y un vector unitario.

Los ejes cartesianos $\color{#0000FF} X,Y,Z$ no son vectores , son direcciones, sin embargo sobre ellos, sobre sus planos, o sobre su volumen se pueden graficar vectores, esto con la ayuda de los vectores unitarios. Para el eje $\color{#0000FF} X$ existe un vector unitario llamado $\color{#0000FF} \widehat {i}$, para el eje $\color{#0000FF} Y$ un vector unitario llamado $\color{#0000FF} \widehat {j}$, y para el eje $\color{#0000FF} Z$ un vector unitario llamado $\color{#0000FF} \widehat {k}$.
Como ya vimos, los escalares pueden afectar a los vectores, de manera que un vector unitario puede verse afectado por un escalar; por ejemplo podemos tener $\color{#0000FF} 5\widehat {i}$, cinco veces el vector unitario $\color{#0000FF} \widehat {i}$, o tener $\color{#0000FF} 0.5\widehat {i}$ o cambiar el sentido del vector $\color{#0000FF} \widehat {i}$, segun sea el signo y el valor del escalar. Igual sucede con los vectores unitarios $\color{#0000FF} \widehat {j}$ y $\color{#0000FF} \widehat {k}$, podemos tener por ejemplo $\color{#0000FF} 4\widehat {j}$, $\color{#0000FF} -3\widehat {k}$, etc.
• En la escena interactiva, tome los botones controladores de los ejes $\color{#0000FF} X, Y, Z$, mueva cada control a la posición $1$.
Observe que los ejes $\color{#0000FF} X$, $\color{#0000FF} Y$, $\color{#0000FF} Z$ no son vectores y que sobre cada eje aparece un vector llamado unitario, que tiene una magnitud igual a $\color{#0000FF} 1$. Sobre el eje $\color{#0000FF} X$ el vector unitario $\color{#0000FF} \widehat {i}$, sobre el eje $\color{#0000FF} Y$ el vector unitario $\color{#0000FF} \widehat {j}$, sobre el eje $\color{#0000FF} Z$ el vector unitario $\color{#0000FF} \widehat {k}$.
• Tome los botones controladores de los ejes $\color{#0000FF} X, Y, Z$, mueva cada control a la posición $\color{#0000FF} (-1)$. Los vectores unitarios cambian su sentido y se expresan como $\color{#0000FF} -\widehat {i}$, $\color{#0000FF} -\widehat {j}$, $\color{#0000FF} -\widehat {k}$.
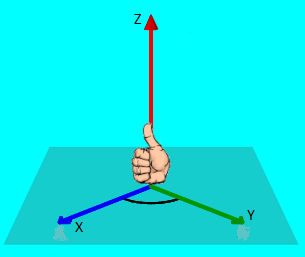
Los ejes $\color{#0000FF} X,Y,Z$ obedecen a la regla de la mano derecha o dextrógiro, que funciona de la siguiente forma: se pone la palma de la mano derecha sobre la parte positiva eje $\color{#0000FF} X$, se giran los dedos buscando la parte positiva del eje $\color{#0000FF} Y$ y el dedo pulgar nos indica la dirección y sentido positivo del eje $\color{#0000FF} Z$.
El procedimiento en el caso en que conozcamos la parte positiva del eje $\color{#0000FF} Y$ y del eje $\color{#0000FF} Z$ es análogo, ponemos la palma de la mano derecha sobre el eje $\color{#0000FF} Y$ en su parte positiva, se giran los dedos buscando la parte positiva del eje $\color{#0000FF} Z$ y el dedo pulgar nos indica la dirección y sentido positivo del eje $\color{#0000FF} Z$.En el plano $\color{#0000FF} x,y$ se dibuja el vector con el origen del sistema de coordenadas en la cola o en la punta del vector, se trazan paralelas a los ejes $\color{#0000FF} x,y$, se forma un triángulo rectángulo; de éste triángulo tomamos uno de los ángulos diferentes del de $\color{#0000FF} 90°$ y aplicamos las funciones trigonométricas $\color{#0000FF} Sen \theta$, y $\color{#0000FF} Cos \theta$ para determinar el valor de las componentes a lo largo de los ejes $\color{#0000FF} x,y$. Si el vector se llama $\color{#0000FF} F$, las componentes se llaman $\color{#0000FF} F_x$ y $\color{#0000FF} F_y$. si el ángulo que tomamos $\color{#0000FF} \theta$ toca al eje $\color{#0000FF} x$ o a la paralela con el eje $\color{#0000FF} x$, entonces la componente respecto al eje $\color{#0000FF} x$ se llama $\color{#0000FF} F Cos \theta$, y la componente con el eje $\color{#0000FF} y$ se llama $\color{#0000FF} F Sen \theta$. Si el ángulo que tomamos toca al eje $\color{#0000FF} y$ o a la paralela con el eje $\color{#0000FF} y$, la componente respecto al eje $\color{#0000FF} x$ se llama $\color{#0000FF} F Sen \theta$, y la componente con el eje $\color{#0000FF} \color{#0000FF} y$ se llama $\color{#0000FF} F Cos \theta$.
Escena interactiva, diseñada por Juan Guillermo Rivera B.Juan Guillermo Rivera B. es autor de la red Descartes quien publico la escena interactiva "Componentes Rectangulares de un Vector".
Estas componentes se llaman componentes escalares del vector, que no son vectores, son escalares positivos, sin embargo podemos convertirlos en vectores con ayuda de los vectores unitarios $\color{#0000FF} \widehat {i}$, $\color{#0000FF} \widehat {j}$, llamándose así componentes vectoriales del vector:
$\color{#0000FF} \overrightarrow {F_x}=F Cos \theta \widehat {i}$, $\color{#0000FF} \overrightarrow {F_y}=F Cos \theta \widehat {j}$ esto en el caso de haber tomado el ángulo $\color{#0000FF} \theta$ tocando al eje $\color{#0000FF} X$ o a su paralela.
Los vectores se pueden sumar por el método grafico o por el método analítico.
siempre que sumamos cantidades físicas, estas deben ser de la misma especie, entonces se suman vectores de fuerza con vectores de fuerza, vectores de velocidad con vectores de velocidad, vectores de aceleración con vectores de aceleración; no existe la suma de la combinación de vectores de diferente especie, no existe la suma de vector fuerza con vector velocidad.
Para sumar vectores por el método grafico, tomamos dos vectores y formamos con ellos un triángulo o un paralelogramo.
$\blacktriangleright\hspace{0.2cm}$ Método Grafico del TriánguloSe dibuja un vector y en la punta de este se pone la cola del otro vector; la suma de estos dos vectores es el vector que sale de la cola del primer vector y va hasta la punta del último vector, formando un triángulo. Para determinar la magnitud y dirección del vector suma se aplica lo visto respecto de los triángulos.
El video fue creado por Juan Guillermo Rivera B.Juan Guillermo Rivera B. es autor en la red Descartes. El video enseña la suma de dos vectores por el método del triángulo.
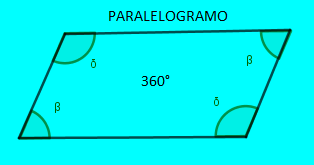
$\blacktriangleright\hspace{0.2cm}$ Método Grafico del Paralelogramo• Un paralelogramo es una figura geometrica que tiene cuatro lados formados por dos juegos de paralelas.
• Sus ángulos internos suman $\color{#0000FF} 360°$.
• Los ángulos opuestos son iguales.
• la suma de dos ángulos vecinos es de $\color{#0000FF} 180°$.• Las diagonales de un paralelogramo dividen los ángulos en partes iguales únicamente cuando el paralelogramo tiene todos sus lados iguales.
• Cuando se trace una de las diagonales del paralelogramo se forman dos triángulos exactamente iguales.
• Dentro de los paralelogramos se encuentran los cuadrados y los rectángulos.
Con el método del paralelogramo, se toman dos vectores por las colas, en la punta de cada vector se traza una paralela al otro vector formando un paralelogramo; la suma de los dos vectores es el vector que sale de la unión de las colas de los vectores y sigue la diagonal del paralelogramo.
Como al trazar la diagonal de un paralelogramo se forman dos triángulos idénticos, entonces podemos aplicar los modelos matemáticos aplicados a los triángulos y los modelos matemáticos aplicados a los paralelogramos.
El video fue creado por Juan Guillermo Rivera B.Juan Guillermo Rivera B. es autor en la red Descartes. El video enseña la suma de dos vectores por el método del paralelogramo.
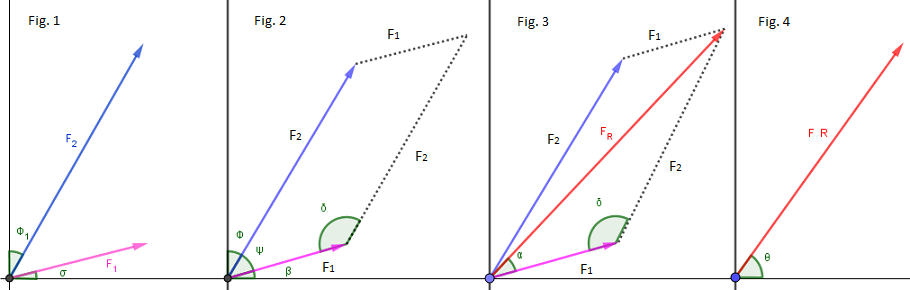
| Ejercicio 2.1: Hallar la fuerza resultante del sistema mostrado en la (Figura 1), aplicando el método grafico de suma de vectores, si se sabe que $\color{#0000FF} \sigma = 10°$, $\color{#0000FF} \phi = 20°$, $\color{#0000FF} F_1 = 10N$, y $\color{#0000FF} F_2 = 20N$. |
|
• Con los datos del ejercicio 2.1 representados en la figura 1 construimos la (Figura 2). Estando los dos vectores unidos por las colas hacemos en la punta de cada uno de ellos una paralela al otro vector formando un paralelogramo. • Del paralelogramo que construimos podemos en principio afirmar que el ángulo $\color{#0000FF} \psi = 60°$ formado por las colas de los vectores, esto en razón a que el ángulo entre los ejes es de $\color{#0000FF} 90°$, del que ya conocemos $\color{#0000FF} 30°$ que corresponde a $\color{#0000FF} \sigma = 10°$ que forma el vector $\color{#0000FF} F_1$ con el eje horizontal más $\color{#0000FF} \color{#0000FF} \phi = 20°$ que forma el vector $\color{#0000FF} \color{#0000FF} F_2$ con el eje vertical, de tal manera que el ángulo $\color{#0000FF} \psi = 60°$ que es ángulo interno del paralelogramo. • En la misma (Figura 2) aplicamos el concepto de que dos ángulos vecinos en un paralelogramo suman $\color{#0000FF} 180°$, entonces el ángulo $\color{#0000FF} \gamma = 120°$ • Hacemos la (Figura 3), en la que trazamos la diagonal del paralelogramo que parte de la unión de las colas de los vectores y que corresponde al vector suma del vector $\color{#0000FF} \overrightarrow {F_1} + \overrightarrow {F_2}$ y que llamaremos $\color{#0000FF} \overrightarrow {F_R}$ . • El vector fuerza resultante es un lado de uno cualquiera de los dos triángulos en que este vector dividió el paralelogramo. Tomaremos el triángulo más cercano al eje horizontal y aplicamos los conceptos de los triángulos para hallar su magnitud. |
|
• El triángulo escogido tiene un lado con magnitud $\color{#0000FF} F_1 = 10N$, otro lado de magnitud $\color{#0000FF} F_2 = 20N$ y conocemos el ángulo entre ellos que es $\color{#0000FF} \gamma = 120°$; entonces aplicamos ley del Coseno para hallar la magnitud de la $\color{#0000FF} F_R$. $\color{#0000FF} F_R=\sqrt {10^{2}+20^{2}-2.{10}.{20}\cos 120}$ $\color{#FF0000}F_R=26.46N$ • En la (Figura 4) observamos que la dirección de la fuerza resultante esta indicada por el ángulo $\color{#0000FF} \theta$ que es la suma de $\color{#0000FF} \sigma = 10°$ que forma el vector $\color{#0000FF} F_1$ con el eje horizontal más el ángulo $\color{#0000FF} \alpha$ que pertenece al triángulo que estamos analizando. $\color{#0000FF} \theta = 10° + \alpha$. Aplicamos la ley del Seno para conocer $\color{#0000FF} \alpha$. $\color{#0000FF} \dfrac {sen\alpha }{20}=\dfrac {sen 120° }{26.46}$ $\color{#0000FF} {sen\alpha }=\dfrac {20 sen 120° }{26.46}$ $\color{#0000FF} \alpha =Sen^{-1}\dfrac {20 sen 120° }{26.46}$ $\color{#FF0000} \alpha = 40.89°$ • Como $\color{#0000FF} \theta = 10° + \alpha$, entonces: $\color{#0000FF} \theta = 10° + 40.89°$,$\color{#0000FF} \color{#FF0000} \theta = 59.89°$. • Finalmente diremos que la Figura 4 muestra que la fuerza resultante es el vector $\color{#0000FF} \color{#FF0000} \overrightarrow {F_R}$ que tiene por magnitud $\color{#0000FF} \color{#FF0000} F_R = 26.46N$ y una dirección ,$\color{#FF0000} \theta = 59.89°$, dirigida hacia arriba de la horizontal. |
Cuando vimos las componentes vectoriales de un vector sección 2.3.3. entendimos que con ayuda de las funciones trigonométricas Seno y Coseno obteníamos las componentes escalares y luego las convertíamos en componentes vectoriales con el eje $\color{#0000FF} x$ y con el eje $\color{#0000FF} y$
$\color{#0000FF} \overrightarrow {F_x}=F Cos \theta \widehat {i}$, $\color{#0000FF} \overrightarrow {F_y}=F Cos \theta \widehat {j}$ esto en el caso de haber tomado el ángulo $\color{#0000FF} \theta$ tocando al eje $\color{#0000FF} x$ o a su paralela.
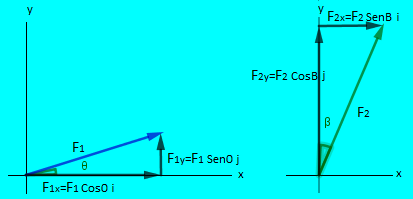
Observemos que el vector $\color{#0000FF} \overrightarrow {F_1}$ puede expresarse como la suma de las dos vectores llamados componentes vectoriales del vector $\color{#0000FF} \overrightarrow {F_1}$ que al alinearse punta con cola se puede formar un triángulo rectángulo cuya hipotenusa es el vector $\color{#0000FF} \overrightarrow {F_1}$, eso gráficamente, pero analíticamente podemos dar al vector $\color{#0000FF} \overrightarrow {F_1}$ también como la suma de sus componentes vectoriales o en forma cartesiana:
$\color{#0000FF} \overrightarrow {F_1} = \overrightarrow {F_1x} + \overrightarrow {F_1y}$ $\color{#0000FF} \overrightarrow {F_1} = F_1 Cos \theta \widehat {i} + F_1 Sen \theta \widehat {j}$Observemos que para el vector $\color{#0000FF} F_2$ se a tomado el ángulo $\color{#0000FF} \beta $ que es el ángulo que hace el vector $\color{#0000FF} F_2$ con el eje $\color{#0000FF} Y$, de tal manera que la.
componente vectorial con respecto al eje $\color{#0000FF} X$ es $\color{#0000FF} \overrightarrow {F_2x} = F_2 Sen \beta \widehat {i}$ y la componente vectorial con respecto al eje $\color{#0000FF} Y$ es $\color{#0000FF} \overrightarrow {F_2x} = F_2 Cos \beta \widehat {j}$.
Podemos ahora expresar al vector $\color{#0000FF} F_2$ como la suma en forma analítica de sus componentes vectoriales o en forma cartesiana:
$\color{#0000FF} \color{#0000FF} \overrightarrow {F_2} = F_2 Sen \beta \widehat {i} + F_1 Cos \beta \widehat {j}$
Cuando un vector se describe en forma cartesiana es porque sus componentes escalares que luego las convertimos en componentes vectoriales provienen de un triángulo rectángulo ( sección 2.3.3. y sección 2.4.2.).
Si queremos hallar la magnitud de un vector descrito en forma cartesiana aplicamos la ecuación de Pitágoras (para los triángulos rectángulos) donde los catetos son las componentes escalares del vector y la hipotenusa del triángulo es la magnitud del vector.
Supóngase que tenemos un vector cartesiano descrito como:
$\color{#0000FF} \overrightarrow {F} = \overrightarrow {Fx} + \overrightarrow {Fy}$
Donde $\color{#0000FF} F_x = F Cos \theta$ y $\color{#0000FF} F_y = F Sen \theta$
Entonces $\color{#0000FF} \overrightarrow {F} = F Cos \theta \widehat {i} + F Sen \theta \widehat {j}$
Su magnitud es $\color{#0000FF} F = \sqrt {F_x^{2}+F_y^{2}}$
$\color{#0000FF} F = \sqrt {(F Cos \theta)^{2}+ (F Sen \theta)^{2}}$
Este método de sumar vectores consiste en describir cada uno de los vectores en forma cartesiana, luego se suman las componentes vectoriales $\color{#0000FF} \widehat {i}$ con las $\widehat {i}$, las componentes vectoriales $\widehat {j}$ con las $\color{#0000FF} \widehat {j}$, las componentes vectoriales $\color{#0000FF} \widehat {k}$ con las $\color{#0000FF} \widehat {k}$; el resultado será un vector descrito en forma cartesiana llamado vector resultante.
Solución:
• tomamos cada vector por separado y le describimos sus componentes escalares.
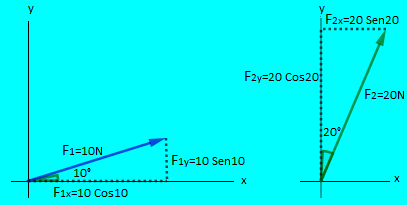
• Las componentes escalares las convertimos en componentes vectoriales y con estas describimos a cada vector en forma cartesiana.
$\color{#0000FF} \overrightarrow {F_1} = 10 Cos 10° \widehat {i} + 10 sen 10° \widehat {j}$
$\color{#0000FF} \overrightarrow {F_2} = 20 Sen 20° \widehat {i} + 20 Cos 20° \widehat {j}$
• Sumamos las componentes vectoriales $\color{#0000FF} \widehat {i}$ con las $\widehat {i}$, las componentes vectoriales $\color{#0000FF} \widehat {j}$ con las $\widehat {j}$
$\color{#0000FF} \overrightarrow {F_1} = 9.85 \widehat {i} + 1.74 \widehat {j}$
$\color{#0000FF} \dfrac {\overrightarrow {F_2} = 6.84 \widehat {i} + 18.79 \widehat {j}}{\overrightarrow {F_R} = 16.69 \widehat {i} + 20.53 \widehat {j}}$
Fuerza resultante en forma vectorial o cartesiana.
• Para determinar la magnitud de la fuerza resultante, aplicamos lo visto en la sección 2.4.2.1.
$\color{#0000FF} F_R = \sqrt {(16.69)^{2}+(20.53)^{2}}$, $\color{#FF0000} F_R = 26.46N$
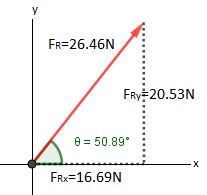
• Para determinar la dirección $\color{#0000FF} \theta$ del vector fuerza resultante, aprovechamos el hecho de que las componentes escalares de la fuerza resultante son los catetos de un triángulo rectángulo en el que la hipotenusa es la magnitud de la fuerza resultante; entonces aplicamos la función trigonométrica;
$\color{#0000FF} tg \theta =\dfrac {20.53}{16.69}$ $\color{#0000FF} \theta =tag^{-1} {1.23}$ $\color{#FF0000} \theta = 50.89°$
• La fuerza resultante es el vector $\color{#FF0000} \overrightarrow {F_R}$ que tiene por magnitud $\color{#FF0000} F_R = 26.46N$ y una dirección ,$\color{#FF0000} \theta = 59.89°$, dirigida hacia arriba de la horizontal, como lo muestra la figura.
• El resultado obtenido es exactamente igual al resultado del ejercicio 2.1..la suma de vectores por el método gráfico y por el método analítico tiene que arrojar el mismo resultado.
• La suma incluye la resta, de manera que la suma de vectores incluye la resta de vectores.
• Para efectos de la resta de vectores, cuando nos dicen $\color{#0000FF} -\overrightarrow {F}$, significa que el vector $\color{#0000FF} \overrightarrow {F}$ cambia de sentido, de manera que si nos piden realizar la resta de vectores por el método grafico lo que tenemos que hacer es dibujar el vector que se va ha restar en sentido contrario y se traza el triángulo o paralelogramo correspondiente.
• Cuando se desea restar vectores por el método analítico se procede igualmente a describir los vectores en forma cartesiana y ya no se suman ahora se restan según el caso.
• Cuando queremos sumar por el método grafico del triángulo o del paralelogramo más de dos vectores tenemos que hacer la suma primero de dos vectores (hacemos el triángulo o el paralelogramo y resolvemos), la resultante de esos dos se suma con otro de los vectores realizando nuevamente el triángulo o el paralelogramo. Si son más vectores se continúa este procedimiento hasta lograr la suma de todos los vectores.
• Cuando vamos a sumar más de dos vectores por el método analítico de sumar vectores se procede igual que al sumar dos vectores; sencillamente se describen todos los vectores en forma cartesiana, se alinean se suman todos al mismo tiempo, se suman las componentes vectoriales $\color{#0000FF} \widehat {i}$ con las $\color{#0000FF} \widehat {i}$, las componentes vectoriales $\color{#0000FF} \widehat {j}$ con las $\widehat {j}$; el resultado será un vector descrito en forma cartesiana llamado vector resultante.
Es una forma de multiplicar vectores. Por definición, el producto punto o producto escalar de dos vectores es: $\color{#0000FF} \overrightarrow {A} \cdot \overrightarrow {B} = A \cdot B Cos \theta$.
se lee, el producto punto de los vectores $\color{#0000FF} \overrightarrow {A} \cdot \overrightarrow {B}$, es igual a la magnitud del vector $\color{#0000FF} \left| \overrightarrow {A}\right|= A$, multiplicada por la magnitud del vector $\color{#0000FF} \left| \overrightarrow {B}\right|= B$, multiplicado por el coseno del ángulo formado entre el vector $\color{#0000FF} \overrightarrow {A}$ y el vector $\color{#0000FF} \overrightarrow {B}$. El ángulo entre dos vectores lo vimos en la sección 2.1.4..
El producto punto de dos vectores arroja como resultado un escalar. Téngase en cuenta que la magnitud de un vector es un escalar positivo; el coseno de un ángulo es un escalar que puede ser positivo, negativo o valer cero. Es por esta razón que al producto punto se le conoce como producto escalar.
El signo del producto punto finalmente lo da el signo del coseno del ángulo entre los vectores.
El producto punto de vectores se puede realizar entre vectores de igual o de diferente especie, por ejemplo se puede realizar el producto punto entre un vector de fuerza y un vector de velocidad, entre un vector de posición y un vector de aceleración, entre un vector de fuerza y un vector unitario, entre dos vectores unitarios, entre dos vectores de fuerza, etc.
Tener en cuenta que al ser el producto punto una multiplicación de vectores, también se debe realizar la multiplicación de las unidades.
$\color{#0000FF} \widehat {i} \cdot \widehat {i} = (1)(1) Cos 0 = 1$
$\color{#0000FF} \widehat {i} \cdot \widehat {j} = (1)(1) {\color{Red}\bcancel {{\color{blue}Cos 90}}} = 0$
$\color{#0000FF} \widehat {j} \cdot \widehat {j} = (1)(1) Cos 0 = 1$
$\color{#0000FF} \widehat {j} \cdot \widehat {k} = (1)(1) {\color{Red}\bcancel {{\color{blue}Cos 90}}} = 0$
$\color{#0000FF} \widehat {k} \cdot \widehat {k} = (1)(1) Cos 0 = 1$
$\color{#0000FF} \widehat {k} \cdot \widehat {j} = (1)(1) {\color{Red}\bcancel {{\color{blue}Cos 90}}} = 0$
$\color{#0000FF} \widehat {k} \cdot \widehat {i} = (1)(1) {\color{Red}\bcancel {{\color{blue}Cos 90}}} = 0$
El producto punto entre los vectores unitarios $\color{#0000FF} \widehat {i},\widehat {j},\widehat {k}$ es $\color{#0000FF} 1$ o $\color{#0000FF} 0$. Es $\color{#0000FF} 1$ cuando el producto punto es entre ellos mismos y es $\color{#0000FF} 0$ cuando el producto punto es con otro diferente de ellos mismos. Esto se debe a que cuando el producto punto es entre el mismo vector unitario, el ángulo con ellos mismos es de $\color{#0000FF} 0°$ y el $\color{#0000FF} Cos 0 = 1$ y cuando el producto punto es con otro vector unitario diferente de ellos mismos el ángulo entre ellos es de $\color{#0000FF} 90°$ y el $\color{#0000FF} Cos 90 = 0$. Cuando nos piden hallar el producto punto entre vectores descritos en forma cartesiana aprovechamos los resultados de los producto punto entre vectores unitarios $\color{#0000FF} \widehat {i},\widehat {j},\widehat {k}$.
Hallar el producto punto entre los vectores
$\color{#0000FF} \overrightarrow {F_1} = ( 3 \widehat {i} + 4 \widehat {j}) N$, $\color{#0000FF} \overrightarrow {F_2} = ( 12 \widehat {i} + 5 \widehat {j}) N$
Solución:
• Se disponen los vectores para la multiplicación.
$\color{#0000FF} \overrightarrow {F_1} \cdot \overrightarrow {F_2}= ( 3 \widehat {i} + 4 \widehat {j}) \cdot ( 12 \widehat {i} + 5 \widehat {j})$
• Se realiza la el producto punto de los vectores unitarios $\color{#0000FF} \widehat {i}$ con $\color{#0000FF} \widehat {i}$ que es igual a $\color{#0000FF} 1$ y se realiza el producto escalar de las componentes en $\color{#0000FF} X$, en este caso $\color{#0000FF} (3) \cdot (12) = 36$
• Se realiza la el producto punto de los vectores unitarios $\color{#0000FF} \widehat {j}$ con $\color{#0000FF} \widehat {j}$ que es igual a $\color{#0000FF} 1$ y se realiza el producto escalar de las componentes en $\color{#0000FF} Y$, en este caso $\color{#0000FF} (4) \cdot (5) = 20$
$\color{#0000FF} \overrightarrow {F_1} \cdot \overrightarrow {F_2}= ( 3 \widehat {i} + 4 \widehat {j}) \cdot ( 12 \widehat {i} + 5 \widehat {j}) = (36 +20) $
$\color{#FF0000} \overrightarrow {F_1} \cdot \overrightarrow {F_2} = 56 N^2$
Una aplicación del producto punto es calcular el ángulo entre dos vectores, especialmente cuando los vectores están descritos en tres dimensiones.
De la definición de producto punto despejamos el ángulo.
$\color{#0000FF} \overrightarrow {A} \cdot \overrightarrow {B} = AB Cos \theta$ $\color{#0000FF} \dfrac {\overrightarrow {A} \cdot \overrightarrow {B}}{A \cdot B} = Cos \theta$
$\color{#0000FF} Cos \theta = \dfrac {\overrightarrow {A} \cdot \overrightarrow {B}}{A \cdot B}$ $ \color{#0000FF} \theta = Cos ^{-1}\dfrac {\overrightarrow {A} \cdot \overrightarrow {B}}{A \cdot B}$
$\color{#0000FF} \overrightarrow {F_1} = ( \widehat {i} + 3 \widehat {j} - 2 \widehat {k} ) Lb$
$\color{#0000FF} \overrightarrow {F_2} = ( -3 \widehat {i} - 2 \widehat {j} + 2 \widehat {k} ) ft$
Solución: Sabemos que: $\color{#0000FF} \color{#0000FF} \theta = Cos ^{-1}\dfrac {\overrightarrow {F_1} \cdot \overrightarrow {F_2}}{F_1 \cdot F_2}$
• La fórmula nos dice que si queremos hallar el ángulo $\color{#0000FF} \theta$ entre el vector$\color{#0000FF} \overrightarrow {F_1}$ y el vector $\color{#0000FF} \overrightarrow {F_2}$ debemos calcular primero el producto punto entre estos dos vectores.
$\color{#0000FF} \overrightarrow {F_1} = ( \widehat {i} + 3 \widehat {j} - 2 \widehat {k} ) Lb$
$\color{#0000FF} \dfrac {\overrightarrow {F_2} = ( -3 \widehat {i} - 2 \widehat {j} + 2 \widehat {k} ) ft}{\overrightarrow {F_1}.\overrightarrow {F_2} = (- 3 - 6 - 4) Lb.ft}$
$\color{#FF0000} \overrightarrow {F_1}.\overrightarrow {F_2} = - 13 Lb.ft$
En el procedimiento lo que hicimos fue aplicar lo del ejercicio 2.3. con la novedad de agregarle una la componente $\color{#0000FF} \widehat {k}$ aplicando el mismo procedimiento para esta componente.
• Hallamos la magnitud de cada uno de los vectores $\color{#0000FF} \overrightarrow {F_1}$ y $\color{#0000FF} \overrightarrow {F_2}$ aplicando lo conceptuado en la sección 2.4.2.1., pero incluyendo la componente escalar positiva $\color{#0000FF} Z$ de cada vector.
$\color{#0000FF} F = \sqrt {F_x^{2}+F_y^{2}+F_Z^{2}}$
$\color{#0000FF} F_1 = \sqrt {1^{2}+3^{2}+2^{2}}$ $\color{#0000FF} \color{#FF0000} F_1 = \sqrt {14} Lb$
$\color{#0000FF} F_2 = \sqrt {3^{2}+2^{2}+2^{2}}$ $\color{#FF0000} F_2 = \sqrt {17} ft$
• Los valores obtenidos los remplazamos en la ecuación:
$\color{#0000FF} \theta = Cos ^{-1}\dfrac {\overrightarrow {F_1} \cdot \overrightarrow {F_2}}{F_1 \cdot F_2}$ $\color{#0000FF} \theta = Cos ^{-1}\dfrac {-13 {\color{Red}\bcancel {{\color{blue}Lb}}} . {\color{Red}\bcancel {{\color{blue}ft}}} }{(\sqrt {14}) {\color{Red}\bcancel {{\color{blue}Lb}}} . (\sqrt {17}) {\color{Red}\bcancel {{\color{blue}ft}}}}$
• Cancelamos unidades $\color{#0000FF} \theta = Cos ^{-1}\dfrac {-13}{(\sqrt {14}).(\sqrt {17})}$
• Operamos para $\color{#0000FF} \theta$. $\color{#FF0000}\theta = 147.42°$
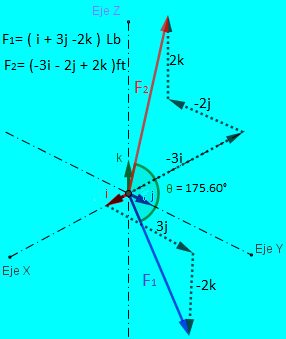
• Utilizando la escena interactiva desarrollar el Ejercicio 2.4.:
Hallar el ángulo entre los vectores
$\color{#0000FF} \overrightarrow {F_1} = ( \widehat {i} + 3 \widehat {j} - 2 \widehat {k} ) Lb$
$\color{#0000FF} \overrightarrow {F_2} = ( -3 \widehat {i} - 2 \widehat {j} + 2 \widehat {k} ) ft$
• En la escena interactiva tome al vector $\color{#0000FF} \overrightarrow {F_1}$ como el vector $\color{#0000FF} \overrightarrow {G}$ y tome al vector $\color{#0000FF} \overrightarrow {F_2}$ como el vector $\color{#0000FF} \overrightarrow {N}$
• El vector $\color{#0000FF} \overrightarrow {G}$ contiene $\color{#0000FF} 3$ deslizadores $\color{#0000FF} a,b,c$ que controlan los valores $\color{#0000FF} xi,yj,zk$ del vector $\color{#0000FF} \overrightarrow {F_1}$. El vector $\color{#0000FF} \overrightarrow {N}$ contiene $\color{#0000FF} 3$ deslizadores $\color{#0000FF} i,j,h$ que controlan los valores $\color{#0000FF} xi,yj,zk$ del vector $\color{#0000FF} \overrightarrow {F_2}$.
• Utilizando los deslizadores grafique los vectores $\color{#0000FF} \overrightarrow {F_1}$ y $\color{#0000FF} \overrightarrow {F_2}$ que serán los vectores $\color{#0000FF} \overrightarrow {G}$ y $\color{#0000FF} \overrightarrow {N}$ respectivamente.
• Haga clic sostenido en cualquier lugar de la escena interactiva y mueva muy suavemente el cursor en forma horizontal a la izquierda y observe como el sistema tridimensional gira. Encuentre la mejor posición para observar el ángulo entre los dos vectores.
• Haga clic sostenido en cualquier lugar de la escena interactiva y mueva muy suavemente el cursor en forma vertical hacia abajo y observe como el sistema tridimensional gira. Encuentre la mejor posición para observar el ángulo entre los dos vectores.
• Compare los valores obtenidos por medio de los modelos matemáticos tales como la magnitud del vector $\color{#0000FF} \overrightarrow {F_1}$ que es la magnitud del vector $\color{#0000FF} \overrightarrow {G}$, la magnitud del vector $\color{#0000FF} \overrightarrow {F_2}$ que es la magnitud del vector $\color{#0000FF} \overrightarrow {N}$; el producto punto entre el vector $\color{#0000FF} \overrightarrow {F_1}$ y el vector $\color{#0000FF} \overrightarrow {F_2}$ que es el producto punto entre los vectores $\color{#0000FF} \overrightarrow {G}$ con el vector $\color{#0000FF} \overrightarrow {N}$;
• Compare el modelo matemático utilizado por usted para hallar el ángulo entre los vectores $\color{#0000FF} \overrightarrow {F_1}$ y $\color{#0000FF} \overrightarrow {F_2}$ con el modelo matemático mostrado en la escena interactiva para el producto punto entre los vectores $\color{#0000FF} \overrightarrow {G}$ y el vector $\color{#0000FF} \overrightarrow {N}$.
• Encuentre por medio de los modelos matemáticos vistos el ángulo entre los vectores $\color{#0000FF} \overrightarrow {r_1} = ( 3 \widehat {i} - 2 \widehat {j} - 4 \widehat {k} ) ft $ $\color{#0000FF} \overrightarrow {r_2} = ( \widehat {i} + 5 \widehat {j} - 3 \widehat {k} ) ft$
• Realice cada uno de los pasos para comparar sus resultados con los arrojados por la escena interactiva.
Se llama momento de una fuerza o torque al giro o tendencia de giro que una fuerza produce sobre un cuerpo. Por lo general se toman como positivos los momentos o torques es en sentido contrario al movimiento de las manecillas del reloj y negativos los momentos o torques en el sentido de las manecillas del reloj; sin embargo para la solución de algunos ejercicios se pueden tomar contrario los signos, esto por facilidad, por ejemplo en casos en que la mayoría de los momentos son en uno de los sentidos se pueden tomar esas tendencias como positivas.
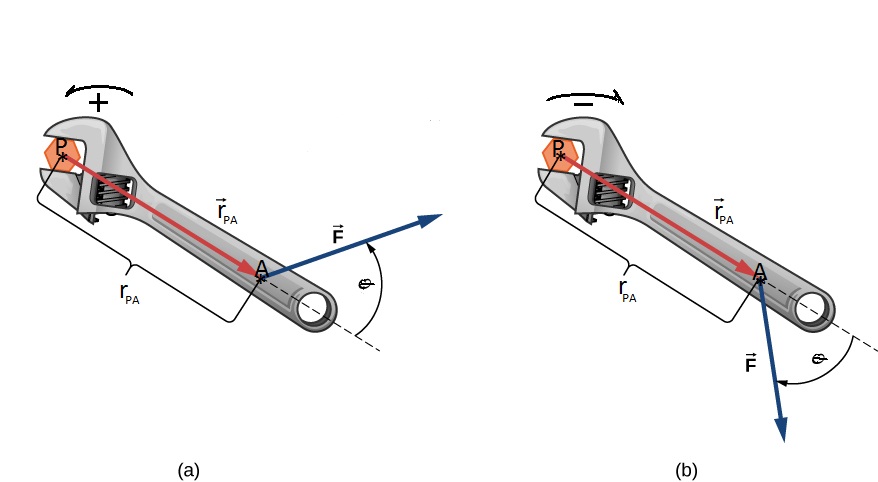
Para entender el concepto imaginemos que queremos aflojar una tuerca de rosca derecha (ajusta con el giro a la derecha), con una llave expansiva, como se muestra en la figura $\color{#0000FF} (a)$. La tuerca esta fija en el punto $\color{#0000FF} P$ y nosotros tomamos la llave por el punto $\color{#0000FF} A$ y hacemos fuerza en la dirección y sentido mostrado en la figura $\color{#0000FF} (a)$. Del punto $\color{#0000FF} P$ al punto $\color{#0000FF} A$ trazamos el vector de posición $\color{#0000FF} \overrightarrow {r_{PA}}$ en metros o en pies.
Ahora, realizamos la multiplicación de la magnitud del vector de
posición $\color{#0000FF} \left| \overrightarrow {r_{PA}}\right|$ por la magnitud de la fuerza $\color{#0000FF} \left| \overrightarrow {F}\right|$ y esto por el Seno del ángulo $\color{#0000FF} \theta$ que es ángulo entre el vector de posición $\color{#0000FF} \overrightarrow {r_{PA}}$ y el vector de fuerza $\color{#0000FF} \overrightarrow {F}$, sección 2.1.4. (sección 2.1.4.).
El momento de una fuerza se define como $\color{#0000FF} M^{F} = {r} {F} Sen \theta $ unidades de fuerza por distancia. En el sistema Internacional las unidades son Newton por metro $\color{#0000FF} (Nm)$ y en el sistema Técnico Ingles F.P.S. las unidades son de Libra por Pies $\color{#0000FF} (Lbft)$.
De la figura (a) de la sección 2.6. podemos tomar la fuerza $\color{#0000FF} \overrightarrow {F}$ y descomponerla en dos componentes, una a lo largo de la dirección del vector de posición $\color{#0000FF} F Cos \theta $ y otra componente perpendicular al mismo vector de posición $\color{#0000FF} F Sen \theta $. Ver la siguiente figura $\color{#0000FF} (C)$.

Observamos desde la figura $\color{#0000FF} (C)$ que la componente $\color{#0000FF} F Cos \theta$ No produce tendencia de giro. En este caso concreto la componente $\color{#0000FF} F Cos \theta$ lo que pretende hacer es sacar de la tuerca la llave expansiva.
Cuando una fuerza actúa en la misma dirección del vector de posición, esta fuerza No produce tendencia de giro.
Si miramos la componente $\color{#0000FF} F Sen \theta$ concluimos que esta componente es la que produce tendencia de giro. Esta conclusión es consecuente con la definición de momento de una fuerza $\color{#0000FF} M^{F} = {r} {F} Sen \theta $, pues al aplicar esta ecuación queda: $\color{#0000FF} M^{F} = {r} ({F} Sen \theta) Sen 90°$ como $\color{#0000FF} Sen 90° = 1$ entonces $\color{#0000FF} M^{F} = {r} {F} Sen \theta$
Este principio afirma que una fuerza puede desplazarse por su misma línea de acción (dirección) y el efecto que produce sobre el cuerpo en el que actúa es el mismo. En la figura (C) y figura (d) vemos claramente casos como el de la fuerza $\color{#0000FF} \color{#0000FF} F Sen \theta $ que se puede desplazar por su misma línea de acción y el efecto sobre la llave expansiva es el mismo. La fuerza $\color{#0000FF} \color{#0000FF} F Cos \theta $ se puede desplazar por su misma línea de acción y en cualquier lugar donde se ponga no produce tendencia de giro. Observe que cuando se ubicó esta fuerza en el punto $\color{#0000FF} \color{#0000FF} P$ lo que produce es empujar la tuerca y no produce tendencia de giro.
En la figura (d) la fuerza $\color{#0000FF} \color{#0000FF} F$ se desplaza por su línea de acción, hacia adelante o hacia atrás y el efecto sobre la llave expansiva es el mismo.
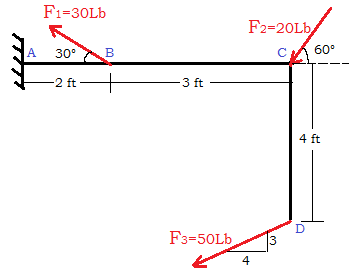
Hallar el momento resultante con respecto del punto $\color{#0000FF} A$ producido por las fuerzas aplicadas sobre la varilla en forma de ele $\color{#0000FF} L$. El punto $\color{#0000FF} A$ es el lugar donde está empotrada la varilla a la pared. Solución: Hallamos los momentos de cada una de fuerzas respecto al punto $\color{#0000FF} A$ y se suman. 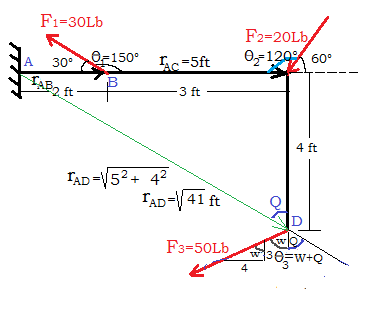
De la figura se obtiene que: $\color{#0000FF} M^{F_1}_{A}={r_{AB}}{F_1}Sen \theta_1$ Contra Manecillas del Reloj $\color{#0000FF} M^{F_1}_{A}={(2)}{(30)}Sen {150}$ $\color{#0000FF} \color{#FF0000} M^{F_1}_{A}={30Lb.ft}$ $\color{#0000FF} M^{F_2}_{A}={r_{AC}}{F_2}Sen \theta_2$ A favor Manecillas del Reloj $\color{#0000FF} M^{F_2}_{A}={(5)}{(20)}Sen {120}$ $\color{#0000FF} \color{#FF0000} M^{F_2}_{A}={-86.60Lb.ft}$ |
$\color{#0000FF} M^{F_3}_{A}={r_{AD}}{F_3}Sen \theta_3$ A favor Manecillas del Reloj.
Obsérvese que: $\color{#0000FF} r_{AD}={\sqrt {41}} ft$
$\color{#0000FF} \theta_3 = Q + W$
El ángulo $\color{#0000FF} Q$ del triángulo que forma la varilla es:
$\color{#0000FF} Q =tag^{-1}\dfrac {5}{4}$ $\color{#0000FF} Q=51.34°$
El ángulo $\color{#0000FF} W$ del triángulo pequeño que indica la inclinación de la $\color{#0000FF} \overrightarrow {F_3}$ es:
$\color{#0000FF} W=tag^{-1}\dfrac {4}{3}$ $\color{#0000FF} W=53.13°$
$\color{#0000FF} \theta_3 = Q + W$ $\color{#0000FF} \theta_3 = 51.34° + 53.13°$ $\color{#0000FF} \theta_3 = 104.47°$
$\color{#0000FF} M^{F_3}_{A}={({\sqrt {41}})}{(50)}Sen {104.47°}$ $\color{#0000FF} \color{#FF0000} M^{F_3}_{A}={-310Lb.ft}$
El Momento resultante es la suma de los momentos:
$\color{#0000FF} M^{R}_{A}= M^{F_1}_{A} + M^{F_2}_{A} + M^{F_3}_{A}$
$\color{#0000FF} M^{R}_{A}= (30 - 86.60 - 310)$ $\color{#0000FF} \color{#FF0000} M^{R}_{A}= -366.60 Lb.ft$
El signo negativo indica que la tendencia de giro que le generan entre las tres fuerzas a la varilla doblada en forma de ele $\color{#0000FF} L$ respecto del punto $\color{#0000FF} A$, es en sentido de las manecillas del reloj.
Hallar el momento de la $\color{#0000FF} {\overrightarrow {F_3}}$ puede resultar para algunos con un cierto grado de dificultad. Por ello analizaremos otras formas de hallarlo.
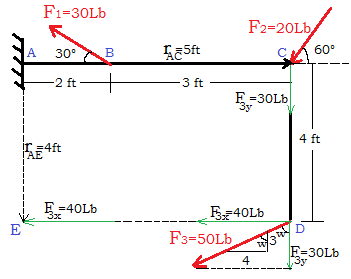
se descompone la $\color{#0000FF} {\overrightarrow {F_3}}$ en dos componentes $\color{#0000FF} {\overrightarrow {F_{3x}}}$ y $\color{#0000FF} {\overrightarrow {F_{3y}}}$; aplicamos el principio de transmisibilidad. Trasladamos cada una de las componentes vectoriales de la fuerza a un lugar (un punto) en el que un vector de posición $\color{#0000FF} {\overrightarrow {r}}$ y la componente de la fuerza trasladada formen un ángulo de $\color{#0000FF} 90°$ o un ángulo que conozcamos o que sea fácil de hallar. El momento de la fuerza descompuesta es la suma del los momentos de cada una de sus componentes vectoriales respecto del punto $\color{#0000FF} A$.
De la figura: El ángulo $\color{#0000FF} W=tag^{-1}\dfrac {4}{3}=53.13$
$\color{#0000FF} {F_{3x}}=50 Sen 53.13=40Lb$
$\color{#0000FF} {F_{3y}}=50 Cos 53.13=30Lb$
Trasladamos la fuerza $\color{#0000FF} {\overrightarrow {F_{3y}}}$ al punto $\color{#0000FF} C$, observando que en el punto $\color{#0000FF} C$ la fuerza $\color{#0000FF} {\overrightarrow {F_{3y}}}$ y el vector de posición $\color{#0000FF} {\overrightarrow {r_{AC}}}$ forman un ángulo de $\color{#0000FF} 90°$ y trasladamos la fuerza $\color{#0000FF} {\overrightarrow {F_{3x}}}$ al punto $\color{#0000FF} E$, observando que la fuerza$\color{#0000FF} {\overrightarrow {F_{3x}}}$ y el vector de posición $\color{#0000FF} {\overrightarrow {r_{AE}}}$ forman un ángulo de $\color{#0000FF} 90°$. Aplicamos el modelo matemático de momento de una fuerza a cada una de las componentes vectoriales de la fuerza $\color{#0000FF} {\overrightarrow {F_3}}.$
$\color{#0000FF} M^{F_3}_{A}= M^{F_{3x}}_{A} + M^{F_{3y}}_{A}$
$\color{#0000FF} M^{F_3}_{A}= -{r_{AE}}{F_{3x}}Sen 90° - {r_{Ac}}{F_{3y}}Sen 90°$
$\color{#0000FF} Sen90°=1$ $\color{#0000FF} M^{F_3}_{A}= - (4)(40)(1) - (5)(30)(1)$
$\color{#FF0000} M^{F_3}_{A}= -310 Lb.ft$
El signo negativo indica que la tendencia de giro es en sentido contrario a las manecillas del reloj.
Como se puede observar el momento de la $\color{#0000FF} \overrightarrow {F_3}$ respecto del punto $\color{#0000FF} A$ da exactamente igual por los métodos vistos.
Aun así, podemos hallar el momento de la $\color{#0000FF} \overrightarrow {F_3}$ respecto del punto $\color{#0000FF} A$ por otro método. Se trata de utilizar el modelo matemático del producto cruz de dos vectores.
El producto Cruz de vectores es otra forma de multiplicar vectores (recordar que la otra forma de multiplicar vectores es a través del producto punto que da como resultado un escalar). El producto cruz de dos vectores da como resultado otro vector que es perpendicular al plano formado por los dos vectores involucrados. La nomenclatura para el producto cruz es $\color{#0000FF} \overrightarrow A X \overrightarrow B$, $\color{#0000FF} \overrightarrow r X \overrightarrow F$, y se opera de la siguiente manera: Se escribe cada vector en forma cartesiana en tres dimensiones y los organizamos en una matriz de tres por tres.
$\color{#0000FF} \overrightarrow {A}\times \overrightarrow {B}=\begin{vmatrix} \widehat {i} & \widehat {j} & \widehat {k} \\ A_x & A_y & A_z \\ B_x & B_y & B_z \end{vmatrix}$
$\color{#0000FF} \overrightarrow {A}\times \overrightarrow {B}=\widehat {i}\left[ \left( A_{y}\cdot B_{z}\right) -\left( B_{y}\cdot A_{z}\right) \right]-\widehat {j}\left[ \left( A_{x}\cdot B_{z}\right) -\left( B_{x}\cdot A_{z}\right) \right]+$
$\color{#0000FF} \widehat {k}\left[ \left( A_{x}\cdot B_{y}\right) -\left( B_{x}\cdot A_{y}\right) \right]$
Para hallar el momento de una fuerza:
$\color{#0000FF} \overrightarrow {r}\times \overrightarrow {F}=\begin{vmatrix} \widehat {i} & \widehat {j} & \widehat {k} \\ r_x & r_y & r_z \\ F_x & F_y & F_z \end{vmatrix}= \overrightarrow M^{F}$$\color{#0000FF} \overrightarrow {r}\times \overrightarrow {F}=\widehat {i}\left[ \left( r_{y}\cdot F_{z}\right) -\left( F_{y}\cdot r_{z}\right) \right]-\widehat {j}\left[ \left( r_{x}\cdot F_{z}\right) -\left( F_{x}\cdot r_{z}\right) \right]+$
$\color{#0000FF} \widehat {k}\left[ \left( r_{x}\cdot F_{y}\right) -\left( F_{x}\cdot r_{y}\right) \right]= \overrightarrow M^{F}$
Para hallar el momento de la $\color{#0000FF} {\overrightarrow {F_3}}$ respecto del punto $\color{#0000FF} A$ en el ejercicio 2.6. Podemos aplicar el Producto Cruz $\color{#0000FF} \overrightarrow {r_{AD}}\times \overrightarrow {F_3}$. Describimos el vector de posición $\color{#0000FF} \overrightarrow {r_{AD}}$ como un vector cartesiano en tres dimensiones, describimos el vector de fuerza $\color{#0000FF} {\overrightarrow {F_3}}$ como un vector cartesiano en tres dimensiones y aplicamos el Producto Cruz $\color{#0000FF} \overrightarrow {r_{AD}}\times \overrightarrow {F_3}$:
Describimos el vector $\color{#0000FF} \overrightarrow {r_{AD}}$ recorriéndolo desde la cola a la punta por los ejes coordenados x,y.z:
$\color{#0000FF} \overrightarrow {r_{AD}} = 5\widehat {i} -4\widehat {j} + 0\widehat {k}$ en el eje $\color{#0000FF} Z$ el recorrido es cero
Describimos el vector $\color{#0000FF} \overrightarrow {F_3}$ recorriéndolo desde la cola a la punta por los ejes coordenados $\color{#0000FF} x,y,z$:
$\color{#0000FF} \overrightarrow {F_3} = -40\widehat {i} -30\widehat {j} + 0\widehat {k}$ en el eje $\color{#0000FF} Z$ el recorrido es cero
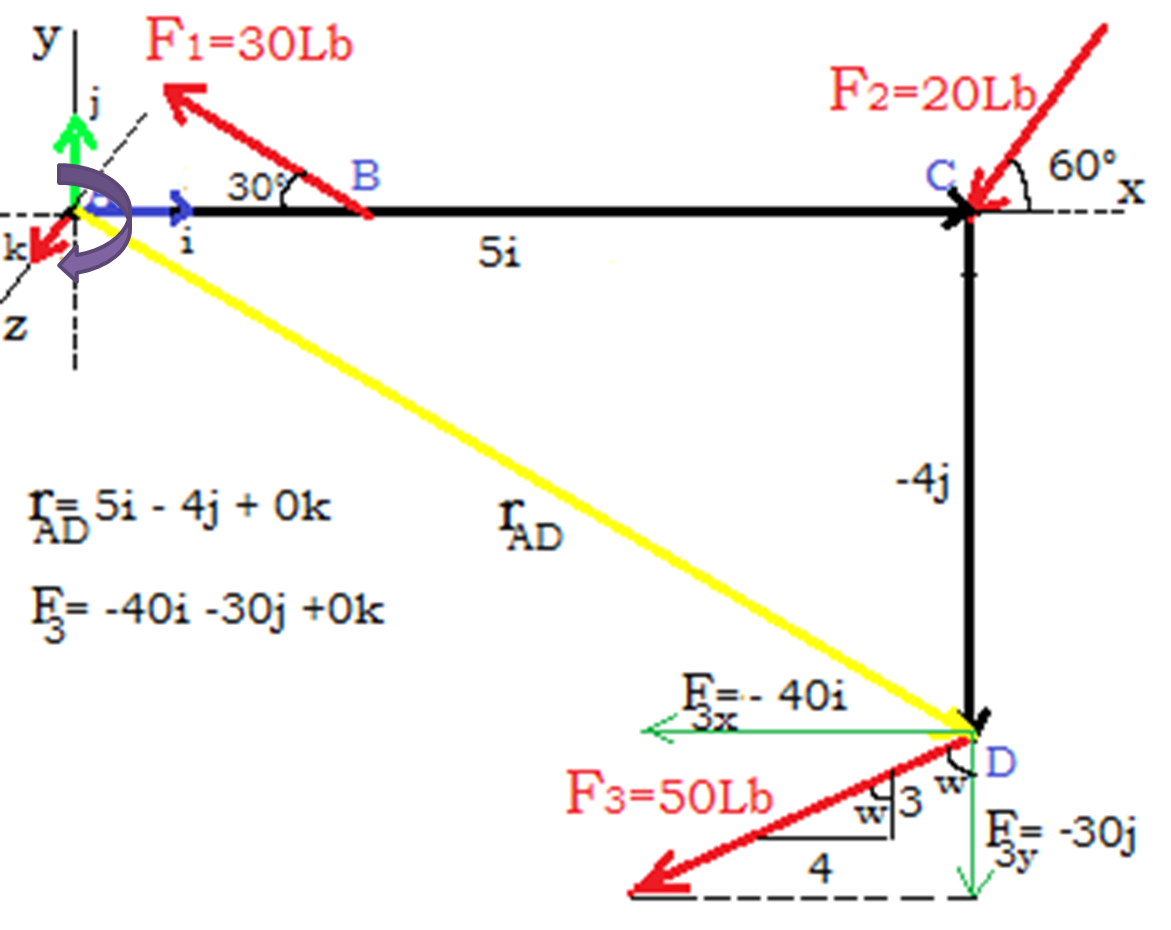
$\color{#0000FF} \overrightarrow {r_{AD}}\times \overrightarrow {F_3}=\begin{vmatrix} \widehat {i} & \widehat {j} & \widehat {k} \\ 5 & -4 & 0 \\ -40 & -30 & 0 \end{vmatrix}=\overrightarrow M^{F_{3}}_{A}$
$\color{#0000FF} \overrightarrow M^{F_{3}}_{A}=\overrightarrow {r_{AD}}\times \overrightarrow {F_3}=\widehat {i}\left[ \left( -4\cdot 0\right) -\left( -30\cdot 0\right) \right]-$
$\color{#0000FF} \widehat {j}\left[ \left( 5\cdot 0\right) -\left( -40\cdot 0\right) \right]+$
$\color{#0000FF} \widehat {k}\left[ \left( 5\cdot -30\right) -\left( -40\cdot -4\right) \right]$
$\color{#0000FF} \overrightarrow M^{F_{3}}_{A}= 0\widehat {i} + 0\widehat {j} + \widehat {k}\left[ \left( -150\right) -\left( 160\right) \right]$
$\color{#0000FF} \overrightarrow M^{F_{3}}_{A}= 0\widehat {i} + 0\widehat {j} - 310\widehat {k}$
$\color{#FF0000} \overrightarrow M^{F_{3}}_{A}= ( 0\widehat {i} + 0\widehat {j} - 310\widehat {k} ) Lb.ft$
• La $\color{#0000FF} \overrightarrow {F_3}$ No le produce tendencia de giro a la varilla doblada en forma de ele $\color{#0000FF} L$ respecto del punto $\color{#0000FF} A$ al rededor del vector unitario $\color{#0000FF} \widehat {i}$
• La $\color{#0000FF} \overrightarrow {F_3}$ No le produce tendencia de giro a la varilla doblada en forma de ele $\color{#0000FF} L$ respecto del punto $\color{#0000FF} A$ al rededor del vector unitario $\color{#0000FF} \widehat {j}$
• La $\color{#0000FF} \overrightarrow {F_3}$ produce tendencia de giro a la varilla doblada en forma de ele $\color{#0000FF} L$ respecto del punto $\color{#0000FF} A$. La varilla tiende a girar al rededor del vector unitario $\color{#0000FF} \widehat{k}$ en sentido de las manecillas del reloj con un valor de $\color{#0000FF} -310 Lb.ft$
La magnitud del producto Cruz de los vectores $\color{#0000FF} \overrightarrow A X \overrightarrow B$ es por definición $\color{#0000FF} \left|\overrightarrow A X \overrightarrow B \right| =\left|\overrightarrow A\right| \left|\overrightarrow B\right| Sen \theta $. Donde $\color{#0000FF} \theta$ es el ángulo entre el vector $\color{#0000FF} \overrightarrow A$ y el vector $\color{#0000FF} \overrightarrow B$.
Para el caso del momento de una fuerza La magnitud del producto Cruz de los vectores $\color{#0000FF} \overrightarrow F X \overrightarrow r$ es :
$\color{#0000FF} M^{F}=\left|\overrightarrow F X \overrightarrow r \right| =\left|\overrightarrow F\right| \left|\overrightarrow r\right| Sen \theta $. Donde $\color{#0000FF} \theta$ es el ángulo entre el vector $\color{#0000FF} \overrightarrow F$ y el vector $\color{#0000FF} \overrightarrow r$: Por ello $\color{#0000FF} \color{#0000FF} M^{F} = {r} {F} Sen \theta $
El producto cruz como concepto tiene otras propiedades que son estudiadas en un curso llamado algebra lineal; hemos tomado lo estrictamente necesario para este curso de Física mecánica.
En la escena interactiva realice los siguientes pasos:
• Mueva el punto del vector de fuerza, manteniendo su magnitud $\color{#0000FF} \overrightarrow F$ y ubíquelo en la misma dirección y sentido del vector de posición.
• Gire el vector de fuerza $\color{#0000FF} \overrightarrow F$ en sentido contrario a las manecillas del reloj lentamente y manteniendo constante la magnitud del vector $\color{#0000FF} \overrightarrow F$. Mientras gira el vector $\color{#0000FF} \overrightarrow F$ observe que el vector momento de la fuerza $\color{#0000FF} \overrightarrow M^{F}$ empieza a crecer. Gire el vector $\color{#0000FF} \overrightarrow F$ hasta lograr un ángulo de $180°$
• ¿Para qué valor del ángulo $\color{#0000FF} \theta$ el vector $\color{#0000FF} \overrightarrow M^{F}$ es máximo?
• ¿Para qué valores del ángulo $\color{#0000FF} \theta$ el vector $\color{#0000FF} \overrightarrow M^{F}$ es mínimo?
• Continúe girando el vector $\color{#0000FF} \overrightarrow F$ entre $\color{#0000FF} 180°$ y $\color{#0000FF} 360°$, observando en cada instante lo que sucede con el vector momento de la fuerza.
• Hacia arriba del eje $\color{#0000FF} z$ el sentido es $\color{#0000FF} \widehat {k}$ y hacia abajo del eje $\color{#0000FF} z$ el sentido es $\color{#0000FF} \widehat {-k}$. Con esto, diga para que valores del ángulo $\color{#0000FF} \theta$ el momento es positivo, negativo y cero
• Manteniendo el ángulo de $ \hspace{0.1cm} \color{#0000FF} 90° $ entre los vectores $ \hspace{0.1cm} \color{#0000FF} r $ y $ \hspace{0.1cm} \color{#0000FF} F $ manipule el vector $ \hspace{0.1cm} \color{#0000FF} F $ lentamente volviéndolo cada vez más pequeño. Observe que pasa con el vector momento. Deje la escena como estaba originalmente.
• Manteniendo el ángulo de $ \hspace{0.1cm} \color{#0000FF} 90° $ entre los vectores $ \hspace{0.1cm} \color{#0000FF} r $ y $ \hspace{0.1cm} \color{#0000FF} F $ manipule el vector $ \hspace{0.1cm} \color{#0000FF} r $ lentamente volviéndolo cada vez más pequeño. Observe que pasa con el vector momento.
• Realiza el producto cruz entre los vectores $\color{#0000FF} \overrightarrow {r}$ y $\color{#0000FF} \overrightarrow {F}$ con los valores mostrados en la escena interactiva. Compara el resultado obtenido con el de la escena interactiva.
• Observe que el resultado del producto cruz es un vector perpendicular al plano formado por los vectores $\color{#0000FF} \overrightarrow {r}$ y el vector $\color{#0000FF} \overrightarrow {F}$
• Haga clic sostenido en cualquier punto de la pantalla y mueva suavemente en forma horizontal y observe que la escena tridimensional gira. Busque varias opciones para observar el producto cruz.
• Haga clic sostenido en cualquier punto de la pantalla u mueva suavemente en forma vertical y observe que la escena tridimensional gira. Busque varias opciones para observar el producto cruz.
• Encuentre en la escena interactiva el producto cruz entre los vectores $\color{#0000FF} \overrightarrow {r} = ( 3 \widehat {i} - 2 \widehat {j} - 4 \widehat {k} ) m $ y el vector $\color{#0000FF} \overrightarrow {F} = ( \widehat {i} + 5 \widehat {j} - 3 \widehat {k} ) KN$ y realice los pasos anteriores.
El video introductorio hace parte de la serie Universo MecánicoLa serie educativa Universo Mecánico es una colección de 52 videos creados por el Instituto de Tecnología de California cuyo director y anfitrión es el Dr. David L. Goodtein.
Vivimos en un mundo, en un universo que se caracteriza por el movimiento. el movimiento es la característica general, el reposo es una creación humana. Solo existe un cuerpo en reposo cuando lo hacemos parecer así respecto de un marco de referencia. La superficie de la tierra gira alrededor de su eje a la nada despreciable velocidad de $\color{#0000FF} 1670 \dfrac {Km}{h}$ y sin embargo cuando realizamos ejercicios de movimientos de cuerpos sobre la tierra, consideramos para la ejecución del ejercicio que la tierra está en reposo. El estudio del movimiento de los cuerpos ha permitido al hombre desarrollar maquinas potentes que le facilitan la subsistencia en la tierra, le ha permitido la conquista del espacio al punto de lograr llevar una maquina a sitios tan lejanos como el planeta marte.
En la cinemática estudiaremos el movimiento de los cuerpos sin tener en cuenta las fuerzas externas o internas que actúan sobre ellos.
La cinemática es el estudio del movimiento de los cuerpos teniendo como base la geometría del movimiento. Se analiza la trayectoria que describe el cuerpo durante su movimiento. El movimiento del cuerpo puede ser a lo largo de una línea recta o a lo largo de una línea curva.
El análisis del movimiento será referido al centro de masa del cuerpo, como si toda la masa del cuerpo estuviera concentrada en éste punto (centro de masa), tomaremos el cuerpo como una partícula.
Un cuerpo cuando se mueve puede girar (una pelota de béisbol lanzada por el pícher al bateador), puede vibrar (el movimiento de un avión sobre la pista de aterrizaje), puede deformarse (las llantas de un automóvil al contacto con el suelo). Estos efectos de los cuerpos cuando están en movimiento afectan el movimiento de los cuerpos y requieren de unos conceptos que se verán más adelante.
Las partículas no tienen dimensiones, no tienen extensión, la partícula es un punto, las partículas no giran, no vibran, no se deforman. Realizar el análisis del movimiento de los cuerpos considerándolos partículas resulta muy útil pues en condiciones especiales se aproximan bastante a la realidad y nos permite comprender los conceptos fundamentales del movimiento de los cuerpos.
La cinemática estudia la posición, velocidad y aceleración de un cuerpo. Si en un ejercicio nos piden hallar la cinemática de un cuerpo, debemos hallar su posición, velocidad y aceleración a partir de la geometría del movimiento.
La posición es un vector que nos indica el lugar donde se encuentra la partícula respecto de un punto de referencia en un instante determinado.
En la figura 3.1 si nos ubicamos en el punto $\color{#0000FF} A$ podemos definir el vector de posición de una partícula cuando se encuentra en el punto $\color{#0000FF} P_1$ como el vector de posición $\color{#0000FF} \overrightarrow {r_1}$ y si en otro momento la partícula se encuentra en el punto $\color{#0000FF} P_2$, desde el mismo punto $\color{#0000FF} A$ definimos el vector de posición $\color{#0000FF} \overrightarrow {r_2}$.
$\blacktriangleright \hspace{0.2cm}$ Magnitud del vector de PosiciónEn la figura 3.1 se aprecia que la magnitud del vector de posición $\color{#0000FF} \overrightarrow {r_1}$ es $\color{#0000FF} S_1$ y La magnitud del vector de posición $\color{#0000FF} \overrightarrow {r_2}$ es $S_2$. En general la magnitud del vector de posición $\color{#0000FF} \overrightarrow {r}$ es $\color{#0000FF} S$.
Cuando una partícula está por ejemplo en la posición $\color{#0000FF} P_1$ y en otro instante se encuentra en la posición $\color{#0000FF} P_2$ como se muestra en la figura 3.1 decimos que la partícula sufrió un cambio en la posición o desplazamiento $\color{#0000FF} \Delta \overrightarrow {{r}}$ . El cambio de posición o desplazamiento $\color{#0000FF} \Delta \overrightarrow {{r}}$ es un vector que va desde la punta de $\color{#0000FF} P_1$ a la punta de $\color{#0000FF} P_2$, (figura 3.1).
El símbolo $\color{#0000FF} {\Delta}$ significa algo final menos algo inicial $\color{#0000FF}\Delta \overrightarrow {{x}} = \overrightarrow {x_2} - \overrightarrow {x_1}$
Aplicando suma de vectores vemos en la figura 3.1 que:
$\color{#0000FF} \overrightarrow {r_1} + \Delta \overrightarrow {{r}} = \overrightarrow {r_2}$ de donde $\color{#0000FF}\Delta \overrightarrow {{r}} = \overrightarrow {r_2} - \overrightarrow {r_1}$
El modelo matemático para denotar el cambio de posición o desplazamiento es por medio de una ecuación que puede ser una constante o una función del tiempo. Ejemplo:
$\color{#0000FF} \overrightarrow {r}= 3\widehat {i}$ Constante.
$\color{#0000FF} \overrightarrow {r_t}= 2t\widehat {i} + 6t^{2}\widehat {j}$ Variable
$\color{#0000FF} \overrightarrow {r_t}= 7t^{3}\widehat {i} - 4t^{2}\widehat {j} + 2t^{5}\widehat {k}$ Variable
$\blacktriangleright\hspace{0.2cm}$ Magnitud del vector Cambio de Posición $\color{#0000FF} \Delta \overrightarrow {{r}}$
La magnitud del vector cambio de posición o desplazamiento $\color{#0000FF}\Delta \overrightarrow {{r}}$ es $\color{#0000FF}\Delta {S}$. El manejo de los conceptos de vector y magnitud de un vector es de suma importancia a la hora de realizar análisis de los movimientos rectilíneo y parabólico pues se pueden estos analizar a partir de escalares (magnitud de los vectores) y luego volver al modelo vectorial.
En la escena interactiva podemos mover los puntos $\color{#0000FF} A$, $\color{#0000FF} P_1$ y $\color{#0000FF} P_2$.
• El punto $\color{#0000FF} A$ es el lugar desde donde el analista se ubica para observar la partícula. debe ser un lugar desde donde pueda tomar mediciones de posición, velocidad, aceleración según el caso.
• El punto $\color{#0000FF} P_1$ es el lugar donde inicialmente se encuentra la partícula.
• El punto $\color{#0000FF} P_2$ es el lugar donde finalmente se encuentra la partícula.
• El vector $\color{#0000FF} \overrightarrow {r_1}$ es el vector de posición inicial de la partícula.
• El vector $\color{#0000FF} \color{#0000FF} \overrightarrow {r_2}$ es el vector de posición final de la partícula.
• El vector $\color{#0000FF} \Delta \overrightarrow {{r}}$ es el vector cambio de posición o desplazamiento de la partícula.
Si movemos el punto A observamos que el vector $\color{#0000FF} \Delta \overrightarrow {{r}}$ no cambia porque la ubicación del analista no puede afectar el desplazamiento
de la partícula. El analista se puede ubicar en cualquier punto siempre y cuando desde ese punto pueda realizar mediciones.
Si movemos el punto $\color{#0000FF} P_2$ muy despacio, lento de tal forma que se vallan alineando el punto $\color{#0000FF} A$, el punto $\color{#0000FF} P_1$ y el punto $\color{#0000FF} P_2$, podemos observar que la magnitud de la suma vectorial del vector $\color{#0000FF} \overrightarrow {r_1}$ mas el vector $\color{#0000FF} \overrightarrow {\Delta {r}}$ es exactamente igual a la suma escalar de las distancias $\color{#0000FF} S_1$ mas la distancia $\color{#0000FF} \Delta {S}$, que se concreta en que $\color{#0000FF} \left|\overrightarrow {r_2} \right| = S_2$.
$\color{#0000FF} \left|\overrightarrow {r_1} + \Delta \overrightarrow {{r}}\right| = S_1 + \Delta {S} = S_2 = \left|\overrightarrow {r_2} \right|$
Es la única forma en que la suma vectorial numéricamente coincide con la suma escalar. Esto permite que al analizar más adelante el movimiento rectilíneo lo podamos realizar en forma escalar que es metodológicamente más sencillo.
Ahora, hacemos coincidir con el punto $\color{#0000FF} P_2$ con el punto $\color{#0000FF} P_1$ y desde ese instante vamos a identificar el desplazamiento $\color{#0000FF} \Delta \overrightarrow {{r}}$ de la partícula, entonces, con clic sostenido sobre $\color{#0000FF} P_2$ vamos a desplazarnos aleatoriamente por toda la pantalla, observando cuidadosamente al vector desplazamiento $\color{#0000FF} \Delta \overrightarrow {{r}}$ (unas veces más largo, otras veces más corto) y muy despacio hacemos nuevamente coincidir el punto $\color{#0000FF} P_2$ con el punto $\color{#0000FF} P_1$ manteniendo la observación sobre el vector $\color{#0000FF} \Delta \overrightarrow {{r}}$. La pregunta que nos hacemos es ¿cuánto se desplazó la partícula? y la respuesta es: El desplazamiento de la partícula es $\color{#0000FF} 0m$. Cuando hacemos coincidir el punto $\color{#0000FF} P_2$ con el punto $P_1$ el vector desplazamiento $\color{#0000FF} \Delta \overrightarrow {{r}}$ desaparece (se vuelve de $\color{#0000FF} 0m$).
Cuando un cuerpo sale de un punto, se mueve y vuelve al mismo punto, su desplazamiento es $\color{#0000FF} 0m$.
Es la suma escalar positiva (suma de magnitudes) de todos y cada uno de los puntos de la trayectoria por donde se movió la partícula. Una persona que viaja $\color{#0000FF} 400Km$ de Medellín a Bogotá, llega a Bogotá y se devuelve a Medellín, podemos afirmar que la distancia recorrida por esta persona es de $\color{#0000FF} 800Km$, pero su desplazamiento es de $\color{#0000FF} 0Km$.
Una persona que viaja $\color{#0000FF} 400Km$ de Medellín a Bogotá, llega a Bogotá y se devuelve $\color{#0000FF} 300Km$ habrá recorrido una distancia de $\color{#0000FF} 700Km$ y su desplazamiento es de $\color{#0000FF} 100Km$.
Es el cambio del vector desplazamiento respecto de un cambio en el tiempo $\color{#0000FF} \overrightarrow {v}=\dfrac { \Delta \overrightarrow {{r}}}{\Delta t}$. La velocidad es un vector que proviene del cociente entre el vector cambio de posición o desplazamiento $\color{#0000FF} \Delta \overrightarrow {{r}}$ y el escalar cambio en el tiempo $\color{#0000FF} {\Delta {t}}$.
Las unidades de la velocidad en el Sistema Internacional es de metros sobre segundos (se suele decir metros por segundos entendiendo este lenguaje como la razón entre metros y segundos) $\color{#0000FF} \dfrac {m}{s}$ y en el Sistema Técnico Ingles F.P.S. en pies sobre segundos $\color{#0000FF} \dfrac {ft}{s}$.
La velocidad por ser un vector contiene dos partes esenciales Magnitud (magnitud y unidad) y Dirección (dirección y sentido) y cada una de estas partes puede cambiar por separado o cambiar juntas a la vez. Las consecuencias de estos cambios será objeto de estudio más adelante.
Es el promedio de la velocidad: $\color{#0000FF}\overrightarrow {v_m}=\dfrac {\Delta \overrightarrow {{r}}}{\Delta t} = \dfrac{\overrightarrow {r_2}-\overrightarrow {r_1}}{t_2-t_1}$
Recordemos que el símbolo $\color{#0000FF} {\Delta}$ significa algo final menos algo inicial $\color{#0000FF}\Delta \overrightarrow {{x}} = \overrightarrow {x_2} - \overrightarrow {x_1}$
En el concepto de velocidad media el valor del tiempo $\color{#0000FF} t_2$ puede estar tan cerca o tan lejos del valor del tiempo $\color{#0000FF} t_1$ como se nos indique en el ejercicio dado.
Ejercicio 3.1: Un automóvil se desplaza de Medellín a Bogotá $400Km$ en 8 horas, determine la velocidad media. Solución: Tomaremos vectorialmente el sentido de Medellín a Bogotá como $\color{#0000FF} \widehat {i}$
$\color{#0000FF}\overrightarrow {v_m}=\dfrac {\Delta \overrightarrow {{r}}}{\Delta t} = \dfrac{\overrightarrow {r_2}-\overrightarrow {r_1}}{t_2-t_1} = \dfrac{400\widehat {i} - 0\widehat {i}}{8 - 0}$ $\color{#FF0000} \overrightarrow {v_m} = 50 \widehat {i} \dfrac {Km}{h}$.
La velocidad media es de poca importancia para la física en la medida que no arroja muchos datos respecto a la trayectoria.
En el ejercicio 3.1. la velocidad media nos dice que un automóvil que salga de Medellín a una velocidad de $\color{#0000FF} 50 \dfrac{Km}{h}$ llegara a la ciudad de Bogotá en 8 horas; pero esto no se ajusta a la realidad; no existirá un automóvil que salga de Medellín a $\color{#0000FF} 50 \dfrac{Km}{h}$ y sin ninguna variante llegue a Bogotá a esa misma velocidad.
La velocidad media le sirve a la estadística para revisar que pasa con la movilidad en las carreteras. la velocidad media no nos dice nada de la trayectoria.
A la física le sirve es poder saber la velocidad de una partícula en cualquier instante, en un instante determinado, es decir la velocidad instantánea.
Es el cambio del vector desplazamiento respecto de un cambio infinitesimal del tiempo.
$\color{#0000FF} \overrightarrow {v}= \lim_{ t\to 0 }\dfrac {\Delta \overrightarrow {{r}}}{\Delta t} = \dfrac {\overrightarrow {dr}}{dt}$
Resaltamos que en la velocidad instantánea $\color{#0000FF} t_1$ y $\color{#0000FF} t_2$ están infinitesimalmente cercanos.
Nótese que la velocidad instantánea aparece cuando hacemos tender a cero $\color{#0000FF} {\Delta t}$, es decir estamos mirando lo que pasa en la relación desplazamiento tiempo pero en lo más pequeño que nos podamos imaginar del tiempo ($\color{#0000FF} {\Delta t}$ tiende a cero).
La velocidad instantánea es la velocidad de la partícula en cada punto de la trayectoria. Al analizar el movimiento de un cuerpo seguramente queremos saber su velocidad en un momento determinado.
La velocidad instantánea se expresa con una ecuación y esta puede ser una constante o puede ser una variable. Ejemplo:
(a) $\color{#0000FF} \overrightarrow {v} = 8\dfrac {{m}}{s} \widehat {i}$ Constante (b) $\color{#0000FF} \overrightarrow {v} = 4 t^3\dfrac {{m}}{s} \widehat {i} $ Variable
Ejercicio 3.2: Una motocicleta parte de reposo a lo largo de una recta a una velocidad de $\color{#0000FF} 8\dfrac {{m}}{s}$ y un automóvil parte del reposo por la misma recta a una velocidad de $\color{#0000FF} 4 t^3\dfrac {{m}}{s}$. Determine la velocidad la motocicleta y del automóvil pasados 2 segundos.
Solución:El sentido de la recta será $\color{#0000FF} \widehat {i}$.
Para la motocicleta: $\color{#0000FF} \overrightarrow {v} = 8\dfrac {{m}}{s} \widehat {i}$ Esta velocidad es constante; quiere decir que para cualquier valor del tiempo su valor no cambia, entonces al pasar 5 segundos la velocidad será de:
$\color{#FF0000} \overrightarrow {v} = 8\widehat {i} \dfrac {{m}}{s} $
Para el automóvil: $\color{#0000FF} \overrightarrow {v} = 4 t^3\dfrac {{m}}{s} \widehat {i} $ Esta velocidad es variable, es una función del tiempo. Para $\color{#0000FF} t=5s$ la velocidad es:
$\color{#0000FF} \overrightarrow {v} = (4) (2^3) \widehat {i}$ $\color{#FF0000} v=32 \widehat {i} \dfrac {{m}}{s}$.
• Para que la velocidad sea constante se requiere que tanto la magnitud como la dirección permanezcan constantes. Obsérvese que para la motocicleta se cumple con esta regla $\color{#0000FF} \overrightarrow {v} = 8\dfrac {{m}}{s} \widehat {i}$ .
• La velocidad del automóvil aparece como variable por el hecho de cambiar su magnitud ($\color{#0000FF} 4 t^3\dfrac {{m}}{s}$), así permanezca constante la dirección ($\color{#0000FF} \widehat {i}$).
Es la magnitud de la velocidad. Lo que mide la velocidad. Por lo tanto, la Rapidez es un escalar.
$\color{#0000FF} {v} = \left| {\overrightarrow {v}} \right| = \left|\dfrac {d \overrightarrow {r}}{dt} \right| = \dfrac {\left| d \overrightarrow {r}\right|}{dt} = \dfrac {{ds}}{dt} $ La Rapidez $\color{#0000FF} {v} = \dfrac {{ds}}{dt}$Donde $\color{#0000FF} {ds} = {\left|\overrightarrow {dr}\right|}$ lo que mide el vector diferencial de desplazamiento.
El concepto de Rapidez es de suma importancia en el desarrollo de muchos ejercicios pues por ser la rapidez un escalar facilita el análisis por el manejo algebraico que es más sencillo que el manejo vectorial y al momento de lograr resultados fácilmente se puede volver al modelo vectorial a partir de los signos positivo o negativo de las operaciones algebraicas.
Es el cambio de la velocidad respecto de un cambio en el tiempo. $\color{#0000FF} \overrightarrow {a}=\dfrac { \Delta \overrightarrow {{v}}}{\Delta t}$. Las unidades de la aceleración en el Sistema Internacional S.I. son de metros sobre segundos al cuadrado.
$\color{#0000FF} a = \dfrac {{\dfrac {{m}}{s}}}{s} = \dfrac {{m}}{s^2}$ Esto se debe a que las unidades de la aceleración son unidades de velocidad sobre tiempo.
Las unidades de la aceleración en el Sistema técnico Ingles F.P.S. son de pies sobre segundos al cuadrado.
$\color{#0000FF} a = \dfrac {{\dfrac {{ft}}{s}}}{s} = \dfrac {{ft}}{s^2}$
En el concepto de aceleración media el valor del tiempo $\color{#0000FF} t_2$ puede estar tan cerca o tan lejos del valor del tiempo $\color{#0000FF} t_1$ como se nos indique en el ejercicio dado.
La aceleración media tiene gran importancia en la física en casos donde al tomar esta aceleración media en diferentes intervalos de tiempo, la variación de la aceleración este en rangos similares y se pueda tomar un valor promedio haciendo que la aplicación de ésta en muchos modelos de ejercicios se aproximen los resultados a la realidad. Es el caso de la aceleración de la gravedad que en realidad es variable; la aceleración de la gravedad responde a la ecuación: $\color{#0000FF} g = G \dfrac {{m_1 . m_2}}{r^2}$. La aceleración de la gravedad varia con el radio de la tierra y el radio de la tierra es variable casi en cada punto, en cada lugar; es mayor el radio de la tierra en Bogotá que en Cartagena, esto hace que la aceleración de la gravedad sea mayor en Cartagena que en Bogotá. Pero ésta variación no es tan grande lo que permite que a nivel científico se tome un promedio del valor de la gravedad que es aceptable y permite y facilita el estudio de muchos fenómenos tales como el movimiento rectilíneo y el movimiento parabólico entre otros.
$\color{#0000FF} \overrightarrow {a}= \lim_{ t\to 0 }\dfrac {\Delta \overrightarrow {v}}{\Delta t} = \dfrac {d \overrightarrow {v}}{dt}$
$\color{#0000FF} \overrightarrow {a} = \dfrac {d \overrightarrow {v}}{dt}$
$\color{#0000FF} \overrightarrow {a} = \dfrac {d \overrightarrow {v}}{dt}$ Es la ecuación más importante de la Física Mecánica, de ella se derivan todos los modelos matemáticos que explican los fenómenos físicos de la naturaleza que se relacionan con cuerpos que se mueven con velocidades mucho menores a la velocidad de la luz.
$\color{#0000FF} \overrightarrow {a} = \dfrac {d \overrightarrow {v}}{dt}$ Es una expresión de la aceleración en función del tiempo. $\color{#0000FF} d \overrightarrow {v}$ es el cambio en el vector velocidad. El vector velocidad puede cambiar por dos razones; cuando cambia la magnitud de la velocidad (la rapidez) y cuando cambia la dirección de la velocidad. Éste análisis nos permite decir que existen dos tipos de aceleración: una aceleración que aparece por el cambio en la magnitud de la velocidad y otra que aparece por el cambio en la dirección de la velocidad.
En esta sección nos ocuparemos de la aceleración que aparece por el cambio en la magnitud de la velocidad $\color{#0000FF} a=\dfrac {d{v}}{dt}$. Al final del capítulo haremos un estudio completo de las componentes de la aceleración.
Aplicaremos el siguiente artificio matemático:
$\color{#0000FF} a=\dfrac {d{v}}{dt} \dfrac {d{s}}{ds}=(\dfrac {d{s}}{dt}) \dfrac {d{v}}{ds}$ Recordemos que $\color{#0000FF} v= \dfrac {d{s}}{dt}$
Entonces $\color{#0000FF} \color{#0000FF} a=v\dfrac {d{v}}{ds}$
Tenemos así dos expresiones para la aceleración:
$\color{#0000FF} a=\dfrac {d{v}}{dt}$ Aceleración en función del tiempo.
$\color{#0000FF} a=v\dfrac {d{v}}{ds}$ Aceleración en función de la posición.
La aceleración es constante cuando su valor no cambia cuando cambia el tiempo, no cambia cuando cambia la posición, es decir la aceleración es constante cuando su valor es un número. Ejemplo: $\color{#0000FF} a=5\dfrac {m}{s^2}$, $\color{#0000FF} a=9.81\dfrac {m}{s^2}$, $\color{#0000FF} a=32.2\dfrac {ft}{s^2}$.
La aceleración es variable cuando su valor cambia cuando cambia el tiempo, cambia cuando cambia la posición, es decir la aceleración es variable cuando su valor depende del tiempo o de la posición. Ejemplo: $\color{#0000FF} a=5t^3\dfrac {m}{s^2}$, $\color{#0000FF} a=4s^2\dfrac {m}{s^2}$, $\color{#0000FF} a=(0.5s^4 + 2s + 3)\dfrac {ft}{s^2}$.
Un cuerpo está en movimiento rectilíneo cuando su trayectoria es a lo largo de una línea recta. La trayectoria rectilínea puede ser vertical, horizontal, oblicua, ascendente, descendente.
En el movimiento rectilíneo ocurre que la magnitud de la suma vectorial es exactamente igual a la suma escalar. Esto hace que podamos analizar el movimiento rectilíneo en forma escalar para facilitar los cálculos.
Un cuerpo en movimiento rectilíneo no cambia de dirección, siempre se mantendrá en la misma recta (el mismo eje), solo podrá cambiar es de sentido. El signo positivo o negativo indicará el sentido de la posición, velocidad o aceleración según convenio del analista.
Bajo este análisis la ecuación vectorial $\color{#0000FF} \overrightarrow {a} = \dfrac {d \overrightarrow {v}}{dt}$ queda $\color{#0000FF} a=\dfrac {d{v}}{dt}$.
Hecho que permite también la utilización de la ecuación $\color{#0000FF} a=v\dfrac {d{v}}{ds}$
De $\color{#0000FF} a=\dfrac {d{v}}{dt}$ $\color{#0000FF} dv=a.dt$ Integramos $\color{#0000FF} \displaystyle \int_{v_{0}}^{v}{dv}=\int_{t_{0}}^{t}{a.dt}$
$\color{#0000FF} \displaystyle v-v_0=\int_{t_{0}}^{t} {a.dt}$ $\color{#0000FF} \displaystyle v = v_0 + \int_{t_{0}}^{t} {a.dt}$
En este momento tenemos que preguntarnos si la aceleración es constante o es variable. Si la aceleración es constante la sacamos de la integral. Si la aceleración es variable remplazamos su ecuación en la integral y realizamos la respectiva integral.
Para $\color{#0000FF} a$ Constante: $\hspace{0.2cm} \color{#0000FF} \displaystyle v = v_0 + a\int_{t_{0}}^{t} {dt}$
$\color{#0000FF} v = v_0 + a(t-t_0)$ Generalmente hacemos $\color{#0000FF} t_0=0$
$\color{#008000} v = v_0 + at$ Velocidad en cualquier instante.
Como $\color{#0000FF} v= \dfrac {d{s}}{dt}$ $\color{#0000FF} \dfrac {d{s}}{dt} = v_0 + at$
$\color{#0000FF} ds = v_0dt + atdt$ Integramos $\color{#0000FF} \displaystyle \int_{s_{0}}^{s} {ds} = \int_{t_{0}}^{t} {v_{0}dt} + \int_{t_{0}}^{t} {atdt}$
La aceleración es constante y los valores $\color{#0000FF} v_0, t_0, s_0, x_0, y_0, Z_0, a_0, ....$ son valores que aunque no sabemos cuánto valen, si sabemos que son valores de condiciones iniciales y por lo tanto son constantes y cuando estas condiciones iniciales están dentro de una integral salen de ellas por ser constantes. Hacemos $\color{#0000FF} t_0=0$
$\color{#0000FF} \displaystyle \int_{s_{0}}^{s} {ds} = v_0\int_{t_{0}}^{t} {dt} + a\int_{t_{0}}^{t} {t.dt}$ $\Rightarrow$ $\color{#0000FF} s-s_0 = v_0t + \dfrac {1}{2}at^2$
$\color{#008000} s = s_0 + v_0t + \dfrac {1}{2}at^2$ Posición en cualquier instante.
Ahora, tomamos la ecuación de la aceleración en función de la posición $\color{#0000FF} a=v\dfrac {d{v}}{ds}$
Despejamos para la velocidad $\color{#0000FF} vdv = ads$
Aplicamos integral a ambos lados de la ecuación. Teniendo en cuenta que la aceleración es constante, la sacamos de la integral.
$\color{#0000FF} \displaystyle \int_{v_{0}}^{v} {vdv} = \int_{s_{0}}^{s} {ads}$ Como $\color{#0000FF} a=Cte$ $\Rightarrow$ $\color{#0000FF} \displaystyle \int_{v_{0}}^{v} {vdv} = a\int_{s_{0}}^{s} {ds}$
Desarrollamos la integral y despejamos para $\color{#0000FF} v^2$
$\color{#0000FF} \dfrac {1}{2}(v^2-v_0^2) = a(s-s_0)$ $\color{#0000FF} (v^2-v_0^2) = 2a(s-s_0)$
$\color{#008000} v^2 = v_0^2 + 2a(s-s_0)$ Velocidad en función de la posición.
Es una ecuación que facilita encontrar velocidad, aceleración, posición cuando no tenemos como referencia el tiempo.
Para estudiantes que no estén familiarizados con el tema de las integrales pueden hacer uso de las ecuaciones que ya están desarrolladas y que presentamos a continuación:
Cinemática Rectilínea.
Aceleración: $\color{#0000FF} a = Constante$
Velocidad: $\color{#0000FF} v = v_0 + at$
Posición: $\color{#0000FF} s = s_0 + v_0t + \dfrac {1}{2}at^2$
Velocidad: $\color{#0000FF} v^2 = v_0^2 + 2a(s-s_0)$
Con estas ecuaciones el estudiante estará en capacidad de desarrollar cualquier ejercicio relacionado con cinemática rectilínea, siempre que la aceleración del cuerpo sea una constante.
Ejercicio 3.2: Un avión aterriza en una pista a $\color{#0000FF} 120\dfrac {m}{s}$. El avión frena a razón de $\color{#0000FF} 10\dfrac {m}{s^2}$. Cuánto tiempo le toma al avión detenerse? Que distancia recorre el avión sobre la pista hasta detenerse?
Si se requiere que el avión se detenga en la mitad de la distancia, que valor tendrá su aceleración? Cuanto tiempo le tomara detenerse?
Solución:
Del enunciado se extraen todos los datos y son representados en un gráfico junto con las condiciones iniciales y finales además de los interrogantes a resolver. En el gráfico tomaremos como positivo el sentido en que el avión recorre la pista de tal forma que la aceleración será de signo negativo.
Del enunciado se extrae que la aceleración es constante (El avión frena a razón de $\color{#0000FF} 10\dfrac {m}{s^2}$, dice el enunciado "el avión frena", indica que la velocidad y la aceleración van en sentido contrario.
El modelo matemático a utilizar es el de la cinemática rectilínea con aceleración constante cuyas ecuaciones son:
Aceleración: $\color{#008000} a = Constante$
Velocidad: $\color{#008000} v = v_0 + at$
Posición: $\color{#008000} s = s_0 + v_0t + \dfrac {1}{2}at^2$
Velocidad: $\color{#008000} v^2 = v_0^2 + 2a(s-s_0)$
• Para determinar cuánto tiempo le toma al avión detenerse tomamos la ecuación de velocidad en función del tiempo y lo despejamos teniendo en cuenta que la velocidad final al detenerse es de $\color{#0000FF} 0\dfrac {m}{s}$
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue} {v}}}} = v_0 + at$ $\color{#0000FF} 0 = v_0 + at$ $\color{#0000FF} -v_0 = at$ $\color{#0000FF} t = \dfrac {-v_0}{a}$
$\color{#0000FF} t = \dfrac {-120}{-10}$ $\color{#0000FF} \color{#FF0000} t = 12 s$ Al avión le toma $\color{#0000FF} 12$ segundos detenerse desde el momento que toca la pista.
• Para determinar la distancia que recorre el avión sobre la pista hasta detenerse tomamos la ecuación de posición en función del tiempo, tomando como referencia que la posición inicial es cero metros $\color{#0000FF} s_0 = 0$
$\color{#0000FF} s = {\color{Red}\bcancel {{\color{blue} {s_0}}}} + v_0t + \dfrac {1}{2}at^2$ $\color{#0000FF} s = v_0t + \dfrac {1}{2}at^2$
$\color{#0000FF} s = 120(12) + \dfrac {1}{2}(-10)(12^2)$ $\color{#FF0000} s = 720 m$ El avión recorre $\color{#0000FF} 720 m$ desde el momento que toca la pista hasta detenerse.
• Se obtiene el mismo resultado para la distancia recorrida si utilizamos la ecuación de la velocidad en función de la posición.
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue} {v^2}}}} = v_0^2 + 2a(s-s_0)$ $\color{#0000FF} 0 = v_0^2 + 2a(s)$ $\color{#0000FF} -v_0^2 = 2a(s)$
$\color{#0000FF} s = \dfrac {-v_0^2}{2a}$ $\color{#0000FF} s = \dfrac {-120^2}{2(-10)}$ $\color{#0000FF} \color{#FF0000} s = 720 m$
• Si se desea que el avión se detenga en la mitad de la distancia, que valor tendrá su aceleración?, podemos tomar nuevamente la ecuación de la velocidad en función del tiempo y despejamos la aceleración. La mitad de la distancia es:
$\color{#0000FF} \dfrac {720}{2} = 360 m$
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue} {v^2}}}} = v_0^2 + 2a(s-s_0)$ $\color{#0000FF} 0 = v_0^2 + 2a(s)$ $\color{#0000FF} -v_0^2 = 2a(s)$
$\color{#0000FF} -v_0^2 = 2a(s)$ $\color{#0000FF} \dfrac {-v_0^2}{2(s)} = a$ $\color{#0000FF} a = \dfrac {-120^2}{2(360)}$ $\color{#FF0000} a = -20\dfrac {m}{s^2}$
• El tiempo que le tomara detenerse en estas condiciones lo encontramos con la ecuación de la velocidad en función del tiempo:
$v = v_0 + at$ $\color{#0000FF} 0 = v_0 + at$ $\color{#0000FF} -v_0 = at$ $\color{#0000FF} t = \dfrac {-v_0}{a}$
$\color{#0000FF} t = \dfrac {-120}{-20}$ $\color{#FF0000} t = 6 s$ Al avión le toma $\hspace {0.1cm} \color{#0000FF} 6 \ $ segundos en detenerse bajo estas nuevas condiciones.
Un cuerpo está en caída libre cuando su trayectoria es a lo largo de una recta perpendicular a la tierra y este cuerpo queda afectado únicamente por la aceleración de la gravedad. No se tendrá en cuenta los efectos del aire ni de ninguna otra clase, solo los efectos de la gravedad.
Existen tres casos en que un cuerpo estará en caída libre:
$\color{#0000FF} \blacktriangleright\hspace{0.1cm}$ Primer Caso: Se deja caer libremente un cuerpo hacia la tierra. En este caso la velocidad inicial del cuerpo es de $\color{#0000FF} v_0 = 0 \dfrac {m}{s}$.
La velocidad y la gravedad van en el mismo sentido (tienen el mismo signo)
Como cuando desde la altura de un metro dejamos caer una piedra hacia la tierra.
$\color{#0000FF} \blacktriangleright\hspace{0.1cm}$ Segundo Caso: Se lanza un cuerpo verticalmente en dirección y sentido hacia la tierra. En este caso la velocidad inicial de la piedra es diferente de cero $\color{#0000FF} v_0 {\color{Red}\bcancel {{\color{blue} {=}}}} 0 \dfrac {m}{s}$.
La velocidad inicial y la gravedad tienen el mismo sentido (tienen el mismo signo)
Desde el balcón de un apartamento se lanza verticalmente hacia abajo (hacia la tierra) una piedra.
$\color{#0000FF} \blacktriangleright\hspace{0.1cm}$ Tercer Caso: Se lanza cuerpo verticalmente hacia arriba de la tierra. En este caso la velocidad inicial de la piedra es diferente de cero $\color{#0000FF} v_0 {\color{Red}\bcancel {{\color{blue} {=}}}} 0 \dfrac {m}{s}$.
La velocidad inicial y la gravedad tienen sentido contrario (tienen diferente signo)
Se lanza una piedra verticalmente hacia arriba de la tierra.
Podemos lanzar verticalmente hacia arriba de la tierra un objeto y es posible que no vuelva a bajar, como en el caso en que lanzamos un confite a una persona que está en un segundo piso y esta persona atrapa el confite mientras este está subiendo. A pesar de que el confite siempre estuvo moviéndose verticalmente hacia arriba de la tierra, su movimiento cumple las características esenciales del movimiento de caída libre.
El movimiento de caída libre es un caso particular del movimiento rectilíneo en el cual ya se conoce la aceleración que es la aceleración de la gravedad que se considera constante por zonas; por lo que en el movimiento de caída libre utilizaremos las ecuaciones desarrolladas para la cinemática rectilínea con aceleración constante.
Para el caso de movimiento de caída libre tomaremos como positivo todo eje vertical hacia arriba de la tierra; es decir que la aceleración de la gravedad tendrá en caída libre un signo negativo por apuntar hacia el centro de la tierra.
Recordemos que la aceleración de la gravedad tiene un valor en el Sistema Internacional SI de $\color{#0000FF} g = 9.81 \dfrac {m}{s^2}$, y un valor en el Sistema Ingles FPS de $\color{#0000FF} g = 32.2 \dfrac {ft}{s^2}.$
Para el movimiento de caída libre se acostumbra nombrar el eje vertical a la tierra como eje $\color{#0000FF} y$. No olvidar que este eje $\color{#0000FF} y$ lo tomamos positivo hacia arriba.
Cinemática Rectilínea: Caída Libre
Aceleración: $\color{#0000FF} a = -g Constante$
Velocidad: $\color{#0000FF} v = v_0 - gt$
Posición: $\color{#0000FF} y = y_0 + v_0t - \dfrac {1}{2}gt^2$
Velocidad: $\color{#0000FF} v^2 = v_0^2 - 2g(y-y_0)$
Ejercicio 3.3: Un maestro de obra subido en un andamio $\color{#0000FF} 6m$ arriba de su ayudante que está $\color{#0000FF} 2m$ arriba del suelo, le solicita que le lance un alicate verticalmente. El ayudante le lanza el alicate verticalmente hacia arriba y es atrapado por el maestro de obra $\color{#0000FF} 2$ segundos más tarde.
a) Con qué velocidad fue lanzado el alicate?
b) Con qué velocidad fue atrapado el alicate?
c) Si el maestro de obra no atrapa el alicate, con qué velocidad el alicate golpea el suelo?
d) Cual es el tiempo desde que es lanzado el alicate hasta que cae al suelo?
e) Cual es la altura máxima alcanzada por el alicate?
f) Si el maestro de obra no atrapa el alicate, con qué velocidad los atrapa el ayudante?
Solución: Hacemos un diagrama de lo sucedido:
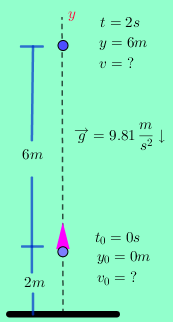
El modelo matemático a aplicar son las ecuaciones del movimiento rectilíneo aplicadas al movimiento de caída libre.
Aceleración: $\color{#008000} a = -g Constante$
Velocidad: $\color{#008000} v = v_0 - gt$ $\color{#008000} v^2 = v_0^2 - 2g(y-y_0)$
Posición: $\color{#008000} y = y_0 + v_0t - \dfrac {1}{2}gt^2$
Una vez realizado el diagrama donde se colocan los datos dados en el enunciado, las condiciones iniciales, las condiciones finales y los interrogantes a resolver, procedemos a ir contestando cada una de las preguntas:
Nosotros como analistas nos ubicaremos en la base del andamio (en el piso).
a) Con que velocidad fue lanzado el alicate?. Para ello aplicamos la ecuación de la posición en función del tiempo:
$\color{#0000FF} y = y_0 + v_0t - \dfrac {1}{2}gt^2$ La única incógnita es $\color{#0000FF} v_0$
$\color{#0000FF} y - y_0 + \dfrac {1}{2}gt^2 = v_0t$ $\color{#0000FF} v_0 = \dfrac {y - y_0 + \dfrac {1}{2}gt^2}{t}$
$\color{#0000FF} v_0 = \dfrac {8 - 2 + \dfrac {1}{2}(9.81)(2)^2}{2}$ $\color{#FF0000} v_0 = 12.81\dfrac {m}{s}$ El signo positivo indica que el alicate fue lanzado hacia arriba.
b) Con qué velocidad fue atrapado el alicate?. Ya conocida la velocidad inicial $\color{#0000FF} v_0$ podemos hallar la velocidad con que fueron atrapados los alicates con la ecuación de la velocidad en función del tiempo.
$\color{#0000FF} v = v_0 - gt$ $\color{#0000FF} v = 12.81 - (9.81)2$ $\color{#0000FF} \color{#FF0000} v_0 = -6.81\dfrac {m}{s}$ El signo negativo indica que el alicate fue atrapado cuando estaba bajando.
c) Si el maestro de obra no atrapa el alicate, con qué velocidad el alicate golpea el suelo? Si el maestro de obra no atrapa el alicate, éste caerá al suelo, es decir cae a la posición final $\color{#0000FF} y = 0$. Como sabemos la posición inicial, la posición final y la velocidad inicial, entonces utilizamos la ecuación de velocidad en función de la posición.
$\color{#0000FF} v^2 = v_0^2 - 2g({\color{Red}\bcancel {{\color{blue} {y}}}}-y_0)$ $\color{#0000FF} v^2 = 12.81^2 - 2(9.81)(0 - 2)$
$\color{#0000FF} v^2 = 203.34$ $\color{#0000FF} v = \pm \sqrt {203.34}$ $\color{#0000FF} v = \pm14.26\dfrac {m}{s}$
$\color{#FF0000} v = -14.26\dfrac {m}{s}$ Hemos tomado el signo negativo por el hecho de que los alicates caen al suelo.
d) Cual es el tiempo desde que es lanzado el alicate hasta que cae al suelo?. Conocidas la velocidad inicial $\color{#0000FF} v_0$, la velocidad final al caer al piso, utilizamos la ecuación de la velocidad en función del tiempo y de ésta despejamos el tiempo:
$\color{#0000FF} v = v_0 - gt$ $gt = v_0 - v$ $\color{#0000FF} t = \dfrac {v_0 - v}{g}$
$\color{#0000FF} t = \dfrac {12.81 - (-14.26 )}{9.81}$ $\color{#FF0000} t = 2.76 s$ Tiempo desde que es lanzado el alicate hacia arriba hasta que cae al piso.
e) Cual es la altura máxima alcanzada por el alicate?. En la altura máxima la velocidad es cero $\color{#0000FF} v = 0 \dfrac {m}{s}$; Remplazamos en la ecuación de velocidad en función de la posición y despejamos la altura $\color{#0000FF} y$.
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue} {v^2}}}} = v_0^2 - 2g(y-y_0)$ $\color{#0000FF} 0 = v_0^2 - 2g(y_{max}-y_0)$
$\color{#0000FF} 2g(y_{max}-y_0) = v_0^2$ $\color{#0000FF} y_{max}-y_0 = \dfrac {v_0^2}{2g}$
$\color{#0000FF} y_{max} = y_0 + \dfrac {v_0^2}{2g}$ $\color{#0000FF} y_{Max} = 2 + \dfrac {12.81^2}{2(9.81)}$
$\color{#FF0000} y_{max} = 10.36 m$ Altura máxima alcanzada por el alicate.
f) Si el maestro de obra no atrapa el alicate, con qué velocidad los atrapa el ayudante?. En éste caso la posición inicial $\color{#0000FF} y_0 = 2m$ y la posición final $\color{#0000FF} (y = 2m)$ son iguales (los alicates vuelven a las manos de quien los lanzo) entonces, el factor $\color{#0000FF} (y - y_0) = 0$. Tenemos la velocidad inicial $\color{#0000FF} v_0$ y la aceleración $\color{#0000FF} g$; entonces utilizamos la ecuación de la velocidad en función de la posición y despejamos la velocidad final $\color{#0000FF} v$
$\color{#0000FF} v^2 = v_0^2 - 2g(y-y_0)$ $\color{#0000FF} v^2 = v_0^2$ $\color{#0000FF} v = \pm \sqrt {v_0^2}$ $\color{#0000FF} v = - v_0$
$\color{#FF0000} v = - 12.81 \dfrac {m}{s}$ Tomamos el signo negativo en el entendido de que el ayudante atrapa los alicates cuando estos caen; a la misma velocidad con que los lanzo pero en sentido contrario.
Nota: Otra forma seria tomar la ecuación de posición en función del tiempo y despejar el tiempo que gasta el alicate en volver a las manos del ayudante; lo remplazamos en la ecuación de la velocidad en función del tiempo y así obtenemos la velocidad con que el ayudante atrapa los alicates. Este procedimiento se lo dejamos para que el estudiante lo verifique.
Hasta ahora hemos analizado la cinemática (posición, velocidad y aceleración) de una partícula utilizando las ecuaciones derivadas del cálculo.
Para realizar ejercicios nos dan una serie de datos que provienen de situaciones especiales del movimiento de una partícula y luego los llevamos a los modelos matemáticos correspondientes y solucionamos correctamente.
En ocasiones nos pedirán encontrar la cinemática de una partícula pero ahora a partir de datos representados por graficas que relacionan las variables $\hspace{0.1cm} \color{#0000FF} a, v, s, t \ $.
Cuando en una gráfica se relacionan dos de estas variables es posible realizar las gráficas que describen la relación entre las otras variables, lo que conlleva a poder obtener a partir de las gráficas las ecuaciones cinemáticas correspondientes y obtener de ellas los resultados esperados en un ejercicio particular.
Basta una gráfica que relacione dos de estas variables y con ayuda de las relaciones:
$ \color{#008000} a= \dfrac {dv}{dt} \hspace{0.8cm} v= \dfrac {ds}{dt} \hspace{0.8cm} a= v \dfrac {dv}{ds} \ $
Obtendremos soluciones para la cinemática de partículas que se mueven como en el caso de un automóvil que realiza un viaje y por intervalos de tiempo cambia la aceleración, la velocidad y finalmente tenemos de este automóvil gráficas de su movimiento.
Ejercicio 3.4:
El automóvil deportivo arranca desde el reposo por una pista recta generando la gráfica $\hspace{0.1cm} \color{#0000FF} v_{vs} t \ $. Determine la aceleración y la posición del automóvil para $\hspace{0.1cm} \color{#0000FF} t=6 \ s \ $ y $\hspace{0.1cm} \color{#0000FF} t=12 \ s \ $
Solución: La aceleración para $\hspace{0.1cm} \color{#0000FF} t=6 \ s \ $ es $\hspace{0.1cm} \color{#0000FF} a_6=0 \dfrac {m}{s^2} \ $ ya que nos encontramos en el intervalo de tiempo $\hspace{0.1cm} \color{#0000FF} t=3 \ s \ $ a $\hspace{0.1cm} \color{#0000FF} t=8 \ s \ $ donde la velocidad es constante:
$\hspace{0.1cm} \color{#0000FF} a_{3-8}= \dfrac {dv}{dt} = \dfrac {v_8 - v_3}{t_8 - t_3} = \dfrac {4-4}{8-3} = 0 \Rightarrow $ $\hspace{0.1cm} \color{#FF0000} a_6=0 \ \dfrac {m}{s^2} $
Para la posición en $\hspace{0.1cm} \color{#0000FF} t=6 \ s \ $ tenemos que sumar el cambio de posición durante el intervalo de $\hspace{0.1cm} \color{#0000FF} t=0 \ s \ $ a $\hspace{0.1cm} \color{#0000FF} t=3 \ s \ $ más el cambio de posición de $\hspace{0.1cm} \color{#0000FF} t=3 \ s \ $ a $\hspace{0.1cm} \color{#0000FF} t=6 \ s \ $. Hallamos la aceleración para el primer intervalo:
$\hspace{0.1cm} \color{#0000FF} a_{0-3}= \dfrac {dv}{dt} = \dfrac {v_3 - v_0}{t_3 - t_0} = \dfrac {4-0}{3-0} = \dfrac {4}{3} \Rightarrow$ $\hspace{0.5cm} \color{#008000} a_{0-3} = \dfrac {4}{3} \ \dfrac {m}{s^2}$
$\hspace{0.1cm} \color{#0000FF} S_{0-3}= {\color{Red}\bcancel {{\color{blue} {S_0}}}} + {\color{Red}\bcancel {{\color{blue} {v_0}}}}t + \dfrac {1}{2}at^2 $ $\hspace{0.5cm} \color{#0000FF} S_{0-3} = \dfrac {1}{2} (\dfrac {4}{3}) 3^2 $ $\hspace{0.3cm} \color{#008000} S_{0-3}=6 \ {m} $
$\color{#0000FF} S_{3-6}= {\color{Red}\bcancel {{\color{blue} {S_0}}}} + {v_{0}}t + \dfrac {1}{2} {\color{Red}\bcancel {{\color{blue} {a}}}} t^2 $ $\hspace{0.4cm} \color{#0000FF} S_{3-6} = 4(3) $ $\hspace{0.2cm} \color{#FF0000} S_{3-6}=12 \ {m} $
Al sumar: $\hspace{0.2cm} \color{#0000FF} S_{0-6}= 6 + 12 \ \Rightarrow $ $\hspace{0.8cm} \color{#FF0000} S_{0-6}= 18 \ {m} $
La aceleración para $\hspace{0.1cm} \color{#0000FF} t=12 \ s \ $ es la pendiente de la recta en el intervalo desde $\hspace{0.1cm} \color{#0000FF} t=8 \ s \ $ a $\hspace{0.1cm} \color{#0000FF} t=12 \ s \ $:
$\color{#0000FF} a_{8-16}= \dfrac {dv}{dt} = \dfrac {v_6 - v_8}{t_6 - t_8} = \dfrac {0-4}{16-8} = \dfrac {1}{4} \Rightarrow$ $\color{#FF0000} a_{8-16} = - \dfrac {1}{4} \ \dfrac {m}{s^2}$
Para la posición en $\hspace{0.1cm} \color{#0000FF} t=12 \ s \ $ tenemos que sumar el cambio de posición durante el intervalo de $\hspace{0.1cm} \color{#0000FF} t=0 \ s \ $ a $\hspace{0.1cm} \color{#0000FF} t=3 \ s \ $ más el cambio de posición de $\hspace{0.1cm} \color{#0000FF} t=3 \ s \ $ a $\hspace{0.1cm} \color{#0000FF} t=8 \ s \ $ más el cambio de posición de $\hspace{0.1cm} \color{#0000FF} t=8 \ s \ $ a $\hspace{0.1cm} \color{#0000FF} t=12 \ s \ $ .
$\hspace{0.1cm} \color{#0000FF} S_{0-3}= {\color{Red}\bcancel {{\color{blue} {S_0}}}} + {\color{Red}\bcancel {{\color{blue} {v_0}}}}t + \dfrac {1}{2}at^2 $ $\hspace{0.5cm} \color{#0000FF} S_{0-3} = \dfrac {1}{2} (\dfrac {4}{3}) 3^2 $ $\hspace{0.3cm} \color{#008000} S_{0-3}=6 \ {m} $
$\color{#0000FF} S_{3-8}= {\color{Red}\bcancel {{\color{blue} {S_0}}}} + {v_{0}}t + \dfrac {1}{2} {\color{Red}\bcancel {{\color{blue} {a}}}} t^2 $ $\hspace{0.4cm} \color{#0000FF} S_{3-8} = 4(5) $ $\hspace{0.8cm} \color{#008000} S_{3-8}=20 \ {m} $
$\color{#0000FF} S_{8-12}= {\color{Red}\bcancel {{\color{blue} {S_0}}}} + {v_{0}}t + \dfrac {1}{2} a t^2 $ $\hspace{0.4cm} \color{#0000FF} S_{8-12} = 4(4) - \dfrac {1}{2} (\dfrac {1}{4}) 4^2 $
$\hspace{0.2cm} \color{#008000} S_{8-12}=14 \ {m} $
Al sumar: $\hspace{0.2cm} \color{#0000FF} S_{0-12}= 6 + 20 + 14 \ \Rightarrow $ $\hspace{0.8cm} \color{#FF0000} S_{0-12}= 40 \ {m} $
La siguiente es una escena interactiva, adaptada de Plantillas con descartes_JSLas escenas de Descartes son recursos interactivos que pueden insertarse o embeberse en múltiples soportes y medios como páginas web, blogs, wikispaces, o plataformas de aprendizaje como Moodle, entre otras herramientas., y diseñada por Juan Guillermo Rivera B.
La unidad interactiva permite obtener las gráficas de aceleración, velocidad y posición del automóvil que se desplaza con movimiento errático en un máximo de tiempo de $\hspace{0.1cm} \color{#0000FF} t=10 \ s \ $. La unidad interactiva cuenta con un botón abajo a la derecha identificado con la letra $\hspace{0.1cm} \color{#0000FF} i \ $ con las instrucciones para manipular la escena.
Ejercicio 3.5: Luego de leer las instrucciones para manipular la escena interactiva y haber simulado el movimiento del automóvil para los intervalos de $\hspace{0.1cm} \color{#0000FF} 0 \ $ a $\hspace{0.1cm} \color{#0000FF} 3 \ s \ $, de $\hspace{0.1cm} \color{#0000FF} 3 \ $ a $\hspace{0.1cm} \color{#0000FF} 6 \ s \ $ y de $\hspace{0.1cm} \color{#0000FF} 6 \ $ a $\hspace{0.1cm} \color{#0000FF} 10 \ s \ $, la escena arrojo las gráficas de aceleración, velocidad y posición que a continuación se presenta:
A partir de las gráficas determine la aceleración, velocidad y posición del automóvil a los $\hspace{0.1cm} \color{#0000FF} 5 \ s \ $ de haberse puesto en marcha la escena interactiva.
Solución: En $\hspace{0.1cm} \color{#0000FF} t=5 \ s \ $ el automóvil se encuentra en el segundo intervalo (de $\hspace{0.1cm} \color{#0000FF} t=3 \ s \ $ a $\hspace{0.1cm} \color{#0000FF} t=6 \ s \ $). Para la aceleración:
Hallamos la velocidad para $\hspace{0.1cm} \color{#0000FF} t=3 \ s \ $:
$\hspace{0.1cm} \color{#0000FF} v= {\color{Red}\bcancel {{\color{blue}v_0}}} + at = 12.5(3) \Rightarrow$ $\hspace{0.1cm} \color{#008000} v_3 = 37.5 \dfrac {m}{s} \ $
De la gráfica de la velocidad vemos que la velocidad es constante en el intervalo de $\hspace{0.1cm} \color{#0000FF} t=3 \ s \ $ a $\hspace{0.1cm} \color{#0000FF} t=6 \ s \ $ Entonces la velocidad para $\hspace{0.1cm} \color{#0000FF} t=5 \ s \ $ es: $\hspace{2cm} \color{#FF0000} v_5 = 37.5 \dfrac {m}{s} \ $
Como la velocidad es constante en el intervalo de $\hspace{0.1cm} \color{#0000FF} t=3 \ s \ $ a $\hspace{0.1cm} \color{#0000FF} t=6 \ s \ $ Entonces la aceleración es $\hspace{0.1cm} \color{#0000FF} a_{3-6}=0 \dfrac {m}{s^2} \ $
$ \color{#0000FF} a= \dfrac {dv}{dt} = \ \dfrac {v_6-v_3}{t_6-t_3} = \dfrac {37.5 - 37.5}{6 - 3} \hspace{0.3cm} \Rightarrow$ $\hspace{0.4cm} \color{#FF0000} a_{5}= 0 \dfrac {m}{s^2} $
Para la posición: Hallamos la posición alcanzada en el intervalo de $\hspace{0.1cm} \color{#0000FF} t=0 \ s \ $ a $\hspace{0.1cm} \color{#0000FF} t=3 \ s \ $
$\hspace{0.1cm} \color{#0000FF} S = {\color{Red}\bcancel {{\color{blue}S_0}}} + {\color{Red}\bcancel {{\color{blue}v_0}}} t + \dfrac {1}{2} a t^2 \ $ $\hspace{0.1cm} \color{#0000FF} S = \dfrac {1}{2} a t^2 \ $
$\hspace{0.1cm} \color{#0000FF} S = \dfrac {1}{2} 12.5 (3^2) \hspace{1cm} \Rightarrow $ $\hspace{1cm} \color{#008000} S_{0-3} = 56.25 \ m $
Nos falta $\hspace{1cm} \color{#0000FF} S_{3-5} = {\color{Red}\bcancel {{\color{blue}S_0}}} + v_0 t + \dfrac {1}{2} {\color{Red}\bcancel {{\color{blue}a}}} t^2 \ $
$\hspace{0.1cm} \color{#0000FF} S_{3-6} = v_0 t \ $ $\hspace{1cm} \color{#0000FF} S_{3-5} = 37.5 (2) \ $ $\hspace{1cm} \color{#008000} S_{3-5} = 75 \ m \ $
La posición para $\hspace{0.1cm} \color{#0000FF} t=5 \ s \ $ es:
$\hspace{0.1cm} \color{#0000FF} S_5 = 56.25 + 75 \ $ $\hspace{3cm} \color{#FF0000} S_5 = 131.25 \ m \ $
Para el estudiante:
• A partir de la misma gráfica determine aceleración, velocidad y posición del automóvil para $\hspace{0.1cm} \color{#0000FF} t=9 \ s \ $.
$ \color{#FF0000} R // \hspace{0.5cm} a_9 = -5 \dfrac {m}{s^2} \hspace{0.5cm} v_{9} = 22.5 \dfrac {m}{s} \hspace{0.5cm} S_9 \ = 258.75 \ m \ $
• Manipule la escena interactiva para $\hspace{0.1cm} \color{#0000FF} 3 \ $ intervalos repartidos en $\hspace{0.1cm} \color{#0000FF} 10 \ s \ $ y a partir de la gráfica generada encuentre la aceleración, velocidad y posición en la mitad de cada intervalo.
Un cuerpo está en movimiento parabólico cuando su trayectoria es a lo largo de un plano vertical a la tierra y éste cuerpo en su trayectoria queda afectado únicamente por la acción de la gravedad. Ejemplos de movimiento parabólico los vemos en el lanzamiento de la bola de basquetbol por parte del jugador a la cesta, el lanzamiento del tejo con ánimo de lograr una mecha, el disparo de un arma de fuego no hecha en forma vertical a la tierra, el movimiento de la bola en el juego de ping pon, lanzamiento de la bola de voleibol a la zona contraria, etc.
Para el análisis del Movimiento Parabólico. Trazamos un eje horizontal $\color{#0000FF} x$, trazamos un eje vertical $\color{#0000FF} y$ paralelo a la dirección de la gravedad. En cada punto de la trayectoria la partícula tiene una posición respecto a $\color{#0000FF} x$ y una posición respecto a $\color{#0000FF} y$, siendo la posición inicial $\color{#0000FF} (x_{0}, y_{0})$.
En la gráfica Movimiento Parabólico. en cada punto de la trayectoria hemos representado la velocidad tangente a la trayectoria. La velocidad inicial $\color{#0000FF} v_0$ forma un ángulo $\color{#0000FF} \theta_{0}$ respecto del eje horizontal. Con el ángulo $\color{#0000FF} \theta_{0}$ obtenemos las componentes de la velocidad inicial en cada uno de los ejes $\color{#0000FF} x$, $\color{#0000FF} y$:
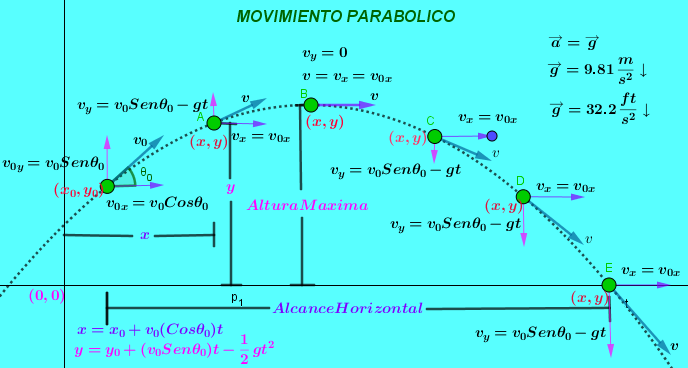
$\color{#0000FF} v_{0x}=v_0 Cos \theta_{0}$ $\color{#0000FF} v_{0y}=v_0 Sen \theta_{0}$.
Como el movimiento parabólico se da a lo largo de un plano vertical a la tierra, esto trae como consecuencia que la única aceleración que aparece es la aceleración de la gravedad $\color{#0000FF} g$ que actúa sobre el eje vertical $\color{#0000FF} y$, $\color{#0000FF} a_{y}= -g$; el signo negativo indica que hemos tomado el eje vertical como positivo alejándose de la tierra. A lo largo del eje horizontal $\color{#0000FF} x$ no existe aceleración, entonces $\color{#0000FF} a_{x}=0$.
De la gráfica Movimiento Parabólico. se observa que en cualquier instante la partícula experimenta una posición en $\color{#0000FF} x$, una posición en $\color{#0000FF} y$, una velocidad en $\color{#0000FF} x$, $\color{#0000FF} v_{x}$, una velocidad en $\color{#0000FF} y$, $\color{#0000FF} v_{y}$, una aceleración en $\color{#0000FF} x$, $\color{#0000FF} a_{x}=0$, una aceleración en $\color{#0000FF} y$ $\color{#0000FF} a_{y}=-g$.
El movimiento parabólico se puede analizar como un movimiento rectilíneo en $x$ sumado a un movimiento rectilíneo en $\color{#0000FF} y$ que suceden en el mismo instante, es decir que en el mismo momento que se mueve en $\color{#0000FF} x$, en ese mismo instante se mueve por $\color{#0000FF} y$.
Así las cosas, para el análisis del movimiento parabólico planteamos las ecuaciones de movimiento rectilíneo para el movimiento por el eje $\color{#0000FF} x$, y para el movimiento por el eje $\color{#0000FF} y$.
$\color{#0000FF} \blacktriangleright\hspace{0.2cm}$ Movimiento Horizontal $x$$\color{#0000FF} a_x = 0 Constante$
$\color{#0000FF} v_x = v_{0x} + a_xt$ $\Rightarrow$ $\color{#0000FF} v_{x}=v_0 Cos \theta_{0}$
$\color{#0000FF} x = x_{0} + v_{0x}t + \dfrac {1}{2}a_xt^2$ $\Rightarrow$ $\color{#0000FF} x = x_{0} + v_{0}(Cos\theta_{0})t$
$\color{#0000FF} v_x^2 = v_{0x}^2 + 2a_x(x-x_0)$ $\Rightarrow$ $\color{#0000FF} v_x^2 = v_{0x}^2$ $\Rightarrow$ $\color{#0000FF} v_{x}=v_0 Cos \theta_{0}$
$\color{#0000FF} \blacktriangleright\hspace{0.2cm}$ Movimiento Vertical $y$$\color{#0000FF} a_y = -g Constante$
$\color{#0000FF} v_y = v_{0y} - gt$ $\Rightarrow$ $\color{#0000FF} v_y = v_0 Sen \theta_{0} - gt$
$\color{#0000FF} y = y_0 + v_{0y}t - \dfrac {1}{2}gt^2$ $\Rightarrow$ $\color{#0000FF} y = y_0 + (v_0 Sen \theta_{0})t - \dfrac {1}{2}gt^2$
$\color{#0000FF} v_y^2 = v_{0y}^2 - 2g(y-y_0)$ $\Rightarrow$ $\color{#0000FF} v_y^2 = (v_0 Sen \theta_{0})^2 - 2g(y-y_0)$
El movimiento horizontal ocurre en el mismo instante en que ocurre el movimiento vertical. El tiempo transcurrido en $\color{#0000FF} x$ es el mismo tiempo transcurrido en $\color{#0000FF} y$. El tiempo se constituye así en el puente de conexión entre las ecuaciones de $\color{#0000FF} x$ y las ecuaciones de $\color{#0000FF} y$, permitiendo resolver de manera sencilla interrogantes. Podemos por ejemplo despejar el tiempo en las ecuaciones de $\color{#0000FF} x$ y remplazarlo en las ecuaciones de $\color{#0000FF} y$.

Ejercicio 3.6: En un partido de futbol un jugador patea el balón desde una distancia horizontal de $\color{#0000FF} 30 m$ con una velocidad de $\color{#0000FF} 19.46 \dfrac {m}{s}$. Si la altura de la portería es de $\color{#0000FF} 2.20 m$. Determine:
a) Fue o no fue gol?
b) Por cuanto el balón pasa por encima o por debajo del travesaño de la portería?
c) El balón iba subiendo o iba cayendo cuando paso por la portería?
d) Con qué velocidad pasa el balón por la portería?
e) Cuál es la altura máxima que adquiere el balón en su trayectoria?
f) Si la portería no tiene malla y es gol, cual es el alcance máximo horizontal.
Solución: hacemos un diagrama de lo sucedido.
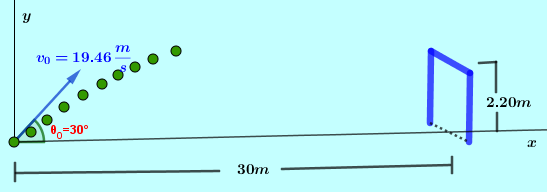
a) Fue o no fue gol? para resolver este interrogante y con base en el diagrama realizado, planteamos las ecuaciones generales del movimiento parabólico aplicadas al caso concreto (al caso particular). Determinamos la altura $\color{#0000FF} y$ del balón a la distancia horizontal $\color{#0000FF} x=30m$. Comparamos esta altura con la altura de la portería; si es menor Fue gol, si es mayor no fue gol.

Como la incógnita es la altura $\color{#0000FF} y$, tomamos la ecuación de posición $\color{#0000FF} y$, $\color{#0000FF} y = y_0 + (v_0 Sen \theta_{0})t - \dfrac {1}{2}gt^2$
En ésta ecuación tenemos dos incógnitas: La altura $\color{#0000FF} y$ y el tiempo $\color{#0000FF} t$. esto nos obliga a ir a las ecuaciones del movimiento horizontal $\color{#0000FF} x$, tomar la ecuación de posición $\color{#0000FF} x$ en la que tenemos como única incógnita el tiempo $\color{#0000FF} t$. Despejamos el tiempo $\color{#0000FF} t$.
$\color{#0000FF} x = x_{0} + v_{0}(Cos\theta_{0})t$ $\Rightarrow$ $\color{#0000FF} x = v_{0}(Cos\theta_{0})t$
$\color{#0000FF} t=\dfrac {x}{v_{0} Cos\theta_{0}}$ $\Rightarrow$ $\color{#0000FF} t=\dfrac {30}{19.46 Cos 30°}$ $\Rightarrow$ $\color{#FF0000} t= 1.78 s$
Éste valor de $\color{#0000FF} t$ lo remplazamos en la ecuación de posición $\color{#0000FF} y$.
$\color{#0000FF} y = y_0 + v_{0y}t - \dfrac {1}{2}gt^2$ $\Rightarrow$ $\color{#0000FF} y = v_{0y}t - \dfrac {1}{2}gt^2$
$\color{#0000FF} y = y_0 + (v_0 Sen \theta_{0})t - \dfrac {1}{2}gt^2$ $\Rightarrow$ $\color{#0000FF} y= (v_0 Sen \theta_{0})t - \dfrac {1}{2}gt^2$
$\color{#0000FF} y= (19.46 Sen 30°)1.78 - \dfrac {1}{2}(9.81)1.78^2$ $\Rightarrow$ $\color{#FF0000} y= 1.78 m$
$\color{#0000FF} y=1.78 m$ es menor que la altura de la portería..."FUE GOL".
b) Por cuanto el balón pasa por encima o por debajo del travesaño de la portería?
Es la diferencia entre la altura de la portería y el valor de $\color{#0000FF} y$ encontrado: $\color{#0000FF}\Delta {y} = \left| 2.20 - 1.78 \right|$ $\Rightarrow$ $\color{#FF0000} \Delta {y} = 0.42m$ Por debajo.
c) El balón iba subiendo o iba cayendo cuando paso por la portería?. El signo de la $\color{#0000FF} v_y$ en $\color{#0000FF} t=1.78 s$ cuando pasa por la portería nos indicara si el balón iba subiendo o iba cayendo: $\color{#0000FF} v_y = v_0 Sen \theta_{0} - gt$ $\color{#0000FF} v_y = 19.46 Sen 30° - (9.81)1.78$
$\color{#FF0000} v_y = -7.73 \dfrac {m}{s}$ El signo (-) indica que el balón iba cayendo.
d) Con que velocidad pasa el balón por la portería?. La velocidad $\color{#0000FF} v$ en ese instante es tangente a la trayectoria y tiene dos componentes, $\color{#0000FF} v_x$ y $\color{#0000FF} v_y$. $\color{#FF0000} v_y = -7.73 \dfrac {m}{s}$. $\color{#0000FF} v_{x}=v_0 Cos \theta_{0}$ $\color{#0000FF} v_{x}=19.46 Cos 30°$ $\color{#FF0000} v_x=16.85\dfrac {m}{s}$
Tenemos que: $\color{#0000FF} \overrightarrow{v}= \overrightarrow{v_x} + \overrightarrow{v_y}$ $\Rightarrow$ $\color{#0000FF} v =\sqrt {v_x^2 + v_y^2}$
$\color{#0000FF} v =\sqrt {{16.85^2} + {7.73^2}}$ $\Rightarrow$ $\color{#FF0000} v = 18.54 \dfrac {m}{s}$ El ángulo $\color{#0000FF} \theta_{v}$ de la velocidad lo hallamos haciendo: $\color{#0000FF} \theta_{v} = tag^{-1}\dfrac {v_y}{v_x}$
$\color{#0000FF} \theta_{v} = tag^{-1}\dfrac {7.73}{16.85}$ $\Rightarrow$ $\color{#FF0000} \theta_{v} = 24.64°$ Abajo de la horizontal.
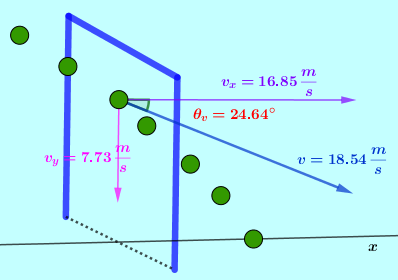
e)Cuál es la altura máxima que adquiere el balón en su trayectoria?. En la altura máxima la $\color{#0000FF} v_y=0$.
$\color{#0000FF} \quad {\color{Red}\bcancel {{\color{blue}v_y}}} = v_0 Sen \theta_{0} - gt$ $\color{#0000FF} 0 = v_0 Sen \theta_{0} - gt$ $\Rightarrow$ $\color{#0000FF} t=\dfrac {v_0 Sen \theta_{0}}{g}$
$\color{#0000FF} t=\dfrac {19.46 Sen {30°}}{9.81}$ $\Rightarrow$ $\color{#FF0000} t=0.99 s$ Tiempo que toma el balón desde que sale hasta alcanzar la altura máxima. Tiempo que remplazamos en ecuación de posición ($\color{#0000FF} y$); así obtenemos el valor de la altura máxima. $\color{#0000FF} y = {\color{Red}\bcancel {{\color{blue}y_0}}} + (v_0 Sen \theta_{0})t - \dfrac {1}{2}gt^2$
$\color{#0000FF} y_{max} = (19.46 Sen 30)0.99 - \dfrac {1}{2}(9.81)0.99^2$ [[$y_{max} = 4.83m$]]
f) Si la portería no tiene malla y es gol, cual es el alcance máximo horizontal. El balón sale a la altura del piso $\color{#0000FF} y_0 = 0$, cae a la misma altura $\color{#0000FF} y=0$; remplazamos en la ecuación de posición $\color{#0000FF} y$; despejamos el tiempo: $\color{#0000FF} \quad {\color{Red}\bcancel {{\color{blue}y}}} = {\color{Red}\bcancel {{\color{blue}y_0}}} + (v_0 Sen \theta_{0})t - \dfrac {1}{2}gt^2$
$\color{#0000FF} 0 = 0 + (v_0 Sen \theta_{0})t - \dfrac {1}{2}gt^2$ $\Rightarrow$ $\color{#0000FF} (v_0 Sen \theta_{0})t = \dfrac {1}{2}gt^2$
$\color{#0000FF} (v_0 Sen \theta_{0}) = \dfrac {1}{2}gt$ $\color{#0000FF} t = \color{#0000FF} \dfrac {2v_0 Sen \theta_{0}}{g}$ $\Rightarrow$ $\color{#0000FF} t = \dfrac {2(19.46) Sen {30}}{9.81}$
$\color{#FF0000} t = 1.98 s$ Es el tiempo que dura el balón desde que sale del piso y vuelve a caer al piso a la misma altura. Tiempo que remplazamos en la ecuación de posición $\color{#0000FF} x$ para obtener el alcance horizontal máximo en este caso particular.
$\color{#0000FF} x = {\color{Red}\bcancel {{\color{blue}x_0}}} + v_{0}(Cos\theta_{0})t$ $\Rightarrow$ $\color{#0000FF} x_{max} = {19.46}(Cos{30})1.98$
$\color{#FF0000} x_{max} = 33.37 m$
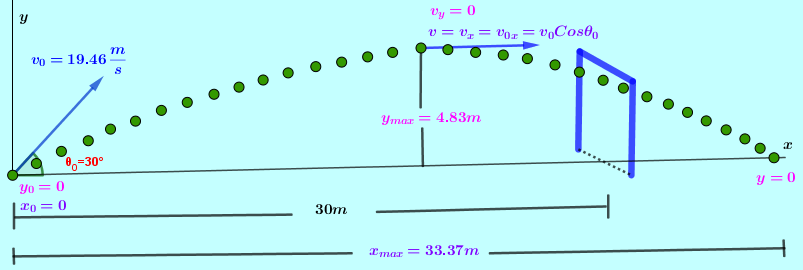
Para el estudiante:
g) Para que el balón pegue en el travesaño (palo horizontal) con qué velocidad debe ser pateado? R// $\color{#FF0000} v_0 = 19.73\dfrac {m}{s}$
h) Si el portero se encuentra $\color{#0000FF} 3m$ adelante de la portería, salta y atrapa el balón. ¿A qué altura lo atrapa? R// $\color{#FF0000} y = 3.01m$
i) Bajo las condiciones del punto (g), si el balón rebota hacia la cancha por el mismo plano sin pérdida de energía y cae al piso a $\color{#FF0000} 20 \ m$ adelante de la portería. ¿ Con que ángulo o ángulos respecto de la horizontal pudo haber rebotado el balón?.
R// $\color{#FF0000} \theta_0 = 73.35° $ R// $\color{#FF0000}\theta_0 = 10.34°$
j) Si en el instante en que el balón rebota en el travesaño con un ángulo de $\color{#0000FF} 73.35°$ respecto de la horizontal, el portero sale corriendo desde una distancia de $\color{#0000FF} 3m$ adelante de la portería con una velocidad constante y patea hacia adelante el balón a
una altura sobre el piso de $\color{#0000FF} 1m$. Determine la velocidad constante del portero. R// $\color{#FF0000} v = 4.52\dfrac {m}{s}$
Escena interactiva, diseñada por Yorman Guillén SalazarYorman Guillén Salazar es autor de la red GeoGebra quien publico la escena interactiva "Movimiento Parabólico".
a) Ubicando los deslizadores para una velocidad inicial $\color{#0000FF} v_i$ en $\color{#0000FF} 40\dfrac {m}{s}$, un ángulo en $\color{#0000FF} 30°$ y el tiempo en $\color{#0000FF} 0s$. Determine aplicando los modelos matemáticos la distancia horizontal que recorre la bola. La altura máxima y la velocidad con la cual la bola impacta el carro tanque.
b) Compare los resultados con los de la escena interactiva.
c) Realice los pasos $\color{#008000} (a)$ y $\color{#008000} (b)$ para una velocidad inicial de $\color{#0000FF} 40\dfrac {m}{s}$, un ángulo $\color{#0000FF} 60°$ y $\color{#0000FF} t=0$.
En la escena interactiva el proyectil es lanzado desde una altura, con una velocidad a un ángulo determinado por los deslizadores.
a) Ubique el deslizador de altura inicial en $4m$, el deslizador de velocidad inicial en $\color{#0000FF} 12\dfrac {m}{s}$ y el deslizador de ángulo inicial en $\color{#0000FF} 0°$.
b) la altura máxima alcanzada por el proyectil medida desde el piso. Determine la velocidad con la cual el proyectil impacta el piso. Determine el alcance horizontal del proyectil. Determine el tiempo que le toma al proyectil entre la parte más alta de la trayectoria y el momento en que toca el piso.
c) Compare los resultados obtenidos con los desarrollados en en la escena interactiva.
d) Realice el pasos (a), (b), (c) para una altura inicial de $\color{#0000FF} 3m$, una velocidad inicial de $\color{#0000FF} 12\dfrac {m}{s}$ a un ángulo de $\color{#0000FF} 45°$.
Ejercicio 3.7:
El jugador de basquetbol lanza el balón a la cesta con una velocidad de $\color{#0000FF} 42 \dfrac {ft}{s}$ con un ángulo de $\color{#0000FF} 50°$ arriba de la horizontal. El balón tarda en llegar a la cesta $\color{#0000FF} 1.86 s$. Determine (a) la distancia horizontal de la que fue lanzado el balón. (b) La altura de la canasta medida desde el piso si el balón se lanzo a una altura de $\color{#0000FF} 5.87 ft$. (c) A que otro ángulo inicial entrará el balón en la cesta, lanzándolo desde la misma posición y la misma velocidad inicial? (d) Determine la velocidad con la que el balón entra en la cesta con el ángulo encontrado.
Solución:

(a) $\color{#0000FF} x= (42 Cos 50°)1.86$ $\color{#FF0000} x= 50.21 ft $
(b) $\color{#0000FF} y= (42 Sen 50°)1.86 - \dfrac {1}{2}32.2 (1.86^2)$ $\color{#FF0000} y= 4.14 ft $ Medido desde la mano del jugador.
$\color{#0000FF} y= 5.87 + 4.14$ $\color{#FF0000} y= 10.01 ft $ Medido desde el piso.
(c) Determinamos la ecuación de la trayectoria $\color{#0000FF} y=F_{(x)}$
$\color{#0000FF} x= (v_0 Cos \theta _0 )t$ $\color{#0000FF} y= (v_0 Sen \theta _0 )t - \dfrac {1}{2}gt^2$
$\color{#0000FF} t= \dfrac {x}{v_0 Cos \theta _0}$
$\color{#0000FF} y= ({\color{Red}\cancel {{\color{blue} {v_0}}}} Sen \theta _0 ){(\dfrac {x}{{\color{Red}\cancel {{\color{blue} {v_0}}}} Cos \theta _0})} - \dfrac {1}{2}g{(\dfrac {x^2}{v_0^2 Cos^2 \theta _0})}$
$\color{#0000FF} y= (tg \theta_0)x -\dfrac {gx^2}{2v_0^2} Sec^2 \theta_0$
$\color{#0000FF} \dfrac {gx^2}{2v_0^2} Sec^2 \theta_0 - (tg \theta_0)x + y= 0$
$\color{#0000FF} Sec^2 \theta = tg^2 \theta + 1$
$\color{#0000FF} \dfrac {gx^2}{2v_0^2} (tg^2 \theta_0 + 1) - (tg \theta_0)x + y= 0$
$\color{#0000FF} \dfrac {gx^2}{2v_0^2} tg^2 \theta_0 - (tg \theta_0)x + (\dfrac {gx^2}{2v_0^2} + y) = 0$
$\color{#0000FF} \dfrac {32.2(50.21^2)}{2(42^2)} tg^2 \theta_0 - (tg \theta_0)50.21 + (\dfrac {32.2(50.21^2)}{2(42^2)} +$
$\color{#0000FF} 4.14) = 0$
$\color{#0000FF} 23.01 tg^2 \theta_0 - 50.21 tg \theta_0 + 27.15 = 0$
• Ecuación cuadrática para $\color{#0000FF} tg \theta_0$ Resolvemos:
$\color{#0000FF} tg \theta_0 = 1.19$ $\color{#0000FF} \theta_0 = tg^{-1} 1.19$ $\color{#FF0000} \theta_0 = 50°$
$\color{#0000FF} tg \theta_0 = 0.9888$ $\color{#0000FF} \theta_0 = tg^{-1} 0.9888$ $\color{#FF0000} \theta_0 = 44.68°$
• Manipulando el deslizador de ángulo en la escena interactiva se puede comprobar el rasultado.
(d) $\color{#0000FF} v_x=42 Cos 44.68°$ $\color{#0000FF} v_x=29.86$ $\color{#FF0000} \overrightarrow v_x=29.86 \dfrac {ft}{s} \rightarrow$
• Para $\color{#0000FF} v_y$ necesitamos el valor de $\color{#0000FF} t$.
$\color{#0000FF} t= \dfrac {x}{v_0 Cos \theta _0}$ $\color{#0000FF} t= \dfrac {50.21}{42 Cos 44.68°}$ $\color{#FF0000} t=1.68 s$
• Manipulando los deslizadores en la escena interactiva se puede comprobar el resultado.
$\color{#0000FF} v_y= (42 Sen 44.68)1.68 - 32.2(1.68)$ $\color{#0000FF} v_y=-24.60$
$\color{#FF0000} \overrightarrow v_y=24.60 \dfrac {ft}{s} \downarrow$
$\color{#0000FF} v= \sqrt {29.86^2 + 24.60^2}$ $\color{#FF0000} v= 38.70\dfrac {ft}{s}$
$\color{#0000FF} \theta_v=tg^{-1} [\dfrac {24.60}{29.86}]$ $\color{#FF0000} \theta_v= \searrow 39.47°$
$\color{#FF0000} \overrightarrow v=38.70 \dfrac {ft}{s} \searrow 39.47°$
• Para el estudiante: Determine la $\color{#0000FF} v_0$ a la que se debe lanzar el balón para lograr la cesta si la distancia horizontal del jugador a la cesta es de $\color{#0000FF} 25 ft$, la altura de la cesta es $\color{#0000FF} 10 ft$, el balón se lanza a la altura de $\color{#0000FF} 7 ft$ a un ángulo de $\color{#0000FF} 30°$. $\color{#0000FF} R//:$ $\color{#FF0000} v_0= 36.70 \dfrac {ft}{s}$
• Manipulando los deslizadores compruebe el resultado.
Todos los cuerpos en la naturaleza buscan que su movimiento sea a lo largo de una línea recta. Muchas veces estos cuerpos se encuentran sometidos a efectos externos que los obligan a tomar trayectorias curvas. En cada punto de la trayectoria el cuerpo tiende a salir en línea recta tangente a la trayectoria que describe.
En la gráfica hemos tomado varios puntos de la trayectoria de una partícula que se mueve de izquierda a derecha. En cada punto de la trayectoria la velocidad la dibujamos tangente a ésta trayectoria.
ponemos sobre la partícula un sistema de ejes móviles, mutuamente ortogonales (perpendiculares), llamados eje tangencial $\color{#0000FF} t_g$, eje normal $\color{#0000FF} n$, eje binormal $\color{#0000FF} b$, que viajan con la partícula.
Para facilitar la observación de los ejes móviles en la FIGURA3D, los hemos dibujado con colores: El eje tangencial $\color{#0000FF} t_g$ color Fucsia, el eje normal $\color{#0000FF} n$ color azul, el eje binormal $\color{#0000FF} b$ color verde.
Por ser la velocidad tangente a la trayectoria dibujamos un eje en la misma dirección de la velocidad (tangente a la trayectoria en cada punto) llamado eje tangencial $t_g$, que es positivo en el sentido de la velocidad y negativo en sentido contrario (la velocidad será siempre positiva por ser el eje tangencial positivo en el sentido de la velocidad.
Perpendicular al eje tangencial y alineado con el centro de la curva que genera la trayectoria de la partícula dibujamos un eje llamado eje normal $n$ que es positivo hacia adentro de la curva y negativo hacia afuera de la curva.
Perpendicular al eje tangencial $t_g$ y a la vez perpendicular al eje normal $n$ dibujamos un eje llamado eje binormal $b$ . Ponemos la palma de la mano derecha sobre el eje tangencial $t_g$, cerramos los dedos buscando el eje normal $n$; observamos el dedo pulgar que nos indica la dirección del eje binormal y su sentido positivo.
$\color{#0000FF} \blacktriangleright\hspace{0.2cm}$ Eje tangencial: Tiene la misma dirección de la velocidad y el sentido positivo es el sentido de la velocidad.
$\color{#0000FF} \blacktriangleright\hspace{0.2cm}$ Eje normal: Tiene dirección perpendicular al eje tangencial pasando por el centro de la curva y es positivo hacia el centro de la curva.
$\color{#0000FF} \blacktriangleright\hspace{0.2cm}$ Eje binormal: Perpendicular al eje tangencial y al eje normal. Ponemos la palma de la mano derecha sobre el eje tangencial $t_g$, cerramos los dedos hacia el eje normal $n$; el dedo pulgar indica la dirección y sentido positivo.
La partícula en cada punto de la trayectoria tiene los ejes ($\color{#0000FF} t_g, n, b$) montados sobre ella.
Por definición, la aceleración es el cambio del vector velocidad respecto de un cambio en el tiempo. La aceleración es por tanto un vector $\color{#0000FF} \overrightarrow {a} = \dfrac {d \overrightarrow {v}}{dt}$
Como la aceleración es el cambio del vector velocidad y el vector velocidad por ser un vector tiene magnitud y dirección, ejemplo: $\color{#0000FF} \overrightarrow {v} = 60 \dfrac {m}{s}\measuredangle 30°$,magnitud: $\color{#0000FF} v = 60 \dfrac {m}{s}$, dirección: $\color{#0000FF} \measuredangle 30°$
Así entonces aparece aceleración cuando cambia la magnitud de la velocidad y aparecerá aceleración cuando cambie la dirección de la velocidad. Analizaremos por separado cada uno estos cambios de la velocidad.
$\blacktriangleright\hspace{0.2cm}$ Cambio en la Magnitud de la Velocidad $a_{t_g}$El cambio en la magnitud de la velocidad (cambio en la rapidez) respecto del tiempo es: $\color{#0000FF} a_{t_g} = \dfrac {dv}{dt} = \dfrac {v-v_{0}}{t-t_{0}}$. Ésta expresión nos indica que se da un cambio en la velocidad debido a un cambio en su magnitud y trae como consecuencia que aparece una aceleración. El cambio en la magnitud de la velocidad se da a lo largo del eje tangencial que es donde esta la magnitud de la velocidad, por ello esta aceleración que aparece se llama aceleración tangencial.
Cuando la partícula cambia la magnitud de la velocidad de menor a mayor valor, la aceleración tangencial tiene el mismo sentido de la velocidad (sobre el eje tangencial sentido positivo). La partícula viaja cada vez mas rápido (acelerando). punto A
Cuando la partícula cambia la magnitud de la velocidad de mayor a menor valor, la aceleración tangencial tiene sentido contrario a la velocidad (sobre el eje tangencial sentido negativo) y la partícula estará viajando cada vez mas despacio (desacelerando). punto B
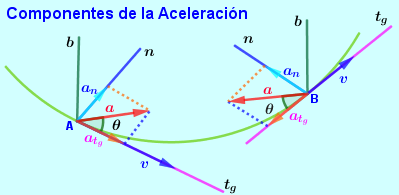
Hagamos el siguiente análisis; cuando viajamos como pasajeros en autobús intermunicipal y vamos por una carretera que tiene muchas curvas, sentimos que nos movemos en cada curva para los lados del asiento. Cuando la curva es a la izquierda sentimos que nos movemos a la derecha, si la curva es a la derecha sentimos que nos movemos a la izquierda. Esto es una pura sensación, porque lo que en realidad sucede es que el vehículo cada ves que toma una curva nos mueve a nosotros hacia la curva (nos hala hacia adentro de la curva). Nosotros vamos viajando en el vehículo en el mismo sentido de su velocidad y de repente el autobús nos cambia el sentido de la velocidad produciendo el efecto analizado.
Ese cambio en la dirección de la velocidad provoca en nosotros ese movimiento lateral que es perpendicular al eje tangencial (es decir, que el efecto es sobre el eje normal) y como ya mencionamos nos hala hacia adentro de la curva y que físicamente se llama aceleración normal. El hecho de que nos hale hacia adentro de la curva indica que la aceleración normal es siempre positiva (el eje normal es positivo hacia adentro de la curva).
Si la curva es muy cerrada (el radio de la curva es pequeño) se corre el riesgo de volcamiento del vehículo dependiendo de la velocidad. Si la curva es amplia (el radio de la curva es grande) es posible viajar a una mas alta velocidad. Podemos afirmar entonces que si se aumenta la velocidad en una curva se corre el riesgo de volcamiento (aumenta la aceleración normal), si se reduce el radio en una curva aumenta la aceleración normal.Así, la aceleración normal es directamente proporcional a la velocidad e inversamente proporcional al radio de curvatura. $\color{#0000FF} a_n \propto \dfrac {v}{r}$
Para lograr una ecuación (quitar la proporcionalidad y lograr una igualdad) se llaga a que la $\color{#0000FF} a_n = \dfrac {v^2}{r}$
$v^2$ es positivo y el radio de una curva siempre es positivo, esto confirma que la aceleración normal $a_n$ es siempre positiva (hacia adentro de la curva). Punto A, punto B
Una vez tenemos el vector aceleración tangencial $\overrightarrow a_{t_g}$ y el vector aceleración normal $\overrightarrow a_{n}$, podemos determinar el vector aceleración de la partícula que es la suma de estos vectores $\color{#0000FF} \overrightarrow {a} = \overrightarrow a_{t_g} + \overrightarrow a_{n}$. Entre la $\color{#0000FF} \overrightarrow a_{t_g}$ y la aceleración $\color{#0000FF} \overrightarrow a_{n}$ existe un ángulo de $\color{#0000FF} 90°$ esto permite que por la ecuación de Pitágoras podamos determinar la magnitud de
la aceleración de la partícula $\color{#0000FF} a =\sqrt {a_{t_g}^2 + a_{n}^2}$ El ángulo de la aceleración respecto del eje tangencial es $\color{#0000FF} \theta = tag^{-1}\dfrac {a_n}{a_{t_g}}$
La magnitud de la velocidad puede cambiar respecto del tiempo y este cambio se da sobre el eje tangencial entonces aparece la aceleración tangencial. $\color{#0000FF} a_{t_g} = \dfrac {dv}{dt} = \dfrac {v-v_{0}}{t-t_{0}}$
Cuando cambia la dirección de la velocidad respecto del tiempo este cambio en la dirección de la velocidad produce efecto sobre el eje normal entonces aparece la aceleración normal. $\color{#0000FF} a_n = \dfrac {v^2}{r}$
Sobre el eje binormal no surten efectos de los cambios en la magnitud ni en la dirección de la velocidad por lo que la aceleración sobre el eje binormal es cero. $\color{#0000FF} a_b = 0$
Ejercicio 3.8: Una partícula se mueve por una trayectoria curva y en un instante determinado el radio de curvatura es de $\color{#0000FF} 4m$, su rapidez es de $\color{#0000FF} 8 \dfrac {m}{s}$. La aceleración de la partícula es de $\color{#0000FF} 25\dfrac {m}{s^2}$. Hallar las componentes de la aceleración y determinar el ángulo de la aceleración respecto del eje tangencial en ese instante, si se sabe que la partícula se está deteniendo. El enunciado no incluye gráfica.
Solución: El primer paso es realizar el grafico que revele todo el contenido literal de enunciado.
Hemos dibujado la aceleración tangencial en sentido contrario a la velocidad (sobre el eje tangencial sentido negativo) porque la partícula se está deteniendo.
Aceleración normal $\color{#0000FF} a_n = \dfrac {v^2}{r}$ $\Rightarrow$ $\color{#0000FF} a_n = \dfrac {8^2}{4}$ $\Rightarrow$ $\color{#FF0000} a_n = 16\dfrac {m}{s^2}$
Aceleración tangencial $\color{#0000FF} a^2 = a_{tg}^2 + a_{n}^2$ $\Rightarrow$ $\color{#0000FF} a_{tg}^2 = a^2 - a_{n}^2$
$\color{#0000FF} a_{t_g} = \pm \sqrt {{a}^2 - {a_n}^2}$ $\color{#0000FF} a_{t_g} = \pm \sqrt {25^{2} - 16^{2}}$ $\Rightarrow$ $\color{#FF0000} a_{t_g} = - 19.21 \dfrac {m}{s^2}$
Hemos tomado el signo negativo en razón a que el enunciado dice que la partícula se está deteniendo
Ángulo de la aceleración $\color{#0000FF} \theta = tag^{-1}\dfrac {a_n}{a_{t_g}}$ $\color{#0000FF} \theta = tag^{-1}\dfrac {16}{19.21}$ $\color{#FF0000} \theta = 39.79°$
Existe movimiento dependiente cuando el movimiento de un cuerpo depende del movimiento de otro cuerpo. En éste curso de física mecánica estudiaremos el movimiento dependiente cuando existen cuerpos que están unidos entre sí por medio de cuerdas que pasan por poleas.
El estudio del movimiento dependiente es importante como herramienta en la solución de muchos ejercicios porque permite relacionar la posición, la velocidad y la aceleración entre cuerpos conectados entre si, permitiendo minimizar incógnitas en las ecuaciones.
Para éste curso se consideraran las cuerdas inextensibles (que no se estiran), es decir que su longitud no cambia (la longitud de la cuerda es constante).
En muchos ejercicios aparecen poleas que pueden estar fijas o ser móviles. Para el desarrollo de éste curso se consideraran las poleas perfectamente lisas permitiendo que la tensión de las cuerdas que pasan sobre ellas sea la misma en cada punto de la cuerda.
En éste tema de movimiento dependiente no aparecen los ejes $\color{#0000FF} x,y,z,t_g,n,b$. En éste tema ubicaremos un nivel de referencia en una polea figa o un muro, un techo que este fijo respecto del sistema que vamos a analizar, con el ánimo de verificar si los cuerpos objeto de análisis se acercan o se alejan de éste nivel de referencia.
Por convención diremos que si un cuerpo se aleja del nivel de referencia su movimiento es positivo y si el cuerpo se acerca al nivel de referencia su movimiento será negativo. Los signos positivo y negativo de éste tema no son algebraicos ( éstos signos son de se aleja o se acerca al nivel de referencia) no son signos compatibles con los signos algebraicos de los ejes $\color{#0000FF} x,y,z,t_g,n,b$, por lo que si por alguna razón los resultados obtenidos en el análisis de movimiento dependiente tienen que ser llevados a un sistema de ejes $\color{#0000FF} x,y,z,t_g,n,b$, se llevaran las relaciones encontradas como una relación simple y sin signos; ya será el analista del ejercicio quien dirá dentro de su modelo matemático con que signo entra en sus ecuaciones.
Para el caso de la gráfica nos ubicamos en la polea fija y desde el centro de la polea tomado como nivel de referencia tomamos la distancia hasta cada uno de los bloques. Del nivel de referencia al bloque $\color{#0000FF} A$ se llama $\color{#0000FF} S_A$, del nivel de referencia al bloque $\color{#0000FF} B$ se llama $\color{#0000FF} S_B$. Ahora modelamos una ecuación que de razón de la longitud de la cuerda. $\color{#0000FF} S_A + \widehat {CD} + S_B = L$ La longitud de la cuerda es la distancia $\color{#0000FF} S_A$ más el pedacito de cuerda en el arco $\color{#0000FF} \widehat {CD}$ de la polea, más la distancia $\color{#0000FF} S_B$.
Aplicamos a cada término de la ecuación de longitud de la cuerda $\color{#0000FF} S_A + \widehat {CD} + S_B = L$ el concepto de cambio:
$\color{#0000FF} \Delta S_A + \Delta \widehat {CD} + \Delta S_B = \Delta L$ Como la cuerda es inextensible (su longitud es constante), el cambio en la longitud de la cuerda es cero $\color{#0000FF} \Delta L = 0$
Por el arco $\color{#0000FF} \widehat {CD}$ pasa cuerda, pero siempre es la misma distancia de cuerda, es decir que el arco $\color{#0000FF}\widehat {CD}$ no cambia, entonces $\color{#0000FF} \Delta \widehat {CD} = 0$
La posición del bloque (A) puede cambiar, es decir que la distancia $S_A$ puede cambiar, sea alejándose o acercándose al nivel de referencia según el caso particular que se esté analizando: $\color{#0000FF} \Delta S_A$ es variable.
La posición del bloque (B) puede cambiar, es decir que la distancia $S_B$ puede cambiar, sea alejándose o acercándose al nivel de referencia según el caso particular que se esté analizando: $\color{#0000FF} \Delta S_B$ es variable.
La ecuación de la cuerda queda $\color{#0000FF} \Delta S_A + {\color{Red}\bcancel {{\color{blue}\Delta \widehat {CD}}}} + \Delta S_B = {\color{Red}\bcancel {{\color{blue}\Delta L}}}$
$\color{#0000FF} \Delta S_A + \Delta S_B = 0$ $\color{#0000FF} \Rightarrow$ $\color{#FF0000} \Delta S_A = - \Delta S_B$ Entonces, para éste caso en particular diremos que:
• Cuando el bloque $\color{#0000FF} A$ se aleja de su nivel de referencia una distancia, el bloque $\color{#0000FF} B$ se acerca a su nivel de referencia la misma distancia.
Recordemos que el signo positivo en el tema de movimiento dependiente significa que el cuerpo analizado se aleja de su nivel de referencia y el signo negativo significa que el cuerpo analizado se acerca a su nivel de referencia.
Ahora podemos dividir ésta ecuación $\color{#0000FF} \Delta S_A = - \Delta S_B$ en un cambio en el tiempo $\color{#0000FF} \Delta {t}$: $\Rightarrow$ $\color{#0000FF} \dfrac {\Delta S_A}{\Delta t} = - \dfrac {\Delta S_B}{\Delta t}$ Recordar que $\color{#0000FF} \dfrac {\Delta S_A}{\Delta t} = v_A$ y que $\color{#0000FF} \dfrac {\Delta S_B}{\Delta t} = v_B$ $\Rightarrow$ $\color{#FF0000} v_A = - v_B$ Entonces diremos en éste caso en particular que:
• Cuando el bloque $\color{#0000FF} A$ se aleja del nivel de referencia a una rapidez, el bloque $\color{#0000FF} B$ se acerca a su nivel de referencia a la misma rapidez.
Hacemos $\color{#0000FF} \Delta v_A = - \Delta v_B$ dividimos en un cambio en el tiempo $\color{#0000FF} \Delta {t}$: $\Rightarrow$ $\color{#0000FF} \dfrac {\Delta v_A}{\Delta t} = - \dfrac {\Delta v_B}{\Delta t}$ Recordar que $\color{#0000FF} \dfrac {\Delta v_A}{\Delta t} = a_A$ y que $\color{#0000FF} \dfrac {\Delta v_B}{\Delta t} = a_B$ $\Rightarrow$ $\color{#0000FF} a_A = - a_B$ Entonces diremos en éste caso en particular que:
• Cuando el bloque $\color{#0000FF} A$ se aleja del nivel de referencia a una aceleración, el bloque $\color{#0000FF} B$ se acerca a su nivel de referencia a la misma aceleración.
Así para éste caso en particular obtenemos las siguientes relaciones de movimiento dependiente entre los bloques $\color{#0000FF} A$ y el bloque $\color{#0000FF} B$:
Posición $\color{#0000FF} \Delta S_A = - \Delta S_B$
Velocidad $\color{#0000FF} v_A = - v_B$
Aceleración $\color{#0000FF} a_A = - a_B$
Nota: Al llevar éstas relaciones a ejercicios que implican sistemas de referencia diferente al concepto de se aleja o se acerca a niveles de referencia, los signos no se llevan. Es decir que las relaciones entre el bloque $\color{#0000FF} A$ y el bloque $\color{#0000FF} B$ quedan de la siguiente manera:
Posición $\color{#0000FF} \Delta S_A = \Delta S_B$ El cambio de posición del bloque $\color{#0000FF} A$ es igual al cambio de posición del bloque $\color{#0000FF} B$.
Velocidad $\color{#0000FF} v_A = v_B$ La velocidad del bloque $\color{#0000FF} A$ es igual a la velocidad del bloque $\color{#0000FF} B$.
Aceleración $\color{#0000FF} a_A = a_B$ La aceleración del bloque $\color{#0000FF} A$ es igual a la aceleración del bloque $\color{#0000FF} B$.
En el sistema existe una polea móvil que por ésta condición no sirve de nivel de referencia.
El movimiento del centro de la polea móvil es el mismo movimiento del bloque $\color{#0000FF} B$.
El nivel de referencia lo hacemos en el centro de la polea fija.
La posición del bloque $\color{#0000FF} B$ se llama $\color{#0000FF} S_B$ y es la distancia desde el centro de la polea fija hasta el centro de la polea móvil.
La porción de cuerda que se encuentra por encima del centro de la polea fija hasta el techo es constante.
la porción de cuerda que se encuentra en el arco $\color{#0000FF} \widehat {CD}$ y la porción de cuerda sobre el arco $\color{#0000FF} \widehat {EF}$ son constantes.
Todas éstas porciones de cuerda que permanecen constantes durante el movimiento de los bloques, por su condición de constantes no sufren cambios; es decir que los cambios en éstas porciones de cuerda es cero y desde ya podemos tomar la decisión de no tenerlos en cuenta la ecuación de longitud de la cuerda, la cual la podemos escribir como: $\color{#0000FF} S_A + 2S_B = L$
$\color{#0000FF} \Delta S_A + \Delta 2S_B = \Delta L$ $\Rightarrow$ $\color{#0000FF} \Delta S_A + \Delta 2S_B = 0$ $\Rightarrow$ $\color{#0000FF} \Delta S_A = - \Delta 2S_B$
Significa que cuando el bloque $\color{#0000FF} A$ se aleja de su nivel de referencia una distancia, el bloque $\color{#0000FF} B$ se acerca la mitad de esa distancia a su nivel de referencia.
Para la velocidad tenemos: $\color{#0000FF} v_A = - 2v_B$
Significa que cuando el bloque $\color{#0000FF} A$ se aleja de su nivel de referencia una velocidad, el bloque $\color{#0000FF} B$ se acerca a la mitad de esa velocidad a su nivel de referencia.
Para la aceleración tenemos: $\color{#0000FF} a_A = - 2a_B$
Significa que cuando el bloque $\color{#0000FF} A$ se aleja de su nivel de referencia una aceleración, el bloque $\color{#0000FF} B$ se acerca a la mitad de esa aceleración a su nivel de referencia.
Nota: Al llevar éstas relaciones a ejercicios que implican sistemas de referencia diferente al concepto de se aleja o se acerca a niveles de referencia, los signos no se llevan. Es decir que las relaciones entre el bloque $\color{#0000FF} A$ y el bloque $\color{#0000FF} B$ quedan de la siguiente manera:
Posición $\color{#0000FF} \Delta S_A = 2\Delta S_B$ El cambio de posición del bloque $\color{#0000FF} A$ es igual al doble del cambio en la posición del bloque $\color{#0000FF} B$.
Velocidad $\color{#0000FF} v_A = 2 v_B$ La velocidad del bloque $\color{#0000FF} A$ es igual al doble de la velocidad del bloque $\color{#0000FF} B$.
Aceleración $\color{#0000FF} a_A = 2 a_B$ La aceleración del bloque $\color{#0000FF} A$ es igual al doble de la aceleración del bloque $\color{#0000FF} B$.
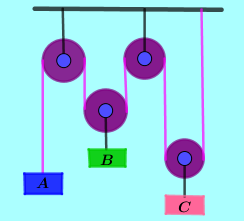
Determine la aceleración del bloque $\color{#0000FF} B$ si el bloque $\color{#0000FF} A$ se mueve hacia abajo con una aceleración de $\color{#0000FF} 2\dfrac {m}{s^2}$ y el bloque $\color{#0000FF} C$ se mueve hacia arriba con aceleración de $\color{#0000FF} 1\dfrac {m}{s^2}$.
Solución: El nivel de referencia es el centro de las poleas fijas.
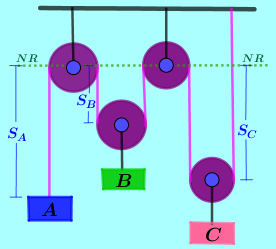
Desde el nivel de referencia tomamos la posición de cada uno de los bloques; logramos la ecuación para la cuerda omitiendo las porciones de cuerda que son constantes por el hecho de no reportar cambios cuando los cuerpos se desplazan:
$\color{#0000FF} S_A + 2S_B + 2S_C = L$ aplicamos el concepto de cambio
$\color{#0000FF} \Delta S_A + 2\Delta S_B + 2\Delta S_C = {\color{Red}\bcancel {{\color{blue}\Delta L}}}$
$\color{#0000FF} \Delta S_A + 2\Delta S_B + 2\Delta S_C = 0$
Si dividimos por $\color{#0000FF} \Delta t$ obtenemos la relación para las velocidades:
$\color{#0000FF}v_A + 2v_B + 2v_C = 0$ si dividimos un cambio de la velocidad respecto de un cambio en el tiempo $\color{#0000FF} \Delta t$ aparece la relación para la aceleración:
$\color{#0000FF} a_A + 2a_B + 2a_C = 0$ Remplazamos los valores dados en el
enunciado interpretando con los signos de se aleja $\color{#0000FF} (+)$ y se acerca $\color{#0000FF} (-)$, así obtenemos la aceleración del bloque $\color{#0000FF} B$:
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue}2}}} + 2a_B - {\color{Red}\bcancel {{\color{blue}2(1)}}} = 0$ $\Rightarrow$ $\color{#FF0000} a_B = 0 \dfrac {m}{s^2}$
Para el estudiante.
• Si el sistema parte del reposo, cual es la posición de cada bloque pasados dos segundos? R//
$\color{#FF0000} S_A = 4m$ alejándose del nivel de referencia
$\color{#FF0000} S_B = 0m$
$\color{#FF0000} S_C = 2m$ acercándose del nivel de referencia
• Halle la velocidad de cada bloque para $\color{#0000FF} t =4s$. R//
$\color{#FF0000} v_A = 8 \dfrac {m}{s}$ alejándose del nivel de referencia
$\color{#FF0000} v_B = 0 \dfrac {m}{s}$
$\color{#FF0000} v_A = 4 \dfrac {m}{s}$ acercándose del nivel de referencia
•Si la posición del bloque (B) es de $1.5m$ luego de liberarse el sistema cual es la rapidez de cada boque? R//
$\color{#FF0000} v_A = 3.46 \dfrac {m}{s}$ $\color{#FF0000} v_B = 0$ $\color{#FF0000} v_C = 1:73 \dfrac {m}{s}$
En muchos casos vamos a necesitar saber la cinemática (posición, velocidad, aceleración) de un cuerpo que se mueve respecto de otro cuerpo que se mueve respecto de un marco de referencia fijo, como cuando queremos saber la cinemática del émbolo de un motor que se mueve por la acción de la biela, que a su vez se mueve por la acción de la manivela.
En el sistema mostrado la manivela tiene movimiento circular, la biela tiene un movimiento llamado movimiento plano (tiene movimiento de rotación y translación al mismo tiempo) y la punta de la biela donde se ubica el embolo tiene movimiento rectilíneo a lo largo de la guía.
Primero se analiza el movimiento del pasador manivela-biela visto desde un marco de referencia fijo y luego se le suma vectorialmente el movimiento de la biela referido al marco de referencia móvil que es el pasador manivela-biela
Para éste curso de física mecánica consideraremos solamente para movimiento relativo aquellos sistemas que se mueven sobre marcos de referencia en translación. en un curso de dinámica del cuerpo rígido abordaremos movimiento relativo para el caso de sistemas de referencia giratorios.
$\blacktriangleright\hspace{0.2cm}$ Posición
Las partículas $\color{#0000FF} A$ y $\color{#0000FF} B$ se mueven por trayectorias arbitrarias. Las posiciones absolutas serán $\color{#0000FF} \overrightarrow r_A$ y $\color{#0000FF} \overrightarrow r_B$ respectivamente por ser obtenidas desde el marco de referencia fijo $\color{#0000FF} x,y,z$. El vector $\color{#0000FF} \overrightarrow r_{B/A}$ es la posición relativa de $\color{#0000FF} B$ visto desde $\color{#0000FF} A$ que porta un marco de referencia en translación $\color{#0000FF} x_1, y_1, z_1$. Por suma de vectores:
$\color{#008000} \overrightarrow r_B = \overrightarrow r_A + \overrightarrow r_{B/A}$
$\blacktriangleright\hspace{0.2cm}$ Velocidad
Si realizamos la derivada de la posición respecto del tiempo obtenemos la relación para las velocidades.
$\color{#0000FF} \dfrac {\overrightarrow r_B}{dt} = \dfrac {\overrightarrow r_A}{dt} + \dfrac {\overrightarrow r_{B/A}}{dt}$ $\color{#008000} \overrightarrow v_B = \overrightarrow v_A + \overrightarrow v_{B/A}$
$\blacktriangleright\hspace{0.2cm}$ Aceleración
Si realizamos la derivada de la velocidad respecto del tiempo obtenemos la relación para las aceleraciones.
$\color{#0000FF} \dfrac {\overrightarrow v_B}{dt} = \dfrac {\overrightarrow v_A}{dt} + \dfrac {\overrightarrow v_{B/A}}{dt}$ $\color{#008000} \overrightarrow a_B = \overrightarrow a_A + \overrightarrow a_{B/A}$
En la escena interactiva, el tren $\color{#0000FF} A$ sale de la ciudad $\color{#0000FF} A$, con velocidad constante, en el mismo instante el tren $\color{#0000FF} B$ sale de la ciudad $\color{#0000FF} B$ con velocidad constante. Determine la velocidad del tren $\color{#0000FF} B$ visto desde el tren $\color{#0000FF} A$, $\hspace{0.1cm} \color{#0000FF} v_{B/A}$, si los dos trenes se cruzan luego de una hora de viaje.
Solución:Conocemos de la escena interactiva las coordenadas del punto donde se cruzan, las posiciones iniciales de cada tren y la geometría del movimiento de cada uno de los trenes (movimiento rectilíneo con velocidad constante). Hallamos $\color{#0000FF} \overrightarrow v_A $ y $\color{#0000FF} \overrightarrow v_B$.
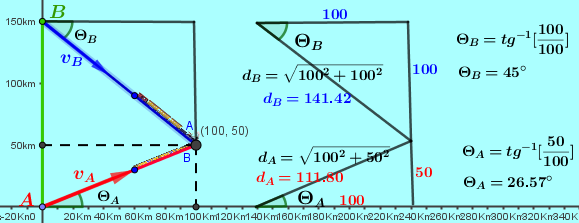
$\color{#0000FF} v_A= \dfrac {d_A}{t_A}$ $\color{#0000FF} v_A= \dfrac {111.80}{1}$ $\color{#0000FF} \overrightarrow v_A = 111.80 \nearrow 26.57° \dfrac {Km}{h}$
$\color{#0000FF} v_B= \dfrac {d_B}{t_B}$ $\color{#0000FF} v_B= \dfrac {141.42}{1}$ $\color{#0000FF} \overrightarrow v_B = 141.42 \searrow 45° \dfrac {Km}{h}$
$\color{#008000} \overrightarrow v_B = \overrightarrow v_A + \overrightarrow v_{B/A}$ $\color{#0000FF} \overrightarrow v_{B/A} = \overrightarrow v_B - \overrightarrow v_A$
$\color{#0000FF} v_{(B/A)_x} \rightarrow + v_{(B/A)_y} \uparrow = 141.42 \searrow 45°- 111.80 \nearrow 26.57°$
$\color{#0000FF} v_{(B/A)_x} = 141.42 Cos45° - 111.80 Cos26.57°$
$\color{#0000FF} v_{(B/A)_x} = 10$ $\color{#FF0000} \overrightarrow v_{(B/A)_x} = 10 \rightarrow \dfrac {Km}{h}$
$\color{#0000FF} v_{(B/A)_y} = -141.42 Sen45° - 111.80 Sen26.57°$
$\color{#0000FF} v_{(B/A)_y} = -150$ $\color{#FF0000} \overrightarrow v_{(B/A)_y} = 150 \downarrow \dfrac {Km}{h}$
$\color{#0000FF} v_{B/A} = \sqrt {10^2+150^2}=150.33$ $\color{#0000FF} \theta = tg^{-1} \dfrac {150}{10}=86.19°$
$\color{#FF0000} \overrightarrow v_{B/A} = 150.33 \searrow 86.19° \dfrac {Km}{h}$
Un punto se caracteriza por no tener dimensiones, es por ello que "los puntos no rotan".
Los puntos se pueden trasladar de un lugar a otro.
Observemos que en el análisis que realizamos de cinemática de la partícula siempre tomamos la masa de los cuerpos como si ésta estuviera concentrada en un punto llamado centro de gravedad. Con ello se pudo determinar Posición, Velocidad y Aceleración de dichos cuerpos según la gráfica que generaba la trayectoria de ese punto llamado centro de gravedad (Traslación Rectilínea como Movimiento Rectilíneo, Caída Libre, Traslación Curvilínea como Movimiento Parabólico).
Un cuerpo rígido es aquel cuerpo que tiene dimensiones y que para efectos de diferentes análisis sus dimensiones no cambian, es decir que éste cuerpo conserva su forma.
La mínima expresión de un cuerpo rígido son dos puntos y dos puntos definen una recta; así una recta es la mínima expresión de un cuerpo rígido. Cuando una recta está sobre un plano puede generar dos tipos de movimiento Rotación y traslación (Rotación pura, Traslación pura o Rotación y Traslación al mismo tiempo).
Para que exista movimiento angular se requiere de un cuerpo con dimensiones. Si un cuerpo está sobre un plano puede girar alrededor de un punto cualquiera del mismo cuerpo. Cada punto describe una
trayectoria circular.
En la práctica se presenta una analogía entre la cinemática de una partícula (Determinar Posición Lineal $\color{#0000FF} S$, velocidad lineal $\color{#0000FF} v$, aceleración lineal $\color{#0000FF} a$) y la cinemática angular (Determinar Posición angular $\color{#0000FF} \theta$, velocidad angular $\color{#0000FF} w$, aceleración angular $\color{#0000FF} \alpha$) de un cuerpo con dimensiones en un plano.
En este curso de Física Mecánica hablaremos de aceleración angular constante $\color{#0000FF} \alpha=Cte$, de tal manera que las ecuaciones que utilizamos para la cinemática de la partícula en su estructura son válidas para el movimiento angular utilizando la correspondiente simbología.
Cuando una línea rota su posición en un instante determinado queda definida por el ángulo $\color{#0000FF} \theta$ respecto de otra línea de referencia. El ángulo $\color{#0000FF} \theta$ se mide en radianes $\color{#0000FF} rad$.
El desplazamiento angular hace referencia al cambio en la posición angular:
Para Movimiento Rectilíneo de partícula con aceleración constante: $\color{#0000FF} s = s_0 + v_0t + \dfrac {1}{2}at^2$
Para Movimiento Angular con aceleración angular constante su analogía es : $\color{#0000FF} \theta = \theta_0 + w_0t + \dfrac {1}{2}\alpha t^2$
El desplazamiento angular se mide en radianes $\color{#0000FF} rad$.
Es el cambio de la posición angular $\color{#0000FF} \Delta\theta$ respecto de un cambio en el tiempo $\color{#0000FF} \Delta t$: $\color{#0000FF} w=\dfrac {d\theta}{dt}$ $\color{#0000FF} w=\dfrac {\Delta\theta}{\Delta t}$ $\color{#0000FF} w=\dfrac {\theta - \theta_0}{t - t_0}$
Para el movimiento Rectilíneo de partícula: $\color{#0000FF} v=v_0 + at$
Para Movimiento Angular con aceleración angular constante su analogía es: $\color{#0000FF} w=w_0 + \alpha t$
Para el movimiento Rectilíneo de partícula: $\color{#0000FF} v^2=v^2_0 + 2a(S - S_0)$
Para Movimiento Angular con aceleración angular constante su analogía es: $\color{#0000FF} w^2=w^2_0 + 2a(\theta - \theta_0) $
La velocidad angular se mide en $\color{#0000FF} \dfrac {rad}{s}$
Es el cambio que sufre la velocidad angular $\color{#0000FF} \Delta w$ respecto de un cambio en el tiempo $\color{#0000FF} \Delta t$: $\color{#0000FF} \alpha=\dfrac {dw}{dt}$ $\color{#0000FF} \alpha=\dfrac {\Delta w}{\Delta t}$ $\color{#0000FF} \alpha=\dfrac {w - w_0}{t - t_0}$
Recordamos que para este curso de Física Mecánica vamos a considerar ejercicios que implican aceleración angular constante.
La Aceleración angular se mide en $\color{#0000FF} \dfrac {rad}{s^2}$
En resumen, las ecuaciones cinemáticas para el movimiento angular con aceleración angular constante son:
Posición Angular $\color{#008000} \theta = \theta_0 + w_0t + \dfrac {1}{2}\alpha t^2 rad$
Velocidad Angular $\color{#008000} w=w_0 + \alpha t \dfrac {rad}{s}$
Aceleración Angular $\color{#008000} \alpha=\dfrac {dw}{dt}$ $\color{#008000} \alpha=\dfrac {w - w_0}{t - t_0} \alpha=Cte$ $\color{#008000} \dfrac {rad}{s^2}$
Ecuación auxiliar para Velocidad Angular $\color{#008000} w^2=w^2_0 + 2a(\theta - \theta_0) $
En ocasiones es necesario conocer la longitud de una parte de una circunferencia o longitud de un arco de una curva.
Para desarrollar una ecuación para la longitud de arco partimos de la ecuación de la longitud de una circunferencia $\color{#0000FF} l=2\pi r$ que podemos escribir $\color{#0000FF} l=r(2\pi)$ donde $\color{#0000FF} (2\pi)$ indica el ángulo de una vuelta completa de la circunferencia en radianes. Si queremos saber ahora la longitud $\color{#0000FF} S$ de una parte de esa circunferencia, el ángulo ya no será $\color{#0000FF} (2\pi)$ sino un ángulo $\color{#0000FF} \theta$ determinado para el ejercicio que estemos analizando. Entonces: de $\color{#0000FF} l=r(2\pi)$ que representa la longitud de toda la circunferencia pasamos a $\color{#0000FF} S=r\theta$ que es la ecuación que define la longitud de cualquier segmento de arco de la circunferencia incluyendo la circunferencia completa para cuando $\color{#0000FF} \theta=2\pi$.
Longitud de Arco $\color{#0000FF} S=r\theta$ $m$, ft Desaparecen los radianes por ser $\color{#0000FF} S$ una longitud
Bajo los parámetros que nos ofrece el concepto de longitud de arco podemos determinar el desplazamiento lineal realizado por un punto en el cuerpo con dimensiones que se mueve con movimiento angular:
Desplazamiento lineal $\color{#008000} S=r\theta m$, $\color{#008000} ft$
Con la ecuación de desplazamiento lineal podemos determinar la velocidad lineal de cualquier punto en el cuerpo con dimensiones que se mueve con movimiento angular:
Velocidad lineal
$\color{#0000FF} S=r\theta$ ; $\color{#0000FF} \dfrac {dS}{dt}=r \dfrac {d\theta}{dt}$ ; $\color{#0000FF} \dfrac {dS}{dt}=v$ ; $\color{#0000FF} \dfrac {d\theta}{dt}=w$ $\Rightarrow$ $\color{#0000FF} v=rw$
$\color{#0000FF} v=rw$ $\color{#008000} v=m\dfrac {rad}{s}$ $\Rightarrow$ $\color{#008000} v=\dfrac {m}{s}$ ; $\color{#008000} v=\dfrac {ft}{s}$
Con la ecuación de Velocidad lineal podemos determinar la Aceleración lineal de cualquier punto en el cuerpo con dimensiones que se mueve con movimiento angular:
Cada punto del cuerpo con dimensiones recorre una trayectoria curva. El cuerpo puede experimentar un cambio en la velocidad angular $\color{#0000FF} w$ que traen como consecuencia un cambio en la velocidad lineal que a su vez produce una aceleración tangencial a un punto cualquiera del cuerpo rígido. Obsérvese que como el cuerpo rígido está en movimiento angular siempre existirá por ese hecho (cuerpo en rotación) una aceleración normal.
Aceleración Tangencial
$\color{#0000FF} v=rw$ ; $\color{#0000FF} \dfrac {dv}{dt}=r \dfrac {dw}{dt}$ ; $\color{#0000FF} \dfrac {dv}{dt}=a_t$ ;; $\color{#0000FF} \dfrac {dw}{dt}=\alpha$ $\Rightarrow$ $\color{#008000} a_t=r\alpha$
$\color{#0000FF} a_t=r\alpha$ $\color{#008000} a_t=m\dfrac {rad}{s^2}$ $\Rightarrow$ $\color{#008000} a_t=\dfrac {m}{s^2}$ ; $\color{#008000} a_t=\dfrac {ft}{s^2}$
Aceleración Normal
$\color{#0000FF} a_n=\dfrac {v^2}{r}$ ; $\color{#0000FF} v=rw$ ; $\color{#0000FF} a_n=\dfrac {(rw)^2}{r}$ ; $\color{#0000FF} a_n=\dfrac {r^2w^2}{r}$ $\Rightarrow$ $\color{#0000FF} a_n=rw^2$ ; $\color{#008000} a_n=\dfrac {m}{s^2}$ ; $\color{#008000} a_n=\dfrac {ft}{s^2}$
Cuando un cuerpo rota alrededor de un punto (centro de giro) describe una trayectoria circular. La distancia de un punto cualquiera al punto centro de giro se llama el radio $\color{#0000FF} r$.
Cuando un punto de ese cuerpo al girar completa una vuelta (vuelve a pasar por el punto de partida) y tomamos el tiempo que le tomo realizar esa vuelta, ese tiempo se llama el periodo $\color{#0000FF} T$.
Cuando una partícula se mueve por una línea con la magnitud de la velocidad constante se puede determinar su desplazamiento como $\color{#0000FF} X=Vt$. En forma análoga, cuando un cuerpo con dimensiones rota al rededor de un punto con velocidad angular constante (llamado Movimiento Circular Uniforme), su desplazamiento angular lo podemos determinar como $\color{#0000FF} \theta=wt$
Cuando el cuerpo con dimensiones a completado una vuelta el ángulo $\color{#0000FF} \theta=2\pi$ y el tiempo que le toma dar esa vuelta se convierte en el periodo $\color{#0000FF} T$. $\color{#0000FF} 2\pi=wT$
Despejamos para la velocidad Angular: $\color{#0000FF} w= \dfrac {2\pi}{T}$ $\color{#008000} \dfrac {rad}{s}$
Despejamos para el periodo: $\color{#0000FF} T=\dfrac {2\pi}{w}$ Segundos $\color{#008000} s$
Al inverso del periodo se le llama la frecuencia $\color{#008000} f$ del movimiento: $\color{#0000FF} f= \dfrac {1}{T}$ $\color{#008000} [\dfrac {1}{s}=H_z]$ Número de vueltas en la unidad de tiempo.
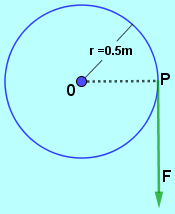
A la rueda que está en reposo se le enrolla una cuerda a la que se le aplica una fuerza que le produce a la cuerda una aceleración de $\color{#0000FF} 4\dfrac {m}{s^2}$. Determine la velocidad angular de la rueda, la posición angular de la línea $\color{#0000FF} 0P$, la magnitud de la aceleración y la velocidad lineal del punto $\color{#0000FF} P$ a los $\color{#0000FF} 2$ segundos de ser aplicada la fuerza. Determine el periodo y la frecuencia del movimiento.
Solución: La rueda está en reposo en $\color{#0000FF} t_0=0$, entonces la velocidad angular inicial es $\color{#0000FF} w_0=0$, la velocidad lineal inicial $\color{#0000FF} v_0=0$, la posición inicial angular es $\color{#0000FF} \theta_0=0$ y la posición inicial lineal es $\color{#0000FF} S_0=0$. La aceleración en la cuerda de $\color{#0000FF} 4\dfrac {m}{s^2}$ es la aceleración tangencial $\color{#0000FF} a_t$ en cualquier punto de la polea cuando
el radio es $\color{#0000FF} r=0.5m$. Ésta aceleración tangencial es constante ($\color{#0000FF} 4\dfrac {m}{s^2}$) por lo que la aceleración angular en la rueda también es constante.$\color{#0000FF} a_t=r\alpha$ $\color{#0000FF} \dfrac {a_t}{r}=\alpha$ $\color{#0000FF} \dfrac {4}{0.5}=\alpha$ $\color{#FF0000} \alpha=8\dfrac {rad}{s^2}$
Para determinar la velocidad angular: $\color{#0000FF} w= {\color{Red}\bcancel {{\color{blue}w_0}}} + \alpha t$
$\color{#0000FF} w=\alpha t$ $\color{#0000FF} w= 8(2)$ $\color{#FF0000} w= 16 \dfrac {rad}{s}$
Para determinar la posición angular de la línea $\color{#0000FF} OP$:
$\color{#0000FF} \theta = {\color{Red}\bcancel {{\color{blue}\theta_0}}} + {\color{Red}\bcancel {{\color{blue}w_0}}}t + \dfrac {1}{2}\alpha t^2$ ; $\color{#0000FF} \theta = \dfrac {1}{2}\alpha t^2$ ; $\color{#0000FF} \theta = \dfrac {1}{2} (8)2^2$
$\color{#FF0000} \theta =16rad$
Para determinar la aceleración del punto $\color{#0000FF} P$ pasados $\color{#0000FF}2$ segundos de ser aplicada la fuerza nos falta conocer la aceleración normal del punto $\color{#0000FF} P$. $\color{#0000FF} a_n=rw^2$ $\color{#0000FF} a_n=(0.5)16^2$ $\color{#FF0000} a_n=128\dfrac {m}{s^2}$
La aceleración total será $\color{#0000FF} a=\sqrt {a_t^{2}-a_n^{2}}$ $\color{#0000FF} a=\sqrt {4^{2}-128^{2}}$ $\color{#FF0000} a=128.06\dfrac {m}{s^2}$
Para la velocidad lineal $\color{#0000FF} v=rw$ $\color{#0000FF} v=(0.5)16$ $\color{#FF0000} v=8\dfrac {m}{s}$
Para el Periodo $\color{#0000FF} T=\dfrac {2\pi}{w}$ $\color{#0000FF} T=\dfrac {2\pi}{16}$ $\color{#FF0000} T=0.3927_s$
Para la frecuencia del movimiento $\color{#0000FF} f=\dfrac {1}{T}$ $\color{#0000FF} f=\dfrac {1}{0.3927}$ $\color{#FF0000} f=2.55H_z$
La siguiente escena interactiva, diseñada por Amaia San SebastianAmaia San Sebastian es un autor de la red GeoGebra que publico la escena interactiva "Movimiento Circular Uniforme".
• En la escena interactiva cuando transcurre un tiempo $\color{#0000FF} t=1$, significa que en tiempo real es de $\color{#0000FF} 10.5$ segundos (esto para que el estudiante haga la respectiva conversión al momento de realizar los ejercicios prácticos).
• En la escena interactiva donde dice datos iniciales, acomode el deslizador de aceleración tangencial al valor de $\color{#0000FF} a_t=0.25\pi \dfrac {m}{s^2}$. Verifique que la escena interactiva este en la posición angular de $\color{#0000FF} \theta_0=0\pi rad$
• Tome un cronometro y póngalo a correr en el mismo instante que pone en marcha la escena interactiva. Detenga el cronometro y la escena interactiva cuando ha transcurrido aproximadamente $\color{#0000FF} 20$ segundos (es posible que el cronometro se detenga antes o después de los $\color{#0000FF} 20$ segundos). Tome el dato exacto del tiempo y el valor del ángulo recorrido en la escena interactiva.
• El valor del tiempo tomado en el cronometro divídalo entre $\color{#0000FF} 10.5$ (el resultado es el tiempo que maneja la escena interactiva). Este resultado remplácelo en la ecuación de la posición angular: $\color{#0000FF} \theta = \theta_0 + w_0t + \dfrac {1}{2}\alpha t^2$ habiendo hallado previamente el valor de la aceleración angular $\color{#0000FF} \alpha=a_t R$. verifique que el valor de la posición angular que da como resultado coincida o este muy cercana al resultado que aparece en la escena interactiva.
• Remplace también el valor del tiempo en la ecuación de la velocidad angular $\color{#0000FF} w=w_0 + \alpha t$; el resultado compárelo con el resultado dado en la escena interactiva.
• Haga las operaciones correspondientes para hallar las magnitudes lineales $\color{#0000FF} a_n, v, a_{total}$. Compare sus respuestas con las expresadas en la escena interactiva. De clic en mostrar vectores y compare con sus respuestas.
• Determine el tiempo real (de un cronometro) que le tomaría a un punto en el extremo del radio en dar la primera vuelta. El tiempo que le tomaría en dar la segunda vuelta. ¿Son iguales los dos tiempos? Explique.
• Repetir los mismos pasos para un valor de la aceleración tangencial de $\color{#0000FF} a_t=0.75\pi \dfrac {m}{s^2}$ y un tiempo en el cronometro de $\color{#0000FF} 10$ segundos.
Podemos utilizar la misma escena interactiva para analizar un movimiento circular con aceleración angular $\color{#0000FF}\alpha =0\dfrac {rad}{s^2}$, llamado Movimiento Circular Uniforme que ocurre cuando la velocidad angular es $\color{#0000FF} w=Cte$.
• En la escena interactiva donde dice datos iniciales ponga el valor del deslizador para la aceleración tangencial en cero $\color{#0000FF} a_t =0\dfrac {m}{s^2}$.
• Tome un cronometro y póngalo a correr en el mismo instante que pone en marcha la escena interactiva. Detenga el cronometro y la escena interactiva cuando ha transcurrido aproximadamente 15 segundos (es posible que el cronometro se detenga antes o después de los 15 segundos). Tome el dato exacto del tiempo y el valor del ángulo recorrido en la escena interactiva.
• El valor del tiempo tomado en el cronometro divídalo entre $\color{#0000FF} 10.5$ (el resultado es el tiempo que maneja la escena interactiva). Este resultado remplácelo en la ecuación de la posición angular: $\color{#0000FF} \theta = \theta_0 + w_0t + \dfrac {1}{2}\alpha t^2$ habiendo hallado previamente el valor de la aceleración angular $\color{#0000FF} \alpha=a_t(R)$. Verifique que el valor de la posición angular que da como resultado coincida o este muy cercana al resultado que aparece en la escena interactiva.
• Remplace también el valor del tiempo en la ecuación de la velocidad angular $\color{#0000FF} w=w_0 + \alpha t$; el resultado compárelo con el resultado dado en la escena interactiva. Note que en este caso la velocidad angular es cero $\color{#0000FF}\alpha =0\dfrac {rad}{s^2}$.
• Haga las operaciones correspondientes para hallar las magnitudes de $\color{#0000FF} a_t, a_n, v, a \ total$. Compare sus respuestas con las
expresadas en la escena interactiva. De clic en mostrar vectores y compare con sus respuestas.
• Determine el tiempo real (de un cronometro) que le tomaría a un punto en el extremo del radio en dar la primera vuelta. El tiempo que le tomaría en dar la segunda vuelta. Note que en este caso el tiempo en dar la primera vuelta es el mismo tiempo en dar la segunda vuelta. Este tiempo es el que se llama el Periodo. Verifique el valor del periodo con la ecuación $\color{#0000FF} T= \dfrac {2\pi}{w}$.
• Tome el valor del periodo y divídalo por $\color{#0000FF} 10.5$. Este resultado remplácelo en la ecuación de posición angular y verifique que el radio está en la posición inicial.
• Con el valor del periodo determine la frecuencia del movimiento.
• Determine cuantas vuelta da el radio en un tiempo real (del cronometro) de $\color{#0000FF} 100$ segundos. Exprese el resultado en revoluciones por minuto $\color{#0000FF} rpm$.
Nota:
$\color{#0000FF} rpm=\dfrac {revolución}{minuto} \cdot \dfrac {vuelta}{revolución} \cdot \dfrac {2\pi rad}{Vuelta} \cdot \dfrac {minuto}{60 segundos}$
El video introductorio hace parte de la serie Universo MecánicoLa serie educativa Universo Mecánico es una colección de 52 videos creados por el Instituto de Tecnología de California cuyo director y anfitrión es el Dr. David L. Goodtein.
En el capítulo anterior estudiamos la cinemática (posición, velocidad y aceleración), de los cuerpos a partir de la geometría del movimiento de este cuerpo.
En este capítulo veremos la cinética que es el estudio del movimiento de los cuerpos (posición, velocidad y aceleración) a partir de las fuerzas externas que actúan sobre dichos cuerpos. La cinética responde al interrogante de cual es la causa del movimiento o la causa del no movimiento de un cuerpo.
La cinética se desarrolla a través de tres grandiosas leyes propuestas por Isaac Newton en el Siglo XIIV.
Cuando sobre una partícula actúan fuerzas y la suma de estas fuerzas es igual a cero, el cuerpo estará en equilibrio. $\color{#0000FF} \Sigma \overrightarrow {F} = 0$
Debemos recordar que estamos realizando el estudio de la cinética de la partícula y se tendrá que entender que la masa del cuerpo está concentrada en el centro de gravedad que es un punto y los puntos no rotan. En este caso es como si todas las fuerzas estuvieran actuando en ese punto llamado centro de gravedad y por esta razón el cuerpo no sufre los efectos de la rotación.
Cuando la suma de todas las fuerzas que actúan sobre un cuerpo es igual a cero, la aceleración es cero.
$\color{#0000FF} \Sigma \overrightarrow {F} = 0$ $\Rightarrow$ $\color{#0000FF} \overrightarrow {a} = 0$
Estar en equilibrio no significa que el cuerpo tenga que estar en reposo. Estar en equilibrio significa no estar acelerado; el cuerpo se puede estar moviendo con velocidad constante (en magnitud y dirección) y por ello su aceleración es cero y se está moviendo. Ejemplo: un avión viajando en línea recta con la magnitud de la velocidad constante. Un vaso con agua puede estar en el piso del avión y no regarse.
Cuando sobre un cuerpo actúan fuerzas y la suma de estas fuerzas es diferente de cero, el cuerpo estará acelerado.
$\color{#0000FF} \Sigma \overrightarrow {F} \quad {\color{Red}\bcancel {{\color{blue}=}}} 0$ $\Rightarrow$ $\color{#0000FF} a \quad {\color{Red}\bcancel {{\color{blue}=}}} 0$
Estar acelerado significa que la velocidad está cambiando (en magnitud y/o dirección).
La segunda ley de Newton se fundamenta en dos fenómenos físicos:
• La aceleración es directamente proporcional a la fuerza resultante: $\color{#0000FF} \overrightarrow {a} \alpha \overrightarrow {F_R}$
• La aceleración es inversamente proporcional a la masa: $\color{#0000FF} \overrightarrow {a} \alpha \dfrac {1}{m}$
Para entender estos conceptos pensemos en un automóvil que se encuentra apagado, en reposo en una calle y una persona quiere moverlo pero con su fuerza no lo logra, llegan dos personas más a ayudar; aportan sus fuerzas y logran poner en movimiento el automóvil (el automóvil se acelera), el automóvil salió de su estado de reposo.
Supongamos que llegan tres personas más y aportan sus fuerzas haciendo que el automóvil aumente más su velocidad (aumenta su aceleración). Notemos que la aceleración aumenta cuando aumenta la fuerza resultante: $\color{#0000FF} \overrightarrow {a} \alpha \overrightarrow {F_R}$
Ahora que el automóvil está en movimiento pensemos en que llegan otras dos personas y en lugar de ayudar a empujar lo que hacen es que se montan en el automóvil. Lo que sucede en este caso es que el automóvil pierde velocidad (disminuye la velocidad) y por tanto su aceleración disminuye: $\color{#0000FF} \overrightarrow {a} \alpha \dfrac {1}{m}$.
Con estos dos fenómenos físicos basados en la proporcionalidad Isaac Newton llego a una igualdad: $\color{#0000FF} \overrightarrow {a} = \dfrac {\overrightarrow {F_R}}{m}$ $\Rightarrow$ $\color{#0000FF} \overrightarrow {F_R} = m\overrightarrow {a}$
La $\color{#0000FF} \overrightarrow {F_R}= \Sigma \overrightarrow {F}$ $\Rightarrow$ $\color{#008000} \Sigma \overrightarrow {F} = m\overrightarrow {a}$
$\color{#0000FF} \Sigma \overrightarrow {F} = m\overrightarrow {a}$ es una ecuación vectorial, la fuerza es un vector, la masa es un escalar, la aceleración es un vector y el producto de un escalar por un vector da como resultado un vector.
$\color{#0000FF} \Sigma \overrightarrow {F} = m\overrightarrow {a}$ da lugar a las siguientes ecuaciones escalares:
$\color{#0000FF} \Sigma F_x=ma_x$ $\color{#0000FF} \Sigma F_y=ma_y$ $\color{#0000FF} \Sigma F_z=ma_z$
Estas ecuaciones las aplicamos cuando los cuerpos se mueven por trayectorias rectas.
$\color{#0000FF} \Sigma F_t=ma_t$ $\color{#0000FF} \Sigma F_n=ma_n$ $\color{#0000FF} \Sigma F_b=0$ ; $\color{#0000FF} a_b=o$
Estas ecuaciones las aplicamos cuando los cuerpos se mueven por trayectorias curvas.
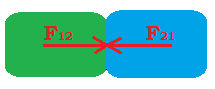
La tercera ley de Newton nos enseña que las fuerzas no aparecen solas, siempre aparecen en pareja. Si una persona hace una fuerza a una pared, la pared responde con una fuerza exactamente igual y de sentido contrario.
Para una eficaz aplicación de las leyes de Newton es necesario realizar sumatorias de fuerzas que obligan a elaborar previamente diagramas de cuerpo libre según sea el caso a resolver.
Es un gráfico, un dibujo, un esquema en el cual se dibuja el cuerpo y sobre el diagrama se colocan todas las fuerzas externas que actúan.
El diagrama que se hace del cuerpo debe realizarse tal cual está el cuerpo en el ejercicio o según las indicaciones de este. si el cuerpo está o dice que está sobre un plano inclinado debe dibujarse el bloque igual como se ve o como dice que está en el plano inclinado.
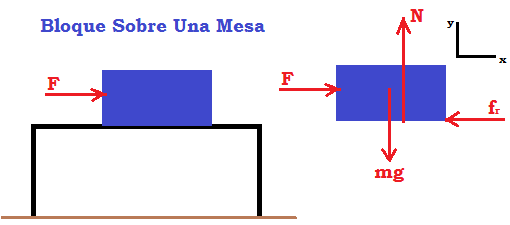
Las fuerzas externas que actúan sobre el bloque de la figura son:
$\blacktriangleright\hspace{0.2cm}$ La Fuerza Normal $\color{#0000FF} \overrightarrow {N}$: Se presenta cuando existe contacto entre dos superficies. La fuerza Normal es siempre perpendicular a las dos superficies en contacto. La fuerza Normal se dibuja desde donde se presenta el contacto entre las dos superficies.
$\blacktriangleright\hspace{0.2cm}$ La Fuerza Aplicada $\color{#0000FF} \overrightarrow {F}$: Se dibuja tal cual aparece o lo indica el ejercicio y siempre en el punto donde se aplica sobre el cuerpo.
$\blacktriangleright\hspace{0.2cm}$ La Fuerza de Gravedad $\color{#0000FF} \overrightarrow {mg}$ Es la fuerza con que la tierra atrae los cuerpos y por ello es una fuerza externa al cuerpo. Se dibuja desde el centro de gravedad del cuerpo y siempre dirigida al centro de la tierra.
Algunos autores identifican la fuerza de gravedad $\color{#0000FF} \overrightarrow {mg}$ como $\color{#0000FF} \overrightarrow {w}$.
$\blacktriangleright\hspace{0.2cm}$ La Fuerza de rozamiento $\color{#0000FF} \overrightarrow {f}$: Las fuerzas de rozamiento son fuerzas que se oponen al movimiento de los cuerpos. Las fuerzas de rozamiento se deben al contacto de los cuerpos con el medio que los rodea.
Las fuerzas de rozamiento pueden ser fuerzas de rozamiento fluidas o fuerzas de rozamiento secas.
$\blacktriangleright\hspace{0.2cm}$ La Fuerza de rozamiento fluidas $\overrightarrow {f}$: Son aquellas que se oponen al movimiento de los cuerpos y se deben al contacto de los cuerpos con medios fluidos, ejemplo de ello es cuando un ciclista hace contacto con el aire; un disparo de una bala en el agua. En este curso no haremos referencia a las fuerzas de rozamiento fluidas.
$\blacktriangleright\hspace{0.2cm}$ La Fuerza de rozamiento Seca $\color{#0000FF} \overrightarrow {f}$: Son aquellas fuerzas que se oponen al movimiento de los cuerpos y se deben al contacto de los cuerpos con superficies secas. Ejemplo de ello es un bloque se mueve sobre la superficie rugosa de una mesa.
Las fuerzas de rozamiento secas pueden ser, Fuerza de rozamiento estática $\color{#0000FF} \overrightarrow {f_s}$ y Fuerza de rozamiento cinética Dinámica $\color{#0000FF} \overrightarrow {f_k}$
$\blacktriangleright\hspace{0.2cm}$ La Fuerza de rozamiento Estática $\color{#0000FF} \overrightarrow {f_s}$: Con la nomenclatura $\color{#0000FF} \overrightarrow {f_s}$ hace referencia a la máxima resistencia que se presenta entre dos superficies en contacto que impide que el cuerpo salga de la posición de reposo.
$\blacktriangleright\hspace{0.2cm}$ La Fuerza de rozamiento Cinética o Dinámica $\overrightarrow {f_k}$: Se presenta cuando un cuerpo se desliza por una superficie rugosa.
La fuerza de rozamiento estática $\color{#0000FF} \overrightarrow {f_s}$ es ligeramente mayor que la fuerza de rozamiento cinética o dinámica $\color{#0000FF} \overrightarrow {f_k}$. Esto se debe a que cuando un cuerpo sale del reposo las fuerzas de ligadura entre las superficies en contacto (fuerzas electrostáticas entre las superficies en contacto) se rompen y hacen que el rozamiento disminuya.
Para la realización de ejercicios prácticos se requiere de un modelo matemático para las fuerzas de rozamiento estático y cinético o dinámico.
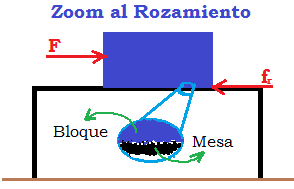
Para llegar al modelo matemático pensemos en el bloque que esta sobre la mesa y pensemos en que con la fuerza que se le está aplicando el bloque está a punto de moverse (punto de movimiento inminente) y en ese instante se coloca otro bloque encima de nuestro bloque; una de las consecuencias inmediatas es que la mesa tiene que hacer más fuerza hacia arriba para sostener los dos bloques y evitar que estos caigan al suelo (Aumenta el valor de la fuerza Normal $\color{#0000FF} \overrightarrow {N}$ ), la otra consecuencia es que el contacto entre las superficies en contacto (nuestro primer boque y la mesa) es mayor y por consiguiente la fuerza de rozamiento aumenta.
Estas reflexiones nos llevan a concluir que las fuerzas de rozamiento son directamente proporcionales a la fuerza Normal $\color{#0000FF} \overrightarrow {f_r} \alpha \overrightarrow {N}$
Para eliminar la proporcionalidad y llegar a una igualdad (Ecuación) se debe encontrar una constante (constante de proporcionalidad) que en este caso se llama Coeficiente de Rozamiento $\color{#0000FF} \mu$. Así, para la fuerza de rozamiento estático $\color{#0000FF} \overrightarrow {f_s}=\mu_s \overrightarrow {N}$ donde $\color{#0000FF} \mu_s$ es el coeficiente de rozamiento estático. Para la fuerza de rozamiento cinético o
dinámico $\color{#0000FF} \overrightarrow {f_k}=\mu_k \overrightarrow {N}$ donde $\color{#0000FF} \mu_k$ es el coeficiente de rozamiento cinético o dinámico.
Los valores del coeficiente de rozamiento hallados experimentalmente se encuentran entre $\color{#0000FF} 0.05 \leq \mu \geq 1.5 $ y sus unidades estarán dadas en $\color{#0000FF} \dfrac {N}{N}$ en el Sistema Internacional de Unidades y de $\color{#0000FF} \dfrac {lb}{lb}$ en el Sistema Ingles de Unidades F.P.S. esto porque al despejar $\color{#0000FF} \mu$ de la ecuación $\color{#0000FF} \overrightarrow {f_r}=\mu \overrightarrow {N}$ queda $\color{#0000FF} \mu = \dfrac {\overrightarrow {f_r}}{\overrightarrow {N}}$; es decir, que el coeficiente de rozamiento $\color{#0000FF} \mu$ responde a una relación entre dos fuerzas, Newton sobre Newton, Libras sobre Libras.
En Muchos textos afirman que el coeficiente de rozamiento $\color{#0000FF} \mu$ es una cantidad "Adimensional", hecho que no compartimos por las razones expresadas. Si compartimos el hecho de que matemáticamente se cancelan las unidades, pero no por ello se vuelve una cantidad adimensional.
Aceptar que el coeficiente de rozamiento $\color{#0000FF} \mu$ es adimensional seria desnaturalizar el fenómeno físico que representa.
Los valores del coeficiente de rozamiento estático $\color{#0000FF} \mu_s$ y $\color{#0000FF} \mu_k$ dependen del material de las superficies en contacto y no del area de estas.
Ingenieros Mecánicos estudiosos del coeficiente de rozamiento han elaborado tablas con valores del $\color{#0000FF} \mu_s$ y $\color{#0000FF} \mu_k$ para el contacto entre diferentes materiales tales como Hierro sobre Cobre, Aluminio sobre Acero, Madera sobre Vidrio, Caucho sobre Asfalto entre otras relaciones.
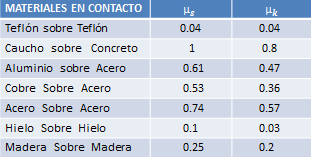 $$
$$
Tabla 4.1: La tabla muestra los valores para el coeficiente de rozamiento estático $\color{#0000FF} \mu_s$ y cinético o dinámico $\color{#0000FF} \mu_k$ para diferentes materiales en contacto.
En éste curso de Física Mecánica se consideran las cuerdas como inextensibles (que no se estiran), la longitud de la cuerda no cambia. La tensión en las cuerdas es la misma en cada punto de la cuerda.
Las fuerzas que se realizan con una cuerda son de tensión; las cuerdas sirven para halar, jalar, tensionar no para comprimir.
A nivel de nomenclatura a la fuerza realizada por una cuerda se le denota con una $\color{#0000FF} T$ mayúscula, de Tensión.
Cuando una cuerda se tensiona, la tensión es la misma en cada punto de la cuerda.
La masa de las cuerdas es despreciable en comparación con las masas de los cuerpos sobre la que la cuerda actúa.
Para éste curso de Física Mecánica se considera que las poleas son completamente lisas (lubricadas) de tal forma que al pasar una cuerda sobre ellas no afectan la tensión en la cuerda (la tensión en la cuerda sigue siendo la misma en cada punto de la cuerda).
En general la masa de las poleas es despreciable a no ser que el enunciado del ejercicio le atribuya una masa.
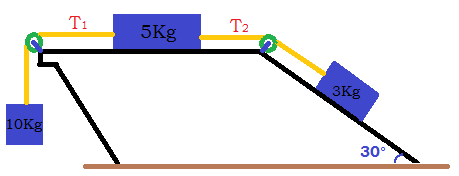
Los tres bloques están conectados por medio de cuerdas ligeras que pasan por las poleas sin fricción. El coeficiente de rozamiento entre los bloques y la superficie es de $\color{#0000FF} 0.1$. El sistema se libera desde el reposo. Determine: (a) La aceleración de cada bloque, (b) La Tensión en cada cuerda, (c) El desplazamiento de cada bloque a los dos segundos de ser liberados, (d) La velocidad de cada bloque a los dos segundos de ser liberados.
Solución:
(a) La aceleración de cada bloque: Luego de leer detenidamente el ejercicio dos o tres veces, entendemos que la aceleración de
cada bloque en magnitud es la misma $\color{#0000FF} a_{10}=a_5=a_3=a$. La aceleración de cada bloque en dirección es diferentes.
Hacemos los diagramas de cuerpo libre de cada uno de los bloques teniendo cuidado en dibujar en cada diagrama todas las fuerzas externas que actúan en cada bloque. Realizamos las sumatorias de fuerzas a que haya lugar para cada bloque.
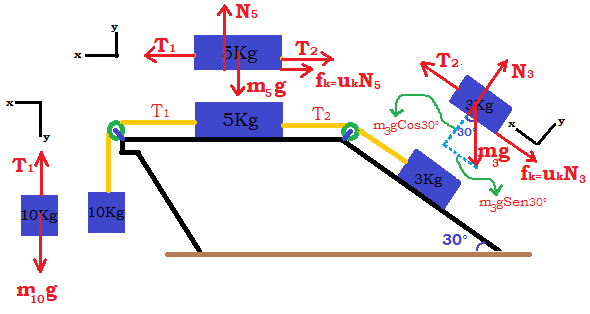
Para el Bloque de 10Kg:
Tomamos el eje $\color{#0000FF} y$ positivo en la dirección del movimiento del bloque de 10Kg tal como se muestra la figura, entonces:
$\color{#0000FF} \Sigma F_y=m_{10}a_{10}$ $\color{#0000FF} a_{10}=a$ $\Rightarrow$ $\color{#008000} m_{10}a=m_{10}g-T_1$ $\color{#0000FF} (1)$
En esta ecuación tenemos dos incógnitas $\color{#0000FF} a$ y la $\color{#0000FF} T_{1}$. Necesitamos otra ecuación porque una ecuación con dos incógnitas no se puede resolver. Vamos a cualquiera de los otros dos bloques.
Para el Bloque de $5Kg$:
Tomamos el eje $\color{#0000FF} x$ positivo en la dirección del movimiento del bloque de $\color{#0000FF} 10Kg$ tal como se muestra la figura, entonces:
$\color{#0000FF} \Sigma F_x=m_{5}a_{5}$ $\color{#0000FF} a_{5}=a$ $\Rightarrow$ $\color{#0000FF} m_{5}a=T_1-T_2-\mu_kN_5$
En ésta ecuación tenemos cuatro incógnitas: La $\color{#0000FF} a$, la $\color{#0000FF} T_{1}$, la $\color{#0000FF} T_{2}$ y la $\color{#0000FF} N_{5}$. La $\color{#0000FF} N_{5}$ la podemos determinar haciendo:
$\color{#0000FF} \Sigma F_y=0$ $\color{#0000FF} 0=N_5-M_5g$ $\Rightarrow$ $\color{#FF0000} N_5=M_5g$ Remplazamos
$\color{#008000} m_{5}a=T_1-T_2-\mu_km_5g$ $\color{#0000FF} (2)$
Entre las ecuaciones para el bloque de $\color{#0000FF}10Kg$ y del bloque de $\color{#0000FF}5Kg$ tenemos tres incógnitas La $\color{#0000FF} a$, la $\color{#0000FF} T_{1}$, la $\color{#0000FF} T_{2}$. Necesitamos otra ecuación, entonces vamos al bloque de $\color{#0000FF} 3Kg$
Para el Bloque de $3Kg$:
Tomamos el eje $\color{#0000FF} x$ positivo en la dirección del movimiento del bloque de $\color{#0000FF} 3Kg$ tal como se muestra la figura, entonces:
$\color{#0000FF} \Sigma F_x=m_{3}a_{3}$ $\color{#0000FF} a_{3}=a$ $\Rightarrow$ $\color{#0000FF} m_{3}a=T_2-m_3gsen\theta-\mu_kN_3$
En ésta ecuación tenemos tres incógnitas: La $\color{#0000FF} a$, la $\color{#0000FF} T_{2}$ y la $\color{#0000FF} N_{3}$. La $\color{#0000FF} N_{3}$ la podemos determinar haciendo:
$\color{#0000FF} \Sigma F_y=0$ $\color{#0000FF} 0=N_3-M_3gCos\theta$ $\Rightarrow$ $\color{#FF0000} N_3=M_3gCos\theta$ Remplazamos $\color{#008000} m_{3}a=T_2-m_3gsen\theta-\mu_kM_3gCos\theta$ $\color{#0000FF} (3)$
Tenemos tres ecuaciones con tres incógnitas La $\color{#0000FF} a$, la $\color{#0000FF} T_{1}$, y la $\color{#0000FF} T_{2}$ Sumamos las tres ecuaciones (se cancelan las tensiones):
$\color{#008000} m_{10}a=m_{10}g-T_1$ $\color{#0000FF} (1)$
$\color{#008000} m_{5}a=T_1-T_2-\mu_km_5g$ $\color{#0000FF} (2)$
$\color{#008000} m_{3}a=T_2-m_3gsen\theta-\mu_kM_3gCos\theta$ $\color{#0000FF} (3)$
$\color{#0000FF} m_{10}a + m_{5}a + m_{3}a = m_{10}g -\mu_km_5g -m_3gsen\theta - \mu_kM_3gCos\theta$
$\color{#0000FF} a(m_{10}+m_5+m_3)= g(m_{10} -\mu_km_5 -m_3sen\theta - \mu_kM_3Cos\theta)$
$\color{#0000FF} a=\dfrac {g(m_{10} -\mu_km_5 -m_3sen\theta -\mu_kM_3Cos\theta)}{(m_{10}+m_5+m_3)}$
$\color{#0000FF} a=\dfrac {9.81(10 -0.1*5 -3sen 30° -0.1*3Cos 30°)}{(10+5+3)}$
$\color{#0000FF} a=4.22\dfrac {m}{s^2}$
Hemos determinado la magnitud de la aceleración de cada bloque. Como nos piden la aceleración de cada bloque, debemos dar la aceleración en forma vectorial.
$\color{#FF0000} \overrightarrow {a_{10}}=4.22\dfrac {m}{s^2} \downarrow$ $\color{#FF0000} \overrightarrow {a_{5}}=4.22\dfrac {m}{s^2} \leftarrow$ $\color{#FF0000} \overrightarrow {a_{3}}=4.22\dfrac {m}{s^2} 30° \nwarrow$
(b) La Tensión en cada cuerda: De la ecuación $\color{#0000FF} (1)$ despejamos $\color{#0000FF} T_1$, de la ecuación $\color{#0000FF} (2)$ despejamos $\color{#0000FF} T_2$ y hallamos sus valores remplazando en ellas el valor de la aceleración.
$\color{#008000} m_{10}a=m_{10}g-T_1$ $\color{#0000FF} (1)$
$\color{#0000FF} T_1=m_{10}g - m_{10}a$ $\color{#0000FF} T_1=m_{10}(g - a)$
$\color{#0000FF} T_1={10}(9.81 - 4.22)$ $\color{#FF0000} T_1=55.9N$
$\color{#008000} m_{3}a=T_2-m_3gsen\theta-\mu_kM_3gCos\theta$ $\color{#0000FF} (3)$
$\color{#0000FF} m_{3}a + m_3gsen\theta + \mu_kM_3gCos\theta = T_2$
$\color{#0000FF} T_2 = m_{3}(a + gsen\theta + \mu_kgCos\theta)$
$\color{#0000FF} T_2 = {3}(4.22 + 9.81sen 30° + 0.1*9.81Cos 30°)$
$\color{#FF0000} T_2=29.92N$
(c) El desplazamiento de cada bloque a los dos segundos de ser liberados: El movimiento de cada bloque es rectilíneo. la aceleración en magnitud es $\color{#0000FF} a=4.22\dfrac {m}{s^2}$. El desplazamiento de cada bloque es el mismo en magnitud; utilizamos la ecuación de posición en función del tiempo para el movimiento rectilíneo con aceleración constante.
El sistema se libera desde el reposo $\color{#0000FF} v_0=0$ $\color{#0000FF} S_0=0$
$\color{#0000FF} s = {\color{Red}\bcancel {{\color{blue}s_0}}} + {\color{Red}\bcancel {{\color{blue}v_0}}}t + \dfrac {1}{2}at^2$ $\color{#0000FF} s = \dfrac {1}{2}at^2$
$\color{#0000FF} s = \dfrac {1}{2}4.22(2^2)$ $\color{#0000FF} s =8.44m$ el mismo para cada bloque.
$\color{#FF0000} \overrightarrow {S_{10}}=8.44{m} \downarrow$ $\color{#FF0000} \overrightarrow {S_{5}}=8.44{m} \leftarrow$ $\color{#FF0000} \overrightarrow {S_{3}}=8.44{m} 30° \nwarrow$
(d) La velocidad de cada bloque a los dos segundos de ser liberados: Vamos a la ecuación de la velocidad en función del tiempo para el movimiento rectilíneo con aceleración constante.
$\color{#0000FF} v = {\color{Red}\bcancel {{\color{blue}v_0}}} + at$ $\color{#0000FF} v = at$ $\color{#0000FF} v =(4.22)2$ $\color{#0000FF} v =8.44\dfrac {m}{s}$
$\color{#FF0000} \overrightarrow {v_{10}}=8.44\dfrac {m}{s} \downarrow$ $\color{#FF0000} \overrightarrow {v_{5}}=8.44\dfrac {m}{s} \leftarrow$ $\color{#FF0000} \overrightarrow {v_{3}}=8.44\dfrac {m}{s} 30° \nwarrow$
La escena interactiva, diseñada por Alberto Rubio, Agustin JiménezAlberto Rubio, Agustin Jiménez, son autores de la red GeoGebra quienes publicaron la escena interactiva "Simulación plano inclinado".
La escena interactiva muestra un bloque sobre un plano inclinado. El ángulo del plano inclinado se puede variar con el deslizador desde $\color{#0000FF} 0°$ (plano horizontal) hasta una inclinación de $\color{#0000FF} 30°$. La masa varia con el deslizador entre $\color{#0000FF} 20Kg$ hasta $\color{#0000FF} 50Kg$. La fuerza aplicada al bloque varia con el deslizador desde $\color{#0000FF} 0 N$ hasta $\color{#0000FF} 500 N$. el coeficiente de rozamiento cinético varia con el deslizador desde $\color{#0000FF} 0$ hasta $\color{#0000FF} 0.7$.
La escena interactiva cuenta con tres botones que se deben utilizar en el siguiente orden; botón de INICIO, botón de EMPEZAR, botón de PARAR.
Adicionalmente la escena interactiva cuenta con un botón (al lado derecho abajo) que al activarse muestra o deja de mostrar las componentes del peso (una componente a lo largo del plano y otra componente perpendicular al plano).
• Manipule los deslizadores dejándolos en los siguientes valores $\color{#0000FF} \theta = 30°$, $\color{#0000FF} m_{(Kg)} = 50$, $\color{#0000FF} F_{(N)}=100$, $\color{#0000FF} \mu = 0.05$
• Sin manipular la escena interactiva determine con los modelos matemáticos explicados: (a) El peso del bloque, (b) La componente del peso a lo largo del plano, (c) La componente del peso perpendicular al plano, (d) la fuerza de rozamiento, (e) la aceleración del bloque.
• Pulse el botón EMPEZAR y deje correr la escena interactiva.
• Cuando el boque llega al final del recorrido aparece en la pantalla los valores de (a) El peso del bloque, (b) La componente del peso a lo largo del plano, (c) La componente del peso perpendicular al plano, (d) la fuerza de rozamiento, (e) la aceleración del bloque.
• Compare los valores obtenidos por medio de los modelos matemáticos con los valores arrojados en la escena interactiva.
Desde una plataforma circular giratoria de $\color{#0000FF} 6m$ de diámetro giran unas sillas de $\color{#0000FF} 8Kg$. Las sillas giran por medio de una cuerda de $\color{#0000FF} 3m$ de longitud. En el instante mostrado las cuerdas forman un ángulo de $\color{#0000FF} 30°$ con la vertical y éste ángulo se mantiene constante. Determine: (a) La tensión en la cuerda, (b) La velocidad de la silla, (c) La tensión en la cuerda y la velocidad de la silla si un niño de $\color{#0000FF} 50Kg$ va sentado en la silla.
Solución:
Cuando los cuerpos se mueven por trayectorias curvas es
Hacemos el diagrama de cuerpo libre de la silla. Ubicamos los ejes móviles $\color{#0000FF} t, n, b$. El eje tangencial se ve como un punto y su parte positiva es hacia adentro de la hoja (de la pantalla), el eje normal en su parte positiva va dirigido hacia el centro de la trayectoria circular de la silla, el eje binormal en su parte positiva es hacia arriba.
Dibujamos desde el origen del sistema coordenado móvil todas las fuerzas externas que actúan obre la silla en un comienzo vacía, la Tensión y el peso de la silla. Observamos que no existen fuerzas sobre el eje tangencial, la Tensión tiene una componente (positiva) a lo largo del eje normal $\color{#0000FF} T Sen 30°$ y una componente (positiva) a lo largo del eje binormal $\color{#0000FF} T Cos 30°$. El peso $\color{#0000FF} mg$ es hacia el centro de la tierra y coincide con la parte negativa del eje binormal.
(a) La tensión en la cuerda: Hacemos sumatoria de fuerzas binormales: $\color{#0000FF} \Sigma F_{b}=ma_{b}$ $\color{#0000FF} a_{b}=0$ $\Rightarrow$ $\color{#0000FF} 0=T Cos 30 - mg$ $\color{#0000FF} mg=T Cos 30$ $\Rightarrow$ $\color{#0000FF} T = \dfrac {mg}{Cos 30}$ $\color{#0000FF} T = \dfrac {8*9.81}{Cos 30}$ $\color{#FF0000} T =90.62 N$
(b) La Velocidad de la silla: Hacemos sumatoria de fuerzas normales: $\color{#0000FF} \Sigma F_{n}=ma_{n}$ $\color{#0000FF} a_n = \dfrac {v^2}{R}$ $\color{#0000FF} \Sigma F_{n}=m \dfrac {v^2}{R}$
$\color{#0000FF} m \dfrac {v^2}{R}= T Sen 30$ $\color{#0000FF} v^2=\dfrac {RT Sen 30}{m}$ $\color{#0000FF} v=\pm\sqrt \dfrac {RT Sen 30}{m}$
De la ecuación debemos tomar el valor positivo porque la velocidad siempre tiene su sentido en la dirección positiva del eje tangencial. En el diagrama de cuerpo libre se aprecia que el radio $\color{#0000FF} R = 3 + 3 Sen 30$ $\color{#0000FF} R = 4.5m$
$\color{#0000FF} v=\sqrt \dfrac {4.5 \cdot 90.62 Sen 30}{8}$ $\color{#FF0000} v=5.05\dfrac {m}{s}$
(c) La Tensión en la cuerda y la velocidad de la silla si un niño de $\color{#0000FF} 50Kg$ va sentado en la silla:
Las ecuaciones de las sumatorias de fuerzas no cambian. Lo que cambia es el valor de la masa (a la masa de la silla se le suma la masa del niño $\color{#0000FF} m=(8+50)Kg)$:
$\color{#0000FF} T = \dfrac {mg}{Cos 30}$ $\Rightarrow$ $\color{#0000FF} T = \dfrac {(8 + 50)9.81}{Cos 30}$ $\color{#FF0000} T = 657 N$
$\color{#0000FF} v=\pm\sqrt \dfrac {RT Sen 30}{m}$ $\color{#0000FF} v=\sqrt \dfrac {R\dfrac {mg}{Cos 30} Sen 30}{m}$
$\color{#0000FF} v=\sqrt \dfrac {R {\color{Red}\bcancel {{\color{blue}m}}}g tag 30}{ {\color{Red}\bcancel {{\color{blue}m}}}}$ $\color{#0000FF} v=\sqrt {Rg tag 30}$
$\color{#0000FF} v=\sqrt {4.5 \cdot 9.81 tag 30}$ $\color{#FF0000} v=5.05\dfrac {m}{s}$
La masa se cancela. Quiere esto decir que la velocidad de las sillas no depende de la masa de quien este en la silla. Para cualquier valor de la masa la velocidad será la misma; es por ésta razón que en las sillas se pueden montar personas con diferentes masas e incluso puede haber sillas vacías.
Un avión de $\color{#0000FF} 80000Lb$ gira en una trayectoria circular horizontal de $\color{#0000FF} 300 Ft$ de diámetro alrededor de un globo estático con una rapidez constante de $\color{#0000FF} 64 \dfrac {ft}{s}$. Determine: (a) el ángulo $\color{#0000FF} \theta$ respecto de la vertical que debe tener el avión para lograr la maniobra. (b) Determine la fuerza centrípeta que soporta el avión. (c) Determine la fuerza de elevación.
Solución: para que un avión pueda sostenerse en el aire viajando en línea recta a una altura constante (las alas del avión estarán horizontales) actúan básicamente dos fuerzas, el peso del avión $\color{#0000FF} mg$ y la fuerza de elevación $\color{#0000FF} F_E$ que serán exactamente iguales y de sentido contrario sobre la vertical. La fuerza de elevación es siempre perpendicular a las alas del avión y el peso siempre dirigido al centro de la tierra.
Para el caso que nos presenta el ejercicio en que el avión hace un giro alrededor de un globo estático; el avión tiene que desnivelar las alas (ya no estarán horizontales) de tal forma que la fuerza de elevación se inclinara buscando el radio sobre el
cual girara el avión. Esto hace que aparezca una fuerza resultante de la suma entre el peso del avión y la fuerza de elevación dirigida hacia el centro de curvatura (radio) llamada fuerza centrípeta.
(a) el ángulo respecto de la vertical que debe tener el avión para lograr la maniobra: sobre el dibujo hemos hecho el diagrama de cuerpo libre del avión. El eje tangencial positivo es perpendicular a la hoja (la pantalla) hacia afuera, el eje normal positivo es hacia adentro de la curva, el eje binormal positivo es hacia arriba.
$\color{#0000FF} \Sigma F_{n}=ma_{n}$ $\color{#008000} ma_{n}=F_E Sen \theta$ $\color{#008000} (1)$
$\color{#0000FF} \Sigma F_{b}=m {\color{Red}\bcancel {{\color{blue}a_b}}}$ $\color{#0000FF} 0=F_E Cos \theta - mg$ $\color{#008000} mg=F_E Cos \theta$ $\color{#008000} (2)$
Dividimos la ecuación $\color{#008000} (1)$ con la ecuación $\color{#008000} (2)$
$\color{#0000FF} \dfrac {{\color{Red}\bcancel {{\color{blue}m}}}a_n}{{\color{Red}\bcancel {{\color{blue}m}}}g}=\dfrac {{\color{Red}\bcancel {{\color{blue}F_E}}} Sen\theta}{{\color{Red}\bcancel {{\color{blue}F_E}}} Cos \theta}$ $\color{#0000FF} a_n=\dfrac {v^2}{R}$ $\color{#0000FF} \dfrac {v^2}{Rg}=tag \theta$
$\color{#0000FF} \theta=tag^{-1}(\dfrac {v^2}{Rg})$ $\color{#0000FF} \theta=tag^{-1}(\dfrac {64^2}{150 \cdot 32.2})$ $\color{#FF0000} \theta=40.30°$
(b) Determine la fuerza centrípeta que soporta el avión: La fuerza centrípeta va dirigida hacia el centro curvatura.
$\color{#0000FF} F_c=ma_n$ $\color{#0000FF} F_c=m\dfrac {v^2}{R}$ $\color{#0000FF} mg=Peso$ $\Rightarrow$ $\color{#0000FF} m=\dfrac {Peso}{g}$
$\color{#0000FF} F_c=\dfrac {mg}{g}(\dfrac {v^2}{R})$ $\color{#0000FF} F_c=\dfrac {80000}{32.2}(\dfrac {64^2}{150})$ $\color{#FF0000} F_c=67842.65Lb$
(c) Determine la fuerza de elevación: Fuerza que permite que el avión se mantenga a la misma altura mientras realiza la maniobra de girar al rededor del globo estático. Fuerza que la podemos despejar de la sumatoria de fuerzas binormales en la ecuación $\color{#008000} (2)$
$\color{#008000} mg=F_E Cos \theta$ $\color{#008000} (2)$ $\color{#0000FF} F_E=\dfrac {mg}{Cos \theta}$ $\color{#0000FF} F_E=\dfrac {80000}{Cos 30°}$
$\color{#FF0000} F_E=92376.04 Lb$
Sobre éste ejercicio podemos resolver otros conceptos:
(d) Si consideramos la recta que une el centro de gravedad del avión con el globo estático (El Radio). Determine la velocidad angular de ésta línea. Conocemos la velocidad del centro de gravedad del avión que es un punto de la recta llamada el radio entonces podemos hallar la velocidad angular $\color{#0000FF} w$.
$\color{#0000FF} v=wR$ $\color{#0000FF} w=\dfrac {v}{R}$ $\color{#0000FF} w=\dfrac {64}{150}$ $\color{#FF0000} w=0.4267 \dfrac {rad}{s}$
(e) Determine el tiempo que le toma al avión en dar una vuelta al rededor del globo. Nos piden el periodo:
$\color{#0000FF} T=\dfrac {2\pi}{w}$ $\color{#0000FF} T=\dfrac {2\pi}{w}$ $\color{#0000FF} T=\dfrac {2\pi}{0.4267}$ $\color{#FF0000} T=14.73 {s}$
(f) Determine la frecuencia del movimiento.
$\color{#0000FF} f=\dfrac {1}{T}$ $\color{#0000FF} f=\dfrac {1}{14.73}$ $\color{#FF0000} f=0.0679 {H_z}$
(g) A cuantas revoluciones por minuto gira el avión.
$\color{#0000FF} w=0.4267\dfrac {\quad{\color{Red}\bcancel {{\color{blue}rad}}}}{\quad{\color{Red}\bcancel {{\color{blue}s}}}} \cdot \dfrac {\quad{\color{Red}\bcancel {{\color{blue}vuelta}}}}{2\pi \quad{\color{Red}\bcancel {{\color{blue}rad}}}} \cdot \dfrac {revolución}{\quad{\color{Red}\bcancel {{\color{blue}vuelta}}}} \cdot \dfrac {60 \quad{\color{Red}\bcancel {{\color{blue}s}}}}{minuto}$
$\color{#0000FF} w=4.07 \dfrac {\quad{\color{Red}\bcancel {{\color{blue}rev}}}}{\quad{\color{Red}\bcancel {{\color{blue}min}}}} \cdot \dfrac {rpm}{\dfrac {\quad{\color{Red}\bcancel {{\color{blue}rev}}}}{\quad{\color{Red}\bcancel {{\color{blue}min}}}}}$ $\color{#FF0000} w=4.07 rpm$
(h) Si el avión mide 64 metros de largo y su centro de gravedad ésta justo en la mitad de ésta distancia, determine la velocidad en la punta del avión. Todo el avión gira en torno al globo estático con la misma velocidad angular. para hallar la velocidad de la punta del avión necesitamos el radio desde el globo a la punta del avión. el avión gira tangencialmente a la trayectoria circular en el punto de su centro de gravedad. Así se forma un triángulo rectángulo que muestra la figura:
$\color{#0000FF} v=wR_P$ $\color{#0000FF} R_P=\sqrt {{150^2} + {32^2}}$ $\color{#0000FF} R_P=153.38 ft$
$\color{#0000FF} v=0.4267(153.38)$ $\color{#FF0000} v=65.44 \dfrac {ft}{s}$
El video introductorio hace parte de la serie Universo MecánicoLa serie educativa Universo Mecánico es una colección de 52 videos creados por el Instituto de Tecnología de California cuyo director y anfitrión es el Dr. David L. Goodtein.
El trabajo $\color{#0000FF} W$ físicamente hablando es la capacidad que tienen los cuerpos de producir energía. La energía $\color{#0000FF} E$ es la capacidad que tienen los cuerpos de producir trabajo. Dos conceptos que van de la mano, el uno nos lleva al otro. El trabajo y la energía son un mismo concepto, $\color{#0000FF} W=E$
Para que exista trabajo se requiere que exista una fuerza aplicada a un cuerpo y que la fuerza o una componente de ésta produzca un desplazamiento del cuerpo o que ésta fuerza se oponga al desplazamiento del cuerpo cuando el cuerpo se mueve.
El trabajo puede ser realizado por una fuerza constante o por una fuerza variable, en éste capítulo veremos ambos tipos de trabajo con sus respectivas aplicaciones.
La figura muestra una fuerza constante que se aplica a un bloque y produce un desplazamiento horizontal desde el punto $\color{#0000FF} (1)$ hasta el punto $\color{#0000FF} (2)$.
Veamos las características de la fuerza constante que produce el desplazamiento:
Descomponemos la fuerza en dos componentes, una componente paralela al desplazamiento $\color{#0000FF} F Cos \theta$ y otra componente perpendicular al desplazamiento $\color{#0000FF} F sen \theta$.
La fuerza $\color{#0000FF} F sen \theta$ no colabora, no aporta en nada para que el bloque se desplace de la posición $\color{#0000FF} (1)$ a la posición $\color{#0000FF} (2)$. Ésta fuerza es perpendicular al desplazamiento del bloque, $\color{#0000FF} F sen \theta$ forma un ángulo de $\color{#0000FF} 90°$ con el desplazamiento.
La fuerza $\color{#0000FF} F Cos \theta$ es la responsable de que el bloque se desplace de la posición $\color{#0000FF} (1)$ a la posición $\color{#0000FF} (2)$. La fuerza $\color{#0000FF} F Cos \theta$ es la componente de la fuerza $\color{#0000FF} F$ a lo largo del desplazamiento.
En conclusión, el Trabajo $\color{#0000FF} W$ es el producto de $\color{#0000FF} F Cos \theta$ por el desplazamiento $\color{#0000FF} d$.
$\color{#0000FF} W=(F Cos \theta)d$ que se puede escribir: $\color{#0000FF} W=Fd Cos \theta$.
Observamos que la fuerza $\color{#0000FF} \overrightarrow {F}$ es un vector, que el desplazamiento $\color{#0000FF} \overrightarrow {d}$ es un vector y que si realizamos el producto punto:
$\color{#0000FF} \overrightarrow {F} \cdot \overrightarrow {d}=W=Fd Cos \theta$
El ángulo $\color{#0000FF} \theta$ es entre el vector desplazamiento $\color{#0000FF} \overrightarrow {d}$ y el vector fuerza $\color{#0000FF} \overrightarrow {F}$. Recordemos que el producto punto de vectores da por resultado un escalar; entonces el trabajo $\color{#0000FF} W$ y la Energía $\color{#0000FF} E$ son escalares.
$\color{#0000FF} W=Fd Cos \theta$ es la ecuación para el trabajo realizado por una fuerza constante (que la fuerza no cambia ni en magnitud ni dirección), que no cambia durante el desplazamiento.
Las unidades del trabajo las obtenemos de la ecuación:
$\color{#0000FF} W=Fd Cos \theta$ $\color{#0000FF} W=[Nm]$ $\color{#0000FF} W=[Lbft]$
$\color{#0000FF} Trabajo=W=[Nm]=[J]=[Julios]=E=Energía$.
Es claro con el análisis de unidades que el trabajo es energía y la energía es trabajo.
Vemos que para evaluar el trabajo realizado por una fuerza no se requiere de los ejes $\color{#0000FF} x,y,z,t,n,b$; se requiere el valor de la magnitud de la fuerza $\color{#0000FF} {F}$ (positivo), el valor de la magnitud del desplazamiento $\color{#0000FF} {d}$ (positivo) y conocer el Coseno del ángulo $\color{#0000FF} \theta$ entre la fuerza y el desplazamiento. Así que el signo del trabajo lo pone $\color{#0000FF} Cos \theta$.
En la ecuación de trabajo $\color{#0000FF} W=Fd Cos \theta$, el $\color{#0000FF} Cos \theta$ puede ser positivo, negativo o valer cero. El signo positivo de $\color{#0000FF} Cos \theta$ indica que la fuerza le inyecta energía al sistema (que la fuerza colabora con el desplazamiento del cuerpo), que el ángulo entre la fuerza y el desplazamiento está entre $\color{#0000FF} 0\leq \theta < 90$. El ángulo entre la fuerza y el desplazamiento en la práctica se mide entre $\color{#0000FF} 0\leq \theta \geq 180$
El signo negativo de $\color{#0000FF} Cos \theta$ indica que la fuerza le quita energía al sistema (que la fuerza se opone al movimiento del cuerpo), que el ángulo entre la fuerza y el desplazamiento está entre $\color{#0000FF} 90< \theta \geq 180$.
El valor de cero del $\color{#0000FF} Cos \theta$ se da para cuando $\color{#0000FF} \theta =90°$, indica que la fuerza ni aporta ni le quita energía al sistema (la fuerza no interviene en el movimiento del cuerpo ni le ayuda a desplazarse ni se opone al desplazamiento).
en ocasiones en el tema de trabajo y energía se recurre a las leyes de Newton y será necesario aplicar los ejes $\color{#0000FF} x,y,z,t,n,b$, pero solo para encontrar alguna incógnita tal como el valor de una fuerza normal $N$.
Cuando el cuerpo se desplaza de la posición $\color{#0000FF} (1))$ a la posición $\color{#0000FF} (2))$ actúan varias fuerzas y podemos encontrar el trabajo realizado por cada una de éstas Fuerzas.
En el tema de trabajo y energía el diagrama de cuerpo libre no se realiza en el inicio del desplazamiento, ni se realiza al final del desplazamiento, se realiza en un lugar cualquiera de la trayectoria entre la posición $\color{#0000FF} (1)$ y la posición $\color{#0000FF} (2)$. Sobre el diagrama se deben dibujar todas las fuerzas que actuaron durante la trayectoria entre la posición $\color{#0000FF} (1)$ y la posición $\color{#0000FF} (2)$.
$\color{#0000FF} W_{12}^F=Fd Cos \theta$
$\color{#0000FF} W_{12}^N=Nd {\color{Red}\bcancel {{\color{blue}Cos 90°}}} = 0$
$\color{#0000FF} W_{12}^{F_g}=mgd {\color{Red}\bcancel {{\color{blue}Cos 90°}}} = 0$
$\color{#0000FF} W_{12}^{f_k}=f_kd Cos 180° = - f_kd = - u_k Nd$
A nivel de nomenclatura, la expresión $\color{#0000FF} W_{12}^F=Fd Cos \theta$ se lee así: El trabajo realizado por la fuerza para cuando el cuerpo se desplaza de la posición $\color{#0000FF} (1))$ a la posición $\color{#0000FF} (2))$ es igual a la magnitud de la fuerza $\color{#0000FF} F$ multiplicada por la magnitud del desplazamiento $\color{#0000FF} d$, multiplicado por el ángulo entre el vector fuerza $\color{#0000FF} \overrightarrow {F}$ y el vector distancia $\color{#0000FF} \overrightarrow {d}$.
La expresión $\color{#0000FF} W_{12}^N=Nd Cos 90$ se lee así: El trabajo realizado por la fuerza Normal para cuando el cuerpo se desplaza de la posición $\color{#0000FF} (1))$ a la posición $\color{#0000FF} (2))$ es igual a la magnitud de la fuerza Normal $\color{#0000FF} N$ multiplicada por la magnitud del desplazamiento $\color{#0000FF} d$, multiplicado por el ángulo entre el vector Fuerza Normal $\color{#0000FF} \overrightarrow {N}$ y el vector distancia $\color{#0000FF} \overrightarrow {d}$, que en este cao es de $\color{#0000FF} 90°$ y $\color{#0000FF} cos 90° = 0$, es por ello que el $\color{#0000FF} W_{12}^N=Nd {\color{Red}\bcancel {{\color{blue}Cos 90°}}} = 0$.
La expresión $\color{#0000FF} W_{12}^{F_g}=md Cos 90$ se lee así: El trabajo realizado por la
fuerza de gravedad $\color{#0000FF} \overrightarrow F_g$ para cuando el cuerpo se desplaza de la posición $\color{#0000FF} (1))$ a la posición $\color{#0000FF} (2))$ es igual a la magnitud de la fuerza de gravedad $\color{#0000FF} mg$ multiplicada por la magnitud del desplazamiento $\color{#0000FF} d$, multiplicado por el ángulo entre el vector Fuerza de gravedad $\color{#0000FF} \overrightarrow {F_g}$ y el vector distancia $\color{#0000FF} \overrightarrow {d}$, que en este cao es de $\color{#0000FF} 90°$ y $\color{#0000FF} cos 90° = 0$, es por ello que el $\color{#0000FF} W_{12}^{F_g}=mgd{\color{Red}\bcancel {{\color{blue}Cos 90°}}} = 0$.
La expresión $\color{#0000FF} W_{12}^{f_k}=f_kd Cos 180°$ se lee así: El trabajo realizado por la fuerza de rozamiento cinético para cuando el cuerpo se desplaza de la posición $\color{#0000FF} (1))$ a la posición $\color{#0000FF} (2))$ es igual a la magnitud de la fuerza de rozamiento cinético $\color{#0000FF} f_k$ multiplicada por la magnitud del desplazamiento $\color{#0000FF} d$, multiplicado por el ángulo entre el vector Fuerza de rozamiento cinético $\color{#0000FF} \overrightarrow {f_k}$ y el vector distancia $\color{#0000FF} \overrightarrow {d}$, que en éste y en todos lo caso el ángulo es de $\color{#0000FF} 180°$, y $\color{#0000FF} cos 180° = -1$, entonces diremos que $\color{#0000FF} W_{12}^{f_k}= -f_kd$. Recordemos que $\color{#0000FF} f_k=u_k N$ es por ello que el $\color{#0000FF} W_{12}^{f_k}= -u_k Nd$.
La fuerza de rozamiento cinético y el desplazamiento siempre forman un ángulo de $\color{#0000FF} 180°$ sin importar la trayectoria tomada por el cuerpo.
En una trayectoria curva el desplazamiento del cuerpo siempre es tendiente a la parte positiva del eje tangencial y el rozamiento siempre es sobre el eje tangencial en su parte negativa, así que existirá en todos los casos un ángulo de $\color{#0000FF} 180°$ entre el desplazamiento y la fuerza de rozamiento.
$\color{#0000FF} W_{12}^{f_k}=f_kd Cos 180° = - f_kd = - u_k Nd$ es una expresión que podemos tenerla como fórmula para cuando buscamos determinar el trabajo realizado por la fuerza de rozamiento cinético.
Una vez hemos encontrado el trabajo de cada una de las fuerza, podemos determinar el trabajo Neto realizado sobre el cuerpo cuando éste se desplazó de la posición $\color{#0000FF} (1))$ a la posición $\color{#0000FF} (2))$
El trabajo Neto es la sumatoria de todos trabajos realizados por todas y cada una de las fuerzas para cuando el cuerpo se desplazó de la posición $\color{#0000FF} (1)$ a la posición $\color{#0000FF} (2)$: $\hspace{0.2cm} \color{#0000FF} W_{Neto}=\Sigma W_{12}$.
Para el caso del ejercicio que estamos realizando, el trabajo Neto es:
$$\color{#0000FF} W_{Neto}=\Sigma W_{12} = W_{12}^F + W_{12}^N + W_{12}^{F_g} + W_{12}^{f_k}$$
$\color{#0000FF} W_{12}^F=Fd Cos \theta$
$\color{#0000FF} W_{12}^N=Nd {\color{Red}\bcancel {{\color{blue}Cos 90°}}} = 0$
$\color{#0000FF} W_{12}^{F_g}=mgd {\color{Red}\bcancel {{\color{blue}Cos 90°}}} = 0$
$\color{#0000FF} \dfrac {W_{12}^{f_k}=f_kd Cos 180° = - f_kd = - u_k Nd}{W_{Neto} = Fd Cos \theta - u_k Nd}$
Supongamos que para nuestro ejemplo la masa es de $\color{#0000FF} 10Kg$, el desplazamiento es de $\color{#0000FF} 4m$, la fuerza aplicada es de $\color{#0000FF} 50N$, el ángulo $\color{#0000FF} \theta =30°$ y el coeficiente de rozamiento cinético es$\color{#0000FF} u_k=0.1$. El trabajo Neto sera:$\color{#0000FF} {W_{Neto} = Fd Cos \theta - u_k Nd}$
$\color{#0000FF} {W_{Neto} = 50(4) Cos 30° - 0.1 N (4)}$
Para hallar el trabajo Neto falta conocer la Magnitud de la fuerza normal. Recurrimos al tema de Leyes de Newton.
Como ya tenemos el diagrama de cuerpo libre del bloque, asignamos ejes $\color{#0000FF} x,y$ para realizar la sumatoria de fuerzas en $\color{#0000FF} y$ para despejar el valor de a fuerza Normal.
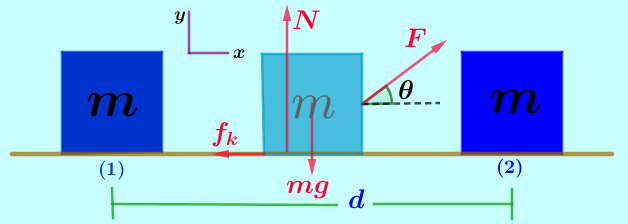
$\color{#0000FF} \Sigma F_y=0=N+F Sen \theta - mg$ $\Rightarrow$ $\color{#FF0000} N=mg-F Sen \theta$
Remplazamos en la ecuación de trabajo Neto.
$\color{#0000FF} {W_{Neto} = Fd Cos \theta - u_k Nd}$ $\color{#0000FF} {W_{Neto} = 50(4) Cos 30° - 0.1 N (4)}$
$\color{#0000FF} {W_{Neto} = 50(4) Cos 30° - 0.1 (mg-F Sen \theta) (4)}$
$\color{#0000FF} {W_{Neto} = 50(4) Cos 30° - 0.1 (10*9.81-50* Sen 30)(4)}$
$\color{#FF0000} W_{Neto} = 143.97N.m$
El trabajo Neto $\color{#FF0000}W_{Neto} = 143.97 N.m$ positivo, indica que al sumar el trabajo realizado por todas la fuerzas, el resultado es que se le inyecto energía al sistema y el bloque pudo desplazarse desde la posición $\color{#0000FF} (1))$ a la posición $\color{#0000FF} (2))$.
Al analizar el trabajo de una fuerza contante se utilizó entre otras el trabajo de la fuerza de gravedad para el caso en que la fuerza de gravedad actúa en forma perpendicular al movimiento del cuerpo.
Ahora analizaremos el trabajo de la fuerza de gravedad para cualquier desplazamiento del cuerpo sin importar la trayectoria que tome el cuerpo siempre y cuando se conozca la altura inicial de la que sale el cuerpo y la altura final a donde llega el cuerpo.

Supongamos que el bloque se mueve hacia arriba de la superficie inclinada.
Podemos observar que el la fuerza de gravedad (peso) y el desplazamiento no forman un ángulo de $\color{#0000FF} 90°$ (si la fuerza de gravedad y el desplazamiento forman ángulo de $\color{#0000FF} 90°$, el trabajo de la fuerza de gravedad es cero), entonces descomponemos la fuerza de gravedad en dos componentes, una componente perpendicular al desplazamiento ($\color{#0000FF} mg Cos\theta)$ y otra componente a lo largo del desplazamiento ($\color{#0000FF} mg Sen\theta$) como se muestra en la figura.
Podemos ahora decir que el trabajo de la fuerza de gravedad es el trabajo realizado por estas componentes.
$\color{#0000FF} W_{12}^{F_g}= W_{12}^{mgSen\theta}+W_{12}^{mgCos\theta}$$\color{#0000FF} W_{12}^{F_g}=(mg Sen \theta)d Cos 180° + (mg Cos \theta)d {\color{Red}\cancel {{\color{blue}Cos 90°}}}$
$\color{#0000FF} W_{12}^{F_g}=-(mg Sen \theta)d$ $\color{#008000} W_{12}^{F_g}=-mgd Sen \theta$
Ahora, de la grafica: En el triangulo grande (la plataforma)
$\color{#0000FF} Sen \theta = \dfrac {h}{d}$ $\Rightarrow$ $\color{#0000FF} dSen \theta =h$ Remplazamos en $\color{#008000} W_{12}^{F_g}=-mgd Sen \theta$
$\color{#0000FF} W_{12}^{F_g}=-mgh$ Como $\color{#0000FF} h=(y_2-y_1)$ $\Rightarrow$ $\color{#FF0000} W_{12}^{F_g}=-mg(y_2-y_1)$
Ésta es la ecuación general para encontrar el trabajo de la fuerza de gravedad. El trabajo de la fuerza de la gravedad ha quedado en función de la altura $\color{#0000FF} h=(y_2-y_1)$, donde $\color{#0000FF} y_1$ es la altura inicial del cuerpo y $\color{#0000FF} y_2$ es la altura final del cuerpo, sin importar la trayectoria que tome el cuerpo.
Podemos utilizar ésta ecuación para encontrar el trabajo de la fuerza de gravedad sin importar la trayectoria del bloque, tomemos el caso en que el bloque se desplaza horizontalmente
Tomamos como nivel de referencia para medir las alturas $\color{#0000FF} NR$ la superficie horizontal por la que se desplaza el bloque. Nótese que el cuerpo sale de la altura $\color{#0000FF} y_1=0$ en la posición $\color{#0000FF} (1)$ hasta la altura $\color{#0000FF} y_2=0$ en la posición $\color{#0000FF} y_2=0$. Si remplazamos éstos valores en la ecuación de trabajo de la fuerza de gravedad queda:
$\color{#0000FF} W_{12}^{F_g}=-mg(\quad{\color{Red}\bcancel {{\color{blue}y_2}}}-\quad{\color{Red}\bcancel {{\color{blue}y_1}}})$ $\Rightarrow$ $\color{#FF0000} W_{12}^{F_g}=0$
Cuando un cuerpo recorre una trayectoria desde una posición $\color{#0000FF} (1)$ hasta una posición $\color{#0000FF} (2)$ puede ocurrir que sobre el cuerpo actúen fuerzas constante y/o fuerzas variables. Para el trabajo de las fuerzas constantes aplicamos los conceptos vistos hasta ahora en este capítulo. Respecto de las fuerzas variables en este curso haremos el estudio de la fuerza elástica como fuerza variable, será en un curso mas adelante que veamos el trabajo de las fuerzas variables en general.
Cuando a un cuerpo se le aplica una fuerza y éste reacciona contra la fuerza deformadora buscando recuperar su estado original decimos que éste cuerpo ejerce una fuerza elástica. Pensamos inmediatamente en un resorte.
Veamos algunas características de la fuerza elástica en su forma mas sencilla como lo es en un resorte
• Cuando un resorte se encuentra en su estado natural (sin estirar, sin encoger), su longitud se llama longitud normal $\color{#0000FF} L_0$ y diremos que el resorte está en equilibrio. La fuerza que hace el resorte cuando está en equilibrio (en estado natural) es cero $\color{#0000FF} F_e=0$. La deformación del resorte es $\color{#0000FF} x=0$.
• Los resortes se pueden estirar, se pueden encoger y en cualquiera de éstos casos su longitud se llama $\color{#0000FF} L$.
• La distancia desde el punto de equilibrio hasta donde el resorte se estira o se encoge se llama deformación y se representa por $\color{#0000FF} x$. El valor de la distancia que se deforma el resorte $\color{#0000FF} x$ se toma siempre positivo sin importar si el resorte se estira o se encoge.
• De la grafica se observa que $\color{#0000FF} x=\left| L_0-L \right|$ o $\color{#0000FF} x=\left| L-L_0 \right|$, Siempre positivo
En el siglo $\color{#0000FF} XVII$ el físico Ingles Robert Hooke realizo estudios acerca del comportamiento de los resortes, encontrando y desarrollando los siguientes conceptos.
• La fuerza realizada por un resorte es igual y de sentido contrario a la fuerza aplicada al resorte.
• Un resorte siempre hace fuerza buscando el equilibrio, por ello a la fuerza realizada por un resorte se le llama fuerza recuperadora.
• La fuerza realizada por un resorte es directamente proporcional y de sentido contrario a la deformación $\color{#0000FF} x$ (alargamiento o
encogimiento) del resorte medido a partir del punto de equilibrio: $\color{#0000FF} F_e \alpha -x$, el signo negativo indica el hecho de que la fuerza elástica $\color{#0000FF} F_e$ es en sentido contrario a la deformación del resorte $\color{#0000FF} x$.
• Para lograr una igualdad (una ecuación) a partir de la proporcionalidad analizada, Hooke agrega una constante de proporcionalidad llamada constante elástica $\color{#0000FF} k$ y logra la igualdad: $\color{#0000FF} F_e = -kx$ donde $\color{#0000FF} k$, la constante elástica es característica para cada resorte; ésta constante tiene valores pequeños para resortes muy suaves (el resorte de un lapicero) y valores altos para resortes duros (el resorte de un amortiguador de un automóvil).
$\color{#0000FF} F_e=-kx$ Es una fuerza Variable que depende de la deformación $\color{#0000FF} x$. Cuando $\color{#0000FF} x$ aumenta, aumenta la fuerza elástica, Cuando $\color{#0000FF} x$ disminuye, disminuye la fuerza elástica.
$\color{#0000FF} x$: Es la deformación del resorte medida desde el punto de equilibrio. Se mide en metros $\color{#0000FF} m$ o en pies $\color{#0000FF} ft$. De la ecuación es claro que cuando $\color{#0000FF} x=0$ la fuerza elástica es cero $\color{#0000FF} F_e=-k(0)=0$ que ocurre cuando el resorte está en equilibrio.
$\color{#0000FF} F_e=-kx$ El signo negativo indica que la fuerza elástica siempre se opone a la deformación del resorte, quiere esto decir que al llevar la fuerza elástica a un sistema de referencia de ejes coordenados como el caso de leyes de Newton el signo no va (el signo negativo es un atributo de la fuerza por ser contraria a la deformación del resorte). Los signos que imponen los sistemas de referencia utilizados en las leyes de newton son signos algebraicos para sumatorias y la fuerza elástica se expresara: $\color{#0000FF} F_e=kx$.
Las unidades de la constante elástica $\color{#0000FF} k$ se deducen al despejarla de la ecuación $\color{#0000FF} F_e=kx$ donde $\color{#0000FF} k=\dfrac {F_x}{x}$. Así $\color{#0000FF} k=[\dfrac {N}{m}]$ o $\color{#0000FF} k=[\dfrac {Lb}{ft}]$.
La fuerza de un resorte puede aplicarse a un cuerpo y eventualmente producir trabajo. Podemos adherir a uno de los extremos de un resorte un bloque, alargar el resorte con el bloque adherido y soltarlo, es posible que se produzca el desplazamiento del bloque por la acción de la fuerza recuperadora del resorte y producirse un trabajo.
El bloque se desplazara desde una posición $\color{#0000FF} (1)$ hasta una posición $\color{#0000FF} (2)$, se presenta entonces un trabajo realizado por una fuerza variable.
El trabajo realizado por una fuerza variable se define como
$\color{#0000FF} \displaystyle W_{12}^{F_vble}=\int ^{x_1}_{x_2}F_x dx$ Remplazamos para la fuerza elástica $\color{#0000FF} F_e=-kx$
$\color{#0000FF} \displaystyle W_{12}^{F_e}=-\int ^{x_1}_{x_2}kx dx$ $\color{#008000} W_{12}^{F_e}= - \dfrac {1}{2}k(x_2^2 - x_1^2)$.
Con ésta ecuación hallamos el trabajo realizado por un resorte cuando al actuar sobre un cuerpo, éste se desplaza de una posición $\color{#0000FF} (1)$ hasta una posición $\color{#0000FF} (2)$.$\color{#0000FF} x_1$: Deformación inicial del resorte medido desde el punto de equilibrio.
$\color{#0000FF} x_2$: Deformación final del resorte medido desde el punto de equilibrio.
En éste curso para encontrar el trabajo realizado por un resorte vamos directamente a la formula sin necesidad de recurrir a la integral.
Escena interactiva, diseñada por Elvira Martinez y Carlos RomeroElvira Martinez y Carlos Romero son autores de la red GeoGebra quienes publicaron la escena interactiva "Fuerza que actúa sobre un muelle".
Ejercicio 5.1: La escena interactiva muestra un resorte adherido a un muro. En el otro extremo del resorte se adhiere un bloque. El bloque se lleva al extremo derecho y se libera del reposo y comienza a oscilar armónicamente.
• Determine el valor de la constante elástica del resorte si la fuerza máxima ejercida por el resorte es de $\color{#0000FF} 5 Lb$
$\color{#0000FF} F_e=kx$ $\Rightarrow$ $\color{#0000FF} k=\dfrac {F_e}{x}$ $\color{#0000FF} k=\dfrac {5}{1.4}$ $\color{#FF0000} k= 3.57 \dfrac {Lb}{ft}$
• Determine el trabajo realizado por el resorte para cuando el bloque se desplaza desde el extremo derecho hasta cuando pasa
por la posición de equilibrio.
$\color{#008000} W_{12}^{F_e}= - \dfrac {1}{2}k(x_2^2 - x_1^2)$ $\color{#0000FF} W_{12}^{F_e}= - \dfrac {1}{2}3.57(0^2 - 1.4^2)$
$\color{#FF0000} W_{12}^{F_e}= 3.5 Lb.ft$
La energía es la capacidad que tienen los cuerpos de generar trabajo, la energía se asocia con la transformación de algo, los niños crecen, los animales corren, las maquinas realizan alguna tarea, el universo cambia a cada instante.
El universo tiene una cantidad de energía que se mantiene constante desde su creación, "La energía no se crea ni se destruye, la energía se transforma".
La energía se manifiesta de muchas formas, energía química, Energía nuclear, energía térmica, energía mecánica, energía eólica, energía eléctrica, energía luminosa, energía solar, entre otras. En éste curso nos concentraremos en la energía mecánica.
La energía mecánica es la capacidad que tienen los cuerpos de producir un trabajo mecánico una transformación o un movimiento
La energía mecánica es la sumatoria de la energía cinética y la energía potencial: $\color{#0000FF} E=E_k+E_p$
La energía potencial es la capacidad que tienen los cuerpos de producir trabajo en virtud de su posición o configuración. en este curso nos concentraremos en la energía potencial gravitacional y en la energía potencial elástica.
$\blacktriangleright\hspace{0.2cm}$ Energía Potencial GravitacionalCuando un cuerpo se encuentra a una determinada altura respecto de un nivel de referencia, por ese solo hecho tiene energía potencial, el cuerpo puede caer y producir trabajo, tal es el caso del agua cuando cae en una represa que es capaz de mover las aspas de unos motores (Dinamos) y generar energía eléctrica. Como ya vimos la expresión matemática para el trabajo realizado por la fuerza de gravedad $\color{#0000FF} W_{12}^{Fg}=mgh$, es la misma expresión de la energía potencial gravitacional: $\color{#0000FF} E_{Pg}=mgh$
$\blacktriangleright\hspace{0.2cm}$ Energía Potencial ElásticaCuando un cuerpo es un resorte o se comporta con características iguales a las de un resorte, es decir que la fuerza que realiza es de la forma $\color{#0000FF} F_{e}=-kx$ y este cuerpo es capaz de producir trabajo que se representa como $\color{#0000FF} W_{12}^{F_e}=-\dfrac {1}{2} kx$, obtenemos la expresión para la energía potencial elástica: $\color{#0000FF} E_{Pe}=-\dfrac {1}{2} kx$
Una fuerza es conservativa cuando el trabajo realizado por esta fuerza sobre un cuerpo, el trabajo no depende de la trayectoria que tome el cuerpo en su trayectoria y que el trabajo de ir y volver a la misma posición es igual a cero.
Entre las fuerzas conservativas tenemos la fuerza de gravedad y la fuerza elástica entre otras.
Recordemos que el trabajo de la fuerza de gravedad se describe como $\color{#0000FF} W_{12}^{F_g}=-mg(y_2-y_1)$, trabajo que depende de la altura inicial del cuerpo y de la altura final sin importar la trayectoria que tome el cuerpo desde la posición inicial a la posición final y si el cuerpo se desplaza y vuelve a la misma altura de la que salió el trabajo de la fuerza de gravedad es cero, quedaría que $\color{#0000FF} y_2=y_1$ y el factor $\color{#0000FF} (y_2-y_1)=0$. El trabajo no depende de la trayectoria que le tome al cuerpo al pasar de una altura inicial hasta una altura final.
Recordemos también el trabajo realizado por la fuerza elástica $\color{#0000FF} W_{12}^{F_e}= - \dfrac {1}{2}k(x_2^2 - x_1^2)$, trabajo que depende de la deformación final del resorte medida desde el punto de equilibrio y de la deformación inicial del resorte medida desde el punto de equilibrio y el trabajo de la fuerza elástica es cero cuando el resorte se deforma desde una deformación inicial y finalmente vuelve a la misma deformación inicial ya que $\color{#0000FF} x_2=x_1$ y el factor $\color{#0000FF} (x_2^2 - x_1^2)=0$. El trabajo no depende de la trayectoria que le tome al resorte al deformarse desde la deformación inicial hasta la deformación final.
Una fuerza es No conservativa o disipativa cuando el trabajo realizado sobre un cuerpo depende de la trayectoria que tome el cuerpo al desplazarse de un lugar a otro; y el trabajo realizado por ésta fuerza para cuando el cuerpo se desplazó y volvió a la misma posición de la que salió es diferente de cero.
Lo que hacen estas fuerzas no conservativas es disipar energía del sistema como el caso de las fuerzas de rozamiento cinético que
provocan perdidas de energía al sistema en forma de calor (el motor que se calienta).
Entre las muchas fuerzas no conservativas en éste curso estudiaremos la fuerza de rozamiento cinético como única fuerza no conservativa.
Recordemos que el trabajo realizado por la fuerza de rozamiento es $\color{#0000FF} W_{12}^{f_k}=-f_kNd=-u_kNd$ donde $\color{#0000FF} d$ es el camino, la trayectoria recorrida por el cuerpo siempre sumando positivamente cada punto de la trayectoria.
La energía cinética es la capacidad que tienen los cuerpos de producir trabajo en virtud de su movimiento.
Cuando un cuerpo se desplaza (se mueve) de una posición a otra está generando energía mecánica. Es por esto que a la energía cinética se le conoce como la energía del movimiento.
$\color{#0000FF} E_k= \dfrac {1}{2}mv^2$
El teorema del trabajo y la energía cinética afirma que el trabajo neto realizado sobre un cuerpo es igual cambio en la energía cinética del cuerpo.
$\color{#0000FF} W_{Neto}=\Delta E_k$
$\color{#0000FF} W_{Neto}=E_{k_2}-E_{k_1}$
$\color{#0000FF} W_{Neto}=\dfrac{1}{2}mv_2^2-\dfrac{1}{2}mv_1^2$
Ahora contamos con dos formas de calcular el trabajo neto realizado sobre un cuerpo:
Una es haciendo un diagrama de cuerpo libre en un lugar cualquiera de la trayectoria del cuerpo entre las posiciones inicial y final, determinamos el trabajo realizado por cada una de las fuerzas y luego sumamos todos los trabajos.
La otra forma es aplicando el teorema del trabajo y la energía cinética, esto cuando conocemos o podemos determinar la velocidad inicial y la velocidad final del cuerpo.
Un vehículo de $\color{#0000FF} 1000Kg$ pasa un semáforo en verde a una velocidad de $\color{#0000FF} 10 \dfrac {m}{s}$, al pasar por el próximo semáforo lo hace a una velocidad de $\color{#0000FF} 20 \dfrac {m}{s}$; determine el trabajo neto realizado sobre el vehículo.
Solución: Conocemos la velocidad inicial, la velocidad final y la masa del vehículo, entonces aplicamos el teorema del trabajo y la energía cinética para determinar el trabajo neto.
$\color{#0000FF} W_{Neto}=\dfrac{1}{2}mv_2^2-\dfrac{1}{2}mv_1^2$ $\color{#0000FF} W_{Neto}=\dfrac{1}{2}m(v_2^2-v_1^2)$
$\color{#0000FF} W_{Neto}=\dfrac{1}{2}1000(20^2-10^2)$ $\color{#FF0000} W_{Neto}=150000Nm$
Un cuerpo de $\color{#0000FF} 1 Slug$ tiene una velocidad de $\color{#0000FF} 2 \dfrac{ft}{s}$ en un punto $\color{#0000FF} A$ y una energía cinética de $\color{#0000FF} 5 Lb.ft$ en un punto $\color{#0000FF} B$. Determine $\color{#0000FF} (a)$ el trabajo neto sobre el cuerpo entre los puntos $\color{#0000FF} A$ y $\color{#0000FF} B$, $\color{#0000FF} (b)$ La velocidad del cuerpo en el punto $\color{#0000FF} (B)$
Solución:$\color{#0000FF} (a)$ $\color{#0000FF} W_{AB}=E_{k_B}-E_{k_A}$ Tenemos la $\color{#0000FF} E_{kB}=5 Lb.ft$, la $\color{#0000FF} v_A=2 \dfrac{ft}{s}$ y la masa del cuerpo $\color{#0000FF} 1 Slug$
$\color{#0000FF} W_{AB}=E_{k_B}-\dfrac {1}{2}mv_A^2$ $\color{#0000FF} W_{AB}=5-\dfrac {1}{2}1(2^2)$ $\color{#FF0000} W_{AB}=3Lb.ft$
$\color{#0000FF} (b)$ $\color{#0000FF} W_{AB}=\dfrac{1}{2}mv_B^2-\dfrac{1}{2}mv_A^2$ $\color{#0000FF} W_{AB}+\dfrac{1}{2}mv_A^2=\dfrac{1}{2}mv_B^2$
$\color{#0000FF}\sqrt {\dfrac {2(W_{AB}+\dfrac{1}{2}mv_A^2)}{m}}=v_B=\sqrt {\dfrac {2({3}+\dfrac{1}{2}(1)2^2)}{1}}$ $\color{#FF0000} v=3.16\dfrac{ft}{s}$
"La energía no se crea ni se destruye, la Energía se transforma"
En un sistema donde No existen fuerzas No conservativas (No existen fuerzas de rozamiento), la energía inicial es exactamente igual a la energía final $\color{#0000FF} E_1=E_2$.
La energía mecánica es la suma de la energía cinética más la energía potencial entonces:
$\color{#0000FF} E_1=E_2$
$\color{#0000FF} E_{k_1}+E_{P_1}=E_{k_2}+E_{P_2}$
$\color{#0000FF} E_{k_1}+E_{Pg_1}+E_{Pe_1}=E_{k_2}+E_{Pg_2}+E_{Pe_2}$
$\color{#0000FF} \dfrac{1}{2}mv_1^2+mgh_1+\dfrac{1}{2}kx_1^2=\dfrac{1}{2}mv_2^2+mgh_2+\dfrac{1}{2}kx_2^2$
Escena interactiva, diseñada por Pablo PiedrahitaPablo Piedrahita es autor de la red GeoGebra quien publico la escena interactiva "Movimiento circular uniforme".
• La escena interactiva muestra un sistema masa resorte que se mueve horizontalmente sobre una superficie sin fricción.
• El resorte está adherido al bloque y es desplazado al extremo derecho y se libera desde el reposo.
• En ese instante la velocidad inicial es cero y por tanto la energía
cinética del sistema es cero $\color{#0000FF} \dfrac{1}{2}mv_2^2=0$ pero como el resorte está estirado, el sistema tiene pura energía potencial $\color{#0000FF} \dfrac{1}{2}kx_2^2$. Observe en la gráfica que la energía potencial en este instante (la curva color verde) es máxima e igual a la energía total.
• Recordemos que la energía mecánica es la suma de la energía cinética y la energía potencial $\color{#0000FF} E= E_k+E_p$. Para éste sistema (masa resorte) la energía total es $\color{#0000FF} E=\dfrac{1}{2}mv_2^2 + \dfrac{1}{2}kx_2^2$ y como no tenemos energía disipadora, la energía total es una constante. Una vez se libera el bloque, el movimiento será de un extremo al otro en forma perpetua.
• Al darle PLAY (en el botón abajo a la izquierda), el boque sale de la velocidad cero y empieza a ganar velocidad (gana energía cinética $\color{#0000FF} \dfrac{1}{2}mv_2^2$) y el resorte empieza a perder deformación (pierde energía potencial $\color{#0000FF} \dfrac{1}{2}kx_2^2$), lo que se pierde en energía potencial se gana en energía cinética manteniéndose constante la energía total.
• Deje correr la escena interactiva y observe como en cada instante existe intercambio entre energía cinética y energía potencial.
• Cuando el resorte recupera su longitud normal (cuando no está deformado) la energía potencial es cero y la energía cinética es máxima e igual a la energía total.
• El bloque continua su movimiento a la izquierda. Ahora empieza a perder velocidad (energía cinética) y empieza a ganar deformación (energía potencial) el resorte y así en forma perpetua se mantendrá el intercambio de energía cinética y de energía potencial manteniéndose la energía total constante.
En un sistema donde existen fuerzas No conservativas (existen fuerzas de rozamiento), la energía inicial del sistema se ve menguada (disminuida) por el efecto de las fuerzas no conservativas.
La Energía ya no se conserva entre dos posiciones $\color{#0000FF} E_1>E_2$ entonces $\color{#0000FF} E_1+W_{12}^{F_{NC}}=E_2$, que para este curso la única fuerza no conservativa que trataremos es la fuerza de rozamiento cinético $\color{#0000FF} E_1+W_{12}^{F_{f_k}}=E_2$
Recordemos que el trabajo de la fuerza de rozamiento cinético es negativo $\color{#0000FF} W_{12}^{f_k}=-f_kNd=-u_kNd$ y por lo tanto en la ecuación de la energía le esta es robando a la energía inicial $\color{#0000FF} E_1$:
$\color{#0000FF} E_1+W_{12}^{F_{f_k}}=E_2$
$\color{#0000FF} E_{k_1}+E_{P_1}+W_{12}^{F_{f_k}}=E_{k_2}+E_{P_2}$
$\color{#0000FF} E_{k_1}+E_{Pg_1}+E_{Pe_1}W_{12}^{F_{f_k}}=E_{k_2}+E_{Pg_2}+E_{Pe_2}$
$\color{#0000FF} \dfrac{1}{2}mv_1^2+mgh_1+\dfrac{1}{2}kx_1^2+W_{12}^{F_{f_k}}=\dfrac{1}{2}mv_2^2+mgh_2+\dfrac{1}{2}kx_2^2$
Para el caso en que se trate de dos o más cuerpos, dos o mas resortes, dos o más fuerzas de rozamiento cinético la ecuación de la energía será:
$\color{#0000FF} \Sigma\dfrac{1}{2}mv_1^2+\Sigma mgh_1+\Sigma\dfrac{1}{2}kx_1^2+\Sigma W_{12}^{f_k}=\Sigma\dfrac{1}{2}mv_2^2+\Sigma mgh_2+$
$\color{#0000FF} \Sigma\dfrac{1}{2}kx_2^2$
Es ésta la ecuación de la energía que vamos a utilizar para desarrollar los ejercicios que a continuación plantearemos.
Escena interactiva, diseñada por Jhon AtencioJhon Atencio es autor de la red GeoGebra quien publico la escena interactiva "Trabajo".
De acuerdo con el modelo de la escena interactiva, un bloque de masa $\color{#0000FF} m$ parte del reposo desde la parte superior del plano inclinado un ángulo $\color{#0000FF} \theta°$ , se desliza por el plano inclinado una distancia $\color{#0000FF} d$ hasta que hace contacto con un resorte no deformado de masa despreciable. El bloque se desliza una distancia adicional $\color{#0000FF} x$ comprimiendo el resorte de constante elástica $\color{#0000FF} k$ alcanzando momentáneamente el reposo. Entre el bloque y el plano inclinado existe fricción con coeficiente de rozamiento cinético $\color{#0000FF} u_k$. (a) Demuestre que para el caso planteado la distancia $\color{#0000FF} d= \dfrac {kx^2}{2mg(Sen \theta -u_k Cos \theta} - x$
(b) Con los datos que muestra la escena interactiva demuestre que la distancia $\color{#0000FF} d=10m$
Solución:
(a) Por tratarse de un solo bloque, un resorte, un rozamiento, entonces aplicamos la ecuación energía:
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue}\dfrac{1}{2}mv_1^2}}} +mgh_1+ {\color{Red}\bcancel {{\color{blue}\dfrac{1}{2}kx_1^2}}}+W_{12}^{F_{f_k}}= {\color{Red}\bcancel {{\color{blue}\dfrac{1}{2}mv_2^2}}}+$
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue}mgh_2}}}+\dfrac{1}{2}kx_2^2$
Cancelamos las energías cinéticas inicial y final. Nos ubicamos en la parte más baja del movimiento del bloque como nivel de referencia para mirar las alturas $\color{#0000FF} h_1$ y $\color{#0000FF} h_2$ de las energías potenciales gravitacionales inicial y final, así $\color{#0000FF} h_2=0$ y cancelamos la energía potencial gravitacional final. Cancelamos la energía potencial elástica inicial porque el resorte no tiene deformación cuando el bloque está en el punto $\color{#0000FF} (1)$
$\color{#0000FF} mgh_1+W_{12}^{F_{f_k}}=\dfrac{1}{2}kx_2^2$
El trabajo realizado por la fuerza de rozamiento cinético es $\color{#0000FF} W_{12}^{f_k}=-u_kN(d+x)$. En la gráfica hemos realizado la deducción para la Fuerza Normal por medio de las leyes de Newton $\color{#0000FF} N=mgCos\theta$. También en la gráfica se deduce la altura inicial del bloque $\color{#0000FF} h_1= (d+x)Sen\theta$. Remplazamos:
$\color{#0000FF} mg(d+x)Sen\theta + -u_kmg Cos\theta (d+x) =\dfrac{1}{2}kx_2^2$
Al lado izquierdo de la ecuación factorizamos los términos comunes $\color{#0000FF} mg(d+x)$
$\color{#0000FF} mg(d+x)(Sen\theta + -u_kCos\theta) =\dfrac{kx_2^2}{2}$
$\color{#0000FF} (d+x)=\dfrac{kx_2^2}{2mg(Sen\theta + -u_kCos\theta)}$
$\color{#FF0000} d=\dfrac{kx_2^2}{2mg(Sen\theta -u_kCos\theta)}-x$
(b) La escena interactiva tiene los siguientes datos:
$\color{#0000FF} m=2Kg$, $\color{#0000FF} k=50 \dfrac {N}{m}$, $\color{#0000FF} \theta = 30°$, $\color{#0000FF} u_k=0.3$, $\color{#0000FF} x=1.47m$:
$\color{#0000FF} d=\dfrac{50(1.47)^2}{2(2)9.81(Sen 30°- 0.3Cos 30°)}- 1.47$
$\Rightarrow$ $\color{#FF0000} d=10m$
La potencia $\color{#0000FF} P$ es la cantidad de trabajo realizado en la unidad de tiempo. Es la cantidad de energía entregada en la unidad de tiempo. La potencia es la razón a la que se entrega energía, la razón a la que se realiza trabajo.
El concepto de potencia nos permite conocer por ejemplo que máquina, que fuerza, que sistema nos realiza un trabajo en el menor tiempo posible. La potencia es el cociente entre dos escalares, el trabajo y el tiempo, por lo que la potencia es un escalar.
$\color{#0000FF} P=\dfrac {dE}{dt}$ $\color{#0000FF} P=\dfrac {\Delta E}{\Delta t}$ $\color{#0000FF} P=\dfrac {E_2-E_1}{t_2-t_1}$
$\color{#0000FF} P=\dfrac {dW}{dt}$ $\color{#0000FF} P=\dfrac {\Delta W}{\Delta t}$ $\color{#0000FF} P=\dfrac {W_2-W_1}{t_2-t_1}$
Como la potencia es $\color{#0000FF} P=\dfrac {dW}{dt}$ y el trabajo de una fuerza constante es $\color{#0000FF} W_{12}^{F_{cte}}=FSCos \theta$, donde $\color{#0000FF} S$ es el desplazamiento, entonces un deferencial de trabajo será $\color{#0000FF} dW_{12}^{F_{cte}}=F(dS)Cos\theta$ así:
$\color{#0000FF} P=\dfrac {dW}{dt}$ $\color{#0000FF} P=\dfrac {F(dS)Cos\theta} {dt}$ $\color{#0000FF} P=F \dfrac {ds}{dt}Cos \theta$
como: $\color{#0000FF} \dfrac {ds}{dt}=v$ $\Rightarrow$ $\color{#008000} P={FvCos\theta}$ $\color{#008000} P= \overrightarrow F \cdot \overrightarrow v $
Unidades: $\color{#0000FF} P=\dfrac {dW}{dt}$ $[\color{#0000FF} \dfrac {N.m}{s}= '\dfrac {J}{s} = watt]$ [SI]
$\color{#0000FF} P=\dfrac {dW}{dt}$ $[\color{#0000FF} \dfrac {Lb.ft}{s}]$ [FPS]
En el sistema [FPS] frecuentemente se da la potencia en "caballos de potencia" [hp]
$\color{#0000FF} [hp]=550 \dfrac {Lb.ft}{s}$ al pasar al sistema [SI] es $\color{#0000FF} [hp]=746 [watt = w]$
Escena interactiva, diseñada por Steve CheungSteve Cheung es autor de la red GeoGebra quien publico la escena interactiva "Problem Work Energy Q4".
Un esquiador parte del reposo en el punto $\color{#0000FF} A$, la parte superior de una colina que no presenta fricción y le toma $\color{#0000FF} 3.41$ segundos llegar al punto$\color{#0000FF} B$. Determine la velocidad en $\color{#0000FF} B$, el trabajo de $\color{#0000FF} A \ $ a $\color{#0000FF} B \ $ y la potencia promedio en $\color{#0000FF} hp$ entregada por el esquiador entre el punto $\color{#0000FF} A$ y el punto $\color{#0000FF} B$.
• Por conservación de la energía mecánica:
$\color{#0000FF} E_1=E_2$
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue}\dfrac{1}{2}mv_A^2}}}+mgh_A=\dfrac{1}{2}mv_B^2+ {\color{Red}\bcancel {{\color{blue}mgh_B}}}$
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue}m}}}gh_A=\dfrac{1}{2} {\color{Red}\bcancel {{\color{blue}m}}}v_A^2$
$\color{#0000FF} v_B=\sqrt {2gh}$ $\color{#0000FF} v_B=\sqrt {2(9.81)57.11}$ $\color{#FF0000} v_B=33.47 \dfrac {m}{s}$• Por el teorema del trabajo y la energía cinética:
$\color{#0000FF} W_{Neto}= \dfrac {1}{2}mv_f^2-\dfrac {1}{2}mv_i^2$ $\color{#0000FF} W_{AB}= \dfrac {1}{2}mv_B^2- {\color{Red}\bcancel {{\color{blue}\dfrac{1}{2}mv_A^2}}}$
$\color{#0000FF} {W_{AB}}=\dfrac {1}{2}mv_B^2$ $\color{#0000FF} {W_{AB}}=\dfrac {1}{2}100(33.47^2)$
$\color{#FF0000} {W_{AB}}=56012.05 J$
• Por definición de Potencia:
$\color{#0000FF} P=\dfrac {\Delta W}{\Delta t}=\dfrac {W_B-W_A}{t_2-t_1}=\dfrac {W_{AB}}{t_{12}}$
$\Rightarrow$ $\color{#0000FF} P= \dfrac {{W_{AB}}}{t_{12}}$ $\color{#0000FF} P= \dfrac {{56012.05}}{3.41}$ $\color{#FF0000} P=16425.82 Watt$
$\color{#0000FF} P=16425.82 {\color{Red}\bcancel {{\color{blue}Watt}}} * \dfrac {hp}{746 {\color{Red}\bcancel {{\color{blue}Watt}}} }$ $\color{#FF0000} P=22.02 hp$
El video introductorio hace parte de la serie Universo MecánicoLa serie educativa Universo Mecánico es una colección de 52 videos creados por el Instituto de Tecnología de California cuyo director y anfitrión es el Dr. David L. Goodtein.
Existen unos fenómenos físicos que merecen ser tratados en física mecánica como el caso del impacto dado por un bate de beisbol a la bola en el cual la bola está en contacto con el bate apenas un instante de tiempo y esto es suficiente para cambiar completamente el estado de movimiento que tenía la bola antes del contacto con el bate.
Fenómenos como el impacto entre dos bolas de billar, el choque entre dos vehículos son el tema de estudio en éste capítulo. El camino a seguir para el análisis de estos eventos es tomar la segunda ley de Newton y llevarla a una integral respecto del tiempo y lograr así unos modelos matemáticos que nos llevaran al principio del Impulso y conservación del momentum lineal.
Cuando la bola de beisbol es golpeada por el bate, éste le imprime por un tiempo muy corto una fuerza que produce en la bola un cambio en su velocidad y aceleración muy grandes que hacen posible que la bola sobrepase la cerca. De la segunda ley de Newton:
$\color{#0000FF} \Sigma \overrightarrow {F}=m\overrightarrow {a}$ $\color{#0000FF} \overrightarrow {a}=\dfrac {d\overrightarrow {v}}{dt}$ $\color{#0000FF} \Sigma \overrightarrow {F}=m\overrightarrow \dfrac {d\overrightarrow {v}}{dt}$
$\color{#0000FF} \Sigma \overrightarrow {F}dt=md\overrightarrow {v}$ $\color{#0000FF} \displaystyle \Sigma \int ^{t_2}_{t_1} \overrightarrow {F}dt=m\int ^{v_2}_{v_1}d\overrightarrow {v}$
$\color{#0000FF} \displaystyle \Sigma \int ^{t_2}_{t_1} \overrightarrow {F}dt=m(\overrightarrow {v_2}- \overrightarrow {v_1})$ $\color{#008000} \displaystyle \Sigma \int ^{t_2}_{t_1} \overrightarrow {F}dt=m\overrightarrow {v_2}- m\overrightarrow {v_1}$
De la parte izquierda de la ecuación, la suma de todas las fuerzas que actúan durante un tiempo determinado sobre un cuerpo se llama Impulso$\color{#0000FF} \overrightarrow {I}$: $\color{#0000FF} \displaystyle \overrightarrow {I}=\Sigma \int ^{t_2}_{t_1} \overrightarrow {F}dt$
$\color{#008000} \overrightarrow {I}=m\overrightarrow {v_2}- m\overrightarrow {v_1}$
En la parte derecha de la ecuación, el termino $\color{#0000FF} m\overrightarrow {v}=\overrightarrow {P}$ donde $\color{#0000FF} \overrightarrow {P}$ es Momentum Lineal
$\color{#008000} \overrightarrow {I}=\overrightarrow {P_2}- \overrightarrow {P_1}$
$\color{#008000} \overrightarrow {I}=\Delta \overrightarrow {P}$
Ésta ecuación se llama Principio del Impulso y Momento Lineal.Las unidades del Impulso y del momento Lineal son las mismas:
$\color{#0000FF} \displaystyle \overrightarrow {I}=\Sigma \int ^{t_2}_{t_1} \overrightarrow {F}dt=[Ns]$ [SI] $\color{#0000FF} \displaystyle \overrightarrow {I}=\Sigma \int ^{t_2}_{t_1} \overrightarrow {F}dt=[Lbs]$ [FPS]
$\color{#0000FF} \overrightarrow {P} = m\overrightarrow {v}= [Kg\dfrac {m}{s}]$ [SI] $\color{#0000FF} \overrightarrow {P} = m\overrightarrow {v}= [Slug\dfrac {ft}{s}]$ [FPS]
$\color{#0000FF} \overrightarrow {I}=[Ns=\dfrac {Kgm}{s^{{\color{Red}\bcancel {{\color{blue}2}}}}} \cdot {{\color{Red}\bcancel {{\color{blue}s}}}}]=[Kg\dfrac {m}{s}]=\overrightarrow {P}$ [SI]
$\color{#0000FF} \overrightarrow {I}=[Lbs=\dfrac {Slug.ft}{s^{{\color{Red}\bcancel {{\color{blue}2}}}}} \cdot {{\color{Red}\bcancel {{\color{blue}s}}}}]=[Slug\dfrac {ft}{s}]=\overrightarrow {P}$ [FPS]
La ecuación del Principio del Impulso y Momento Lineal:
$\color{#0000FF} \overrightarrow {I}=m\overrightarrow {v_2}- m\overrightarrow {v_1}$ se puede escribir de la siguiente manera que nos parece más didáctica: ; $\color{#0000FF} m\overrightarrow {v_1}+ \overrightarrow {I}=m\overrightarrow {v_2}$
Una buena interpretación del Principio del Impulso y Momento Lineal será:
Un cuerpo con Momentum inicial $\color{#0000FF} \overrightarrow {P_1}=m\overrightarrow {v_1}$ que es sometido a un Impulso dado por fuerzas externas durante un tiempo $\color{#0000FF} \displaystyle \overrightarrow {I}=\Sigma \int ^{t_2}_{t_1} \overrightarrow {F}dt$, el cuerpo quedara con un momentum final $\color{#0000FF} \overrightarrow {P_2}=m\overrightarrow {v_2}$.$\color{#008000} \displaystyle m\overrightarrow {v_1}+\Sigma \int ^{t_2}_{t_1} \overrightarrow {F}dt=m\overrightarrow {v_2}$
Con el Principio del Impulso y Momento Lineal se resuelven problemas que involucran fuerzas, tiempo y velocidad.
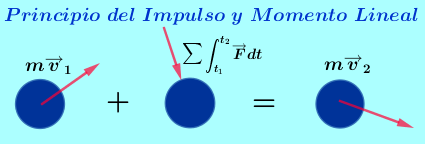
La figura representa el diagrama de Impulso y Momento Lineal que es la representación vectorial de los tres pasos consecutivos que se siguen en el proceso en el que un cuerpo es sometido a fuerzas externas en un periodo de tiempo.
El primer término representa vectorialmente el instante antes de efectuarse el o los impulsos sobre el cuerpo, este primer término indica el momento lineal inicial del cuerpo $\color{#0000FF} m\overrightarrow {v_1}$.
El Segundo término representa vectorialmente la fuerza o las fuerzas en el tiempo que produce el o los impulsos sobre el cuerpo. Representado este fenómeno por medio de una sumatoria de cada una de las fuerzas involucradas en ese tiempo $\color{#0000FF} \displaystyle \Sigma \int ^{t_2}_{t_1} \overrightarrow {F}dt$.
El tercer término es el resultado en forma vectorial de los dos primeros términos, representa el instante después de el o los impulsos a que fue sometido el cuerpo. El cuerpo queda con un momento lineal final $\color{#0000FF} m\overrightarrow {v_2}$.
Al momento de resolver ejercicios que involucran vectores como es el caso de la aplicación del principio del Impulso y Momento Lineal es conveniente descomponer la ecuación del principio del Impulso y Momento Lineal en componentes escalares $\color{#0000FF} x$ $\color{#0000FF} y$ $\color{#0000FF} z$ ya que se facilita los cálculos en forma algebraica.
$\color{#008000} \displaystyle m{v_{1_x}}+\Sigma \int ^{t_2}_{t_1} {F_x}dt=m{v_{2_x}}$
$\color{#008000} \displaystyle m{v_{1_y}}+\Sigma \int ^{t_2}_{t_1} {F_y}dt=m{v_{2_y}}$
$\color{#008000} \displaystyle m{v_{1_z}}+\Sigma \int ^{t_2}_{t_1} {F_z}dt=m{v_{2_z}}$
El automóvil de $\color{#0000FF} 2000 Kg$ se encuentra originalmente en reposo sobre la superficie horizontal. si durante $\color{#0000FF} 12$ segundos el motor ejerce una fuerza de $\color{#0000FF} 5000$ newton determine la velocidad final del automóvil.
Solución:
El problema involucra Fuerza, tiempo y velocidad, entonces aplicamos el Principio del Impulso y Momento Lineal:
$\color{#008000} \displaystyle m\overrightarrow {v_1}+\Sigma \int ^{t_2}_{t_1} \overrightarrow {F}dt=m\overrightarrow {v_2}$
El automóvil se mueve durante $\color{#0000FF} 12$ segundos sobre la superficie horizontal bajo la acción de una fuerza de constante. El Impulso se halla con el producto de la fuerza por el tiempo.
$\color{#0000FF} \displaystyle \Sigma \int ^{t_2}_{t_1} \overrightarrow {F_x}dt=\overrightarrow {F_x} \int ^{t_2}_{t_1} dt$
$\color{#0000FF} \displaystyle \Sigma \int ^{t_2}_{t_1} \overrightarrow {F_x}dt=\overrightarrow {F_x}(t_2-t_1)$ $\color{#0000FF} \displaystyle \Sigma \int ^{t_2}_{t_1} \overrightarrow {F_x}dt=\overrightarrow {F_x}\Delta t$
Aplicamos el principio del Impulso y Momento Lineal en su componente Horizontal.
$\color{#008000} \displaystyle m{v_{1_x}}+\Sigma \int ^{t_2}_{t_1} {F_x}dt=m{v_{2_x}}$
$\color{#0000FF} m{\color{Red}\bcancel {{\color{blue}{v_{1_x}}}}}+F_x\Delta t=m{v_{2_x}}$
$\color{#0000FF} \dfrac {F_x\Delta t}{m}=v_2$ $\color{#008000} v_2=\dfrac {(5000)(12)}{2000}$ $\color{#0000FF} v_2=30 \dfrac {m}{s}$
$\color{#FF0000} \overrightarrow v_2=30 \dfrac {m}{s} \rightarrow$
Recordemos la Tercera Ley de Newton, Acción y Reacción: Cuando dos cuerpos interactúan entre si (cuerpo $\color{#0000FF} 1$ y cuerpo $\color{#0000FF}2$), la fuerza que el cuerpo $\color{#0000FF} 1$ ejerce sobre el cuerpo $\color{#0000FF} 2$ es igual y de sentido contrario a la fuerza que el cuerpo $\color{#0000FF} 2$ ejerce sobre el cuerpo $\color{#0000FF} 1$.

La tercera ley de Newton nos enseña que las fuerzas no aparecen solas, siempre aparecen en pareja. Si una persona hace una fuerza a una pared, la pared responde con una fuerza exactamente igual y de sentido contrario. Entonces:
$\color{#0000FF} \overrightarrow {F_{12}}= -\overrightarrow {F_{21}}$ $\Leftrightarrow$ $\color{#0000FF} -\overrightarrow {F_{12}}= \overrightarrow {F_{21}}$
$\color{#0000FF} \overrightarrow {F_{12}}= m_1\overrightarrow {a_1}$ y $\color{#0000FF} \overrightarrow {F_{21}}=m_2\overrightarrow {a_2}$ $\Rightarrow$ $\color{#0000FF} -m_1\overrightarrow {a_1}=\color{#0000FF} m_2\overrightarrow {a_2}$
$\color{#0000FF} -m_1\dfrac {d\overrightarrow {v_1}}{{\color{Red}\bcancel {{\color{blue}dt}}}}=\color{#0000FF} m_2\dfrac {d\overrightarrow {v_2}}{{\color{Red}\bcancel {{\color{blue}dt}}}}$ $\color{#0000FF} -m_1{d\overrightarrow {v_1}}=m_2{d\overrightarrow {v_2}}$
$\color{#0000FF} -m_1({\overrightarrow {v_{1_f}}}-\overrightarrow {v_{1_i}})=m_2({\overrightarrow {v_{2_f}}-\overrightarrow {v_{2_i}}})$
$\color{#0000FF} -m_1{\overrightarrow {v_{1_f}}}+m_1{\overrightarrow {v_{1_i}}}=m_2{\overrightarrow {v_{2_f}}}-m_2{\overrightarrow {v_{2_i}}}$
Acomodamos condiciones iniciales al lado izquierdo y condiciones finales al lado derecho de la ecuación para llegar a la ecuación de la Conservación del Momento Lineal.
$\color{#008000}m_1{\overrightarrow {v_{1_i}}}+m_2{\overrightarrow {v_{2_i}}}= m_1{\overrightarrow {v_{1_f}}}+m_2{\overrightarrow {v_{2_f}}}$
Para un sistema de partículas (varios cuerpos) la ecuación de la Conservación del Momento Lineal es:
$\color{#008000} \Sigma m{\overrightarrow {v_{i}}}= \Sigma m{\overrightarrow {v_{f}}}$
Como $\color{#0000FF} m\overrightarrow {v}=\overrightarrow {P}$ Momentum Lineal
$\color{#0000FF} {\overrightarrow {P_{1_i}}}+{\overrightarrow {P_{2_i}}}= {\overrightarrow {P_{1_f}}}+{\overrightarrow {P_{2_f}}}$
Ésta ecuación nos indica que el momento inicial de las partículas viéndolas en conjunto es igual al momento final de ellas en conjunto. De manera más simplificada:
$\color{#008000} \Sigma {\overrightarrow {P_i}}= \Sigma{\overrightarrow {P_f}}$
La ecuación para la Conservación del Momento Lineal es una ecuación vectorial que permite ser analizada a partir de componentes escalares $\color{#0000FF} x$ $\color{#0000FF} y$ $\color{#0000FF} z$ ya que se facilita los cálculos en forma algebraica.
$\color{#008000}m_1{{v_{1_{xi}}}}+m_2{{v_{2_{xi}}}}= m_1{{v_{1_{xf}}}}+m_2{{v_{2_{xf}}}}$
$\color{#008000}m_1{{v_{1_{yi}}}}+m_2{{v_{2_{yi}}}}= m_1{{v_{1_{yf}}}}+m_2{{v_{2_{yf}}}}$
$\color{#008000}m_1{{v_{1_{zi}}}}+m_2{{v_{2_{zi}}}}= m_1{{v_{1_{zf}}}}+m_2{{v_{2_{zf}}}}$
Otra Forma de llegar a la ecuación de la Conservación del Momento Lineal es analizar lo que sucede cuando dos cuerpos impactan. Miramos a cada cuerpo por separado aplicándole a cada uno de ellos el principio del Impulso y Momento Lineal en el instante del impacto:
Para el cuerpo $\color{#0000FF}{1}$: $\color{#008000} \displaystyle m_1\overrightarrow {v_{1i}}+\Sigma \int ^{t_2}_{t_1} \overrightarrow {F}dt=m_1\overrightarrow {v_{1f}}$
Para el cuerpo $\color{#0000FF}{2}$: $\color{#008000} \displaystyle m_1\overrightarrow {v_{2i}}+\Sigma \int ^{t_2}_{t_1} \overrightarrow {F}dt=m2\overrightarrow {v_{2f}}$
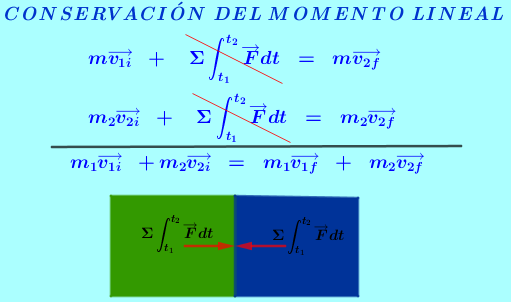
De la gráfica se observa que al momento de interactuar los cuerpos, los Impulsos aplicados al cuerpo $\color{#0000FF}{1}$ son iguales y de sentido contrario a los Impulsos aplicados al cuerpo $\color{#0000FF}{2}$. Ahora sumamos la aplicación del principio del Impulso y Momento Lineal de los dos cuerpos, vemos que se cancelan los impulsos por ser iguales y de sentido contrario, además analicemos que en el momento de la interacción los dos cuerpos se pueden apreciar como un solo sistema y las fuerzas que interactúan entre ellos serán fuerzas internas que se traducen en Impulsos internos que se cancelan.
La aplicación del principio del Impulso y Momento Lineal queda:
$\color{#008000}m_1\overrightarrow {v_{1i}}+m_2\overrightarrow {v_{2i}}=m_1\overrightarrow {v_{1f}}+m_2\overrightarrow {v_{2f}}$
$\color{#008000} \Sigma m{\overrightarrow {v_{i}}}= \Sigma m{\overrightarrow {v_{f}}}$
$\color{#008000} \Sigma {\overrightarrow {P_i}}= \Sigma{\overrightarrow {P_f}}$
Con las respectivas ecuaciones escalares:
$\color{#008000}m_1{{v_{1_{xi}}}}+m_2{{v_{2_{xi}}}}= m_1{{v_{1_{xf}}}}+m_2{{v_{2_{xf}}}}$
$\color{#008000}m_1{{v_{1_{yi}}}}+m_2{{v_{2_{yi}}}}= m_1{{v_{1_{yf}}}}+m_2{{v_{2_{yf}}}}$
$\color{#008000}m_1{{v_{1_{zi}}}}+m_2{{v_{2_{zi}}}}= m_1{{v_{1_{zf}}}}+m_2{{v_{2_{zf}}}}$
Escena interactiva, diseñada por Bard NewittBard Newitt es autor de la red GeoGebra quien publico la escena interactiva "Momentum and Kinetic in collisions".
Ejercicio 6.2:
En la escena interactiva, el bloque $\color{#0000FF} 1$ de $\color{#0000FF} 5 Kg$ se desplaza libremente a $\color{#0000FF} 4 \dfrac {m}{s}$ sobre la pista horizontal. Un bloque $\color{#0000FF} 2$ de $\color{#0000FF} 3 Kg$ se desplaza $\color{#0000FF} 10m$ más adelante a $\color{#0000FF} 3 \dfrac {m}{s}$ sobre la misma pista y en sentido contrario al del bloque $\color{#0000FF} 1$ y justo a encontrarse con él. Si los bloques hacen contacto y se acoplan. Determine: $\color{#0000FF} (a)$ La velocidad de ambos bloques un instante luego del acoplamiento, $\color{#0000FF} (b)$ La fuerza promedio entre ambos bloques si el acoplamiento dura $\color{#0000FF} 0.05$ segundos, $\color{#0000FF} (c)$ a que distancia medida desde el bloque $\color{#0000FF} 1$ hacen contacto los bloques.
Solución: En la escena interactiva manipulamos las casillas de entrada de datos para los valores expresados en el enunciado: Posición inicial del bloque $\color{#0000FF} 1=0m$, Posición inicial del bloque $\color{#0000FF} 2=10m$, Velocidad inicial del bloque $\color{#0000FF} 1=4 \dfrac {m}{s}$, Velocidad inicial del bloque $\color{#0000FF} 2=-3 \dfrac {m}{s}$, masa del bloque $\color{#0000FF} 1=5 Kg$, masa del bloque $\color{#0000FF} 2=3 Kg$
(a) Damos clic al botón "RESET" para asegurar que la escena este en las condiciones iniciales, clic al botón "START" y la escena corre; observamos que todo transcurre sobre el eje de la pista (horizontal).
• En la escena se observa que un instante luego de acoplarse, los bloques quedan unidos (en un solo sistema) y se mueven con la misma velocidad a la derecha $\color{#0000FF} v_{1_{xf}}=v_{2_{xf}}=v_{xf}$
• Aplicamos conservación del Momento Lineal sobre el eje $\color{#0000FF} x$
$\color{#008000}m_1\overrightarrow {v_{1i}}+m_2\overrightarrow {v_{2i}}=m_1\overrightarrow {v_{1f}}+m_2\overrightarrow {v_{2f}}$
$\color{#0000FF}m_1{{v_{1_{xi}}}}+m_2{{v_{2_{xi}}}}= m_1{{v_{1_{xf}}}}+m_2{{v_{2_{xf}}}}$
$\color{#0000FF} m_1{{v_{1_{xi}}}}+m_2{{v_{2_{xi}}}}= {v_{xf}}(m_1+m_2)$
$\color{#0000FF} v_{xf} = \dfrac {m_1{{v_{1_{xi}}}}+m_2{{v_{2_{xi}}}}}{(m_1+m_2)}$ $\color{#0000FF} v_{xf} = \dfrac {5(4)+3(-3)}{(5+3)}$
$\color{#0000FF} v_{xf}=1.38 \dfrac {m}{s}$ $\color{#FF0000} \overrightarrow v_{xf}=1.38 \dfrac {m}{s} \rightarrow$
(b) La fuerza promedio es una constante y es fuerza impulsiva. Aplicamos el Principio del Impulso y Momento Lineal a uno cualquiera de los bloques.
Para el Bloque $\color{#0000FF} 1$: $\color{#008000} \displaystyle m_1\overrightarrow {v_{1i}}+\Sigma \int ^{t_2}_{t_1} \overrightarrow {F}dt=m_1\overrightarrow {v_{1f}}$
$\color{#0000FF} m_1\overrightarrow {v_{1i}}+ \overrightarrow {F} \Delta t=m_1\overrightarrow {v_{1f}}$
• El Impulso sobre $\color{#0000FF} m_1$ en la ecuación es de signo negativo.
$\color{#0000FF} m_1 {v_{1_{xi}}} - {F_x} \Delta t=m_1 {v_{1_{xf}}}$ $\color{#0000FF} m_1 {v_{1_{xi}}} - m_1 {v_{1_{xf}}} = {F_x} \Delta t$
$\color{#0000FF} F_x= \dfrac {m_1 {v_{1_{xi}}} - m_1 {v_{1_{xf}}}}{\Delta t}$ $\color{#0000FF} F_x= \dfrac {m_1 ({v_{1_{xi}}} - {v_{1_{xf}}})}{\Delta t}$
$\color{#0000FF} F_x= \dfrac {5 ({4} - {1.38})}{0.05}$ $\color{#FF0000} F_x=262.5 N$
(c) Ambos bloques se desplazan con velocidad constante en movimiento rectilíneo. En el punto donde hacen contacto la posición del bloque $\color{#0000FF} 1$ es igual a la posición del bloque $\color{#0000FF} 2$.
$\color{#0000FF} x_1=x_2$
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue}x_{1_0}}}}+ v_{1_0}t+ {\color{Red}\bcancel {{\color{blue}\dfrac {1}{2}a_1t^2}}}=x_{2_0}+ v_{2_0}t+ {\color{Red}\bcancel {{\color{blue}\dfrac {1}{2}a_2t^2}}}$
$\color{#0000FF} v_{1_0}t=x_{2_0}+ v_{2_0}t$
$\color{#0000FF} v_{1_0}t-v_{2_0}t = x_{2_0}$ $\color{#0000FF} t(v_{1_0}-v_{2_0}) = x_{2_0}$
$\color{#0000FF} t= \dfrac {x_{2_0}}{(v_{1_0}-v_{2_0})}$ $\color{#0000FF} t= \dfrac {10}{[4-(-3)]}$ $\color{#FF0000} t=1.43s$
• Remplazamos el valor del tiempo en la ecuación de posición para el bloque $\color{#0000FF} 1$:
$\color{#0000FF} x_1=v_{1_0}t$ $\color{#0000FF} x_1=4(1.43)$ $\color{#FF0000} x_1=5.71m$
Para el estudiante: En la escena interactiva ubique los siguientes valores: Posición inicial del bloque $\color{#0000FF} 1=0m$, Posición inicial del bloque $\color{#0000FF} 2=12m$, Velocidad inicial del bloque $\color{#0000FF} 1=2 \dfrac {m}{s}$, Velocidad inicial del bloque $\color{#0000FF} 2=1 \dfrac {m}{s}$, masa del bloque $\color{#0000FF} 1=3 Kg$, masa del bloque $\color{#0000FF} 2=5 Kg$. Determine: $\color{#0000FF} (a)$ La velocidad de ambos bloques un instante después del acoplamiento, $\color{#0000FF} (b)$ La fuerza promedio entre ambos bloques si el acoplamiento dura $\color{#0000FF} 0.06$ segundos, $\color{#0000FF} (c)$ a que distancia medida desde el bloque $\color{#0000FF} 2$ hacen contacto los bloques.
Es un fenómeno Físico que ocurre cuando chocan dos cuerpos en un instante de tiempo. Durante el impacto se ejercen fuerzas muy grandes (fuerzas impulsivas) entre ambos cuerpos haciendo que cualquier impulso provocado por alguna fuerza externa al sistema formado por los dos cuerpos que colisionan sea despreciable.
El impacto entre el bate de beisbol y la bola, entre el palo de golf y la bola, entre el martillo y la puntilla son ejemplos de impactos.
Si los cuerpos que impactan no están sujetos a impulsos externos o estos se pueden despreciar, la cantidad de momento Lineal se conserva.
$\color{#008000}m_1\overrightarrow {v_{1i}}+m_2\overrightarrow {v_{2i}}=m_1\overrightarrow {v_{1f}}+m_2\overrightarrow {v_{2f}}$
En los problemas que involucran impactos generalmente las incógnitas son las velocidades.
Es la línea que une los centros de masa de los dos cuerpos al momento del Impacto.
Es el plano perpendicular a la línea de impacto y coincide con un punto de contacto, el plano de contacto resulta ser tangente al Impacto.
El Impacto entre dos cuerpos es central cuando la dirección de las velocidades de los centro de masa de los dos cuerpos al momento del impacto coinciden con la línea de impacto.
El Impacto entre dos cuerpos es oblicuo cuando la dirección de las velocidades de los centro de masa de los dos cuerpos o una de ellas al momento del impacto no coinciden con la línea de impacto.
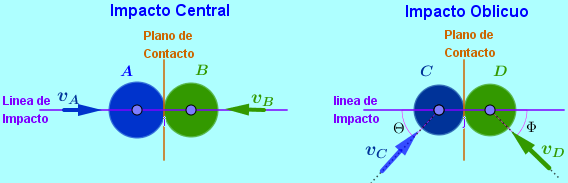
Cuando dos cuerpos impactan sufren un proceso de deformación y una restitución generando pérdidas de energía como cuando dejamos caer un balón de basquetbol al piso y observamos que el balón no regresa a la misma altura de la que fue lanzado; esto se debe a que al momento del impacto del balón con el suelo, sufre una deformación y restitución en la que se pierde energía. En la deformación aparece un impulso de deformación $\color{#0000FF} \displaystyle \int ^{t_2}_{t_1} \overrightarrow {F_D}dt$ , en la restitución aparece un impulso de restitución $\color{#0000FF} \displaystyle \int ^{t_2}_{t_1} \overrightarrow {F_R}dt$.
Entre el impulso de deformación y el impulso de restitución existe una relación llamada Coeficiente de Restitución $\color{#0000FF} e$
$\color{#0000FF} e=\dfrac {\displaystyle \int ^{t_2}_{t_1} \overrightarrow {F_D}dt}{\displaystyle \int ^{t_2}_{t_1} \overrightarrow {F_R}dt}$ $\color{#0000FF} e=-\dfrac {v_{B2}-v_{A2}}{v_{B1}-v_{A1}}$
El coeficiente de restitución se obtiene del cociente entre los impulsos de deformación y restitución o del cociente entre la diferencia de las velocidades finales y las velocidades iniciales. El coeficiente de restitución matemáticamente no tiene unidades pero físicamente si por ser el resultado de una relación entre dos fenómenos físicos que contienen unidades.
$\color{#0000FF} e=[\dfrac {Ns}{Ns}]$ $\color{#0000FF} e= [\dfrac {\dfrac {m}{s}}{\dfrac {m}{s}}]$ $\color{#0000FF} e=[\dfrac {Lbs}{Lbs}]$ $\color{#0000FF} e= [\dfrac {\dfrac {ft}{s}}{\dfrac {ft}{s}}]$
El coeficiente de restitución tiene un valor que esta entre $\color{#0000FF} 0$ y $\color{#0000FF} 1$
El impacto es perfectamente elástico cuando el coeficiente de restitución $\color{#0000FF} e=1$ indicando que el impulso de deformación es exactamente igual al impulso de restitución.
$\color{#0000FF} e=\dfrac {\displaystyle \int ^{t_2}_{t_1} \overrightarrow {F_D}dt}{\displaystyle \int ^{t_2}_{t_1} \overrightarrow {F_R}dt}=1$ $\color{#0000FF} e=-\dfrac {v_{B2}-v_{A2}}{v_{B1}-v_{A1}}=1$
Obsérvese que $\color{#0000FF} e=1$ indica también que la relación entre las diferencias entre las velocidades finales y la diferencia entre las velocidades iniciales es igual a $\color{#0000FF} =1$.
$\color{#0000FF} e=1$ es un caso ideal pues en la realidad en todo impacto existe algo que se pierde de energía, se pierde energía en las deformaciones permanentes en los cuerpos, las vibraciones durante la colisión, el sonido que produce el impacto entre otros factores.
Cuando el coeficiente de Restitución $\color{#0000FF} e=1$ (impacto perfectamente elástico) la energía cinética total se conserva:
$\color{#0000FF} \quad{\color{Red}\bcancel {{\color{blue}\dfrac{1}{2}}}}m_{A}v_{Ai}^2+\quad{\color{Red}\bcancel {{\color{blue}\dfrac{1}{2}}}}m_{B}v_{Bi}^2=\quad{\color{Red}\bcancel {{\color{blue}\dfrac{1}{2}}}}m_{A}v_{Af}^2+\quad{\color{Red}\bcancel {{\color{blue}\dfrac{1}{2}}}}m_{B}v_{Bf}^2$
$\color{#0000FF} m_{A}v_{Ai}^2+m_{B}v_{Bi}^2=m_{A}v_{Af}^2+m_{B}v_{Bf}^2$
El impacto es Inelástico cuando el coeficiente de restitución $\color{#0000FF} e=0$, indicando que en el impacto no se da lugar a la existencia del impulso de restitución.
Analizando el coeficiente de restitución $\color{#0000FF} e=0$ desde la relación entre las diferencias entre las velocidades finales y la diferencia entre las velocidades iniciales:
$\color{#0000FF} e=0=-\dfrac {v_{B2}-v_{A2}}{v_{B1}-v_{A1}}$ $\color{#0000FF} 0={v_{B2}-v_{A2}}$ $\Rightarrow$ $\color{#008000} v_{A2}=v_{B2}$
La consecuencia de un coeficiente de restitución $\color{#0000FF} e=0$ es que los dos cuerpos quedan unidos, acoplados como un solo sistema.
Escena interactiva, diseñada por Elvira Martinez y Carlos RomeroElvira Martinez y Carlos Romero son autores de la red GeoGebra quienes publicaron la escena interactiva "Choque lateral elástico".
Ejercicio 6.2: En la escena interactiva la bola lisa verde $\color{#0000FF} m_1$ de $\color{#0000FF} 1 Kg$ se desplaza horizontalmente a $\color{#0000FF} 0.8 \dfrac {m}{s}$ cuando impacta en forma oblicua con la bola lisa azul $\color{#0000FF} m_2$ de $\color{#0000FF} 1 Kg$ que se encuentra en reposo. Si se conoce la rapidez final de cada bola, $\color{#0000FF} v_{1f}= 0.16 \dfrac {m}{s}$ y $\color{#0000FF} v_{2f}= 0.784 \dfrac {m}{s}$. Determine el ángulo $\color{#0000FF} \Phi$ y $\color{#0000FF} \Theta$ correspondiente a las velocidades final e inicial de la bola $\color{#0000FF} m_1$
Solución:
• Hacemos el diagrama para la línea de impacto y plano de contacto.
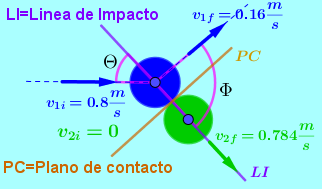
• Sobre la línea de impacto al momento del choque, las fuerzas impulsivas entre las bolas se cancelan y siendo las bolas lisas hacen posible la aplicación sobre la línea de impacto del principio de conservación del momento lineal.
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue}m_1}}}\overrightarrow {v_{1i}}+ {\color{Red}\bcancel {{\color{blue}m_2}}}\overrightarrow {v_{2i}}= {\color{Red}\bcancel {{\color{blue}m_1}}}\overrightarrow {v_{1f}}+ {\color{Red}\bcancel {{\color{blue}m_2}}}\overrightarrow {v_{2f}}$
• Operamos a nivel de componentes:
$\color{#0000FF} {v_{1i} Cos \Theta} + {\color{Red}\bcancel {{\color{blue}{v_{2i}}}}} = {v_{1f}} Cos \Phi + {v_{2f}}$
$\color{#0000FF} {0.8 Cos \Theta} = {0.16} Cos \Phi + {0.784}$
Ecuación que contiene dos incógnitas $\color{#0000FF} \Theta$ y $\color{#0000FF} \Phi$, necesitamos otra ecuación.
Sobre la línea de impacto no existe deformación al momento del impacto, indica que no se pierde energía cinética la cual se conserva.
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue}\dfrac{1}{2}}}}m_{1}v_{1i}^2+ {\color{Red}\bcancel {{\color{blue}\dfrac{1}{2}}}}m_{2}v_{2i}^2= {\color{Red}\bcancel {{\color{blue}\dfrac{1}{2}}}}m_{1}v_{1f}^2+ {\color{Red}\bcancel {{\color{blue}\dfrac{1}{2}}}}m_{2}v_{2f}^2$
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue}m_{1}}}}v_{1i}^2+ {\color{Red}\bcancel {{\color{blue}m_{2}}}} {\color{Red}\bcancel {{\color{blue}v_{2i}^2}}}= {\color{Red}\bcancel {{\color{blue}m_{1}}}}v_{1f}^2+ {\color{Red}\bcancel {{\color{blue}m_{2}}}}v_{2f}^2$
$\color{#0000FF} (v_{1i} Cos \Theta)^2 = (v_{1f} Cos \Phi)^2 + v_{2f}^2$
$\color{#0000FF} (0.8 Cos \Theta)^2 = (0.16 Cos \Phi)^2 + 0.784^2$
• Tenemos dos ecuaciones (principio de conservación del momento lineal y conservación de la energía cinética) con dos incógnitas $\color{#0000FF} \Theta$ y $\color{#0000FF} \Phi$. De la conservación del Momento Lineal:
$\color{#0000FF} {0.8 Cos \Theta} = {0.16} Cos \Phi + {0.784}$
$\color{#0000FF} (0.8 Cos \Theta)^2 = ({0.16} Cos \Phi + {0.784})^2$
$\color{#0000FF} (0.8 Cos \Theta)^2 = {0.16^2} (Cos \Phi)^2 + 2(0.16)o.784 Cos \Phi + {0.784^2}$
• Remplazamos este resultado en la ecuación de energía.
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue}({0.16} Cos \Phi)^2}}} + 2(0.16)0.784 Cos \Phi + {\color{Red}\bcancel {{\color{blue} 0.784^2}}}=$
$\color{#0000FF} {\color{Red}\bcancel {{\color{blue}({0.16} Cos \Phi)^2}}} + {\color{Red}\bcancel {{\color{blue} 0.784^2}}}$
$\color{#0000FF} 2(0.16)0.784 Cos \Phi=0$ $\Rightarrow$ $\color{#0000FF} \Phi= Cos^{-1} 0$ $\color{#FF0000} \Phi=90°$
• Remplazamos $\color{#0000FF} \Phi=90°$ en la ecuación de conservación del Momento Lineal:
$\color{#0000FF} {0.8 Cos \Theta} = {0.16} Cos \Phi + {0.784}$
$\color{#0000FF} {0.8 Cos \Theta} = {0.16} {\color{Red}\bcancel {{\color{blue} Cos 90°}}} + {0.784}$
$\color{#0000FF} {0.8 Cos \Theta} =0.784$ $\color{#0000FF} \Theta=Cos_{-1} \dfrac {0.784}{0.8}$ $\Rightarrow$ $\color{#FF0000} \Theta=11.48°$
Ejercicio 6.2:
En la escena interactiva, si el impacto tiene un coeficiente de restitución de $\color{#0000FF} e=0.8$, el ángulo $\color{#0000FF} \Theta =30°$, el ángulo $\color{#0000FF} \Phi =60°$, $\color{#0000FF} m_1=1 Kg$, $\color{#0000FF} m_2=1 Kg$, la rapidez de $\color{#0000FF} m_1$ es de $\color{#0000FF} 0.8 \dfrac {m}{s}$ y la rapidez de $\color{#0000FF} m_2$ es de $\color{#0000FF} 0 \dfrac {m}{s}$. Determine las velocidades finales de cada bola un instante luego del impacto.
Solución: Diagrama línea de impacto y plano de contacto.
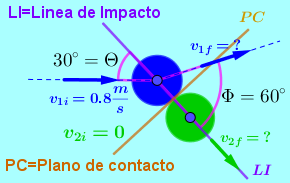
• Sobre la línea de impacto aplicamos el principio de conservación del momento lineal y el coeficiente de restitución.
$\color{#008000} {\color{Red}\bcancel {{\color{blue}m_1}}}\overrightarrow {v_{1i}}+ {\color{Red}\bcancel {{\color{blue}m_2}}} {\color{Red}\bcancel {{\color{blue}\overrightarrow {v_{2i}}}}}= {\color{Red}\bcancel {{\color{blue}m_1}}}\overrightarrow {v_{1f}}+ {\color{Red}\bcancel {{\color{blue}m_2}}}\overrightarrow {v_{2f}}$
$\color{#008000} v_1 Cos \Theta= v_{1f} Cos \Phi + v_{2f}$ $\color{#0000FF} e=- \dfrac {v_{2f}-v_{2i}}{ {\color{Red}\bcancel {{\color{blue}v_{2i}}}}-v_{1i}}$
$\color{#0000FF} ev_1 Cos \Theta = v_{2f} - v_{1f} Cos \Phi$ $\color{#008000} ev_1 Cos \Theta + v_{1f} Cos \Phi = v_{2f} $
Remplazamos $\color{#0000FF} v_{2f}$ en la ecuación de conservación del momento lineal.
$\color{#0000FF} v_1 Cos \Theta= v_{1f} Cos \Phi + ev_1 Cos \Theta + v_{1f} Cos \Phi$
$\color{#0000FF} v_1 Cos \Theta - ev_1 Cos \Theta = 2v_{1f} Cos \Phi$
$\color{#0000FF} \dfrac {v_1 Cos \Theta - ev_1 Cos \Theta}{2Cos \Phi}=v_{1f}$ $\color{#0000FF} v_{1f}=\dfrac {v_1 Cos \Theta (1 - e)}{2Cos \Phi}$
$\color{#0000FF} v_{1f}=\dfrac {0.8 Cos \Theta (1 - 0.8)}{2Cos 60°}$ $\color{#FF0000} v_{1f}= 0.14 \dfrac {m}{s}$
$\color{#0000FF} ev_1 Cos \Theta + v_{1f} Cos \Phi = v_{2f}$ $\color{#FF0000} v_{2f}= 0.71 \dfrac {m}{s}$
• Para el estudiante:
Manipule el deslizador para $\color{#0000FF} m_1$ y fíjelo el $\color{#0000FF} m_1=0.5 Kg$, el deslizador para $\color{#0000FF} m_2$ Fíjelo en $\color{#0000FF} m_2=2 Kg$. Haga correr la escena interactiva y obtenga de ella los valores de las velocidades iniciales y finales de $\color{#0000FF} m_1$ y de $\color{#0000FF} m_2$. Determine el ángulo $\color{#0000FF} \Phi$ y $\color{#0000FF} \Theta$ correspondiente a las velocidades final e inicial de la bola $\color{#0000FF} m_1$. $\color{#FF0000} \Phi=115.12°$ $\color{#FF0000} \Theta=52°$
Manipule el deslizador para $\color{#0000FF} m_1$ y fíjelo el $\color{#0000FF} m_1=0.6 Kg$, el deslizador para $\color{#0000FF} m_2$ Fíjelo en $\color{#0000FF} m_2=1.8 Kg$. Haga correr la escena interactiva y obtenga de ella los valores de las velocidades iniciales y finales de $\color{#0000FF} m_1$ y de $\color{#0000FF} m_2$. Determine el ángulo $\color{#0000FF} \Phi$ y $\color{#0000FF} \Theta$ correspondiente a las velocidades final e inicial de la bola $\color{#0000FF} m_1$. $\color{#FF0000} \Phi=132.25°$ $\color{#FF0000} \Theta=12.84°$
Momento angular $\color{#0000FF} \overrightarrow {H_0}$ es el Momento del Momento Lineal de un cuerpo alrededor de un punto de referencia.
Matemáticamente el Momento angular se define como:
$\color{#0000FF} \overrightarrow {H_0} = \overrightarrow r \times m \overrightarrow v [Kg \dfrac {m^2}{s}] ; [Slug \dfrac {ft^2}{s}]$
$\color{#0000FF} \overrightarrow {r}$ es el vector de posición que va desde el punto de referencia $\color{#0000FF} o$ hasta el centro de masa del cuerpo.
m $\color{#0000FF} \overrightarrow {v}$ es el vector cantidad de movimiento que es tangencial a la trayectoria del centro de masa del cuerpo.
$\color{#0000FF} \overrightarrow {H_0}$ es el vector Momento Angular que es perpendicular al plano formado por $\color{#0000FF} \overrightarrow {r}$ y $\color{#0000FF} m \overrightarrow {v}$
Para hallar el Momento Angular $\color{#0000FF} \overrightarrow {H_0}$:
$\color{#0000FF} \overrightarrow {r}\times m \overrightarrow {v}=\begin{vmatrix} \widehat {i} & \widehat {j} & \widehat {k} \\ r_x & r_y & r_z \\ mv_x & mv_y & mv_z \end{vmatrix}= \overrightarrow {H_0}$De Newton $\color{#0000FF} \Sigma \overrightarrow {F} = m \overrightarrow {a}$ $\color{#0000FF} \Sigma \overrightarrow {F} = m \dot {\overrightarrow {v}}$
El Momento Angular $\color{#0000FF} \overrightarrow {H_0} = \overrightarrow {r} \times m \overrightarrow v$
Hacemos $\color{#0000FF} \dfrac {d \overrightarrow H_0}{dt} = \dot {\overrightarrow {H_0}} = \dfrac {d}{dt} (\overrightarrow {r} \times m \overrightarrow {v})$
$\color{#0000FF} \dot {\overrightarrow {H_0}} = {\color{Red}\bcancel {{\color{blue}\dfrac {d \overrightarrow {r}}{dt} \times m \overrightarrow {v}}}} + \overrightarrow {r} \times m \dot {\overrightarrow {v}}$ Observemos que $\color{#0000FF} \dfrac {d \overrightarrow {r}}{dt} = \overrightarrow {v}$ y $\color{#0000FF} \overrightarrow {v} \times m \overrightarrow {v} = 0$ Son vectores paralelos.
$\color{#0000FF} \dot {\overrightarrow {H_0}} = \overrightarrow {r} \times m \dot {\overrightarrow v} = \overrightarrow {r} \times m \overrightarrow {a} = \overrightarrow {r} \times \overrightarrow {F} = \Sigma \overrightarrow {M_0}$
$\color{#0000FF} \dot {\overrightarrow {H_0}} = \Sigma \overrightarrow {M_0}$
El Momento alrededor de un punto de todas las fuerzas que actúan sobre un cuerpo es igual al cambio respecto del tiempo del Momento Angular del cuerpo alrededor del mismo punto.
De la relación de Momento de Fuerza y Momento Angular:
$\color{#0000FF} \Sigma \overrightarrow {M_0} = \dot {\overrightarrow {H_0}} = \dfrac {d}{dt} H_0$
$\color{#0000FF} \displaystyle \Sigma \int ^{t_{2}}_{t_{1}} \overrightarrow {M_0} {dt} = \int ^{{H_0}_{2}}_{{H_0}_{1}} d\overrightarrow {H_0}$ $\color{#0000FF} \displaystyle \Sigma \int ^{t_{2}}_{t_{1}} \overrightarrow {M_0} {dt} = \overrightarrow H_{02} - \overrightarrow H_{01}$
$\color{#008000} \displaystyle \overrightarrow H_{01} + \Sigma \int ^{t_{2}}_{t_{1}} \overrightarrow {M_0} {dt} = \overrightarrow H_{02}$
$\color{#008000} \overrightarrow H_{01}$ $\color{#0000FF} = \overrightarrow r_1 \times m \overrightarrow v_1$ es el Momento del Momento Inicial.
$\color{#008000} \overrightarrow H_{02}$ $\color{#0000FF} = \overrightarrow r_2 \times m \overrightarrow v_2$ es el Momento del Momento Final.
$\color{#008000} \displaystyle \Sigma \int ^{t_{2}}_{t_{1}} \overrightarrow {M_0} {dt}$ es el Impulso Angular. Representa los momentos de todas las fuerzas que actúan sobre el cuerpo desde el instante $\color{#0000FF} t_1$ hasta el instante $\color{#0000FF} t_2$.
$\color{#008000} \displaystyle \Sigma \int ^{t_{2}}_{t_{1}} \overrightarrow {M_0} {dt} = \Sigma \int ^{t_{2}}_{t_{1}} (\overrightarrow r \times \overrightarrow F) dt$
Ejercicio 6.3:
Una esfera de $\color{#0000FF} 10 Kg$ está en reposo sobre el plano circular liso como se muestra en la escena interactiva. La esfera está unida al extremo de una varilla de $\color{#0000FF} 0.4m$ de masa despreciable que puede girar desde el otro extremo al rededor del punto $\color{#0000FF} o$.
Se aplica a la varilla un momento de $\color{#0000FF} 12\widehat {k} Nm$, a la esfera se le aplica una fuerza $\color{#0000FF} P=6N$ perpendicular a la varilla y paralela al plano circular. Determine la rapidez del bloque $\color{#0000FF} 0.5$ segundos después y el Impulso Angular en éste tiempo.
Solución: Diagrama de Cuerpo libre.
Para el diagrama de cuerpo libre consideramos un solo cuerpo la esfera y la varilla.
Aplicamos el principio del impulso y momento Angular al rededor del eje $\color{#0000FF} z$. Obsérvese que la esfera gira al rededor del eje $\color{#0000FF} z$ comenzando desde el reposo, el momento de $\color{#0000FF} 12\widehat {k} Nm$ genera impulso angular respecto del eje $\color{#0000FF} z$, la fuerza $\color{#0000FF} P=6N$ también genera momento angular respecto del eje $\color{#0000FF} z$. La fuerza de gravedad $\color{#0000FF} mg$ y la fuerza Normal $\color{#0000FF} N$ no generan momento angular respecto del eje $\color{#0000FF} z$, matemáticamente es demostrable ya que en éste caso los vectores fuerza de gravedad $\color{#0000FF} mg$ y fuerza Normal $\color{#0000FF} N$ son paralelos al eje $\color{#0000FF} z$ y el producto vectorial de dos vectores paralelos es cero.
No genera momento angular la fuerza de reacción $\color{#0000FF} F_0$ por estar aplicada en el punto de referencia para el momento angular donde es cero el valor de $\color{#0000FF} r$. Al rededor del eje $\color{#0000FF} z$ el principio de impulso y momento angular en forma escalar queda:
$\color{#0000FF} \displaystyle H_{z1} + \Sigma \int ^{t_{2}}_{t_{1}} {M_z} {dt} = H_{z2}$
$\color{#0000FF} \displaystyle {\color{Red}\bcancel {{\color{blue} {r(mv_1)Sen 90°}}}} + \int ^{t_{2}}_{t_{1}} [{M_z} {dt} + r(P)Sen 90° dt] =$
$\color{#0000FF} r(mv_2)Sen 90°$
$\color{#0000FF} 0 + [12(0.5) + 0.4(6)0.5] = 0.4(10)v_2$
$\color{#0000FF} v_2= \dfrac {[12(0.5) + 0.4(6)0.5]}{0.4(10)}$ $\color{#FF0000} v_2= 1.8 \dfrac {m}{s}$
Para determinar el Impulso Angular durante los primeros $\color{#0000FF} 0.5$ segundos utilizamos en forma escalar la ecuación vectorial de Impulso Angular aplicada al eje $\color{#0000FF} z$.
$\color{#0000FF} \displaystyle \Sigma \int ^{t_{2}}_{t_{1}} {M_z} {dt}$
$\color{#0000FF} \displaystyle \int ^{t_{2}}_{t_{1}} [{M_z} {dt} + r(P)Sen 90° dt] = [12(0.5) + 0.4(6)0.5]$
$\color{#FF0000} \displaystyle \Sigma \int ^{t_{2}}_{t_{1}} {M_z} {dt} = 7.2 Nms$
Ejercicio 6.4:
Un disco de $\color{#0000FF} 1 Slug$ se adhiere a una cuerda elástica que en éste instante mide $\color{#0000FF} 3ft$. En ese instante se le imprime una rapidez de $\color{#0000FF} 2 \dfrac {ft}{s}$ y se desplaza sobre un plano horizontal liso. Mientras el disco se desplaza la cuerda se recoge como muestra la escena interactiva. La cuerda tiene una longitud normal de $\color{#0000FF} 1 ft$ y una constante elástica de $\color{#0000FF} 15 \dfrac {Lb}{ft}$.
Determine la velocidad con que se recoge la cuerda en el instante que la cuerda no ésta estirada.
Solución: Diagrama de Cuerpo libre.
La fuerza de gravedad y la fuerza Normal son paralelas al eje $\color{#0000FF} z$ y el momento respecto al eje $\color{#0000FF} z$ es cero. La fuerza elástica apunta al eje $\color{#0000FF} z$ por lo que el momento respecto del eje $\color{#0000FF} z$ también es cero. así las cosas no existen impulsos angulares respecto del eje $\color{#0000FF} z$; Se concluye que se conserva el momento angular respecto del eje $\color{#0000FF} z$.
$\color{#0000FF} \displaystyle H_{z1} + {\color{Red}\bcancel {{\color{blue} {\Sigma \int ^{t_{2}}_{t_{1}} {M_z} {dt}}}}} = H_{z2}$
$\color{#0000FF} H_{z1} = H_{z2}$
$\color{#0000FF} r_1 {\color{Red}\bcancel {{\color{blue} {m}}}} v_1 = r_2 {\color{Red}\bcancel {{\color{blue} {m}}}} v_2$ $\color{#0000FF} \dfrac {r_1 v_1}{r_2} = v_{2t}$
$\color{#0000FF} v_{2t} = \dfrac {3(2)}{1}$ $\color{#FF0000} v_{2t} = 6 \dfrac {ft}{s}$
$\color{#0000FF} v_{2t} = 6 \dfrac {ft}{s}$ es la velocidad tangencial del disco cuando la cuerda se a recogido y está en su longitud normal.
Debemos ahora encontrar la velocidad total del disco y aplicando el teorema de Pitágoras encontraremos la velocidad con la que se recoge la cuerda que llamaremos $\color{#0000FF} v_n$
No existen fuerzas de rozamiento, se conserva la energía.
$\color{#0000FF} E_1 = E_2$
$\color{0000FF} \dfrac {1}{2}mv_1^2 + {\color{Red}\bcancel {{\color{blue} {mgh_1}}}} + \dfrac {1}{2}kx_1^2 = \dfrac {1}{2}mv_{2}^2 + {\color{Red}\bcancel {{\color{blue} {mgh_2}}}} + {\color{Red}\bcancel {{\color{blue} {\dfrac {1}{2}kx_2^2}}}}$
$\color{0000FF} {\color{Red}\bcancel {{\color{blue} {\dfrac {1}{2}}}}} mv_1^2 + {\color{Red}\bcancel {{\color{blue} {\dfrac {1}{2}}}}}kx_1^2 = {\color{Red}\bcancel {{\color{blue} {\dfrac {1}{2}}}}}mv_{2}^2$
$\color{0000FF} mv_1^2 + kx_1^2 = mv_{2}^2$ $\color{0000FF} v_{2} = \sqrt {\dfrac {mv_1^2 + kx_1^2}{m}}$
$\color{0000FF} v_{2} = \sqrt {\dfrac {1(2^2)+ 15(2^2)}{1}}$ $\color{FF0000} v_{2} =8 \dfrac {ft}{s}$
$\color{#0000FF} v_{2} = 8 \dfrac {ft}{s}$ Es la velocidad total del disco cuando la cuerda se a recogido y está en su longitud normal.
Aplicamos Pitágoras con la velocidad total $\color{#0000FF} v_{2}$ y la velocidad tangencial $\color{#0000FF} v_{2t}$ para hallar la velocidad normal $\color{#0000FF} v_{2n}$ que es la velocidad con la que se recoge la cuerda.
$\color{0000FF} v_{2n} = \sqrt {v_2^2 - v_{2t}^2}$
$\color{0000FF} v_{2n} = \sqrt {8^2 - 6^2}$ $\color{FF0000} v_{2n} = 5.29 \dfrac {ft}{s}$