Respuestas - Capítulo V
Excepto por las preguntas de los apartados de Comprueba tu aprendizaje, sólo se dan las respuestas de los numerales impares
Comprueba tu aprendizaje
5.1 La fuerza apuntaría hacia afuera.
5.2 La fuerza neta apuntaría a 58° debajo del eje -x.
5.3 E→ = 1/4πε0q/r2r^
5.4 Ya no podremos aprovechar la simetría. En cambio, necesitaremos calcular cada uno de los dos componentes del campo eléctrico con su propia integral.
5.5 La carga puntual sería Q = σab donde a y b son los lados del rectángulo pero por lo demás idénticos.
5.6 El campo eléctrico sería cero en el medio, y tiene una magnitud σ/ε0 en cualquier otro lugar.
Preguntas conceptuales
1. En su mayoría, hay la misma cantidad de cargas positivas y negativas presentes, lo que hace que el objeto sea eléctricamente neutro.
3. a. sí; b. sí
5. Toma un objeto con una carga conocida, ya sea positiva o negativa, y acércalo a la barra. Si el objeto cargado conocido es positivo y es repelido de la varilla, la varilla se carga positivamente. Si el objeto con carga positiva es atraído por la varilla, la varilla está cargada negativamente.
7. No, el polvo es atraído por ambos porque las moléculas de partículas de polvo se polarizan en la dirección de la seda.
9. Sí, la carga de polarización se induce en el conductor de modo que la carga positiva esté más cerca de la varilla cargada, causando una fuerza atractiva.
11. La carga por conducción se realiza por contacto donde la carga se transfiere al objeto. La carga por inducción implica primero producir una carga de polarización en el objeto y luego conectar un cable a tierra para permitir que parte de la carga abandone el objeto, dejando el objeto cargado.
13. Esto es para que cualquier exceso de carga se transfiera al suelo, manteniendo los receptáculos de gasolina neutros. Si hay un exceso de carga en el receptáculo de gasolina, una chispa podría encenderlo.
15. La secadora carga la ropa. Si están húmedos, la presencia de moléculas de agua suprime la carga.
17. Solo hay dos tipos de carga, atractiva y repulsiva. Si llevas un objeto cargado cerca del cuarzo, solo se producirá uno de estos dos efectos, demostrando que no hay un tercer tipo de carga.
19. a. No, ya que se induce una carga de polarización. b. Sí, ya que la carga de polarización produciría solo una fuerza atractiva.
21. La fuerza que mantiene el núcleo unido debe ser mayor que la fuerza de repulsión electrostática en los protones.
23. Cualquiera de los dos signos de la carga de prueba podría ser utilizado, pero la convención es usar una carga de prueba positiva.
25. Las cargas son del mismo signo.
27. En el infinito, esperaríamos que el campo fuera cero, pero debido a que la hoja es de extensión infinita, este no es el caso. Donde quiera que estés, ves un plano infinito en todas las direcciones.
29. La placa con carga infinita tendría E = σ/2ε0 en todas partes. El campo apuntaría hacia la placa si estuviera cargada negativamente y apuntará lejos de la placa si estuviera cargada positivamente. El campo eléctrico de las placas paralelas sería cero entre ellas si tuvieran la misma carga, y E sería E = σ/ε0 en cualquier otro lugar. Si las cargas eran opuestas, la situación se invierte, cero fuera de las placas y E = σ/ε0 entre ellas.
31. sí; no
33. En la superficie de la Tierra, el campo gravitacional siempre se dirige hacia el centro de la Tierra. Un campo eléctrico podría mover una partícula cargada en una dirección diferente que hacia el centro de la Tierra. Esto indicaría que hay un campo eléctrico presente.
35. 10
Problemas
37. a. 2.00 × 10-9 C[1/(1.602 × 10-19e/C)] = 1.248 × 1010 electrones;
b. 0.500 × 10-6 C[1/(1.602 × 10-19e/C)] = 3.121 × 1012 electrones
39. 3.750 × 1021e/6.242 × 1018e/C = 600.8 C
41. a. 2.0 × 10-9 C(6.242 × 1018 e/C) = 1.248 × 1010 e;
b. 9.109 × 10-31 kg(1.248 × 1010e) = 1.137 × 10-20 kg, 1.137 × 10-20 kg/2.5 × 10-3 kg = 4.548 × 10-18 o 4.545 × 10-16%
43. 5.00 × 10-9 C(6.242 × 1018 e/C) = 3.121 × 1019e;
3.121 × 1019 e + 1.0000 × 1012 e = 3.1210001 × 1019 e
45. masa atómica de átomos de cobre multiplicada por 1u = 1.055 × 10-25 kg;
cantidad de átomos de cobre = 4.739 × 1023 átomos;
el número de electrones es igual a 29 veces el número de átomos o 1.374 × 1025 electrones;
2.00 × 10-6 C(6.242 × 1018 e/C)/ 1.374 × 1025 e = 9.083 × 10-13 o 9.083 × 10-11%
47. 244.00 u(1.66 × 10-27 kg/u) = 4.050 × 10-25kg;
4.00kg/4.050 × 10-25 kg = 9.877 × 1024 átomos
9.877 × 1024(94) = 9.284 × 1026 protones;
9.284 × 1026(1.602 × 10-19 C/p) = 1.487 × 108 C
49. a. la carga 1 es 3μC; la carga 2 es 12μC, F31 = 2.16 × 10-4 N a la izquierda,
F32 = 8.63 × 10-4 N a la derecha,
Fneta = 6.47 × 10-4 N a la derecha;
b. F31 = 2,16 × 10-4 N a la derecha,
F32 = 9.59 × 10-5 N a la derecha,
Fneta = 3.12 × 10-4 N a la derecha,

c. F→31x = -2.76 × 10-5 Ni^,
F→31y = -1.38 × 10-5 Nj^,
F→32y = -8.63 × 10-4 Nj^,
F→neta = -3.86 × 10-5 Ni^ - 8.83 × 10-4 Nj^
51. F = 230.7 N
53. F = 53.94 N
55. La tensión es T = 0.049 N. El componente horizontal de la tensión es 0.0043 N
d = 0.088 m, q = 6.1 × 10-8C.
Las cargas pueden ser positivas o negativas, pero ambas tienen que ser del mismo signo.
57. Deja que la carga en una de las esferas sea nQ, donde n es una fracción entre 0 y 1. En el numerador de la ley de Coulomb, el término que implica las cargas es nQ(1 - n)Q. Esto es igual a (n - n2)Q2. Encontrar el máximo de este término da 1 - 2n = 0 ⇒ n = 1259. Define el eje derecho como la dirección positiva y, por lo tanto, a la izquierda, es la dirección negativa, luego F = -0.05N
61. Las partículas forman el triángulo de los lados 13, 13 y 24 cm. Los componentes x se cancelan, mientras que hay una contribución al componente y de ambas cargas a una distancia de 24 cm. El eje y que pasa por la tercera carga divide en dos la línea de 24 cm, creando dos triángulos rectángulos de 5, 12 y 13 cm.
Fy = 2.56 N en la dirección y negativa ya que la fuerza es atractiva. La fuerza neta de ambas cargas es F→neta = -5.12 Nj^.
63. La diagonal es 2√a y las componentes de la fuerza debidas a la carga diagonal tienen un factor cosθ = 1/√2;
F→neta = [kq2/a2 + kq2/2a21/√2]i^ - [kq2/a2 + kq2/2a21/√2]j^
65. a. E = 2.0 × 10-2 NC arriba;
b. F = 2.0 × 10-6 N hacia abajo
67. a. E = 2,88 × 1011 N/C;
b. E = 1,44 × 1011 N/C;
c. F = 4.61 × 10-8 N en partículas alfa;
F = 4.61 × 10-8 N en el electrón
69. E = (- 2.0i^ + 3.0j^) N
71. F = 3.204 × 10-14 N,
a = 3.517 × 1016 m/s2
73. q = 2,78 × 10-9 C
75. a. E = 1,15 × 1012 N/C;
b. F = 1.47 × 10-6 N
77. Si q2 está a la derecha de q1, el vector del campo eléctrico de ambas cargas apunta hacia la derecha. a. E = 2.70 × 106 N/C;
b. F = 54.0 N
79. Hay una geometría de triángulo rectángulo de 45°. Los componentes x del campo eléctrico en y = 3 m se cancelan. Los componentes y dan E(y = 3m) = 2.83 × 103 N/C.
En el origen tenemos una carga negativa de magnitud q = -2.83 × 10-6 C.
81. E→(z) = 3.6 × 104 N/Ck^
83. dE = 1/4πε0λdx/(x + a)2, E = λ/4πε0 [1/l + a- 1/a]
85. σ = 0.02 C/m2 E = 2.26 × 109 N/C
87. En P1: E→(y) = 1/4πε0λL/y(y2 + L2/4)1/2j^ ⇒ 1/4πε0q/(a/2)((a/2)2 + L2/4)1/2j^ = 1/πε0q/a(a2 + L2)1/2j^
En P2: coloca el origen al final de L.
dE = 1/4πε0λdx/(x + a)2, E = -q/4πε0l [1/l + a- 1/a]i^
89. a. E→(r→) = 1/4πε02λx/bi^ + 1/4πε02λy/aj^;
b. 1/4πε02(λx + λy)/ck^
91. a. F→ = 3.2 × 10-17 Ni^,
a→ = 1,92 × 1010 m/s2i^;
b. E→ = -3.2 × 10-17 Ni^,
a→ = -3.51 × 1013 m/s2i^
93. m = 6.5 × 10-11kg,
E = 1,6 × 107 N/C
95. E = 1.70 × 106 N/C,
F = 1.53 × 10-3 N Tcosθ = mg, Tsenθ = qE,
tanθ = 0.62 ⇒θ = 32.0°,
Esto es independiente de la longitud de la cadena.
97. arco circular dEx(-i^) = 1/4πε0λds/r2cosθ (-i^),
E→x = 1/4πε0r(-i^),
dEy(i^) = 1/4πε0λds/r2senθ (-j^),
E→y = 1/4πε0r(-j^),
eje y: E→x = λ/4πε0r(-i^);
eje x: E→y = λ/4πε0r(-j^);
E→ = λ/2πε0r(-i^) +λ/2πε0r(-j^)
99. a. W = 1/2m(v2 - v02),
Qq/4πε0r(1/r - 1/r0) = 1/2m(v2 - v02) ⇒ r0 - r = 4πε0/Qq1/2rr0m(v2 - v02);
b. r0 - r es negativo; por lo tanto, v0 > v, r → ∞, y v → 0: Qq/4πε0r(-1/r0) = - 1/2mv02 ⇒v0 = √Qq/2πε0mr0/
101.
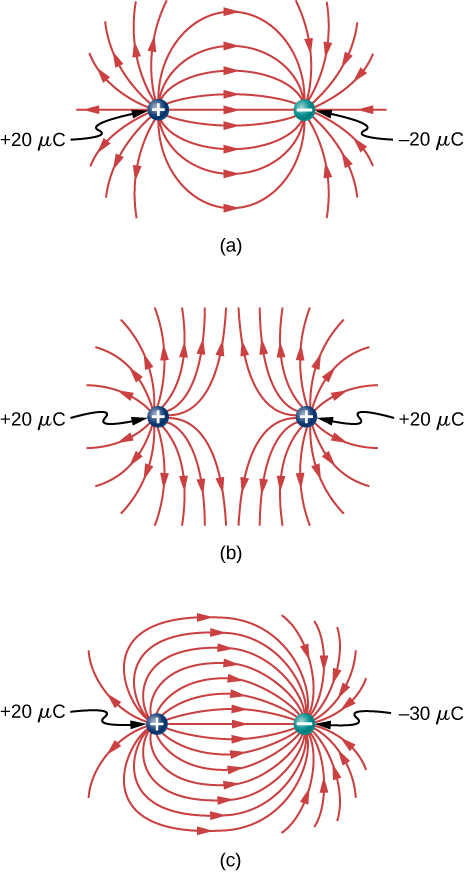
103.

105. Ex = 0,
Ey = 1/4πε0[2q/(x2 + a2)a/√(x2 + a2)/]
⇒ x >> a ⇒ 1/2πε0qa/x3,
Ey = q/4πε0[2ya + 2ya/(y - a)2(y + a)2]
⇒ y >> a ⇒ 1/πε0qa/y3
107. El momento dipolar neto de la molécula es la suma del vector de los momentos dipolares individuales entre los dos O-H. La separación O-H es 0.9578 angstroms:
p→ = 1.889 × 10-29 Cmi^
Problemas Adicionales
109.F→neta = [−8.99 × 1093.0 × 10-6(5.0 × 10-6)/(3.0 m)2 − 8.99 × 1099.0 × 10-6(5.0 × 10-6)/(3.0 m)2]i^
−8.99 × 1096.0 × 10-6(5.0 × 10-6)/(3.0 m)2j^ = −0.06 Ni^ −0.03 Nj^
111. Las cargas Q y q forman un triángulo rectángulo de lados de 1 m y 3 + √3 m. Las cargas 2Q y q forman un triángulo rectángulo de lados de 1 m y √3 m.
Fx = 0.036 N,
Fy = 0.09 N,
F→neta = 0.036 Ni^ + 0.09 Nj^
113. W = 0.054 J
115. a. E→ = 1/4πε0[q/2(a)2 - q/a2]i^
b. E→ = √3/4πε0q/a2(-j^)
c. E→ = 2/πε0q/a21/√2(-j^)
117. E→neta = E→1 + E→2 + E→3 + E→4 = (4.65i^ + 1.44j^) × 107 N/C
119. F = qE0(1 + x/a), W = 1/2m(v2 − v02),
1/2mv2 = qE0(15a/2) J
121. Campo eléctrico del alambre en x:
E→x = 1/4πε02λy/xi^,
dF = λxλy/2πε0(lnb − lna)
123.
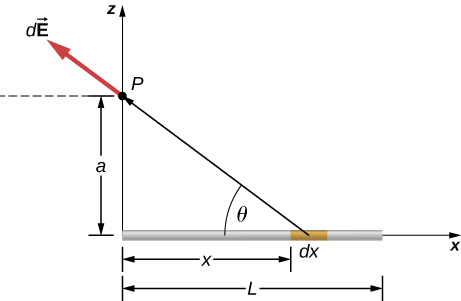
dEx = 1/4πε0λdx/(x2 + a2)x/√(x2 + a2)/
E→x = λ/4πε0[1/√(L2 + a2)/ - 1/a]i^,
dEz = 1/4πε0λdx/(x2 + a2)a/√(x2 + a2)/
E→z = λ/4πε0L/√(L2 + a2)/k^
Sustituyendo z por a, tenemos:
E→(z) = λ/4πε0[1/√(L2 + z2)/ - 1/z]i^ + λ/4πε0L/√(L2 + z2)/k^
125. Hay una fuerza neta solo en la dirección y. Sea θ el ángulo que hace el vector desde dx a q con el eje x. Las componentes a lo largo del eje x se cancelan debido a la simetría, dejando el componente y de la fuerza.
dFy = 1/4πε0aqλdx/(x2 + a2)3/2
Fy = 1/2πε0qλ/a[l/2/[(l/2)2 + a2]1/2



