Preguntas y problemas - Capítulo VII

Preguntas conceptuales

7.1 Energía potencial eléctrica

1. ¿La energía potencial eléctrica sería significativa si el campo eléctrico no fuera conservador?

2. ¿Por qué tenemos que tener cuidado con el trabajo realizado en el sistema en comparación con el trabajo realizado por el sistema en los cálculos?

3. ¿El orden en el que reunimos un sistema de cargas puntuales afecta el trabajo total realizado?

7.2 Potencial eléctrico y diferencia de potencial

4. Discute cómo se relacionan la diferencia de potencial y la intensidad del campo eléctrico. Da un ejemplo.

5. ¿Cuál es la fuerza del campo eléctrico en una región donde el potencial eléctrico es constante?

6. Si un protón se libera del reposo en un campo eléctrico, ¿se moverá en la dirección del potencial de aumento o disminución? También responde esta pregunta para un electrón y un neutrón. Explicar por qué.

7. El voltaje es la palabra común para la diferencia de potencial. ¿Qué término es más descriptivo, voltaje o diferencia de potencial?

8. Si el voltaje entre dos puntos es cero, ¿se puede mover una carga de prueba entre ellos sin que se realice ningún trabajo de red? ¿Se puede hacer esto necesariamente sin ejercer una fuerza? Explica.

9. ¿Cuál es la relación entre el voltaje y la energía? Más precisamente, ¿cuál es la relación entre la diferencia de potencial y la energía potencial eléctrica?

10. Los voltajes siempre se miden entre dos puntos. ¿Por qué?

11. ¿Cómo se relacionan las unidades de voltios y electrón-voltios? ¿Cómo difieren?

12. ¿Puede una partícula moverse en una dirección de aumento del potencial eléctrico, y aún así tener su potencial eléctrico disminuyendo? Explica

7.3 Cálculos del potencial eléctrico

13. Compara los momentos dipolares eléctricos de cargas ± Q separados por una distancia d y cargas ± Q/2 separados por una distancia d/2.

14. ¿Sería útil la ley de Gauss para determinar el campo eléctrico de un dipolo? ¿Por qué?

15. ¿En qué región del espacio se encuentra el potencial debido a una esfera cargada uniformemente igual a la de una carga puntual? ¿En qué región difiere de la de una carga puntual?

16. ¿Puede el potencial de una esfera no uniformemente cargada ser el mismo que el de una carga puntual? Explica.

7.4 Determinación del campo del potencial

17. Si el campo eléctrico es cero en una región, ¿el potencial eléctrico también debe ser cero en esa región?

18. Explica por qué el conocimiento de E→(x, y, z) no es suficiente para determinar V(x, y, z).

7.5 Superficies equipotenciales y conductores

19. Si dos puntos tienen el mismo potencial, ¿hay alguna línea de campo eléctrico que los conecte?

20. Supón que tienes un mapa de superficies equipotenciales separadas 1,0 V. ¿Qué te dicen las distancias entre las superficies de una región en particular acerca de la fuerza del E→ en esa región?

21. ¿Es el potencial eléctrico necesariamente constante sobre la superficie de un conductor?

22. En condiciones electrostáticas, el exceso de carga en un conductor reside en su superficie. ¿Esto significa que todos los electrones de conducción en un conductor están en la superficie?

23. ¿Puede un conductor con carga positiva tener un potencial negativo? Explica.

24. ¿Pueden las superficies equipotenciales cruzarse?

7.6 Aplicaciones de la Electrostática

25. ¿Por qué las varillas de soporte de metal para platos de red de satélite generalmente están conectadas a tierra?

26. a) ¿Por qué los peces son razonablemente seguros en una tormenta eléctrica? (b) ¿Por qué, sin embargo, se ordena a los nadadores salir del agua en la misma circunstancia?

27. ¿Cuáles son las similitudes y diferencias entre los procesos en una fotocopiadora y un precipitador electrostático?

28. ¿Qué magnitud de potencial se usa para cargar el tambor de una fotocopiadora? Una búsqueda web de "xerografía" puede ser útil.

Problemas

7.1 Energía potencial eléctrica

29. Considere una carga Q₁(+ 5.0 μC) fija en un sitio con otra carga Q₂(carga + 3.0 μC, masa 6.0 μg) moviéndose en el espacio vecino. (a) Evalúa la energía potencial de Q₂ cuando está a 4.0 cm de Q₁. (b) Si Q₂ comienza desde el reposo desde un punto 4.0 cm desde Q₁, ¿cuál será su velocidad cuando esté 8.0 cm desde Q₁₂? (Nota: Q₂ se mantiene fijo en su lugar).

30. Dos cargas Q₁ (+ 2.00μC) y Q₂ (+ 2.00 μC) se colocan simétricamente a lo largo del eje x a x = ± 3.00 cm. Considera una carga Q₃ de carga + 4.00 μC y masa 10.0 mg moviéndose a lo largo del eje y. Si Q₃ comienza desde el reposo a y = 2.00cm, ¿cuál es su velocidad cuando alcanza y = 4.00 cm?

31. Para formar un átomo de hidrógeno, se fija un protón en un punto y se lleva un electrón desde muy lejos a una distancia de 0,529 × 10^-10 m, la distancia promedio entre el protón y el electrón en un átomo de hidrógeno. ¿Cuánto trabajo se hace?

32. (a) ¿Cuál es la potencia de salida promedio de un desfibrilador cardíaco que disipa 400 J de energía en 10.0 ms? (b) Considerando la salida de alta potencia, ¿por qué el desfibrilador no produce quemaduras graves?

7.2 Potencial eléctrico y diferencia de potencial

33. Encuentra la relación de velocidades de un electrón y un ion de hidrógeno negativo (uno que tiene un electrón extra) acelerado a través del mismo voltaje, asumiendo velocidades finales no relativistas. Tome la masa del ion de hidrógeno para que sea 1,67 × 10^-27 kg.

34. Un tubo de vacío utiliza un voltaje de aceleración de 40 kV para acelerar los electrones y golpear una placa de cobre y producir rayos X. No relativísticamente, ¿cuál sería la velocidad máxima de estos electrones?

35. Demostrar que las unidades de V/m y N/C para la intensidad del campo eléctrico son de hecho equivalentes.

36. ¿Cuál es la intensidad del campo eléctrico entre dos placas conductoras paralelas separadas por 1,00 cm y que tienen una diferencia de potencial (voltaje) entre ellas de 1,50 × 10⁴ V?

37. La intensidad del campo eléctrico entre dos placas conductoras paralelas separadas por 4,00 cm es de 7,50 × 10⁴ V/m. (a) ¿Cuál es la diferencia de potencial entre las placas? (b) La placa con el potencial más bajo se toma como cero voltios. ¿Cuál es el potencial de 1.00 cm de esa placa y 3.00 cm de la otra?

38. El voltaje a través de una membrana que forma una pared celular es de 80.0 mV y la membrana tiene un espesor de 9.00 nm. ¿Cuál es la intensidad del campo eléctrico? (El valor es sorprendentemente grande, pero correcto). Puedes suponer un campo eléctrico uniforme.

39. Dos placas conductoras paralelas están separadas por 10.0 cm, y una de ellas está tomada a cero voltios. (a) ¿Cuál es la intensidad del campo eléctrico entre ellos, si el potencial de 8.00 cm desde la placa de cero voltios (y 2.00 cm desde el otro) es de 450 V? (b) ¿Cuál es el voltaje entre las placas?

40. Encuentra la diferencia de potencial máxima entre dos placas conductoras paralelas separadas por 0.500 cm de aire, dado que la máxima intensidad de campo eléctrico sostenible en el aire es de 3.0 × 10⁶ V/m.

41. Se debe acelerar un electrón en un campo eléctrico uniforme con una fuerza de 2.00 × 10⁶ V/m. (a) ¿Qué energía en keV se le da al electrón si se acelera a través de 0.400 m? (b) ¿A qué distancia debería acelerarse para aumentar su energía en 50.0 GeV?

42. Usa la definición de diferencia de potencial en términos de campo eléctrico para deducir la fórmula para la diferencia de potencial entre r = r_a y r = r_b para una carga puntual ubicada en el origen. Aquí r es la coordenada radial esférica.

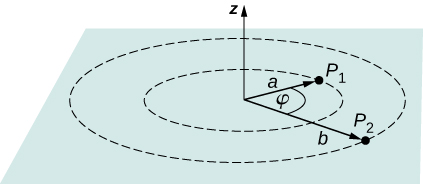
43. El campo eléctrico en una región apunta hacia el eje z y la magnitud depende de la distancia s del eje. La magnitud del campo eléctrico se da como E = αs donde α es una constante. Encuentra la diferencia de potencial entre los puntos P₁ y P₂, indicando explícitamente la ruta sobre la que realiza la integración para la integral de línea.



44. Los iones de carga cargados individualmente se aceleran desde el reposo a través de un voltaje de 13.0 V. ¿A qué temperatura la energía cinética promedio de las moléculas de gas será la misma que la de estos iones?

7.3 Cálculos del potencial eléctrico

45. Una esfera de plástico de 0.500 cm de diámetro, utilizada en una demostración de electricidad estática, tiene una carga de 40.0 pC uniformemente distribuida en su superficie. ¿Cuál es el potencial cerca de su superficie?

46. ​​¿Qué tan lejos de una carga puntual de 1.00 μC es el potencial de 100 V? ¿A qué distancia es 2.00 × 10² V?

47. Si el potencial debido a una carga puntual es 5.00 × 10² V a una distancia de 15.0 m, ¿cuál es el signo y la magnitud de la carga?

48. En la fisión nuclear, un núcleo se divide aproximadamente por la mitad. (a) ¿Cuál es el potencial de 2.00 × 10^-14 m de un fragmento que tiene 46 protones? (b) ¿Cuál es la energía potencial en MeV de un fragmento con una carga similar a esta distancia?

49. Un generador Van de Graaff de investigación tiene una esfera de metal de 2,00 m de diámetro con una carga de 5,00 mC sobre él. (a) ¿Cuál es el potencial cerca de su superficie? (b) ¿A qué distancia de su centro está el potencial de 1.00 MV? (c) Un átomo de oxígeno con tres electrones faltantes se libera cerca del generador Van de Graaff. ¿Cuál es su energía en MeV cuando el átomo está en la distancia que se encuentra en la parte b?

50. Un pulverizador de pintura electrostática tiene una esfera metálica de 0.200 m de diámetro con un potencial de 25.0 kV que repele las gotas de pintura en un objeto con conexión a tierra. (a) ¿Qué carga hay en la esfera? (b) ¿Qué carga debe tener una gota de pintura de 0.100 mg para llegar al objeto con una velocidad de 10.0 m/s?

51. (a) ¿Cuál es el potencial entre dos puntos situados a 10 cm y 20 cm de una carga puntual de 3.0? ΜC? (b) ¿A qué ubicación debe moverse el punto a 20 cm para aumentar esta diferencia de potencial en un factor de dos?

52. Encuentre el potencial en los puntos P₁, P₂, P₃ y P₄ en el diagrama debido a las dos cargas dadas.



53. Dos cargas -2.0μC y + 2.0μC están separadas 4.0 cm en el eje z simétricamente respecto al origen, con el positivo en la parte superior. Dos puntos espaciales de interés P₁ y P₂ están ubicados a 3.0 cm y 30 cm del origen en un ángulo de 30° con respecto al eje z. Evalúa los potenciales eléctricos en P₁ y P₂ de dos maneras: (a) Usando la fórmula exacta para las cargas puntuales, y (b) usando la fórmula del potencial dipolo aproximado.

54. (a) Traza el potencial de una barra de 1 m cargada uniformemente con una carga de 1 C/m como una función de la distancia perpendicular desde el centro. Dibuja tu gráfica desde s = 0.1 m a s = 1.0 m. (b) En el mismo gráfico, traza el potencial de una carga puntual con una carga de 1 C en el origen. (c) ¿Qué potencial es más fuerte cerca de la varilla? (d) ¿Qué pasa con la diferencia a medida que aumenta la distancia? Interpreta tu resultado.

7.4 Determinación del campo del potencial

55. En una región, las superficies equipotenciales vienen dadas por z = constante. Las superficies están equiespaciadas con V = 100 V para z = 0.00 m, V = 200 V para z = 0.50 m, V = 300 V para z = 1.00 m. ¿Cuál es el campo eléctrico en esta región?

56. En una región particular, el potencial eléctrico viene dado por V = -xy²z + 4xy. ¿Cuál es el campo eléctrico en esta región?

57. Calcula el campo eléctrico de una carga lineal infinita, a lo largo del espacio.

7.5 Superficies equipotenciales y conductores

58. Dos placas de metal muy grandes se colocan a 2,0 cm de distancia, con una diferencia de potencial de 12 V entre ellas. Considera que una placa debe estar a 12 V y la otra a 0 V. (a) Dibuja las superficies equipotenciales para 0, 4, 8 y 12 V. (b) Haz un boceto en algunas líneas de campo eléctrico, y confirma que son perpendiculares a las líneas equipotenciales.

59. Una hoja muy grande de material aislante ha tenido un exceso de electrones sobre una densidad de carga superficial de -3.00 nC/m². (a) A medida que aumenta la distancia desde la hoja, ¿el potencial aumenta o disminuye? ¿Puedes explicar por qué, sin ningún cálculo? ¿Importa la ubicación de su punto de referencia? (b) ¿Cuál es la forma de las superficies equipotenciales? (c) ¿Cuál es el espacio entre las superficies que difieren en 1.00 V?

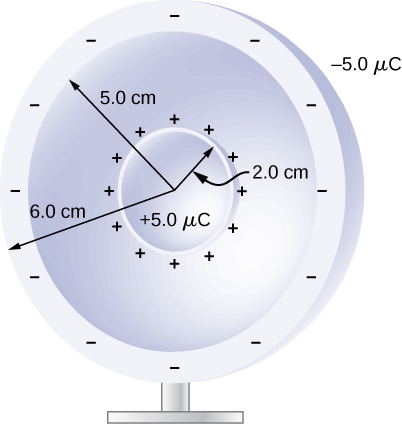
60. Una esfera metálica de radio de 2,0 cm se carga con una carga de +5,0 μC, que se extiende uniformemente sobre la superficie de la esfera. La esfera metálica se encuentra en un soporte aislado y está rodeada por una carcasa esférica metálica más grande, de radio interno 5.0 cm y radio exterior 6.0 cm. Ahora, se coloca una carga de -5.0 μC en el interior de la carcasa esférica, que se extiende uniformemente en la superficie interior de la carcasa. Si el potencial es cero en el infinito, ¿cuál es el potencial de (a) el caparazón esférico, (b) la esfera, (c) el espacio entre los dos, (d) dentro de la esfera y (e) fuera del caparazón?



61. Dos grandes placas cargadas de densidad de carga ± 30 μC/m² se enfrentan entre sí a una separación de 5,0 mm. (a) Encuentra el potencial eléctrico en todas partes. (b) Se libera un electrón del reposo en la placa negativa; ¿con qué velocidad golpeará la placa positiva?

62. Un cilindro largo de aluminio de radio R metros se carga para que tenga una carga uniforme por unidad de longitud en su superficie de λ. (a) Encuentra el campo eléctrico dentro y fuera del cilindro. (b) Encuentra el potencial eléctrico dentro y fuera del cilindro. (c) Traza el campo eléctrico y el potencial eléctrico en función de la distancia desde el centro de la varilla.

63. Dos placas paralelas de 10 cm en un lado reciben cargas iguales y opuestas de magnitud 5.0 × 10^-9 C. Las placas están separadas por 1,5 mm. ¿Cuál es la diferencia de potencial entre las placas?

64. La densidad de carga superficial en un tubo metálico recto largo es σ. ¿Cuál es el potencial eléctrico fuera y dentro de la tubería? Supón que la tubería tiene un diámetro de 2a



65. Las conchas esféricas conductoras concéntricas llevan cargas Q y -Q, respectivamente. La carcasa interna tiene un grosor insignificante. ¿Cuál es la diferencia de potencial entre las conchas?



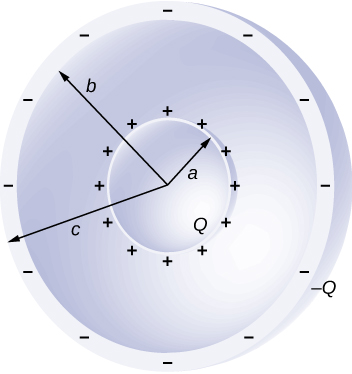
66. A continuación se muestran dos capas esféricas concéntricas de grosores y radios insignificantes R₁ y R₂. La carcasa interna y externa llevan cargas netas q₁ y q₂, respectivamente, donde tanto q₁ como q₂ son positivas. ¿Cuál es el potencial eléctrico en las regiones (a) r < R₁, (b) R₁ < r < R₂ y (c) r > R₂?



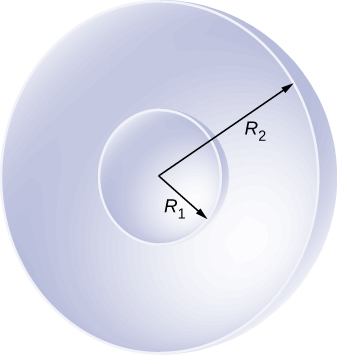
67. Un conductor cilíndrico sólido de radio a, está rodeado por una capa cilíndrica concéntrica de radio interior b. El cilindro sólido y la carcasa llevan cargas Q y -Q, respectivamente. Suponiendo que la longitud L de ambos conductores es mucho mayor que a o b, ¿cuál es la diferencia de potencial entre los dos conductores?

7.6 Aplicaciones de la Electrostática

68. (a) ¿Cuál es el campo eléctrico a 5,00 m del centro de la terminal de un Van de Graaff con una carga de 3,00 mC, teniendo en cuenta que el campo es equivalente al de una carga puntual en el centro de la terminal? (b) A esta distancia, ¿qué fuerza ejerce el campo con una carga de 2.00 μC en el cinturón de Van de Graaff?

69. (a) ¿Cuál es la dirección y la magnitud de un campo eléctrico que soporta el peso de un electrón libre cerca de la superficie de la Tierra? (b) Discute qué implica el valor pequeño para este campo con respecto a la fuerza relativa de las fuerzas gravitacionales y electrostáticas.

70. Una técnica simple y común para acelerar electrones se muestra en la Figura 7.46, donde hay un campo eléctrico uniforme entre dos placas. Los electrones se liberan, generalmente de un filamento caliente, cerca de la placa negativa, y hay un pequeño orificio en la placa positiva que permite que los electrones continúen moviéndose. (a) Calcula la aceleración del electrón si la intensidad del campo es 2.50 × 10⁴ N/C. (b) Explica por qué el electrón no se retraerá a la placa positiva una vez que se mueve a través del agujero.


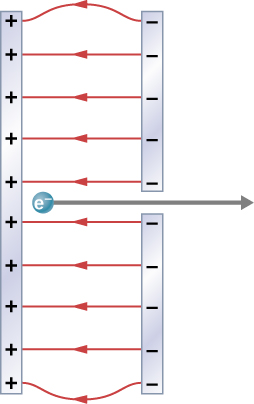
Figura 7.46 Las placas conductoras paralelas con cargas opuestas sobre ellas crean un campo eléctrico relativamente uniforme utilizado para acelerar los electrones hacia la derecha. Aquellos que pasan por el agujero pueden usarse para hacer que un televisor o una pantalla de computadora brillen o para producir rayos X.

71. En un contador Geiger, un cable metálico delgado en el centro de un tubo metálico se mantiene a un alto voltaje con respecto al tubo de metal. La radiación ionizante que entra al tubo hace que los electrones salgan de las moléculas de gas o de los lados del tubo, que luego se aceleran hacia el cable central, eliminando aún más electrones. Este proceso finalmente conduce a una avalancha que es detectable como una corriente. Un contador Geiger particular tiene un tubo de radio R y el cable interno de radio a tiene un potencial de V₀ voltios con respecto al tubo de metal exterior. Considera un punto P a una distancia s del cable central y lejos de los extremos. (a) Encuentra una fórmula para el campo eléctrico en un punto P adentro, usando la aproximación de alambre infinito. (b) Encuentrauna fórmula para el potencial eléctrico en un punto P adentro. (c) Use V₀ = 900 V, a = 3.00 mm, R = 2.00 cm, y encuentra el valor del campo eléctrico en un punto a 1.00 cm del centro.



72. El límite práctico para un campo eléctrico en el aire es de aproximadamente 3,00 × 10⁶ N/C. Por encima de esta fuerza, se producen chispas porque el aire comienza a ionizarse. (a) En esta fuerza de campo eléctrico, ¿qué tan lejos viajaría un protón antes de alcanzar la velocidad de la luz (ignorar los efectos relativistas)? (b) ¿Es práctico dejar aire en aceleradores de partículas?

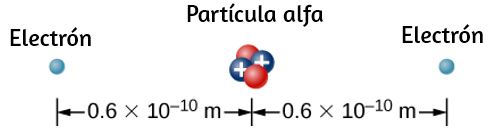
73. Para formar un átomo de helio, una partícula alfa que contiene dos protones y dos neutrones se fija en un lugar, y dos electrones son llevados desde lejos, uno a la vez. El primer electrón se coloca a 0.600 × 10^-10 m de la partícula alfa y se mantiene allí mientras el segundo electrón se lleva a 0.600 × 10^-10 m desde la partícula alfa en el otro lado desde el primer electrón. Ver la configuración final a continuación. (a) ¿Cuánto trabajo se hace en cada paso? (b) ¿Cuál es la energía electrostática de la partícula alfa y dos electrones en la configuración final?



74. Encuentra la energía electrostática de ocho cargas iguales (+ 3μC) cada una fija en las esquinas de un cubo de lado 2 cm.

75. La probabilidad de que se produzca la fusión aumenta mucho cuando se unen los núcleos apropiados, pero se debe superar la repulsión mutua de Coulomb. Esto se puede hacer utilizando la energía cinética de los iones de gas a alta temperatura o acelerando los núcleos uno hacia el otro. (a) Calcula la energía potencial de dos núcleos con carga única separados por 1.00 × 10^-12 m. (b) ¿A qué temperatura tendrán los átomos de un gas una energía cinética promedio igual a esta energía potencial eléctrica necesaria?

76. Un núcleo de helio desnudo tiene dos cargas positivas y una masa de 6.64 × 10^-27 kg. (a) Calcula su energía cinética en joules a 2.00% de la velocidad de la luz. (b) ¿Qué es esto en electron-voltios? (c) ¿Qué voltaje se necesitaría para obtener esta energía?

77. Un electrón entra en una región entre dos grandes placas paralelas hechas de aluminio separadas por una distancia de 2.0 cm y mantenidas a una diferencia de potencial de 200 V. El electrón entra por un pequeño orificio en la placa negativa y se mueve hacia la placa positiva. En el momento en que el electrón está cerca de la placa negativa, su velocidad es de 4.0 × 10⁶ m/s. Supón que el campo eléctrico entre las placas es uniforme, y encuentra la velocidad del electrón en (a) 0.10 cm, (b) 0.50 cm, (c) 1.0 cm y (d) 1.5 cm de la placa negativa, y (e) inmediatamente antes de que golpee la placa positiva.



78. ¿A qué distancia están dos placas conductoras que tienen una intensidad de campo eléctrico de 4.50 × 10³ V/m entre ellas, si su diferencia de potencial es de 15.0 kV?

79. (a) ¿La intensidad del campo eléctrico entre dos placas conductoras paralelas excederá la resistencia a la ruptura del aire seco, que es 3.00 × 10⁶ V/m, si las placas están separadas por 2.00 mm y se aplica una diferencia de potencial de 5.0 × 10³ V? (b) ¿Qué tan juntas pueden estar las placas con este voltaje aplicado?

80. Las paredes de membrana de las células vivas tienen campos eléctricos sorprendentemente grandes a través de ellas debido a la separación de iones. ¿Cuál es el voltaje en una membrana de 8.00 nm de espesor si la intensidad del campo eléctrico es 5.50 MV/m? Puedes suponer un campo eléctrico uniforme.

81. Un ion de doble carga se acelera a una energía de 32.0 keV por el campo eléctrico entre dos placas conductoras paralelas separadas por 2.00 cm. ¿Cuál es la intensidad del campo eléctrico entre las placas?

82. Se cree que la temperatura cerca del centro del Sol es de 15 millones de grados Celsius (1,5 × 10⁷ °C) (o Kelvin). ¿A través de qué voltaje debe acelerarse un ion de carga simple para tener la misma energía que la energía cinética promedio de los iones a esta temperatura?

83. Un rayo golpea un árbol, moviendo 20.0 C de carga a través de una diferencia de potencial de 1.00 × 10² MV. (a) ¿Qué energía se disipó? (b) ¿Qué cantidad de agua se puede elevar desde 15 °C hasta el punto de ebullición? (c) Discute el daño que podría causar al árbol la expansión del vapor hirviendo.

84. ¿Cuál es el potencial de 0.530 × 10^-10 m de un protón (la distancia promedio entre el protón y el electrón en un átomo de hidrógeno)?

85. (a) Una esfera tiene una superficie uniformemente cargada con 1.00 C. ¿A qué distancia de su centro está el potencial de 5.00 MV? (b) ¿Qué implica tu respuesta sobre el aspecto práctico de aislar una carga tan grande?

86. ¿Cuál es el signo y la magnitud de una carga puntual que produce un potencial de -2.00 V a una distancia de 1.00 mm?

87. En uno de los experimentos clásicos de física nuclear a principios del siglo XX, una partícula alfa se aceleró hacia un núcleo de oro, y su trayectoria fue desviada sustancialmente por la interacción de Coulomb. Si la energía del núcleo alfa con carga doble fuera de 5.00 MeV, ¿qué tan cerca del núcleo de oro (79 protones) podría venir antes de desviarse?

Problemas Adicionales

88. Un calentador de biberones operado con batería de 12.0 V calienta 50.0 g de vidrio, 2.50 × 10²g de fórmula para bebés y 2.00 × 10²g de aluminio de 20.0° C a 90.0 °C. (a) ¿Cuánta carga mueve la batería? (b) ¿Cuántos electrones por segundo fluyen si lleva 5.00 minutos calentar la fórmula? (Sugerencia: supón que el calor específico de la fórmula para bebés es aproximadamente el mismo que el calor específico del agua).

89. Un automóvil que funciona con batería usa un sistema de 12.0 V. Encuentra la carga que las baterías deben poder mover para acelerar el automóvil de 750 kg desde el reposo hasta 25.0 m / s, haga subir una colina de 2.00 × 102 my conduzca finalmente a una velocidad constante de 25.0 m / s mientras subes con una fuerza de 5.00 × 10² N durante una hora.

90. (a) Encuentra el voltaje cerca de una esfera de metal de 10.0 cm de diámetro que tiene 8.00 C de carga positiva en exceso. (b) ¿Qué es irracional sobre este resultado? (c) ¿Qué suposiciones son responsables?

91. Un anillo de 10 cm de radio uniformemente colocado se coloca sobre una mesa no conductora. Se encuentra que a 3.0 cm por encima del centro del semianillo el potencial es de -3.0 V con respecto al potencial cero en el infinito. ¿Cuánta carga hay en el medio anillo?

92. Un anillo de vidrio con un radio de 5,0 cm se pinta con una pintura cargada de manera que la densidad de carga alrededor del anillo varía continuamente dada la siguiente función del ángulo polar θ, λ = (3,0 × 10^-6 C/m) cos2θ. Encuentra el potencial en un punto a 15 cm por encima del centro.

93. Un disco CD de radio (R = 3.0cm) se rocía con una pintura cargada de manera que la carga varía continuamente con la distancia radial r desde el centro de la siguiente manera: σ = - (6.0 C/m)r/R. Encuentra el potencial en un punto a 4 cm por encima del centro.

94. (a) ¿Cuál es la velocidad final de un electrón acelerado desde el reposo a través de un voltaje de 25.0 MV por un terminal Van de Graff con carga negativa? (b) ¿Qué es irracional sobre este resultado? (c) ¿Qué suposiciones son responsables?

95. Una placa de metal grande se carga uniformemente a una densidad de σ = 2.0 × 10^-9 C/m². ¿Qué tan separadas están las superficies equipotenciales que representan una diferencia de potencial de 25 V?

96. Tu amigo se emociona mucho con la idea de hacer un pararrayos o tal vez solo un juguete chispeante conectando dos esferas como se muestra en la Figura 7.39, y haciendo R₂ tan pequeño que el campo eléctrico es mayor que la fuerza dieléctrica del aire, solo desde el campo eléctrico habitual de 150 V/m cerca de la superficie de la Tierra. Si R₁ mide 10 cm, ¿qué tan pequeño debe ser R₂, y esto parece práctico? (Sugerencia: recuerda el cálculo del campo eléctrico en la superficie de un conductor de la Ley de Gauss).

97. (a) Encuentra x >> L, límite del potencial de una varilla finita uniformemente cargada y demuestra que coincide con la de una fórmula de carga puntual. (b) ¿Por qué esperarías este resultado?

98. Una pequeña bola de médula esférica de radio de 0,50 cm se pinta con una pintura de plata y luego se le coloca una carga de -10 μC. La bola de médula cargada se coloca en el centro de una cáscara esférica de oro de radio interno de 2,0 cm y un radio exterior de 2,2 cm. (a) Encuentra el potencial eléctrico de la capa de oro con respecto al potencial cero en el infinito. (b) ¿Cuánta carga deberías poner en el caparazón de oro si quieres hacer que su potencial sea de 100 V?

99. Dos placas conductoras paralelas, cada una de secciones transversales de 400 cm², están separadas 2,0 cm y sin carga. Si se transfieren 1.0 × 10¹² electrones de una placa a la otra, (a) ¿cuál es la diferencia de potencial entre las placas? (b) ¿Cuál es la diferencia de potencial entre la placa positiva y un punto a 1.25 cm de ella que está entre las placas?

100. Una carga puntual de q = 5.0 × 10^-8 C se coloca en el centro de una capa esférica no cargada de radio interior 6.0 cm y radio exterior 9.0 cm. Encuentra el potencial eléctrico en (a) r = 4.0 cm, (b) r = 8.0 cm, (c) r = 12.0 cm.

101. La Tierra tiene una carga neta que produce un campo eléctrico de aproximadamente 150 N/C hacia abajo en su superficie. (a) ¿Cuál es la magnitud y el signo del exceso de carga, teniendo en cuenta que el campo eléctrico de una esfera conductora es equivalente a una carga puntual en su centro? (b) ¿Qué aceleración producirá el campo en un electrón libre cerca de la superficie de la Tierra? (c) ¿Qué objeto de masa con un solo electrón extra tendrá su peso soportado por este campo?

102. Las cargas puntuales de 25.0 μC y 45.0 μC se colocan a 0.500 m de distancia. (a) ¿En qué punto a lo largo de la línea entre ellos está el campo eléctrico cero? (b) ¿Cuál es el campo eléctrico a medio camino entre ellos?

103. ¿Qué puedes decir acerca de dos cargas q₁ y q₂, si el campo eléctrico un cuarto del camino desde q₁ a q₂ es cero?

104. Calcula la velocidad angular ω de un electrón que orbita un protón en el átomo de hidrógeno, dado que el radio de la órbita es 0.530 × 10^-10 m. Puedes suponer que el protón es estacionario y que la fuerza centrípeta es suministrada por la atracción de Coulomb.

105. Un electrón tiene una velocidad inicial de 5.00 × 10⁶ m/s en un campo eléctrico uniforme de 2.00 × 10⁵ N/C. El campo acelera el electrón en la dirección opuesta a su velocidad inicial. (a) ¿Cuál es la dirección del campo eléctrico? (b) ¿Qué distancia recorre el electrón antes de detenerse? (c) ¿Cuánto tiempo tarda el electrón en descansar? (d) ¿Cuál es la velocidad del electrón cuando vuelve a su punto de partida?

Problemas de Desafío

106. Tres iones Na⁺ y tres iones Cl^- se colocan alternativamente e igualmente espaciados alrededor de un círculo de radio de 50 nm. Encuentra la energía electrostática almacenada.

107. Mira hacia arriba (presumiblemente en línea, o desmantelando un dispositivo viejo y haciendo mediciones) la magnitud de las placas de deflexión potenciales (y el espacio entre ellas) en una impresora de inyección de tinta. Luego, busca la velocidad con la que sale la tinta de la boquilla. ¿Puedes calcular la masa típica de una gota de tinta?

108. Usa el campo eléctrico de una esfera finita con una densidad de carga de volumen constante para calcular el potencial eléctrico en todo el espacio. Luego verifica tus resultados calculando el campo eléctrico del potencial.
109. Calcula el campo eléctrico de un dipolo a lo largo del espacio desde el potencial.