Preguntas y problemas - Capítulo VI

Preguntas conceptuales

6.1 Flujo eléctrico

1. Discute cómo orientar una superficie plana de área A en un campo eléctrico uniforme de magnitud E₀ para obtener (a) el flujo máximo y (b) el flujo mínimo a través del área.

2. ¿Cuáles son los valores máximos y mínimos del flujo en la pregunta anterior?

3. El flujo eléctrico neto que cruza una superficie cerrada es siempre cero. ¿Verdadero o falso?

4. El flujo eléctrico neto que cruza una superficie abierta nunca es cero. ¿Verdadero o falso?

6.2 Explicando la ley de Gauss

5. Dos superficies esféricas concéntricas encierran una carga puntual q. El radio de la esfera externa es el doble del radio de la interna. Compara los flujos eléctricos que cruzan las dos superficies.

6. Compara el flujo eléctrico a través de la superficie de un cubo de una longitud lateral a que tiene una carga q en su centro hacia el flujo a través de una superficie esférica de radio a con una carga q en su centro.

7. (a) Si el flujo eléctrico a través de una superficie cerrada es cero, ¿el campo eléctrico es necesariamente cero en todos los puntos de la superficie? (b) ¿Cuál es la carga neta dentro de la superficie?

8. Discute cómo la ley de Gauss se vería afectada si el campo eléctrico de una carga puntual no variara como 1/r².

9. Discute las similitudes y diferencias entre el campo gravitacional de una masa puntual m y el campo eléctrico de una carga puntual q.

10. Discute si la ley de Gauss se puede aplicar a otras fuerzas, y si es así, cuáles.

11. ¿Es el término E→ en la ley de Gauss el campo eléctrico producido solo por la carga dentro de la superficie Gaussiana?

12. Reformula la ley de Gauss eligiendo la unidad normal de la superficie de Gauss para ser la dirigida hacia adentro.

6.3 Aplicación de la ley de Gauss

13. ¿Sería útil la ley de Gauss para determinar el campo eléctrico de dos cargas iguales pero opuestas a una distancia fija aparte?

14. Discute el papel que desempeña la simetría en la aplicación de la ley de Gauss. Dá ejemplos de distribuciones de carga continuas en las cuales la ley de Gauss es útil y no útil para determinar el campo eléctrico.

15. Discute las restricciones en la superficie gaussiana usadas para discutir la simetría plana. Por ejemplo, ¿es su longitud importante? ¿La sección transversal tiene que ser cuadrada? ¿Las caras frontales deben estar en lados opuestos de la hoja?

6.4 Conductores en equilibrio electrostático

16. ¿El campo eléctrico dentro de un metal siempre es cero?

17. En condiciones electrostáticas, el exceso de carga en un conductor reside en su superficie. ¿Esto significa que todos los electrones de conducción en un conductor están en la superficie?

18. Una carga q se coloca en la cavidad de un conductor como se muestra a continuación. ¿Experimentará una carga fuera del conductor un campo eléctrico debido a la presencia de q?



19. El conductor en la figura anterior tiene una carga en exceso de -5.0 μC. Si se coloca una carga puntual de 2.0 μC en la cavidad, ¿cuál es la carga neta en la superficie de la cavidad y en la superficie externa del conductor?

Problemas

6.1 Flujo eléctrico

20. Un campo eléctrico uniforme de magnitud 1.1 × 10⁴ N/C es perpendicular a una hoja cuadrada con lados de 2.0 m de largo. ¿Cuál es el flujo eléctrico a través de la hoja?

21. Calcula el flujo a través de la hoja del problema anterior si el plano de la hoja está en un ángulo de 60° con respecto al campo. Encuentra el flujo para ambas direcciones unitarias normales a la hoja.

22. Encuentra el flujo eléctrico a través de un área rectangular de 3 cm × 2 cm entre dos placas paralelas donde hay un campo eléctrico constante de 30 N/C para las siguientes orientaciones del área: (a) paralelo a las placas, (b) perpendicular a las placas, y (c) la normal al área haciendo un ángulo de 30° con la dirección del campo eléctrico. Ten en cuenta que este ángulo también se puede dar como 180° + 30°.

23. El flujo eléctrico a través de un área de forma cuadrada de 5 cm de lado cerca de una gran lámina cargada se encuentra que es 3 × 10^-5 N • m²/C cuando el área es paralela a la placa. Encuentra la densidad de carga en la hoja.

24. Dos grandes placas de aluminio rectangulares de 150 cm² de superficie se enfrentan entre sí con una separación de 3 mm entre ellas. Las placas se cargan con la misma cantidad de cargas opuestas, ± 20μC. Las cargas en las placas se enfrentan entre sí. Encuentre el flujo a través de un círculo de radio de 3 cm entre las placas cuando la normal al círculo forma un ángulo de 5° con una línea perpendicular a las placas. Observa que este ángulo también se puede dar como 180° + 5°.

25. Una superficie cuadrada de 2 cm² de área se encuentra en un espacio de campo eléctrico uniforme de magnitud 10³ N/C. La cantidad de flujo a través de él depende de cómo se oriente el cuadrado en relación con la dirección del campo eléctrico. Encuentra el flujo eléctrico a través del cuadrado, cuando la normal haga los siguientes ángulos con el campo eléctrico: (a) 30°, (b) 90° y (c) 0°. Ten en cuenta que estos ángulos también se pueden dar como 180° + θ.

26. Un campo vectorial apunta hacia el eje z, v→ = α/(x² + y²)z^. (a) Encuentre el flujo del campo vectorial a través de un rectángulo en el plano xy entre a < x < b y c < y < d. (b) Haz lo mismo a través de un rectángulo en el plano yz entre a < z ​​ < b y c < y < d (Presenta tu respuesta como una integral).

27. Considere el campo eléctrico uniforme E→ = (4.0j^ + 3.0k^) × 10³ N/C. ¿Cuál es su flujo eléctrico a través de un área circular de radio de 2,0 m que se encuentra en el plano xy?

28. Repite el problema anterior, dado que el área circular es (a) en el plano yz y (b) 45° por encima del plano xy.

29. Un cable cargado infinitamente con carga por unidad de longitud λ se encuentra a lo largo del eje central de una superficie cilíndrica de radio ry longitud l. ¿Cuál es el flujo a través de la superficie debido al campo eléctrico del cable cargado?

6.2 Explicando la ley de Gauss

30. Determine el flujo eléctrico a través de cada superficie cuya sección transversal se muestra a continuación.



31. Encuentrael flujo eléctrico a través de la superficie cerrada cuyas secciones transversales se muestran a continuación.



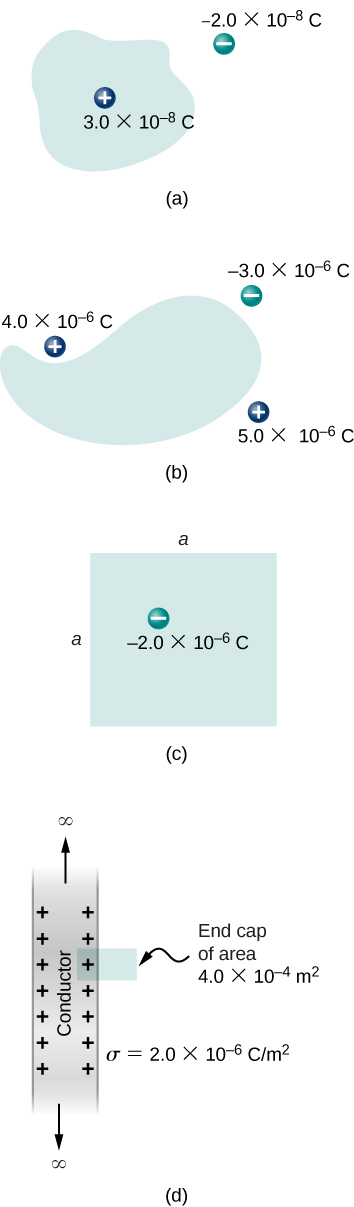
32. Una carga puntual q se encuentra en el centro de un cubo cuyos lados son de longitud a. Si no hay otros cargas en este sistema, ¿cuál es el flujo eléctrico a través de una cara del cubo?

33. Una carga puntual de 10 μC se encuentra en una ubicación no especificada dentro de un cubo de 2 cm de lado. Encuentra el flujo eléctrico neto a través de las superficies del cubo.

34. Un flujo neto de 1.0 × 10⁴ N • m²/C pasa hacia adentro a través de la superficie de una esfera de radio de 5 cm. (a) ¿Cuánta carga hay dentro de la esfera? (b) ¿Con cuánta precisión podemos determinar la ubicación de la carga a partir de esta información?

35. Una carga q se coloca en una de las esquinas de un cubo del lado a, como se muestra a continuación. Encuentra la magnitud del flujo eléctrico a través de la cara sombreada debido a q. Suponer q > 0



36. El flujo eléctrico a través de una caja cúbica de 8.0 cm en un lado es de 1.2 × 10³ N • m²/C. ¿Cuál es la carga total encerrada por la caja?

37. El flujo eléctrico a través de una superficie esférica es de 4,0 × 10⁴ N • m²/C. ¿Cuál es la carga neta encerrada por la superficie?

38. Un cubo cuyos lados son de longitud d se coloca en un campo eléctrico uniforme de magnitud E = 4.0 × 10³ N/C, de modo que el campo es perpendicular a dos caras opuestas del cubo. ¿Cuál es el flujo neto a través del cubo?

39. Repite el problema anterior, suponiendo que el campo eléctrico se dirige a lo largo de una diagonal del cuerpo del cubo.

40. Una carga total de 5.0 × 10^-6 C se distribuye uniformemente a través de un volumen cúbico cuyos bordes son de 8.0 cm de largo. (a) ¿Cuál es la densidad de carga en el cubo? (b) ¿Cuál es el flujo eléctrico a través de un cubo con bordes de 12.0 cm que es concéntrico con la distribución de carga? (c) Haz el mismo cálculo para cubos cuyos bordes tengan 10.0 cm de largo y 5.0 cm de largo. (d) ¿Cuál es el flujo eléctrico a través de una superficie esférica de radio de 3,0 cm que también es concéntrica con la distribución de carga?

6.3 Aplicación de la ley de Gauss

41. Recuerda que en el ejemplo de una esfera cargada uniforme, ρ₀ = Q/(4/3πR³). Reescribe las respuestas en términos de la carga total Q en la esfera.

42. Supón que la densidad de carga de la distribución de carga esférica que se muestra en la Figura 6.23 es ρ(r) = ρ₀r/R para r ≤ R y cero para r > R. Obtén expresiones para el campo eléctrico tanto dentro como fuera de la distribución.

43. Un cable muy largo y delgado tiene una densidad de carga lineal uniforme de 50 μC/m. ¿Cuál es el campo eléctrico a una distancia de 2.0 cm del cable?

44. Una carga de -30 μC se distribuye uniformemente a lo largo de un volumen esférico de radio 10.0 cm. Determina el campo eléctrico debido a esta carga a una distancia de (a) 2.0 cm, (b) 5.0 cm y (c) 20.0 cm desde el centro de la esfera.

45. Repite tus cálculos para el problema anterior, dado que la carga se distribuye uniformemente sobre la superficie de un conductor esférico de radio 10.0 cm.

46. ​​Una carga total Q se distribuye uniformemente a través de una capa esférica de radios internos y externos r₁ y r₂, respectivamente. Demuestra que el campo eléctrico debido a la carga es



47. Cuando una carga se coloca en una esfera de metal, termina en equilibrio en la superficie exterior. Utiliza esta información para determinar el campo eléctrico de carga de + 3.0 μC puesta en una bola esférica de aluminio de 5.0 cm en los siguientes dos puntos en el espacio: (a) un punto a 1.0 cm del centro de la bola (un punto interno) y ( b) un punto a 10 cm del centro de la pelota (un punto exterior).

48. Una gran hoja de carga tiene una densidad de carga uniforme de 10 μC/m². ¿Cuál es el campo eléctrico debido a esta carga en un punto justo arriba de la superficie de la hoja?

49. Determina si la simetría cilíndrica aproximada se cumple para las siguientes situaciones. Indica por qué o por qué no. (a) Una varilla de cobre de 300 cm de largo con un radio de 1 cm se carga con una carga de +500 nC y buscamos un campo eléctrico en un punto a 5 cm del centro de la varilla. (b) Una varilla de cobre de 10 cm de largo con un radio de 1 cm se carga con una carga de +500 nC y buscamos un campo eléctrico en un punto a 5 cm del centro de la varilla. (c) Una varilla de madera de 150 cm se pega a una varilla de plástico de 150 cm para hacer una varilla de 300 cm de largo, que luego se pinta con una pintura cargada para que se obtenga una densidad de carga uniforme. El radio de cada varilla es de 1 cm, y buscamos un campo eléctrico en un punto que está a 4 cm del centro de la varilla. (d) La misma varilla que (c), pero buscamos campo eléctrico en un punto que está a 500 cm del centro de la varilla.

50. Una barra de plata larga de radio 3 cm tiene una carga de -5 μC/cm en su superficie. (a) Encuentra el campo eléctrico en un punto a 5 cm del centro de la varilla (un punto externo). (b) Encuentra el campo eléctrico en un punto a 2 cm del centro de la varilla (un punto interno).

51. El campo eléctrico a 2 cm del centro de la varilla larga de cobre de radio 1 cm tiene una magnitud de 3 N/C y se dirige hacia afuera desde el eje de la varilla. (a) ¿Cuánta carga por unidad de longitud existe en la varilla de cobre? (b) ¿Cuál sería el flujo eléctrico a través de un cubo de 5 cm de lado situado de manera tal que la varilla pasa a través de los lados opuestos del cubo perpendicularmente?

52. Una carcasa cilíndrica de cobre larga de radio interior de 2 cm y radio exterior de 3 cm rodea concéntricamente una varilla de aluminio larga y cargada de radio de 1 cm con una densidad de carga de 4 pC/m. Todas las cargas en la varilla de aluminio residen en su superficie. La superficie interna de la carcasa de cobre tiene una carga exactamente opuesta a la de la varilla de aluminio, mientras que la superficie exterior de la carcasa de cobre tiene la misma carga que la varilla de aluminio. Encuentra la magnitud y dirección del campo eléctrico en puntos que están a las siguientes distancias del centro de la varilla de aluminio: (a) 0.5 cm, (b) 1.5 cm, (c) 2.5 cm, (d) 3.5 cm, y (e) 7 cm.

53. La carga se distribuye uniformemente con una densidad ρ a lo largo de un volumen cilíndrico infinitamente largo de radio R. Demuestra que el campo de esta distribución de carga se dirige radialmente con respecto al cilindro y que



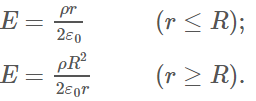
54. La carga se distribuye a lo largo de un volumen cilíndrico muy largo de radio R tal que la densidad de carga aumenta con la distancia r desde el eje central del cilindro de acuerdo con ρ = αr, donde α es una constante. Demuestra que el campo de esta distribución de carga se dirige radialmente con respecto al cilindro y que



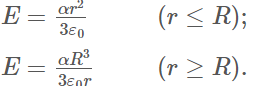
55. El campo eléctrico a 10.0 cm de la superficie de una bola de cobre de radio 5.0 cm se dirige hacia el centro de la bola y tiene una magnitud de 4.0 × 10² N/C. ¿Cuánta carga hay en la superficie de la bola?

56. La carga se distribuye a lo largo de un caparazón esférico de radio interior r₁ y radio exterior r₂ con una densidad de volumen dada por ρ = ρ₀r₁/r, donde ρ₀ es una constante. Determina el campo eléctrico debido a esta carga en función de r, la distancia desde el centro de la carcasa.

57. La carga se distribuye en un volumen esférico de radio R con una densidad ρ = αr², donde α es una constante. Determina el campo eléctrico debido a la carga en los puntos tanto dentro como fuera de la esfera.

58. Considera que un núcleo de uranio es una esfera de radio R = 7.4 × 10^-15 m con una carga de 92e distribuida uniformemente en todo su volumen. (a) ¿Cuál es la fuerza eléctrica ejercida sobre un electrón cuando está a 3,0 × 10^-15 m del centro del núcleo? (b) ¿Cuál es la aceleración del electrón en este punto?

59. La densidad de carga volumétrica de una distribución de carga esférica está dada por ρ(r) = ρ₀e - αr, donde ρ₀ y α son constantes. ¿Cuál es el campo eléctrico producido por esta distribución de carga?

6.4 Conductores en equilibrio electrostático

60. En la figura siguiente se muestra un conductor sin carga con una cavidad interna. Utiliza la superficie cerrada S junto con la ley de Gauss para mostrar que cuando se coloca una carga q en la cavidad, se induce una carga total -q en la superficie interna del conductor. ¿Cuál es la carga en la superficie externa del conductor?



Figura 6.46 Una carga dentro de la cavidad de un metal. Las cargas en la superficie externa no dependen de cómo se distribuyan las cargas en la superficie interna ya que el campo E dentro del cuerpo del metal es cero.

61. Un conductor esférico no cargado S de radio R tiene dos cavidades esféricas A y B de radios a y b, respectivamente, como se muestra a continuación. Dos cargas puntuales + q_a y + q_b se colocan en el centro de las dos cavidades mediante el uso de soportes no conductores. Además, una carga puntual + q₀ se coloca afuera a una distancia r del centro de la esfera. (a) Dibuja distribuciones de carga aproximadas en el metal, aunque la esfera metálica no tiene carga neta. (b) Dibuja líneas de campo eléctrico. Dibuja suficientes líneas para representar todos los lugares claramente diferentes.



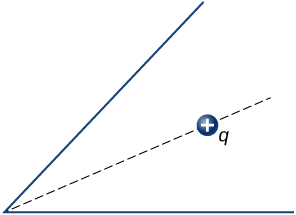
62. Se coloca una carga puntual positiva en la bisectriz angular de dos conductores planos no cargados que forman un ángulo de 45°. Dibuja las líneas del campo eléctrico.



63. Se carga un cilindro largo de cobre de radio de 3 cm para que tenga una carga uniforme por unidad de longitud en su superficie de 3 C/m. (a) Encuentra el campo eléctrico dentro y fuera del cilindro. (b) Dibuja líneas de campo eléctrico en un plano perpendicular a la barra.

64. Una bola esférica de aluminio de radio 4 cm se carga con 5 μC de carga. Una capa esférica de cobre de radio interior de 6 cm y un radio exterior de 8 cm lo rodea. Se coloca una carga total de -8 μC en la carcasa de cobre. (a) Encuentra el campo eléctrico en todos los puntos del espacio, incluidos los puntos dentro de la carcasa de aluminio y cobre cuando la cubierta de cobre y la esfera de aluminio son concéntricas. (b) Encuentra el campo eléctrico en todos los puntos del espacio, incluidos los puntos dentro de la carcasa de aluminio y cobre cuando los centros de la cubierta de cobre y la esfera de aluminio estén a una distancia de 1 cm.

65. Un cilindro largo de aluminio de radio R metros se carga para que tenga una carga uniforme por unidad de longitud en su superficie λ. (a) Encuentra el campo eléctrico dentro y fuera del cilindro. (b) Traza el campo eléctrico como una función de la distancia desde el centro de la varilla.

66. En la superficie de cualquier conductor en equilibrio electrostático, E = σ/ε₀. Demuestra que esta ecuación es consistente con el hecho de que E = kq/r² en la superficie de un conductor esférico.

67. Dos placas paralelas de 10 cm en un lado reciben cargas iguales y opuestas de magnitud 5.0 × 10^-9 C. Las placas están separadas por 1,5 mm. ¿Cuál es el campo eléctrico en el centro de la región entre las placas?

68. Dos placas conductoras paralelas, cada una de las secciones transversales de 400 cm², están separadas 2,0 cm y sin carga. Si se transfieren 1.0 × 10¹² electrones de una placa a la otra, ¿cuál es (a) la densidad de carga en cada placa? (b) ¿El campo eléctrico entre las placas?

69. La densidad de carga superficial en un tubo metálico recto largo es σ. ¿Cuál es el campo eléctrico afuera y dentro de la tubería? Supón que la tubería tiene un diámetro de 2a.



70. Una carga puntual q = -5.0 × 10^-12 C se coloca en el centro de una carcasa esférica conductora de radio interior 3.5 cm y radio exterior 4.0 cm. El campo eléctrico justo por encima de la superficie del conductor se dirige radialmente hacia afuera y tiene una magnitud de 8.0 N/C. (a) ¿Cuál es la densidad de carga en la superficie interna de la carcasa? (b) ¿Cuál es la densidad de carga en la superficie exterior de la carcasa? (c) ¿Cuál es la carga neta en el conductor?

71. Un conductor cilíndrico sólido de radio a está rodeado por una concha cilíndrica concéntrica de radio interior b. El cilindro sólido y la carcasa llevan cargas + Q y -Q, respectivamente. Suponiendo que la longitud L de ambos conductores es mucho mayor que a o b, determina el campo eléctrico como una función de r, la distancia desde el eje central común de los cilindros, para (a) r < a; (b) a < r < b; y (c) r > b.

Problemas Adicionales

72. Un campo vectorial E→ (no necesariamente un campo eléctrico) viene dado por E→ = 3x²k^. Calcula ∫_SE→ • n^da, donde S es el área que se muestra a continuación. Supongamos que n^ = k^.



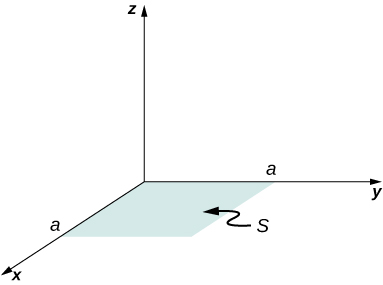
73. Repite el problema anterior, con E→ = 2xi^ + 3x²k^.

74. Un área circular S es concéntrica con el origen, tiene radio a, y se encuentra en el plano yz. Calcula ∫_SE→ • n^dA para E→ = 3z²i^.

75. (a) Calcula el flujo eléctrico a través de la superficie hemisférica abierta debido al campo eléctrico E→ = E₀k^ (ver figura a continuación). (b) Si el hemisferio gira 90° alrededor del eje x, ¿cuál es el flujo a través de él?



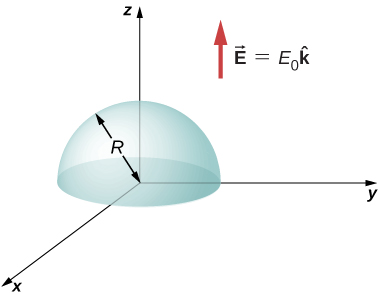
76. Supongamos que el campo eléctrico de una carga puntual aislada fuera proporcional a 1/r^{2 + σ} en lugar de 1/r². Determina el flujo que pasa a través de la superficie de una esfera de radio R centrada en la carga. ¿La ley de Gauss seguirá siendo válida?

77. El campo eléctrico en una región viene dado por E→ = a/(b + cx)i^, donde a = 200 N • m/C, b = 2.0m, y c = 2.0. ¿Cuál es la carga neta encerrada por el volumen sombreado que se muestra a continuación?



78. Dos cargas iguales y opuestas de magnitud Q están ubicadas en el eje x en los puntos + a y -a, como se muestra a continuación. ¿Cuál es el flujo neto debido a estas cargas a través de una superficie cuadrada del lado 2a que se encuentra en el plano yz y se centra en el origen? (Sugerencia: determina el flujo debido a cada carga por separado, luego usa el principio de superposición. Puedes hacer un argumento de simetría).



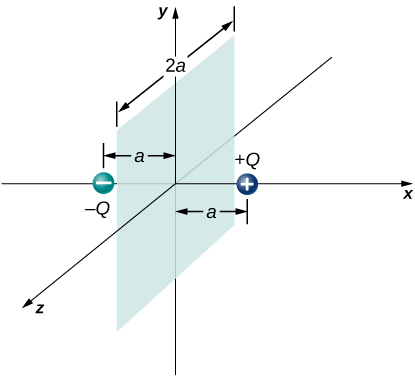
79. Un compañero estudiante calculó el flujo a través de un cuadrado para el sistema en el problema anterior y obtuvo 0. ¿Qué salió mal?

80. Una pieza de aluminio de 10 cm × 10 cm de espesor de 0,1 mm tiene una carga de 20 μC que se extiende uniformemente en ambas caras laterales. Puedes ignorar las cargas en los lados delgados de los bordes. (a) Encuentra la densidad de carga. (b) Encuentra el campo eléctrico a 1 cm del centro, suponiendo una simetría plana aproximada.

81. Dos láminas de aluminio de 10 cm × 10 cm de espesor de 0,1 mm se enfrentan entre sí con una separación de 5 mm. Una de las láminas tiene una carga de + 30 μC y la otra tiene -30 μC. (a) Encuentra la densidad de carga en todas las superficies, es decir, en aquellas enfrentadas entre sí y las que están orientadas hacia afuera. (b) Encuentra el campo eléctrico entre las placas cerca del centro asumiendo la simetría plana.

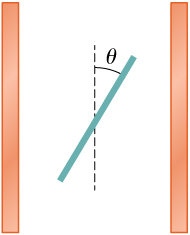
82. Dos placas de cobre grandes enfrentadas tienen densidades de carga ± 4.0 C/m² en la superficie enfrentada a la otra placa, y cero entre las placas. Encuentra el flujo eléctrico a través de un área rectangular de 3 cm × 4 cm entre las placas, como se muestra a continuación, para las siguientes orientaciones del área. (a) Si el área es paralela a las placas, y (b) si el área está inclinada θ = 30° desde la dirección paralela. Ten en cuenta que este ángulo también puede ser θ = 180° + 30°.



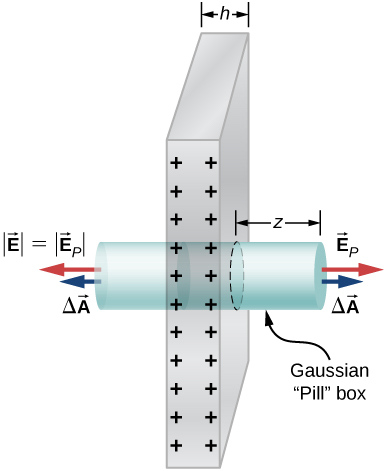
83. La losa infinita entre los planos definidos por z = -a/2 y z = a/2 contiene una densidad de carga de volumen uniforme ρ (ver figura abajo). ¿Cuál es el campo eléctrico producido por esta distribución de carga, tanto dentro como fuera de la distribución?



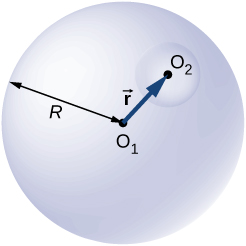
84. Una carga total Q se distribuye uniformemente a través de un volumen esférico que se centra en O₁ y tiene un radio R. Sin perturbar la carga restante, la carga se elimina del volumen esférico que está centrado en O₂ (ver figura a continuación). Demuestra que el campo eléctrico en todas partes en la región vacía está dado por E→ = Qr→/4πε₀R³ , donde r→ es el vector de desplazamiento dirigido desde O₁ a O₂.



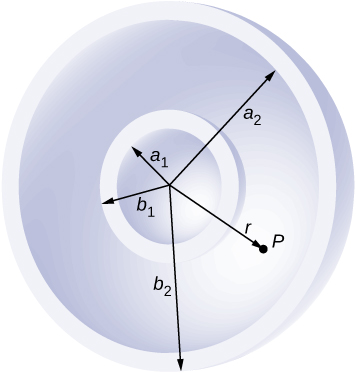
85. Una carcasa esférica no conductora de radio interior a₁ y radio exterior b₁ está uniformemente cargada con densidad de carga ρ₁ dentro de otra capa esférica no conductora de radio interior a₂ y radio exterior b₂ que también está uniformemente cargada con densidad de carga ρ₂. Encuentra el campo eléctrico en el punto espacial P a una distancia r del centro común tal que (a) r > b₂, (b) a₂ < r < b₂, (c) b₁ < r < a₂, (d) a₁ < r < b₁, y (e) r < a₁.



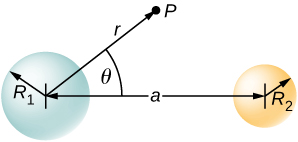
86. Dos esferas no conductoras de radios R₁ y R₂ están uniformemente cargadas con densidades de carga ρ₁ y ρ₂, respectivamente. Están separados a una distancia de centro a centro a (ver figura a continuación). Encuentra el campo eléctrico en el punto P ubicado a una distancia r del centro de la esfera 1 y está en la dirección θ de la línea que une las dos esferas, suponiendo que sus densidades de carga no se ven afectadas por la presencia de la otra esfera (Sugerencia: trabaja una esfera a la vez y usa el principio de superposición).



87. Un disco de radio R se corta en una placa grande no conductora que está uniformemente cargada con una densidad de carga σ (culombio por metro cuadrado). Ver figura abajo. Encuentra el campo eléctrico a una altura h por encima del centro del disco. (h >> R, h << l o w). (Sugerencia: llena el agujero con ± σ)



88. Las conchas esféricas conductoras concéntricas llevan cargas Q y -Q, respectivamente (ver figura abajo). La carcasa interna tiene un grosor insignificante. Determina el campo eléctrico para (a) r < a; (b) a < r < b; (c) b < r < c; y (d) r > c.



89. A continuación se muestran dos capas esféricas conductoras concéntricas de radios R₁ y R₂, cada una de espesor finito mucho menor que cualquiera de los dos radios. La carcasa interna y externa llevan cargas netas q₁ y q₂, respectivamente, donde tanto q₁ como q₂ son positivas. ¿Cuál es el campo eléctrico para (a) r < R₁; (b) R₁ < r < R₂; y (c) r > R₂? (d) ¿Cuál es la carga neta en la superficie interna de la carcasa interna, la superficie exterior de la capa interior, la superficie interna de la capa externa y la superficie externa de la capa exterior?



90. Una carga puntual de q = 5.0 × 10^-8 C se coloca en el centro de una carcasa esférica sin carga de radio interior 6.0 cm y radio exterior 9.0 cm. Encuentra el campo eléctrico en (a) r = 4.0 cm, (b) r = 8.0 cm, y (c) r = 12.0 cm. (d) ¿Cuáles son las cargas inducidas en las superficies interna y externa de la carcasa?

Problemas Reto

91. El Telescopio Espacial Hubble puede medir el flujo de energía de objetos distantes como supernovas y estrellas. Los científicos luego usan estos datos para calcular la energía emitida por ese objeto. Elige un objeto interestelar con el que los científicos hayan observado el flujo en el Hubble (por ejemplo, Vega3), encuentra la distancia hasta ese objeto y el tamaño del espejo primario del Hubble, y calcula el flujo de energía total. (Sugerencia: el Hubble intercepta solo una pequeña parte del flujo total).

92. Re-deriva la ley de Gauss para el campo gravitatorio, con g→ dirigido positivamente hacia afuera.

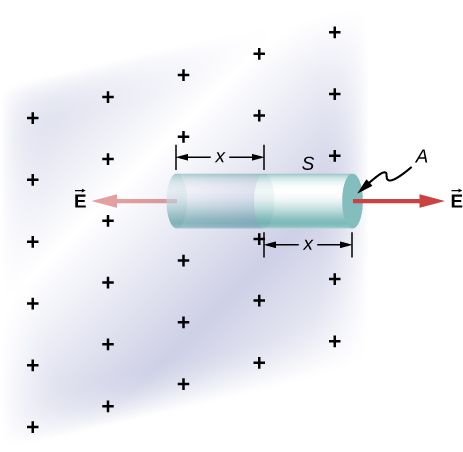
93. Abajo se muestra una hoja de carga de placa infinita de densidad de carga superficial σ. ¿Cuál es el campo eléctrico a una distancia x de la hoja? Compara el resultado de este cálculo con el calculado en el texto.



94. Un globo esférico de goma lleva una carga total Q distribuida uniformemente sobre su superficie. En t = 0, el radio del globo es R. Luego, el globo se infla lentamente hasta que su radio alcance 2R en el momento t₀. Determina el campo eléctrico debido a esta carga en función del tiempo (a) en la superficie del globo, (b) en la superficie del radio R y (c) en la superficie del radio 2R. Ignora cualquier efecto en el campo eléctrico debido al material del globo y supón que el radio aumenta uniformemente con el tiempo.

95. Encuentra el campo eléctrico de una gran placa conductora que contiene una carga neta q. Supón que A es el área de un lado de la placa y h el espesor de la placa (ver figura más abajo). La carga en la placa de metal se distribuirá principalmente en los dos lados planos y muy poco en los bordes si la placa es delgada.

<
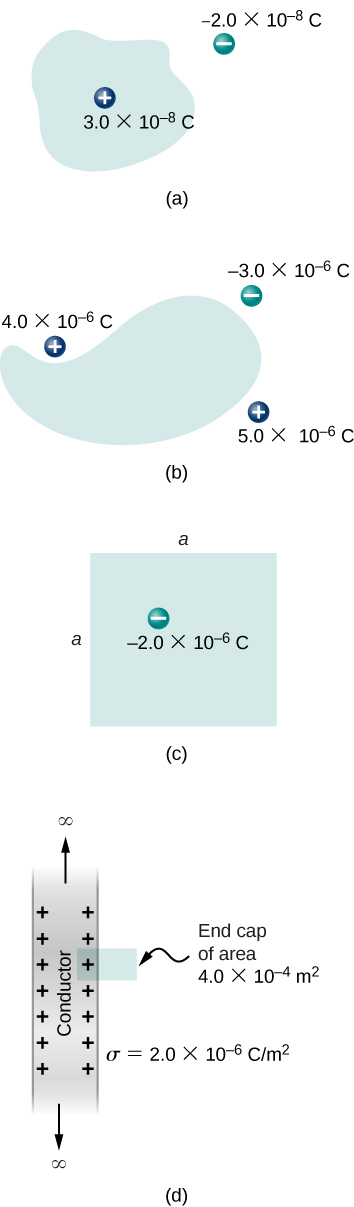
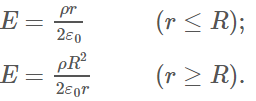
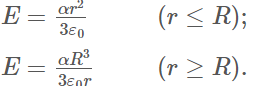