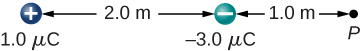Preguntas y problemas - Capítulo V

Preguntas conceptuales

5.1 Carga eléctrica

1. Hay una gran cantidad de partículas cargadas en la mayoría de los objetos. ¿Por qué, entonces, la mayoría de los objetos no muestran electricidad estática?

2. ¿Por qué la mayoría de los objetos tienden a contener cantidades casi iguales de cargas positivas y negativas?

3. Una barra con carga positiva atrae una pequeña pieza de corcho. (a) ¿Podemos concluir que el corcho está cargado negativamente? (b) La varilla repele otra pequeña pieza de corcho. ¿Podemos concluir que esta pieza está cargada positivamente?

4. Dos cuerpos se atraen entre sí eléctricamente. ¿Ambos tienen que estar cargados? Responde la misma pregunta si los cuerpos se repelen entre sí.

5. ¿Cómo determinarías si la carga en una varilla en particular es positiva o negativa?

5.2 Conductores, aislantes y carga por inducción

6. Un inventor excéntrico intenta levitar una bola de corcho envolviéndola con papel de aluminio y colocando una gran carga negativa sobre la bola y luego colocando una gran carga positiva en el techo de su taller. Pero, al intentar colocar una gran carga negativa en la pelota, la lámina se va volando. Explica.

7. Cuando una varilla de vidrio se frota con seda, se vuelve positiva y la seda se vuelve negativa, pero ambas atraen el polvo. ¿El polvo tiene un tercer tipo de carga que se ve atraída tanto por positivo como por negativo? Explica.

8. ¿Por qué un automóvil siempre atrae polvo justo después de pulirlo? (Ten en cuenta que la cera del automóvil y las llantas de automóviles son aislantes).

9. ¿El conductor descargado que se muestra a continuación experimenta una fuerza eléctrica neta?



10. Al caminar sobre una alfombra, una persona con frecuencia es cargada debido al roce entre sus zapatos y la alfombra. Esta carga causa una chispa y un ligero golpe cuando la persona se acerca a un objeto de metal. ¿Por qué estos shocks son mucho más comunes en un día seco?

11. Compara la carga por conducción con la carga por inducción.

12. Pequeños pedazos de tejido son atraídos por un peine cargado. Poco después de pegarse al peine, los pedazos de tejido son repelidos. Explica.

13. Los camiones que llevan gasolina a menudo tienen cadenas colgando y cepillando el suelo. ¿Por qué?

14. ¿Por qué los experimentos electrostáticos funcionan tan mal en climas húmedos?

15. ¿Por qué algunas prendas se adhieren después de haberlas quitado de la secadora? ¿Esto sucede si todavía están húmedos?

16. ¿Se puede usar la inducción para producir carga en un aislante?

17. Supongamos que alguien te dice que frotes cuarzo con un paño de algodón que produce un tercer tipo de carga en el cuarzo. Describe lo que podrías hacer para probar esta afirmación.

18. Una varilla de cobre portátil no adquiere una carga cuando la frotas con un paño. Explicar por qué.

19. Supón que colocas una carga q cerca de una placa de metal grande. (a) Si atraen q a la placa, ¿la placa está cargada necesariamente? (b) Si q es repelido por la placa, ¿la placa está necesariamente cargada?

5.3 Ley de Coulomb

20. ¿Definir la carga de un electrón como positiva tiene algún efecto sobre la ley de Coulomb?

21. Un núcleo atómico contiene protones con carga positiva y neutrones sin carga. Dado que los núcleos permanecen juntos, ¿qué debemos concluir acerca de las fuerzas entre estas partículas nucleares?

22. ¿La fuerza entre dos cargas fijas está influenciada por la presencia de otras cargas?

5.4 Campo eléctrico

23. Al medir un campo eléctrico, ¿podríamos usar una carga de prueba negativa en lugar de positiva?

24. Cuando hace buen tiempo, el campo eléctrico debido a la carga neta en la Tierra apunta hacia abajo. ¿La Tierra está cargada positivamente o negativamente?

25. Si el campo eléctrico en un punto de la línea entre dos cargas es cero, ¿qué sabes de las cargas?

26. Dos cargas se encuentran a lo largo del eje x. ¿Es cierto que el campo eléctrico neto siempre desaparece en algún punto (que no sea infinito) a lo largo del eje x?

5.5 Cálculo de los campos eléctricos de distribuciones de carga

27. Da un argumento plausible de por qué el campo eléctrico fuera de una hoja infinita cargada es constante.

28. Compara los campos eléctricos de una hoja de carga infinita, una placa conductora cargada infinitamente e infinitas placas paralelas cargadas opuestamente.

29. Describe los campos eléctricos de una placa cargada infinitamente y de dos placas paralelas cargadas infinitamente en términos del campo eléctrico de una hoja infinita de carga.

30. Una carga negativa se coloca en el centro de un anillo de carga positiva uniforme. ¿Cuál es el movimiento (si hay alguno) de la carga? ¿Qué pasa si la carga se coloca en un punto en el eje del anillo que no sea el centro?

5.6 Líneas de campo eléctrico

31. Si una carga puntual se libera del reposo en un campo eléctrico uniforme, ¿seguirá una línea de campo? ¿Lo hará si el campo eléctrico no es uniforme?

32. ¿Bajo qué condiciones, si hay alguna, la trayectoria de una partícula cargada no seguirá una línea de campo?

33. ¿Cómo distinguirías experimentalmente un campo eléctrico de un campo gravitacional?

34. Una representación de un campo eléctrico muestra 10 líneas de campo perpendiculares a una placa cuadrada. ¿Cuántas líneas de campo deberían pasar perpendicularmente a través de la placa para representar un campo con el doble de magnitud?

35. ¿Cuál es la relación entre el número de líneas de campo eléctrico que dejan una carga de 10q y una carga q?

5.7 Dipolos eléctricos

36. ¿Cuál es la orientación estable (s) para un dipolo en un campo eléctrico externo? ¿Qué sucede si el dipolo está ligeramente perturbado por estas orientaciones?

Problemas

5.1 Carga eléctrica

37. La electricidad estática común implica cargas que van desde nanocoulombs a microcoulombs. (a) ¿Cuántos electrones se necesitan para formar una carga de -2.00 nC? (b) ¿Cuántos electrones deben eliminarse de un objeto neutral para dejar una carga neta de 0.500 μC?

38. Si 1.80 × 10²⁰ electrones se mueven a través de una calculadora de bolsillo durante la operación de un día completo, ¿cuántos coulombs de carga se movieron a través de ella?

39. Para encender el motor de un automóvil, la batería del automóvil mueve 3.75 × 10²¹ electrones a través del motor de arranque. ¿Cuántos coulombs de carga se movieron?

40. Un cierto rayo mueve 40.0 C de carga. ¿Cuántas unidades fundamentales de carga es esta?

41. Un centavo de cobre de 2.5 g recibe una carga de -2.0 × 10^-9 C. (a) ¿Cuántos electrones en exceso hay en el centavo? (b) ¿En qué porcentaje el exceso de electrones cambia la masa del centavo?

42. Un centavo de cobre de 2.5 g recibe una carga de 4.0 × 10^-9 C. (a) ¿Cuántos electrones se eliminan del centavo? (b) Si no se elimina más de un electrón de un átomo, ¿qué porcentaje de los átomos se ionizan con este proceso de carga?

5.2 Conductores, aislantes y carga por inducción

43. Supón que una mota de polvo en un precipitador electrostático tiene 1.0000 × 10¹² protones y tiene una carga neta de -5.00 nC (una carga muy grande para una pequeña mancha). ¿Cuántos electrones tiene?

44. Una ameba tiene 1.00 × 10¹⁶ protones y una carga neta de 0.300 pC. (a) ¿Cuántos menos electrones hay que protones? (b) Si los empareja, ¿qué fracción de los protones no tendría electrones?

45. Una bola de cobre de 50.0 g tiene una carga neta de 2.00 μC. ¿Qué fracción de los electrones de cobre se ha eliminado? (Cada átomo de cobre tiene 29 protones, y el cobre tiene una masa atómica de 63.5)

46. ¿Qué carga neta colocarías en un pedazo de azufre de 100 g si pones un electrón extra en 1 de cada 10¹² de sus átomos? (El azufre tiene una masa atómica de 32.1 u)

47. ¿Cuántos coulombs de carga positiva hay en 4.00 kg de plutonio, dado que su masa atómica es 244 y que cada átomo de plutonio tiene 94 protones?

5.3 Ley de Coulomb

48. Las fuerzas 3-N en cada carga mantienen en su lugar dos partículas puntuales con cargas + 3μC y + 5μC en las direcciones apropiadas. (a) Dibuja un diagrama de cuerpo libre para cada partícula. (b) Encuentra la distancia entre las cargas.

49. Dos cargas + 3μC y + 12μC se fijan a 1 m de distancia, con la segunda a la derecha. Encuentra la magnitud y dirección de la fuerza neta en una carga de -2 nC cuando se coloque en los siguientes lugares: (a) a mitad de camino entre las dos (b) medio metro a la izquierda de la carga de + 3μC (c) medio metro por encima de la carga +12 μC en una dirección perpendicular a la línea que une las dos cargas fijas

50. En un cristal de sal, la distancia entre los iones de sodio y cloruro adyacentes es de 2,82 × 10^-10 m. ¿Cuál es la fuerza de atracción entre los dos iones con carga única?

51. Los protones en un núcleo atómico son típicamente 10^-15 m de diferencia. ¿Cuál es la fuerza eléctrica de repulsión entre los protones nucleares?

52. Supongamos que la Tierra y la Luna tienen una carga neta negativa -Q. Aproximar ambos cuerpos como puntos de masas y puntos de carga. (a) ¿Qué valor de Q se requiere para equilibrar la atracción gravitacional entre la Tierra y la Luna? (b) ¿La distancia entre la Tierra y la Luna afecta tu respuesta? Explica. (c) ¿Cuántos electrones se necesitarían para producir esta carga?

53. Las cargas puntuales q₁ = 50 μC y q₂ = -25 μC se colocan a una distancia de 1,0 m. ¿Cuál es la fuerza en una tercera carga q₃ = 20 μC colocada a mitad de camino entre q₁ y q₂?

54. ¿Dónde debe colocarse q₃ del problema anterior para que la fuerza neta sobre él sea cero?

55. Dos bolas pequeñas, cada una de 5.0 g de masa, están unidas a hilos de seda de 50 cm de largo, que a su vez están atados al mismo punto en el techo, como se muestra a continuación. Cuando las bolas reciben la misma carga Q, los hilos cuelgan a 5.0° con respecto a la vertical, como se muestra a continuación. ¿Cuál es la magnitud de Q? ¿Cuáles son los signos de las das cargas?



56. Las cargas de punto Q₁ = 2.0 μC y Q₂ = 4.0 μC se encuentran en r→₁ = (4.0i^ - 2.0j^ + 5.0k^) m y r→₂ = (8.0i^ + 5.0j^ - 9.0k^)m. ¿Cuál es la fuerza de Q₂ en Q₁?

57. El exceso neto de carga en dos pequeñas esferas (lo suficientemente pequeño para ser tratado como cargas puntuales) es Q. Demuestra que la fuerza de repulsión entre las esferas es mayor cuando cada esfera tiene una carga en exceso Q/2. Supongamos que la distancia entre las esferas es tan grande en comparación con sus radios que las esferas se pueden tratar como cargas puntuales.

58. Dos pequeñas esferas conductoras idénticas se repelen entre sí con una fuerza de 0.050 N cuando están a 0.25 m de distancia. Después de que un cable conductor se conecta entre las esferas y luego se retira, se repelen entre sí con una fuerza de 0.060 N. ¿Cuál es la carga original en cada esfera?

59. Una carga q = 2.0 μC se coloca en el punto P que se muestra a continuación. ¿Cuál es la fuerza sobre q?



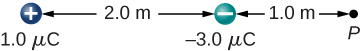
60. ¿Cuál es la fuerza eléctrica neta en la carga ubicada en la esquina inferior derecha del triángulo que se muestra aquí?



61. Dos partículas fijas, cada una de carga 5.0 × 10^-6 C, están separadas por 24 cm. ¿Qué fuerza ejercen sobre una tercera partícula de carga -2.5 × 10^-6 C que está a 13 cm de cada una de ellas?

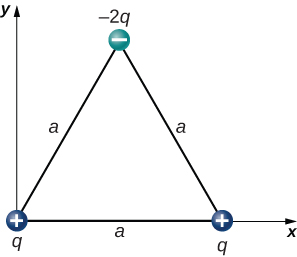
62. Las cargas q₁ = 2.0 × 10^-7 C, q₂ = -4.0 × 10^-7 C, y q₃ = -1.0 × 10^-7 C se colocan en las esquinas del triángulo que se muestra a continuación. ¿Cuál es la fuerza en q₁?



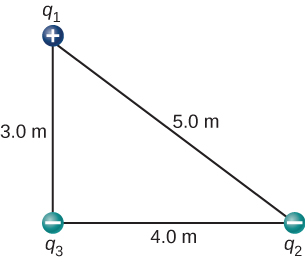
63. ¿Cuál es la fuerza sobre la carga q en la esquina inferior derecha del cuadrado que se muestra aquí?



64. Las cargas de punto q₁ = 10 μC y q₂ = -30 μC se fijan en r₂ = (3.0i^ - 4.0j^)m y r₂ = (9.0i^ + 6.0j^)m. ¿Cuál es la fuerza de q₂ sobre q₁?

5.4 Campo eléctrico

65. Una partícula de carga 2.0 × 10^-8 C experimenta una fuerza ascendente de magnitud 4.0 × 10^-6 N cuando se coloca en un punto particular en un campo eléctrico. (a) ¿Cuál es el campo eléctrico en ese punto? (b) Si se coloca allí una carga q = -1.0 × 10^-8 C, ¿cuál es la fuerza sobre ella?

66. En un día despejado típico, el campo eléctrico atmosférico apunta hacia abajo y tiene una magnitud de aproximadamente 100 N/C. Compara las fuerzas gravitacionales y eléctricas en una pequeña partícula de polvo de masa 2.0 × 10^-15 g que lleva una sola carga de electrones. ¿Cuál es la aceleración (tanto de magnitud como de dirección) de la partícula de polvo?

67. Considera un electrón que está a 10^-10 m de una partícula alfa (q = 3.2 × 10^-19 C). (a) ¿Cuál es el campo eléctrico debido a la partícula alfa en la ubicación del electrón? (b) ¿Cuál es el campo eléctrico debido al electrón en la ubicación de la partícula alfa? (c) ¿Cuál es la fuerza eléctrica sobre la partícula alfa? En el electrón?

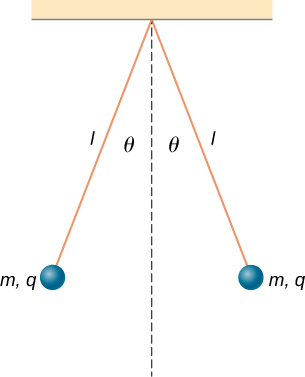
68. Cada una de las bolas que se muestran a continuación lleva una carga q y tiene una masa m. La longitud de cada hilo es l, y en equilibrio, las bolas están separadas por un ángulo 2θ. ¿Cómo varía θ con q y l? Muestra que θ satisface sen(θ)²tan (θ) = q²/16πε₀gl²m.



69. ¿Cuál es el campo eléctrico en un punto donde la fuerza en una carga de -2.0 × 10^-6-C es (4.0i^ - 6.0j^) × 10^-6 N?

70. Un protón se suspende en el aire por un campo eléctrico en la superficie de la Tierra. ¿Cuál es la fuerza de este campo eléctrico?

71. El campo eléctrico en una tormenta particular es 2.0 × 10⁵ N/C. ¿Cuál es la aceleración de un electrón en este campo?

72. Un pequeño trozo de corcho cuya masa es de 2,0 g recibe una carga de 5,0 × 10^-7 C. ¿Qué campo eléctrico se necesita para colocar el corcho en equilibrio bajo las fuerzas eléctricas y gravitacionales combinadas?

73. Si el campo eléctrico es de 100 N/C a una distancia de 50 cm de una carga puntual q, ¿cuál es el valor de q?

74. ¿Cuál es el campo eléctrico de un protón en la primera órbita de Bohr para hidrógeno (r = 5.29 × 10^-11 m)? ¿Cuál es la fuerza sobre el electrón en esa órbita?

75. (a) ¿Cuál es el campo eléctrico de un núcleo de oxígeno en un punto que está a 10^-10 m del núcleo? (b) ¿Cuál es la fuerza que ejerce este campo eléctrico sobre un segundo núcleo de oxígeno colocado en ese punto?

76. Dos cargas puntuales, q₁ = 2.0 × 10^-7 C y q₂ = -6.0 × 10^-8 C, se mantienen separadas 25.0 cm. (a) ¿Cuál es el campo eléctrico en un punto a 5.0 cm de la carga negativa y a lo largo de la línea entre las dos cargas? (b) ¿Cuál es la fuerza sobre un electrón colocado en ese punto?

77. Las cargas puntuales q₁ = 50 μC y q₂ = -25 μC se colocan a una distancia de 1,0 m. (a) ¿Cuál es el campo eléctrico en un punto intermedio entre ellos? (b) ¿Cuál es la fuerza sobre una carga q₃ = 20 μC situada allí?

78. ¿Puedes organizar las dos cargas de puntos q₁ = -2.0 × 10^-6 C y q₂ = 4.0 × 10^-6 C a lo largo del eje x de modo que E = 0 en el origen?

79. Las cargas de punto q₁ = q₂ = 4.0 × 10^-6 C se fijan en el eje x en x = -3.0 m y x = 3.0 m. ¿Qué carga q debe colocarse en el origen para que el campo eléctrico desaparezca en x = 0, y = 3.0 m?

5.5 Cálculo de los campos eléctricos de distribuciones de carga

80. Una placa conductora delgada de 1,0 m en el lado recibe una carga de -2,0 × 10^-6 C. Un electrón se coloca 1,0 cm por encima del centro de la placa. ¿Cuál es la aceleración del electrón?

81. Calcula la magnitud y la dirección del campo eléctrico 2.0 m desde un cable largo que se carga uniformemente a λ = 4.0 × 10^-6 C/m.

82. Dos placas conductoras delgadas, cada una de 25.0 cm de lado, están situadas paralelas entre sí y separadas 5.0 mm. Si 10^-11 electrones se mueven de una placa a la otra, ¿cuál es el campo eléctrico entre las placas?

83. La carga por unidad de longitud en la varilla delgada que se muestra a continuación es λ. ¿Cuál es el campo eléctrico en el punto P? (Sugerencia: Resuelve este problema considerando primero el campo eléctrico dE→ en P debido a un pequeño segmento dx de la varilla, que contiene la carga dq = λdx. Luego, encuentra el campo de red integrando dE→ sobre la longitud de la varilla).



84. La carga por unidad de longitud en el alambre semicircular delgado que se muestra a continuación es λ. ¿Cuál es el campo eléctrico en el punto P?



85. Dos placas conductoras paralelas delgadas se colocan a 2,0 cm de distancia. Cada plato mide 2.0 cm en un lado; una placa tiene una carga neta de 8.0 μC y la otra placa tiene una carga neta de -8.0 μC. ¿Cuál es la densidad de carga en la superficie interior de cada placa? ¿Cuál es el campo eléctrico entre las placas?

86. Una placa conductora delgada de 2,0 m de lado recibe una carga total de -10,0 μC. (a) ¿Cuál es el campo eléctrico de 1,0 cm por encima de la placa? (b) ¿Cuál es la fuerza sobre un electrón en este punto? (c) Repite estos cálculos para un punto 2.0 cm por encima de la placa. (d) Cuando el electrón se mueve de 1.0 a 2.0 cm por encima de la placa, ¿cuánto trabajo le realiza el campo eléctrico?

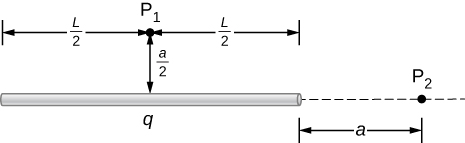
87. Una carga total q se distribuye uniformemente a lo largo de una barra delgada y recta de longitud L (ver más abajo). ¿Cuál es el campo eléctrico en P₁? ¿en P₂?



88. La carga se distribuye a lo largo de todo el eje x con densidad uniforme λ. ¿Cuánto trabajo hace el campo eléctrico de esta distribución de carga en un electrón que se mueve a lo largo del eje y desde y = a y = b?

89. La carga se distribuye a lo largo de todo el eje x con densidad uniforme λx y a lo largo de todo el eje y con densidad uniforme λy. Calcula el campo eléctrico resultante en (a) r→ = ai^ + bj^ y (b) r→ = ck^.

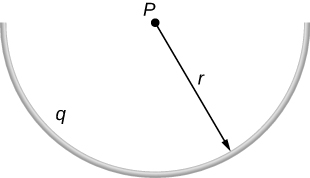
90. Una vara doblada en el arco de un círculo subtiende un ángulo 2θ en el centro P del círculo (ver figura). Si la varilla se carga uniformemente con una carga total Q, ¿cuál es el campo eléctrico en P?



91. Un protón se mueve en el campo eléctrico E→ = 200i^ N/C. (a) ¿Cuál es la fuerza y la aceleración del protón? (b) Haga el mismo cálculo para un electrón que se mueve en este campo.

92. Un electrón y un protón, cada uno comenzando desde el reposo, son acelerados por el mismo campo eléctrico uniforme de 200 N/C. Determina la distancia y el tiempo para que cada partícula adquiera una energía cinética de 3.2 × 10^-16 J.

93. Una gota de agua esférica de radio de 25 μm lleva un exceso de 250 electrones. ¿Qué campo eléctrico vertical se necesita para equilibrar la fuerza gravitacional en la gota en la superficie de la tierra?

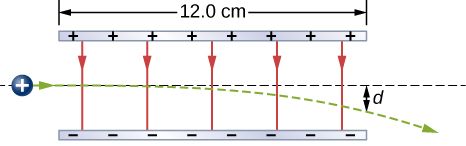
94. Un protón entra en el campo eléctrico uniforme producido por las dos placas cargadas que se muestran a continuación. La magnitud del campo eléctrico es 4.0 × 10⁵ N/C, y la velocidad del protón cuando entra es 1.5 × 10⁷ m/s. ¿Qué distancia d tiene el protón desviado hacia abajo cuando sale de las placas?



95. A continuación se muestra una pequeña esfera de masa de 0.25 g que lleva una carga de 9.0 × 10^-10 C. La esfera está unida a un extremo de una cuerda de seda muy delgada de 5.0 cm de largo. El otro extremo de la cuerda está unido a una gran placa conductora vertical que tiene una densidad de carga de 30 × 10^-6 C/m². ¿Cuál es el ángulo que la cuerda hace con la vertical?



96. Dos barras infinitas, cada una con una densidad de carga uniforme λ, son paralelas entre sí y perpendiculares al plano de la página. ( ¿Cuál es el campo eléctrico en P₁? En P₂?



97. La carga positiva se distribuye con una densidad uniforme λ a lo largo del eje x positivo desde r a ∞, a lo largo del eje y positivo desde r a ∞, y a lo largo de un arco de 90° de un círculo de radio r, como se muestra a continuación. ¿Cuál es el campo eléctrico en O?



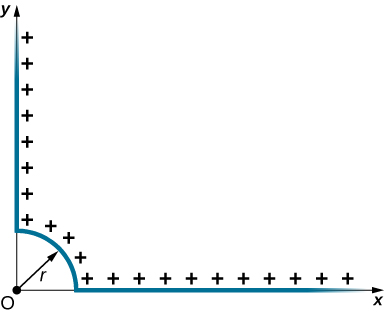
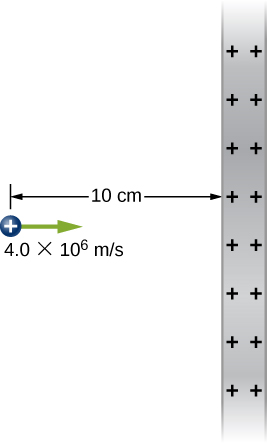
98. Desde una distancia de 10 cm, se proyecta un protón con una velocidad de v = 4.0 × 10⁷ m/s directamente en una placa grande, con carga positiva, cuya densidad de carga es σ = 2.0 × 10^-5 C/m². (a) ¿El protón llega a la placa? (b) Si no, ¿qué tan lejos de la placa gira?



99. Una partícula de masa m y carga -q se mueve a lo largo de una línea recta lejos de una partícula fija de carga Q. Cuando la distancia entre las dos partículas es r₀, -q se mueve con una velocidad v₀. (a) Usa el teorema del trabajo y la energía para calcular la separación máxima de las cargas. (b) ¿Qué tienes que asumir sobre v₀ para hacer este cálculo? (c) ¿Cuál es el valor mínimo de v₀ tal que -q escapa de Q?

5.6 Líneas de campo eléctrico

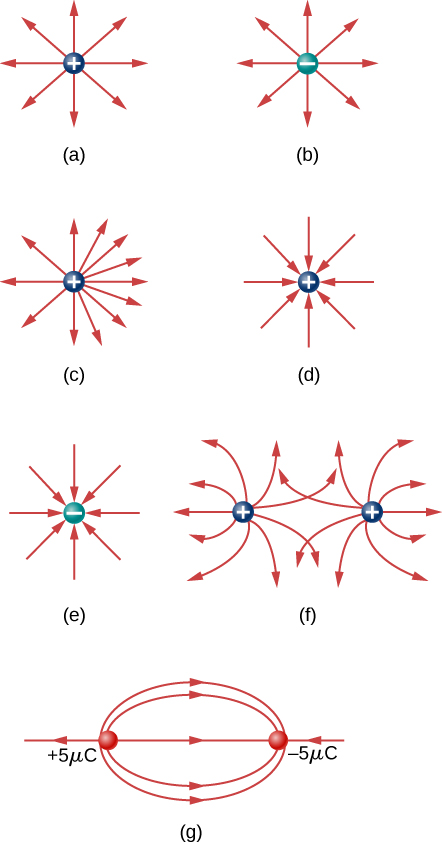
100. ¿Cuál de las siguientes líneas de campo eléctrico son incorrectas para las cargas puntuales? Explicar por qué.



101. En este ejercicio, practicarás dibujando líneas de campo eléctrico. Asegúrete de representar adecuadamente tanto la magnitud como la dirección del campo eléctrico. Ten en cuenta que el número de líneas dentro o fuera de las cargas es proporcional a las cargas. (a) Dibuja el mapa de líneas de campo eléctrico para dos cargas + 20 μC y -20 μC situadas a 5 cm una de la otra. (b) Dibuja el mapa de líneas de campo eléctrico para dos cargas + 20 μC y + 20 μC situadas a 5 cm una de la otra. (c) Dibuja el mapa de líneas de campo eléctrico para dos cargas + 20 μC y -30 μC situadas a 5 cm una de la otra.

102. Dibuja el campo eléctrico para un sistema de tres partículas de cargas + 1 μC, + 2 μC y -3 μC fijadas en las esquinas de un triángulo equilátero de lado 2 cm.

103. Dos cargas de igual magnitud pero de signo opuesto conforman un dipolo eléctrico. Un cuadripolo consiste en dos dipolos eléctricos que se colocan antiparalelos en dos bordes de un cuadrado como se muestra en la figura.



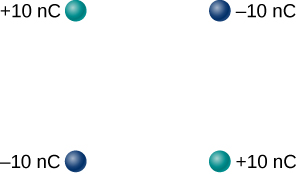
Dibuja el campo eléctrico de la distribución de carga.

104. Supongamos que el campo eléctrico de una carga puntual aislada disminuyó con la distancia como 1/r^{2 + δ} en lugar de 1/r². Demuestra que es imposible dibujar líneas de campo continuas para que su número por unidad de área sea proporcional a E.

5.7 Dipolos eléctricos

105. Considera las cargas iguales y opuestoas que se muestran a continuación. (a) Muestra eso en todos los puntos en el eje x para el cual |x| >> a, E ≈ Qa/2πε₀x³. (b) Muestra eso en todos los puntos en el eje y para el que |y| >> a, E ≈ Qa/πε₀y³.



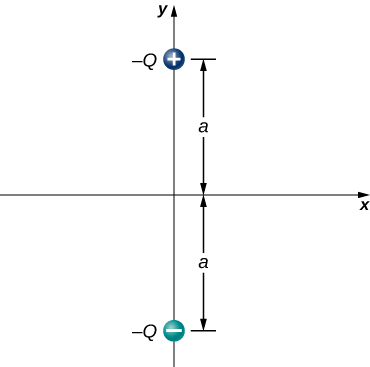
106. (a) ¿Cuál es el momento dipolar de la configuración que se muestra arriba? Si Q = 4.0 μC, (b) ¿cuál es el par en este dipolo con un campo eléctrico de 4.0 × 10⁵ N/Ci^? (c) ¿Cuál es el par en este dipolo con un campo eléctrico de -4.0 × 10⁵ N/Ci^? (d) ¿Cuál es el par en este dipolo con un campo eléctrico de ± 4.0 × 10⁵ N/Cj^?

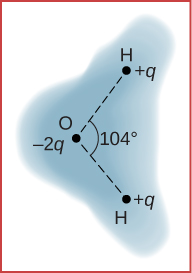
107. Una molécula de agua consiste en dos átomos de hidrógeno unidos con un átomo de oxígeno. El ángulo de enlace entre los dos átomos de hidrógeno es 104° (ver abajo). Calcula el momento dipolar neto de una molécula de agua que se coloca en un campo eléctrico horizontal uniforme de magnitud 2,3 × 10^-8 N/C. (Falta información para resolver este problema, deberás determinar qué información necesitas y buscarla).

Problemas Adicionales

108. Las cargas de punto q₁ = 2.0 μC y q₁ = 4.0 μC se encuentran en r₁ = (4.0i^ - 2.0j^ + 2.0k^)m y r₂ = (8.0i^ + 5.0j^ - 9.0k^)m. ¿Cuál es la fuerza de q₂ sobre q₁?

109. ¿Cuál es la fuerza sobre la carga de 5.0 μC que se muestra a continuación?



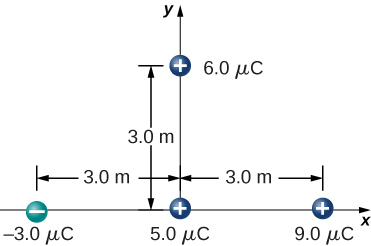
110. ¿Cuál es la fuerza sobre la carga de 2.0 μC colocada en el centro del cuadrado que se muestra abajo?



111. Cuatro partículas cargadas se colocan en las esquinas de un paralelogramo como se muestra a continuación. Si q = 5.0 μC y Q = 8.0 μC, ¿cuál es la fuerza neta sobre q?



112. Una carga Q se fija en el origen y una segunda carga q se mueve a lo largo del eje x, como se muestra a continuación. ¿Cuánto trabajo se hace en q por la fuerza eléctrica cuando q se mueve desde x₁ a x₂?



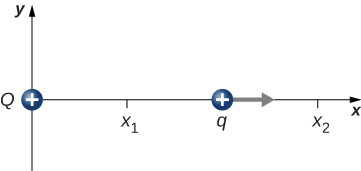
113. Una carga q = -2.0 μC se libera del reposo cuando está a 2.0 m de una carga fija Q = 6.0 μC. ¿Cuál es la energía cinética de q cuando está a 1.0 m de Q?

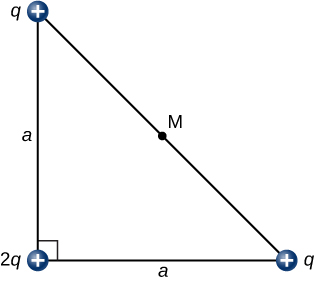
114. ¿Cuál es el campo eléctrico en el punto medio M de la hipotenusa del triángulo que se muestra a continuación?



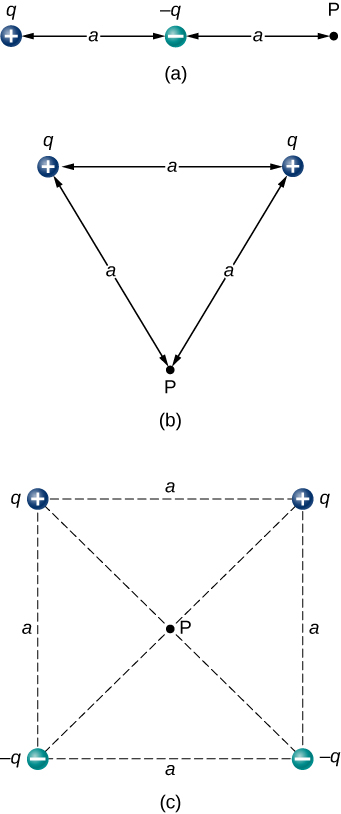
115. Encuentre el campo eléctrico en P para las configuraciones de carga que se muestran a continuación.



116. (a) ¿Cuál es el campo eléctrico en la esquina inferior derecha del cuadrado que se muestra abajo? (b) ¿Cuál es la fuerza sobre una carga q colocada en ese punto?



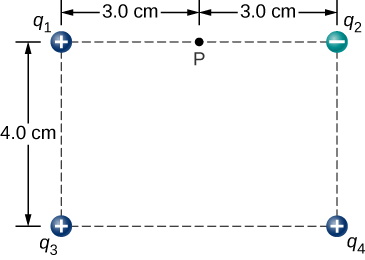
117. Las cargas puntuales se colocan en las cuatro esquinas de un rectángulo como se muestra a continuación: q₁ = 2.0 × 10^-6 C, q₂ = -2.0 × 10^-6 C, q₃ = 4.0 × 10^-6 C y q₄ = 1.0 × 10^-6 C . ¿Cuál es el campo eléctrico en P?



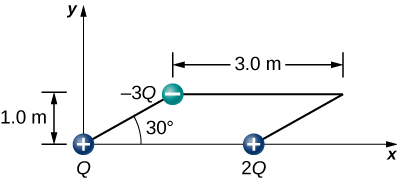
118. Tres cargas se colocan en las esquinas de un paralelogramo como se muestra a continuación. (a) Si Q = 8.0 μC, ¿cuál es el campo eléctrico en la esquina desocupada? (b) ¿Cuál es la fuerza en una carga de 5.0 μC colocada en esta esquina?



119. Una carga positiva q se libera del reposo en el origen de un sistema de coordenadas rectangulares y se mueve bajo la influencia del campo eléctrico E→ = E₀(1 + x/a)i^. ¿Cuál es la energía cinética de q cuando pasa a través de x = 3a?

120. Una partícula de carga -q y masa m se coloca en el centro de un anillo uniformemente cargado de carga total Q y radio R. La partícula se desplaza una pequeña distancia a lo largo del eje perpendicular al plano del anillo y se libera. Suponiendo que la partícula está obligada a moverse a lo largo del eje, demuestra que la partícula oscila en un movimiento armónico simple con una frecuencia
f = 1/2π(qQ/4πε₀mR³)^1/2. 121. La carga se distribuye uniformemente a lo largo de todo el eje y con una densidad λy a lo largo del eje x positivo de x = a a x = b con una densidad λx. ¿Cuál es la fuerza entre las dos distribuciones?

122. El arco circular que se muestra a continuación tiene una carga por unidad de longitud λ= λ₀cosθ, donde θ se mide desde el eje x. ¿Cuál es el campo eléctrico en el origen?



123. Calcula el campo eléctrico debido a una barra uniformemente cargada de longitud L, alineada con el eje x con un extremo en el origen; en un punto P en el eje z.

124. La carga por unidad de longitud en la barra delgada que se muestra a continuación es λ. ¿Cuál es la fuerza eléctrica en la carga puntual? Resuelva este problema considerando primero la fuerza eléctrica dF→ en q debido a un pequeño segmento dx de la varilla, que contiene carga λdx. Luego, encuentre la fuerza neta integrando dF→ sobre la longitud de la barra



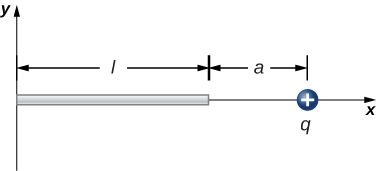
125. La carga por unidad de longitud en la varilla delgada que se muestra aquí es λ. ¿Cuál es la fuerza eléctrica en la carga puntual? (Ver el problema anterior)



126. La carga por unidad de longitud en el alambre semicircular delgado que se muestra a continuación es λ. ¿Cuál es la fuerza eléctrica en la carga puntual? (Ver los problemas anteriores).