Preguntas y problemas - Capítulo IV

Preguntas conceptuales

4.1 Procesos reversibles e irreversibles

1. Indica un ejemplo de un proceso que ocurre en la naturaleza que es lo más cercano a lo reversible que puede ser.

4.2 Máquinas térmicas o de Calor

2. Explica en términos prácticos por qué la eficiencia se define como W/Q_h.

4.3 Refrigeradores y bombas de calor

3. Si la puerta del refrigerador se deja abierta, ¿qué ocurre con la temperatura de la cocina?

4. ¿Es posible que la eficiencia de un motor reversible sea mayor que 1.0? ¿Es posible que el coeficiente de rendimiento de un refrigerador reversible sea inferior a 1,0?

4.4 Declaraciones de la segunda ley de la termodinámica

5. En el texto, mostramos que si la declaración Clausius es falsa, la declaración Kelvin también debe ser falsa. Ahora muestra el reverso, de modo que si la declaración de Kelvin es falsa, se deduce que la declaración de Clausius es falsa.

6. ¿Por qué no operamos transatlánticos extrayendo calor del océano u operando aviones extrayendo calor de la atmósfera?

7. Discute las ventajas y desventajas prácticas de las bombas de calor y la calefacción eléctrica.

8. La producción de energía de una bomba de calor es mayor que la energía utilizada para operar la bomba. ¿Por qué esta afirmación no viola la primera ley de la termodinámica?

9. Especula sobre por qué las plantas de energía nuclear son menos eficientes que las plantas de combustibles fósiles basadas en argumentos de temperatura.

10. Un gas ideal pasa del estado (p_i, V_i) al estado (p_f, V_f) cuando se le permite expandirse libremente. ¿Es posible representar el proceso real en un diagrama pV? Explica.

4.5 El ciclo de Carnot

11. Para aumentar la eficiencia de un motor Carnot, ¿debería elevarse o bajarse la temperatura del depósito caliente? ¿Qué pasa con el depósito frío?

12. ¿Cómo podrías diseñar un motor Carnot con una eficiencia del 100%?

13. ¿Qué tipo de procesos ocurren en un ciclo de Carnot?

4.6 Entropía

14. ¿La entropía aumenta para un motor de Carnot para cada ciclo?

15. ¿Es posible que un sistema tenga un cambio de entropía si no absorbe ni emite calor durante una transición reversible? ¿Qué pasa si el proceso es irreversible?

4.7 Entropía a escala microscópica

16. ¿Los cambios de entropía de los sistemas en los siguientes procesos son positivos o negativos? (a) vapor de agua que se condensa en una superficie fría; (b) gas en un contenedor que se filtra a la atmósfera circundante; (c) un cubo de hielo que se derrite en un vaso de agua tibia; (d) el agua tibia de la parte (c); (e) un motor térmico real que realiza un ciclo; (f) comida enfriada en un refrigerador.

17. Discute los cambios de entropía en los sistemas de la Pregunta 16 en términos de desorden.

Problemas

4.1 Procesos reversibles e irreversibles

18. Un tanque contiene 111.0 g de cloro gaseoso (Cl₂), que está a una temperatura de 82.0 °C y una presión absoluta de 5.70 × 10⁵ Pa. La temperatura del aire fuera del tanque es de 20.0 °C. La masa molar de Cl₂ es 70,9 g/mol. (a) ¿Cuál es el volumen del tanque? (b) ¿Cuál es la energía interna del gas? (c) ¿Cuál es el trabajo realizado por el gas si la temperatura y la presión dentro del tanque caen a 31.0 °C y 3.80 × 10⁵ Pa, respectivamente, debido a una fuga?

19. Un mol de gas monoatómico ideal a 0 °C y 1,00 atm se calienta para expandirse isobáricamente hasta triplicar su volumen. ¿Cuánto calor se transfiere durante el proceso?

20. Un mol de un gas ideal a una presión de 4.00 atm y una temperatura de 298 K se expande isotérmicamente para duplicar su volumen. ¿Cuál es el trabajo realizado por el gas?

21. Después de una expansión libre para cuadruplicar su volumen, un mol de gas diatómico ideal se comprime de nuevo a su volumen original isobáricamente y luego se enfría a su temperatura original. ¿Cuál es el calor mínimo eliminado del gas en el paso final para restaurar su estado?

4.2 Máquinas térmicas o de Calor

22. Se encuentra que un motor tiene una eficiencia de 0.40. Si realiza 200 J de trabajo por ciclo, ¿cuáles son las cantidades correspondientes de calor absorbido y descargado?

23. Al realizar 100.0 J de trabajo, un motor descarga 50.0 J de calor. ¿Cuál es la eficiencia del motor?

24. Un motor con una eficiencia de 0.30 absorbe 500 J de calor por ciclo. (a) ¿Cuánto trabajo realiza por ciclo? (b) ¿Cuánto calor descarga por ciclo?

25. Se encuentra que un motor descarga 100.0 J mientras absorbe 125.0 J en cada ciclo de operación. (a) ¿Cuál es la eficiencia del motor? (b) ¿Cuánto trabajo realiza por ciclo?

26. La temperatura del depósito frío del motor es de 300 K. Tiene una eficiencia de 0.30 y absorbe 500 J de calor por ciclo. (a) ¿Cuánto trabajo realiza por ciclo? (b) ¿Cuánto calor descarga por ciclo?

27. Un motor absorbe tres veces más calor a medida que se descarga. El trabajo realizado por el motor por ciclo es 50 J. Calcula (a) la eficiencia del motor, (b) el calor absorbido por ciclo y (c) el calor descargado por ciclo.

28. Una central de carbón consume 100.000 kg de carbón por hora y produce 500 MW de potencia. Si el calor de la combustión del carbón es de 30 MJ/kg, ¿cuál es la eficiencia de la planta de energía?

4.3 Refrigeradores y bombas de calor

29. Un refrigerador tiene un coeficiente de rendimiento de 3.0. (a) Si requieres 200 J de trabajo por ciclo, ¿cuánto calor por ciclo elimina el depósito frío? (b) ¿Cuánto calor por ciclo se descarta al depósito caliente?

30. Durante un ciclo, un refrigerador extrae 500 J de un depósito frío y descarga 800 J en su depósito caliente. (a) ¿Cuál es su coeficiente de rendimiento? (b) ¿Cuánto trabajo por ciclo requiere para operar?

31. Si un refrigerador descarta 80 J de calor por ciclo y su coeficiente de rendimiento es 6.0, ¿cuáles son (a) la cantidad de calor que elimina por ciclo de un depósito frío y (b) la cantidad de trabajo por ciclo requerido para su ¿operación?

32. Un refrigerador tiene un coeficiente de rendimiento de 3.0. (a) Si requieres 200 J de trabajo por ciclo, ¿cuánto calor por ciclo elimina el depósito frío? (b) ¿Cuánto calor por ciclo se descarta al depósito caliente?

4.5 El ciclo de Carnot

33. La temperatura de los depósitos fríos y calientes entre los que funciona un frigorífico Carnot es de -73 °C y 270 °C, respectivamente. ¿Cuál es su coeficiente de rendimiento?

34. Supongamos que un frigorífico Carnot funciona entre T_c y T_h. Calcula la cantidad de trabajo requerido para extraer 1,0 J de calor del depósito frío si (a) T_c = 7 °C, T_h = 27 °C; (b) T_c = -73 °C, T_h = 27 °C; (c) T_c = -173 °C, T_h = 27 °C; y (d) T_c = -273 °C, T_h = 27 °C.

35. Un motor Carnot opera entre los depósitos a 600 y 300 K. Si el motor absorbe 100 J por ciclo en el depósito caliente, ¿cuál es su rendimiento de trabajo por ciclo?

36. Un motor de 500 W opera un refrigerador Carnot entre -5 °C y 30 °C. (a) ¿Cuál es la cantidad de calor por segundo extraído del interior del refrigerador? (b) ¿Cuánto calor se consume en el aire exterior por segundo?

37. Dibuja un ciclo de Carnot en un diagrama de temperatura y volumen.

38. Una bomba de calor Carnot funciona entre 0 °C y 20 °C. ¿Cuánto calor se agota en el interior de una casa por cada 1,0 J de trabajo realizado por la bomba?

39. Un motor que funciona entre los depósitos de calor a 20 °C y 200 °C extrae 1000 J por ciclo del depósito caliente. (a) ¿Cuál es el trabajo máximo que el motor puede hacer por ciclo? (b) Para este trabajo máximo, ¿cuánta calor se descarga al depósito frío por ciclo?

40. Supongamos que un motor Carnot puede funcionar entre dos depósitos como una máquina térmica o un refrigerador. ¿Cómo se relaciona el coeficiente de rendimiento del refrigerador con la eficiencia del motor térmico?

41. Un motor Carnot se usa para medir la temperatura de un depósito de calor. El motor funciona entre el depósito de calor y un depósito que consiste en agua en su punto triple. (a) Si se retiran 400 J por ciclo del depósito de calor mientras se depositan 200 J por ciclo en el depósito del punto triple, ¿cuál es la temperatura del depósito de calor? (b) Si se retiran 400 J por ciclo del depósito de triple punto mientras se depositan 200 J por ciclo en el depósito de calor, ¿cuál es la temperatura del depósito de calor?

42. ¿Cuál es el trabajo mínimo requerido de un refrigerador si se trata de extraer 50 J por ciclo del interior de un congelador a -10 °C y expulsar el calor al aire a 25 °C?

4.6 Entropía

43. Doscientos julios de calor se eliminan de un depósito de calor a una temperatura de 200 K. ¿Cuál es el cambio de entropía del depósito?

44. En una expansión isotérmica reversible a 27 °C, un gas ideal produce 20 J de trabajo. ¿Cuál es el cambio de entropía del gas?

45. Un gas ideal a 300 K se comprime isotérmicamente hasta una quinta parte de su volumen original. Determina el cambio de entropía por mol del gas.

46. ​​¿Cuál es el cambio de entropía de 10 g de vapor a 100 °C cuando se condensa en agua a la misma temperatura?

47. Una varilla de metal se usa para conducir calor entre dos depósitos a temperaturas T_h y T_c, respectivamente. Cuando una cantidad de calor Q fluye a través de la varilla desde el depósito caliente al frío, ¿cuál es el cambio neto de entropía de la varilla, el depósito caliente, el depósito frío y el universo?

48. Para el ciclo de Carnot de la Figura 4.12, ¿cuál es el cambio de entropía del depósito caliente, el depósito frío y el universo?

49. Una pieza de plomo de 5.0 kg a una temperatura de 600 °C se coloca en un lago cuya temperatura es de 15 °C. Determina el cambio de entropía de (a) la pieza principal, (b) el lago y (c) el universo.

50. Una mol de un gas ideal dobla su volumen en una expansión isotérmica reversible. (a) ¿Cuál es el cambio en la entropía del gas? (b) Si se agregan 1.500 J de calor en este proceso, ¿cuál es la temperatura del gas?

51. Una mol de un gas monoatómico ideal está confinado a un contenedor rígido. Cuando el calor se agrega reversiblemente al gas, su temperatura cambia de T₁ a T₂. (a) ¿Cuánto calor se agrega? (b) ¿Cuál es el cambio en la entropía del gas?

52. (a) Una roca de 5,0 kg a una temperatura de 20 °C se deja caer en un lago poco profundo también a 20 °C desde una altura de 1,0 × 10³ m. ¿Cuál es el cambio resultante en la entropía del universo? (b) Si la temperatura de la roca es de 100 °C cuando se cae, ¿cuál es el cambio de entropía del universo? Supón que la fricción del aire es insignificante (no es una buena suposición) y que c = 860 J/kg•K es el calor específico de la roca.

4.7 Entropía a escala microscópica

53. Una varilla de cobre con una sección transversal de 5.0 cm² y una longitud de 5.0 m conduce el calor desde un depósito de calor a 373 K a uno a 273 K. ¿Cuál es la tasa de cambio de tiempo de la entropía del universo para este proceso?

54. Se calientan cincuenta gramos de agua a 20 °C hasta que se convierte en vapor a 100 °C. Calcula el cambio en la entropía del agua en este proceso.

55. Cincuenta gramos de agua a 0 °C se transforman en vapor a 100 °C. ¿Cuál es el cambio en la entropía del agua en este proceso?

56. En un proceso isocórico, se agrega calor a 10 moles de gas ideal monoatómico cuya temperatura aumenta de 273 a 373 K. ¿Cuál es el cambio de entropía del gas?

57. Doscientos gramos de agua a 0 °C se ponen en contacto con un depósito de calor a 80 °C. Después de que se alcanza el equilibrio térmico, ¿cuál es la temperatura del agua? Del depósito? ¿Cuánto calor se ha transferido en el proceso? ¿Cuál es el cambio de entropía del agua? Del depósito? ¿Cuál es el cambio de entropía del universo?

58. Supón que la temperatura del agua en el problema anterior se eleva al ponerla primero en equilibrio térmico con un depósito a una temperatura de 40 °C y luego con un depósito a 80 °C. Calcula los cambios de entropía de (a) cada depósito, (b) del agua y (c) del universo.

59. Doscientos gramos de agua a 0 °C se ponen en contacto en equilibrio térmico sucesivamente con los depósitos a 20 °C, 40 °C, 60 °C y 80 °C. (a) ¿Cuál es el cambio de entropía del agua? (b) Del depósito? (c) ¿Cuál es el cambio de entropía del universo?

60. (a) Diez gramos de H₂O comienzan en forma de hielo a 0 °C. El hielo absorbe calor del aire (justo por encima de 0 °C) hasta que todo se derrita. Calcula el cambio de entropía del H₂O, del aire y del universo. (b) Supón que el aire en la parte (a) está a 20 °C en lugar de 0 °C y que el hielo absorbe calor hasta que se convierte en agua a 20 °C. Calcula el cambio de entropía del H₂O, del aire y del universo. (c) ¿Es reversible alguno de estos procesos?

61. El ciclo de Carnot está representado por el diagrama de temperatura-entropía que se muestra a continuación. (a) ¿Cuánto calor se absorbe por ciclo en el depósito de alta temperatura? (b) ¿Cuánto calor se agota por ciclo en el depósito de baja temperatura? (c) ¿Cuánto trabajo se realiza por ciclo por el motor? (d) ¿Cuál es la eficiencia del motor?



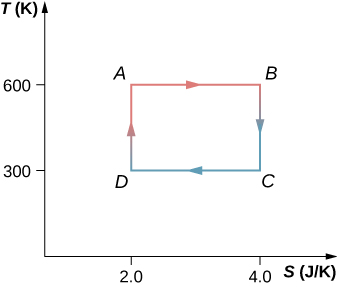
62. Un motor Carnot que funciona entre los depósitos de calor a 500 y 300 K absorbe 1500 J por ciclo en el depósito de alta temperatura. (a) Representar el ciclo del motor en un diagrama de temperatura-entropía. (b) ¿Cuánto trabajo por ciclo realiza el motor?

63. Un gas ideal monoatómico (n moles) pasa por un proceso cíclico que se muestra a continuación. Encuentra el cambio en la entropía del gas en cada paso y la entropía total cambia durante todo el ciclo.



64. Un motor Carnot tiene una eficiencia de 0.60. Cuando la temperatura de su depósito frío cambia, la eficiencia cae a 0.55. Si inicialmente T_c = 27 °C, determina (a) el valor constante de T_h y (b) el valor final de T_c.

65. Un motor Carnot realiza 100 J de trabajo mientras descarga 200 J de calor en cada ciclo. Después de que la temperatura del depósito caliente solo se ajusta, se encuentra que el motor ahora hace 130 J de trabajo mientras descarta la misma cantidad de calor. (a) ¿Cuáles son las eficiencias inicial y final del motor? (b) ¿Cuál es el cambio fraccional en la temperatura del depósito caliente?

66. Un frigorífico Carnot extrae calor del aire, que está a una temperatura de 25 °C. ¿Cuánta energía usa el refrigerador si se congela 1.5 g de agua por segundo? Supongamos que el agua está a 0 °C.

Problemas Adicionales

67. Una bomba de calor de 300 W funciona entre el suelo, cuya temperatura es de 0 °C, y el interior de una casa a 22 °C. ¿Cuál es la cantidad máxima de calor por hora que la bomba de calor puede suministrar a la casa?

68. Un ingeniero debe diseñar un refrigerador que haga 300 J de trabajo por ciclo para extraer 2100 J de calor por ciclo de un congelador cuya temperatura es de -10 °C. ¿Cuál es la temperatura máxima del aire para la cual se puede cumplir esta condición? ¿Es esta una condición razonable para imponer en el diseño?

69. Un motor Carnot emplea 1,5 mol de gas nitrógeno como sustancia de trabajo, que se considera como un gas diatómico ideal con γ = 7,5 a las temperaturas de trabajo del motor. El ciclo de Carnot entra en el ciclo ABCDA siendo AB una expansión isotérmica. El volumen en los puntos A y C del ciclo es 5.0 × 10^-3 m³ y 0.15 L, respectivamente. El motor funciona entre dos baños termales de temperatura de 500 K y 300 K. (a) Encuentra los valores de volumen en B y D. (b) ¿Cuánto calor es absorbido por el gas en la expansión isotérmica AB? (c) ¿Cuánto trabajo realiza el gas en la expansión isotérmica de AB? (d) ¿Cuánto calor se pierde por el gas en la expansión isotérmica CD? (e) ¿Cuánto trabajo realiza el gas en la compresión isotérmica CD? (f) ¿Cuánto trabajo realiza el gas en la expansión adiabática de BC? (g) ¿Cuánto trabajo realiza el gas en la compresión adiabática DA? (h) Encuentre el valor de la eficiencia del motor basado en el trabajo neto y la entrada de calor. Compara este valor con la eficiencia de un motor Carnot en función de la temperatura de los dos baños.

70. Un bloque de madera de 5.0 kg comienza con una velocidad inicial de 8.0 m/s y se desliza por el suelo hasta que la fricción lo detiene. Estima el cambio resultante en la entropía del universo. Supongamos que todo permanece a una temperatura ambiente de 20 °C.

71. Un sistema que consiste en 20.0 mol de un gas ideal monoatómico se enfría a presión constante desde un volumen de 50.0 L a 10.0 L. La temperatura inicial fue de 300 K. ¿Cuál es el cambio en la entropía del gas?

72. Un vaso de precipitados de 400 g de masa contiene 500 g de agua a 27 °C. El vaso de precipitados se calienta de forma reversible, de modo que la temperatura del vaso de precipitados y el agua ascienden gradualmente a 57 °C. Encuentra el cambio en la entropía del vaso de precipitados y el agua juntos.

73. Un motor Carnot funciona entre baños de 550 °C y 20 °C y produce 300 kJ de energía en cada ciclo. Encuentra el cambio en la entropía del (a) baño caliente y (b) baño frío, en cada ciclo de Carnot?

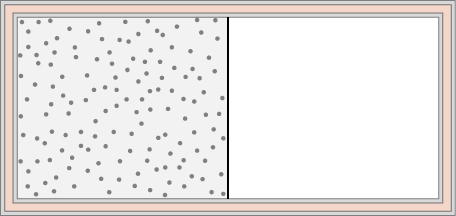
74. Un gas ideal a temperatura T se almacena en la mitad izquierda de un contenedor aislante de volumen V utilizando una partición de volumen insignificante (ver figura a continuación). ¿Cuál es el cambio de entropía por mol del gas en cada uno de los siguientes casos? (a) La partición se elimina de repente y el gas llena rápidamente todo el contenedor. (b) Se perfora un pequeño orificio en la partición y después de un largo período, el gas alcanza un estado de equilibrio tal que no hay flujo neto a través del orificio. (c) La partición se mueve muy lenta y adiabáticamente hasta la pared derecha, de modo que el gas finalmente llena todo el contenedor.



75. Se deja caer una pieza de aluminio de 0,50 kg a 250 °C en 1,0 kg de agua a 20 °C. Después de alcanzar el equilibrio, ¿cuál es el cambio neto de entropía del sistema?

76. Supón que se agregan 20 g de hielo a 0 °C a 300 g de agua a 60 °C. ¿Cuál es el cambio total en la entropía de la mezcla después de alcanzar el equilibrio térmico?

77. Un motor térmico funciona entre dos temperaturas, de modo que la sustancia activa del motor absorbe 5000 J de calor del baño de alta temperatura y descarga 3000 J al baño de baja temperatura. El resto de la energía se convierte en energía mecánica de la turbina. Encuentra (a) la cantidad de trabajo producido por el motor y (b) la eficiencia del motor.

78. Un motor térmico produce 4 MJ de energía eléctrica mientras opera entre dos baños termales de diferentes temperaturas. La sustancia de trabajo del motor descarga 5 MJ de calor al baño de temperatura fría. ¿Cuál es la eficiencia del motor?

79. Una central de carbón consume 100.000 kg de carbón por hora y produce 500 MW de potencia. Si el calor de la combustión del carbón es de 30 MJ/kg, ¿cuál es la eficiencia de la planta de energía?

80. Un motor Carnot funciona en un ciclo de Carnot entre una fuente de calor a 550 °C y un disipador de calor a 20 °C. Encuentra la eficiencia del motor Carnot.

81. Un motor Carnot que funciona entre dos baños de calor de temperaturas de 600 K y 273 K completa cada ciclo en 5 segundos. En cada ciclo, el motor absorbe 10 kJ de calor. Encuentra la potencia del motor.

82. Un ciclo de Carnot que trabaja entre 100 °C y 30 °C se usa para conducir un refrigerador entre -10 °C y 30 °C. ¿Cuánta energía debe producir el motor Carnot por segundo para que el refrigerador pueda descartar 10 J de energía por segundo?

Problemas Desafío

83. (a) Una cantidad infinitesimal de calor se agrega reversiblemente a un sistema. Al combinar las leyes primera y segunda, muestra que dU = TdS - dW. (b) Cuando se agrega calor a un gas ideal, su temperatura y volumen cambian de T₁ y V₁ a T₂ y V₂. Demuestra que el cambio de entropía de n moles del gas viene dado por ΔS = nC_vln(T₂/T₁) + nRln(V₂/V₁).

84. Utilizando el resultado del problema anterior, demuestra que para un gas ideal sometido a un proceso adiabático, TV^γ-1 es constante.

85. Con la ayuda de los dos problemas anteriores, muestra que ΔS entre los estados 1 y 2 de n moles un gas ideal está dado por ΔS = nC_pln(T₂/T₁) - nRln(p₂/p₁).

86. Un cilindro contiene 500 g de helio a 120 atm y 20 °C. La válvula tiene fugas y todo el gas escapa lentamente isotérmicamente a la atmósfera. Usa los resultados del problema anterior para determinar el cambio resultante en la entropía del universo.

87. Un gas ideal diatómico se lleva de un estado de equilibrio inicial a p₁ = 0.50 atm y T₁ = 300 K a una etapa final con p₂ = 0.20 atm y T₂ = 500 K. Usa los resultados del problema anterior para determinar el cambio de entropía por mol del gas.

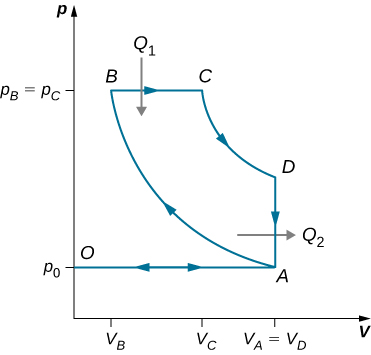
88. El motor de combustión interna de gasolina funciona en un ciclo que consta de seis partes. Cuatro de estas partes involucran, entre otras cosas, fricción, intercambio de calor a través de diferencias finitas de temperatura y aceleraciones del pistón; es irreversible Sin embargo, está representado por el ciclo reversible ideal de Otto, que se ilustra a continuación. Se supone que la sustancia de trabajo del ciclo es aire. Los seis pasos del ciclo de Otto son los siguientes:

1. Golpe de admisión isobarico (OA). Se introduce una mezcla de gasolina y aire en la cámara de combustión a la presión atmosférica p₀ a medida que el pistón se expande, aumentando el volumen del cilindro de cero a V_A.
2. Movimiento de compresión adiabático (AB). La temperatura de la mezcla aumenta cuando el pistón la comprime adiabáticamente desde un volumen V_A a V_B.
3. Encendido a volumen constante (BC). La mezcla se enciende por una chispa. La combustión ocurre tan rápido que esencialmente no hay movimiento del pistón. Durante este proceso, el calor adicional Q₁ hace que la presión aumente desde p_B a p_C al volumen constante V_B = V_C.
4. Expansión adiabática (CD). La mezcla calentada de gasolina y aire se expande contra el pistón, aumentando el volumen de V_C a V_D. Esto se llama golpe de potencia, ya que es la parte del ciclo que entrega la mayor parte de la potencia al cigüeñal.
5. Salida de volumen constante (DA). Cuando se abre la válvula de escape, algunos de los productos de combustión escapan. Casi no hay movimiento del pistón durante esta parte del ciclo, por lo que el volumen permanece constante en V_A (= V_D). La mayor parte de la energía disponible se pierde aquí, como se representa por el escape de calor Q₂.
6. Compresión isobárica (AO). La válvula de escape permanece abierta, y la compresión de V_A a cero expulsa los productos de combustión restantes.

(a) Usando (i) e = W/Q₁; (ii) W = Q₁ - Q₂; y (iii) Q₁ = nC_v(T_C - T_B), Q₂ = nC_v(T_D - T_A), muestran que e = 1 - T_D - T_A/T_C - T_B.

(b) Usa el hecho de que los pasos (ii) y (iv) son adiabáticos para mostrar que e = 1 - 1/r^γ-1, donde r = V_A/V_B. La cantidad r se denomina relación de compresión del motor.

(c) En la práctica, r se mantiene por debajo de 7. Para valores más grandes, la mezcla de gasolina-aire se comprime a temperaturas tan altas que explota antes de que se entregue la chispa finamente sincronizada. Esta preignición causa golpes en el motor y pérdida de potencia. Muestrae eso para r = 6 y γ = 1.4 (el valor para el aire), e = 0.51, o una eficiencia del 51%. Debido a los muchos procesos irreversibles, un motor de combustión interna real tiene una eficiencia mucho menor que este valor ideal. Una eficiencia típica para un motor sintonizado es de aproximadamente 25% a 30%



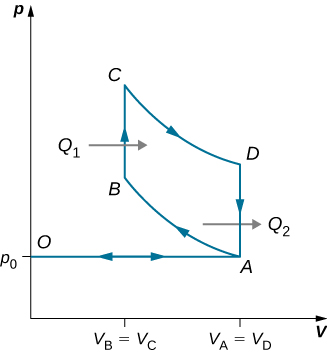
89. A continuación se muestra un ciclo diésel ideal. Este ciclo consiste en cinco golpes. En este caso, solo se aspira aire a la cámara durante la carrera de admisión OA. Luego, el aire se comprime adiabáticamente del estado A al estado B, elevando su temperatura lo suficiente como para que cuando se agrega combustible durante la carrera de energía BC, se encienda. Después de que el encendido termina en C, hay un CD de trazo de potencia adiabático adicional. Finalmente, hay un escape a volumen constante a medida que la presión cae de p_D a p_A, seguido de un escape adicional cuando el pistón comprime el volumen de la cámara a cero. (a) Usa W = Q₁ - Q₂, Q₁ = nC_p(T_C - T_B) y Q₂ = nC_v(T_D - T_A) para mostrar que e = W/Q₁ = 1 - T_D - T_A/γ(T_C - T_B).
(b) Usa el hecho de que A → B y C → D son adiabáticos para mostrar que e = 1 - 1/γ (V_C/V_D)^γ - (V_B/V_A)^γ/(V_C/V_D) - (V_B/V_A).
(c) Como no hay preignición (recuerda, la cámara no contiene combustible durante la compresión), la relación de compresión puede ser mayor que la de un motor de gasolina. Típicamente, V_A/V_B = 15 y V_D/V_C = 5. Para estos valores y γ = 1.4, muestra que ε = 0.56, o una eficiencia del 56%. Los motores diesel realmente funcionan con una eficiencia de aproximadamente 30% a 35% en comparación con 25% a 30% para los motores de gasolina.



90. Considera un ciclo de Joule de gas ideal, también llamado ciclo de Brayton, que se muestra a continuación. Encuentra la fórmula de eficiencia del motor usando este ciclo en términos de P₁, P₂ y γ.



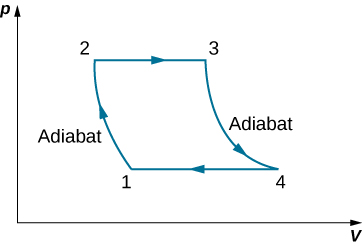
91. Deriva una fórmula para el coeficiente de rendimiento de un refrigerador utilizando un gas ideal como sustancia de trabajo que opera en el ciclo que se muestra a continuación en términos de las propiedades de los tres estados etiquetados como 1, 2 y 3.



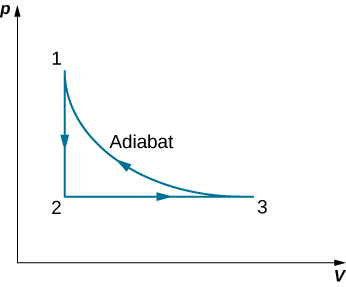
92. Dos moles de gas nitrógeno, con γ = 7/5 para los gases diatómicos ideales, ocupa un volumen de 10^-2 m³ en un cilindro aislado a una temperatura de 300 K. El gas se comprime adiabática y reversiblemente a un volumen de 5 L. el pistón del cilindro está bloqueado en su lugar, y el aislamiento alrededor del cilindro se elimina. El cilindro conductor de calor se coloca luego en un baño de 300 K. El calor del gas comprimido abandona el gas y la temperatura del gas vuelve a ser de 300 K. Luego, el gas se expande lentamente a la temperatura fija de 300 K hasta que el volumen del gas se convierte en 10^-2 m³, formando así un ciclo completo para el gas. Para todo el ciclo, calcula (a) el trabajo realizado por el gas, (b) el calor dentro o fuera del gas, (c) el cambio en la energía interna del gas y (d) el cambio en la entropía de el gas.

93. Un refrigerador Carnot, que funciona entre 0 °C y 30 °C, se usa para enfriar un balde de agua que contiene de 10 a 2 m³ de agua a una temperatura de 30 °C a 5 °C en 2 horas. Encuentre la cantidad total de trabajo necesaria.