Preguntas y problemas - Capítulo III
Preguntas conceptuales
3.1 Sistemas termodinámicos
1. Considera estos escenarios y establece si el sistema realiza el trabajo en el entorno (SE) o el entorno en el sistema (ES): (a) abriendo una bebida carbonatada; (b) llenar una rueda pinchada; (c) un gas vacío sellado se puede expandir en un día caluroso, haciendo una inclinación en las paredes.
3.2 Trabajo, calor y energía interna
2. ¿Es posible determinar si un cambio en la energía interna es causado por el calor transferido, por el trabajo realizado o por una combinación de ambos?
3. Cuando un líquido se vaporiza, su cambio en la energía interna no es igual al calor agregado. ¿Por qué?
4. ¿Por qué una bomba de bicicleta se siente caliente al inflar su neumático?
5. ¿Es posible que la temperatura de un sistema permanezca constante cuando entra o sale calor? Si es así, da ejemplos.
3.3 Primera ley de la termodinámica
6. ¿Qué nos dice la primera ley de la termodinámica sobre la energía del universo?
7. ¿Agregar calor a un sistema siempre aumenta su energía interna?
8. Se ha gastado una gran cantidad de esfuerzo, tiempo y dinero en la búsqueda de una máquina llamada de movimiento perpetuo, que se define como una máquina hipotética que opera o produce trabajo útil indefinidamente y/o una máquina hipotética que produce más trabajo o energía de la que consume. Explica, en términos de la primera ley de la termodinámica, por qué o por qué no es probable que se construya una máquina de este tipo.
3.4 Procesos termodinámicos
9. Cuando un gas se expande isotérmicamente, trabaja. ¿Cuál es la fuente de energía necesaria para hacer este trabajo?
10. Si se dan la presión y el volumen de un sistema, ¿la temperatura siempre se determina de manera única?
11. Es poco probable que un proceso pueda ser isotérmico a menos que sea un proceso muy lento. Explicar por qué. ¿Es lo mismo cierto para los procesos isobáricos e isocóricos? Explica tu respuesta.
3.5 Capacidades de calor de un gas ideal
12. ¿Cómo puede un objeto transferir calor si el objeto no posee una cantidad discreta de calor?
13. La mayoría de los materiales se expanden cuando se calientan. Una excepción notable es el agua entre 0 °C y 4 °C, que en realidad disminuye en volumen con el aumento de la temperatura. ¿Cuál es mayor para el agua en esta región de temperatura, Cp o CV?
14. ¿Por qué hay dos calores específicos para gases Cp y CV, pero solo uno dado para un sólido?
3.6 Procesos adiabáticos para un gas ideal
15. ¿Es posible que γ sea más pequeño que la unidad?
16. ¿Esperarías que γ sea más grande para un gas o un sólido? Explica.
17. No hay cambio en la energía interna de un gas ideal que se somete a un proceso isotérmico ya que la energía interna depende solo de la temperatura. ¿Es correcto decir que un proceso isotérmico es lo mismo que un proceso adiabático para un gas ideal? Explica tu respuesta.
18. ¿Hace algún trabajo un gas cuando se expande adiabáticamente? Si es así, ¿cuál es la fuente de la energía necesaria para hacer este trabajo?
Problemas
3.1 Sistemas termodinámicos
19. Un gas sigue la ecuación pV = bp + cT en una curva isotérmica, donde p es la presión, V es el volumen, b es una constante, y c es una función de la temperatura. Demostrar que se puede establecer una escala de temperatura bajo un proceso isocórico con este gas y es idéntica a la de un gas ideal.
20. Una mole de gas tiene un coeficiente de expansión isobárico dV/dT = R/p y un coeficiente de presión-temperatura isocórico dp/dT = p/T. Encuentra la ecuación de estado del gas.
21. Halla la ecuación de estado de un sólido que tiene un coeficiente de expansión isobórica dV/dT = 2cT - bp y un coeficiente de presión/volumen isotérmico dV/dp = -bT.
3.2 Trabajo, calor y energía interna
22. Un gas a una presión de 2.00 atm sufre una expansión isobárica cuasiestática de 3.00 a 5.00 L. ¿Cuánto trabajo realiza el gas?
23. Se necesitan 500 J de trabajo para comprimir cuasi-estáticamente 0,50 mol de un gas ideal a una quinta parte de su volumen original. Calcula la temperatura del gas, suponiendo que permanezca constante durante la compresión.
24. Se encuentra que, cuando un gas diluido se expande cuasi-estáticamente de 0.50 a 4.0 L, hace 250 J de trabajo. Suponiendo que la temperatura del gas permanece constante a 300 K, ¿cuántos moles de gas hay?
25. En una expansión isobárica cuasiestática, el gas realiza 500 J de trabajo. Si la presión del gas es 0.80 atm, ¿cuál es el incremento fraccional en el volumen del gas, suponiendo que originalmente era a 20.0 L?
26. Cuando un gas sufre un cambio isobárico cuasiestático en volumen de 10.0 a 2.0 L, se requieren 15 J de trabajo de una fuente externa. ¿Cuál es la presión del gas?
27. Un gas ideal se expande de forma cuasi-estática e isotérmica desde un estado con presión p y volumen V a un estado con volumen 4V. Demuestra que el trabajo realizado por el gas en la expansión es pV(ln 4).
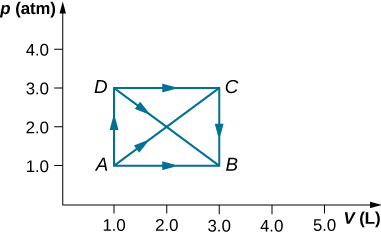
28. Como se muestra a continuación, calcula el trabajo realizado por el gas en los procesos cuasiestáticos representados por las trayectorias (a) AB; (b) ADB; (c) ACB; y (d) ADCB.
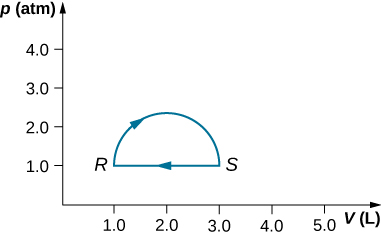
29. (a) Calcula el trabajo realizado por el gas a lo largo de la trayectoria cerrada que se muestra a continuación. La sección curva entre R y S es semicircular. (b) Si el proceso se lleva a cabo en la dirección opuesta, ¿cuál es el trabajo realizado por el gas?
30. Un gas ideal se expande cuasi-estáticamente a tres veces su volumen original. ¿Qué proceso requiere más trabajo del gas, un proceso isotérmico o uno isobárico? Determina la relación del trabajo realizado en estos procesos.
31. Un gas diluido a una presión de 2.0 atm y un volumen de 4.0 L se toma a través de los siguientes pasos cuasi-estáticos: (a) una expansión isobárica a un volumen de 10.0 L, (b) un cambio isocórico a una presión de 0.50 atm, (c) una compresión isobárica a un volumen de 4.0 L, y (d) un cambio isocórico a una presión de 2.0 atm. Muestre estos pasos en un diagrama pV y determine desde su gráfico el trabajo neto realizado por el gas.
32. ¿Cuál es la energía mecánica promedio de los átomos de un gas monoatómico ideal a 300 K?
33. ¿Cuál es la energía interna de 6.00 mol de un gas monoatómico ideal a 200 °C?
34. Calcula la energía interna de 15 mg de helio a una temperatura de 0 °C.
35. Dos gases monoatómicos ideales A y B están a la misma temperatura. Si 1,0 g de gas A tiene la misma energía interna que 0,10 g de gas B, ¿cuál es (a) la relación entre el número de moles de cada gas y (b) la relación de las masas atómicas de los dos gases?
36. Los coeficientes de van der Waals para el oxígeno son a = 0.138J•m3/mol2 y b = 3.18 × 10-5m3/mol. Usa estos valores para dibujar una isoterma de oxígeno de Van der Waals a 100 K. En el mismo gráfico, dibuja isotermas de un mol de un gas ideal.
37. Encuentra el trabajo realizado en los procesos cuasiestáticos que se muestran a continuación. Los estados se dan como valores (p, V) para los puntos en el plano pV: 1 (3 atm, 4 L), 2 (3 atm, 6 L), 3 (5 atm, 4 L), 4 (2 atm , 6 l), 5 (4 atm, 2 l), 6 (5 atm, 5 l) y 7 (2 atm, 5 l).

3.3 Primera ley de la termodinámica
38. Cuando un gas diluido se expande cuasi-estáticamente de 0.50 a 4.0 L, hace 250 J de trabajo. Suponiendo que la temperatura del gas permanezca constante a 300 K, (a) ¿cuál es el cambio en la energía interna del gas? (b) ¿Cuánto calor es absorbido por el gas en este proceso?
39. En una expansión isobárica cuasiestática, el gas realiza 500 J de trabajo. La presión del gas es 0.80 atm y originalmente estaba en 20.0 L. Si la energía interna del gas aumenta en 80 J en la expansión, ¿cuánto calor absorbe el gas?
40. Un gas ideal se expande cuasi-estáticamente e isotérmicamente desde un estado con presión p y volumen V a un estado con volumen 4V. ¿Cuánto calor se agrega al gas en expansión?
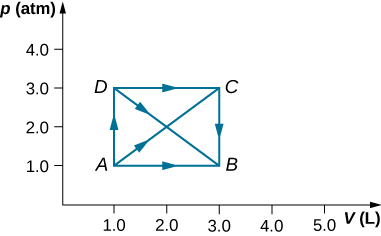
41. Como se muestra a continuación, si el calor absorbido por el gas a lo largo de AB es 400 J, determine las cantidades de calor absorbido a lo largo de (a) ADB; (b) ACB; y (c) ADCB
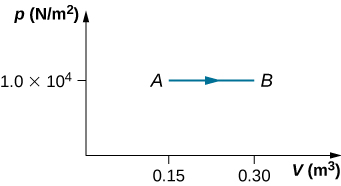
42. Durante la expansión isobárica de A a B representada a continuación, se eliminan 130 J de calor del gas. ¿Cuál es el cambio en su energía interna?
43. (a) ¿Cuál es el cambio en la energía interna para el proceso representado por la trayectoria cerrada que se muestra a continuación? (b) ¿Cuánto calor se intercambia? (c) Si la ruta se atraviesa en la dirección opuesta, ¿cuánta calor se intercambia?

44. Cuando un gas se expande a lo largo del camino AC que se muestra a continuación, realiza 400 J de trabajo y absorbe 200 o 400 J de calor. (a) Supón que te dicen que a lo largo del camino ABC, el gas absorbe 200 o 400 J de calor. ¿Cuál de estos valores es correcto? (b) Da la respuesta correcta de la parte (a), ¿cuánto trabajo realiza el gas a lo largo de ABC? (c) A lo largo de CD, la energía interna del gas disminuye en 50 J. ¿Cuánto calor intercambia el gas a lo largo de este camino?
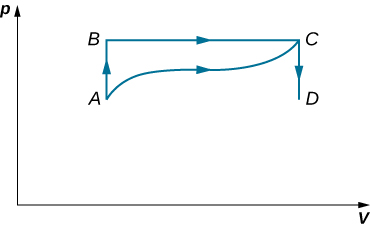
45. Cuando un gas se expande a lo largo de AB (ver abajo), realiza 500 J de trabajo y absorbe 250 J de calor. Cuando el gas se expande a lo largo de AC, realiza 700 J de trabajo y absorbe 300 J de calor. (a) ¿Cuánto calor intercambia el gas a lo largo de BC? (b) Cuando el gas realiza la transmisión de C a A a lo largo de CDA, se realizan 800 J de trabajo de C a D. ¿Cuánto calor intercambia a lo largo de CDA?
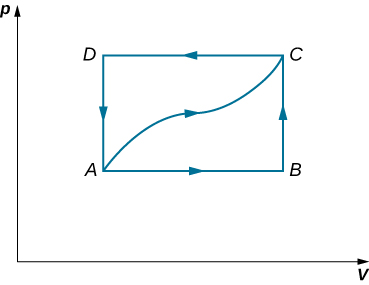
46. Un gas diluido se almacena en la cámara izquierda de un contenedor cuyas paredes son perfectamente aislantes (ver abajo), y la cámara derecha es evacuada. Cuando se elimina la partición, el gas se expande y llena todo el contenedor. Calcula el trabajo realizado por el gas. ¿La energía interna del gas cambia en este proceso?
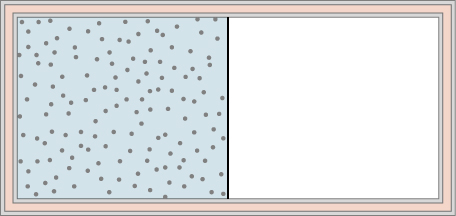
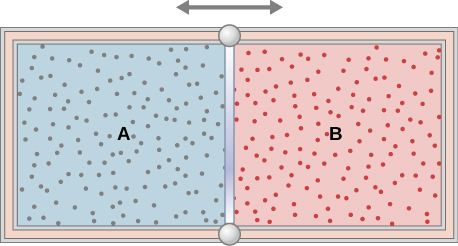
47. Los gases ideales A y B se almacenan en las cámaras izquierda y derecha de un contenedor aislado, como se muestra a continuación. La partición se elimina y los gases se mezclan. ¿Se ha hecho algún trabajo en este proceso? Si las temperaturas de A y B son inicialmente iguales, ¿qué ocurre con su temperatura común después de mezclarse?
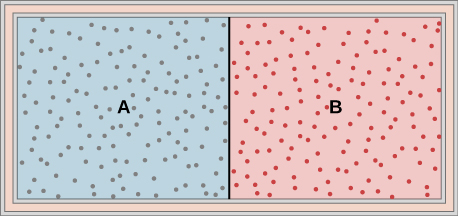
48. Un gas monoatómico ideal a una presión de 2.0 × 105 N/m2 y una temperatura de 300 K sufre una expansión isobárica cuasiestática de 2.0 × 103 a 4.0 × 103 cm3. (a) ¿Cuál es el trabajo realizado por el gas? (b) ¿Cuál es la temperatura del gas después de la expansión? (c) ¿Cuántos moles de gas hay? (d) ¿Cuál es el cambio en la energía interna del gas? (e) ¿Cuánto calor se agrega al gas?
49. Considera el proceso de vapor en un cilindro que se muestra a continuación. Supongamos que el cambio en la energía interna en este proceso es de 30 kJ. Encuentra el calor entrando al sistema.
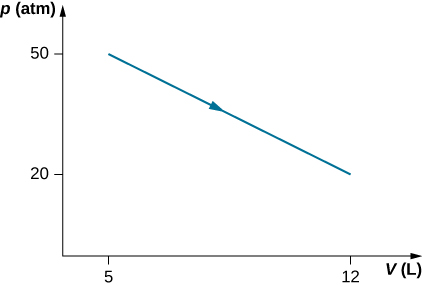
50. El estado de 30 moles de vapor en un cilindro se cambia cíclicamente de a-b-c-a, donde la presión y el volumen de los estados son: a (30 atm, 20 L), b (50 atm, 20 L) y c (50 atm, 45 L). Supongamos que cada cambio tiene lugar a lo largo de la línea que conecta los estados inicial y final en el plano pV. (a) Visualiza el ciclo en el plano pV. (b) Encuentra el trabajo neto realizado por el vapor en un ciclo. (c) Encuentra la cantidad neta de flujo de calor en el vapor en el transcurso de un ciclo.
51. Un gas ideal monoatómico se somete a un proceso cuasiestático que se describe mediante la función p(V) = p1 + 3(V - V1), donde el estado inicial es (p1, V1) y el estado final (p2, V2) Supongamos que el sistema consiste en n moles del gas en un contenedor que puede intercambiar calor con el medio ambiente y cuyo volumen puede cambiar libremente. (a) Evalúa el trabajo realizado por el gas durante el cambio en el estado. (b) Encuentra el cambio en la energía interna del gas. (c) Encuentra la entrada de calor al gas durante el cambio. (d) ¿Cuáles son las temperaturas iniciales y finales?
52. Un contenedor metálico de volumen fijo de 2,5 × 10-3 m3 inmerso en un tanque grande de temperatura de 27 °C contiene dos compartimentos separados por una pared libremente movible. Inicialmente, la pared se mantiene en su lugar mediante un tapón, de modo que hay 0.02 mol del gas nitrógeno en un lado y 0.03 mol del gas oxígeno en el otro lado, ocupando cada uno la mitad del volumen. Cuando se quita el tapón, la pared se mueve y llega a una posición final. El movimiento de la pared se controla de modo que la pared se mueva en pasos cuasi-estáticos infinitesimales. (a) Encuentra los volúmenes finales de los dos lados asumiendo el comportamiento ideal del gas para los dos gases. (b) ¿Cuánto trabajo hace cada gas en el otro? (c) ¿Cuál es el cambio en la energía interna de cada gas? (d) Encuentra la cantidad de calor que entra o sale de cada gas.
53. Un gas en un contenedor cilíndrico cerrado se expande adiabática y cuasi-estáticamente desde un estado A (3 MPa, 2 L) a un estado B con un volumen de 6 L a lo largo del camino 1.8pV = constante. (a) Traza la trayectoria en el plano pV. (b) Encuentra la cantidad de trabajo realizado por el gas y el cambio en la energía interna del gas durante el proceso.
3.4 Procesos termodinámicos
54. Dos moles de un gas ideal monoatómico a (5 MPa, 5 L) se expanden isotérmicamente hasta que el volumen se duplica (paso 1). Luego se enfría isocóricamente hasta que la presión sea de 1 MPa (paso 2). La temperatura baja en este proceso. El gas ahora se comprime isotérmicamente hasta que su volumen vuelva a 5 L, pero su presión es ahora de 2 MPa (paso 3). Finalmente, el gas se calienta isocóricamente para volver al estado inicial (paso 4). (a) Dibujalos cuatro procesos en el plano pV. (b) Encuentra el trabajo total realizado por el gas.
55. Considera una transformación del punto A al B en un proceso de dos pasos. Primero, la presión se reduce de 3 MPa en el punto A a una presión de 1 MPa, mientras se mantiene el volumen a 2 L al enfriar el sistema. El estado alcanzado se etiqueta como C. Luego, el sistema se calienta a una presión constante para alcanzar un volumen de 6 L en el estado B. (a) Encuentra la cantidad de trabajo realizado en la trayectoria de ACB. (b) Encuentra la cantidad de calor intercambiado por el sistema cuando va de A a B en la trayectoria ACB. (c) Compara el cambio en la energía interna cuando el proceso AB ocurre adiabáticamente con el cambio AB a través del proceso de dos pasos en la trayectoria ACB.
56. Considera un cilindro con un pistón móvil que contiene n moles de un gas ideal. Todo el aparato está sumergido en un baño de temperatura constante T kelvin. El pistón se empuja lentamente para que la presión del gas cambie cuasi-estáticamente de p1 a p2 a temperatura constante T. Encuentra el trabajo realizado por el gas en términos de n, R, T, p1 y p2.
57. Un gas ideal se expande isotérmicamente a lo largo de AB y realiza 700 J de trabajo (ver abajo). (a) ¿Cuánto calor intercambia el gas a lo largo de AB? (b) El gas luego se expande adiabáticamente a lo largo de BC y hace 400 J de trabajo. Cuando el gas vuelve a A a lo largo de CA, agota 100 J de calor en su entorno. ¿Cuánto trabajo se hace en el gas a lo largo de este camino?
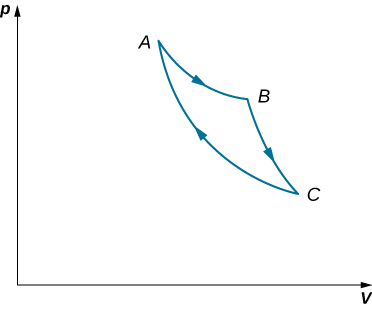
58. Considera los procesos que se muestran a continuación. En los procesos AB y BC, se agregan 3600 J y 2400 J de calor al sistema, respectivamente. (a) Encuentrael trabajo realizado en cada uno de los procesos AB, BC, AD y DC. (b) Encuentra el cambio de energía interno en los procesos AB y BC. (c) Encuentra la diferencia de energía interna entre los estados C y A. (d) Encuentra el calor total agregado en el proceso de CAD. (e) A partir de la información facilitada, ¿puedes encontrar el calor agregado en el proceso AD? ¿Por qué o por qué no?

59. Dos moles de gas de helio se colocan en un recipiente cilíndrico con un pistón. El gas está a temperatura ambiente de 25 °C y bajo una presión de 3.0 × 105 Pa. Cuando la presión desde el exterior disminuye mientras se mantiene la temperatura igual a la temperatura ambiente, el volumen del gas se duplica. (a) Encuentra el trabajo que el agente externo hace en el gas en el proceso. (b) Encuentra el calor intercambiado por el gas e indica si el gas absorbe o cede el calor. Supón el comportamiento ideal del gas.
60. Una cantidad de n moles de un gas ideal monoatómico en un contenedor conductor con un pistón móvil se coloca en un gran baño de calor térmico a temperatura T1 y se permite que el gas llegue al equilibrio. Después de que se alcanza el equilibrio, la presión sobre el pistón se reduce de modo que el gas se expande a temperatura constante. El proceso se continúa cuasi-estáticamente hasta que la presión final es 4/3 de la presión inicial p1. (a) Encuentra el cambio en la energía interna del gas. (b) Encuentra el trabajo realizado por el gas. (c) Encuentra el calor intercambiado por el gas e indica si el gas absorbe o cede el calor.
3.5 Capacidades de calor de un gas ideal
61. La temperatura de un gas monoatómico ideal aumenta en 8.0 K. ¿Cuál es el cambio en la energía interna de 1 mol del gas a volumen constante?
62. Para un aumento de la temperatura de 10 °C a volumen constante, ¿cuál es el calor absorbido por (a) 3,0 mol de un gas monoatómico diluido; (b) 0,50 mol de un gas diatómico diluido; y (c) 15 mol de un gas poliatómico diluido?
63. Si los gases del problema anterior son inicialmente de 300 K, ¿cuáles son sus energías internas después de que absorben el calor?
64. Considera 0.40 mol de dióxido de carbono diluido a una presión de 0.50 atm y un volumen de 50 L. ¿Cuál es la energía interna del gas?
65. Cuando 400 J de calor se agregan lentamente a 10 mol de un gas monoatómico ideal, su temperatura aumenta en 10 °C. ¿Cuál es el trabajo realizado en el gas?
66. Un mol de un gas diatómico diluido que ocupa un volumen de 10.00 L se expande contra una presión constante de 2.000 atm cuando se calienta lentamente. Si la temperatura del gas aumenta en 10.00 K y se agregan 400.0 J de calor en el proceso, ¿cuál es su volumen final?
3.6 Procesos adiabáticos para un gas ideal
67. Un gas ideal monoatómico experimenta una expansión adiabática cuasiestática en la que su volumen se duplica. ¿Cómo se modifica la presión del gas?
68. Un gas ideal tiene una presión de 0.50 atm y un volumen de 10 L. Se comprime adiabática y cuasi-estáticamente hasta que su presión es 3.0 atm y su volumen es 2.8 L. ¿El gas es monoatómico, diatómico o poliatómico?
69. Las mediciones de presión y volumen de un gas diluido sometido a una expansión adiabática cuasi estática se muestran a continuación. Traza ln p vs. V y determina γ para este gas de tu gráfica.
| P (atm)20.0 | V (L) |
| 20.0 | 1.0 |
| 17.0 | 1.1 |
| 14.0 | 1.3 |
| 11.0 | 1.5 |
| 8.0 | 2.0 |
| 5.0 | 2.6 |
| 2.0 | 5.2 |
| 1.0 | 8.4 |
70. Un gas monoatómico ideal a 300 K se expande adiabática y reversiblemente al doble de su volumen. ¿Cuál es su temperatura final?
71. Un gas diatómico ideal a 80 K se comprime lentamente adiabática y reversiblemente al doble de su volumen. ¿Cuál es su temperatura final?
72. Un gas diatómico ideal a 80 K se comprime lentamente adiabáticamente a un tercio de su volumen original. ¿Cuál es su temperatura final?
73. Compara la carga en energía interna de un gas ideal para una expansión adiabática cuasiestática con la de una expansión isotérmica cuasiestática. ¿Qué sucede con la temperatura de un gas ideal en una expansión adiabática?
74. La temperatura de n moles de un gas ideal cambia de T1 a T2 en una transición adiabática cuasiestática. Demuestra que el trabajo realizado por el gas viene dado por W = nR/(γ-1)(T1 - T2).
75. Un gas diluido se expande cuasi-estáticamente a tres veces su volumen inicial. ¿La presión final del gas es mayor para una expansión isotérmica o adiabática? ¿Tu respuesta depende de si el gas es monoatómico, diatómico o poliatómico?
76. (a) Un gas ideal se expande adiabáticamente desde un volumen de 2.0 × 10-3 m3 a 2.5 × 10-3 m3. Si la presión y la temperatura iniciales fueron de 5,0 × 105 Pa y 300 K, respectivamente, ¿cuál es la presión y la temperatura finales del gas? Usa γ = 5/3 para el gas. (b) En un proceso isotérmico, un gas ideal se expande de un volumen de 2.0 × 10-3 m3 a 2.5 × 10-3 m3. Si la presión y la temperatura iniciales fueron de 5,0 × 105 Pa y 300 K, respectivamente, ¿cuál es la presión y la temperatura finales del gas?
77. En un proceso adiabático de una presión de gas ideal, el volumen y la temperatura cambian de tal manera que pVγ sea constante con γ = 5/3 para gas monatómico como helio y γ = 7/5 para gas diatómico como el hidrógeno a temperatura ambiente. Usa valores numéricos para trazar dos isotermas de 1 mol de gas de helio usando la ley de los gases ideales y dos procesos adiabáticos que median entre ellos. Utilice T1 = 500K, V1 = 1 L y T2 = 300K para su trazado.
78. Dos moles de un gas ideal monoatómico como el helio se comprimen adiabáticamente y reversiblemente desde un estado (3 atm, 5 L) a un estado con una presión de 4 atm. (a) Encuentra el volumen y la temperatura del estado final. (b) Encuentra la temperatura del estado inicial del gas. (c) Encuentra el trabajo realizado por el gas en el proceso. (d) Encuentra el cambio en la energía interna del gas en el proceso.
Problemas Adicionales
79. Considera el proceso que se muestra a continuación. Durante los pasos AB y BC, se agregan 3600 J y 2400 J de calor, respectivamente, al sistema. (a) Encuentra el trabajo realizado en cada uno de los procesos AB, BC, AD y DC. (b) Encuentra el cambio de energía interno en los procesos AB y BC. (c) Encuentra la diferencia de energía interna entre los estados C y A. (d) Encuentra el calor total agregado en el proceso de CAD. (e) A partir de la información proporcionada, ¿puedes encontrar el calor agregado en el proceso AD? ¿Por qué o por qué no?
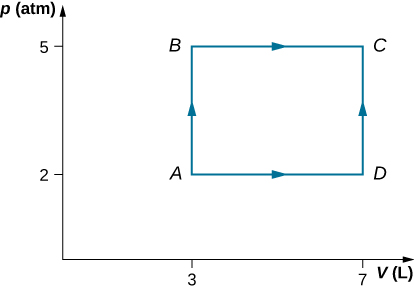
80. Un neumático de automóvil contiene 0.0380 m3 de aire a una presión de 2.20 × 105 Pa (aproximadamente 32 psi). ¿Cuánta más energía interna tiene este gas que el mismo volumen tiene a presión manométrica cero (que es equivalente a la presión atmosférica normal)?
81. Un globo de juguete lleno de helio tiene una presión manométrica de 0.200 atm y un volumen de 10.0 L. ¿Cuánta mayor es la energía interna del helio en el globo de lo que sería con una presión manométrica cero?
82. El vapor para conducir una locomotora de vapor antigua se suministra a una presión manométrica constante de 1.75 × 106 N/m2 (aproximadamente 250 psi) a un pistón con un radio de 0.200 m. (a) Calculando pΔV, encuentra el trabajo realizado por el vapor cuando el pistón se mueve 0.800 m. Ten en cuenta que esta es la salida neta de trabajo, ya que se utiliza presión manométrica. (b) Ahora encuentra la cantidad de trabajo calculando la fuerza ejercida multiplicada por la distancia recorrida. ¿Es la respuesta la misma que en la parte (a)?5
83. Una bomba de neumático manual tiene un pistón con un diámetro de 2.50 cm y una carrera máxima de 30.0 cm. (a) ¿Cuánto trabajo hace de un golpe si la presión manométrica promedio es de 2.4 × 105 N/m2 (alrededor de 35 psi)? (b) ¿Qué fuerza media ejerce sobre el pistón, despreciando la fricción y la fuerza gravitacional?
84. Calcula la salida neta de trabajo de un motor térmico siguiendo la trayectoria ABCDA como se muestra a continuación.
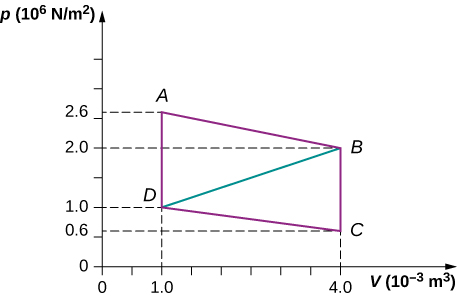
85. ¿Cuál es la producción neta de trabajo de un motor térmico que sigue el camino ABDA en el problema anterior con una línea recta de B a D? ¿Por qué la salida de trabajo es menor que para la ruta ABCDA?
86. Cinco moles de un gas ideal monoatómico en un cilindro a 27 °C se expanden isotérmicamente desde un volumen de 5 L a 10 L. (a) ¿Cuál es el cambio en la energía interna? (b) ¿Cuánto trabajo se hizo con el gas en el proceso? (c) ¿Cuánto calor se transfirió al gas?
87. Se expanden cuatro moles de un gas ideal monoatómico en un cilindro a 27 °C a una presión constante igual a 1 atm hasta que su volumen se duplique. (a) ¿Cuál es el cambio en la energía interna? (b) ¿Cuánto trabajo hizo el gas en el proceso? (c) ¿Cuánto calor se transfirió al gas?
88. El gas de helio se enfría de 20 °C a 10 °C al expandirse de 40 atm a 1 atm. Si hay 1,4 mol de helio, (a) ¿Cuál es el volumen final de helio? (b) ¿Cuál es el cambio en la energía interna?
89. En un proceso adiabático, el gas oxígeno en un contenedor se comprime a lo largo de una trayectoria que se puede describir mediante la siguiente presión en atm en función del volumen V, con V0 = 1 L: p = (3.0atm)(V/V0) - 1.2. Los volúmenes inicial y final durante el proceso fueron de 2 L y 1,5 L, respectivamente. Encuentra la cantidad de trabajo realizado en el gas.
90. Un cilindro que contiene tres moles de un gas ideal monoatómico se calienta a una presión constante de 2 atm. La temperatura del gas cambia de 300 K a 350 K como resultado de la expansión. Encuentra el trabajo realizado (a) en el gas; y (b) por el gas.
91. Un cilindro que contiene tres moles de gas nitrógeno se calienta a una presión constante de 2 atm. La temperatura del gas cambia de 300 K a 350 K como resultado de la expansión. Encuentra el trabajo realizado (a) en el gas y (b) en el gas usando la ecuación de estado de van der Waals en lugar de la ley de los gases ideales.
92. Dos moles de un gas ideal monoatómico, como el oxígeno, se comprimen adiabática y reversiblemente desde un estado (3 atm, 5 L) a un estado con una presión de 4 atm. (a) Encuentra el volumen y la temperatura del estado final. (b) Encuentra la temperatura del estado inicial. (c) Encuentra el trabajo realizado por el gas en el proceso. (d) Encuentra el cambio en la energía interna en el proceso. Supón CV = 5R y Cp = CV + R para el gas ideal diatómico en las condiciones dadas.
93. Un recipiente aislado contiene 1,5 moles de argón a 2 atm. El gas ocupa inicialmente un volumen de 5 L. Como resultado de la expansión adiabática, la presión del gas se reduce a 1 atm. (a) Encuentra el volumen y la temperatura del estado final. (b) Encuentra la temperatura del gas en el estado inicial. (c) Encuentra el trabajo realizado por el gas en el proceso. (d) Encuentra el cambio en la energía interna del gas en el proceso.
Problemas Desafío
94. Un mol de un gas monoatómico ideal ocupa un volumen de 1.0 × 10-2 m3 a una presión de 2.0 × 105 N/m2. (a) ¿Cuál es la temperatura del gas? (b) El gas se somete a una compresión adiabática cuasi estática hasta que su volumen se reduce a 5.0 × 10-3 m3. ¿Cuál es la nueva temperatura del gas? (c) ¿Cuánto trabajo se realiza en el gas durante la compresión? (d) ¿Cuál es el cambio en la energía interna del gas?
95. Un mol de un gas ideal se encuentra inicialmente en una cámara de volumen de 1.0 × 10-2 m3 y a una temperatura de 27 °C. (a) ¿Cuánto calor absorbe el gas cuando se expande isotérmicamente hasta el doble de su volumen inicial? (b) Supongamos que el gas se transforma lentamente en el mismo estado final disminuyendo primero la presión a volumen constante y luego expandiéndolo isobáricamente. ¿Cuál es el calor transferido para este caso? (c) Calcula el calor transferido cuando el gas se transforma cuasi-estáticamente en el mismo estado final al expandirlo isobáricamente, luego disminuyendo su presión a un volumen constante.
96. Una bala de 10 g de masa viaja horizontalmente a 200 m/s cuando golpea e incrusta en una sacudida de péndulo de 2,0 kg de masa. (a) ¿Cuánta energía mecánica se disipa en la colisión? (b) Suponiendo que Cv para la bala bob plus es 3R, calcula el aumento de temperatura del sistema debido a la colisión. Toma la masa molecular del sistema para que sea de 200 g/mol.
97. El cilindro aislado que se muestra a continuación está cerrado en ambos extremos y contiene un pistón aislante que se puede mover libremente sobre cojinetes sin fricción. El pistón divide la cámara en dos compartimentos que contienen los gases A y B. Originalmente, cada compartimento tiene un volumen de 5,0 × 10-2 m3 y contiene un gas ideal monoatómico a una temperatura de 0 °C y una presión de 1,0 atm. (a) ¿Cuántos moles de gas hay en cada compartimento? (b) El calor Q se agrega lentamente a A para que se expanda y B se comprima hasta que la presión de ambos gases sea de 3,0 atm. Usa el hecho de que la compresión de B es adiabática para determinar el volumen final de ambos gases. (c) ¿Cuáles son sus temperaturas finales? (d) ¿Cuál es el valor de Q?
98. En un motor diesel, el combustible se enciende sin una bujía. En cambio, el aire en un cilindro se comprime adiabáticamente a una temperatura superior a la temperatura de ignición del combustible; en el punto de máxima compresión, el combustible se inyecta en el cilindro. Supongamos que el aire a 20 °C se introduce en el cilindro a un volumen V1 y luego se comprime adiabática y cuasi-estáticamente a una temperatura de 600 °C y un volumen V2. Si γ = 1.4, ¿cuál es la relación V1/V2? (Nota: en un motor diesel en funcionamiento, la compresión no es cuasiestática).















