Preguntas y problemas - Capítulo II

Preguntas conceptuales

2.1 Modelo molecular de un gas ideal

1. Dos moléculas de H₂ pueden reaccionar con una molécula de O₂ para producir dos moléculas de H₂O. ¿Cuántos moles de moléculas de hidrógeno se necesitan para reaccionar con un mol de moléculas de oxígeno?

2. ¿Bajo qué circunstancias esperarías que un gas se comportara de manera significativamente diferente a lo predicho por la ley de los gases ideales?

3. Un termómetro de gas de volumen constante contiene una cantidad fija de gas. ¿Qué propiedad del gas se mide para indicar su temperatura?

4. Infla un globo a temperatura ambiente. Deja el globo inflado en el refrigerador durante la noche. ¿Qué le sucede al globo y por qué?

5. En el último capítulo, se explicó la convección libre como el resultado de las fuerzas de flotación sobre los fluidos calientes. Explica el movimiento ascendente del aire ardiente basado en la ley de los gases ideales.

2.2 Presión, temperatura y velocidad RMS

6. ¿Cómo se relaciona el momento con la presión ejercida por un gas? Explica a nivel molecular, considerando el comportamiento de las moléculas.

7. Si un tipo de molécula tiene el doble del radio de otra y ocho veces la masa, ¿cómo se comparan sus trayectorias libres medias en las mismas condiciones? ¿Cómo se comparan sus tiempos libres?

8. ¿Cuál es la velocidad promedio de las moléculas de aire en la habitación donde estás ahora?

9. ¿Por qué las atmósferas de Júpiter, Saturno, Urano y Neptuno, que son mucho más masivas y más alejadas del Sol que la Tierra, contienen grandes cantidades de hidrógeno y helio?

10. La mecánica estadística dice que en un gas mantenido a temperatura constante por contacto térmico con un sistema más grande (un "depósito") a esa temperatura, las fluctuaciones en la energía interna son típicamente una fracción 1/√N de la energía interna. Como una fracción de la energía interna total de una mole de gas, ¿cuán grandes son las fluctuaciones en la energía interna? ¿Estamos justificados al ignorarlos?

11. ¿Cuál es más peligroso, un armario donde se almacenan tanques de nitrógeno, o uno donde se almacenan tanques de dióxido de carbono?

2.3 Capacidad de calor y equipartición de energía

12. Experimentalmente, parece que los grados de libertad vibratorios de muchas moléculas poliatómicas pueden contribuir en cierta medida a su energía a temperatura ambiente. ¿Esperarías el aumento o disminuciónde su capacidad de calor desde el valor R? Explica.

13. Se podría pensar que la energía interna de los gases diatómicos viene dada por E_int = 5RT/2. ¿Los gases diatómicos cercanos a la temperatura ambiente tienen más o menos energía interna que eso? Sugerencia: Su energía interna incluye la energía total añadida al elevar la temperatura desde el punto de ebullición (muy bajo) a la temperatura ambiente.

14. Mezclas 5 moles de H₂ a 300 K con 5 moles de He a 360 K en un calorímetro perfectamente aislado. ¿La temperatura final es más alta o más baja que 330 K?

2.4 Distribución de velocidades moleculares

15. Un cilindro contiene gas de helio y otro contiene gas de criptón a la misma temperatura. Marca cada una de estas afirmaciones como verdaderas, falsas o imposibles de determinar a partir de la información dada. (a) Las velocidades eficaces de los átomos en los dos gases son las mismas. (b) Las energías cinéticas promedio de los átomos en los dos gases son las mismas. (c) Las energías internas de 1 mol de gas en cada cilindro son las mismas. (d) Las presiones en los dos cilindros son las mismas.

16. Repite la pregunta anterior si un gas todavía es helio pero el otro se cambia a flúor, F₂. 17. Un gas ideal está a una temperatura de 300 K. Para duplicar la velocidad promedio de sus moléculas, ¿a qué se debe cambiar la temperatura?

Problemas

2.1 Modelo molecular de un gas ideal

18. La presión manométrica en los neumáticos de tu automóvil es de 2.50 × 10⁵ N/m² a una temperatura de 35.0 °C cuando lo conduces a un barco en Los Ángeles para enviarlo a Alaska. ¿Cuál es su presión manométrica en una noche en Alaska cuando la temperatura ha bajado a -40.0 °C? Supongamos que los neumáticos no han ganado ni perdido aire.

19. Supón que una bombilla incandescente llena de gas está fabricada de manera que el gas dentro de la bombilla se encuentre a presión atmosférica cuando la bombilla tiene una temperatura de 20.0 °C. (a) Encuentra la presión manométrica dentro de una bombilla cuando está caliente, suponiendo que su temperatura promedio es de 60.0 °C (una aproximación) y desprecia cualquier cambio en el volumen debido a la expansión térmica o fugas de gas. (b) La presión final real para la bombilla será menor que la calculada en la parte (a) porque la bombilla de vidrio se expandirá. Es este efecto significativo?

20. Las personas que compran alimentos en bolsas selladas a grandes alturas a menudo notan que las bolsas están hinchadas porque el aire interior se ha expandido. Se empaquetó una bolsa de pretzels a una presión de 1.00 atm y una temperatura de 22.0 °C. Cuando se abre en un picnic de verano en Santa Fe, Nuevo México, a una temperatura de 32.0 °C, el volumen del aire en la bolsa es 1,38 veces su volumen original. ¿Cuál es la presión del aire?

21. ¿Cuántos moles hay en (a) 0.0500 g de gas N₂ (M = 28.0 g/mol)? (b) 10.0 g de gas CO₂ (M = 44.0g/mol)? (c) ¿Cuántas moléculas hay en cada caso?

22. Un contenedor cúbico de volumen 2.00 L contiene 0.500 mol de gas nitrógeno a una temperatura de 25.0 °C. ¿Cuál es la fuerza neta debida al nitrógeno en una pared del contenedor? Compara esa fuerza con el peso de la muestra.

23. Calcula la cantidad de moles en el volumen de aire de 2.00 l en los pulmones de la persona promedio. Ten en cuenta que el aire está a 37.0 °C (temperatura corporal) y que el volumen total en los pulmones es varias veces la cantidad inhalada en una respiración típica como se indica en el Ejemplo 2.2.

24. Un pasajero del avión tiene 100 cm³ de aire en el estómago justo antes de que el avión despegue de un aeropuerto a nivel del mar. ¿Qué volumen tendrá el aire a la altitud de crucero si la presión de la cabina cae a 7.50 × 10⁴ N/m²?

25. Una compañía anuncia que suministra helio a una presión manométrica de 1.72 × 10⁷ Pa en un cilindro de volumen 43.8 L. ¿Cuántos globos pueden inflarse a un volumen de 4.00 L con esa cantidad de helio? Supón que la presión dentro de los globos es de 1.01 × 10⁵ Pa y la temperatura en el cilindro y los globos es de 25.0 °C.

26. Según http://hyperphysics.phy-astr.gsu.edu/hbase/solar/venusenv.html, la atmósfera de Venus es aproximadamente 96.5% de CO₂ y 3.5% de N₂ en volumen. En la superficie, donde la temperatura es de aproximadamente 750 K y la presión es de aproximadamente 90 atm, ¿cuál es la densidad de la atmósfera?

27. Un costoso sistema de vacío puede alcanzar una presión tan baja como 1.00 × 10^-7 N/m² a 20.0 °C. ¿Cuántas moléculas hay en un centímetro cúbico a esta presión y temperatura?

28. La densidad numérica N/V de las moléculas de gas en un lugar determinado en el espacio sobre nuestro planeta es de aproximadamente 1.00 × 10¹ m^-3, y la presión es de 2.75 × 10^-10 N/m² en este espacio. ¿Cuál es la temperatura allí?

29. Un neumático de bicicleta contiene 2.00 L de gas a una presión absoluta de 7.00 × 10⁵ N/m² y una temperatura de 18.0 °C. ¿Cuál será su presión si dejas salir una cantidad de aire que tiene un volumen de 100 cm³ a presión atmosférica? Supongamos que la temperatura y el volumen de los neumáticos permanecen constantes.

30. En una demostración común, una botella se calienta y se tapona con un huevo duro que es un poco más grande que el cuello de la botella. Cuando se enfría la botella, la diferencia de presión entre el interior y el exterior obliga al huevo a entrar en la botella. Supongamos que la botella tiene un volumen de 0.500 L y la temperatura en su interior se eleva a 80.0 °C mientras que la presión permanece constante a 1.00 atm porque la botella está abierta. (a) ¿Cuántos moles de aire hay adentro? (b) Ahora el huevo se pone en su lugar, sellando la botella. ¿Cuál es la presión manométrica en el interior después de que el aire se enfría de nuevo a la temperatura ambiente de 25 °C, pero antes de que el huevo se introduzca en la botella?

31. Un cilindro de gas a alta presión contiene 50.0 L de gas tóxico a una presión de 1.40 × 107N / m2 y una temperatura de 25.0 ° C. El cilindro se enfría a la temperatura del hielo seco (-78,5 ° C) para reducir la tasa de fugas y la presión, de modo que pueda repararse con seguridad. (a) ¿Cuál es la presión final en el tanque, suponiendo una cantidad insignificante de fugas de gas mientras se enfría y que no hay cambio de fase? (b) ¿Cuál es la presión final si escapa una décima parte del gas? (c) ¿A qué temperatura debe enfriarse el tanque para reducir la presión a 1.00 atm (suponiendo que el gas no cambia de fase y que no hay fugas durante el enfriamiento)? (d) ¿Parece que la refrigeración del tanque como en la parte (c) es una solución práctica? 32. Encuentre la cantidad de moles en 2.00 L de gas a 35.0 ° C y bajo 7.41 × 10⁷ N/m² de presión.

33. Calcula la profundidad a la que la cantidad de bolas de tenis de mesa de Avogadro cubriría la Tierra. Cada bola tiene un diámetro de 3.75 cm. Asume que el espacio entre las bolas agrega un 25.0% extra a su volumen y asume que no son aplastados por su propio peso.

34. (a) ¿Cuál es la presión manométrica en un neumático para automóvil a 25.0 °C que contiene 3.60 mol de gas en un volumen de 30.0 l? (b) ¿Cuál será su presión manométrica si agrega 1.00 L de gas originalmente a presión atmosférica y 25.0 °C? Supongamos que la temperatura permanece a 25.0 °C y el volumen permanece constante.

2.2 Presión, temperatura y velocidad RMS

En los problemas de esta sección, supón que todos los gases son ideales.

35. Una persona golpea una pelota de tenis con una masa de 0.058 kg contra una pared. El componente promedio de la velocidad de la bola perpendicular a la pared es 11 m/s, y la pelota golpea la pared cada 2.1 s en promedio, rebotando con la componente de velocidad perpendicular opuesta. (a) ¿Cuál es la fuerza promedio ejercida sobre la pared? (b) Si la parte de la pared que golpea la persona tiene un área de 3.0 m², ¿cuál es la presión promedio en esa área?

36. Una persona está en una habitación cerrada (una cancha de ráquetbol) con V = 453 m³ golpeando una pelota (m = 42.0g) alrededor al azar sin pausas. La energía cinética promedio de la pelota es 2.30 J. (a) ¿Cuál es el valor promedio de v_2x? ¿Importa qué dirección tomes para ser x? (b) Aplicando los métodos de este capítulo, ¿encuentra la presión promedio en las paredes? (c) Aparte de la presencia de una sola "molécula" en este problema, ¿cuál es la suposición principal en presión, temperatura y velocidad RMS que no se aplica aquí?

37. Cinco ciclistas recorren las siguientes velocidades: 5.4 m/s, 5.7 m/s, 5.8 m/s, 6.0 m/s, y 6.5 m/s. (a) ¿Cuál es su velocidad promedio? (b) ¿Cuál es su velocidad rms?

38. Algunas bombillas incandescentes están llenas de gas argón. ¿Cuál es la v_rms para los átomos de argón cerca del filamento, suponiendo que su temperatura es de 2500 K?

39. Las velocidades moleculares típicas (v_rms) son grandes, incluso a bajas temperaturas. ¿Cuál es la v_rms para los átomos de helio a 5.00 K, menos de un grado por encima de la temperatura de licuefacción del helio?

40. ¿Cuál es la energía cinética promedio en julios de átomos de hidrógeno en la superficie de 5500 °C del Sol? (b) ¿Cuál es la energía cinética promedio de los átomos de helio en una región de la corona solar donde la temperatura es de 6.00 × 10⁵ K?

41. ¿Cuál es la relación de la energía cinética de traslación promedio de una molécula de nitrógeno a una temperatura de 300 K a la energía potencial gravitacional de un sistema de molécula de nitrógeno-Tierra en el techo de una habitación de 3 m de altura con respecto al mismo sistema con la molécula en el piso?

42. ¿Cuál es la energía cinética de traslación total de las moléculas de aire en una sala de volumen de 23 m³ si la presión es de 9,5 × 10⁴ Pa (la habitación tiene una elevación bastante alta) y la temperatura es de 21 °C? ¿Hay algún elemento de datos innecesario para la solución?

43. El producto de la presión y el volumen de una muestra de gas de hidrógeno a 0.00 °C es 80.0 J. (a) ¿Cuántos moles de hidrógeno hay? (b) ¿Cuál es la energía cinética de traslación promedio de las moléculas de hidrógeno? (c) ¿Cuál es el valor del producto de presión y volumen a 200 °C?

44. ¿Cuál es la presión manométrica dentro de un tanque de 4,86 ​​× 10⁴ mol de nitrógeno comprimido con un volumen de 6,56 m³ si la velocidad eficaz es de 514 m/s?

45. Si la velocidad rms de las moléculas de oxígeno dentro de un refrigerador de volumen 22.0 pies³ es 465 m/s, ¿cuál es la presión parcial del oxígeno? Hay 5,71 moles de oxígeno en el refrigerador, y la masa molar de oxígeno es 32,0 g/mol.

46. ​​La velocidad de escape de cualquier objeto de la Tierra es de 11.1 km/s. ¿A qué temperatura las moléculas de oxígeno (la masa molar es igual a 32,0 g/mol) tienen una velocidad media cuadrática v_rms igual a la velocidad de escape de la Tierra de 11,1 km/s?

47. La velocidad de escape desde la Luna es mucho más pequeña que la de la Tierra, solo 2.38 km/s. ¿A qué temperatura las moléculas de hidrógeno (la masa molar es igual a 2.016 g/mol) tienen una velocidad media cuadrática v_rms igual a la velocidad de escape de la Luna?

48. La fusión nuclear, la fuente de energía del Sol, las bombas de hidrógeno y los reactores de fusión, se produce mucho más fácilmente cuando la energía cinética promedio de los átomos es alta, es decir, a altas temperaturas. Supongamos que quieres que los átomos en su experimento de fusión tengan energías cinéticas promedio de 6.40 × 10^-14 J. ¿Qué temperatura es necesaria?

49. Supongamos que la velocidad típica (v_rms) de las moléculas de dióxido de carbono (la masa molar es 44.0 g/mol) en una llama se encuentra en 1350 m/s. ¿Qué temperatura indica esto?

50. (a) Las moléculas de hidrógeno (la masa molar es igual a 2.016 g/mol) tienen v_rms igual a 193 m/s. ¿Cual es la temperatura? (b) Gran parte del gas cerca del Sol es hidrógeno atómico (H en lugar de H₂). Su temperatura tendría que ser de 1.5 × 10⁷ K para que la velocidad rms, v_rms, sea igual a la velocidad de escape del sol. ¿Cuál es esa velocidad?

51. Hay dos isótopos importantes de uranio, ²³⁵U y ²³⁸U; estos isótopos son casi idénticos químicamente pero tienen diferentes masas atómicas. Solo ²³⁵U es muy útil en reactores nucleares. Separar los isótopos se llama enriquecimiento de uranio (y suele aparecer en las noticias al momento de escribir esto, debido a la preocupación de que algunos países estén enriqueciendo uranio con el objetivo de fabricar armas nucleares). Una de las técnicas de enriquecimiento, difusión de gases, se basa en las diferentes velocidades moleculares del gas de hexafluoruro de uranio, UF₆. (a) Las masas molares de ²³⁵U y ²³⁸UF₆ son 349.0 g/mol y 352.0 g/mol, respectivamente. ¿Cuál es la razón de sus velocidades típicas v_rms? (b) ¿A qué temperatura diferirían sus velocidades típicas en 1,00 m/s? (c) ¿Tus respuestas en este problema implican que esta técnica puede ser difícil?

52. La presión parcial del dióxido de carbono en los pulmones es de alrededor de 470 Pa cuando la presión total en los pulmones es de 1.0 atm. ¿Qué porcentaje de las moléculas de aire en los pulmones es dióxido de carbono? Compara tu resultado con el porcentaje de dióxido de carbono en la atmósfera, alrededor de 0.033%.

53. El aire seco consiste en aproximadamente 78% de nitrógeno, 21% de oxígeno y 1% de argón por mol, con trazas de otros gases. Un tanque de aire comprimido seco tiene un volumen de 1.76 pies cúbicos a una presión manométrica de 2200 libras por pulgada cuadrada y una temperatura de 293 K. ¿Cuánto oxígeno contiene en moles?

54. (a) Utilizando datos del problema anterior, encuentra la masa de nitrógeno, oxígeno y argón en 1 mol de aire seco. La masa molar de N₂ es 28.0 g/mol, la de O₂ es 32.0 g/mol y la de argón es 39.9 g/mol. (b) El aire seco se mezcla con pentano (C₅H₁₂, masa molar 72,2 g/mol), un constituyente importante de la gasolina, en una relación aire-combustible de 15:1 en masa (aproximadamente típico para los motores de los automóviles). Encuentra la presión parcial de pentano en esta mezcla a una presión total de 1.00 atm.

55. (a) Dado que el aire contiene 21% de oxígeno, encuentra la presión atmosférica mínima que proporcione una presión parcial de oxígeno relativamente segura de 0.16 atm. (b) ¿Cuál es la presión mínima que da una presión parcial de oxígeno por encima del nivel rápidamente fatal de 0.06 atm? (c) La presión del aire en la cima del Monte Everest (8848 m) es 0.334 atm. ¿Por qué algunas personas lo subieron sin oxígeno, mientras que algunos que lo han intentado, a pesar de haber entrenado a gran altura, tuvieron que retroceder?

56. (a) Si la presión parcial del vapor de agua es de 8.05 torr, ¿cuál es el punto de rocío? (760 torr = 1atm = 101,325 Pa) (b) En un día cálido cuando la temperatura del aire es de 35 °C y el punto de rocío es de 25 °C, ¿cuál es la presión parcial del agua en el aire y la humedad relativa?

2.3 Capacidad de calor y equipartición de energía

57. Para dar un átomo de helio, el momento angular distinto de cero requiere aproximadamente 21.2 eV de energía (es decir, 21.2 eV es la diferencia entre las energías del estado más bajo de energía o fundamental y el estado de energía más baja con momento angular). El electrón-voltio o eV se define como 1.60 × 10^-19 J. Encuentra la temperatura T donde esta cantidad de energía es igual a k_BT/2. ¿Esto explica por qué podemos ignorar la energía de rotación del helio para la mayoría de los propósitos? (Los resultados para otros gases monoatómicos y para gases diatómicos que giran alrededor del eje que conecta los dos átomos tienen órdenes de magnitud comparables).

58. (a) ¿Cuánto calor se debe agregar para elevar la temperatura de 1.5 mol de aire de 25.0 °C a 33.0 °C a volumen constante? Supongamos que el aire es completamente diatómico. (b) Repite el problema para la misma cantidad de moles de xenón, Xe.

59. Un recipiente sellado y rígido de 0.560 mol de un gas ideal desconocido a una temperatura de 30.0 °C se enfría a -40.0 °C. En el proceso, se eliminan 980 J de calor del gas. ¿El gas es monoatómico, diatómico o poliatómico?

60. Una muestra de gas de neón (Ne, masa molar M = 20,2 g/mol) a una temperatura de 13,0 °C se coloca en un recipiente de acero con una masa de 47,2 g que está a una temperatura de -40,0 °C. La temperatura final es -28.0 °C (No se intercambia calor con el entorno, y puedes despreciar cualquier cambio en el volumen del contenedor) ¿Cuál es la masa de la muestra de neón?

61. Un recipiente de acero de 135 g de masa contiene 24,0 g de amoníaco, NH₃, que tiene una masa molar de 17,0 g/mol. El contenedor y el gas están en equilibrio a 12.0 °C. ¿Cuánto calor se tiene que eliminar para alcanzar una temperatura de -20,0 °C? Ignora el cambio en el volumen del acero.

62. Una habitación sellada tiene un volumen de 24 m³. Está lleno de aire, que puede suponerse que es diatómico, a una temperatura de 24 °C y una presión de 9.83 × 10⁴ Pa. Un bloque de 1.00 kg de hielo en su punto de fusión se coloca en la habitación. Supongamos que las paredes de la sala no transmiten calor. ¿Cuál es la temperatura de equilibrio?

63. Heliox, una mezcla de helio y oxígeno, a veces se administra a pacientes del hospital que tienen problemas para respirar, ya que la baja masa de helio facilita la respiración en comparación con el aire. Supongamos que el helio a 25 °C se mezcla con oxígeno a 35 °C para formar una mezcla que es 70% de helio por mol. ¿Cuál es la temperatura final? Ignora cualquier flujo de calor hacia o desde el entorno, y supón que el volumen final es la suma de los volúmenes iniciales.

64. Los buceadores profesionales a veces usan heliox, que consiste en 79% de helio y 21% de oxígeno por mol. Supongamos que un tanque de buceo perfectamente rígido con un volumen de 11 L contiene heliox a una presión absoluta de 2.1 × 10⁷ Pa a una temperatura de 31 °C. (a) ¿Cuántos moles de helio y cuántos moles de oxígeno hay en el tanque? (b) El buceador baja a un punto donde la temperatura del mar es de 27 °C mientras usa una cantidad insignificante de la mezcla. A medida que el gas en el tanque alcanza esta nueva temperatura, ¿cuánto calor se elimina de ella?

65. En las carreras de autos, una de las ventajas de mezclar óxido nitroso líquido (N₂O) con aire es que la ebullición del "nitroso" absorbe el calor latente de vaporización y enfría el aire y finalmente la mezcla aire-combustible, permitiendo más mezcla combustible-aire para entrar en cada cilindro. Como una mirada muy aproximada a este proceso, supongamos que 1.0 mol de gas de óxido nitroso en su punto de ebullición, -88 °C, se mezcla con 4.0 mol de aire (supuestamente diatómico) a 30 °C. ¿Cuál es la temperatura final de la mezcla? Use la capacidad de calor medida de N₂O a 25 °C, que es 30.4 J/ mol °C (La principal ventaja del óxido nitroso es que consiste en 1/3 de oxígeno, que es más de lo que contiene el aire, por lo que suministra más oxígeno para quemar el combustible. Otra ventaja es que su descomposición en nitrógeno y oxígeno libera energía en el cilindro).

2.4 Distribución de velocidades moleculares

66. En una muestra de sulfuro de hidrógeno (M = 34.1 g/mol) a una temperatura de 3.00 × 10² K, estima la relación del número de moléculas que tienen velocidades muy cercanas a v_rms al número que tienen velocidades muy cercanas a 2v_rms.

67. Usando la aproximación ∫_v1v1+Δvf(v)dv ≈ f(v₁)Δv para Δv pequeña, estima la fracción de moléculas de nitrógeno a una temperatura de 3.00 × 10² K que tienen velocidades entre 290 m/s y 291 m/s.

68. Utilizando el método del problema anterior, estime la fracción de moléculas de óxido nítrico (NO) a una temperatura de 250 K que tenga energías entre 3.45 × 10^-21 J y 3.50 × 10^-21 J.

69. Contando cuadrados en la siguiente figura, estima la fracción de átomos de argón a T = 300 K que tienen velocidades entre 600 m/s y 800 m/s. La curva está correctamente normalizada. El valor de un cuadrado es su longitud medida en el eje x por su altura medida en el eje y, con las unidades dadas en esos ejes.



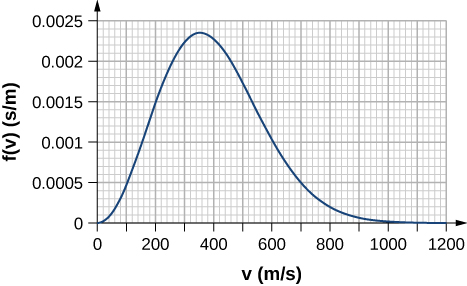
70. Utilizando un método de integración numérica como la regla de Simpson, encuentra la fracción de moléculas en una muestra de gas oxígeno a una temperatura de 250 K que tenga velocidades entre 100 m/s y 150 m/s. La masa molar de oxígeno (O₂) es 32.0 g/mol. Una precisión de dos dígitos significativos es suficiente.

71. Halla (a) la velocidad más probable, (b) la velocidad promedio, y (c) la velocidad rms para las moléculas de nitrógeno a 295 K.

72. Repite el problema anterior para las moléculas de nitrógeno a 2950 K.

73. ¿A qué temperatura es la velocidad promedio de las moléculas de dióxido de carbono (M = 44.0 g/mol) 510 m/s?

74. La velocidad más probable para las moléculas de un gas a 296 K es 263 m/s. ¿Cuál es la masa molar del gas? (Tal vez desees averiguar cuál es el gas probable).

75. a) ¿A qué temperatura tienen las moléculas de oxígeno la misma velocidad promedio que los átomos de helio (M = 4.00 g/mol) a 300 K? b) ¿Cuál es la respuesta a la misma pregunta sobre las velocidades más probables? c) ¿Cuál es la respuesta a la misma pregunta sobre las velocidades rms?

Problemas Adicionales

76. En el espacio profundo entre las galaxias, la densidad de las moléculas (que son en su mayoría átomos individuales) puede ser tan baja como 10⁶ átomos/m³, y la temperatura es una frígida de 2.7 K. ¿Cuál es la presión? (b) ¿Qué volumen (en m³) está ocupado por 1 mol de gas? (c) Si este volumen es un cubo, ¿cuál es la longitud de sus lados en kilómetros?

77. (a) Encuentra la densidad en unidades SI de aire a una presión de 1.00 atm y una temperatura de 20 °C, suponiendo que el aire es 78% N₂, 21% O₂, y 1% Ar, (b) Encuentra la densidad de la atmósfera en Venus, suponiendo que es 96% de CO₂ y 4% de N₂, con una temperatura de 737 K y una presión de 92.0 atm.

78. El aire dentro de un globo de aire caliente tiene una temperatura de 370 K y una presión de 101,3 kPa, la misma que la del aire exterior. Usando la composición del aire como 78% N₂, 21% O₂ y 1% Ar, encuentra la densidad del aire dentro del globo.

79. Cuando una burbuja de aire asciende desde el fondo hasta la parte superior de un lago de agua dulce, su volumen aumenta en un 80%. Si las temperaturas en la parte inferior y superior del lago son de 4.0 y 10 °C, respectivamente, ¿qué tan profundo es el lago?

80. (a) Usa la ecuación del gas ideal para estimar la temperatura a la que 1.00 kg de vapor (masa molar M = 18.0 g/mol) a una presión de 1.50 × 10⁶ Pa ocupa un volumen de 0.220 m³. (b) Las constantes de van der Waals para el agua son a = 0.5537 Pa • m⁶/mol² y b = 3.049 × 10^-5 m³/mol. Usa la ecuación de estado de Van der Waals para estimar la temperatura en las mismas condiciones. (c) La temperatura real es 779 K. ¿Qué estimación es mejor?

81. Un proceso para descafeinar el café utiliza dióxido de carbono (M = 44.0 g/mol) a una densidad molar de alrededor de 14,600 mol/m³ y una temperatura de alrededor de 60 °C. (a) ¿Es el CO₂ un líquido sólido, líquido, gaseoso o supercrítico en esas condiciones? (b) Las constantes de van der Waals para el dióxido de carbono son a = 0.3658 Pa • m⁶/mol² y b = 4.286 × 10^-5m³/mol. Usando la ecuación de van der Waals, calcula la presión del CO₂ a esa temperatura y densidad.

82. En un día de invierno cuando la temperatura del aire es de 0 °C, la humedad relativa es del 50%. El aire exterior entra y se calienta a una temperatura ambiente de 20 °C. Cuál es la humedad relativa del aire dentro de la habitación (¿Este problema muestra por qué el aire interior es tan seco en invierno?)

83. En un día cálido, cuando la temperatura del aire es de 30 °C, una lata de metal se enfría lentamente añadiendo trozos de hielo al agua líquida. La condensación aparece por primera vez cuando la lata alcanza los 15 °C. ¿Cuál es la humedad relativa del aire?

84. (a) La gente a menudo piensa que el aire húmedo es "pesado". Compara las densidades del aire con 0% de humedad relativa y 100% de humedad relativa cuando ambas están a 1 atm y 30 °C. Supongamos que el aire seco es un gas ideal compuesto de moléculas con una masa molar de 29.0 g/mol y el aire húmedo es el mismo gas mezclado con vapor de agua. (b) Como se discutió en el capítulo sobre las aplicaciones de las leyes de Newton, la resistencia del aire que sienten los proyectiles como pelotas de béisbol y pelotas de golf es aproximadamente F_D = CρAv²/2, donde ρ es la densidad másica del aire, A es el área seccional del proyectil, y C es el coeficiente de arrastre del proyectil. Para una presión de aire fija, describe cualitativamente cómo cambia el alcance de un proyectil con la humedad relativa. (c) Cuando llega una tormenta eléctrica, generalmente la humedad es alta y la presión del aire es baja. ¿Estas condiciones dan una ventaja o desventaja a los bateadores locales?

85. La trayectoria libre media para el helio a una determinada temperatura y presión es de 2,10 × 10^-7 m. El radio de un átomo de helio se puede tomar como 1.10 × 10^-11 m. ¿Cuál es la medida de la densidad del helio en esas condiciones (a) en moléculas por metro cúbico y (b) en moles por metro cúbico?

86. El camino libre medio para el metano a una temperatura de 269 K y una presión de 1,11 × 10⁵ Pa es de 4,81 × 10^-8 m. Encuentra el radio efectivo r de la molécula de metano.

87. En el capítulo sobre mecánica de fluidos, la ecuación de Bernoulli para el flujo de fluidos incompresibles se explicó en términos de cambios que afectan a un pequeño volumen dV de fluido. Dichos volúmenes son una idea fundamental en el estudio del flujo de fluidos compresibles, como los gases también. Para que se apliquen las ecuaciones de hidrodinámica, la trayectoria libre media debe ser mucho menor que el tamaño lineal de dicho volumen, a ≈ dV₁/3. Para el aire en la estratosfera a una temperatura de 220 K y una presión de 5,8 kPa, ¿qué tan grande debe ser para que sea 100 veces la trayectoria libre medio? Tome el radio efectivo de las moléculas de aire para que sea 1.88 × 10^-11 m, que es aproximadamente correcto para N₂.

88. Encuentra el número total de colisiones entre moléculas en 1.00 s en 1.00 L de gas nitrógeno a temperatura y presión estándar (0 °C, 1.00 atm). Use 1.88 × 10-10m como el radio efectivo de una molécula de nitrógeno. (El número de colisiones por segundo es el recíproco del tiempo de colisión). Ten en cuenta que cada colisión involucra dos moléculas, por lo que si una molécula colisiona una vez en un período de tiempo determinado, la colisión de la molécula que golpeó no puede contarse.

89. (a) Estima la capacidad calorífica específica del sodio de la Ley de Dulong y Petit. La masa molar de sodio es 23.0 g/mol. (b) ¿Cuál es el porcentaje de error de su estimación del valor conocido, 1230 J/kg • °C?

90. Un envase sellado y perfectamente aislado contiene 0,630 moles de aire a 20,0 °C y una barra de agitación de hierro de 40,0 g de masa. La barra de agitación es impulsada magnéticamente a una energía cinética de 50.0 J y permite disminuir la velocidad por la resistencia del aire. ¿Cuál es la temperatura de equilibrio?

91. Halla la relación f(v_p)/f(v_rms) para gas de hidrógeno (M = 2.02 g/mol) a una temperatura de 77.0 K.

92. Resultados irracionales. (a) Encuentra la temperatura de 0.360 kg de agua, modelada como un gas ideal, a una presión de 1.01 × 10⁵ Pa si tiene un volumen de 0.615 m³. (b) ¿Qué es irracional acerca de esta respuesta? ¿Cómo podrías obtener una mejor respuesta?

93. Resultados irracionales. (a) Encuentra la velocidad promedio del sulfuro de hidrógeno, H₂S, moléculas a una temperatura de 250 K. Su masa molar es de 31.4 g/mol (b) El resultado no es muy irrazonable, pero ¿por qué es menos confiable que aquellos para decir, neón o nitrógeno?

Problemas Desafío

94. Un dispensador hermético para agua potable mide 25 cm × 10 cm en dimensiones horizontales y 20 cm de alto. Tiene un grifo de volumen insignificante que se abre al nivel de la parte inferior del dispensador. Inicialmente, contiene agua a un nivel de 3.0 cm desde la parte superior y aire a la presión ambiente, 1.00 atm, desde allí hasta la parte superior. Cuando se abre el grifo, el agua fluirá hasta que la presión manométrica en la parte inferior del dispensador, y por lo tanto en la apertura del grifo, sea 0. ¿Qué volumen de agua sale? Supongamos que la temperatura es constante, el dispensador es perfectamente rígido y el agua tiene una densidad constante de 1000 kg/m³.

95. Ocho coches de choque, cada uno con una masa de 322 kg, se deslizan en una sala de 21,0 m de largo y 13,0 m de ancho. No tienen controladores, por lo que solo andan por su cuenta. La velocidad efectiva de los autos es de 2.50 m/s. Repitiendo los argumentos de presión, temperatura y velocidad RMS, encuentra la fuerza promedio por unidad de longitud (análoga a la presión) que los autos ejercen en las paredes.

96. Verifique que v_p = √2k_BT/m/.

97. Verifica la ecuación de normalización ∫_0∞f(v)dv = 1. Al hacer la integral, primero realiza la sustitución u = √m/2k_BT/ = v/v_p. Esta transformación de "escalado" te brinda todas las características de la respuesta, excepto la integral, que es un factor numérico adimensional. Necesitarás la fórmula ∫_0∞x²e^-x2dx = √π/4 para encontrar el factor numérico y verificar la normalización.

98. Verifica que v_ = √(8/π)(k_BT/m)/. Haz la misma transformación de escala que en el problema anterior.

99. Verifica que v_rms = √v²_/ = √3k_BT/m/.