Preguntas y problemas - Capítulo I

Preguntas conceptuales

1.1 Temperatura y equilibrio térmico

1. ¿Qué significa decir que dos sistemas están en equilibrio térmico?

2. Dá un ejemplo en el cual A tenga algún tipo de relación de equilibrio no térmico con B, y B tenga la misma relación con C, pero A no tenga esa relación con C.

1.2 Termómetros y escalas de temperatura

3. Si se permite que un termómetro se equilibre con el aire y un vaso de agua no esté en equilibrio con el aire, ¿qué le sucederá al termómetro cuando se lo coloca en el agua?

4. Dá un ejemplo de una propiedad física que varía con la temperatura y describe cómo se usa para medir la temperatura.

1.3 Expansión térmica

5. Verter agua fría en vidrio caliente o utensilios de cocina de cerámica puede romperla fácilmente. ¿Qué causa la ruptura? Explica por qué Pyrex®, un vidrio con un pequeño coeficiente de expansión lineal, es menos susceptible.

6. Un método para obtener un ajuste apretado, por ejemplo, de una clavija de metal en un agujero en un bloque de metal, es fabricar la clavija un poco más grande que el agujero. La clavija se inserta cuando está a una temperatura diferente que el bloque. ¿Debería el bloque estar más caliente o más frío que la clavija durante la inserción? Explica tu respuesta.

7. ¿Realmente ayuda correr agua caliente sobre una tapa de metal apretada en un frasco de vidrio antes de tratar de abrirlo? Explica tu respuesta.

8. Cuando se coloca un termómetro de alcohol frío en un líquido caliente, la columna de alcohol baja un poco antes de subir. Explicar por qué.

9. Calcula la longitud de una varilla de 1 metro de un material con coeficiente de expansión térmica α cuando la temperatura se eleve de 300 K a 600 K. Tomando la respuesta como la nueva longitud inicial, encuentra la longitud después de que la varilla se enfríe nuevamente a 300 K. ¿Tu respuesta es de 1 metro? ¿Debería ser? ¿Cómo puedes explicar el resultado que obtuviste?

10. Observando las grandes tensiones que puede causar la expansión térmica, un inventor de armas aficionado decide usarla para fabricar un nuevo tipo de arma. Él planea meter una bala contra una varilla de aluminio dentro de un tubo de invar cerrado. Cuando calienta el tubo, la varilla se expandirá más que el tubo y se acumulará una fuerza muy fuerte. Luego, por un método aún por determinar, abrirá el tubo en una fracción de segundo y permitirá que la fuerza de la barra lance la bala a una velocidad muy alta. ¿Qué está pasando por alto?

1.4 Transferencia de calor, calor específico y calorimetría

11. ¿Cómo se relaciona la transferencia de calor con la temperatura?

12. Describe una situación en la que se produce la transferencia de calor.

13. Cuando el calor se transfiere a un sistema, ¿la energía se almacena en forma de calor? Explicar brevemente.

14. Los frenos en un automóvil aumentan la temperatura en ΔT cuando el automóvil se detiene a partir de una velocidad v. ¿Cuánto mayor sería ΔT si el automóvil inicialmente tuviera el doble de velocidad? Puedes suponer que el automóvil se detiene lo suficientemente rápido como para que no se transfiera el calor de los frenos.

1.5 Cambios de fase

15. Una olla a presión contiene agua y vapor en equilibrio a una presión mayor que la presión atmosférica. ¿Cómo aumenta esta mayor presión la velocidad de cocción?

16. Como se muestra a continuación, ¿cuál es el diagrama de fases para el dióxido de carbono, cuál es la presión de vapor del dióxido de carbono sólido (hielo seco) a -78.5 °C? (Ten en cuenta que los ejes en la figura son no lineales y el gráfico no está a escala).



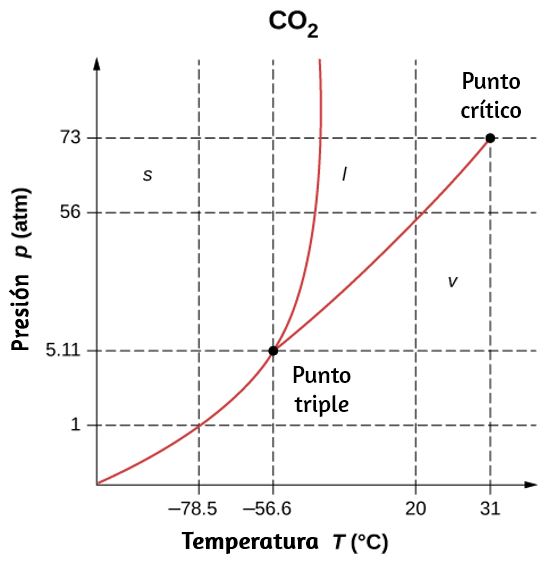
17. ¿Puede el dióxido de carbono licuarse a temperatura ambiente (20 °C)? ¿Si es así, cómo? ¿Si no, porque no? (Ver el diagrama de fases en el problema anterior).

18. ¿Cuál es la distinción entre gas y vapor?

19. La transferencia de calor puede causar cambios de temperatura y fase. ¿Qué más puede causar estos cambios?

20. ¿De qué manera el calor latente de fusión del agua ayuda a disminuir la temperatura del aire, evitando que las temperaturas caigan significativamente por debajo de 0 °C, en las cercanías de grandes masas de agua?

21. ¿Cuál es la temperatura del hielo inmediatamente después de que se forma con agua helada?

22. Si colocas hielo a 0 °C en agua a 0 °C en un recipiente aislado, ¿cuál será el resultado neto? ¿Habrá menos hielo y más agua líquida, o más hielo y menos agua líquida, o las cantidades permanecerán iguales?

23. ¿Qué efecto tiene la condensación en un vaso de agua helada en la velocidad a la que se derrite el hielo? ¿La condensación acelerará el proceso de fusión o lo desacelerará?

24. En Miami, Florida, que tiene un clima muy húmedo y numerosos cuerpos de agua cerca, es inusual que las temperaturas se eleven por encima de los 38 °C (100 °F). Sin embargo, en el clima desértico de Phoenix, Arizona, las temperaturas superan casi todos los días en julio y agosto. Explica cómo la evaporación del agua ayuda a limitar las altas temperaturas en climas húmedos.

25. En invierno, a menudo es más cálido en San Francisco que en Sacramento, 150 km hacia el interior. En verano, casi siempre es más caluroso en Sacramento. Explica cómo los cuerpos de agua que rodean a San Francisco moderan sus temperaturas extremas.

26. Los alimentos liofilizados se han deshidratado en el vacío. Durante el proceso, la comida se congela y debe calentarse para facilitar la deshidratación. Explica cómo el vacío acelera la deshidratación y por qué la comida se congela como resultado.

27. En una demostración de aula de física, un instructor infla un globo por la boca y luego lo enfría en nitrógeno líquido. Cuando está frío, el globo encogido tiene una pequeña cantidad de líquido azul claro, así como algunos cristales parecidos a la nieve. A medida que se calienta, el líquido hierve, y parte de los cristales sublimados, con algunos cristales que permanecen por un tiempo y luego producen un líquido. Identifica el líquido azul y los dos sólidos en el globo frío. Justifique sus identificaciones usando los datos de la Tabla 1.4.

1.6 Mecanismos de transferencia de calor

28. ¿Cuáles son los principales métodos de transferencia de calor desde el núcleo caliente de la Tierra hasta su superficie? ¿De la superficie de la Tierra al espacio exterior?

29. Cuando nuestros cuerpos se calientan demasiado, responden sudando e incrementando la circulación sanguínea a la superficie para transferir la energía térmica lejos del núcleo. ¿Qué efecto tendrán esos procesos en una persona en un jacuzzi de 40.0 °C?

30. A continuación se muestra un dibujo recortado de una botella termo (también conocida como frasco Dewar), que es un dispositivo diseñado específicamente para ralentizar todas las formas de transferencia de calor. Explica las funciones de las distintas partes, como el vacío, el plateado de las paredes, el cuello de vidrio largo de pared delgada, el soporte de goma, la capa de aire y el tapón.



31. Algunas estufas eléctricas tienen una superficie plana de cerámica con elementos calentadores ocultos debajo. Una olla colocada sobre un elemento calefactor se calentará, mientras que la superficie a solo unos centímetros de distancia es segura para tocar. ¿Por qué la cerámica, con una conductividad menor que la de un metal pero mayor que la de un buen aislante, es una opción ideal para la parte superior de la estufa?

32. La ropa blanca holgada que cubre la mayor parte del cuerpo, que se muestra a continuación, es ideal para los habitantes del desierto, tanto en el sol caliente como durante las noches frías. Explica cómo esa ropa es ventajosa durante el día y la noche.



33. Una forma de hacer que una chimenea sea más eficiente en cuanto a la energía, es hacer circular el aire de la habitación por el exterior de la caja de fuego y volver a la habitación. Detallar los métodos de transferencia de calor involucrados.

34. En noches frías y claras, los caballos dormirán bajo la cubierta de grandes árboles. ¿Cómo les ayuda esto a mantenerse calientes?

35. Al observar un circo durante el día en una carpa grande de color oscuro, se percibe una importante transferencia de calor desde la tienda. Explica por qué ocurre esto.

36. Los satélites diseñados para observar la radiación del espacio oscuro frío (3 K) tienen sensores que están sombreados por el sol, la tierra y la luna y se enfrían a temperaturas muy bajas. ¿Por qué los sensores deben estar a baja temperatura?

37. ¿Por qué los termómetros que se usan en las estaciones meteorológicas están protegidos del sol? ¿Qué mide un termómetro si está protegido del sol? ¿Qué mide si no lo es?

38. Poner una tapa en una olla hirviendo reduce en gran medida la transferencia de calor necesaria para mantenerla hirviendo. Explicar por qué.

39. Tu casa estará vacía por un tiempo cuando hace frío y quieres ahorrar energía y dinero. ¿Deberías bajar el termostato al nivel más bajo que protegerá la casa de daños como la congelación de las tuberías o dejarlo a la temperatura normal? (Si no te gusta regresar a una casa fría, imagina que un temporizador controla el sistema de calefacción para que la casa esté caliente cuando regreses). Explica tu respuesta.

40. Verter café en una taza sin tapa, con la intención de beberlo 5 minutos más tarde. Puedes agregar crema cuando viertes la taza o justo antes de beberla (La crema está a la misma temperatura. Suponga que la crema y el café entran en equilibrio térmico entre sí muy rápidamente), ¿De qué manera te dará café más caliente? ¿Qué característica de esta pregunta es diferente de la anterior?

41. Asar a la parrilla es un método de cocción por radiación, que produce resultados algo diferentes de la cocción por conducción o por convección. Una llama de gas o elemento de calentamiento eléctrico produce una temperatura muy alta cerca de la comida y encima de ella. ¿Por qué la radiación es el método de transferencia de calor dominante en esta situación?

42. En una fría mañana de invierno, ¿por qué el metal de una bicicleta se siente más frío que la madera de un porche?

Problemas

1.2 Termómetros y escalas de temperatura

43. Mientras viajas fuera de tu país, te sientes enfermo. Un compañero te consigue un termómetro, que dice que tu temperatura es de 39. ¿Qué escala tiene? ¿Cuál es tu temperatura Fahrenheit? ¿Deberías buscar ayuda médica?

44. ¿Cuáles son las siguientes temperaturas en la escala Kelvin? (a) 68.0 °F, una temperatura interior a veces recomendada para la conservación de energía en invierno (b) 134 °F, una de las temperaturas atmosféricas más altas jamás registradas en la Tierra (Death Valley, California, 1913) (c) 9890 °F, temperatura de la superficie del sol.

45. (a) Supón que un frente frío sopla en tu localidad y baja la temperatura en 40.0 grados Fahrenheit. ¿Cuántos grados Celsius disminuye la temperatura cuando disminuye en 40.0 °F? (b) Demuestra que cualquier cambio en la temperatura en grados Fahrenheit es nueve quintos del cambio en grados Celsius.

46. ​​Un artículo de The Associated Press sobre el cambio climático dijo: "Parte de la desaparición de la plataforma de hielo fue probablemente en épocas en que el planeta estaba entre 36 grados Fahrenheit (2 grados Celsius) y 37 grados Fahrenheit (3 grados Celsius) más cálido que hoy". ¿Qué error cometió el periodista?

47. (a) ¿A qué temperatura tienen las escalas Fahrenheit y Celsius el mismo valor numérico? (b) ¿A qué temperatura tienen las escalas Fahrenheit y Kelvin el mismo valor numérico?

48. Una persona que toma la lectura de la temperatura en un congelador en grados Celsius comete dos errores: primero omite el signo negativo y luego piensa que la temperatura es Fahrenheit. Es decir, la persona lee -x °C como x °F. Por extraño que parezca, el resultado es la temperatura Fahrenheit correcta. ¿Cuál es la lectura Celsius original? Redondea tu respuesta a tres cifras significativas.

1.3 Expansión térmica

49. La altura del monumento a Washington se mide en 170.00 m en un día cuando la temperatura es de 35.0 °C. ¿Cuál será su altura en un día cuando la temperatura cae a -10.0 °C? Aunque el monumento está hecho de piedra caliza, supongamos que su coeficiente de expansión térmica es el mismo que el del mármol. Da tu respuesta a cinco cifras significativas.

50. ¿Cuánto más alta se convierte la Torre Eiffel al final de un día cuando la temperatura ha aumentado en 15 °C? Su altura original es de 321 m y se puede suponer que está hecha de acero.

51. ¿Cuál es el cambio en la longitud de una columna de mercurio de 3.00 cm de longitud si su temperatura cambia de 37.0 °C a 40.0 °C, suponiendo que el mercurio está restringido a un cilindro pero no restringido en longitud? Tu respuesta mostrará por qué los termómetros contienen bulbos en la parte inferior en lugar de simples columnas de líquido.

52. ¿Qué tan grande debe quedar una brecha de expansión entre los rieles ferroviarios de acero si pueden alcanzar una temperatura máxima de 35.0 °C mayor que cuando se colocaron? Su longitud original es de 10.0 m.

53. Estás buscando comprar un pequeño pedazo de tierra en Hong Kong. El precio es "solo" $ 60,000 por metro cuadrado. El título de la tierra dice que las dimensiones son de 20 m × 30 m. ¿En cuánto cambiaría el precio total si midiera el paquete con una cinta métrica de acero el día en que la temperatura era 20 °C superior a la temperatura para la que se diseñó la cinta métrica? Las dimensiones de la tierra no cambian.

54. El calentamiento global producirá un aumento del nivel del mar, en parte debido al derretimiento de los casquetes polares y, en parte, debido a la expansión del agua a medida que aumenta la temperatura media del océano. Para tener una idea del tamaño de este efecto, calcula el cambio en la longitud de una columna de agua de 1.00 km de altura para un aumento de temperatura de 1.00 °C. Supón que la columna no es libre de expandirse hacia los lados. Como modelo del océano, esa es una aproximación razonable, ya que solo partes del océano muy cercanas a la superficie pueden expandirse lateralmente hacia la tierra, y solo en un grado limitado. Como otra aproximación, desprecia el hecho de que el calentamiento de los océanos no es uniforme con la profundidad.

55. (a) Supón que un metro de acero y uno de aluminio tienen la misma longitud a 0 °C. ¿Cuál es su diferencia de longitud a 22.0 °C? (b) Repite el cálculo para dos cintas de topógrafo de 30.0 m de longitud.

56. (a) Si un vaso de precipitados de vidrio de 500 ml se llena hasta el borde con alcohol etílico a una temperatura de 5.00 °C, ¿cuánto se desbordará cuando la temperatura del alcohol alcance la temperatura ambiente de 22.0 °C? (b) ¿Cuánto menos agua rebosaría en las mismas condiciones?

57. La mayoría de los automóviles tienen un depósito de refrigerante para atrapar el líquido del radiador que puede desbordarse cuando el motor está caliente. Un radiador está hecho de cobre y se llena hasta su capacidad de 16.0 L cuando está a 10.0 °C. ¿Qué volumen de fluido del radiador se desbordará cuando el radiador y el fluido alcancen una temperatura de 95,0 °C, dado que el coeficiente de expansión del volumen del fluido es β = 400 × 10^-6/°C? (Tu respuesta será una estimación conservadora, ya que la mayoría de los radiadores de automóviles tienen temperaturas de funcionamiento superiores a 95,0 °C).

58. Un físico prepara una taza de café instantáneo y nota que, a medida que el café se enfría, su nivel cae 3,00 mm en el vaso de vidrio. Demuestra que esta disminución no puede deberse a la contracción térmica al calcular la disminución de nivel si los 350 cm³ de café están en una copa de 7,00 cm de diámetro y la temperatura disminuye de 95,0 °C a 45,0 °C (La mayor parte del descenso en el nivel se debe en realidad a burbujas de aire que escapan).

59. La densidad del agua a 0 °C es muy cercana a los 1000 kg/m³ (en realidad es de 999.84 kg/m³), mientras que la densidad del hielo a 0 °C es de 917 kg/m³. Calcula la presión necesaria para evitar que el hielo se expanda cuando se congela, despreciando el efecto que una presión tan grande tendría sobre la temperatura de congelación (Este problema solo proporciona una indicación de la magnitud de las fuerzas asociadas al agua helada).

60. Demuestre que β = 3α, calculando el cambio infinitesimal en el volumen dV de un cubo con lados de longitud L cuando la temperatura cambia por dT.

1.4 Transferencia de calor, calor específico y calorimetría

61. En un día caluroso, la temperatura de una piscina de 80,000 L aumenta en 1.50 °C. ¿Cuál es la transferencia de calor neta durante este calentamiento? Ignora cualquier complicación, como la pérdida de agua por evaporación.

62. Para esterilizar un biberón de vidrio de 50.0 g, debemos elevar su temperatura de 22.0 °C a 95.0 °C. ¿Cuánta transferencia de calor se requiere?

63. La misma transferencia de calor en masas idénticas de diferentes sustancias produce diferentes cambios de temperatura. Calcula la temperatura final cuando 1.00 kcal de calor se transfiere a 1.00 kg de lo siguiente, originalmente a 20.0 °C: (a) agua; (b) hormigón; (c) acero; y (d) mercurio.

64. Frotarse las manos las calienta al convertir el trabajo en energía térmica. Si una mujer se frota las manos hacia adelante y hacia atrás por un total de 20 roces, a una distancia de 7.50 cm por frotación, y con una fuerza de fricción promedio de 40.0 N, ¿cuál es el aumento de temperatura? La masa de los tejidos calentados es de solo 0.100 kg, principalmente en las palmas y los dedos.

65. Un bloque de 0.250 kg de un material puro se calienta de 20.0 °C a 65.0 °C mediante la adición de 4.35 kJ de energía. Calcula su calor específico e identifica la sustancia de la cual es más probable que esté compuesto.

66. Supón cantidades idénticas de transferencia de calor en diferentes masas de cobre y agua, causando cambios idénticos en la temperatura. ¿Cuál es la razón entre la masa de cobre y agua?

67. a) El número de kilocalorías en los alimentos se determina mediante técnicas de calorimetría en las que se quema el alimento y se mide la cantidad de transferencia de calor. ¿Cuántas kilocalorías por gramo hay en un maní de 5,00 g si la energía que se quema se transfiere a 0,500 kg de agua contenida en una taza de aluminio de 0,100 kg, causando un aumento de la temperatura de 54,9 °C? Supongamos que el proceso tiene lugar en un calorímetro ideal, en otras palabras, un contenedor perfectamente aislado. (b) Compara tu respuesta con la siguiente información de etiquetado que se encuentra en un paquete de cacahuetes tostados secos: una ración de 33 g contiene 200 calorías. Comenta si los valores son consistentes.

68. Después de un ejercicio vigoroso, la temperatura corporal de una persona de 80.0 kg es de 40.0 °C. ¿A qué velocidad en vatios debe la persona transferir energía térmica para reducir la temperatura corporal a 37.0 °C en 30.0 min, suponiendo que el cuerpo continúa produciendo energía a una velocidad de 150 W? (1 watt = 1 joule/segundo o 1W = 1 J/s)

69. En un estudio de hombres jóvenes sanos, haciendo 20 flexiones de brazos en 1 minuto quemaban una cantidad de energía por kg que para un hombre de 70.0 kg corresponde a 8.06 calorías (kcal). ¿Cuánto aumentaría la temperatura de un hombre de 70.0 kg si no perdiera calor durante ese tiempo?

70. Una muestra de agua de 1.28 kg a 10.0 °C se encuentra en un calorímetro. Se deja caer una pieza de acero con una masa de 0,385 kg a 215 °C. Después de que el chisporroteo disminuye, ¿cuál es la temperatura de equilibrio final? (Haz las suposiciones razonables de que cualquier vapor producido se condensa en agua líquida durante el proceso de equilibrado y que la evaporación y la condensación no afectan el resultado, como veremos en la siguiente sección).

71. Repite el problema anterior, suponiendo que el agua está en un vaso de precipitados con una masa de 0.200 kg, que a su vez está en un calorímetro. El vaso de precipitados está inicialmente a la misma temperatura que el agua. Antes de resolver el problema, ¿debería la respuesta ser más alta o más baja que la respuesta anterior? Al comparar la masa y el calor específico del vaso de precipitados con los del agua, ¿crees que el vaso de precipitados hará mucha diferencia?

1.5 Cambios de fase

72. ¿Cuánta transferencia de calor (en kilocalorías) se requiere para descongelar un paquete de 0,450 kg de verduras congeladas originalmente a 0 °C si su calor de fusión es el mismo que el del agua?

73. Una bolsa que contiene hielo a 0 °C es mucho más efectiva para absorber energía que una que contiene la misma cantidad de agua a 0 °C. (a) ¿Cuánta transferencia de calor es necesaria para elevar la temperatura de 0.800 kg de agua de 0 °C a 30.0 °C? (b) ¿Cuánta transferencia de calor se requiere para fundir primero 0.800 kg de hielo a 0 °C y luego elevar su temperatura? (c) Explica cómo tu respuesta respalda la afirmación de que el hielo es más efectivo.

74. a) ¿Cuánta transferencia de calor se requiere para elevar la temperatura de una olla de aluminio de 0.750 kg que contiene 2,50 kg de agua desde 30,0 °C hasta el punto de ebullición y luego evaporar 0,750 kg de agua? (b) ¿Cuánto tiempo dura esto si la tasa de transferencia de calor es de 500 W?

75. La condensación en un vaso de agua helada hace que el hielo se derrita más rápido de lo que lo haría de otra manera. Si 8,00 g de vapor se condensan en un vaso que contiene agua y 200 g de hielo, ¿cuántos gramos de hielo se derretirán como resultado? Supón que no ocurre otra transferencia de calor. Usa L_v para agua a 37 °C como una mejor aproximación que L_v para agua a 100 °C.)

76. En un viaje, observas que una bolsa de hielo de 3.50 kg dura un promedio de un día en tu refrigerador. ¿Cuál es la potencia promedio en vatios que ingresa al hielo si comienza a 0 °C y se derrite completamente a 0 °C de agua en exactamente un día?

77. En un día seco y soleado, la temperatura de la piscina aumentaría en 1.50 °C si no fuera por la evaporación. ¿Qué fracción del agua debe evaporarse para llevar la energía lo suficientemente precisa como para mantener constante la temperatura?

78. a) ¿Cuánta transferencia de calor es necesaria para elevar la temperatura de un trozo de hielo de 0,200 kg de -20,0 °C a 130,0 °C, incluida la energía necesaria para los cambios de fase? (b) ¿Cuánto tiempo se requiere para cada etapa, suponiendo una tasa constante de 20.0 kJ/s de transferencia de calor? (c) Haz un gráfico de temperatura versus tiempo para este proceso.

79. En 1986, un enorme iceberg se separó de la plataforma de hielo Ross en la Antártida. Era un prisma aproximadamente rectangular de 160 km de largo, 40.0 km de ancho y 250 m de espesor. (a) ¿Cuál es la masa de este iceberg, dado que la densidad del hielo es de 917 kg/m³? (b) ¿Cuánta transferencia de calor (en julios) se necesita para derretirla? (c) ¿Cuántos años tomaría la luz solar sola para derretir el hielo de este grosor, si el hielo absorbe un promedio de 100 W/m², 12.00 h por día?

80. ¿Cuántos gramos de café deben evaporarse de 350 g de café en un vaso de vidrio de 100 g, para enfriar el café y la taza de 95.0 °C a 45.0 °C? Supongamos que el café tiene las mismas propiedades térmicas que el agua y que el calor promedio de vaporización es de 2340 kJ/kg (560 kcal/g). Desprecia las pérdidas de calor a través de procesos que no sean la evaporación, así como el cambio en la masa del café a medida que se enfría. ¿Las dos últimas suposiciones hacen que tu respuesta sea mayor o menor que la respuesta verdadera?

81. a) Es difícil extinguir un incendio en un petrolero de petróleo crudo, porque cada litro de petróleo crudo libera 2,80 × 10⁷ J de energía cuando se quema. Para ilustrar esta dificultad, calcula el número de litros de agua que se deben gastar para absorber la energía liberada al quemar 1,00 l de petróleo crudo, si la temperatura del agua aumenta de 20,0 °C a 100 °C, hierve y en el vapor resultante la temperatura aumenta a 300 °C a presión constante. (b) Discute las complicaciones adicionales causadas por el hecho de que el petróleo crudo es menos denso que el agua.

82. La energía liberada por la condensación en tormentas eléctricas puede ser muy grande. Calcula la energía liberada en la atmósfera para una pequeña tormenta de radio de 1 km, suponiendo que precipite 1,0 cm de manera uniforme sobre esta área.

83. Para ayudar a prevenir el daño por heladas, se ha rociado 4.00 kg de agua a 0 °C sobre un árbol frutal. (a) ¿Cuánta transferencia de calor ocurre cuando el agua se congela? (b) ¿Cuánto disminuiría la temperatura del árbol de 200 kg si se transfiriera esta cantidad de calor del árbol? Toma el calor específico como 3.35 kJ/kg • °C, y supón que no ocurre ningún cambio de fase en el árbol.

84. Un recipiente de aluminio de 0.250 kg que contiene 0.800 kg de sopa a 25.0 °C se coloca en un congelador. ¿Cuál es la temperatura final si se transfieren 388 kJ de energía del recipiente y la sopa, suponiendo que las propiedades térmicas de la sopa son las mismas que las del agua?

85. Un cubo de hielo de 0,0500 kg a -30,0 °C se coloca en 0.400 kg de agua a 35.0 °C en un recipiente muy bien aislado. ¿Cuál es la temperatura final?

86. Si vierte 0.0100 kg de agua a 20.0 °C en un bloque de hielo de 1.20 kg (que inicialmente está a -15.0 °C), ¿cuál es la temperatura final? Puedes suponer que el agua se enfría tan rápidamente que los efectos del entorno son insignificantes.

87. Los indígenas a veces cocinan en cestas herméticas al colocar rocas calientes en el agua para llevarlas a ebullición. ¿Qué masa de granito a 500 °C debe colocarse en 4.00 kg de agua a 15.0 °C para llevar su temperatura a 100 °C, si se escapan 0.0250 kg de agua en forma de vapor del chisporroteo inicial? Puedes despreciar los efectos del entorno.

88. ¿Cuál sería la temperatura final de la bandeja y el agua en el ejemplo 1.7 si se colocaran 0,260 kg de agua en la bandeja y se evaporaran inmediatamente 0,0100 kg de agua, dejando que el resto alcance una temperatura común con la bandeja?

1.6 Mecanismos de transferencia de calor

89. (a) Calcula la tasa de conducción de calor a través de las paredes de una casa con un espesor de 13.0 cm y una conductividad térmica promedio dos veces mayor que la de la lana de vidrio. Supongamos que no hay ventanas o puertas. La superficie de las paredes es de 120 m² y su superficie interior está a 18.0 °C, mientras que su superficie exterior está a 5.00 °C. (b) ¿Cuántos calentadores de habitación de 1 kW se necesitarían para equilibrar la transferencia de calor debido a la conducción?

90. La velocidad de conducción de calor desde una ventana en un día de invierno es lo suficientemente rápida como para enfriar el aire que está al lado. Para ver qué tan rápido las ventanas transfieren calor por conducción, calcula la tasa de conducción en vatios a través de una ventana de 3.00 m² que tiene 0.634 cm de grosor (1/4 pulg.) Si las temperaturas de las superficies interna y externa son de 5.00 °C y -10.0 °C, respectivamente (Esta velocidad rápida no se mantendrá: la superficie interna se enfriará, incluso hasta el punto de formación de escarcha).

91. Calcula la tasa de conducción de calor fuera del cuerpo humano, suponiendo que la temperatura interna del núcleo es 37.0 °C, la temperatura de la piel es 34.0 °C, el grosor de los tejidos grasos entre el núcleo y la piel es de 1.00 cm, y el área de superficie es de 1.40 m².

92. Supón que te paras con un pie en el piso de cerámica y un pie en una alfombra de lana, haciendo contacto en un área de 80.0 cm² con cada pie. Tanto la cerámica como la alfombra tienen un grosor de 2.00 cm y están a 10.0 °C en sus lados inferiores. ¿A qué velocidad debe producirse la transferencia de calor desde cada pie para mantener la parte superior de la cerámica y la alfombra a 33.0 °C?

93. Un hombre consume 3000 kcal de alimento en un día, convirtiendo la mayor parte en energía térmica para mantener la temperatura corporal. Si pierde la mitad de esta energía al evaporar el agua (mediante la respiración y la sudoración), ¿cuántos kilogramos de agua se evaporan?

94. Un caminante de fuego corre por un lecho de brasas sin sufrir quemaduras. Calcula el calor transferido por conducción a la planta de un pie de un caminante de fuego, dado que la parte inferior del pie es un callo de 3,00 mm de grosor con una conductividad en el extremo inferior del rango de la madera y su densidad es de 300 kg/m³. El área de contacto es de 25.0 cm², la temperatura de los carbones es de 700 °C, y el tiempo de contacto es de 1.00 s. Ignora el enfriamiento evaporativo del sudor.

95. (a) ¿Cuál es la tasa de conducción de calor a través del pelaje de 3,00 cm de espesor de un animal grande que tiene una superficie de 1,40 m²? Supón que la temperatura de la piel del animal es 32.0 °C, que la temperatura del aire es -5.00 °C, y que la piel tiene la misma conductividad térmica que el aire. (b) ¿Qué ingesta de alimentos necesitará el animal en un día para reemplazar esta transferencia de calor?

96. Una morsa transfiere energía por conducción a través de su grasa a una velocidad de 150 W cuando se sumerge en agua a -1,00 °C. La temperatura interna del cuerpo de la morsa es de 37.0 °C, y tiene una superficie de 2.00 m². ¿Cuál es el grosor promedio de su grasa, que tiene la conductividad de los tejidos grasos?

97. Compara la tasa de conducción de calor a través de una pared de 13.0 cm de espesor que tiene un área de 10.0 m² y una conductividad térmica dos veces la de lana de vidrio con la tasa de conducción de calor a través de una ventana de 0.750 cm de espesor que tiene un área de 2.00 m², suponiendo la misma diferencia de temperatura entre cada uno.

98. Supón que una persona está cubierta de pies a cabeza por ropa de lana con un grosor promedio de 2.00 cm y transfiere energía por conducción a través de la ropa a razón de 50.0 W. ¿Cuál es la diferencia de temperatura entre la ropa, dado que la superficie es de 1.40 m²?

99. Algunas estufas de cocina son de cerámica lisa para facilitar la limpieza. Si la cerámica tiene un espesor de 0.600 cm y la conducción de calor ocurre a través de la misma área y a la misma velocidad que la calculada en el ejemplo 1.11, ¿cuál es la diferencia de temperatura entre ellas? La cerámica tiene la misma conductividad térmica que el vidrio y el ladrillo.

100. Una manera fácil de reducir los costos de calefacción (y refrigeración) es agregar aislamiento adicional en el ático de una casa. Supongamos que una casa cúbica de una sola planta ya tiene 15 cm de aislamiento de fibra de vidrio en el ático y en todas las superficies exteriores. Si agregaste 8,0 cm adicionales de fibra de vidrio al ático, ¿en qué porcentaje bajaría el costo de calefacción de la casa? Toma la casa para tener dimensiones de 10 m por 15 m por 3.0 m. Ignora la infiltración de aire y la pérdida de calor a través de ventanas y puertas, y supón que el interior está uniformemente a una temperatura y el exterior está uniformemente en otra.

101. Muchas decisiones se toman sobre la base del período de recuperación de la inversión: el tiempo que llevará ahorrar para igualar el costo de capital de una inversión. Los tiempos de amortización aceptables dependen del negocio o la filosofía que uno tenga (Para algunas industrias, un período de recuperación de la inversión es tan pequeño como 2 años). Supón que deseas instalar el aislamiento adicional en el problema anterior. Si la energía costaba $ 1.00 por millón de joules y el aislamiento era de $ 4.00 por metro cuadrado, entonces calcula el tiempo de recuperación simple. Tome el ΔT promedio para la temporada de calefacción de 120 días a 15.0 °C.

Problemas Adicionales

102. En 1701, el astrónomo danés Ole Rømer propuso una escala de temperatura con dos puntos fijos, agua helada a 7.5 grados y agua hirviendo a 60.0 grados. ¿Cuál es el punto de ebullición del oxígeno, 90.2 K, en la escala de Rømer?

103. ¿Cuál es el porcentaje de error al pensar que el punto de fusión del tungsteno es 3695 °C en lugar del valor correcto de 3695 K?

104. Un ingeniero desea diseñar una estructura en la que la diferencia de longitud entre una viga de acero y una viga de aluminio permanezca a 0.500 m, independientemente de la temperatura, para temperaturas normales. ¿Cuáles deben ser las longitudes de los rayos?

105. ¿Cuánta tensión se crea en una viga de acero si su temperatura cambia de -15 °C a 40 °C pero no puede expandirse? Para el acero, el módulo de Young Y = 210 × 10⁹ N/m² (Ignora el cambio en el área resultante de la expansión).

106. Una varilla de latón (Y = 90 × 10⁹ N/m²), con un diámetro de 0,800 cm y una longitud de 1,20 m cuando la temperatura es de 25 °C, se fija en ambos extremos. ¿A qué temperatura está la fuerza en 36,000 N?

107. Un termómetro de mercurio todavía en uso para la meteorología tiene un bulbo con un volumen de 0.780 cm³ y un tubo para que el mercurio se expanda en un diámetro interno de 0.130 mm. (a) Despreciando la expansión térmica del vidrio, ¿cuál es el espaciado entre las marcas a 1 °C de distancia? (b) Si el termómetro está hecho de vidrio ordinario (no es una buena idea), ¿cuál es el espaciado?

108. Incluso cuando se cierra después de un período de uso normal, un gran reactor nuclear comercial transfiere energía térmica a razón de 150 MW por la descomposición radiactiva de los productos de fisión. Esta transferencia de calor provoca un rápido aumento de la temperatura si falla el sistema de enfriamiento (1 vatio = 1 joule/segundo o 1 W = 1 J/s y 1 MW = 1 megawatt). (a) Calcula la tasa de aumento de la temperatura en grados Celsius por segundo (°C/s) si la masa del núcleo del reactor es de 1,60 × 10³ kg y tiene un calor específico promedio de 0.3349 kJ/kg • °C. (b) ¿Cuánto tiempo tomaría obtener un aumento de temperatura de 2000 °C, que podría causar que algunos metales que contienen los materiales radioactivos se derritan? (La tasa inicial de aumento de temperatura sería mayor que la calculada aquí porque la transferencia de calor se concentra en una masa más pequeña. Más tarde, sin embargo, el aumento de temperatura se ralentizaría porque el recipiente de contención de acero de 500,000 kg también comenzaría a calentarse).

109. Dejas un pastel en el refrigerador en un plato y le pides a tu compañero que lo saque antes de llegar a casa para que puedas comerlo a temperatura ambiente, de la manera que te guste. En cambio, tu compañero de cuarto juega videojuegos durante horas. Cuando regresas, notas que el pastel todavía está frío, pero la consola del juego se ha calentado. Molesto, y sabiendo que la masa no será buena si está en el microondas, calientas la masa desenchufando la consola y colocándola en una bolsa de basura limpia (que actúa como un calorímetro perfecto) con la masa en el plato. Después de un tiempo, encuentras que la temperatura de equilibrio es agradable, cálida 38.3 °C. Sabes que la consola de juegos tiene una masa de 2.1 kg. Aproxímalo teniendo una temperatura inicial uniforme de 45 °C. La masa tiene una masa de 0.16 kg y un calor específico de 3.0 kJ/(kg • ºC), y tiene una temperatura inicial uniforme de 4.0 °C. La placa está a la misma temperatura y tiene una masa de 0.24 kg y un calor específico de 0.90 J/(kg•ºC). ¿Cuál es el calor específico de la consola?

110. Dos esferas sólidas, A y B, hechas del mismo material, están a temperaturas de 0 °C y 100 °C, respectivamente. Las esferas se colocan en contacto térmico en un calorímetro ideal, y alcanzan una temperatura de equilibrio de 20 °C. ¿Cuál es la esfera más grande? ¿Cuál es la proporción de sus diámetros?

111. En algunos países, el nitrógeno líquido se utiliza en camiones de leche en lugar de refrigeradores mecánicos. Un viaje de entrega de 3.00 horas requiere 200 L de nitrógeno líquido, que tiene una densidad de 808 kg/m³. (a) Calcula la transferencia de calor necesaria para evaporar esta cantidad de nitrógeno líquido y eleve su temperatura a 3.00 °C. (Usa cP y supón que es constante en el rango de temperatura). Este valor es la cantidad de enfriamiento que suministra el nitrógeno líquido. (b) ¿Cuál es la tasa de transferencia de calor en kilovatios-hora? (c) Compara la cantidad de enfriamiento obtenido de la fusión de una masa idéntica de 0 °C de hielo con la de la evaporación del nitrógeno líquido.

112. Algunos pistoleros hacen sus propias balas, lo que implica derretir el plomo y convertirlo en lingotes de plomo. ¿Cuánta transferencia de calor se necesita para elevar la temperatura y fundir 0.500 kg de plomo, a partir de 25.0 °C?

113. Se deja caer un cilindro de hierro de 0,800 kg a una temperatura de 1,00 × 10³ °C en un cofre aislado de 1,00 kg de hielo en su punto de fusión. ¿Cuál es la temperatura final y cuánto hielo se derritió?

114. Repite el problema anterior con 2,00 kg de hielo en lugar de 1,00 kg.

115. Repite el problema anterior con 0,500 kg de hielo, suponiendo que el hielo está inicialmente en un recipiente de cobre de masa 1,50 kg en equilibrio con el hielo.

116. Un cubo de hielo de 30,0 g en su punto de fusión se deja caer en un calorímetro de aluminio de 100,0 g de masa en equilibrio a 24,0 °C con 300,0 g de un líquido desconocido. La temperatura final es 4.0 °C. ¿Cuál es la capacidad de calor del líquido?

117. (a) Calcula la tasa de conducción de calor a través de una ventana de doble pared que tiene un área de 1.50 m² y está hecha de dos paneles de vidrio de 0.800 cm de espesor separados por un espacio de aire de 1.00 cm. La temperatura de la superficie interior es de 15.0 °C, mientras que en el exterior es de -10.0 °C (Sugerencia: Hay caídas de temperatura idénticas en los dos paneles de vidrio. Primero, encuentra estos y luego la temperatura baja en el entrehierro. Este problema ignora la mayor transferencia de calor en el entrehierro debido a la convección). (b) Calcula la tasa de conducción de calor a través de una ventana de 1,60 cm de espesor de la misma área y con las mismas temperaturas. Compare tu respuesta con la de la parte (a).

118. (a) Una pared exterior de una casa mide 3 m de altura y 10 m de ancho. Consiste en una capa de paneles de yeso con un factor R de 0,56, una capa de 3,5 pulgadas de espesor rellena con bloques de fibra de vidrio y una capa de revestimiento aislante con un factor R de 2,6. La pared está construida tan bien que no hay fugas de aire a través de ella. Cuando el interior de la pared está a 22 °C y el exterior a -2 °C, ¿cuál es la velocidad de flujo de calor a través de la pared? (b) De manera más realista, el espacio de 3.5 pulgadas también contiene tachuelas de 2 por 4, tablas de madera de 1.5 pulgadas por 3.5 pulgadas orientadas para que la dimensión de 3.5 pulgadas se extienda desde el panel de yeso hasta el revestimiento. Están "en centros de 16 pulgadas", es decir, los centros de los postes están a 16 pulgadas de distancia. ¿Cuál es la corriente de calor en esta situación? No te preocupes por un clavo más o menos.

119. Para el cuerpo humano, ¿cuál es la tasa de transferencia de calor por conducción a través del tejido corporal con las siguientes condiciones: el grosor del tejido es de 3,00 cm, la diferencia de temperatura es de 2,00 °C y el área de la piel es de 1,50 m². ¿Cómo se compara esto con la tasa promedio de transferencia de calor al cuerpo que resulta de una ingesta de energía de alrededor de 2400 kcal por día? (No se incluye ejercicio)

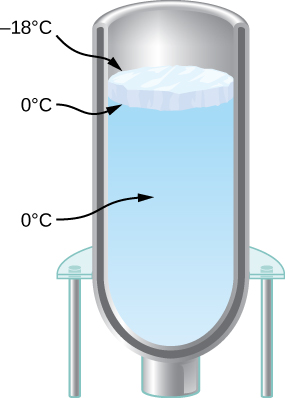
120. Tienes una matraz de Dewar (un matraz al vacío de laboratorio) que tiene una parte superior abierta y lados rectos, como se muestra a continuación. Lo llenas con agua y lo pones en el congelador. Es efectivamente un aislante perfecto, bloqueando toda la transferencia de calor, excepto en la parte superior. Después de un tiempo, se forma hielo en la superficie del agua. El agua líquida y la superficie inferior del hielo, en contacto con el agua líquida, están a 0 °C. La superficie superior del hielo está a la misma temperatura que el aire en el congelador, -18 °C. Establece la tasa de flujo de calor a través del hielo igual a la tasa de pérdida de calor de fusión a medida que el agua se congela. Cuando la capa de hielo tenga un grosor de 0.700 cm, encuentra la velocidad en m/s a ​​la cual el hielo se está espesando



121. Un calentador de infrarrojos para un sauna tiene una superficie de 0.050 m² y una emisividad de 0.84. ¿A qué temperatura debe funcionar si la potencia requerida es de 360 W? Desprecia la temperatura del medio ambiente.

122. (a) Determina la potencia de la radiación del Sol al observar que la intensidad de la radiación a la distancia de la Tierra es de 1370 W/m². Sugerencia: Esa intensidad se encontrará en todas partes en una superficie esférica con un radio igual al de la órbita de la Tierra. (b) Suponiendo que la temperatura del Sol es 5780 K y que su emisividad es 1, encuentra su radio.

Problemas Desafío

123. Un péndulo está hecho de una varilla de longitud L y una masa despreciable, pero capaz de expansión térmica, y un peso de tamaño insignificante. (a) Demuestra que cuando la temperatura aumenta en dT, el período del péndulo aumenta en una fracción αLdT/2. (b) Un reloj controlado por un péndulo de bronce mantiene el tiempo correcto a 10 °C. Si la temperatura ambiente es de 30 °C, ¿el reloj funciona más rápido o más lento? ¿Cuál es su error en segundos por día?

124. A temperaturas de unos pocos cientos de Kelvin la capacidad de calor específica del cobre sigue aproximadamente la fórmula empírica c = α + βT + δT^-2, donde α = 349 J/kg•K, β = 0.107 J kg•K² y δ = 4.58 × 10⁵J•kg•K. ¿Cuánto calor se necesita para elevar la temperatura de una pieza de cobre de 2.00 kg de 20 °C a 250 °C?

125. En un calorímetro de capacidad calorífica insignificante, se mezclan 200 g de vapor a 150 °C y 100 g de hielo a -40 °C. La presión se mantiene a 1 atm. ¿Cuál es la temperatura final y cuánto vapor, hielo y agua hay?

126. Un astronauta que realiza una actividad extravehicular (caminata espacial) sombreada por el Sol lleva puesto un traje espacial que puede aproximarse perfectamente blanco (e = 0) a excepción de un parche de 5 cm × 8 cm en forma de bandera nacional del astronauta. El parche tiene una emisividad 0.300. El traje espacial debajo del parche tiene 0.500 cm de grosor, con una conductividad térmica k = 0.0600 W/m °C, y su superficie interna está a una temperatura de 20.0 °C. ¿Cuál es la temperatura del parche y cuál es la tasa de pérdida de calor a través de él? Supongamos que el parche es tan delgado que su superficie exterior está a la misma temperatura que la superficie exterior del traje espacial debajo de él. También supón que la temperatura del espacio exterior es 0 K. Obtendrás una ecuación que es muy difícil de resolver en forma cerrada, por lo que puedes resolverla numéricamente con una calculadora gráfica, con software o incluso mediante prueba y error con una calculadora.

127. El objetivo en este problema es encontrar el crecimiento de una capa de hielo como una función del tiempo. Llama el grosor de la capa de hielo L. (a) Obtén una ecuación para dL/dt en términos de L, la temperatura T sobre el hielo y las propiedades del hielo (que puedes dejar en forma simbólica en lugar de sustituir los números). (b) Resuelve esta ecuación diferencial suponiendo que en t = 0, tiene L = 0. Si has estudiado ecuaciones diferenciales, conocerás una técnica para resolver ecuaciones de este tipo: manipula la ecuación para obtener dL/dt multiplicado por una función (muy simple) de L en un lado, e integra ambos lados con respecto al tiempo. Alternativamente, puedes usar tu conocimiento de las derivadas de varias funciones para adivinar la solución, que tiene una dependencia simple de t. (c) ¿Se congelará eventualmente el agua hasta el fondo del matraz?

128. Como el primer rudimento de la climatología, calcula la temperatura de la Tierra. Asume que es una esfera perfecta y que su temperatura es uniforme. Ignora el efecto invernadero. La radiación térmica del Sol tiene una intensidad (la "constante solar" S) de aproximadamente 1370 W/m² en el radio de la órbita de la Tierra.

(a) Suponiendo que los rayos del Sol son paralelos, ¿para qué área se debe multiplicar S para obtener la radiación total interceptada por la Tierra? Será más fácil responder en términos del radio de la Tierra, R.

(b) Supongamos que la Tierra refleja aproximadamente el 30% de la energía solar que intercepta. En otras palabras, la Tierra tiene un albedo con un valor de A = 0.3. En términos de S, A y R, ¿cuál es la velocidad a la que la Tierra absorbe la energía del Sol?

(c) Encuentra la temperatura a la cual la Tierra irradia energía a la misma velocidad. Supón que en las longitudes de onda infrarrojas donde se irradia, la emisividad e es 1. ¿Muestra tu resultado que el efecto invernadero es importante? (d) ¿Cómo depende tu respuesta del área de la Tierra?

129. Vamos a dejar de ignorar el efecto invernadero e incorporarlo en el problema anterior de una manera muy aproximada. Supongamos que la atmósfera es una capa única, una capa esférica alrededor de la Tierra, con una emisividad e = 0.77 (elegida simplemente para dar la respuesta correcta) a las longitudes de onda infrarrojas emitidas por la Tierra y por la atmósfera. Sin embargo, la atmósfera es transparente a la radiación solar (es decir, supón que la radiación está en longitudes de onda visibles sin infrarrojos), por lo que la radiación solar llega a la superficie. El efecto invernadero proviene de la diferencia entre la transmisión de luz visible de la atmósfera y su absorción más bien intensa de infrarrojos. Ten en cuenta que el radio de la atmósfera no es significativamente diferente de la de la Tierra, pero dado que la atmósfera es una capa sobre la Tierra, emite radiación tanto hacia arriba como hacia abajo, por lo que tiene dos veces el área de la Tierra. Hay tres transferencias de energía radiativa en este problema: radiación solar absorbida por la superficie de la Tierra; radiación infrarroja de la superficie, que es absorbida por la atmósfera de acuerdo con su emisividad; y la radiación infrarroja de la atmósfera, la mitad de la cual es absorbida por la Tierra y la otra mitad sale al espacio. Aplica el método del problema anterior para obtener una ecuación para la superficie de la Tierra y otra para la atmósfera, y resuélvelas para las dos temperaturas, superficie y atmósfera desconocidas.

a. En términos del radio de la Tierra, la constante σ, y la temperatura desconocida T_s de la superficie, ¿cuál es la potencia de la radiación infrarroja de la superficie?

b. ¿Cuál es la potencia de la radiación de la Tierra absorbida por la atmósfera?

c. En términos de la temperatura desconocida T_e de la atmósfera, ¿cuál es la potencia irradiada de la atmósfera?

d. Escribe una ecuación que diga que la potencia de la radiación que la atmósfera absorbe de la Tierra es igual a la potencia de la radiación que emite.

e. La mitad de la potencia irradiadapor la atmósfera golpea a la Tierra. Escribe una ecuación que diga que la potencia que la Tierra absorbe de la atmósfera y el Sol es igual a la potencia que emite.

f. Resuelve tus dos ecuaciones para la temperatura desconocida de la Tierra.

Para conocer los pasos que hacen que este modelo sea menos burdo, observa, por ejemplo, las conferencias de Paul O'Gorman.