Respuestas - Capítulo IX
Sólo se dan las respuestas de los numerales impares
Preguntas conceptuales
1. La imagen virtual no se puede proyectar en una pantalla. No puedes distinguir una imagen real de una imagen virtual simplemente juzgando a partir de la imagen percibida con su ojo.
3. Sí, puedes fotografiar una imagen virtual. Por ejemplo, si fotografías tu reflejo desde un espejo plano, obtienes una fotografía de una imagen virtual. La cámara enfoca la luz que entra en tu lente para formar una imagen; no importa si la fuente de la luz es un objeto real o un reflejo del espejo (es decir, una imagen virtual).
5. No, puedes ver la imagen real de la misma manera que puedes ver la imagen virtual. La retina de tu ojo sirve efectivamente como una pantalla.
7. El espejo debe ser la mitad de tu tamaño y su borde superior debe estar al nivel de tus ojos. El tamaño no depende de tu distancia del espejo.
9. Cuando el objeto está en el infinito; ver la ecuación del espejo
11. Sí, la ampliación negativa simplemente significa que la imagen está al revés; esto no evita que la imagen sea más grande que el objeto. Por ejemplo, para un espejo cóncavo, si la distancia al objeto es mayor que una distancia focal pero menor que dos distancias focales, la imagen se invertirá y se ampliará.
13. las respuestas pueden variar
15. La distancia focal de la lente es fija, por lo que la distancia de la imagen cambia en función de la distancia del objeto.
17. Sí, la distancia focal cambiará. La ecuación del fabricante de lentes muestra que la distancia focal depende del índice de refracción del medio que rodea la lente. Debido a que el índice de refracción del agua difiere del aire, la distancia focal de la lente cambiará cuando se sumerja en agua.
19. Un ojo relajado con visión normal enfocará rayos de luz paralelos sobre la retina.
21. Una persona con una lente interna necesitará gafas para leer porque sus músculos no pueden distorsionar la lente como lo hacen con las lentes biológicas, por lo que no pueden enfocar objetos cercanos. Para corregir la miopía, la potencia de la lente intraocular debe ser menor que la de la lente extraída.
23. Los microscopios crean imágenes de tamaño macroscópico, por lo que se aplica la óptica geométrica.
25. El ocular se movería un poco más lejos del objetivo, de modo que la imagen formada por el objetivo caiga justo más allá de la longitud focal del ocular.
Problemas
27.
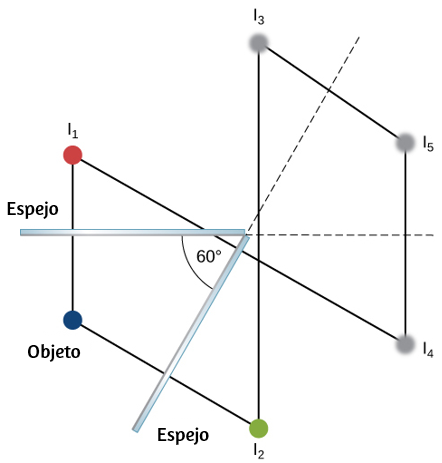
29. Está en el punto focal del espejo grande y en el centro de curvatura del espejo pequeño.
31. f = R/2 ⇒ R = + 1.60 m
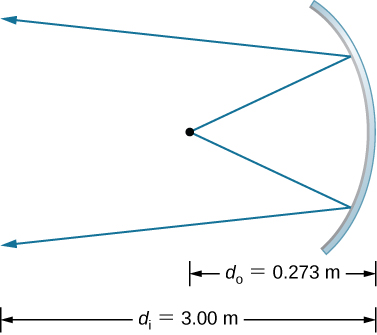
33. do = 27.3 cm
35. Paso 1: La formación de imágenes por un espejo está involucrada.
Paso 2: Dibuja la configuración del problema cuando sea posible.
Paso 3: Usa ecuaciones de lente delgada para resolver este problema.
Paso 4: Encuentra f.
Paso 5: Dado: m = 1.50, do = 0.120 m.
Paso 6: No se necesita trazado de rayos.
Paso 7: Utilizando m = di/do, di = −0.18 0m. Entonces, f = 0.360 m.
Paso 8: La imagen es virtual porque la distancia de la imagen es negativa. La distancia focal es positiva, por lo que el espejo es cóncavo.
37. a. para un espejo convexo di < 0 ⇒ m > 0. m = + 0.111; b. di = −0.334 cm (detrás de la córnea);
c. f = −0.376 cm, por lo que R = −0.752 cm
39. m = hi/ho = −di/do = −-do/do = do/do = 1 ⇒ hi = ho
41.
m = −11.0
A' =0 .110 m2
I = 6.82 kW/m2
43. x2m = −x2m - 1, (m = 1,2,3,...),
x2m + 1 = b - x2m, (m = 0,1,2,...),
45. di =− 55 cm; m = +1.8
47. di = −41 cm, m = 1.4
49. Prueba
51. a. 1/di + 1/do = 1/f ⇒ di = 3.43m;
b. m = −33.33, de modo que (2.40 × 10−2 m)(33.33) = 80.0cm, y (3.60 × 10−2 m)(33.33) = 1.20 m ⇒ 0.800 m × 1.20 m o 80.0 cm × 120 cm
53. a. 1/di + 1/do = 1/f, di = 5.08 cm
b. m = −1.695 × 10−2, por lo que la altura máxima es 0.036 m/1.695 × 10−2 = 2.12 m ⇒ 100%;
c. Esto parece bastante razonable, ya que a 3,00 m es posible obtener una imagen completa de una persona.
55. a. 1/di + 1/do = 1/f ⇒ d0 = 2.55m;
b. hi/ho = -di/do ⇒ do = 1.00m
57. a. Usando 1/di + 1/do = 1/f, di = −56.67 cm. Entonces podemos determinar el aumento, m = 6.67. b. di = −190 cm y m = + 20.0; c. El aumento m aumenta rápidamente a medida que aumenta la distancia del objeto hacia la distancia focal.
59. 1/di + 1/do = 1/f
di = 1/(1/f) − (1/do)
di/do = 6.667 × 10−13 = hi/ho
hi = −0.933 mm
61. di = −6.7 cm
hi = 4.0 cm
63. 83 cm a la derecha de la lente convergente, m = −2.3, hi = 6.9 cm
65. P = 52.0 D
67. hi/ho = −di/do ⇒ hi = −ho(di/do) = -(3.50 mm)(2.00 cm/30.0 cm) = - 0.233 mm
69. a. P = + 62.5 D;
b. hi/ho = −di/do ⇒ hi = −0.250 mm;
c. hi = −0.0800 mm
71. P = 1/di + 1/do ⇒ do = 28.6 cm
73. Originalmente, la visión de cerca era 51.0 D. Por lo tanto, P = 1/di + 1/do ⇒ do = 1.00 m
75. originalmente, P = 70.0 D; Debido a que la potencia para la visión distante normal es 50.0 D, la potencia se debe disminuir en 20.0 D
77. P = 1/di + 1/do ⇒ do = 0.333 m
79. a. P = 52.0 D;
b. 1/di + 1/do = P ⇒ do = 16.2 cm
81. Necesitamos di = −18.5 cm cuando do = ∞, entonces P = −5.41 D
83. Sea x = punto lejano
⇒ P = 1/−(x − 0.0175 m) + 1/∞ ⇒ −xP + (0.0175 m)P = 1
85. M = 6×
87. M = (25 cm/L)(1 + L - ℓ/f)
L - ℓ = do
do = 13 cm
89. M = 2.5×
91. M = −2.1×
93. M = 25 cm/f
Mmax = 5
95. Mmax(nuevo) = 1 + 18 cm/f ⇒ f = 18 cm/Mmax(nuevo)
Mmax(anterior) = 9.8×
97. a. 1/di + 1/do = 1/f ⇒ di = 4.65 cm ⇒ m = -30.0
b. Mneto = -240
99. a. 1/diobj + 1/doobj = 1/fobj ⇒ diobj = 18.3 cm detrás de la lente objetivo
b. mobj = -60.0
c. doojo = 1.70 cm; diojo = -11.3 cm
101. M = −40.0
103. fobj = R/2, M = −1.67
105. M = −fobj/fojo, ojo = + 10.0 cm
107. Las respuestas variarán.
109. 12 cm a la izquierda del espejo, m = 3/5
111. 27 cm delante del espejo, m = 0,6, hi = 1,76 cm, orientación vertical
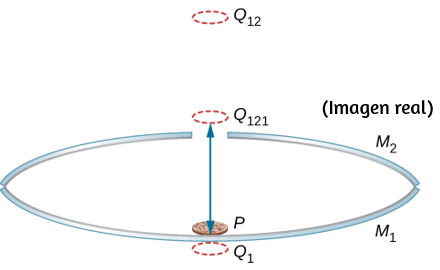
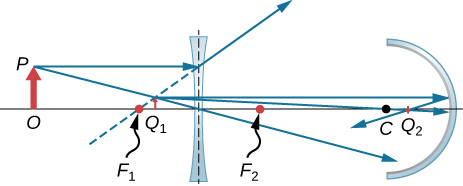
113. La siguiente figura muestra tres imágenes sucesivas que comienzan con la imagen Q1 en el espejo M1. Q1 es la imagen en el espejo M11, cuya imagen en el espejo M2 es Q12 cuya imagen en el espejo M1 es la imagen real
115. 5.4 cm del eje.
117. Deja que el vértice del espejo cóncavo sea el origen del sistema de coordenadas. La imagen 1 está a −10/3 cm (−3.3 cm), la imagen 2 está a −40/11 cm (−3.6 cm). Estos sirven como objetos para imágenes posteriores, que están a −310/83 cm (−3.7 cm), −9340/2501 cm (−3.7 cm), −140,720/37,681 cm (−3,7 cm). Todas las imágenes restantes están a aproximadamente −3.7 cm.
119.
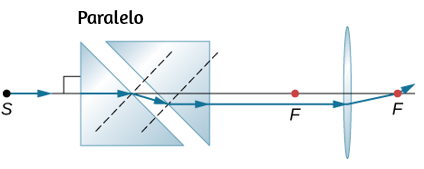
121.
123. −5 D
125. 11
Problemas Adicionales
127.
a.
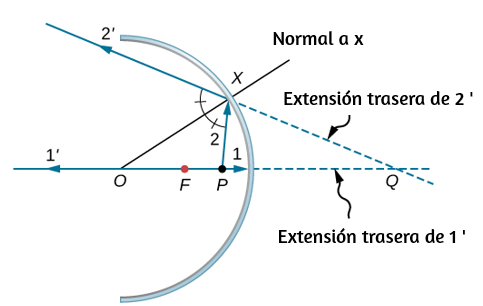
b.
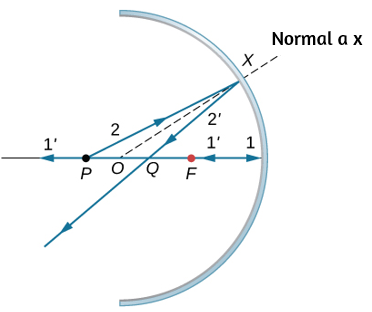
c.

d. Similar a la imagen anterior pero con el punto P fuera de la distancia focal;
e. Repite (a) - (d) para un objeto puntual fuera del eje. Para un objeto puntual colocado fuera del eje frente a un espejo cóncavo correspondiente a las partes (a) y (b), para el espejo convexo se deja como ejercicio.
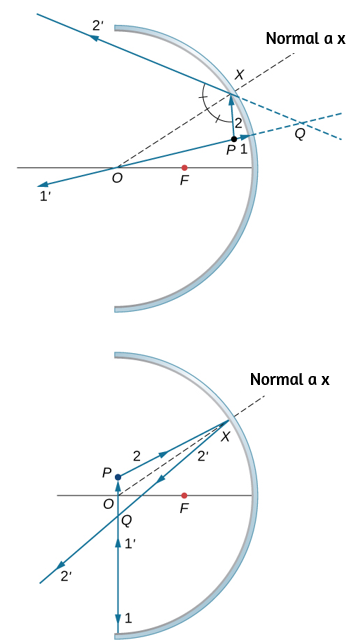
129. di = −10/3 cm, hi = 2 cm, vertical
131. prueba
133.

Los triángulos BAO y B1A1O son triángulos similares. Por lo tanto, A1B1/AB = di/do. Los triángulos NOF y B1A1F son triángulos similares. Por lo tanto, NO/f = A1B1/di - f. Notando que NO = AB da AB/f = A1B1/di - f o AB/A1B1 = f/di - f. Invirtiendo esto se obtiene A1B1/AB = di - f/f. Al igualar las dos expresiones para la relación A1B1/AB se obtiene di/do = di - f/f. Al dividir por di da 1/do = 1/f − 1/di o 1/do + 1/di = 1/f.
135. 70 cm
137. El espejo plano tiene un punto focal infinito, de modo que di = −do. La distancia aparente total del hombre en el espejo será su distancia real, más la distancia aparente de la imagen, o do + (-di) = 2do. Si esta distancia debe ser inferior a 20 cm, debe estar parado a do = 10 cm.
139. Aquí queremos do = 25 cm − 2.20 cm = 0.228 m. Si x = punto cercano, di = - (x − 0.0220 m). Por lo tanto, P = 1/do + 1/di = 1/0.228 m + 1/x − 0.0220 m. Usando P = 0.75 D da x = 0.253 m, entonces el punto cercano es 25.3 cm.
141. Suponiendo una lente a 2.00 cm del ojo del niño, la distancia de la imagen debe ser di = - (500 cm − 2.00 cm) = - 498 cm. Para un objeto de distancia infinita, la potencia requerida es P = 1/di = −0.200 D. Por lo tanto, la lente de −4.00 D corregirá la miopía.
143. 87 μmd
145. Uso, Mneto = −diobj(fojo + 25 cm)/fobjfojo. La distancia de la imagen para el objetivo es diobj = −Mnetofobjfojo/fobj + 25 cm. Usando fobj = 3.0 cm, fojo = 10 cm, y M = −10 da diobj = 8.6 cm. Queremos que esta imagen se encuentre en el punto focal del ocular para que el ocular forme una imagen en el infinito para una visualización cómoda. Por lo tanto, la distancia d entre las lentes debe ser d = fojo + diobj = 10 cm + 8.6 cm = 19 cm.
147. a. longitud focal de la lente correctiva fc = −80 cm; b. −1.25 D
149. 2 × 1016 km
151. 105 m









