Respuestas - Capítulo VI
Excepto por las preguntas de los apartados de Comprueba tu aprendizaje, sólo se dan las respuestas de los numerales impares
Comprueba tu aprendizaje
6.1 La longitud de onda de las ondas depende de la frecuencia y la velocidad de la onda. La frecuencia de la onda de sonido es igual a la frecuencia de la onda en la cuerda. Las longitudes de onda de las ondas de sonido y las ondas en la cuerda son iguales solo si las velocidades de las ondas son las mismas, lo que no siempre es así. Si la velocidad de la onda de sonido es diferente de la velocidad de la onda en la cuerda, las longitudes de onda son diferentes.
6.2 En una onda transversal, la onda puede moverse a una velocidad de propagación constante a través del medio, pero el medio oscila perpendicularmente al movimiento de la onda. Si la onda se mueve en la dirección x positiva, el medio oscila hacia arriba y hacia abajo en la dirección y. Por lo tanto, la velocidad del medio no es constante, pero la velocidad y la aceleración del medio son similares a las del movimiento armónico simple de una masa en un resorte.
6.3 Sí, una función coseno es igual a una función sinusoidal con un cambio de fase, y cualquiera de las dos funciones puede usarse en una función de onda. La función más conveniente de usar depende de las condiciones iniciales. En la figura 6.11, la ola tiene una altura inicial de y(0.00,0.00) = 0 y luego la altura de la ola aumenta a la altura máxima en la cresta. Si la altura inicial en el momento inicial era igual a la amplitud de la onda y(0.00,0.00) = +A, entonces podría ser más conveniente modelar la onda con una función de coseno.
6.4 Esta onda, con una amplitud A = 0.5 m, longitud de onda λ = 10.00 m, período T = 0.50 s, es una solución a la ecuación de onda con una velocidad de onda v = 20.00 m/s.
6.5 Dado que la velocidad de una onda en una cuerda es proporcional a la raíz cuadrada de la tensión dividida por la densidad lineal, la velocidad de la onda aumentaría en √2.
6.6 A primera vista, la potencia promediada en el tiempo de una onda sinusoidal en una cuerda puede parecer proporcional a la densidad lineal de la cuerda porque
P = 1/2μA2ω2v; Sin embargo, la velocidad de la onda depende de la densidad lineal. Reemplazar la velocidad de onda con 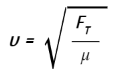 muestra que la potencia es proporcional a la raíz cuadrada de la tensión y proporcional a la raíz cuadrada de la densidad de masa lineal:
muestra que la potencia es proporcional a la raíz cuadrada de la tensión y proporcional a la raíz cuadrada de la densidad de masa lineal:
P = 1/2μA2ω2v = 1/2μA2ω2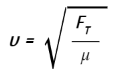 = 1/2A2ω2√μFT/
= 1/2A2ω2√μFT/
6.7 Sí, las ecuaciones funcionarían igual de bien para las condiciones de límites simétricas de un medio libre para oscilar en cada extremo donde había un antinodo en cada extremo. Los modos normales de los tres primeros modos se muestran a continuación. La línea de puntos muestra la posición de equilibrio del medio.
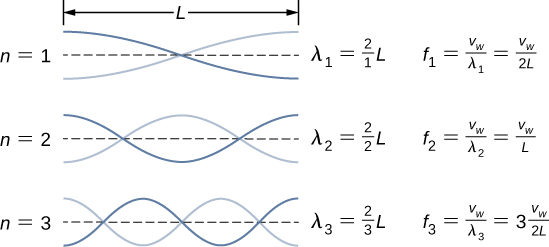
Observa que el primer modo es dos cuartos, o la mitad, de una longitud de onda. El segundo modo es un cuarto de una longitud de onda, seguido por la mitad de una longitud de onda, seguido por un cuarto de una longitud de onda, o una longitud de onda completa. El tercer modo es una longitud y media de onda. Estos son los mismos resultados que la cuerda con un nodo en cada extremo. Las ecuaciones para condiciones de límites simétricos funcionan igualmente bien para condiciones de límites fijos y condiciones de límites libres.
Preguntas conceptuales
1. Una onda en una cuerda de guitarra es un ejemplo de una onda transversal. La perturbación de la cuerda se mueve perpendicular a la propagación de la onda. El sonido producido por la cuerda es una onda longitudinal donde la perturbación del aire se mueve paralela a la propagación de la onda.
3. La velocidad de propagación es la velocidad de la onda que se propaga a través del medio. Si la velocidad de onda es constante, la velocidad se puede encontrar mediante v = λ/T = λf. La frecuencia es el número de onda que pasa un punto por unidad de tiempo. La longitud de onda es directamente proporcional a la velocidad de la onda e inversamente proporcional a la frecuencia.
5. No, la distancia que mueva tu mano hacia arriba y hacia abajo determinará la amplitud de la onda. La longitud de onda dependerá de la frecuencia con la que muevas tu mano hacia arriba y hacia abajo, y la velocidad de la onda a través del resorte.
7. La luz del Sol y las estrellas llegan a la Tierra a través de un espacio vacío donde no hay un medio presente.
9. La longitud de onda es igual a la velocidad de la onda por la frecuencia y el número de onda es igual a k = 2π/λ, por lo tanto la respuesta es sí, el número de onda dependerá de la frecuencia y también dependerá de la velocidad de la onda que se propaga a través del resorte.
11. El medio se mueve en un movimiento armónico simple a medida que la onda se propaga a través del medio, cambiando continuamente la velocidad, por lo tanto, acelera. La aceleración del medio se debe a la fuerza restauradora del medio, que actúa en la dirección opuesta al desplazamiento.
13. La velocidad de la onda es proporcional a la raíz cuadrada de la tensión, por lo que la velocidad se duplica.
15. Dado que la velocidad de una onda en una cuerda es inversamente proporcional a la raíz cuadrada de la densidad de masa lineal, la velocidad sería mayor en la densidad de masa lineal baja de la cuerda.
17. La tensión en el cable se debe al peso del cable de alimentación eléctrica.
19. La potencia promediada en el tiempo es P = Eλ/T = 1/2μA2ω2λ/T = 1/2μA2ω2v. Si la frecuencia o la amplitud se reducen a la mitad, la potencia disminuye en un factor de 4.
21. A medida que una parte de la cuerda se mueve verticalmente, ejerce una fuerza sobre la parte adyacente de la cuerda, haciendo un trabajo en dicha parte y transfiriendo la energía.
23. La intensidad de una onda esférica es I = P/4πr2; si no se disipa la energía, la intensidad disminuirá en un factor de nueve a tres metros.
25. En la interfaz, el pulso incidente produce un pulso reflejado y un pulso transmitido. El pulso reflejado estaría fuera de fase con respecto al pulso incidente y se movería a la misma velocidad de propagación que el pulso incidente, pero se movería en la dirección opuesta. El pulso transmitido viajaría en la misma dirección que el pulso incidente, pero a la mitad de la velocidad. El pulso transmitido estaría en fase con el pulso incidente. Tanto el pulso reflejado como el transmitido tendrían amplitudes menores que la amplitud del pulso incidente.
27.
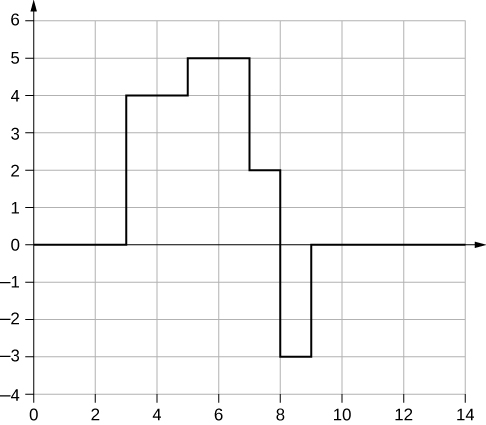
29. Puede ser tan fácil como cambiar la longitud y/o la densidad una pequeña cantidad para que las partes no resuenen a la frecuencia del motor.
31. La energía es suministrada al vidrio por el trabajo realizado por la fuerza de tu dedo sobre el vidrio. Cuando se suministra en la frecuencia correcta, se forman ondas estacionarias. El vidrio resuena y las vibraciones producen sonido.
33. Para la ecuación y(x, t) = 4.00 cmsen(3 m−1x)cos(4 s−1t), hay un nodo porque cuando x = 0.00 m, sen(3 m−1(0.00 m)) = 0.00, entonces y(0.00 m, t) = 0.00 m para todos los tiempos. Para la ecuación y(x, t) = 4.00 cmsen(3 m−1x + π/2)cos(4 s−1t), hay un antinodo porque cuando x = 0.00 m, sen(3 m−1(0.00 m) + π2) = +1.00, entonces y(0.00m , t) oscila entre +A y −A mientras el término coseno oscila entre +1 y -1.
Problemas
35. 2d = vt ⇒ d = 11.25 m
37. v = fλ, por lo que f = 0.125Hz, entonces
N = 7.50 veces
39. v = fλ ⇒ λ = 0.400 m
41. v = fλ ⇒ f = 2.50 × 109 Hz
43. a. Las ondas P superan a las ondas S a una velocidad de v = 3.20 km/s; por lo tanto, Δd = 0.320 km. b. Dado que la incertidumbre en la distancia es inferior a un kilómetro, nuestra respuesta a la parte (a) no parece limitar la detección de detonaciones de bombas nucleares. Sin embargo, si las velocidades son inciertas, entonces la incertidumbre en la distancia aumentaría y podría dificultar la identificación de la fuente de las ondas sísmicas.
45. vΔ = 1900 m/s; t = 1.05 μs
47. y(x, t) = - 0.037 cm
49.
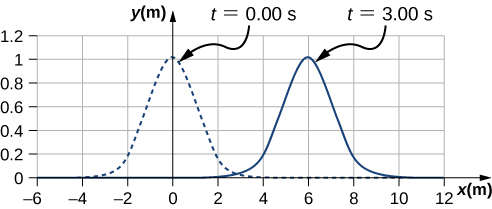
El pulso se moverá Δx = 6.00 m.
51. a. A = 0,25 m; b. k = 0.30 m−1; c. ω = 0.90s−1; d. v = 3,0 m/s; e. φ = π/3 rad; f. λ = 20.93 m; g. T = 6.98 s
53. A = 0.30 m, λ = 4.50 m, v = 18.00 m/s, f = 4.00 Hz, T = 0.25 s
55. y(x, t) = 0.23 msen(3.49 m−1x − 0.63 s−1t)
57. Tienen la misma frecuencia angular, frecuencia y período. Viajan en direcciones opuestas y y2(x, t) tiene el doble de la longitud de onda de y1(x, t) y se mueve a la mitad de la velocidad de la onda.
59. Cada partícula del medio se mueve una distancia de 4A en cada período. El período se puede encontrar al dividir la velocidad por la longitud de onda: t = 10.42 s
61. a. μ = 0.040 kg/m; b. v = 15.75 m/s
63. v = 180 m/s
65. v = 547.723 m/s, t = 5.48 ms
67. 0.707
69. v1t + v2t = 2.00 m, t = 1.69 ms
71. v = 288.68 m/s, λ = 0.73 m
73. a. A = 0.0125 cm; b. FT = 0.96 N
75. v = 74.54 m/s, Pλ = 91.85 W
77. a. I = 20.0 W/m2; b. I = P/A, A = 10.0 m2, A = 4πr2, r = 0.892 m
79. I = 650 W/m2
81. P ∝ E ∝ I ∝ X2 ⇒ P2/P1 = (X2/X1)2
83. I ∝ X2 ⇒ I1/I2 = (X1/X2)2
⇒ I2 = 3.38×10−5 W/m2
85. f = 100.00 Hz, A = 1.10 cm
87. a. I2 = 0.063I1; b. I14πr12 = I24πr22, r2 = 3.16 m
89. 2πr1A12 = 2πr2A22, A1 = (r2/r1)1/2, A1 = 0.17 m
91. y(x,t) = 0.63 m
93. AR = 2Acos(φ/2), φ = 1.17 rad
95. yR = 1.90 cm
97. ω = 6.28 s−1, k=3.00 m−1, φ = π/8 rad,
AR = 2Acos(φ/2), A = 0.37 m
99. a.
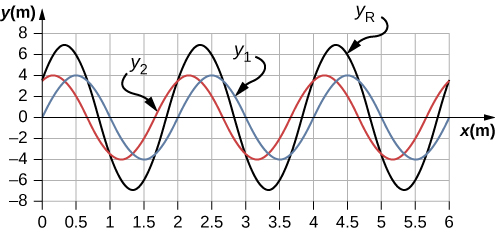
b. λ = 2.0 m, A = 4 m; c. λR = 2.0 m, AR = 6.93 m
101. yR(x, t) = 2Acos(φ/2)cos(kx − ωt + φ/2); El resultado no es sorprendente porque cos(θ) = sen(θ + π/2).
103. λn = 2.00/nL, fn = v/λn
λ1 = 4.00 m, f1 = 12.5 Hz
λ2 = 2.00 m, f2 = 25.00 Hz
λ3 = 1.33 m, f3 = 37.59 Hz
105. v = 158.11 m/s, λ = 4.44 m, f = 35.61 Hz, λs = 9.63 m
107. y(x,t) = [0.60 cmsen(3 m−1x)]cos(4 s−1t)
109. λ100 = 0.06 m, v = 56.8 m/s,
fn = nf1, n=1,2,3,4,5...
f100 = 947 Hz
111. T = 2Δt, v = λ/T, λ = 2.12 m
113. λ1 = 6.00 m, λ2 = 3.00m, λ3 = 2.00 m, λ4 = 1.50m
v = 258.20 m/s = λf
f1 = 43.03 Hz, f2 = 86.07 Hz, f3 = 129.10 Hz, f4 = 172.13 Hz
115. v = 134.16 ms, λ = 1.4m, f = 95.83 Hz, T = 0.0104 s
Problemas Adicionales
117. λ = 0.10 m
119. a. f = 4.74×1014 Hz; b. λ = 422 nm
121. λ = 16.00 m, f = 0.10 Hz, T = 10.00 s, v = 1.6 m/s
123. λ = (vb + v)tb, v = 3.75 m/s, λ = 3.00 m
125. ∂2(y1 + y2)/∂t2 = −Aω2sen(kx − ωt) − Aω2sen(kx − ωt + φ)
∂2(y1 + y2)/∂t2 = −Ak2sen(kx − ωt) − Ak2sen(kx − ωt + φ)
∂2(x, y)/∂x2 = 1/v2∂2(x, y)/∂t2
−Aω2sen(kx − ωt) − Aω2sen(kx − ωt + φ) = (1/v2)(−Ak2sen(kx − ωt) − Ak2sen(kx − ωt + φ))
v = ω/k
127. y(x, t) = 0.40 msen(0.015 m−1x + 1.5 s−1t)
129. v = 223.61 m/s, k = 1.57 m−1, ω = 142.43 s−1
131. P = 1/2A2(2πf)2√μFT/
μ = 2.00×10−4 kg/m
133. P = 1/2
μA2ω2λ/T, μ = 0.0018 kg/m
135. a. AR = 2Acos(φ/2), cos(φ/2) = 1, φ = 0,2π,4π,...; b. AR = 2Acos(φ/2), cos(φ/2) = 0, φ = 0,π,3π,5π...
137. yR(x, t) = 0.6 msen(4 m−1x)cos(3 s−1t)
139. a. (1) FT − 20.00kg(9.80 m/s2)cos45° = 0
2) m(9.80 m/s2) − FT = 0
m = 14.14 kg
b. FT = 138.57 N
v = 67.96m/s
141. FT = 12 N, v = 16.49 m/s
143. a. fn = nv/2L, v = 2Lfn+1/n+1, n+1/n = 2Lfn+1/2Lfn, 1 + 1/n = 1.2, n = 5
λn = 2/nL, λ5 = 1.6m, λ6 = 1.33m
b. FT = 245.76 N
Problemas de Desafío
145. a. Se mueve en la dirección x negativa a una velocidad de propagación de v = 2.00 m/s.
b. Δx = −6.00 m;
c.
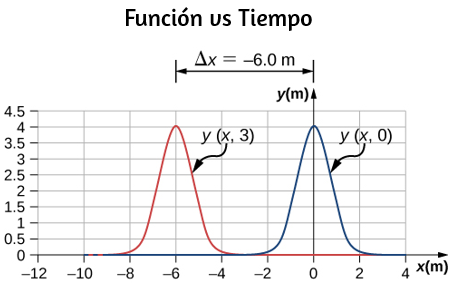
147. sen(kx − ωt) = sen(kx + φ/2)cos(ωt + φ/2) − cos(kx + φ/2)sen(ωt + φ/2)
sen(kx −ωt + φ/2) = sin(kx + φ/2)cos(ωt + φ/2) + cos(kx + φ/2)sen(ωt + φ/2)
sen(kx − ωt) + sen(kx + ωt + φ) = 2sen(kx + φ/2)cos(ωt + φ/2)
yR = 2Asen(kx + φ/2)cos(ωt + φ/2)
149. sen(kx + φ/2) = 0, kx + φ/2 = 0,π, 2π, 1.26 m−1x + π/20 = π, 2π, 3π
x = 2.37 m, 4.86 m, 7.35 m
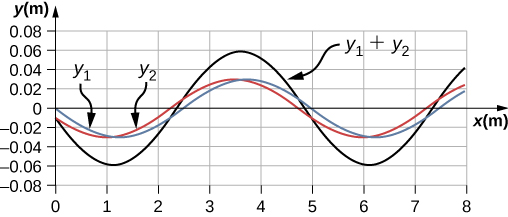
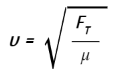 muestra que la potencia es proporcional a la raíz cuadrada de la tensión y proporcional a la raíz cuadrada de la densidad de masa lineal:
muestra que la potencia es proporcional a la raíz cuadrada de la tensión y proporcional a la raíz cuadrada de la densidad de masa lineal: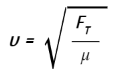 = 12A2ω2√μFT
= 12A2ω2√μFT




