Respuestas - Capítulo II

Excepto por las preguntas de los apartados de Comprueba tu aprendizaje, sólo se dan las respuestas de los numerales impares

Comprueba tu aprendizaje

2.1 a. μ_s ≥ tan θ/1 + (mr²/I_CM); reemplazando el ángulo y observando que para un cilindro hueco I_CM = mr², tenemos μ_s ≥ tan 60°/1 + (mr²/mr²) = 1/2tan60 ° = 0,87; se nos da un valor de 0,6 para el coeficiente de fricción estática, que es menor que 0,87, por lo que la condición no se cumple y el cilindro hueco se deslizará;
b. El cilindro sólido obedece a la condición μ_s ≥ 1/3tanθ = 1/3tan 60° = 0.58. El valor de 0.6 para μ_s cumple esta condición, por lo que el cilindro sólido no se deslizará.

2.2 De la figura, vemos que el producto cruz del vector de radio con el vector de momento proporciona un vector dirigido fuera de la página. Al insertar el radio y el momento en la expresión del momento angular, tenemos

l→ = r→ × p→ = (0.4 mi^) × (1,67 × 10^-27 kg(4,0 × 10⁶ m/s)j^) = 2.7 × 10^-21 kg • m²/sk^

2.3 I_esfera = 2/5mr², I_cilindro = 1/2mr²; tomando la relación de los momentos angulares, tenemos:

L_cilindro/L_esfera = I_cilindroω₀/I_esferaω₀ = (1/2)mr²/(2/5)mr² = 5/4. Por lo tanto, el cilindro tiene un 25% más de momento angular. Esto se debe a que el cilindro tiene más masa distribuida más lejos del eje de rotación.

2.4 Usando la conservación del momento angular, tenemos

I(4.0 rev/min) = 1.25Iω_f, ω_f = 1.0/1.25(4.0 rev/min) = 3.2 rev/min

2.5 La gravedad de la Luna es 1/6 de la de la Tierra. Al examinar la Ecuación 2.12, vemos que la frecuencia de precesión de la parte superior es linealmente proporcional a la aceleración de la gravedad. Todas las demás cantidades, masa, momento de inercia y velocidad de rotación son iguales en la Luna. Por lo tanto, la frecuencia de precesión en la Luna es

ω_P(Luna) = 1/6ω_P(Tierra) = 1/6(5.0 rad/s) = 0.83 rad/s.

Preguntas conceptuales

1. No, la fuerza de fricción estática es cero.

3. Es más probable que la rueda se deslice en una pendiente pronunciada, ya que el coeficiente de fricción estática debe aumentar con el ángulo para mantener el movimiento de rodadura sin deslizarse.

5. El cilindro alcanza una mayor altura. Según la Ecuación 2.4, su aceleración en la dirección hacia abajo de la pendiente sería menor.

7. Todos los puntos en la línea recta darán momento angular cero, porque un vector cruz en un vector paralelo es cero.

9. La partícula debe moverse en una línea recta que pasa por el origen elegido.

11. Sin la pequeña hélice, el cuerpo del helicóptero giraría en el sentido opuesto a la gran hélice para conservar el momento angular. La pequeña hélice ejerce un empuje a una distancia R desde el centro de masa del avión para evitar que esto suceda.

13. La velocidad angular aumenta porque el momento de inercia está disminuyendo.

15. Más masa se concentra cerca del eje de rotación, lo que disminuye el momento de inercia que hace que la estrella aumente su velocidad angular.

17. Se necesita un torque en la dirección perpendicular al vector de momento angular para cambiar su dirección. Estas fuerzas en el vehículo espacial son externas al contenedor en el que está montado el giroscopio y no imparten torques al disco giratorio del giroscopio.

Problemas

19. v_CM = Rω ⇒ ω = 66.7 rad/s

21 α = 3.3 rad/s²

23. I_CM = 2/5mr², a_CM = 3.5 m/s²; x = 15.75 m

25. positivo es el plano inclinado;

a_CM = mg senθ/m + (I_CM/r²) ⇒ I_CM = r²(mgsen30/a_CM - m),
x - x₀ = v₀t - 1/2a_CMt² ⇒ a_CM = 2.96 m/s²,
I_CM = 0.66 mr²

27. α = 67.9 rad/s²
(a_CM)_x = 1.5 m/s²

29. W = -1080.0 J

31. La energía mecánica en la parte inferior es igual a la energía mecánica en la parte superior;

1/2mv₀² + 1/2(1/2mr²)(v₀/r)² = mgh ⇒ h = 1/g(1/2 + 1/4)v₀²,
h = 7.7 m, entonces la distancia arriba de la pendiente es 22.5 m.

33. Usa la conservación de la energía

1/2mv₀² + 1/2I_Cylω₀² = mgh_Cyl,
1/2mv₀² + 1/2I_Sphω₀² = mgh_Sph

Restando las dos ecuaciones, eliminando la energía traslacional inicial, tenemos

1/2I_Cylω₀² = mgh_Cyl - 1/2I_Sphω₀² = mgh_Sph = mg(h_Cyl - h_Sph),
1/2mr²(v₀/r)² - 1/22/3(v₀/r)² = mg(h_Cyl - h_Sph)
1/2v₀² - 1/22/3v₀² = g(h_Cyl - h_Sph),
h_Cyl - h_Sph = 1/g(1/2 - 1/3)v₀² = 1/9.8 m/s²(1/6)(5.0 m/s)² = 0.43 m.

Por lo tanto, la esfera hueca, con el menor momento de inercia, rueda hasta una altura menor de 1.0 - 0.43 = 0.57 m.

35. La magnitud del producto cruz del radio al ave y su vector de momento produce rpsenθ, que da rsenθ como la altitud del ave h. La dirección del momento angular es perpendicular al radio y a los vectores de momento, que elegimos arbitrariamente como k^, que está en el plano del suelo:

L→ = r→ × p→ = hmvk^ = (300.0 m)(2.0 kg)(20.0 m/s)k^ = 12,000.0 kg • m²/s

37. a. l→ = 45.0 kg • m²/sk^;
b. τ = 10.0 N • mk^

39. a. l→₁ = −0.4 kg • m²/sk^, l→₂ = l→₄ = 0,
l→₃ = 1.35 kg • m²/sk^;
L→ = 0.95 kg • m²/sk^

41. a. L = 1.0 × 10¹¹ kg • m²/s; b. No, el momento angular permanece igual ya que el producto cruz involucra solo la distancia perpendicular desde el plano al suelo sin importar a donde se encuentre a lo largo de su trayectoria.

43. a. v→ = -gtj^, r→_⊥ = -di^, l→ = mdgtk^;
b. F→ = -mgj^, ∑τ = dmgk^;
c. Sí

45. a. mgh = 1/2m(rω)² + 1/22/5mr²ω²;

ω = 51.2 rad/s
L = 16.4 kg • m²/s ;
b. ω = 72.5 rad/s;
L = 23.2 kg • m²/s

47. a. I = 720.0 kg • m²; α = 4.20 rad/s²;
ω(10 s) = 42.0 rad/s; L = 3.02 × 10⁴ kg • m²/s;
ω(20 s) = 84.0 rad/s;
b. τ = 3.03 × 10³ N • m

49. a. L = 1.131 × 10⁷ kg • m²/s;
b. τ = 3.77 × 10⁴ N • m

51. ω = 28.6 rad/s ⇒ L = 2.6 kg • m²/s

53. L_f = 2/5M_s(3.5 × 10³ km)²2π/T_f
⇒T_f = 28 días(3.5 × 10³ km)²/(7.0 × 10⁵km)² = 7.0 × 10^-4 día = 60.5 s

55. f_f = 2.1 rev/s ⇒ f₀ = 0.5 rev/s

57. r_Pmv_P = r_Amv_A ⇒ v_P = 18.3 km/s

59. a. I_disco = 5.0 × 10^-4 kg • m²,
I_bicho = 2.0 × 10^-4 kg • m²,
(I_disco + I_bicho)ω₁ = I_discoω₂,
ω₂ = 14.0 rad/s
b. ΔK = 0.014 J;
c. ω₃ = 10.0 rad/s vuelve al valor original;
d. 1/2(I_disco + I_bicho)ω₃² = 0.035 J vuelve al valor original;
e. trabajo del bicho que se arrastra en el disco

61. L_i = 400.0 kg • m²/s,
L_f = 500.0 kg • m²ω,
ω = 0.80 rad/s

63. I₀ = 340.48 kg • m²,
I_f = 268.8 kg • m²,
ω_f = 25.33 rpm

65. a. L = 280 kg • m²/s,
I_f = 89.6 kg • m²,
ω_f = 3.125 rad/s;
b. K_i = 437.5 J,
K_f = 437.5 J

67. Momento de inercia en el giro discográfico: I₀ = 0.5 kg • m²,
I_f = 1.1 kg • m²,
ω_f = I₀/I_fω₀ ⇒ f_f = 155.5 rev/min

69. Su velocidad de giro en el aire es: f_f = 2.0 rev/s;
Puede hacer cuatro volteretas en el aire.

71. Momento de inercia con todos los niños a bordo:

I₀ = 2.4 × 10⁵ kg • m²;
I_f = 1.5 × 10⁵ kg • m²;
f_f = 0.3 rev/s

73. I₀ = 1.00 × 10¹⁰ kg • m²,
I_f = 9.94 × 10⁹ kg • m²,
f_f = 3.32 rev/min

75. I = 2.5 × 10^-3 kg • m¹⁰,
ω_P = 0.78 rad/s

77. a. L_tierra = 7.06 × 10³³ kg • m²/s,
ΔL = 5.63 × 10³³ kg • m²/s;
b. τ = 1.4 × 10²² N • m;
c. Las dos fuerzas en el ecuador tendrían la misma magnitud pero diferentes direcciones, una en la dirección norte y la otra en la dirección sur en el lado opuesto de la Tierra. El ángulo entre las fuerzas y los brazos de palanca en el centro de la Tierra es de 90°, por lo que un torque dado tendría una magnitud τ = FR_Esen90° = FR_E. Ambos proporcionarían un par en la misma dirección:

τ = 2FR_E ⇒ F = 1.3 × 10¹⁵ N

Problemas Adicionales

79. a_CM = -3/10g;
v² = v²₀ + 2a_CMx ⇒ v² = (7.0 m/s)² - 2(3/10g)x;
v² = 0 ⇒ x = 8.34m;
b. t = v - v₀/a_CM, v = v₀ + a_CMt ⇒ t = 2.38 s;

La esfera hueca tiene un mayor momento de inercia y, por lo tanto, es más difícil de detener que la canica o la esfera sólida. La distancia recorrida es más grande y el tiempo transcurrido es más largo.

81. a. W = −500.0 J;
b. K + U_grav = constante,
500 J + 0 = 0 + (6.0 kg)(9.8 m/s²)h,
h = 8.5 m, d = 17.0 m;

El momento de inercia es menor para la esfera hueca, por lo tanto, se requiere menos trabajo para detenerlo. Del mismo modo, sube la inclinación una distancia más corta que el aro.

83. a. τ = 34.0 N • m;
b. l = mr²ω ⇒ ω = 3.6 rad/s

85. a. d_M = 3.85 × 10⁸ mdistancia promedio a la Luna; periodo orbital 27.32d = 2.36 × 10⁶s; velocidad de la luna 2π3.85 × 10⁸ m/2.36 × 10⁶ s = 1.0 × 10³ m/s; masa de la luna 7.35 × 10²²kg,

L = 2.90 × 10³⁴ kgm²/s;

b. radio de la luna 1.74 × 10⁶ m; el período orbital es el mismo que
(a): ω = 2.66 × 10^-6 rad/s,

L = 2.37 × 10²⁹ kg • m²/s;

El momento angular orbital es 1.22 × 10⁵ veces mayor que el momento angular de rotación para la Luna.

87. I = 0.135 kg • m²,
α = 4.19 rad/s², ω = ω₀ + αt,
ω(5 s) = 21.0 rad/s, L = 2.84 kg • m²/s,
ω(10 s) = 41.9 rad/s, L = 5.66 kg • m/s²

89. En la conservación de la ecuación del momento angular, la velocidad de rotación aparece en ambos lados, así que mantenemos la notación (rev/min) ya que la velocidad angular puede multiplicarse por una constante para obtener (rev/min):

L_i = -0.04 kg • m²(300.0 rev/min),
L_f = 0.08 kg • m²f_f ⇒ f_f = -150.0 rev/min agujas del reloj

91. I₀ω₀ = I_fω_f,
I₀ = 6120.0 kg • m²,
I_f = 1180.0 kg • m²,
ω_f = 31.1 rev/min

93. L_i = 1.00 × 10⁷ kg • m²/s,
I_f = 2.025 × 10⁵ kg • m²,
ω_f = 7.86 rev/s

Problemas de Desafío

95. Supongamos que el rodillo acelera hacia adelante con respecto al suelo con una aceleración a'. Luego acelera hacia atrás en relación con el camión con una aceleración (a - a').



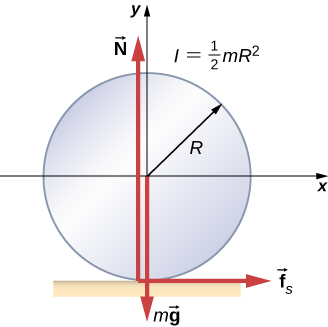
También, Rα = a -a'I = 1/2mR²∑F_x 0 f_s = ma',

∑τ = f_sR = Iα = Ia - a'/Rf_s = I/R²(a - a') = 1/2m(a -a')
Resolviendo para a': f_s = 1/2m(a -a'); a' = a/3,
x - x₀ = v₀t + 1/2at²; d = 1/3at²; t = √3d/a/

entonces, s = 1.5d

97. a. La tensión en la cuerda proporciona la fuerza centrípeta de modo que Tsenθ = mr_⊥ω². El componente de la tensión que es vertical se opone a la fuerza gravitatoria de tal manera que Tcosθ = mg. Esto da T = 5,7 N. Resolvemos para r_⊥ = 0.16 m. Esto da la longitud de la cadena como r = 0.32 m.

En ω = 10.0 rad/s, hay un nuevo ángulo, tensión y radio perpendicular a la barra. Dividiendo las dos ecuaciones que implican la tensión para eliminarlo, tenemos sen θ/cos θ = (0.32 msenθ)ω²/g ⇒ 1/cosθ = 0.32mω²/g;

cosθ = 0.31 ⇒ θ = 72.2°;

b. l_inicial = 0.08 kg • m²/s,
l_final = 0.46 kg • m²/s;

c. No, el coseno del ángulo es inversamente proporcional al cuadrado de la velocidad angular, por lo tanto, para θ → 90°, ω → ∞. La barra debería girar infinitamente rápido.