Preguntas y problemas - Capítulo IX

26. Considera un par de espejos planos que estén colocados de manera que formen un ángulo de 120°. Un objeto se coloca en la bisectriz entre los espejos. Construye un diagrama de rayos como en la figura 9.4 para mostrar cuántas imágenes se forman.

27. Considera un par de espejos planos que estén colocados de manera que formen un ángulo de 60°. Un objeto se coloca en la bisectriz entre los espejos. Construye un diagrama de rayos como en la figura 9.4 para mostrar cuántas imágenes se forman.

28. Al usar más de un espejo plano, construye un diagrama de rayos que muestre cómo crear una imagen invertida.

2.2 Espejos esféricos

29. La siguiente figura muestra una bombilla entre dos espejos esféricos. Un espejo produce un haz de luz con rayos paralelos; el otro evita que la luz se escape sin ser puesta en el haz. ¿Dónde está el filamento de la luz en relación con el punto focal o el radio de curvatura de cada espejo?



30. ¿Por qué los espejos divergentes se usan a menudo para los espejos retrovisores en los vehículos? ¿Cuál es la principal desventaja de usar un espejo de este tipo en comparación con uno plano?

31. Algunas cámaras de teleobjetivo usan un espejo en lugar de una lente. ¿Qué radio de curvatura del espejo se necesita para reemplazar un teleobjetivo de distancia focal de 800 mm?

32. Calcula la longitud focal de un espejo formado por el dorso brillante de una cuchara que tiene un radio de curvatura de 3.00 cm.

33. Los calentadores eléctricos de habitaciones utilizan un espejo cóncavo para reflejar la radiación infrarroja (IR) de las bobinas calientes. Ten en cuenta que la radiación IR sigue la misma ley de reflexión que la luz visible. Dado que el espejo tiene un radio de curvatura de 50.0 cm y produce una imagen de las bobinas a 3.00 m de distancia del espejo, ¿dónde están las bobinas?

34. Encuentra el aumento del elemento calentador en el problema anterior. Ten en cuenta que su gran magnitud ayuda a dispersar la energía reflejada.

35. ¿Cuál es la longitud focal de un espejo de maquillaje que produce un aumento de 1.50 cuando la cara de una persona está a 12.0 cm de distancia? Muestra explícitamente cómo se sigue los pasos en el Ejemplo 9.2.

36. Un comprador que se encuentra a 3.00 m de un espejo de seguridad convexo ve su imagen con un aumento de 0.250. (a) ¿Dónde está su imagen? (b) ¿Cuál es la distancia focal del espejo? (c) ¿Cuál es su radio de curvatura?

37. Un objeto de 1,50 cm de altura se mantiene a 3,00 cm de la córnea de una persona y su imagen reflejada se mide a 0,167 cm de altura. (a) ¿Cuál es el aumento? (b) ¿Dónde está la imagen? (c) Encuentra el radio de curvatura del espejo convexo formado por la córnea (tenga en cuenta que los optometristas utilizan esta técnica para medir la curvatura de la córnea para el ajuste de lentes de contacto. El instrumento utilizado se llama queratómetro o medidor de curva).

38. El trazado de rayos para un espejo plano muestra que la imagen está ubicada a una distancia detrás del espejo igual a la distancia del objeto al espejo. Esto se indica como d_i = −d_o, ya que se trata de una distancia de imagen negativa (es una imagen virtual). ¿Cuál es la longitud focal de un espejo plano?

39. Muestre que, para un espejo plano, h_i = h_o, dado que la imagen está a la misma distancia detrás del espejo que la distancia del objeto al espejo.

40. Usa la ley de reflexión para demostrar que la distancia focal de un espejo es la mitad de su radio de curvatura. Es decir, probar que f = R/2. Ten en cuenta que esto es cierto para un espejo esférico solo si su diámetro es pequeño en comparación con su radio de curvatura.

41. Refiriéndose al calentador eléctrico de la habitación, calcula la intensidad de la radiación IR en W/m² proyectada por el espejo cóncavo en una persona a 3.00 m de distancia. Supón que el elemento de calentamiento irradia 1500 W y tiene un área de 100 cm², y que la mitad de la potencia irradiada se refleja y enfoca en el espejo.

42. Dos espejos están inclinados en un ángulo de 60° y un objeto se coloca en un punto que es equidistante de los dos espejos. Usa un transportador para dibujar los rayos con precisión y localizar todas las imágenes. Puede que tengas que dibujar varias figuras para que los rayos de diferentes imágenes no saturen tu dibujo.

43. Dos espejos paralelos están enfrentados y separados por una distancia de 3 cm. Un objeto puntual se coloca entre los espejos a 1 cm de uno de los espejos. Encuentra las coordenadas de todas las imágenes.

9.3 Imágenes formadas por refracción

44. Un objeto está ubicado en el aire a 30 cm del vértice de una superficie cóncava hecha de vidrio con un radio de curvatura de 10 cm. ¿Dónde se forma la imagen por refracción y cuál es su aumento? Utiliza n_aire = 1 y n_vidrio = 1.5.

45. Un objeto está ubicado en el aire a 30 cm del vértice de una superficie convexa hecha de vidrio con un radio de curvatura de 80 cm. ¿Dónde se forma la imagen por refracción y cuál es su aumento?

46. ​​Un objeto está ubicado en agua a 15 cm del vértice de una superficie cóncava hecha de vidrio con un radio de curvatura de 10 cm. ¿Dónde se forma la imagen por refracción y cuál es su aumento? Utiliza n_agua = 4/3 y n_vidrio = 1.5.

47. Un objeto se encuentra en el agua a 30 cm del vértice de una superficie convexa hecha de plexiglás con un radio de curvatura de 80 cm. ¿Dónde se forma la imagen por refracción y cuál es su aumento? Utiliza n_agua = 4/3 y n_plexiglás = 1.65.

48. Un objeto está ubicado en el aire a 5 cm del vértice de una superficie cóncava hecha de vidrio con un radio de curvatura de 20 cm. ¿Dónde se forma la imagen por refracción y cuál es su aumento? Utiliza n_aire = 1 y n_vidrio = 1.5.

49. Deduce la ecuación de interfaz esférica para la refracción en una superficie cóncava (Sugerencia: sigue la deducción en el texto para la superficie convexa).

9.4 Lentes delgadas

50. ¿A qué distancia de la lente debe estar la película en una cámara, si la lente tiene una distancia focal de 35.0 mm y se utiliza para fotografiar una flor a 75.0 cm de distancia? Muestra explícitamente cómo sigues los pasos de la figura 9.27.

51. Un determinado proyector de diapositivas tiene una lente de 100 mm de distancia focal. (a) ¿A qué distancia se encuentra la pantalla si se coloca una diapositiva a 103 mm del objetivo y produce una imagen nítida? (b) Si la diapositiva es de 24.0 por 36.0 mm, ¿cuáles son las dimensiones de la imagen? Muestra explícitamente cómo sigues los pasos de la figura 9.27.

52. Un médico examina un lunar con una lupa de longitud focal de 15,0 cm sostenida a 13,5 cm del lunar. (a) ¿Dónde está la imagen? (b) ¿Cuál es su aumento? (c) ¿Qué tan grande es la imagen de un lunar de 5.00 mm de diámetro?

53. Se está utilizando una cámara con una lente de 50.0 mm de distancia focal para fotografiar a una persona parada a 3.00 m de distancia. (a) ¿A qué distancia de la lente debe estar la película? (b) Si la película tiene 36.0 mm de altura, ¿qué fracción de una persona de 1.75 m de altura cabrá en ella? (c) Discute cuán razonable parece esto, según tu experiencia al tomar o posar para fotografías.

54. Una lente de cámara utilizada para tomar fotografías en primer plano tiene una distancia focal de 22.0 mm. Lo más lejos que se puede colocar de la película es de 33.0 mm. (a) ¿Cuál es el objeto más cercano que se puede fotografiar? (b) ¿Cuál es el aumento de este objeto más cercano?

55. Supón que tu lente de cámara de 50.0 mm de distancia focal está a 51.0 mm de la película de la cámara. (a) ¿Qué tan lejos está un objeto que está enfocado? (b) ¿Cuál es la altura del objeto si tu imagen tiene 2.00 cm de altura?

56. ¿Cuál es la distancia focal de una lupa que produce un aumento de 3.00 cuando se mantiene a 5.00 cm de un objeto, como una moneda rara?

57. El aumento de un libro de 7.50 cm desde una lente de 10.0 cm de distancia focal es de 3.00. (a) Encuentre el aumento del libro cuando se mantiene a 8,50 cm de la lupa. (b) Repite para el libro sostenido a 9.50 cm de la lupa. (c) Comenta sobre cómo cambia el aumento a medida que aumenta la distancia del objeto como en estos dos cálculos.

58. Supongamos que se está utilizando un teleobjetivo de distancia focal de 200 mm para fotografiar montañas a 10.0 km de distancia. (a) ¿Dónde está la imagen? (b) ¿Cuál es la altura de la imagen de un acantilado de 1000 m de altura en una de las montañas?

59. Se utiliza una cámara con una lente de 100 mm de distancia focal para fotografiar el sol. ¿Cuál es la altura de la imagen del sol en la película, dado que el sol tiene un diámetro de 1.40 × 10⁶ km y está a una distancia de 1.50 × 10⁸ km?

60. Usa la ecuación de lente delgada para mostrar que la ampliación de una lente delgada está determinada por su distancia focal y la distancia del objeto y está dada por m = f/(f − d_o).

61. Un objeto de altura 3,0 cm se coloca 5,0 cm delante de una lente convergente de 20 cm de distancia focal y se observa desde el otro lado. ¿Dónde y cuán grande es la imagen?

62. Un objeto de altura 3,0 cm se coloca a 5,0 cm frente a una lente divergente de distancia focal de 20 cm y se observa desde el otro lado. ¿Dónde y cuán grande es la imagen?

63. Un objeto de altura 3,0 cm se coloca a 25 cm frente a una lente divergente de distancia focal de 20 cm. Detrás de la lente divergente, hay una lente convergente de 20 cm de distancia focal. La distancia entre las lentes es de 5.0 cm. Encuentra la ubicación y el tamaño de la imagen final.

64. Dos lentes convexas con distancias focales de 20 cm y 10 cm se colocan separadas por 30 cm, con la lente con la longitud focal más larga a la derecha. Un objeto de altura 2,0 cm se coloca a medio camino entre ellos y se observa a través de cada lente desde la izquierda y desde la derecha. Describe lo que verás, por ejemplo, dónde aparecerán las imágenes, si estarán verticales o invertidas y sus aumentos.

9.5 El Ojo

A menos que se indique lo contrario, la distancia de la lente a la retina es de 2.00 cm.

65. ¿Cuál es la potencia del ojo al ver un objeto a 50.0 cm de distancia?

66. Calcula la potencia del ojo al ver un objeto a 3.00 m de distancia.

67. La impresión en muchos libros tiene un promedio de 3,50 mm de altura. ¿Qué tan alta es la imagen de la impresión en la retina cuando el libro se sostiene a 30.0 cm del ojo?

68. Supongamos que la agudeza visual de cierta persona es tal que puede ver claramente los objetos que forman una imagen de 4.00 μm de altura en su retina. ¿Cuál es la distancia máxima a la que puedes leer las letras de 75.0 cm de alto en el costado de un avión?

69. Las personas que realizan trabajos muy detallados de cerca, como los joyeros, a menudo pueden ver objetos claramente a una distancia mucho más cercana que los 25 cm normales. (a) ¿Cuál es la potencia de los ojos de una mujer que puede ver claramente un objeto a una distancia de solo 8,00 cm? (b) ¿Cuál es el tamaño de la imagen de un objeto de 1,00 mm, como las letras dentro de un anillo, que se mantiene a esta distancia? (c) ¿Cuál sería el tamaño de la imagen si el objeto se mantuviera a la distancia normal de 25.0 cm?

70. ¿Cuál es el punto lejano de una persona cuyos ojos tienen una potencia relajada de 50.5 D?

71. ¿Cuál es el punto cercano de una persona cuyos ojos tienen una potencia de 53.5 D?

72. (a) Un láser que remodela la córnea de un paciente miope reduce la potencia de su ojo en 9.00 D, con una incertidumbre de ± 5.0% en la corrección final. ¿Cuál es el rango de dioptrías para lentes de anteojos que esta persona podría necesitar después de este procedimiento? (b) ¿La persona fue miope o hipermétrope antes del procedimiento? ¿Cómo lo sabes?

73. La potencia para la visión de cerca normal es de 54.0 D. En un procedimiento de corrección de la visión, la potencia del ojo del paciente aumenta en 3.00 D. Suponiendo que esto produce una visión de cerca normal, ¿cuál era el punto cercano al paciente antes del procedimiento?

74. Para la visión distante normal, el ojo tiene una potencia de 50.0 D. ¿Cuál fue el punto lejano anterior de un paciente que tuvo una corrección de la visión con láser que redujo la potencia de su ojo en 7.00 D, produciendo una visión distante normal?

75. La potencia para la visión distante normal es 50.0 D. Un paciente con miopía severa tiene un punto lejano de 5.00 cm. ¿Cuántas dioptrías debe reducirse la potencia de su ojo en la corrección de la visión con láser para obtener una visión normal a distancia?

76. Los ojos de un estudiante, mientras lee la pizarra, tienen una potencia de 51.0 D. ¿Qué tan lejos está el tablero de sus ojos?

77. La potencia de los ojos de un médico es de 53.0 D al examinar a un paciente. ¿A qué distancia de sus ojos está el objeto que está siendo examinado?

78. La potencia normal para la visión distante es 50.0 D. Una mujer joven con visión distante normal tiene un 10.0% de capacidad para acomodar (es decir, aumentar) la potencia de sus ojos. ¿Cuál es el objeto más cercano que puede ver claramente?

79. El punto lejano de un administrador miope es 50.0 cm. (a) ¿Cuál es la potencia relajada de sus ojos? (b) Si tiene la capacidad normal de 8.00% para acomodarse, ¿cuál es el objeto más cercano que puede ver claramente?

80. Un hombre muy miope tiene un punto lejano de 20.0 cm. ¿Qué lentes de contacto de potencia (cuando está en el ojo) corregirán su visión distante?

81. Repite el problema anterior para anteojos sostenidos a 1,50 cm de los ojos.

82. Una persona miope ve que su receta de lentes de contacto es –4.00 D. ¿Cuál es su punto más lejano?

83. Repite el problema anterior para anteojos que están a 1.75 cm de los ojos.

84. La prescripción de lentes de contacto para una persona con visión lejana moderada es 0.750 D, y la persona tiene un punto cercano de 29.0 cm. ¿Cuál es la potencia de la capa de lágrimas entre la córnea y la lente si la corrección es ideal, teniendo en cuenta la capa de lágrimas?

9.7 La lupa simple

85. Si la imagen formada en la retina subtiende un ángulo de 30° y el objeto subtiende un ángulo de 5°, ¿cuál es el aumento de la imagen?

86. ¿Cuál es el aumento de una lente de aumento con una distancia focal de 10 cm si se mantiene a 3.0 cm del ojo y el objeto está a 12 cm del ojo?

87. ¿Qué tan lejos debe sostener una lupa de 2.1 cm de distancia focal de un objeto para obtener una ampliación de 10×? Supongamos que colocas tu ojo a 5.0 cm de la lupa.

88. Sostienes una lupa de 5.0 cm de distancia focal lo más cerca posible de tu ojo. Si tiene un punto cercano normal, ¿cuál es el aumento?

89. Ves una montaña con una lupa de longitud focal f = 10 cm. ¿Qué es el aumento?

90. Ves un objeto sosteniendo una lupa de 2,5 cm de distancia focal a 10 cm de distancia. ¿A qué distancia de tu ojo debes sostener la lupa para obtener un aumento de 10×?

91. Una lupa forma una imagen de 10 cm en el lado opuesto de la lente del objeto, que está a 10 cm de distancia. ¿Cuál es el aumento de esta lente para una persona con un punto cercano normal si su ojo está a 12 cm del objeto?

92. Un objeto visto a simple vista subtiende un ángulo de 2°. Si ves el objeto a través de una lupa 10×, ¿qué ángulo está subtendido por la imagen formada en tu retina?

93. Para un ojo normal y relajado, una lupa produce un aumento angular de 4.0. ¿Cuál es el mayor aumento posible con esta lupa?

94. ¿Qué rango de aumento es posible con una lente convergente de 7,0 cm de distancia focal?

95. Una lupa produce un aumento angular de 4,5 cuando la utiliza una persona joven con un punto cercano de 18 cm. ¿Cuál es el máximo aumento angular obtenido por una persona mayor con un punto cercano de 45 cm?

9.8 Microscopios y telescopios

96. Un microscopio con un aumento general de 800 tiene un objetivo que aumenta 200. (a) ¿Cuál es el aumento angular del ocular? (b) Si hay otros dos objetivos que se pueden usar, con aumentos de 100 y 400, ¿qué otros aumentos totales son posibles?

97. (a) ¿Qué aumento se produce con un objetivo de microscopio de 0,150 cm de distancia focal que está a 0,155 cm del objeto que se está viendo? (b) ¿Cuál es el aumento general si se usa un ocular de 8× (uno que produce un aumento angular de 8.00)?

98. ¿Dónde debe colocarse un objeto en relación con un microscopio para que su objetivo de distancia focal de 0,50 cm produzca un aumento de −400?

99. Una ameba está a 0.305 cm de la lente objetiva de distancia focal de 0.300 cm de un microscopio. (a) ¿Dónde está la imagen formada por la lente del objetivo? (b) ¿Cuál es el aumento de esta imagen? (c) Un ocular con una distancia focal de 2.00 cm se coloca a 20.0 cm del objetivo. ¿Dónde está la imagen final? (d) ¿Qué aumento angular produce el ocular? (e) ¿Cuál es el aumento general? (Ver figura 9.39).

100. Resultados irrazonables. Tus amigos te muestran una imagen a través de un microscopio. Te dicen que el microscopio tiene un objetivo con una distancia focal de 0.500 cm y un ocular con una longitud focal de 5.00 cm. El aumento global resultante es de 250.000. ¿Son estos valores viables para un microscopio?

A menos que se indique lo contrario, la distancia de la lente a la retina es de 2.00 cm.

101. ¿Cuál es el aumento angular de un telescopio que tiene un objetivo de distancia focal de 100 cm y un ocular de distancia focal de 2,50 cm?

102. Encuentra la distancia entre el objetivo y las lentes oculares en el telescopio en el problema anterior necesario para producir una imagen final muy lejos del observador, donde la visión es más relajada. Ten en cuenta que normalmente se utiliza un telescopio para ver objetos muy distantes.

103. Un gran telescopio reflector tiene un espejo objetivo con un radio de curvatura de 10.0 m. ¿Qué aumento angular se produce cuando se usa un ocular de distancia focal de 3.00 m?

104. Un telescopio pequeño tiene un espejo cóncavo con un radio de curvatura de 2.00 m para su objetivo. Su ocular es una lente focal de 4,00 cm. (a) ¿Cuál es el aumento angular del telescopio? (b) ¿Qué ángulo está subtendido por una mancha solar de 25,000 km de diámetro? (c) ¿Cuál es el ángulo de su imagen telescópica?

105. Un binocular de 7.5× produce un aumento angular de −7.50, actuando como un telescopio (los espejos se usan para colocar la imagen en posición vertical). Si los binoculares tienen lentes objetivas con una distancia focal de 75.0 cm, ¿cuál es la distancia focal de las lentes oculares?

106. Construye tu propio problema. Considera un telescopio del tipo usado por Galileo, que tiene un objetivo convexo y un ocular cóncavo como se ilustra en la parte (a) de la figura 9.40. Crea un problema en el que calcule la ubicación y el tamaño de la imagen producida. Entre las cosas a considerar están las distancias focales de las lentes y sus ubicaciones relativas, así como el tamaño y la ubicación del objeto. Verifica que el aumento angular sea mayor que uno. Es decir, el ángulo subtendido en el ojo por la imagen es mayor que el ángulo subtendido por el objeto.

107. Traza los rayos para encontrar de qué manera emergerá el rayo dado después de la refracción a través de la lente delgada en la siguiente figura. Supongamos una aproximación de lente delgada (Sugerencia: elige un punto P en el rayo dado en cada caso. Trata ese punto como un objeto. Ahora, encuentra su imagen Q. Usa la regla: Todos los rayos en el otro lado de la lente pasarán por Q o aparecerán venir de Q).



108. Copia y dibuja rayos para encontrar la imagen final en el siguiente diagrama (Sugerencia: encuentra la imagen intermedia solo a través de la lente. Usa la imagen intermedia como el objeto del espejo y trabaja solo con el espejo para encontrar la imagen final).



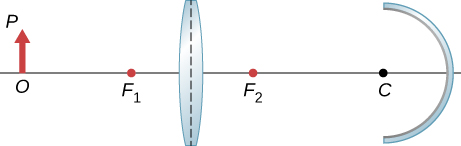
109. Un espejo cóncavo de radio de curvatura de 10 cm se coloca a 30 cm de una lente convexa delgada de 15 cm de longitud focal. Encuentra la ubicación y el aumento de una bombilla pequeña que se encuentra a 50 cm de la lente utilizando el método algebraico.

110. Un objeto de 3 cm de altura se coloca a 25 cm frente a una lente convergente de 20 cm de distancia focal. Detrás de la lente hay un espejo cóncavo de 20 cm de longitud focal. La distancia entre la lente y el espejo es de 5 cm. Encuentra la ubicación, orientación y tamaño de la imagen final.

111. Un objeto de altura de 3 cm se coloca a una distancia de 25 cm frente a una lente convergente de distancia focal de 20 cm, que se conoce como la primera lente. Detrás de la lente hay otra lente convergente de 20 cm de distancia focal colocada a 10 cm de la primera lente. Hay un espejo cóncavo de 15 cm de distancia focal colocado a 50 cm de la segunda lente. Encuentra la ubicación, orientación y tamaño de la imagen final.

112. Un objeto de altura 2 cm se coloca a 50 cm frente a una lente divergente de 40 cm de longitud focal. Detrás de la lente, hay un espejo convexo de 15 cm de distancia focal colocado a 30 cm de la lente convergente. Encuentra la ubicación, orientación y tamaño de la imagen final.

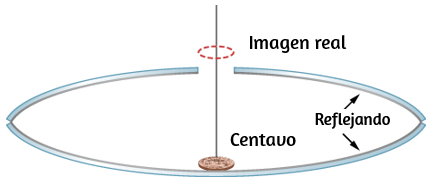
113. Dos espejos cóncavos se colocan uno frente al otro. Uno de ellos tiene un pequeño agujero en el medio. Se coloca un centavo en el espejo inferior (consulta la siguiente figura). Cuando miras de lado, se observa una imagen real del centavo sobre el agujero. Explica cómo podría pasar eso.



114. Una lámpara de altura 5 cm se coloca 40 cm frente a una lente convergente de distancia focal de 20 cm. Hay un espejo plano 15 cm detrás de la lente. ¿Dónde encontrarías la imagen cuando te miras en el espejo?

115. Rayos paralelos de una fuente lejana golpean una lente convergente de distancia focal de 20 cm en un ángulo de 15 grados con la dirección horizontal. Encuentra la posición vertical de la imagen real observada en una pantalla en el plano focal.

116. Los rayos paralelos de una fuente lejana golpean una lente divergente de distancia focal de 20 cm en un ángulo de 10 grados con la dirección horizontal. Al mirar a través de la lente, ¿dónde en el plano vertical aparecerá la imagen?

117. Una bombilla se coloca a 10 cm de un espejo plano, que mira hacia un espejo convexo de radio de curvatura de 8 cm. El espejo plano está situado a una distancia de 30 cm del vértice del espejo convexo. Encuentra la ubicación de dos imágenes en el espejo convexo. ¿Hay otras imágenes? Si es así, ¿dónde están ubicados?

118. Una fuente de luz puntual está 50 cm por delante de una lente convergente con una distancia focal de 30 cm. Un espejo cóncavo con una distancia focal de 20 cm se coloca a 25 cm detrás de la lente. ¿Dónde se forma la imagen final y cuál es su orientación y ampliación?

119. Copia y traza para descubrir cómo sale un rayo horizontal de S después de la lente. Usa n_vidrio = 1.5 para el material del prisma.



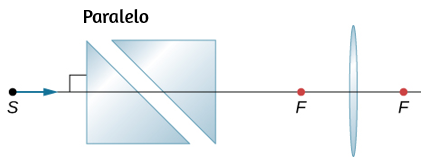
120. Copia y traza cómo un rayo horizontal de S sale después de la lente. Usa n = 1.55 para el vidrio.



121. Copia y dibuja rayos para descubrir la imagen final.



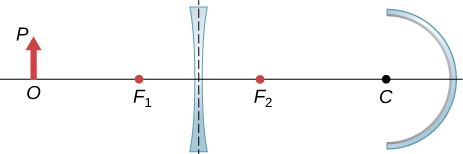
122. Por trazado de rayos o por cálculo, encuentra el lugar dentro del vidrio donde los rayos de S convergen como resultado de la refracción a través de la lente y la interfaz convexa aire-vidrio. Usa una regla para estimar el radio de curvatura.



123. Una lente divergente tiene una longitud focal de 20 cm. ¿Cuál es la potencia de la lente en dioptrías?

124. Dos lentes de distancia focal de f₁ y f₂ están pegadas con un material transparente de grosor insignificante. Demuestra que la potencia total de las dos lentes simplemente se suma.

125. ¿Cuál será el aumento angular de una lente convexa con la longitud focal de 2,5 cm?

126. ¿Cuál será la fórmula para el aumento angular de una lente convexa de distancia focal f si el ojo está muy cerca de la lente y el punto cercano está ubicado a una distancia D del ojo?

Problemas adicionales

127. Usa una regla y un transportador para dibujar rayos para encontrar imágenes en los siguientes casos.

(a) Un objeto puntual ubicado en el eje de un espejo cóncavo ubicado en un punto dentro de la distancia focal desde el vértice.
(b) Un objeto puntual ubicado en el eje de un espejo cóncavo ubicado en un punto más alejado que la distancia focal del vértice.
(c) Un objeto puntual ubicado en el eje de un espejo convexo ubicado en un punto dentro de la distancia focal desde el vértice.
(d) Un objeto puntual ubicado en el eje de un espejo convexo ubicado en un punto más lejano que la distancia focal desde el vértice.
(e) Repite (a) - (d) para un objeto puntual fuera del eje.

128. ¿Dónde debe colocarse un objeto de 3 cm de altura frente a un espejo cóncavo de 20 cm de radio para que su imagen sea real y 2 cm de altura?

129. Un objeto de 3 cm de altura se coloca 5 cm frente a un espejo convexo de radio de curvatura de 20 cm. ¿Dónde se forma la imagen? ¿Qué altura tiene la imagen? ¿Cuál es la orientación de la imagen?

130. Estás buscando un espejo para poder ver una imagen virtual magnificada cuatro veces mayor de un objeto cuando el objeto se coloca a 5 cm del vértice del espejo. ¿Qué tipo de espejo necesitarás? ¿Cuál debería ser el radio de curvatura del espejo?

131. Deduce la siguiente ecuación para un espejo convexo:
1/VO - 1/VI = 1/VF, donde VO es la distancia al objeto O desde el vértice V, VI la distancia a la imagen I desde V y VF es la distancia al punto focal F desde V (Sugerencia: usae dos conjuntos de triángulos similares).

132. (a) Dibuja rayos para formar la imagen de un objeto vertical en el eje óptico y más lejos que el punto focal de una lente convergente. (b) Use la geometría plana en su figura y pruebe que la ampliación m está dada por m = h_i/h_o = −d_i/d_o.

133. Usa otro diagrama de trazado de rayos para la misma situación dada en el problema anterior para derivar la ecuación de lente delgada, 1/d_o + 1/d_i = 1/f.

134. Fotografía a una persona de 2.0 m de altura con una cámara que tiene una lente de distancia focal de 5.0 cm. La imagen de la película no debe tener más de 2,0 cm de altura. (a) ¿Cuál es la distancia más cercana que la persona puede soportar a la lente? (b) Para esta distancia, ¿cuál debe ser la distancia desde la lente a la película?

135. Encuentra la longitud focal de una lente plana convexa delgada. La superficie frontal de esta lente es plana, y la superficie trasera tiene un radio de curvatura de R₂ = −35 cm. Supongamos que el índice de refracción de la lente es 1.5.

136. Encuentra la longitud focal de una lente de menisco con R₁ = 20 cm y R₂ = 15 cm. Supongamos que el índice de refracción de la lente es 1.5.

137. Un hombre miope no puede ver objetos claramente más allá de 20 cm de sus ojos. ¿Qué tan cerca debe estar de pie frente a un espejo para ver lo que está haciendo cuando se afeita?

138. Una madre ve que la prescripción de lentes de contacto de su hijo es 0.750 D. ¿Cuál es el punto cercano del niño?

139. Repite el problema anterior para anteojos que están a 2,20 cm de los ojos.

140. La prescripción de lentes de contacto para una persona miope es −4.00 D y la persona tiene un punto lejano de 22.5 cm. ¿Cuál es la potencia de la capa de lágrimas entre la córnea y la lente si la corrección es ideal, teniendo en cuenta la capa de lágrimas?

141. Resultados irrazonables. Un niño tiene un punto cercano a 50 cm y un punto lejano a 500 cm. ¿Un lente de −4.00 D corregirá su punto lejano al infinito?

142. Encuentra la ampliación angular de una imagen con una lupa de f = 5.0 cm si el objeto se coloca a = 4.0 cm de la lente y la lente está cerca del ojo.

143. El objetivo y el ocular de un microscopio compuesto tienen distancias focales de 2,5 cm y 10 cm, respectivamente, y estan separados por 12 cm. Un objeto de 70 μm se coloca a 6,0 cm del objetivo. ¿Qué tan grande es la imagen virtual formada por el sistema objetivo-ocular?

144. Dibuja rayos a escala para ubicar la imagen en la retina si la lente del ojo tiene una longitud focal de 2,5 cm y el punto cercano es de 24 cm (Sugerencia: coloca un objeto en el punto cercano).

145. El objetivo y el ocular de un microscopio tienen las distancias focales de 3 cm y 10 cm, respectivamente. Decide acerca de la distancia entre el objetivo y el ocular si necesitamos un aumento de 10 aumentos del sistema objetivo/ocular compuesto.

146. Una persona con visión lejana tiene un punto cercano de 100 cm. ¿A qué distancia delante o detrás de la retina se forma la imagen de un objeto colocado a 25 cm del ojo? Utiliza la córnea a la distancia de la retina de 2,5 cm.

147. Una persona miope tiene un punto lejano de 80 cm. (a) ¿Qué tipo de lente correctora necesitará la persona si la lente se coloca a 1.5 cm del ojo? (b) ¿Cuál sería la potencia de la lente de contacto necesaria? Supón que la distancia a la lente de contacto desde el ojo es cero.

148. En un telescopio reflector, el objetivo es un espejo cóncavo de radio de curvatura de 2 m y un ocular es una lente convexa de 5 cm de longitud focal. Encuentra el tamaño aparente de un árbol de 25 m a una distancia de 10 km que percibirá al mirar a través del telescopio.

149. Un telescopio ve dos estrellas que están separadas por 10⁹ km de distancia y se encuentran separadas por un ángulo de 10^-5 radianes. Si el ocular del telescopio tiene una longitud focal de 1,5 cm y el objetivo tiene una longitud focal de 3 metros, ¿a qué distancia están las estrellas del observador?

150. ¿Cuál es el tamaño angular de la Luna si se ve desde un binocular que tiene una longitud focal de 1,2 cm para el ocular y una longitud focal de 8 cm para el objetivo? Utilice el radio de la luna 1.74 × 10⁶ m y la distancia de la luna al observador para que sea 3.8 × 10⁸ m.

151. Un planeta que tiene una distancia focal del ocular de 1 cm y una distancia focal del objetivo de 1 m es la observación de un planeta desconocido a una distancia de 10¹² m de la Tierra. Si se ve que el planeta lejano subtiende un ángulo de 10^-5 radianes en el ocular, ¿cuál es el tamaño del planeta?