
15. Un diamante de alta calidad puede ser bastante claro e incoloro, transmitiendo todas las longitudes de onda visibles con poca absorción. Explica cómo puede brillar con destellos de color brillante cuando se ilumina con luz blanca.
8.1 La propagación de la luz
1. ¿Bajo qué condiciones se puede modelar la luz como un rayo? ¿Como una onda?
2. ¿Por qué el índice de refracción siempre es mayor o igual a 1?
3. ¿El hecho de que el destello de luz de un rayo llegue a ti antes de que su sonido prueba que la velocidad de la luz es extremadamente grande o simplemente es mayor que la velocidad del sonido? Discute cómo podrías usar este efecto para obtener una estimación de la velocidad de la luz.
4. Especula sobre qué proceso físico podría ser responsable de que la luz viaje más lentamente en un medio que en un vacío.
8.2 La ley de reflexión
5. Usando la ley de reflexión, explica cómo el polvo quita el brillo de la nariz de una persona. ¿Cuál es el nombre del efecto óptico?
8.3 Refracción
6. La difusión por reflexión desde una superficie rugosa se describe en este capítulo. La luz también puede ser difundida por refracción. Describe cómo ocurre esto en una situación específica, como la luz que interactúa con el hielo triturado.
7. ¿Cambiará la luz la dirección hacia o desde la perpendicular cuando pase del aire al agua? ¿Agua al vaso? ¿Vidrio al aire?
8. Explica por qué un objeto en el agua siempre parece estar a una profundidad menor de lo que realmente es.
9. Explica por qué las piernas de una persona aparecen muy cortas cuando se baña en una piscina. Justifica tu explicación con un diagrama de rayos que muestra la trayectoria de los rayos desde los pies hasta el ojo de un observador que está fuera del agua.
10. Explica por qué un remo que está parcialmente sumergido en agua parece doblado.
8.4 Reflexión total interna
11. Un anillo con una piedra preciosa incolora se cae al agua. La piedra preciosa se vuelve invisible cuando se sumerge. ¿Puede ser un diamante? Explica.
12. El tipo más común de espejismo es la ilusión de que la luz de los objetos lejanos se refleja en un charco de agua que no está realmente allí. Los espejismos generalmente se observan en los desiertos, cuando hay una capa caliente de aire cerca del suelo. Dado que el índice de refracción del aire es más bajo para el aire a temperaturas más altas, explica cómo se pueden formar los espejismos.
13. ¿Cómo se puede usar la reflexión total interna para estimar el índice de refracción de un medio?
8.5 Dispersión
14. ¿Es posible que la reflexión total interna desempeñe un papel en el arco iris? Explica en términos de índices de refracción y ángulos, quizás refiriéndote a lo que se muestra a continuación. Algunos de nosotros hemos visto la formación de un doble arco iris; ¿Es físicamente posible observar un arco iris triple?

15. Un diamante de alta calidad puede ser bastante claro e incoloro, transmitiendo todas las longitudes de onda visibles con poca absorción. Explica cómo puede brillar con destellos de color brillante cuando se ilumina con luz blanca.
8.6 El Principio de Huygens
16. ¿Cómo dependen los efectos de onda del tamaño del objeto con el que interactúa la onda? Por ejemplo, ¿por qué el sonido se curva en la esquina de un edificio mientras que la luz no?
17. ¿El principio de Huygens se aplica a todos los tipos de ondas?
18. Si se observa difracción para algún fenómeno, es evidencia de que el fenómeno es una onda. ¿Lo contrario es verdad? Es decir, si no se observa difracción, ¿significa eso que el fenómeno no es una onda?
8.7 Polarización
19. ¿Se puede polarizar una onda de sonido en el aire? Explica.
20. Ninguna luz pasa a través de dos filtros polarizadores perfectos con ejes perpendiculares. Sin embargo, si se coloca un tercer filtro polarizador entre los dos originales, puede pasar algo de luz. ¿Por qué es esto? ¿En qué circunstancias pasa la mayor parte de la luz?
21. Explica qué sucede con la energía transportada por la luz que se atenúa pasándola a través de dos filtros polarizados cruzados.
22. Cuando las partículas que dispersan la luz son mucho más pequeñas que su longitud de onda, la cantidad de dispersión es proporcional a 1/λ. ¿Significa esto que hay más dispersión para λ pequeña que λ grande? ¿Cómo se relaciona esto con el hecho de que el cielo es azul?
23. Usando la información dada en la pregunta anterior, explica por qué las puestas de sol son rojas.
24. Cuando la luz se refleja en el ángulo de Brewster desde una superficie lisa, está 100% polarizada en paralelo a la superficie. Parte de la luz será refractada hacia la superficie. Describe cómo harías un experimento para determinar la polarización de la luz refractada. ¿Qué dirección esperarías que tuviera la polarización y esperarías que fuera del 100%?
25. Si te acuestas en una playa mirando el agua con la cabeza inclinada ligeramente de lado, tus gafas de sol polarizadas no funcionan muy bien. Por qué no?
8.1 La propagación de la luz
26. ¿Cuál es la velocidad de la luz en el agua? ¿En la glicerina?
27. ¿Cuál es la velocidad de la luz en el aire? ¿En una copa de cristal?
28. Calcula el índice de refracción para un medio en el que la velocidad de la luz sea de 2.012 × 108 m/s, e identifica la sustancia más probable según la tabla 8.1.
29. ¿De qué sustancia en la tabla 8.1 es la velocidad de la luz 2.290 × 108 m/s?
30. Hubo una gran colisión de un asteroide con la Luna en la época medieval. Fue descrito por monjes en la Catedral de Canterbury en Inglaterra como un brillo rojo en y alrededor de la Luna. ¿Cuánto tiempo después de que el asteroide golpeara la Luna, que está a 3.84 × 105 km de distancia, llegaría la luz a la Tierra por primera vez?
31. Los componentes de algunas computadoras se comunican entre sí a través de fibras ópticas que tienen un índice de refracción n = 1.55. ¿Qué tiempo se requiere en nanosegundos para que una señal viaje 0.200 m a través de dicha fibra?
32. Compara el tiempo que tarda la luz en recorrer 1000 m en la superficie de la Tierra y en el espacio exterior.
33. ¿Hasta dónde viaja la luz bajo el agua durante un intervalo de tiempo de 1.50 × 10−6s?
8.2 La ley de reflexión
34. Supongamos que un hombre está parado frente a un espejo como se muestra a continuación. Sus ojos están a 1.65 m sobre el piso y la parte superior de su cabeza es 0.13 m más arriba. Encuentra la altura sobre el piso de la parte superior e inferior del espejo más pequeño en el que pueda ver tanto la parte superior de su cabeza como sus pies. ¿Cómo se relaciona esta distancia con la altura del hombre?

35. Demuestra que cuando la luz se refleja en dos espejos que se encuentran en ángulo recto, el rayo saliente es paralelo al rayo entrante, como se ilustra a continuación.
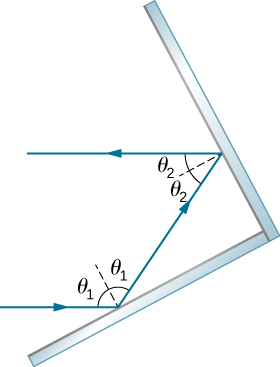
36. En la superficie de la Luna, los astronautas lunares colocaron un reflector de esquina, en el cual se refleja periódicamente un rayo láser. La distancia a la Luna se calcula a partir del tiempo de ida y vuelta. ¿Qué porcentaje de corrección se necesita para explicar el retraso en el tiempo debido a la disminución de la luz en la atmósfera de la Tierra? Supón que la distancia a la Luna es precisamente de 3.84 × 108 m y que la atmósfera de la Tierra (que varía en densidad con la altitud) es equivalente a una capa de 30.0 km de espesor con un índice constante de refracción n = 1.000293.
37. Un espejo plano no es convergente ni divergente. Para probar esto, considera dos rayos que se originan en el mismo punto y divergen en un ángulo θ (ver más abajo). Demuestra que después de golpear un espejo plano, el ángulo entre sus direcciones sigue siendo θ.

8.3 Refracción
A menos que se especifique lo contrario, los índices de refracción del vidrio y el agua deben tomarse como 1,50 y 1,333, respectivamente.
38. Un haz de luz en el aire tiene un ángulo de incidencia de 35° en la superficie de una placa de vidrio. ¿Cuáles son los ángulos de reflexión y refracción?
39. Un haz de luz en el aire incide en la superficie de un estanque, formando un ángulo de 20° con respecto a la superficie. ¿Cuáles son los ángulos de reflexión y refracción?
40. Cuando un rayo de luz cruza del agua al vidrio, emerge en un ángulo de 30° con respecto a la normal de la interfaz. ¿Cuál es su ángulo de incidencia?
41. Una linterna de lápiz sumergida en agua envía un haz de luz hacia la superficie con un ángulo de incidencia de 30°. ¿Cuál es el ángulo de refracción en el aire?
42. Los rayos de luz del sol forman un ángulo de 30° con la vertical cuando se ven desde debajo de la superficie de un cuerpo de agua. ¿En qué ángulo sobre el horizonte está el Sol?
43. La trayectoria de un haz de luz en el aire va desde un ángulo de incidencia de 35° a un ángulo de refracción de 22° cuando entra en un bloque rectangular de plástico. ¿Cuál es el índice de refracción del plástico?
44. Un instructor de buceo en una piscina mira a su instructor como se muestra a continuación. ¿Qué ángulo forma el rayo desde la cara del instructor con la perpendicular al agua en el punto donde entra el rayo? El ángulo entre el rayo en el agua y la perpendicular al agua es de 25.0°.
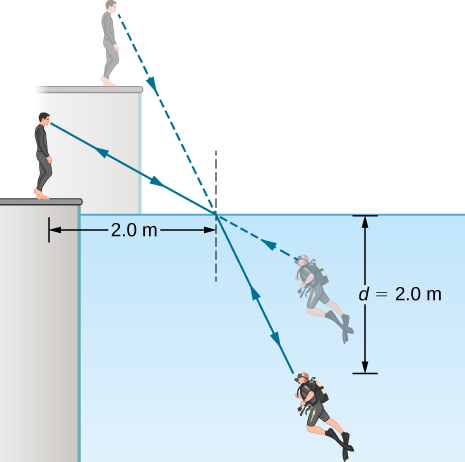
45. (a) Utilizando la información del problema anterior, encuentra la altura de la cabeza del instructor sobre el agua, teniendo en cuenta que primero deberás calcular el ángulo de incidencia. (b) Encuentra la profundidad aparente de la cabeza del buceador debajo del agua como lo ve el instructor.
8.4 Reflexión total interna
46. Verifica que el ángulo crítico para la luz que va del agua al aire sea de 48.6°, como se explicó al final del Ejemplo 8.4, con respecto al ángulo crítico para la luz que viaja en una tubería de poliestireno (un tipo de plástico) rodeada por aire.
47. (a) Al final del Ejemplo 8.4, se indicó que el ángulo crítico para la luz que va del diamante al aire es de 24.4°. Verifica esto. (b) ¿Cuál es el ángulo crítico para la luz que va del zircón al aire?
48. Una fibra óptica utiliza vidrio de sílex revestido con vidrio corona. ¿Cuál es el ángulo crítico?
49. ¿En qué ángulo mínimo obtendrá la reflexión interna total de la luz que viaja en el agua y se refleja en el hielo?
50. Supón que estás utilizando la reflexión total interna para hacer un reflector de esquina eficiente. Si hay aire en el exterior y el ángulo incidente es de 45.0°, ¿cuál debe ser el índice mínimo de refracción del material del que está hecho el reflector?
51. Puedes determinar el índice de refracción de una sustancia determinando su ángulo crítico. (a) ¿Cuál es el índice de refracción de una sustancia que tiene un ángulo crítico de 68.4° cuando está sumergida en el agua? ¿Cuál es la sustancia, basada en la tabla 8.1? (b) ¿Cuál sería el ángulo crítico para esta sustancia en el aire?
52. Un rayo de luz, emitido por debajo de la superficie de un líquido desconocido con aire por encima de él, experimenta una reflexión total interna como se muestra a continuación. ¿Cuál es el índice de refracción para el líquido y su posible identificación?

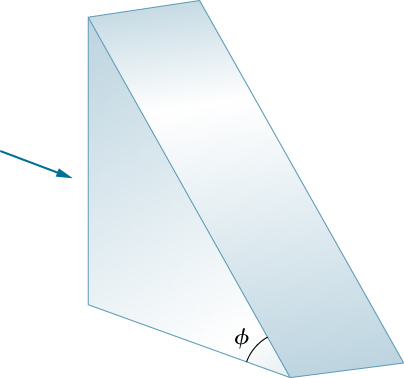
53. Los rayos de luz caen normalmente en la superficie vertical del prisma de vidrio (n = 1.50) que se muestra a continuación. (a) ¿Cuál es el valor más grande para φ tal que el rayo se refleje totalmente en la cara inclinada? (b) Repite el cálculo de la parte (a) si el prisma está sumergido en el agua.
8.5 Dispersión
54. (a) ¿Cuál es la relación entre la velocidad de la luz roja y la luz violeta en el diamante, según la tabla 8.2? (b) ¿Cuál es esta relación en el poliestireno? (c) ¿Cuál es más dispersivo?
55. Un haz de luz blanca pasa del aire al agua en un ángulo incidente de 75.0°. ¿En qué ángulos se refractan las partes roja (660 nm) y violeta (410 nm) de la luz?
56. ¿En qué medida los ángulos críticos para la luz roja (660 nm) y violeta (410 nm) difieren en un diamante rodeado de aire?
57. (a) Un haz de luz estrecho que contiene longitudes de onda amarillas (580 nm) y verdes (550 nm) va del poliestireno al aire, golpeando la superficie a un ángulo incidente de 30.0°. ¿Cuál es el ángulo entre los colores cuando emergen? (b) ¿Qué tan lejos tendrían que viajar para estar separados por 1,00 mm?
58. Un haz de luz paralelo que contiene longitudes de onda de color naranja (610 nm) y violeta (410 nm) pasa del cuarzo fundido al agua, golpeando la superficie entre ellas en un ángulo incidente de 60.0°. ¿Cuál es el ángulo entre los dos colores en el agua?
59. Un rayo de luz de 610 nm pasa del aire al cuarzo fundido en un ángulo incidente de 55.0°. ¿En qué ángulo incidente debe entrar la luz de 470 nm en el vidrio de pedernal para tener el mismo ángulo de refracción?
60. Un haz de luz estrecho que contiene longitudes de onda rojas (660 nm) y azules (470 nm) viaja desde el aire a través de un trozo de vidrio plano de 1.00 cm de espesor y vuelve al aire nuevamente. El rayo golpea en un ángulo incidente de 30.0°. (a) ¿En qué ángulos emergen los dos colores? (b) ¿A qué distancia se separan el rojo y el azul cuando emergen?
61. Un haz estrecho de luz blanca entra en un prisma hecho de vidrio de corona a un ángulo de incidencia de 45.0°, como se muestra a continuación. ¿En qué ángulos, θR y θV, emergen del prisma los componentes rojo (660 nm) y violeta (410 nm) de la luz?

8.7 Polarización
62. ¿Qué ángulo se necesita entre la dirección de la luz polarizada y el eje de un filtro polarizador para reducir su intensidad a la mitad?
63. El ángulo entre los ejes de dos filtros polarizadores es de 45.0°. ¿En qué medida el segundo filtro reduce la intensidad de la luz que llega a través del primero?
64. Dos láminas polarizadoras P1 y P2 se colocan juntas con sus ejes de transmisión orientados en un ángulo θ entre sí. ¿Cuánto vale θ cuando solo el 25% de la intensidad de luz transmitida máxima pasa a través de ellos?
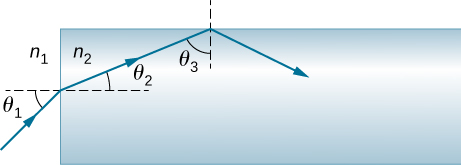
65. Supón que en el problema anterior, la luz incidente en P1 no está polarizada. En el valor determinado de θ, ¿qué fracción de la luz incidente pasa a través de la combinación?
66. Si tiene una luz completamente polarizada de intensidad 150 W/m2, ¿cuál será su intensidad después de pasar a través de un filtro polarizador con su eje en un ángulo de 89.0° con respecto a la dirección de polarización de la luz?
67. ¿Qué ángulo tendría que formar el eje de un filtro polarizador con la dirección de la luz polarizada de intensidad 1.00 kW/m2 para reducir la intensidad a 10.0 W/m2?
68. Al final del Ejemplo 8.7, se indicó que la intensidad de la luz polarizada se reduce a 90.0% de su valor original al pasar a través de un filtro polarizador con su eje en un ángulo de 18.4° con respecto a la dirección de polarización. Verifica esta declaración.
69. Demuestra que si tienes tres filtros polarizadores, con el segundo en un ángulo de 45.0° con respecto al primero y el tercero con un ángulo de 90.0° con el primero, la intensidad de la luz que pasa el primero se reducirá a 25.0% de su valor (esto contrasta con tener solo el primero y el tercero, lo que reduce la intensidad a cero, de modo que colocar el segundo entre ellos aumenta la intensidad de la luz transmitida).
70. Tres hojas polarizadoras se colocan juntas de manera que el eje de transmisión de la segunda hoja esté orientado a 25.0° con respecto al eje de la primera, mientras que el eje de transmisión de la tercera hoja esté orientado a 40.0° (en el mismo sentido) al Eje del primero. ¿Qué fracción de la intensidad de un haz no polarizado incidente se transmite por la combinación?
71. Para rotar el eje de polarización de un haz de luz polarizada linealmente en 90.0°, un alumno coloca las hojas P1 y P2 con sus ejes de transmisión a 45.0° y 90.0°, respectivamente, al eje de polarización del haz. (a) ¿Qué fracción de la luz incidente pasa a través de P1 y (b) a través de la combinación? (c) Repite tus cálculos para la parte (b) para ángulos de eje de transmisión de 30.0° y 90.0°, respectivamente.
72. Se encuentra que cuando la luz que viaja en el agua cae sobre un bloque de plástico, el ángulo de Brewster es de 50.0°. ¿Cuál es el índice de refracción del plástico?
73. ¿En qué ángulo se polarizará completamente la luz reflejada por el diamante?
74. ¿Cuál es el ángulo de Brewster para la luz que viaja en el agua que se refleja desde el cristal de la corona?
75. Un buceador ve la luz reflejada en la superficie del agua. ¿En qué ángulo con respecto a la superficie del agua esta luz estará completamente polarizada?
76. A partir de sus mediciones, Roemer estimó que tomó 22 minutos para que la luz viajara una distancia igual al diámetro de la órbita de la Tierra alrededor del Sol. (a) Usa esta estimación junto con el diámetro conocido de la órbita de la Tierra para obtener un valor aproximado de la velocidad de la luz. (b) En realidad, la luz tarda 16.5 minutos en recorrer esta distancia. Usa este tiempo para calcular la velocidad de la luz.
77. Cornu realizó la medición de Fizeau de la velocidad de la luz utilizando una rueda de 4,00 cm de diámetro que contenía 180 dientes. La distancia desde la rueda hasta el espejo fue de 22,9 km. Suponiendo que midiera la velocidad de la luz con precisión, ¿cuál era la velocidad angular de la rueda?
78. Supón que tienes una sustancia clara desconocida sumergida en el agua, y deseas identificarla al encontrar su índice de refracción. Arreglas que un rayo de luz ingrese a un ángulo de 45.0°, y observas que el ángulo de refracción es de 40.3°. ¿Cuál es el índice de refracción de la sustancia y su identidad probable?
79. Abajo se muestra un rayo de luz que va desde el aire a través del cristal de corona hasta el agua, como entrar en una pecera. Calcula la cantidad de desplazamiento del rayo por el vidrio (Δx), dado que el ángulo incidente es de 40.0° y el vidrio tiene un grosor de 1.00 cm.
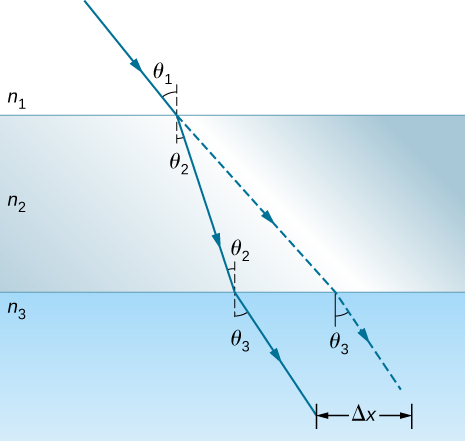
80. Teniendo en cuenta el problema anterior, muestre que θ3 es el mismo que sería si el segundo medio no estuviera presente.
81. ¿En qué ángulo está la luz dentro de la copa de cristal completamente polarizada cuando se refleja en el agua, como en una pecera?
82. La luz reflejada a 55.6° desde una ventana está completamente polarizada. ¿Cuál es el índice de refracción de la ventana y la sustancia probable de la cual está hecho?
83. (a) La luz reflejada a 62.5° de una piedra preciosa en un anillo está completamente polarizada. ¿Puede la gema ser un diamante? (b) ¿En qué ángulo se polarizaría completamente la luz si la gema estuviera en el agua?
84. Si θb es el ángulo de Brewster para la luz reflejada desde la parte superior de una interfaz entre dos sustancias, y θ'b es el ángulo de Brewster para la luz reflejada desde abajo, dedemuestre que θb + θ'b = 90.0°.
85. Resultados irrazonables. Supongamos que la luz viaja desde el agua a otra sustancia, con un ángulo de incidencia de 10.0° y un ángulo de refracción de 14.9°. (a) ¿Cuál es el índice de refracción de la otra sustancia? (b) ¿Qué es irrazonable acerca de este resultado? (c) ¿Qué suposiciones son irrazonables o inconsistentes?
86. Resultados irrazonables. La luz que viaja del agua a una piedra preciosa golpea la superficie en un ángulo de 80.0° y tiene un ángulo de refracción de 15.2°. (a) ¿Cuál es la velocidad de la luz en la piedra preciosa? (b) ¿Qué es irrazonable acerca de este resultado? (c) ¿Qué suposiciones son irrazonables o inconsistentes?
87. Si un filtro polarizador reduce la intensidad de la luz polarizada a 50.0% de su valor original, ¿cuánto se reducen los campos eléctrico y magnético?
88. Supongamos que te pones dos pares de gafas de sol polarizadas con sus ejes en un ángulo de 15.0°. ¿Cuánto tiempo más le tomará a la luz depositar una cantidad determinada de energía en tu ojo en comparación con un solo par de gafas de sol? Supongamos que las lentes son claras excepto por sus características de polarización.
89. (a) En un día en que la intensidad de la luz solar es de 1.00 kW/m2, una lente circular de 0.200 m de diámetro enfoca la luz sobre el agua en un vaso de precipitados negro. Dos láminas de plástico polarizadas se colocan en frente de la lente con sus ejes en un ángulo de 20.0°. Suponiendo que la luz solar no está polarizada y los polarizadores son 100% eficientes, ¿cuál es la velocidad inicial de calentamiento del agua en °C/s, suponiendo que se absorba al 80.0%? El vaso de aluminio tiene una masa de 30.0 gramos y contiene 250 gramos de agua. (b) ¿Se calientan los filtros polarizadores? Explica.
90. Los espectáculos de luz en escena con láseres utilizan espejos móviles para hacer girar los haces y crear efectos coloridos. Demuestra que un rayo de luz reflejado en un espejo cambia de dirección en 2θ cuando el espejo se gira en un ángulo θ.
91. Considera la posibilidad de que la luz solar entre en la atmósfera de la Tierra al amanecer y al atardecer, es decir, a un ángulo de incidencia de 90.0°. Tomando el límite entre el espacio casi vacío y la atmósfera para ser repentino, calcula el ángulo de refracción de la luz solar. Esto alarga el tiempo en que el Sol parece estar sobre el horizonte, tanto al amanecer como al atardecer. Ahora construye un problema en el cual determinas el ángulo de refracción para diferentes modelos de la atmósfera, como varias capas de densidad variable. Es posible que tu instructor desee guiarte sobre el nivel de complejidad a considerar y sobre cómo varía el índice de refracción con la densidad del aire.
92. Un rayo de luz que ingresa a una fibra óptica rodeada por aire primero se refracta y luego se refleja como se muestra a continuación. Demuestra que si la fibra está hecha de vidrio corona, cualquier rayo incidente se reflejará totalmente de manera interna.
93. Un rayo de luz cae sobre la cara izquierda de un prisma (ver más abajo) en el ángulo de incidencia θ para el cual el haz emergente tiene un ángulo de refracción en la cara derecha. Mostrar que el índice de refracción n del prisma de vidrio está dado por
n = sen(1/2)(α + φ) sin(φ/2)
donde φ es el ángulo del vértice del prisma y α es el ángulo a través del cual el haz se ha desviado. Si α = 37.0° y los ángulos base del prisma son cada 50.0°, ¿cuál es n?

94. Si el ángulo del vértice φ en el problema anterior es 20.0° y n = 1.50, ¿cuál es el valor de α?
95. La luz incidente en la lámina de polarización P
96. Demostrar que si I es la intensidad de la luz transmitida por dos filtros polarizadores con ejes en un ángulo θ e I' es la intensidad cuando los ejes están en un ángulo de 90.0° − θ, entonces I + I' = I0, la intensidad original (sugerencia: usa las identidades trigonométricas cos90.0° − θ = senθ y cos2θ + sen2θ = 1).