Preguntas y problemas - Capítulo VII

1. ¿Cuál es la diferencia entre el sonido y la audición?

2. Aprenderás que la luz es una onda electromagnética que puede viajar a través de un vacío. ¿Pueden las ondas sonoras viajar a través de un vacío?

3. Las ondas de sonido se pueden modelar como un cambio en la presión. ¿Por qué se usa el cambio de presión y no la presión real?

7.2 Velocidad del sonido

4. ¿En qué se diferencian las vibraciones sonoras de los átomos del movimiento térmico?

5. Cuando el sonido pasa de un medio a otro donde su velocidad de propagación es diferente, ¿cambia su frecuencia o su longitud de onda? Explica tu respuesta brevemente.

6. Un truco popular es inhalar helio y hablar con una voz graciosa y de alta frecuencia. Explica este fenómeno.

7. Es posible que hayas utilizado un buscador de rango sónico en el laboratorio para medir la distancia de un objeto con un sonido de clic de un transductor de sonido. ¿Cuál es el principio utilizado en este dispositivo?

8. El buscador de rango sónico discutido en la pregunta anterior a menudo necesita ser calibrado. Durante la calibración, el software solicita la temperatura ambiente. ¿Por qué supones que se requiere la temperatura de la habitación?

7.3 Intensidad del sonido

9. Seis miembros de un equipo de natación sincronizada usan tapones para los oídos para protegerse contra la presión del agua en las profundidades, pero aún pueden escuchar la música y realizar las combinaciones en el agua a la perfección. Un día, se les pidió que abandonaran la piscina para que el equipo de buceo pudiera practicar algunas inmersiones, y trataron de practicar en una esterilla, pero parecían tener muchas más dificultades. ¿Por qué podría ser esto?

10. Una comunidad está preocupada por un plan para llevar el servicio de tren a su centro desde las afueras de la ciudad. El nivel actual de intensidad del sonido, a pesar de que el patio ferroviario está a unas cuadras de distancia, es de 70 dB en el centro. El alcalde asegura al público que habrá una diferencia de solo 30 dB en el sonido en el área del centro de la ciudad. ¿Debería preocuparse la gente del pueblo? ¿Por qué?

7.4 Modos normales de una onda de sonido estacionaria

11. Te dan dos instrumentos de viento de idéntica longitud. Uno está abierto en ambos extremos, mientras que el otro está cerrado en un extremo. ¿Cuál es capaz de producir la frecuencia más baja?

12. ¿Cuál es la diferencia entre un sobretono y un armónico? ¿Son todos los sobretonos armónicos? ¿Son todos los armónicos sobretonos?

13. Dos columnas idénticas, abiertas en ambos extremos, están en habitaciones separadas. En la sala A, la temperatura es T = 20 °C y en la sala B, la temperatura es T = 25 °C. Un altavoz está conectado al extremo de cada tubo, lo que hace que los tubos resuenen a la frecuencia fundamental. ¿Es la frecuencia igual para ambos tubos? ¿Cuál tiene la mayor frecuencia?

7.5 Fuentes de sonido musical

14. ¿Cómo una guitarra sin amplificar produce sonidos mucho más intensos que los de una cuerda sostenida por un simple palo?

15. Considera tres tubos de la misma longitud (L). La tubería A está abierta en ambos extremos, la tubería B está cerrada en ambos extremos y la tubería C tiene un extremo abierto y un extremo cerrado. Si la velocidad del sonido es la misma en cada uno de los tres tubos, ¿en cuál de los tubos podría producirse la frecuencia fundamental más baja? ¿En cuál de los tubos podría producirse la frecuencia fundamental más alta?

16. La tubería A tiene una longitud L y está abierta en ambos extremos. La tubería B tiene una longitud L/2 y tiene un extremo abierto y un extremo cerrado. Supón que la velocidad del sonido sea la misma en ambos tubos. ¿Cuál de los armónicos en cada tubo sería igual?

17. Una cuerda está atada entre dos postes de laboratorio a una distancia L de distancia. La tensión en la cuerda y la densidad de masa lineal es tal que la velocidad de una onda en la cuerda es v = 343 m/s. Un tubo con condiciones de contorno simétricas tiene una longitud L y la velocidad del sonido en el tubo es v = 343 m/s. ¿Qué se podría decir acerca de las frecuencias de los armónicos en la cuerda y el tubo? ¿Qué pasa si la velocidad en la cuerda fuera v = 686 m/s?

7.6 Pulsaciones

18. Dos altavoces están conectados al generador de señal de frecuencia variable. El altavoz A produce una onda de sonido de frecuencia constante de 1.00 kHz, y el altavoz B produce un tono de 1.10 kHz. La frecuencia de pulsación es de 0,10 kHz. Si la frecuencia de cada altavoz se duplica, ¿cuál es la frecuencia de pulsación producida?

19. La etiqueta ha sido arrancada de un diapasón y usted necesita saber su frecuencia. Por su tamaño, sospechas que está en algún lugar alrededor de 250 Hz. Encontrarás un diapasón de ajuste de 250 Hz y un diapasón de ajuste de 270 Hz. Cuando golpeas la horquilla de 250 Hz y la horquilla de frecuencia desconocida, se produce una frecuencia de pulsación de 5 Hz. Cuando golpeas la desconocida con la horquilla de 270 Hz, la frecuencia de pulsación es de 15 Hz. ¿Cuál es la frecuencia desconocida? ¿Podrías haber deducido la frecuencia usando solo la horquilla de 250 Hz?

20. Refiriéndose a la pregunta anterior, si solo tuvieras la horquilla de 250 Hz, ¿podría encontrar una solución al problema de encontrar la frecuencia desconocida?

21. Un automóvil "vistoso" hecho a la medida tiene dos bocinas de bronce que se supone que producen la misma frecuencia pero en realidad emiten 263.8 y 264.5 Hz. ¿Qué frecuencia de pulsación se produce?

7.7 El efecto Doppler

22. ¿El cambio Doppler es real o solo una ilusión sensorial?

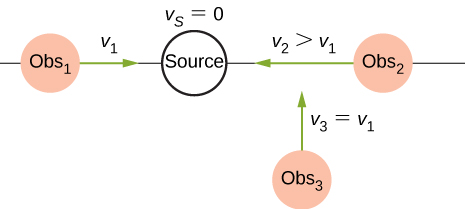
23. Tres observadores estacionarios observan el cambio Doppler desde una fuente que se mueve a una velocidad constante. Los observadores están estacionados como se muestra a continuación. ¿Qué observador observará la frecuencia más alta? ¿Qué observador observará la frecuencia más baja? ¿Qué se puede decir acerca de la frecuencia observada por el observador 3?



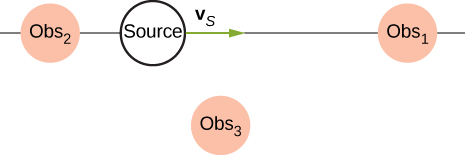
24. A continuación se muestra una fuente estacionaria y observadores en movimiento. Describe las frecuencias observadas por los observadores para esta configuración.



25. Antes de 1980, el radar convencional era utilizado por los meteorólogos. En la década de 1960, los meteorólogos comenzaron a experimentar con el radar Doppler. ¿Cuál crees que es la ventaja de usar el radar Doppler?

7.8 Ondas de choque

26. ¿Cuál es la diferencia entre una explosión sónica y una onda de choque?

27. Debido a consideraciones de eficiencia relacionadas con su estela de proa, el avión de transporte supersónico debe mantener una velocidad de crucero que sea una relación constante con la velocidad del sonido (un número de Mach constante). Si el avión vuela de aire caliente a aire más frío, ¿debería aumentar o disminuir su velocidad? Explica tu respuesta.

28. Cuando escuchas una explosión sónica, a menudo no puedes ver el avión que la hizo. ¿Porqué es eso?

Problemas

7.1 Ondas de sonido

29. Considere una onda de sonido modelada con las ecuación s(x, t) = 4.00 nmcos(3.66 m⁻¹x − 1256 s⁻¹t). ¿Cuál es el desplazamiento máximo, la longitud de onda, la frecuencia y la velocidad de la onda de sonido?

30. Considere una onda de sonido que se mueve a través del aire modelado con las ecuación s(x, t) = 6.00 nmcos(54.93 m⁻¹x − 18.84 × 10³ s⁻¹t). ¿Cuál es el tiempo más corto requerido para que una molécula de aire se mueva entre 3.00 nm y –3.00 nm?

31. Considere un ultrasonido de diagnóstico de frecuencia de 5.00 MHz que se usa para examinar una irregularidad en el tejido blando. (a) ¿Cuál es la longitud de onda en el aire de tal onda de sonido si la velocidad del sonido es 343 m/s? (b) Si la velocidad del sonido en el tejido es de 1800 m/s, ¿cuál es la longitud de onda de esta onda en el tejido?

32. Una onda de sonido se modela como δP = 1.80 Pa sen(55.41 m⁻¹x − 18,840 s⁻¹t). ¿Cuál es el cambio máximo en la presión, la longitud de onda, la frecuencia y la velocidad de la onda de sonido?

33. Una onda de sonido se modela con la función de onda ΔP = 1.20 Pa sen(kx − 6.28 × 10⁴ s⁻¹t) y la onda de sonido viaja en el aire a una velocidad de v = 343.00 m/s. (a) ¿Cuál es el número de onda de la onda de sonido? (b) ¿Cuál es el valor para ΔP(3.00 m, 20.00 s)?

34. El desplazamiento de las moléculas de aire en la onda de sonido se modela con la función de onda s(x, t) = 5.00 nmcos(91.54 m⁻¹x − 3.14 × 10⁴ s⁻¹t). (a) ¿Cuál es la velocidad de onda de la onda de sonido? (b) ¿Cuál es la velocidad máxima de las moléculas de aire cuando oscilan en un movimiento armónico simple? (c) ¿Cuál es la magnitud de la aceleración máxima de las moléculas de aire a medida que oscilan en un movimiento armónico simple?

35. Se coloca un altavoz en la abertura de un tubo horizontal largo. El altavoz oscila a una frecuencia f, creando una onda de sonido que se mueve hacia abajo del tubo. La onda se mueve a través del tubo a una velocidad de v = 340.00 m/s. La onda de sonido se modela con la función de onda s(x, t) = s_maxcos(kx − ωt + φ). En el tiempo t = 0.00 s, una molécula de aire en x = 3.5 m está en el desplazamiento máximo de 7.00 nm. Al mismo tiempo, otra molécula en x = 3.7 m tiene un desplazamiento de 3.00 nm. ¿Cuál es la frecuencia con la que el altavoz está oscilando?

36. Se golpea una horquilla de sintonización de 250 Hz y comienza a vibrar. Un medidor de nivel de sonido se encuentra a 34.00 m de distancia. Se necesita el sonido Δt = 0.10 s para alcanzar el medidor. El desplazamiento máximo del diapasón es de 1,00 mm. Escribe una función de onda para el sonido.

37. Una onda de sonido producida por un transductor ultrasónico, que se mueve en el aire, se modela con la ecuación de onda s(x, t) = 4.50 nmcos(9.15 × 10⁴ m⁻¹x − 2π(5.00 MHz)t). El transductor se utilizará en pruebas no destructivas para detectar fracturas en vigas de acero. La velocidad del sonido en la viga de acero es v = 5950 m/s. Encuentra la función de onda para la onda de sonido en la viga de acero.

38. Las marsopas emiten ondas sonoras que utilizan para la navegación. Si la longitud de onda de la onda de sonido emitida es de 4,5 cm y la velocidad del sonido en el agua es v = 1530 m/s, ¿cuál es el período del sonido?

39. Los murciélagos usan ondas de sonido para atrapar insectos. Los murciélagos pueden detectar frecuencias de hasta 100 kHz. Si las ondas de sonido viajan a través del aire a una velocidad de v = 343 m/s, ¿cuál es la longitud de onda de las ondas de sonido?

40. Un murciélago envía una onda de sonido de 100 kHz y las ondas de sonido viajan a través del aire a una velocidad de v = 343 m/s. (a) Si la diferencia de presión máxima es 1.30 Pa, ¿qué es una función de onda que modelaría la onda de sonido, asumiendo que la onda es sinusoidal? (Supón que el cambio de fase es cero). (b) ¿Cuáles son el período y la longitud de onda de la onda de sonido?

41. Considera la gráfica que se muestra abajo de una onda de compresión. Se muestran instantáneas de la función de onda para t = 0.000 s (azul) y t = 0.005 s (naranja). ¿Cuáles son la longitud de onda, el desplazamiento máximo, la velocidad y el período de la onda de compresión?



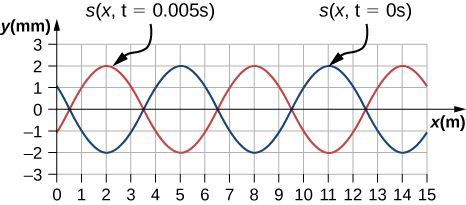
42. Considera la gráfica en el problema anterior de una onda de compresión. Se muestran instantáneas de la función de onda para t = 0.000 s (azul) y t = 0.005 s (naranja). Dado que el desplazamiento de la molécula en el tiempo t = 0.00 s y la posición x = 0.00 m es s(0.00m, 0.00s) = 1.08 mm, deduce una función de onda para modelar la onda de compresión.

43. Una cuerda de guitarra oscila a una frecuencia de 100 Hz y produce una onda de sonido. (a) ¿Cuál crees que es la frecuencia de la onda de sonido que produce la cuerda vibrante? (b) Si la velocidad de la onda sonora es v = 343 m/s, ¿cuál es la longitud de onda de la onda de sonido?

7.2 Velocidad del sonido

44. Cuando es empujada por una lanza, una soprano operística deja escapar un chillido de 1200 Hz. ¿Cuál es su longitud de onda si la velocidad del sonido es de 345 m/s?

45. ¿Qué frecuencia de sonido tiene una longitud de onda de 0,10 m cuando la velocidad del sonido es de 340 m/s?

46. ​​Calcula la velocidad del sonido en un día cuando una frecuencia de 1500 Hz tiene una longitud de onda de 0.221 m.

47. (a) ¿Cuál es la velocidad del sonido en un medio donde una frecuencia de 100 kHz produce una longitud de onda de 5.96 cm? (b) ¿Qué sustancia en la tabla 7.1 es probable que sea?

48. Demuestra que la velocidad del sonido en 20.0 °C de aire es 343 m/s, como se afirma en el texto.

49. La temperatura del aire en el desierto del Sahara puede alcanzar 56.0 °C (aproximadamente 134 °F). ¿Cuál es la velocidad del sonido en el aire a esa temperatura?

50. Los delfines emiten sonidos en el aire y el agua. ¿Cuál es la relación entre la longitud de onda de un sonido en el aire y su longitud de onda en el agua de mar? Supón que la temperatura del aire es de 20.0 °C.

51. Un eco de sonar regresa a un submarino 1,20 s después de ser emitido. ¿Cuál es la distancia al objeto que crea el eco? (Supón que el submarino está en el océano, no en agua dulce).

52. (a) Si el sonar de un submarino puede medir los tiempos de eco con una precisión de 0.0100 s, ¿cuál es la diferencia más pequeña en distancias que puede detectar? (Supón que el submarino está en el océano, no en agua dulce). (b) Discute los límites que esta resolución de tiempo impone sobre la capacidad del sistema de sonar para detectar el tamaño y la forma del objeto que crea el eco.

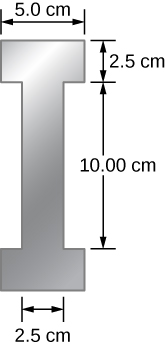
53. Las ondas de sonido ultrasónicas se utilizan a menudo en métodos de prueba no destructiva. Por ejemplo, este método puede usarse para encontrar fallas estructurales en vigas en I de acero utilizadas en edificios. Considera una viga en I de acero de 10.00 metros de largo con una sección que se muestra a continuación. El peso de la viga I es 3846.50 N. ¿Cuál sería la velocidad del sonido en la viga I? (Y_acero = 200 GPa, β_acero = 159 GPa).



54. Un físico en una exhibición de fuegos artificiales cronometra el retraso entre ver una explosión y escuchar su sonido, y encuentra que es de 0.400 s. (a) ¿Qué tan lejos está la explosión si la temperatura del aire es de 24.0 °C y si se desprecia el tiempo que tarda la luz en llegar al físico? (b) Calcula la distancia a la explosión teniendo en cuenta la velocidad de la luz. Ten en cuenta que esta distancia es despreciablemente mayor. 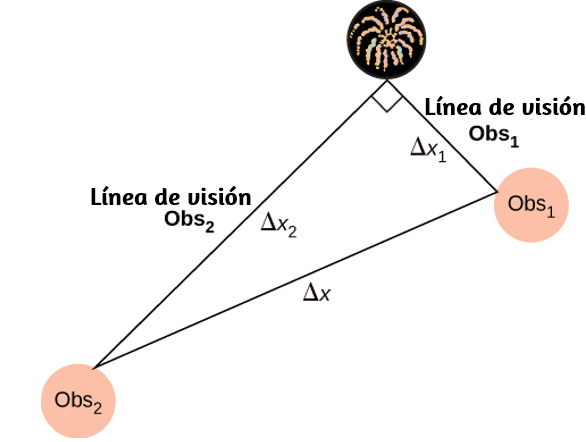55. Durante una celebración del 4 de julio, un fuego artificial M80 estalla en el suelo, produciendo un destello brillante y una fuerte explosión. La temperatura del aire del aire nocturno es T_F = 90.00 °F. Dos observadores ven el flash y escuchan el estallido. El primer observador anota el tiempo entre el flash y la explosión como 1,00 segundo. El segundo observador nota la diferencia como 3,00 segundos. La línea de visión entre los dos observadores se encuentra en un ángulo recto, como se muestra a continuación. ¿Cuál es la distancia Δx entre los dos observadores?



56. La densidad de una muestra de agua es ρ = 998.00 kg/m³ y el módulo de volumen es β = 2.15 GPa. ¿Cuál es la velocidad del sonido a través de la muestra?

57. Supongamos que un murciélago usa ecos de sonido para localizar a su presa de insectos, a 3.00 m de distancia (consulta la Figura 7.6) (a) Calcula los tiempos de eco para temperaturas de 5.00 °C y 35.0 °C. (b) ¿Qué porcentaje de incertidumbre causa esto al murciélago en la localización del insecto? (c) Discute la importancia de esta incertidumbre y si podría causar dificultades para el murciélago (en la práctica, el murciélago continúa utilizando el sonido a medida que se acerca, eliminando la mayoría de las dificultades impuestas por este y otros efectos, como el movimiento de la presa).

7.3 Intensidad del sonido

58. ¿Cuál es la intensidad en vatios por metro cuadrado de un sonido de 85.0 dB?

59. La etiqueta de advertencia en un cortacésped indica que produce ruido a un nivel de 91.0 dB. ¿Qué es esto en vatios por metro cuadrado?

60. Una onda de sonido que viaja en el aire tiene una amplitud de presión de 0.5 Pa. ¿Cuál es la intensidad de la onda?

61. ¿A qué nivel de intensidad corresponde el sonido en el problema anterior?

62. ¿Qué nivel de intensidad de sonido en dB es producido por los auriculares que crean una intensidad de 4.00 × 10⁻² W/m²?

63. ¿Cuál es el nivel de decibelios de un sonido que es dos veces más intenso que un sonido de 90.0 dB? (b) ¿Cuál es el nivel de decibelios de un sonido que es un quinto tan intenso como un sonido de 90.0 dB?

64. ¿Cuál es la intensidad de un sonido que tiene un nivel 7.00 dB más bajo que un sonido de 4.00 × 10⁻⁹ W/m²? (b) ¿Cuál es la intensidad de un sonido que es 3.00 dB más alto que un sonido de 4.00 × 10⁻⁹ W/m²?

65. Las personas con buena audición pueden percibir sonidos tan bajos como −8.00 dB a una frecuencia de 3000 Hz. ¿Cuál es la intensidad de este sonido en vatios por metro cuadrado?

66. Si una mosca doméstica grande a 3.0 m de distancia produce un ruido de 40.0 dB, ¿cuál es el nivel de ruido de 1000 moscas a esa distancia, asumiendo que la interferencia tiene un efecto insignificante?

67. Diez autos en un círculo en una competencia de boom box producen un nivel de intensidad de sonido de 120 dB en el centro del círculo. ¿Cuál es el nivel de intensidad de sonido promedio producido allí por cada estéreo, asumiendo que los efectos de interferencia pueden ser ignorados?

68. La amplitud de una onda de sonido se mide en términos de su presión manométrica máxima. ¿Por qué factor aumenta la amplitud de una onda de sonido si el nivel de intensidad del sonido aumenta en 40.0 dB?

69. Si un nivel de intensidad de sonido de 0 dB a 1000 Hz corresponde a una presión manométrica máxima (amplitud de sonido) de 10⁻⁹ atm, ¿cuál es la presión manométrica máxima en un sonido de 60 dB? ¿Cuál es la presión manométrica máxima en un sonido de 120 dB?

70. Una exposición de 8 horas a un nivel de intensidad de sonido de 90.0 dB puede causar daños auditivos. ¿Qué energía en julios cae sobre un tímpano de 0,800 cm de diámetro tan expuesto?

71. El sonido se transmite más efectivamente en un estetoscopio por contacto directo en lugar de a través del aire, y se intensifica aún más al concentrarse en el área más pequeña del tímpano. Es razonable suponer que el sonido se transmite a un estetoscopio 100 veces más efectivamente en comparación con la transmisión a través del aire. ¿Cuál es, entonces, la ganancia en decibelios producida por un estetoscopio que tiene un área de recolección de sonido de 15.0 cm² y concentra el sonido en dos tímpanos con un área total de 0.900 cm² con una eficiencia del 40.0%?

72. Los altavoces pueden producir sonidos intensos con una entrada de energía sorprendentemente pequeña, a pesar de su baja eficiencia. Calcula la entrada de potencia necesaria para producir un nivel de intensidad de sonido de 90.0 dB para un altavoz de 12.0 cm de diámetro que tenga una eficiencia de 1.00% (este valor es el nivel de intensidad del sonido justo en el altavoz).

73. El factor de 10^-12 en el rango de intensidades a las que el oído puede responder, desde el umbral hasta el que causa el daño después de una breve exposición, es verdaderamente notable. Si pudieras medir distancias en el mismo rango con un solo instrumento y la distancia más pequeña que pudiera medir fuera de 1 mm, ¿cuál sería la mayor?

74. ¿Cuáles son las frecuencias más cercanas a 500 Hz que una persona promedio puede distinguir claramente como diferente en frecuencia de 500 Hz? Los sonidos no están presentes simultáneamente.

75. ¿Puedes decir que tu compañero de cuarto aumentó el sonido en el televisor si su nivel de intensidad de sonido promedio va de 70 a 73 dB?

76. Si una mujer necesita una amplificación de 5.0 × 10⁵ veces el umbral de intensidad para poder escuchar en todas las frecuencias, ¿cuál es su pérdida auditiva general en dB? Ten en cuenta que una amplificación más pequeña es apropiada para sonidos más intensos para evitar un mayor daño a tu audición en niveles superiores a 90 dB.

77. Una persona tiene un umbral de audición de 10 dB por encima de lo normal a 100 Hz y 50 dB por encima de lo normal a 4000 Hz. ¿Cuánto más intenso debe ser un tono de 100 Hz que un tono de 4000 Hz si ambos son apenas audibles para esta persona?

7.4 Modos normales de una onda de sonido estacionaria

78. (a) ¿Cuál es la frecuencia fundamental de un tubo de 0.672 m de largo, abierto en ambos extremos, en un día en que la velocidad del sonido es de 344 m/s? (b) ¿Cuál es la frecuencia de su segundo armónico?

79. ¿Cuál es la longitud de un tubo que tiene una frecuencia fundamental de 176 Hz y un primer sobretono de 352 Hz si la velocidad del sonido es de 343 m/s?

80. El canal auditivo resuena como un tubo cerrado en un extremo (consulta Figura 7.26) Si los canales auditivos varían en longitud desde 1.80 a 2.60 cm en una población promedio, ¿cuál es el rango de las frecuencias resonantes fundamentales? Toma la temperatura del aire a 37.0 °C, que es la misma que la temperatura del cuerpo.

81. Calcula el primer sobretono en un canal auditivo, que resuena como un tubo cerrado de 2.40 cm de largo en un extremo, al tomar la temperatura del aire a 37.0 °C. ¿Es el oído particularmente sensible a tal frecuencia? (Las resonancias del canal auditivo se complican por su forma no uniforme, que ignoraremos).

82. Una aproximación cruda de la producción de voz es considerar que los pasajes respiratorios y la boca son un tubo resonante cerrado en un extremo. (a) ¿Cuál es la frecuencia fundamental si el tubo tiene 0.240 m de largo, tomando la temperatura del aire a 37.0 °C? (b) ¿En qué se convertiría esta frecuencia si la persona reemplazara el aire con helio? Supón la misma dependencia de la temperatura para el helio que para el aire.

83. Un tubo de 4,0 m de largo, abierto en un extremo y cerrado en un extremo, se encuentra en una habitación donde la temperatura es T = 22 °C. Un altavoz capaz de producir frecuencias variables se coloca en el extremo abierto y se usa para hacer que el tubo resuene. (a) ¿Cuál es la longitud de onda y la frecuencia de la frecuencia fundamental? (b) ¿Cuál es la frecuencia y la longitud de onda del primer sobretono?

84. Un tubo de 4.0 m de largo, abierto en ambos extremos, se coloca en una habitación donde la temperatura es T = 25 °C. Un altavoz capaz de producir frecuencias variables se coloca en el extremo abierto y se usa para hacer que el tubo resuene. (a) ¿Cuál es la longitud de onda y la frecuencia de la frecuencia fundamental? (b) ¿Cuál es la frecuencia y la longitud de onda del primer sobretono?

85. Una cuerda de guitarra de nylon se fija entre dos postes de laboratorio a 2,00 m de distancia. La cuerda tiene una densidad de masa lineal de μ = 7.20 g/m y se coloca bajo una tensión de 160.00 N. La cuerda se coloca al lado de un tubo, abierto en ambos extremos, de longitud L. La cuerda se toca y el tubo resuena en el modo n = 3. La velocidad del sonido es de 343 m/s. ¿Cuál es la longitud del tubo?

86. Una horquilla de sintonización de 512 Hz se golpea y se coloca junto a un tubo con un pistón móvil, creando un tubo con una longitud variable. El pistón se desliza por la tubería y se alcanza la resonancia cuando el pistón está a 115,50 cm del extremo abierto. La próxima resonancia se alcanza cuando el pistón está a 82.50 cm del extremo abierto. (a) ¿Cuál es la velocidad del sonido en el tubo? (b) ¿A qué distancia del extremo abierto causará el pistón el siguiente modo de resonancia?

87. Se les pide a los estudiantes en un laboratorio de física que encuentren la longitud de una columna de aire en un tubo cerrado en un extremo que tiene una frecuencia fundamental de 256 Hz. Sostienen el tubo verticalmente y lo llenan con agua hasta la parte superior, luego bajan el agua mientras se toca el diapasón de 256 Hz y escuchan la primera resonancia. (a) ¿Cuál es la temperatura del aire si la resonancia se produce para una longitud de 0.336 m? (b) ¿En qué longitud observarán la segunda resonancia (primer tono)?

7.5 Fuentes de sonido musical

88. Si un instrumento de viento, como una tuba, tiene una frecuencia fundamental de 32.0 Hz, ¿cuáles son sus primeros tres armónicos? Se cierra en un extremo (los armónicos de una tuba real son más complejos que este ejemplo, porque es un tubo cónico).

89. ¿Cuáles son los tres primeros armónicos de un fagot que tiene una frecuencia fundamental de 90.0 Hz? Está abierto en ambos extremos (los armónicos de un fagot real son más complejos que en este ejemplo, porque su doble lengüeta hace que actúe más como un tubo cerrado en un extremo).

90. ¿Cuánto tiempo debe tener una flauta para tener una frecuencia fundamental de 262 Hz (esta frecuencia corresponde a la C media en la escala cromática templada uniformemente) en un día cuando la temperatura del aire es 20.0 °C? Está abierto en ambos extremos.

91. ¿Qué longitud debe tener un oboe para producir una frecuencia fundamental de 110 Hz en un día cuando la velocidad del sonido es de 343 m/s? Está abierto en ambos extremos.

92. (a) Encuentra la longitud de un tubo de órgano cerrado en un extremo que produce una frecuencia fundamental de 256 Hz cuando la temperatura del aire es de 18.0 °C. (b) ¿Cuál es su frecuencia fundamental a 25.0 °C?

93. Un tubo de órgano (L = 3.00 m) está cerrado en ambos extremos. Calcula las longitudes de onda y las frecuencias de los tres primeros modos de resonancia. Supón que la velocidad del sonido es v = 343.00 m/s.

94. Un tubo de órgano (L = 3.00 m) está cerrado en un extremo. Calcula las longitudes de onda y las frecuencias de los tres primeros modos de resonancia. Supón que la velocidad del sonido es v = 343.00 m/s.

95. Una cuerda oscilante en el modo n = 6 produce una onda de sonido de una frecuencia de 2.00 kHz. La densidad de masa lineal de la cuerda es μ = 0.0065 kg/m y la longitud de la cuerda es 1.50 m. ¿Cuál es la tensión en la cuerda?

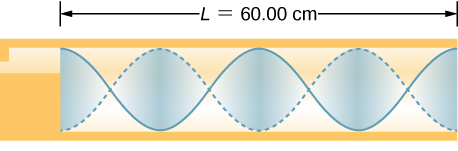
96. Considera el sonido creado al resonar el tubo que se muestra a continuación. La temperatura del aire es T_C = 30.00 °C. ¿Cuáles son la longitud de onda, la velocidad de la onda y la frecuencia del sonido producido?



97. Un estudiante sostiene un palo de laboratorio de 80.00 cm una cuarta parte de la longitud desde el extremo del palo. El poste de laboratorio está hecho de aluminio. El estudiante golpea el poste del laboratorio con un martillo. El polo resuena a la frecuencia más baja posible. ¿Cuál es esa frecuencia?

98. Una cuerda en el violín tiene una longitud de 24.00 cm y una masa de 0.860 g. La frecuencia fundamental de la cuerda es de 1.00 kHz. (a) ¿Cuál es la velocidad de la onda en la cuerda? (b) ¿Cuál es la tensión en la cuerda?

99. ¿En qué fracción cambiarán las frecuencias producidas por un instrumento de viento cuando la temperatura del aire pase de 10.0 °C a 30.0 °C? Es decir, encontrar la relación de las frecuencias a esas temperaturas.

7.6 Pulsaciones

100. ¿Qué frecuencias de pulsación están presentes: (a) Si las notas musicales A y C se tocan juntas (frecuencias de 220 y 264 Hz)? (b) ¿Si D y F se tocan juntos (frecuencias de 297 y 352 Hz)? (c) ¿Si las cuatro se tocan juntas?

101. ¿Qué frecuencias de pulsación resultan si un martillo de piano golpea tres cuerdas que emiten frecuencias de 127.8, 128.1 y 128.3 Hz?

102. Un afinador de piano oye una pulsación cada 2.00 s cuando escucha un diapasón de afinación de 264.0 Hz y una cuerda de piano única. ¿Cuáles son las dos frecuencias posibles de la cuerda?

103. Dos cuerdas idénticas, de longitudes idénticas de 2.00 m y densidad de masa lineal de μ = 0.0065 kg/m, están fijas en ambos extremos. La cuerda A está bajo una tensión de 120.00 N. La cuerda B está bajo una tensión de 130.00 N. Cada una está pulsada y produce sonido en el modo n = 10. ¿Cuál es la frecuencia de pulsación?

104. Un afinador de piano utiliza un diapasón de 512 Hz para afinar un piano. Toca el diapasón y toca una tecla en el piano y oye una frecuencia de pulsación de 5 Hz. Aprieta la cuerda del piano y repite el procedimiento. Una vez más escucha una frecuencia de pulsación de 5 Hz. ¿Que pasó?

105. Una cuerda con una densidad de masa lineal de μ = 0,0062 kg/m se estira entre dos postes separados por 1,30 m. La tensión en la cuerda es 150.00 N. La cuerda oscila y produce una onda de sonido. Se golpea un diapasón de sintonización de 1024 Hz y la frecuencia de pulsación entre las dos fuentes es de 52.83 Hz. ¿Cuáles son la posible frecuencia y longitud de onda de la onda en la cuerda?

106. Un automóvil tiene dos bocinas, una que emite una frecuencia de 199 Hz y la otra que emite una frecuencia de 203 Hz. ¿Qué frecuencia de pulsación producen?

107. El martillo central de un piano golpea dos cuerdas, produciendo pulsaciones de 1,50 Hz. Una de las cuerdas está sintonizada a 260.00 Hz. ¿Qué frecuencias podría tener la otra cuerda?

108. Dos diapasones de sintonización que tienen frecuencias de 460 y 464 Hz se golpean simultáneamente. ¿Qué frecuencia promedio oirás y cuál será la frecuencia de la pulsación?

109. Los motores a reacción dobles en un avión producen una frecuencia de sonido promedio de 4100 Hz con una frecuencia de pulsación de 0.500 Hz. ¿Cuáles son sus frecuencias individuales?

110. Tres teclas adyacentes en un piano (F, F-sharp y G) se tocan simultáneamente, produciendo frecuencias de 349, 370 y 392 Hz. ¿Qué frecuencias de compás son producidas por esta combinación discordante?

7.7 El efecto Doppler

111. (a) ¿Qué frecuencia recibe una persona que mira una ambulancia que se aproxima moviéndose a 110 km/h y emitiendo un sonido constante de 800 Hz desde su sirena? La velocidad del sonido en este día es de 345 m/s. (b) ¿Qué frecuencia recibe después de que la ambulancia haya pasado?

112. (a) En un espectáculo aéreo, un jet vuela directamente hacia las gradas a una velocidad de 1200 km/h, emitiendo una frecuencia de 3500 Hz, en un día en que la velocidad del sonido es de 342 m/s. ¿Qué frecuencia reciben los observadores? (b) ¿Qué frecuencia reciben cuando el avión vuela directamente lejos de ellos?

113. ¿Qué frecuencia recibe un ratón justo antes de ser enviado por un halcón que vuela a 25.0 m/s y emite un chirrido de frecuencia de 3500 Hz? Toma la velocidad del sonido a 331 m/s.

114. Un espectador en un desfile recibe un tono de 888 Hz de un trompetista que está tocando una nota de 880 Hz. ¿A qué velocidad se aproxima el músico si la velocidad del sonido es de 338 m/s?

115. Un tren de cercanías sopla su bocina de 200 Hz cuando se acerca a un cruce. La velocidad del sonido es de 335 m/s. (a) Un observador que espera en el cruce recibe una frecuencia de 208 Hz. ¿Cuál es la velocidad del tren? (b) ¿Qué frecuencia recibe el observador cuando el tren se aleja?

116. ¿Puedes percibir el cambio en la frecuencia producida cuando tiras de un diapasón hacia ti a 10.0 m/s en un día cuando la velocidad del sonido es de 344 m/s? Para responder a esta pregunta, calcula el factor por el cual cambia la frecuencia y observa si es mayor que 0.300%.

117. Dos águilas vuelan directamente una hacia la otra, la primera a 15.0 m/s y la segunda a 20.0 m/s. Ambas chillan, la primera emitiendo una frecuencia de 3200 Hz y la segunda emitiendo una frecuencia de 3800 Hz. ¿Qué frecuencias reciben si la velocidad del sonido es de 330 m/s?

118. El estudiante A corre por el pasillo de la escuela a una velocidad de v_o = 5.00 m/s, cargando un diapasón de sintonización de 1024.00 Hz hacia un muro de concreto. La velocidad del sonido es v = 343.00 m/s. El estudiante B se para en la pared. (a) ¿Cuál es la frecuencia que escucha el estudiante B? (b) ¿Cuál es la frecuencia de pulsación que escucha el estudiante A?

119. Una ambulancia con una sirena (f = 1.00 kHz) a todo volumen se acerca a la escena del accidente. La ambulancia se está moviendo a 70.00 mph. Una enfermera se está acercando a la escena desde la dirección opuesta, corriendo a v_o = 7.00 m/s. ¿Qué frecuencia observa la enfermera? Supón que la velocidad del sonido es v = 343.00 m/s.

120. La frecuencia de la sirena de una ambulancia es de 900 Hz y se acerca a ti. Estás parado en una esquina y observas una frecuencia de 960 Hz. ¿Cuál es la velocidad de la ambulancia (en mph) si la velocidad del sonido es v = 340.00 m/s?

121. ¿Cuál es la velocidad mínima a la que una fuente debe viajar hacia ti para que puedas escuchar que su frecuencia es Doppler cambiada? Es decir, ¿qué velocidad produce un cambio de 0.300% en un día cuando la velocidad del sonido es de 331 m/s?

7.8 Ondas de choque

122. Un avión vuela a Mach 1.50 a una altitud de 7500.00 metros, donde la velocidad del sonido es v = 343.00 m/s. ¿A qué distancia del observador estacionario estará el avión cuando el observador escuche la explosión sónica?

123. Un avión que vuela a una altitud de 8.50 km tiene una velocidad de Mach 2.00, donde la velocidad del sonido es v = 340.00 m/s. ¿Cuánto tiempo después de que el avión esté directamente sobre la cabeza, un observador estacionario oirá la explosión sónica?

124. La onda de choque en la parte delantera de un avión de combate tiene un ángulo de θ = 70.00°. El avión vuela a 1200 km/h. ¿Cuál es la velocidad del sonido?

125. Un avión está volando a Mach 1.2, y un observador en el suelo escucha la explosión sónica 15.00 segundos después de que el avión esté directamente sobre su cabeza. ¿Cuál es la altitud del avión? Supón que la velocidad del sonido es v = 343.00 m/s.

126. Una bala se dispara y se mueve a una velocidad de 1342 mph. Supón que la velocidad del sonido es v = 340.00 m/s. ¿Cuál es el ángulo de la onda de choque producida?

127. Se coloca un altavoz en la abertura de un tubo horizontal largo. El altavoz oscila a una frecuencia de f, creando una onda de sonido que se mueve hacia abajo del tubo. La onda se mueve a través del tubo a una velocidad de v = 340.00 m/s. La onda de sonido se modela con la función de onda s(x, t) = smaxcos (kx − ωt + φ). En el tiempo t = 0.00 s, una molécula de aire en x = 2.3 m está en el desplazamiento máximo de 6.34 nm. Al mismo tiempo, otra molécula en x = 2.7 m tiene un desplazamiento de 2.30 nm. ¿Cuál es la función de onda de la onda de sonido, es decir, encontrar el número de onda, la frecuencia angular y el cambio de fase inicial?

128. Un avión se mueve en Mach 1.2 y produce una onda de choque. (a) ¿Cuál es la velocidad del avión en metros por segundo? (b) ¿Cuál es el ángulo que mueve la onda de choque?

Problemas adicionales

129. Un tubo de 0,80 m de largo se abre en ambos extremos. La temperatura del aire es de 26 °C. El aire en el tubo se oscila mediante un altavoz conectado a un generador de señal. ¿Cuáles son las longitudes de onda y las frecuencias de los dos primeros modos de ondas de sonido que resuenan en el tubo?

130. Un tubo lleno de agua tiene una válvula en la parte inferior para permitir que el agua salga del tubo. A medida que el agua se vacía del tubo, la longitud L de la columna de aire cambia. Se coloca un diapasón de sintonización de 1024 Hz en la abertura del tubo. El agua se retira del tubo hasta que el modo n = 5 de una onda de sonido resuena. ¿Cuál es la longitud de la columna de aire si la temperatura del aire en la habitación es de 18 °C?



131. Considera la siguiente figura. La longitud de la cuerda entre el vibrador de cuerda y la polea es L = 1.00 m. La densidad lineal de la cuerda es μ = 0.006 kg/m. El vibrador de cuerda puede oscilar a cualquier frecuencia. La masa colgante es de 2.00 kg. (a) ¿Cuáles son la longitud de onda y la frecuencia del modo n = 6? (b) La cuerda oscila el aire alrededor de la cuerda. ¿Cuál es la longitud de onda del sonido si la velocidad del sonido es vs = 343.00 m/s?



132. Los primeros experimentos de cambio Doppler se llevaron a cabo utilizando una banda tocando música en un tren. Un trompetista en un vagón de ferrocarril en movimiento toca una nota de 320 Hz. Las ondas de sonido escuchadas por un observador estacionario en una plataforma de tren escuchan una frecuencia de 350 Hz. ¿Cuál es la velocidad del tren en mph? La temperatura del aire es T_C = 22 °C.

133. Dos autos se mueven uno hacia el otro, ambos sonando sus bocinas (f_s = 800 Hz). El auto A se mueve a 65 mph y el auto B está a 75 mph. ¿Cuál es la frecuencia de pulsación que escucha cada conductor? La temperatura del aire es T_C = 22.00 °C.

134. El estudiante A corre después del estudiante B. El estudiante A lleva un diapasón a 1024 Hz, y el estudiante B lleva otros a 1000 Hz. El Estudiante A está corriendo a una velocidad de v_A = 5.00 m/s y el Estudiante B está corriendo a v_B = 6.00 m/s. ¿Cuál es la frecuencia de pulsación escuchado por cada estudiante? La velocidad del sonido es v = 343.00 m/s.

135. Supón que el nivel de sonido de una fuente es de 75 dB y luego cae a 52 dB, con una frecuencia de 600 Hz. Determina la (a) intensidad de sonido inicial y (b) final y las amplitudes de onda de sonido inicial (c) y (d) final. La temperatura del aire es T_C = 24.00 °C y la densidad del aire es ρ = 1.184 kg/m³.

136. El cambio Doppler para un radar Doppler se encuentra con f = f_R(1 + v/c/1 - v/c), donde f_R es la frecuencia del radar, f es la frecuencia observada por el radar, c es la velocidad de la luz y v eEs la velocidad del objetivo. ¿Cuál es la frecuencia de pulsación observada en el radar, asumiendo que la velocidad del objetivo es mucho más lenta que la velocidad de la luz?

137. Un observador estacionario escucha una frecuencia de 1000.00 Hz cuando se aproxima una fuente y una frecuencia de 850.00 Hz cuando sale una fuente. La fuente se mueve a una velocidad constante de 75 mph. ¿Cuál es la temperatura del aire?

138. Una flauta toca una nota con una frecuencia de 600 Hz. La flauta se puede modelar como una tubería abierta en ambos extremos, donde el flautista cambia la longitud con las posiciones de los dedos. ¿Cuál es la longitud del tubo si esta es la frecuencia fundamental?

Problemas de Desafío

139. Dos parlantes de sonido están separados por una distancia d, cada uno con una frecuencia f. Un observador se para en un altavoz y camina en línea recta una distancia x, perpendicular a los dos altavoces, hasta que llega a la primera intensidad máxima de sonido. La velocidad del sonido es v. ¿A qué distancia del parlante está?

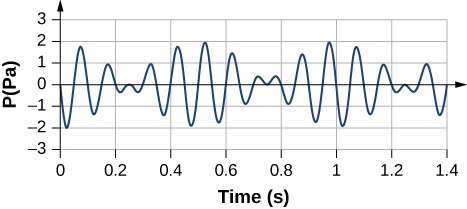
140. Considera las pulsaciones que se muestran a continuación. Este es un gráfico de la presión manométrica en función del tiempo para la posición x = 0.00 m. La onda se mueve con una velocidad de v = 343.00 m/s. (a) ¿Cuántas pulsaciones hay por segundo? (b) ¿Cuántas veces oscila la onda por segundo? (c) Escribe una función de onda para la presión manométrica en función del tiempo.



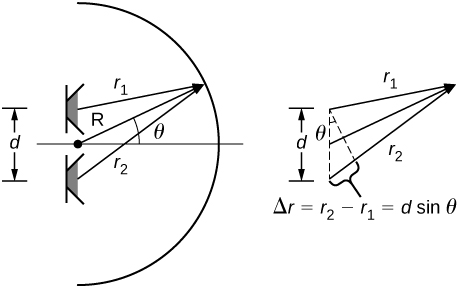
141. Dos altavoces que producen la misma frecuencia de sonido están a una distancia d. Considera un arco a lo largo de un círculo de radio R, centrado en el punto medio de los altavoces, como se muestra a continuación. (a) ¿En qué ángulos habrá máximos? (b) ¿En qué ángulo habrá mínimos?



142. Una cuerda tiene una longitud de 1.5 m, una densidad de masa lineal μ = 0.008 kg/m, y una tensión de 120 N. Si la temperatura del aire es T = 22 °C, ¿cuál debería ser la longitud de una tubería abierta a ambos extremos para que tenga la misma frecuencia para el modo n = 3?

143. Una cuerda (μ = 0,006 kgm, L = 1,50 m) está fija en ambos extremos y está bajo una tensión de 155 N. Oscila en el modo n = 10 y produce sonido. Un diapasón está sonando cerca, produciendo una frecuencia de pulsación de 23.76 Hz. (a) ¿Cuál es la frecuencia del sonido de la cuerda? (b) ¿Cuál es la frecuencia del diapasón si la frecuencia de la misma es menor? (c) ¿Cuál debe ser la tensión de la cuerda para que la frecuencia del tiempo sea cero?

144. Una cuerda tiene una densidad de masa lineal μ, una longitud L y una tensión de F_T, y oscila en un modo n a una frecuencia f. Encuentra la relación de Δf/f para un pequeño cambio en la tensión.

145. Una cuerda tiene una densidad de masa lineal μ = 0.007 kg/m, una longitud L = 0.70 m, una tensión de F_T = 110 N, y oscila en un modo n = 3. (a) ¿Cuál es la frecuencia de las oscilaciones? (b) Usa el resultado en el problema anterior para encontrar el cambio en la frecuencia cuando la tensión aumenta en 1.00%.

146. Un altavoz alimentado por un generador de señal se utiliza para estudiar la resonancia en un tubo. El generador de señal se puede ajustar desde una frecuencia de 1000 Hz a 1800 Hz. Primero, se estudia un tubo de 0,75 m de largo, abierto en ambos extremos. La temperatura en la habitación es T_F = 85.00 °F. (a) ¿Qué modos normales de la tubería se pueden estudiar? ¿Cuáles son las frecuencias y longitudes de onda? A continuación, se coloca una tapa en un extremo del tubo de 0,75 metros de largo. (b) ¿Qué modos normales de la tubería se pueden estudiar? ¿Cuáles son las frecuencias y longitudes de onda?

147. Una cuerda en el violín tiene una longitud de 23.00 cm y una masa de 0.900 gramos. La tensión en la cuerda 850.00 N. La temperatura en la habitación es T_C = 24.00 °C. La cuerda está pulsada y oscila en el modo n = 9. (a) ¿Cuál es la velocidad de la onda en la cuerda? (b) ¿Cuál es la longitud de onda de la onda de sonido producida? (c) ¿Cuál es la frecuencia de la cuerda oscilante? (d) ¿Cuál es la frecuencia del sonido producido? (e) ¿Cuál es la longitud de onda del sonido producido?