Preguntas y problemas - Capítulo VI

1. Da un ejemplo de una onda transversal y un ejemplo de una onda longitudinal, teniendo cuidado de observar las direcciones relativas de la perturbación y la propagación de la onda en cada una.

2. Una onda transversal sinusoidal tiene una longitud de onda de 2,80 m. Se tarda 0.10 s para que una parte de la cuerda en una posición x se mueva desde una posición máxima y = 0.03 m a la posición de equilibrio y = 0. ¿Cuáles son el período, la frecuencia y la velocidad de onda de la onda?

3. ¿Cuál es la diferencia entre la velocidad de propagación y la frecuencia de una onda mecánica? ¿Uno o ambos afectan la longitud de onda? ¿Si es así, cómo?

4. Considera la posibilidad de un resorte estirado, como un slinky. El resorte estirado puede soportar ondas longitudinales y ondas transversales. ¿Cómo se pueden producir ondas transversales en el resorte? ¿Cómo se pueden producir ondas longitudinales en el resorte?

5. Considera una onda producida en un resorte estirado sosteniendo un extremo y agitándolo hacia arriba y hacia abajo. ¿La longitud de onda depende de la distancia que mueva tu mano hacia arriba y hacia abajo?

6. Se produce una onda transversal sinusoidal en un resorte estirado, que tiene un período T. Cada sección del resorte se mueve perpendicular a la dirección de propagación de la onda, en un movimiento armónico simple con una amplitud A. ¿Oscila cada sección con el mismo periodo de la onda o un periodo diferente? Si la amplitud de la onda transversal se duplicara pero el período permanece igual, ¿tu respuesta sería la misma?

7. Una onda electromagnética, como la luz, no requiere un medio. ¿Puedes pensar en un ejemplo que apoye esta afirmación?

6.2 Matematicas de las ondas

8. Si tuviera que sacudir el extremo de un resorte tenso hacia arriba y hacia abajo 10 veces por segundo, ¿cuál sería la frecuencia y el período de la onda sinusoidal producida en el resorte?

9. Si agitas el extremo de un resorte estirado hacia arriba y hacia abajo con una frecuencia f, puedes producir una onda transversal sinusoidal que se propaga por el resorte. ¿El número de onda depende de la frecuencia con la que estás sacudiendo el resorte?

10. ¿La velocidad vertical de un segmento de una cuerda tensa horizontal a través de la cual se propaga una onda transversal sinusoidal depende de la velocidad de onda de la onda transversal?

11. En esta sección, hemos considerado las ondas que se mueven a una velocidad de onda constante. ¿Acelera el medio?

12. Si dejas caer una piedra en un estanque, puedes observar que se producen varias ondulaciones concéntricas, no solo una sola ondulación. ¿Por qué crees que es?

6.3 Velocidad de onda en una cuerda estirada

13. Si la tensión en una cuerda se incrementara en un factor de cuatro, ¿en qué factor aumentaría la velocidad de onda de una onda en la cuerda?

14. ¿Una onda de sonido se mueve más rápido en el agua de mar o en agua dulce, si tanto el agua de mar como el agua dulce están a la misma temperatura y la onda de sonido se mueve cerca de la superficie? (ρ_w ≈ 1000 kg/m³, ρ_s ≈ 1030 kg/m³, B_w = 2.15 × 10⁹ Pa, B_s = 2.34 × 10⁹ Pa)

15. Las guitarras tienen cuerdas de diferente densidad de masa lineal. Si la cuerda de densidad más baja y la cuerda de densidad más alta están bajo la misma tensión, ¿qué cuerda soportaría ondas con la velocidad de onda más alta?

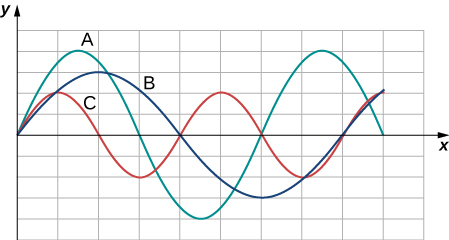
16. A continuación se muestran tres ondas que se enviaron por una cuerda en diferentes momentos. La tensión en la cuerda permanece constante. (a) Clasifica las ondas desde la longitud de onda más pequeña hasta la longitud de onda más grande. (b) Clasifica las ondas de la frecuencia más baja a la frecuencia más alta.



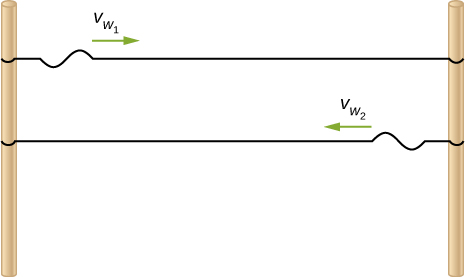
17. En las líneas de energía eléctrica conectadas por dos polos de servicios públicos a veces se oyen zumbidos cuando son empujadas a la oscilación por el viento. La velocidad de las ondas en las líneas eléctricas depende de la tensión. ¿Qué proporciona la tensión en las líneas eléctricas?

18. Dos cuerdas, una con una densidad de masa baja y una con una densidad lineal alta se unen. El extremo de mayor densidad está vinculado a una producción de laboratorio y un estudiante sostiene el extremo libre de la cuerda de baja densidad de masa. El alumno le da un giro a la cuerda y envía un pulso por las cuerdas. Si la tensión es la misma en ambas cuerdas, ¿el pulso se desplaza a la misma velocidad de onda en ambas cuerdas? Si no, ¿a dónde viaja más rápido, en la cuerda de baja densidad o en la de alta densidad?

6.4 Energía y potencia de una onda

19. Considera una cuerda con tensión baja con una densidad de masa lineal constante. Una onda sinusoidal con una frecuencia y amplitud angular producida por alguna fuerza motriz externa. Si la frecuencia de la fuerza motriz se reduce a la mitad de la frecuencia original, ¿cómo se ve afectada la potencia promediada en el tiempo de la onda? Si la amplitud de la fuerza motriz se reduce a la mitad, ¿cómo se ve afectada la potencia promediada en el tiempo? Explica tu respuesta.

20. Las ondas circulares de agua disminuyen en amplitud a medida que se alejan de donde cae una roca. Explicar por qué.

21. En una onda transversal en una cuerda, el movimiento de la cuerda es perpendicular al movimiento de la onda. Si esto es así, ¿cómo es posible mover energía a lo largo de la cuerda?

22. La energía del sol calienta la porción de tierra que mira hacia el sol durante las horas del día. ¿Por qué los polos norte y sur están fríos mientras el ecuador está bastante caliente?

23. La intensidad de las ondas esféricas disminuye a medida que la onda se aleja de la fuente. Si la intensidad de la onda en la fuente es I₀, ¿a qué distancia de la fuente disminuirá la intensidad en un factor de nueve?

6.5 Interferencia de ondas

24. Una onda sinusoidal incidente se envía a lo largo de una cuerda que se fija a la pared con una velocidad de onda v. La onda se refleja en el extremo de la cuerda. Describe la onda reflejada.

25. Una cuerda de una longitud de 2.00 m con una densidad de masa lineal de μ = 0.006 kg/m se une al final de una cuerda de 2.00 m de longitud con una densidad de masa lineal de μ = 0.012 kg/m. El extremo libre de la cuerda de mayor densidad se fija a la pared, y un estudiante sostiene el extremo libre de la cuerda de baja densidad, manteniendo la tensión constante en ambas cuerdas. El alumno envía un pulso por la cuerda. Describe lo que sucede en la interfaz entre las dos cuerdas.

26. Un resorte largo y apretado es sostenido por dos estudiantes, un estudiante sosteniendo cada extremo. Cada estudiante da un giro al final enviando una longitud de onda de una onda sinusoidal a lo largo del resorte en direcciones opuestas. Cuando las ondas se encuentran en el medio, ¿cómo se ve la onda?

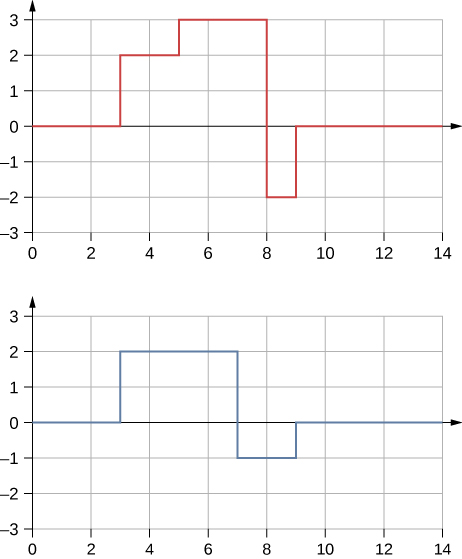
27. Muchos de los temas tratados en este capítulo son útiles más allá de los temas de las ondas mecánicas. Es difícil concebir una onda mecánica con esquinas afiladas, pero podrías encontrar una forma de onda en tu clase de electrónica digital, como se muestra a continuación. Esta podría ser una señal de un dispositivo conocido como convertidor analógico a digital, en el cual una señal de voltaje continuo se convierte en una señal discreta o una grabación digital de sonido. ¿Cuál es el resultado de la superposición de las dos señales?



28. Una cuerda de una densidad de masa lineal constante se mantiene tenso por dos estudiantes, cada uno sosteniendo un extremo. La tensión en la cuerda es constante. Cada uno de los estudiantes envía ondas por la cuerda moviendo la cuerda. (a) ¿Es posible que las ondas tengan diferentes velocidades de onda? (b) ¿Es posible que las ondas tengan diferentes frecuencias? (c) ¿Es posible que las ondas tengan diferentes longitudes de onda?

6.6 Ondas estacionarias y resonancia

29. Un fabricante de camiones encuentra que un puntal en el motor está fallando prematuramente. Un ingeniero de sonido determina que el puntal resuena en la frecuencia del motor y sospecha que este podría ser el problema. ¿Cuáles son las dos características posibles del puntal que pueden modificarse para corregir el problema?

30. ¿Por qué los techos de gimnasios e iglesias parecen fallar más que los hogares familiares cuando ocurre un terremoto?

31. Las copas de vino pueden ponerse en resonancia humedeciendo el dedo y frotándolo alrededor del borde del vaso. ¿Por qué?

32. Las unidades de aire acondicionado a veces se colocan en el techo de las casas en la ciudad. Ocasionalmente, los acondicionadores de aire causan un zumbido indeseable en los pisos superiores de las casas. ¿Por qué pasa esto? ¿Qué se puede hacer para reducir el zumbido?

33. Considera una onda estacionaria modelada como y(x, t) = 4.00 cm sen (3m ^-1x)cos(4 s^-1t). ¿Hay un nodo o un antinodo en x = 0.00 m? ¿Qué pasa con una onda estacionaria modelada como y(x, t) = 4.00 cm sen (3 m^-1x + π/2)cos(4 s^-1t)? ¿Hay un nodo o un antinodo en la posición x = 0.00 m?

Problemas

6.1 Ondas viajeras

34. Las tormentas en el Pacífico Sur pueden crear olas que viajan hasta la costa de California, a 12,000 km. ¿Cuánto tardan en recorrer esta distancia si viajan a 15,0 m/s?

35. Las olas en una piscina se propagan a 0.75 m/s. Salpica el agua en un extremo de la piscina y observas que la ola va hacia el extremo opuesto, refleja y regresa en 30.00 s. ¿A qué distancia está el otro extremo de la piscina?

36. Las ráfagas de viento crean ondulaciones en el océano que tienen una longitud de onda de 5,00 cm y se propagan a 2,00 m/s. ¿Cuál es su frecuencia?

37. ¿Cuántas veces por minuto un barco sube y baja en olas del océano que tienen una longitud de onda de 40.0 m y una velocidad de propagación de 5.00 m/s?

38. Los exploradores en un campamento sacuden el puente de cuerda que acaban de cruzar y observan las crestas de las ondas a 8,00 m de distancia. Si sacuden el puente dos veces por segundo, ¿cuál es la velocidad de propagación de las ondas?

39. ¿Cuál es la longitud de onda de las ondas que creas en una piscina si salpicas tu mano a una velocidad de 2.00 Hz y las ondas se propagan a una velocidad de onda de 0.800 m/s?

40. ¿Cuál es la longitud de onda de un terremoto que se sacude con una frecuencia de 10.0 Hz y llega a otra ciudad a 84.0 km de distancia en 12.0 s?

41. Las ondas de radio transmitidas a través del espacio vacío a la velocidad de la luz (v = c = 3.00 × 10⁸ m/s) por la nave espacial Voyager tienen una longitud de onda de 0.120 m. ¿Cuál es su frecuencia?

42. Tu oído es capaz de diferenciar los sonidos que llegan a cada oído con una diferencia de 0,34 ms, lo que es útil para determinar de dónde se origina el sonido de baja frecuencia. (a) Supón que una fuente de sonido de baja frecuencia se coloca a la derecha de una persona, cuyos oídos están separados aproximadamente 18 cm, y la velocidad del sonido generado es de 340 m/s. ¿Cuánto dura el intervalo entre el sonido cuando llega al oído derecho y el sonido que llega al oído izquierdo? (b) Supón que la misma persona estaba buceando y que una fuente de sonido de baja frecuencia estaba a la derecha del buceador. ¿Cuánto dura el intervalo entre el sonido que llega al oído derecho y el sonido que llega al oído izquierdo, si la velocidad del sonido en el agua es de 1500 m/s? (c) ¿Qué es significativo acerca del intervalo de tiempo de las dos situaciones?

43. (a) Los sismógrafos miden los tiempos de llegada de los terremotos con una precisión de 0.100 s. Para obtener la distancia al epicentro del terremoto, los geólogos comparan los tiempos de llegada de las ondas S y P, que viajan a diferentes velocidades. Si las ondas S y P viajan a 4,00 y 7,20 km/s, respectivamente, en la región considerada, ¿con qué precisión se puede determinar la distancia a la fuente del terremoto? (b) Las ondas sísmicas de detonaciones subterráneas de bombas nucleares pueden usarse para localizar el sitio de prueba y detectar violaciones de las prohibiciones de prueba. Discutea si tu respuesta a (a) implica un límite serio para tal detección (ten en cuenta también que la incertidumbre es mayor si existe una incertidumbre en las velocidades de propagación de las ondas S y P).

44. Una Scout está realizando una caminata de 10.00 km para obtener una insignia de mérito. Mientras que en la caminata, ella ve un acantilado a cierta distancia. Ella desea estimar el tiempo requerido para caminar hasta el acantilado. Ella sabe que la velocidad del sonido es de aproximadamente 343 metros por segundo. Ella grita y encuentra que el eco regresa después de aproximadamente 2.00 segundos. Si puede caminar 1,00 km en 10 minutos, ¿cuánto tiempo le tomará llegar al acantilado?

45. Se solicita a un ingeniero de control de calidad de una empresa de sartenes que califique una nueva línea de sartenes con revestimiento antiadherente. El recubrimiento debe tener un grosor de 1,00 mm. Un método para probar el grosor es que el ingeniero elija un porcentaje de las bandejas fabricadas, quite el recubrimiento y mida el grosor con un micrómetro. Este método es un método de prueba destructiva. En su lugar, el ingeniero decide que cada sartén se probará utilizando un método no destructivo. Se utiliza un transductor ultrasónico que produce ondas de sonido con una frecuencia de f = 25 kHz. Las ondas de sonido se envían a través del recubrimiento y se reflejan en la interfaz entre el recubrimiento y la bandeja de metal, y se registra el tiempo. La longitud de onda de las ondas ultrasónicas en el recubrimiento es de 0.076 m. ¿Cuál debería ser el tiempo registrado si el revestimiento tiene el grosor correcto (1,00 mm)?

6.2 Matematicas de las ondas

46. ​​Un pulso se puede describir como una perturbación de onda única que se mueve a través de un medio. Considera un pulso que se define en el tiempo t = 0.00 s mediante la ecuación y(x)= 6.00 m³/x² + 2.00 m² centrado alrededor de x = 0.00 m. El pulso se mueve con una velocidad de v = 3.00 m/s en la dirección x positiva. (a) ¿Cuál es la amplitud del pulso? (b) ¿Cuál es la ecuación del pulso en función de la posición y el tiempo? (c) ¿Dónde está centrado el pulso en el tiempo t = 5.00 s?

47. Una onda transversal en una cuerda se modela con la función de onda y(x, t) = (0.20 cm)sen(2.00 m^-1x − 3.00 s^-1t + π/16). ¿Cuál es la altura de la cuerda con respecto a la posición de equilibrio en una posición x = 4.00 m y un tiempo t = 10.00 s?

48. Considere la función de onda y(x, t) = (3.00 cm)sen(0.4 m^-1x + 2.00 s^-1t + π/10). ¿Cuáles son el período, la longitud de onda, la velocidad y el cambio de fase inicial de la onda modelada por la función de onda?

49. Un pulso se define como y(x, t) = e^{− 2.77(2.00(x − 2.00 m/s(t))/5.00 m})². Usa una hoja de cálculo u otro programa de computadora para trazar el pulso como la altura del medio y como una función de la posición x. Grafica el pulso en los tiempos t = 0.00 s y t = 3.00 s en el mismo gráfico. ¿Dónde está centrado el pulso en el tiempo t = 3.00 s? Usa tu hoja de cálculo para verificar tu respuesta.

50. Una onda se modela en el tiempo t = 0.00 s con una función de onda que depende de la posición. La ecuación es y(x) = (0.30 m)sen(6.28 m^-1x). La onda recorre una distancia de 4.00 metros en 0.50 s en la dirección x positiva. Escribe una ecuación para la onda en función de la posición y el tiempo.

51. Una onda se modela con la función y(x, t)= (0.25 m)cos(0.30 m^-1x − 0.90 s^-1t + π/3). Encuentra (a) la amplitud, (b) número de onda, (c) frecuencia angular, (d) velocidad de onda, (e) desplazamiento de fase, (f) longitud de onda y (g) período de la onda.

52. Una onda oceánica de superficie tiene una amplitud de 0,60 m, y la distancia de un canal a otro es de 8,00 m. Se mueve a una velocidad de onda constante de 1.50 m/s que se propaga en la dirección x positiva. En t = 0, el desplazamiento del agua en x = 0 es cero, y v_y es positivo. (a) Suponiendo que la onda se puede modelar como una onda sinusoidal, escribe una función de onda para modelar la onda. (b) Usa una hoja de cálculo para trazar la función de onda en los tiempos t = 0.00 s y t = 2.00 s en el mismo gráfico. Verifica que la onda se mueva 3.00 m en esos 2.00 s.

53. Una onda se modela mediante la función de onda y(x, t) = (0.30 m)sen[2π/4.50 m(x − 18.00 m/st)]. ¿Cuáles son la amplitud, longitud de onda, velocidad de la onda, período y frecuencia de la onda?

54. Una onda transversal en una cuerda se describe con la función de onda y(x, t) = (0.50 cm)sen 1.57 m^-11x − 6.28 s^-1t). (a) ¿Cuál es la velocidad de onda de la onda? (b) ¿Cuál es la magnitud de la velocidad máxima de la cuerda perpendicular a la dirección del movimiento?

55. Un nadador en el océano observa un día que las olas de la superficie del océano son periódicas y se parecen a una onda sinusoidal. El nadador estima que la distancia vertical entre la cresta y el canal de cada ola es de aproximadamente 0,45 m, y la distancia entre cada cresta es de aproximadamente 1,8 m. El nadador cuenta que pasan 12 olas cada dos minutos. Determina la función de onda armónica simple que describiría estas ondas.

56. Considera una onda descrita por la función de onda y(x, t) = 0.3 msen(2.00 m^-1x − 628.00 s^-1t). (a) ¿Cuántas crestas pasan por un observador en una ubicación fija en 2.00 minutos? (b) ¿Hasta dónde ha viajado la onda en ese tiempo?

57. Considere dos ondas definidas por las funciones de onda y₁(x, t) = 0.50 msen(2π/3.00 mx + 2π/4.00 st) e y₂(x, t) = 0.50 msen(2π/6.00 mx − 2π/4.00 st). ¿Cuáles son las similitudes y diferencias entre las dos ondas?

58. Considera dos ondas definidas por las funciones de onda y₁(x, t) = 0.20 msen(2π/6.00 mx − 2π/4.00 st) e y₂(x, t) = 0.20 mcos(2π/6.00 mx − 2π/4.00 st). ¿Cuáles son las similitudes y diferencias entre las dos ondas?

59. La velocidad de una onda transversal en una cuerda es de 300.00 m/s, su longitud de onda es de 0.50 m, y la amplitud es de 20.00 cm. ¿Cuánto tiempo se requiere para que una partícula en la cuerda se mueva a través de una distancia de 5.00 km?

6.3 Velocidad de onda en una cuerda estirada

60. Las ondas transversales se envían a lo largo de una cuerda de 5.00 m de largo con una velocidad de 30.00 m/s. La cuerda está bajo una tensión de 10.00 N. ¿Cuál es la masa de la cuerda?

61. Un cable de cobre tiene una densidad ρ = 8920 kg/m³, un radio de 1.20 mm y una longitud L. El cable se mantiene bajo una tensión de 10.00 N. Las ondas transversales se envían por el cable. (a) ¿Cuál es la densidad de masa lineal del cable? (b) ¿Cuál es la velocidad de las ondas a través del cable?

62. Un cable de piano tiene una densidad de masa lineal μ = 4,95 × 10⁻³ kg/m. ¿Bajo qué tensión se debe mantener la cuerda para producir ondas con una velocidad de onda de 500.00 m/s?

63. Una cuerda con una densidad de masa lineal de μ = 0.0060 kg/m está atada al techo. Una masa de 20 kg está atada al extremo libre de la cuerda. La cuerda es pulsada, enviando un pulso por la cuerda. Calcula la velocidad del pulso a medida que se desplaza por la cuerda.

64. Una cuerda tiene una densidad de masa lineal de μ = 0.0075 kg/m y una longitud de tres metros. Se tira del cable y se tarda 0.20 s para que el pulso llegue al final de la cuerda. ¿Cuál es la tensión de la cuerda?

65. Una cuerda mide 3.00 m de largo con una masa de 5.00 g. La cuerda se mantiene tensa con una tensión de 500.00 N aplicada a la cuerda. Un impulso se envía por la cuerda. ¿Cuánto tiempo tarda el pulso en recorrer los 3,00 m de la cuerda?

66. Dos cuerdas están unidas a los polos, sin embargo, la primera cuerda es dos veces más larga que la segunda. Si ambas cuerdas tienen la misma tensión y μ, ¿cuál es la relación de la velocidad del pulso de la onda desde la primera cuerda hasta la segunda?

67. Dos cuerdas están unidas a los polos, sin embargo, la primera cuerda es el doble de la densidad de masa lineal μ de la segunda. Si ambas cuerdas tienen la misma tensión, ¿cuál es la proporción de la velocidad del pulso de la onda desde la primera cuerda hasta la segunda?

68. Las ondas transversales viajan a través de una cuerda donde la tensión es igual a 7.00 N con una velocidad de 20.00 m/s. ¿Qué tensión se requeriría para una velocidad de onda de 25.00 m/s?

69. Dos cuerdas están unidas entre dos polos separados por una distancia de 2,00 m, como se muestra a continuación, ambas bajo la misma tensión de 600,00 N. La cuerda 1 tiene una densidad lineal de μ₁ = 0,0025 kg/m y la cuerda 2 tiene una densidad de masa lineal de μ₂ = 0.0035 kg/m. Los pulsos de onda transversal se generan simultáneamente en los extremos opuestos de las cuerdas. ¿Cuánto tiempo pasa antes de que los pulsos se pasen unos a otros?



70. Dos cuerdas están unidas entre dos polos separados por una distancia de 2.00 metros como se muestra en la figura anterior, ambas cuerdas tienen una densidad lineal μ₁ = 0.0025 kg/m, la tensión en la cuerda 1 es de 600.00 N y la tensión en la cuerda 2 es 700.00 N. Los impulsos de onda transversal se generan simultáneamente en los extremos opuestos de las cuerdas. ¿Cuánto tiempo pasa antes de que los pulsos se pasen unos a otros?

71. La nota E₄ se toca en un piano y tiene una frecuencia de f = 393.88. Si la densidad de masa lineal de esta cuerda del piano es μ = 0.012 kg/m y la cuerda está bajo una tensión de 1000.00 N, ¿cuál es la velocidad de la onda en la cuerda y la longitud de onda de la onda?

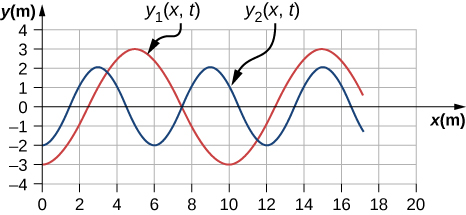
72. Dos ondas transversales viajan a través de una cuerda tensa. La velocidad de cada onda es v = 30.00 m/s. Una gráfica de la posición vertical en función de la posición horizontal se muestra a continuación para el tiempo t = 0.00 s. (a) ¿Cuál es la longitud de onda de cada onda? (b) ¿Cuál es la frecuencia de cada onda? (c) ¿Cuál es la velocidad vertical máxima de cada cuerda?



73. Una onda sinusoidal se desplaza por una cuerda tensa y horizontal con una densidad de masa lineal μ = 0.060 kg/m. La velocidad vertical máxima de la onda es v_ymax = 0.30 cm/s. La onda se modela con la ecuación de onda y(x, t) = Asen(6.00 m⁻¹x − 24.00 s⁻¹t). (a) ¿Cuál es la amplitud de la onda? (b) ¿Cuál es la tensión en la cuerda?

74. La velocidad de una onda transversal en una cuerda es v = 60.00 m/s y la tensión en la cuerda es F_T = 100.00 N. ¿Cuál debe ser la tensión para aumentar la velocidad de la onda a v = 120.00 m/s?

6.4 Energía y potencia de una onda

75. Una cuerda de 5 m de longitud y una masa de 90 g se mantiene bajo una tensión de 100 N. Una onda se desplaza por la cuerda que se modela como y(x, t) = 0.01 msen(0.40 m⁻¹x − 1170.12 s⁻¹). ¿Cuál es la potencia sobre una longitud de onda?

76. La cabeza rectangular de un dispositivo de imagen médica que mide 3,00 cm por 5,00 cm produce un ultrasonido de intensidad de 1,50 × 10² W/m². ¿Cuál es su potencia de salida?

77. El altavoz de baja frecuencia de un conjunto estéreo tiene una superficie de A = 0.05 m² y produce 1 W de potencia acústica. (a) ¿Cuál es la intensidad en el hablante? (b) Si el altavoz proyecta el sonido de manera uniforme en todas las direcciones, ¿a qué distancia del altavoz está la intensidad 0.1 W/m²?

78. Para aumentar la intensidad de una onda en un factor de 50, ¿en qué factor se debe aumentar la amplitud?

79. Un dispositivo llamado medidor de insolación se usa para medir la intensidad de la luz solar. Tiene un área de 100 cm² y registra 6.50 W. ¿Cuál es la intensidad en W/m²?

80. La energía del Sol llega a la cima de la atmósfera de la Tierra con una intensidad de 1400 W/m². ¿Cuánto tiempo demora 1.80 × 10⁹ J en llegar a un área de 1.00 m²?

81. Supón que tienes un dispositivo que extrae energía de los rompeolas en proporción directa a su intensidad. Si el dispositivo produce 10,0 kW de potencia en un día cuando los disyuntores tienen una altura de 1,20 m, ¿cuánto producirá cuando tengan una altura de 0,600 m?

82. Una matriz fotovoltaica de células solares es 10.0% eficiente para recolectar energía solar y convertirla en electricidad. Si la intensidad promedio de la luz solar en un día es de 70.00 W/m², ¿qué área debería tener su matriz para reunir energía a una velocidad de 100 W? (b) ¿Cuál es el costo máximo de la matriz si debe pagarse en dos años de operación con un promedio de 10.0 horas por día? Supón que ganas dinero a una tasa de 9.00 centavos por kilovatio-hora.

83. Un micrófono que recibe un tono de sonido puro alimenta un osciloscopio, produciendo una onda en su pantalla. Si la intensidad del sonido es originalmente de 2.00 × 10^-5 W/m², pero se aumenta hasta que la amplitud aumenta en un 30.0%, ¿cuál es la nueva intensidad?

84. Una cuerda con una masa de 0,30 kg tiene una longitud de 4,00 m. Si la tensión en la cuerda es de 50.00 N y se induce una onda sinusoidal con una amplitud de 2.00 cm en la cuerda, ¿cuál debe ser la frecuencia para una potencia promedio de 100.00 W?

85. En la figura anterior se muestra la potencia en función del tiempo para un punto en una cuerda (μ = 0.05 kg/m) en el que se induce una onda sinusoidal. La onda se modela con la ecuación de onda y(x, t) = Asen(20.93 m^-1x − ωt). ¿Cuál es la frecuencia y amplitud de la onda?

86. Una cuerda está bajo tensión F_T1. La energía es transmitida por una onda en la cuerda a la velocidad P₁ por una onda de frecuencia f₁. ¿Cuál es la relación de la nueva tasa de transmisión de energía P₂ a P₁ si la tensión se duplica?

87. Se golpea una horquilla de sintonización de 250 Hz y la intensidad en la fuente es I₁ a una distancia de un metro de la fuente. (a) ¿Cuál es la intensidad a una distancia de 4.00 m desde la fuente? (b) ¿A qué distancia de la bifurcación está la intensidad en una décima parte de la intensidad en la fuente?

88. Un altavoz de sonido tiene una potencia nominal de P = 120.00 V y una corriente de I = 10.00 A. El consumo de energía eléctrica es P = IV. Para probar el altavoz, se aplica una señal de onda sinusoidal al altavoz. Suponiendo que la onda de sonido se mueve como una onda esférica y que toda la energía aplicada al altavoz se convierte en energía de sonido, ¿a qué distancia del altavoz la intensidad es igual a 3.82 W/m²?

89. La energía de una ondulación en un estanque es proporcional a la amplitud al cuadrado. Si la amplitud de la ondulación es de 0.1 cm a una distancia de la fuente de 6.00 metros, ¿cuál fue la amplitud a una distancia de 2.00 metros de la fuente?

6.5 Interferencia de ondas

90. Considera dos ondas sinusoidales que viajan a lo largo de una cuerda, modeladas como y₁(x, t) = 0.3 msen(4 m^-1x + 3 s^-1t) e y₂(x, t) = 0.6 msen(8 m^-1x − 6 s^-1t). ¿Cuál es la altura de la onda resultante formada por la interferencia de las dos ondas en la posición x = 0.5 m en el tiempo t = 0.2 s?

91. Considera dos ondas sinusoidales que viajan a lo largo de una cuerda, modeladas como y₁(x, t) = 0.3 msen(4 m^-1x + 3 s^-1t + π/3) e y₂(x, t) = 0.6 msen(8 m^-1x − 6 s^-1t). ¿Cuál es la altura de la onda resultante formada por la interferencia de las dos ondas en la posición x = 1.0 m en el tiempo t = 3.0 s?

92. Considera dos ondas sinusoidales que viajan a lo largo de una cuerda, modeladas como y₁(x, t) = 0.3 msen(4 m^-1x − 3 s^-1t) e y₂(x, t) = 0.3 msen(4 m^-1x + 3 s^-1t). ¿Cuál es la función de onda de la onda resultante? [Sugerencia: usa la identidad trigonométrica sen(u ± v) = senucosv ± cosusenv

93. Dos ondas sinusoidales se mueven a través de un medio en la misma dirección, ambas con amplitudes de 3.00 cm, una longitud de onda de 5.20 m y un período de 6.52 s, pero una tiene un desplazamiento de fase de un ángulo φ. ¿Cuál es el cambio de fase si la onda resultante tiene una amplitud de 5.00 cm? [Sugerencia: use la identidad trigonométrica senu + senv = 2sen(u + v/2)cos(u - v/2)

94. Dos ondas sinusoidales se mueven a través de un medio en la dirección x positiva, ambas con amplitudes de 6.00 cm, una longitud de onda de 4.3 m y un período de 6.00 s, pero una tiene un desplazamiento de fase de un ángulo φ = 0.50 rad . ¿Cuál es la altura de la onda resultante en un tiempo t = 3.15 s y una posición x = 0.45 m?

95. Dos ondas sinusoidales se mueven a través de un medio en la dirección x positiva, ambas con amplitudes de 7.00 cm, un número de onda k = 3.00 m^-1, una frecuencia angular de ω = 2.50 s^-1 y un período de 6.00 s, pero uno tiene un desplazamiento de fase de un ángulo φ = π/12 rad. ¿Cuál es la altura de la onda resultante en un tiempo t = 2.00 s y una posición x = 0.53 m?

96. Considera dos ondas y₁(x, t) e y₂(x, t) que son idénticas excepto por un desplazamiento de fase que se propaga en el mismo medio. (a) ¿Cuál es el cambio de fase, en radianes, si la amplitud de la onda resultante es 1.75 veces la amplitud de las ondas individuales? (b) ¿Cuál es el cambio de fase en grados? (c) ¿Cuál es el cambio de fase como porcentaje de la longitud de onda individual?

97. Dos ondas sinusoidales, que son idénticas a excepción de un cambio de fase, viajan en la misma dirección. La ecuación de onda de la onda resultante es y_R(x, t) = 0.70 msen(3.00 m^-1x − 6.28 s^-1t + π/16 rad). ¿Cuáles son la frecuencia angular, el número de onda, la amplitud y el cambio de fase de las ondas individuales?

98. Dos ondas sinusoidales, que son idénticas a excepción de un cambio de fase, viajan en la misma dirección. La ecuación de onda de la onda resultante es y_R(x, t) = 0.35 cmsen(6.28 m^-1x − 1.57 s^-1t + π/4). ¿Cuáles son el período, la longitud de onda, la amplitud y el cambio de fase de las ondas individuales?

99. Considera dos funciones de onda, y₁(x, t) = 4.00 msen(π m^-1x − π s^-1t) e y₂(x, t) = 4.00 msen(π m^-1x − π s^-1t + π/3). (a) Usando una hoja de cálculo, traza las dos funciones de onda y la onda que resulta de la superposición de las dos funciones de onda como una función de la posición (0.00 ≤ x ≤ 6.00m) para el tiempo t = 0.00s. (b) ¿Cuáles son la longitud de onda y la amplitud de las dos ondas originales? (c) ¿Cuáles son la longitud de onda y la amplitud de la onda resultante?

100. Considera dos funciones de onda, y₂(x, t) = 2.00 mssen(π/2 m^-1x − π/3 s^-1t) e y₂(x, t) = 2.00 msen(π2 m ^-1x − π/3 s^-1t + π/6). (a) Verifique que y_R = 2Acos(φ/2 sen(kx − ωt + φ/2) es la solución para la onda que resulta de una superposición de las dos ondas. Haz una columna para x, y₁, y₂, y₁ + y₂, y y_R = 2Acos(φ/2)sen(kx − ωt + φ/2). Grafica cuatro ondas en función de la posición donde el rango de x es de 0 a 12 m.

101. Considera dos funciones de onda que difieren solo por un cambio de fase, y₁(x, t) = Acos(kx − ωt) e y₂(x, t) = Acos (kx − ωt + φ). Usa las identidades trigonométricas cosu + cosv = 2cos(u - v/2)cos(u + v/2) y cos(−θ) = cos(θ) para encontrar una ecuación de onda para la onda que resulta de la superposición de las dos ondas. ¿Te sorprende la función de onda resultante?

6.6 Ondas estacionarias y resonancia

102. Una ola que viaja en un Slinky® que se estira a 4 m tarda 2,4 s en recorrer la longitud del Slinky y luego nuevamente. (a) ¿Cuál es la velocidad de la onda? (b) Utilizando el mismo Slinky estirado a la misma longitud, se crea una onda estacionaria que consta de tres antinodos y cuatro nodos. ¿A qué frecuencia debe estar oscilando el Slinky?

103. Una cuerda de 2 m de largo se estira entre dos soportes con una tensión que produce una velocidad de onda igual a v_w = 50.00 m/s. ¿Cuál es la longitud de onda y la frecuencia de los tres primeros modos que resuenan en la cuerda?

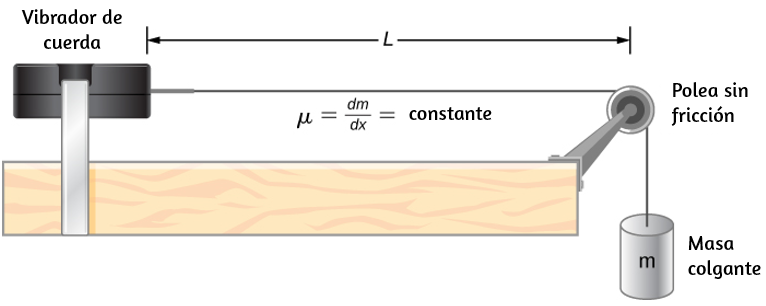
104. Considera la configuración experimental que se muestra a continuación. La longitud de la cuerda entre el vibrador de cuerda y la polea es L = 1.00 m. La densidad lineal de la cuerda es μ = 0.006 kg/m. El vibrador de cuerda puede oscilar a cualquier frecuencia. La masa colgante es de 2.00 kg. (a) ¿Cuáles son la longitud de onda y la frecuencia del modo n = 6? (b) La cuerda oscila el aire alrededor de la cuerda. ¿Cuál es la longitud de onda del sonido si la velocidad del sonido es v_s = 343.00 m/s?



105. Un cable con una densidad lineal de μ = 0.2 kg/m se cuelga de los postes de teléfono. La tensión en el cable es de 500.00 N. La distancia entre los polos es de 20 metros. El viento sopla a través de la línea, haciendo que el cable resuene. Se produce un patrón de ondas estacionarias que tiene 4.5 longitudes de onda entre los dos polos. La temperatura del aire es T = 20 °C. ¿Cuáles son la frecuencia y la longitud de onda del zumbido?

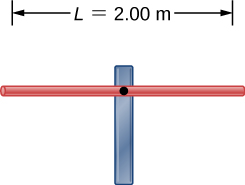
106. Considera una varilla de longitud L, montada en el centro a un soporte. Debe existir un nodo donde la varilla se monta sobre un soporte, como se muestra a continuación. Dibuja los dos primeros modos normales de la barra, ya que se impulsa en resonancia. Etiqueta la longitud de onda y la frecuencia requerida para que la varilla entre en resonancia.



107. Considera dos funciones de onda y(x, t) = 0.30 cmssen(3 m^-1x − 4 s^-1t) e y(x, t) = 0.30 cmsen(3 m^-1x + 4 s^-1t). Escribe una función de onda para la onda estacionaria resultante.

108. Un cable de 2,40 m tiene una masa de 7,50 g y está bajo una tensión de 160 N. El alambre se sostiene rígidamente en ambos extremos y se pone en oscilación. (a) ¿Cuál es la velocidad de las ondas en el cable? La cuerda se activa en resonancia por una frecuencia que produce una onda estacionaria con una longitud de onda igual a 1,20 m. (b) ¿Cuál es la frecuencia utilizada para conducir la cuerda en resonancia?

109. Una cuerda con una densidad de masa lineal de 0,0062 kg/m y una longitud de 3,00 m se establece en el modo de resonancia n = 100. La tensión en la cuerda es 20.00 N. ¿Cuál es la longitud de onda y la frecuencia de la onda?

110. Una cuerda con una densidad de masa lineal de 0,0075 kg/m y una longitud de 6,00 m se establece en el modo n = 4 de resonancia al conducir con una frecuencia de 100,00 Hz. ¿Cuál es la tensión en la cuerda?

111. Dos ondas sinusoidales con longitudes de onda y amplitudes idénticas viajan en direcciones opuestas a lo largo de una cuerda produciendo una onda estacionaria. La densidad de masa lineal de la cuerda es μ = 0.075 kg/m y la tensión en la cuerda es F_T = 5.00 N. El intervalo de tiempo entre instancias de interferencia destructiva total es Δt = 0.13 s. ¿Cuál es la longitud de onda de las ondas?

112. Una cuerda, fija en ambos extremos, tiene una longitud de 5,00 m y una masa de 0,15 kg. La tensión si la cuerda es de 90 N. La cuerda vibra para producir una onda estacionaria en la frecuencia fundamental de la cuerda. (a) ¿Cuál es la velocidad de las ondas en la cuerda? (b) ¿Cuál es la longitud de onda de la onda estacionaria producida? (c) ¿Cuál es el período de la onda estacionaria?

113. Una cuerda está fija en ambos extremos. La masa de la cuerda es de 0,0090 kg y la longitud es de 3,00 m. La cuerda está bajo una tensión de 200.00 N. La cuerda está controlada por una fuente de frecuencia variable para producir ondas estacionarias en la cuerda. Encuentra las longitudes de onda y la frecuencia de los primeros cuatro modos de ondas estacionarias.

114. Las frecuencias de dos modos sucesivos de ondas estacionarias en una cuerda son 258.36 Hz y 301.42 Hz. ¿Cuál es la siguiente frecuencia por encima de 100.00 Hz que produciría una onda estacionaria?

115. Una cuerda está fijada en ambos extremos a soportes separados por 3,50 m y tiene una densidad de masa lineal μ = 0,005 kg/m. La cuerda está bajo una tensión de 90.00 N. Se produce una onda estacionaria en la cuerda con seis nodos y cinco antinodos. ¿Cuáles son la velocidad de onda, la longitud de onda, la frecuencia y el período de la onda estacionaria?

116. Las ondas sinusoidales se envían por una cuerda de 1,5 m de largo fijada en ambos extremos. Las ondas se reflejan de nuevo en la dirección opuesta. La amplitud de la onda es de 4.00 cm. La velocidad de propagación de las ondas es de 175 m/s. Se produce el modo de resonancia n = 6 de la cuerda. Escribe una ecuación para la onda estacionaria resultante.

Problemas adicionales

117. El equipo de ultrasonido utilizado en la profesión médica utiliza ondas de sonido de una frecuencia superior al rango de la audición humana. Si la frecuencia del sonido producido por la máquina de ultrasonido es f = 30 kHz, ¿cuál es la longitud de onda del ultrasonido en el hueso, si la velocidad del sonido en el hueso es v = 3000 m/s?

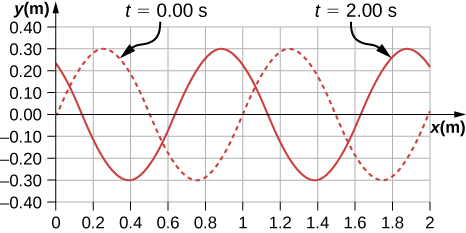
118. A continuación se muestra la gráfica de una función de onda que modela una onda en el tiempo t = 0.00s y t = 2.00 s. La línea de puntos es la función de onda en el tiempo t = 0.00 s y la línea continua es la función en el tiempo t = 2.00 s. Calcula la amplitud, la longitud de onda, la velocidad y el período de la onda.



119. La velocidad de la luz en el aire es aproximadamente v = 3.00 × 10⁸ m/s y la velocidad de la luz en el vidrio es v = 2.00 × 10⁸ m/s. Un láser rojo con una longitud de onda de λ = 633.00 nm ilumina la luz incidente del vidrio, y parte de la luz roja se transmite al vidrio. La frecuencia de la luz es la misma para el aire y el vidrio. (a) ¿Cuál es la frecuencia de la luz? (b) ¿Cuál es la longitud de onda de la luz en el vidrio?

120. Una estación de radio transmite ondas de radio a una frecuencia de 101.7 MHz. Las ondas de radio se mueven por el aire aproximadamente a la velocidad de la luz en el vacío. ¿Cuál es la longitud de onda de las ondas de radio?

121. Una persona que toma el sol se encuentra en la profundidad de la cintura en el océano y observa que cada minuto pasan seis crestas de ondas superficiales periódicas. Las crestas están separadas por 16.00 metros. ¿Cuál es la longitud de onda, la frecuencia, el período y la velocidad de las ondas?

122. Un diapasón vibra produciendo sonido a una frecuencia de 512 Hz. La velocidad del sonido del sonido en el aire es v = 343.00 m/s si el aire está a una temperatura de 20.00 °C. ¿Cuál es la longitud de onda del sonido?

123. Una lancha motora está viajando a través de un lago a una velocidad de v_b = 15.00 m/s. El bote rebota hacia arriba y hacia abajo cada 0.50 s mientras viaja en la misma dirección que una ola. Rebota hacia arriba y hacia abajo cada 0.30 s mientras viaja en una dirección opuesta a la dirección de las olas. ¿Cuál es la velocidad y la longitud de onda de la ola?

124. Usa la ecuación de onda lineal para mostrar que la velocidad de onda de una onda modelada con la función de onda y(x, t) = 0.20 msen(3.00 m^-1x + 6.00 s^-1t) es v = 2.00 m/s. ¿Cuáles son la longitud de onda y la velocidad de la onda?

125. Dadas las funciones de onda y₁(x, t) = Asen(kx − ωt) e y₂(x, t) = Asen(kx − ωt + φ) con φ ≠ π/2, muestra que y₁(x, t) + y₂(x, t) es una solución a la ecuación de onda lineal con una velocidad de onda de v = √ω/k.

126. Una onda transversal en una cuerda se modela con la función de onda y(x, t) = 0.10 msen(0.15 m^-1x + 1.50 s^-1t + 0.20). (a) Encuentra la velocidad de la onda. (b) Encuentra la posición en la dirección y, la velocidad perpendicular al movimiento de la onda y la aceleración perpendicular al movimiento de la onda, de un pequeño segmento de la cuerda centrado en x = 0.40 m en el tiempo t = 5.00 s.

127. Una onda sinusoidal se desplaza por una cuerda tensa y horizontal con una densidad de masa lineal de μ = 0.060 kg/m. La magnitud de la máxima aceleración vertical de la onda es a_ymax = 0.90 cm/s² y la amplitud de la onda es de 0.40 m. La cuerda está bajo una tensión de F_T = 600.00 N. La onda se mueve en la dirección x negativa. Escribe una ecuación para modelar la onda.

128. Una onda transversal en una cuerda (μ = 0.0030 kg/m) se describe con la ecuación y(x, t) = 0.30 msen(2π/4.00 m(x − 16.00 m/st)). ¿Cuál es la tensión bajo la cual la cuerda se mantiene tensa?

129. Una onda transversal en una cuerda horizontal (μ = 0.0060 kg/m) se describe con la ecuación y(x, t) = 0.30 msen(2π/4.00 m(x − v_wt)). La cuerda está bajo una tensión de 300.00 N. ¿Cuál es la velocidad de la onda, el número de onda y la frecuencia angular de la onda?

130. Un estudiante tiene un buscador de rango sónico económico y usa el buscador de rango para encontrar la distancia a la pared. El buscador de rango sónico emite una onda de sonido. La onda de sonido se refleja en la pared y regresa al buscador de rango. El viaje de ida y vuelta tarda 0.012 s. El buscador de rango fue calibrado para uso a temperatura ambiente T = 20 °C, pero la temperatura en la habitación es en realidad T = 23 °C. Suponiendo que el mecanismo de sincronización sea perfecto, ¿qué porcentaje de error puede esperar el estudiante debido a la calibración?

131. Una onda en una cuerda es impulsada por un vibrador de cuerda, que oscila a una frecuencia de 100.00 Hz y una amplitud de 1.00 cm. El vibrador de hilo funciona a una tensión de 12.00 V y una corriente de 0.20 A. La potencia consumida por el vibrador de hilo es P = IV. Supón que el vibrador de cuerda es 90% eficiente en la conversión de energía eléctrica en la energía asociada con las vibraciones de la cuerda. La cuerda tiene una longitud de 3,00 m, y está bajo una tensión de 60,00 N. ¿Cuál es la densidad de masa lineal de la cuerda?

132. Una onda viajera en una cadena se modela mediante la ecuación de onda y(x, t) = 3.00 cmssen(8.00 m^-1x + 100.00 s^-1t). La cuerda está bajo una tensión de 50.00 N y tiene una densidad de masa lineal de μ = 0.008 kg/m. ¿Cuál es la potencia promedio transferida por la onda en la cuerda?

133. Una onda transversal en una cuerda tiene una longitud de onda de 5.0 m, un período de 0.02 s y una amplitud de 1.5 cm. La potencia promedio transferida por la onda es de 5.00 W. ¿Cuál es la tensión en la cuerda?

134. (a) ¿Cuál es la intensidad de un rayo láser utilizado para quemar tejido canceroso que, cuando se absorbe el 90.0%, pone 500 J de energía en un punto circular de 2.00 mm de diámetro en 4.00 s? (b) Discute cómo se compara esta intensidad con la intensidad promedio de la luz solar (aproximadamente) y las implicaciones que tendría si el rayo láser entrara en tu ojo. Notae cómo tu respuesta depende de la duración del tiempo de la exposición.

135. Considera dos funciones de onda periódicas, y₁(x, t) = Asen(kx − ωt) e y₂(x, t) = Asen(kx − ωt + φ). (a) ¿Para qué valores de φ tendrá una amplitud de 2A la onda que resulta de una superposición de las funciones de onda? (b) ¿Para qué valores de φ tendrá una amplitud de cero la onda que resulta de una superposición de las funciones de onda?

136. Considera dos funciones de onda periódicas, y₁(x, t) = Asen(kx − ωt) e y₂(x, t) = Acos(kx − ωt + φ). (a) ¿Para qué valores de φ tendrá una amplitud de 2A la onda que resulta de una superposición de las funciones de onda? (b) ¿Para qué valores de φ tendrá una amplitud de cero la onda que resulta de una superposición de las funciones de onda?

137. Una cubeta con dimensiones de 10,00 metros por 0,10 metros por 0,10 metros se llena parcialmente con agua. Las ondas de agua de la superficie de pequeña amplitud se producen desde ambos extremos del canal mediante paletas que oscilan en un movimiento armónico simple. La altura de las ondas de agua se modelan con dos ecuaciones de onda sinusoidal, y₁(x, t) = 0.3 msen(4 m^-1x − 3 s^-1t) e y₂(x, t) = 0.3 mcos(4 m^-1x + 3 s^-1t − π/2). ¿Cuál es la función de onda de la onda resultante después de que las ondas se alcancen unas a otras y antes de que alcancen el final del canal (es decir, supón que solo hay dos ondas en el canal e ignora los reflejos)? Usa una hoja de cálculo para verificar tus resultados. (Sugerencia: usa las identidades trigonométricas sen(u ± v) = senucosv ± cosusenv y cos(u ± v) = cosucosv∓senusenv)

138. Un sismógrafo registra las ondas S y P de un terremoto con una diferencia de 20.00 s. Si viajaron por el mismo camino a velocidades de onda constantes de v_S = 4.00 km/s y v_P = 7.50 km/s, ¿a qué distancia está el epicentro del terremoto?

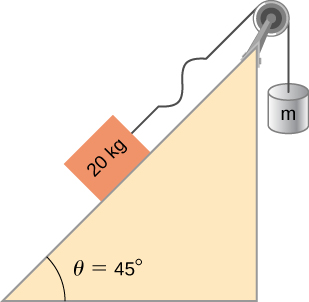
139. Considera lo que se muestra a continuación. Una masa de 20,00 kg descansa sobre una rampa sin fricción inclinada a 45°. Una cuerda con una densidad de masa lineal de μ = 0,025 kg/m está unida a la masa de 20,00 kg. La cuerda pasa sobre una polea sin fricción de masa despreciable y se une a una masa colgante (m). El sistema está en equilibrio estático. Se induce una onda en la cuerda y viaja por la rampa. (a) ¿Cuál es la masa de la masa colgante (m)? (b) ¿A qué velocidad de onda viaja la onda por la cuerda?



140. Considera la superposición de tres funciones de onda y(x, t) = 3.00 cmsen(2 m^-1x − 3 s^-1t), y(x, t) = 3.00 cmsen(6 m^-1x + 3 s^-1t), e y(x, t) = 3.00 cmsen(2 m^-1x − 4 s^-1t). ¿Cuál es la altura de la onda resultante en la posición x = 3.00 m en el tiempo t = 10.0 s?

141. Una cuerda tiene una masa de 150 g y una longitud de 3.4 m. Un extremo de la cuerda se fija a un soporte de laboratorio y el otro se une a un resorte con una constante de resorte de k_s = 100 N/m. El extremo libre del resorte está unido a otro polo de laboratorio. La tensión en la cuerda se mantiene por el resorte. Los polos de laboratorio están separados por una distancia que estira el resorte 2,00 cm. La cuerda es pulsada y un pulso viaja a lo largo de la cuerda. ¿Cuál es la velocidad de propagación del pulso?

142. Una onda estacionaria se produce en una cuerda bajo una tensión de 70.0 N por dos ondas transversales sinusoidales que son idénticas, pero que se mueven en direcciones opuestas. La cadena se fija en x = 0.00 m y x = 10.00 m. Los nodos aparecen en x = 0.00 m, 2.00 m, 4.00 m, 6.00 m, 8.00 m, y 10.00 m. La amplitud de la onda estacionaria es de 3,00 cm. Se necesitan 0.10 s para que los antinodos hagan una oscilación completa. (a) ¿Cuáles son las funciones de onda de las dos ondas sinusoidales que producen la onda estacionaria? (b) ¿Cuál es la velocidad máxima y la aceleración de la cuerda, perpendicular a la dirección de movimiento de las ondas transversales, en los antinodos?

143. Una cuerda con una longitud de 4 m se mantiene bajo una tensión constante. La cuerda tiene una densidad de masa lineal de μ = 0.006 kg/m. Dos frecuencias resonantes de la cuerda son 400 Hz y 480 Hz. No hay frecuencias resonantes entre las dos frecuencias. (a) ¿Cuáles son las longitudes de onda de los dos modos de resonancia? (b) ¿Cuál es la tensión en la cuerda?

Problemas de Desafío

144. Un cable de cobre tiene un radio de 200 μm y una longitud de 5.0 m. El cable se coloca bajo una tensión de 3000 N y el cable se estira en una pequeña cantidad. El cable es arrancado y un pulso viaja por el cable. ¿Cuál es la velocidad de propagación del pulso? (Supón que la temperatura no cambia: (ρ = 8.96 g/cm³, Y = 1.1 × 10¹¹ N/m)).

145. Un impulso que se mueve a lo largo del eje x puede modelarse como la función de onda y(x, t) = 4.00 me^{−(x + (2.00 m/s)t/1.00 m)2}. (a) ¿Cuáles son la dirección y la velocidad de propagación del pulso? (b) ¿Qué tan lejos se ha movido la ola en 3.00 s? (c) Grafica el pulso usando una hoja de cálculo en el tiempo t = 0.00 s y t = 3.00 s para verificar tu respuesta en la parte (b).

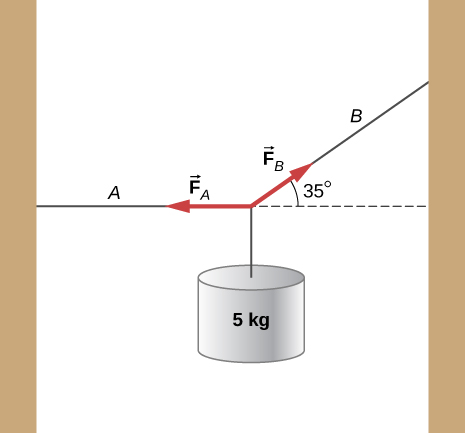
146. Una cuerda con una densidad de masa lineal de μ = 0.0085 kg/m está fijada en ambos extremos. Una masa de 5.0 kg se cuelga de la cuerda, como se muestra a continuación. Si se envía un pulso a lo largo de la sección A, ¿cuál es la velocidad de onda en la sección A y la velocidad de onda en la sección B?



147. Considera dos funciones de onda y₁(x, t) = Asen(kx − ωt) e y₂(x, t) = Asen(kx + ωt + φ). ¿Cuál es la función de onda que resulta de la interferencia de las dos ondas? (Pista: sen (α ± β) = senαcosβ ± cosαsinβ y φ = φ/2 + φ/2).

148. La función de onda que modela una onda estacionaria se da como y_R(x, t) = 6.00 cmsen(3.00 m^-1x + 1.20 rad)cos(6.00 s^-1t + 1.20 rad). ¿Cuáles son las dos funciones de onda que interfieren para formar esta función de onda? Grafica las dos funciones de onda y la suma de las dos funciones de onda en t = 1.00 s para verificar tu respuesta.

149. Considera dos funciones de onda y₁(x, t) = Asen(kx − ωt) e y₂(x, t) = Asen(kx + ωt + φ). La forma de onda resultante cuando agrega las dos funciones es y_R = 2Asen(kx + φ/2)cos(ωt + φ/2). Considera el caso donde A = 0.03 m^-1, k = 1.2 6m^-1, ω = π s^-1, y φ = π/10. (a) ¿Dónde están los primeros tres nodos de la función de onda estacionaria comenzando en cero y moviéndose en la dirección x positiva? (b) Usando una hoja de cálculo, traza las dos funciones de onda y la función resultante en el tiempo t = 1.00 s para verificar tu respuesta.