Preguntas y problemas - Capítulo IV

Preguntas conceptuales

4.1 Fluidos, densidad y presión

1.¿Cuáles de las siguientes sustancias son fluidos a temperatura ambiente y presión atmosférica: aire, mercurio, agua, vidrio?

2. ¿Por qué los gases son más fáciles de comprimir que los líquidos y los sólidos?

3. Explica cómo la densidad del aire varía con la altitud.

4. La imagen muestra un vaso de agua helada llena hasta el borde. ¿Se desbordará el agua cuando el hielo se derrita? Explica tu respuesta.



5. ¿Cómo se relaciona la presión con la agudez de un cuchillo y su capacidad para cortar?

6. ¿Por qué una fuerza ejercida por un fluido estático en una superficie siempre es perpendicular a la superficie?.

7.Imagina que en una ubicación remota cerca del Polo Norte, un trozo de hielo flota en un lago. Junto al lago, un glaciar con el mismo volumen que el hielo flotante se asienta en tierra. Si ambos trozos de hielo se derriten debido al aumento de las temperaturas globales, y todo el hielo derretido entra en el lago, cuál ¿Por qué el nivel del lago se eleva más? Explique.

8. En el ballet, bailar en punta (en la punta de los dedos de los pies) es mucho más difícil en los dedos de los pies que bailar o caminar. Explica por qué, en términos de presión.

9. La presión atmosférica ejerce una gran fuerza (igual al peso de la atmósfera sobre su cuerpo, unas 10 toneladas) sobre la parte superior de su cuerpo cuando está tumbado en la playa tomando el sol. ¿Por qué eres capaz de levantarte?

10. ¿Por qué la presión atmosférica disminuye lineal y rápidamente con la altitud?

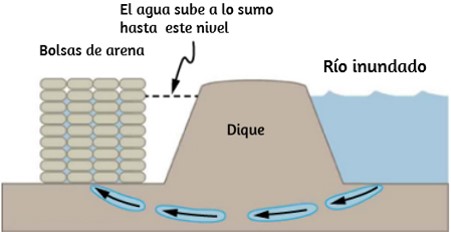
11. La imagen muestra cómo las bolsas de arena colocadas alrededor de una fuga fuera de un dique de un río pueden detener efectivamente el flujo de agua debajo del dique. Explique cómo la pequeña cantidad de agua dentro de la columna de sacos de arena puede equilibrar el cuerpo de agua mucho más grande detrás del dique.



12. ¿Hay una fuerza neta en una presa debido a la presión atmosférica? Explica tu respuesta.

13. ¿La presión atmosférica aumenta la presión del gas en un tanque rígido? ¿En un globo de juguete? ¿Cuándo, en general, la presión atmosférica no afecta a la presión total en un fluido?

14. Puede romper una botella de vino fuerte golpeando un corcho en ella con el puño, pero el corcho debe presionar directamente contra el líquido que llena la botella; no puede haber aire entre el corcho y el líquido. Explique por qué la botella se rompe solo si no hay aire entre el corcho y el líquido.

4.2 Medición de la presión

15. Explique por qué el fluido alcanza niveles iguales a ambos lados de un manómetro si ambos lados están abiertos a la atmósfera, incluso si los tubos tienen diámetros diferentes.

4.3 Principio de Pascal e hidráulica

16.Supongamos que el cilindro maestro en un sistema hidráulico está a una altura mayor que el cilindro que está controlando. Explique cómo afectará esto a la fuerza producida en el cilindro que se está controlando.

4.4 Flotabilidad y principio de Arquímedes

17. Se requiere más fuerza para tirar del tapón en una bañera llena que cuando está vacío. ¿Esto contradice el principio de Arquímedes? Explica tu respuesta.

18. ¿Los fluidos ejercen fuerzas de flotación en un entorno "sin peso", como en el transbordador espacial? Explica tu respuesta.

19. ¿Flotará el mismo barco más alto en agua salada que en agua dulce? Explica tu respuesta.

20. Las canicas cayeron en un fregadero de bañera parcialmente lleno hasta el fondo. Parte de su peso es soportado por la fuerza de flotación, pero la fuerza hacia abajo en el fondo de la bañera aumenta exactamente por el peso de las canicas. Explicar por qué

4.5 Dinámica de fluidos

21. Muchas figuras en el texto muestran líneas de corriente. Explique por qué la velocidad del fluido es mayor cuando las líneas de corriente están más cerca entre sí. (Sugerencia: considere la relación entre la velocidad del fluido y el área de la sección transversal a través de la cual fluye el fluido).

4.6 Ecuación de Bernoulli

22. Puede rociar agua desde una manguera de jardín a una distancia considerablemente mayor si cubre parcialmente la abertura con el pulgar. Explica cómo funciona esto.

23. El agua se dispara casi verticalmente hacia arriba en una fuente decorativa y se observa que la corriente se ensancha a medida que sube. A la inversa, una corriente de agua que cae directamente de un grifo se estrecha. Explicar por qué.

24. Vuelve a la figura 4.29. Responde las siguientes dos preguntas. ¿Por qué es p_o menos que la atmosférica? ¿Por qué p_o es mayor que p_i?

25. Un tubo con un segmento estrecho diseñado para mejorar el arrastre se llama Venturi, como se muestra a continuación. Los venturis son muy utilizados en carburadores y aspiradores. ¿Cómo refuerza esta estructura el arrastre?



26.Algunas tuberías de chimenea tienen forma de T, con un travesaño en la parte superior que ayuda a extraer los gases cuando hay incluso una ligera brisa. Explique cómo funciona esto en términos del principio de Bernoulli.

27.¿Hay un límite a la altura a la que un dispositivo de arrastre puede elevar un fluido? Explica tu respuesta.

28. ¿Por qué es preferible que los aviones despeguen contra el viento en lugar de hacerlo a favor del viento?.

29. Los techos a veces se empujan verticalmente durante un ciclón tropical, y los edificios a veces explotan hacia afuera cuando son golpeados por un tornado. Utilice el principio de Bernoulli para explicar estos fenómenos.

30. Es peligroso pararse cerca de las vías del tren cuando pasa un tren muy cercano y en rápido movimiento. Explica por qué la presión atmosférica te empujaría hacia el tren en movimiento.

31.La presión del agua dentro de una boquilla de manguera puede ser menor que la presión atmosférica debido al efecto Bernoulli. Explique en términos de energía cómo puede salir el agua de la boquilla contra la presión atmosférica opuesta.

32.David bajó la ventanilla de su auto mientras conducía por la autopista. Una bolsa de plástico vacía en el suelo voló rápidamente por la ventana. Explicar por qué.

33.De acuerdo con la ecuación de Bernoulli, ¿cuáles son las tres formas de energía en un fluido? (Tenga en cuenta que estas formas son conservadoras, a diferencia de la transferencia de calor y otras formas disipativas no incluidas en la ecuación de Bernoulli).

34. La vieja bota de goma que se muestra a continuación tiene dos fugas. ¿A qué altura máxima puede rociar el agua de la fuga 1? ¿En qué se diferencia la velocidad del agua que sale de la Fuga 2 de la de la Fuga 1? Explica tus respuestas en términos de energía.



35. La presión del agua dentro de una boquilla de manguera puede ser menor que la presión atmosférica debido al efecto Bernoulli. Explique en términos de energía cómo puede salir el agua de la boquilla contra la presión atmosférica opuesta.

4.7 Viscosidad y turbulencia

36.Explique por qué la viscosidad de un líquido disminuye con la temperatura, es decir, cómo podría un aumento de la temperatura reducir los efectos de las fuerzas cohesivas en un líquido?. También explicar por qué la viscosidad de un gas aumenta con temperatura, es decir, cómo aumenta la temperatura del gas entre átomos y moléculas?.

37.Al remar en una canoa río arriba, lo más prudente es viajar lo más cerca posible de la orilla. Cuando navegue en canoa río abajo, generalmente es mejor permanecer cerca del medio. Explique por qué.

37.La plomería generalmente incluye tubos llenos de aire cerca de los grifos de agua (vea la siguiente figura). Explique por qué se necesitan y cómo funcionan.

39.El ultrasonido Doppler se puede utilizar para medir la velocidad de sangre en el cuerpo. Si hay una constricción parcial de una arteria, donde esperas que la velocidad de la sangre sea mayor: en o después de la constricción? ¿Cuáles son las dos causas distintas de mayor resistencia en la constricción?.

40.Los drenajes de fregadero a menudo tienen un dispositivo como el que se muestra a continuación para ayudar a acelerar el flujo de agua. ¿Cómo funciona esto?.

Problemas

4.1 Líquidos, densidad y presión

41. El oro se vende por onza (31,103 g). ¿Cuanto es el volumen de 1 onza de oro puro?

42. El mercurio se suministra comúnmente en frascos que contienen 34,5 kg (aproximadamente 76 lb.). ¿Cuál es el volumen en litros de esta cantidad de mercurio?.

43.¿Cuál es la masa de una respiración profunda de aire con un volumen de 2.00 L? Discuta el efecto que tiene el tomar tal respiración en el volumen y la densidad de su cuerpo.

44. Un método sencillo para encontrar la densidad de un objeto es medir su masa y luego medir su volumen sumergiéndolo en un cilindro graduado. ¿Qué es el densidad de una roca de 240 g que desplaza 89,0 cm3 de agua? (Tenga en cuenta que la precisión y las aplicaciones prácticas de este son más limitadas que una variedad de otras que son basado en el principio de Arquímedes.)

45.Suponga que tiene una taza de café con una sección transversal circular y lados verticales (radio uniforme). ¿Cuál es su radio interior si contiene 375 g de café cuando se llena a una profundidad de 7,50 cm? Supongamos que el café tiene la misma densidad que el agua.

46. Un tanque rectangular de gasolina puede contener 50,0 kg de gasolina cuando está lleno. ¿Cuál es la profundidad del tanque si es ¿0,500 m de ancho por 0,900 m de largo? (b) Discutir si esto si el tanque de gasolina tiene un volumen razonable para un coche de pasajeros.

47.Un compactador de basura puede comprimir su contenido a 0,350 veces su volumen original. Dejando de lado la masa de aire expulsado, ¿por qué factor aumenta la densidad de la basura?

48. Una lata de gasolina de acero de 2.50 kg puede contener 20.0 L de gasolina cuando está llena. ¿Cuál es la densidad media de la lata llena de gas, teniendo en cuenta el volumen ocupado por el acero y la gasolina?

49. ¿Cuál es la densidad del oro de 18.0 quilates que es una mezcla de 18 partes de oro, 5 partes de plata y 1 parte de cobre? (Estos valores son partes por masa, no por volumen.) Supongamos que se trata de una mezcla simple con una densidad media igual a las densidades ponderadas de sus constituyentes.

50.La punta de un clavo ejerce una presión grande cuando es golpeado por un martillo. Dado que éste ejerce una gran fuerza sobre un área pequeña. ¿Qué fuerza se debe ejercer sobre un clavo con una punta circular de 1.00 mm de diámetro para crear una presión de 3.00 × 109 N / m²? (Esta alta presión es posible porque el martillo que golpea el clavo se detiene en una distancia tan corta).

51.Un tubo de vidrio contiene mercurio. ¿Cuál sería la altura de la columna de mercurio que crearía una presión igual a 1.00 atm? .

52. Las mayores profundidades oceánicas de la Tierra se encuentran en la Fosa de las Marianas, cerca de Filipinas. Calcule la presión debida al océano en la parte inferior de esta zanja, dado que su profundidad es de 11,0 km y se supone que la densidad del agua de mar es constante hasta el final.

53. Verifique que la unidad SI de hρg sea N/m².

54.¿Qué presión se ejerce en el fondo de un tanque de gas que tiene 0.500 m de ancho y 0.900 m de largo y puede contener 50.0 kg de gasolina cuando está lleno?

55. Una presa se utiliza para contener un río. La presa tiene una altura H = 12 m y una anchura W = 10 m. Suponga que la densidad del agua es ρ = 1000 kg/m³. (a) Determine la fuerza neta sobre la presa. (b) ¿Por qué aumenta el espesor de la presa con la profundidad?

4.2 Medición de la Presión

56. Encuentre el manómetro y las presiones absolutas en el frasco de globo y maní que se muestra en la Figura 4.12, suponiendo que el manómetro conectado al globo utiliza agua y el manómetro conectado al frasco contiene mercurio. Exprese en unidades de centímetros de agua para el globo y milímetros de mercurio para la jarra, tomando h = 0.0500m para cada uno ( revisar traducción)

57. ¿Qué altura debe tener un manómetro lleno de agua para medir la presión sanguínea hasta 300 mm Hg?.

58. Suponiendo que los neumáticos de bicicleta sean perfectamente flexibles y soporten el peso de la bicicleta y el ciclista solo con la presión, calcule el área total de los neumáticos en contacto con el suelo si una bicicleta y un ciclista tienen una masa total de 80.0 kg, y la presión manométrica en los neumáticos es de 3.50 × 10⁵ Pa.

4.3 Principio de Pascal e hidráulica.

59. ¿Cuánta presión se transmite en el sistema hidráulico considerado en el Ejemplo 4.3? Expresa tu respuesta en atmósferas.

60. ¿Qué fuerza debe ejercerse sobre el cilindro maestro de un elevador hidráulico para soportar el peso de un automóvil de 2000 kg (un automóvil grande) que descansa sobre un segundo cilindro? El cilindro maestro tiene un diámetro de 2.00 cm y el segundo cilindro tiene un diámetro de 24.0 cm..

61.Una persona vierte los restos de varias botellas de vino en una jarra después de una fiesta. La persona luego inserta un corcho con un diámetro de 2.00 cm en la botella, poniéndolo en contacto directo con el vino. Luego coloca el corcho en su lugar y la parte inferior de la jarra (con un diámetro de 14.0 cm) se desprende. Calcule la fuerza extra ejercida contra el fondo si golpea el corcho con una fuerza de 120N .

62.Un determinado sistema hidráulico está diseñado para ejercer una fuerza 100 veces mayor que la que se le aplica. (a) ¿Cuál debe ser la relación entre el área del cilindro que se está controlando y el área del cilindro maestro? (b) ¿Cuál debe ser la relación de sus diámetros? (c) ¿Por qué factor es la distancia a través de la cual se reduce la fuerza de salida en relación con La distancia a través de la cual se mueve la fuerza de entrada? No asuma pérdidas por fricción.

63. Verifique que el trabajo de entrada sea igual al trabajo de salida para un sistema hidráulico, asumiendo que no hay pérdidas debido a la fricción. Haga esto mostrando que la distancia que se mueve la fuerza de salida se reduce por el mismo factor que la fuerza de salida aumenta. Supongamos que el volumen del fluido es constante. ¿Qué efecto tendría la fricción dentro del fluido y entre ¿Los componentes en el sistema tienen en la fuerza de salida? ¿Dependería esto de si el fluido se está moviendo o no?.

4.4 Principio de Arquímedes y flotabilidad

64. ¿Qué fracción de hielo se sumerge cuando flota en agua dulce, dada la densidad del agua a 0°C es muy cercana a 1000 kg / m³ ?.

65. Si el cuerpo de una persona tiene una densidad de 995 kg / m³, ¿qué fracción del cuerpo quedará sumergido al flotar suavemente en (a) agua dulce? (b) ¿En agua salada con una densidad de 1027 kg /m³ ?.

66. Una roca con una masa de 540 g en el aire tiene una masa aparente de 342 g cuando se sumerge en agua. (a) ¿Qué masa de agua se desplaza? (b) ¿Cuál es el volumen de la roca? (c) ¿Cuál es su densidad media? ¿Es esto consistente con el valor para el granito?.

67. El principio de Arquímedes se puede usar para calcular la densidad de un fluido así como la de un sólido. Supongamos que un trozo de hierro con una masa de 390.0 g en el aire tiene una masa aparente de 350.5 g cuando está completamente sumergido en un líquido desconocido. (a) ¿Qué masa de fluido desplaza el hierro? (b) ¿Cuál es el volumen de hierro, usando su densidad como se indica en la Tabla 4.1? (c) Calcule la densidad del fluido e identifíquelo.

68. Calcule la fuerza de flotación en un globo de helio de 2.00 l. (b) Dada la masa del caucho en el globo es de 1.50 g, ¿cuál es la fuerza vertical neta sobre el globo si se suelta? Desprecie el volumen de la goma.

69. ¿Cuál es la densidad de una mujer que flota en agua dulce con 4.00% de su volumen sobre la superficie? (Esto podría medirse colocándola en un tanque con marcas en el costado para medir la cantidad de agua que desplaza cuando flota y cuando se mantiene bajo el agua). (B) ¿Qué porcentaje de su volumen está por encima de la superficie cuando flota en el agua de mar?.

70. Un hombre tiene una masa de 80 kg y una densidad de 955 kg/m³. (excluyendo el aire en sus pulmones). (a) Calcula su volumen. (b) Encuentra la fuerza de flotación que ejerce el aire sobre él. (c) ¿Cuál es la relación entre la fuerza de flotación y su peso?.

71. Se puede hacer una brújula simple colocando una barra pequeña. Imán sobre un corcho flotando en el agua. (a) ¿Qué fracción de un ¿Se sumergirá el corcho liso al flotar en el agua? (b) si el corcho tiene una masa de 10.0 gy se coloca un imán de 20.0 g En ella, ¿qué fracción del corcho se sumergirá? (c) Will ¿El imán de barra y el corcho flotan en alcohol etílico?.

72. ¿Qué porcentaje del peso de un ancla de hierro será soportado por la fuerza de flotación cuando se sumerge en agua salada?.

73. Refiriéndose a la Figura 4.20, compruebe que la fuerza de flotación en el cilindro es igual al peso del fluido desplazado (principio de Arquímedes). Puede suponer que la fuerza de flotación es F₂ - F₁ y que los extremos del cilindro tengan áreas iguales A. Tenga en cuenta que el volumen del cilindro (y el del fluido que desplaza) es igual a (h₂−h₁) A.

74. Un hombre de 75.0 kg flota en agua dulce con un 3.00% de su volumen sobre el agua cuando sus pulmones están vacíos, y un 5.00% de su volumen sobre el agua cuando sus pulmones están llenos. Calcule el volumen de aire que inhala, llamado su capacidad pulmonar, en litros. (b) ¿Parece razonable este volumen pulmonar?.

4.5 Dinámica de fluídos

75. ¿Cuál es el caudal promedio en cm³/ s de gasolina al motor de un automóvil que viaja a 100 km / h si tiene un promedio de 10.0 km / L?.

76. El corazón de un adulto en reposo bombea sangre a una velocidad de 5.00 L / min. (a) Convierta esto a cm³/s. (b) ¿Cuál es esta tasa en m³/s?.

77. Las cataratas Huka en el río Waikato es una de las atracciones turísticas naturales más visitadas de Nueva Zelanda. En promedio, el río tiene un caudal de alrededor de 300,000 L/s. En el desfiladero, el río se estrecha a 20 m de ancho y tiene un promedio de 20 m de profundidad. (a) ¿Cuál es la velocidad media del río en el ¿garganta? (b) ¿Cuál es la velocidad promedio del agua en el río río abajo de las cataratas cuando se amplía a 60 m y su profundidad aumenta a un promedio de 40 m?.

78. (a) Estime el tiempo que tomaría llenar una piscina privada con una capacidad de 80,000 L con una manguera de jardín que entrega 60 L / min. (b) ¿Cuánto tiempo tomaría si pudiera desviar un río de tamaño moderado, fluyendo a 5000 m³/s hacia la piscina?.

79. ¿Cuál es la velocidad del fluido en una manguera de incendios con un diámetro de 9.00 cm que lleva 80.0 L de agua por segundo? (b) ¿Cuál es el caudal en metros cúbicos por segundo? (c) ¿Serían diferentes sus respuestas si el agua salada reemplazara el agua dulce en la manguera contra incendios?.

80. El agua se mueve a una velocidad de 2.00 m / s a través de una manguera con un diámetro interno de 1,60 cm. (a) Qué es ¿El caudal en litros por segundo? (b) La velocidad del fluido en la boquilla de esta manguera es de 15 m / s. ¿Cuál es el diámetro interior de la boquilla?.

81. Demostrar que la velocidad de un fluido incompresible a través de una constricción, como en un tubo Venturi, aumenta por un factor igual al cuadrado del factor por el cual el El diámetro disminuye. (Lo contrario se aplica para el flujo de un constricción en una región de mayor diámetro.).

82. El agua emerge hacia abajo desde un grifo con un diámetro de 1,80 cm a una velocidad de 0.500 m / s. (Debido a la construcción de la llave, no hay variación en la velocidad a lo largo de la corriente). (A) ¿Cuál es el caudal en cm³/s? (b) ¿Cuál es el diámetro de la corriente a 0.200 m por debajo del grifo? Desprecie cualquier efecto debido a la tensión superficial..

4.6 Ecuación de Bernoulli

83. Verificar que la presión tiene unidades de energía por unidad volumen.

84. Supongamos que tienes un indicador de velocidad del viento como el tubo de pitot mostrado en la figura 4.32. ¿Por qué factor debe viento ¿Incremento de velocidad para duplicar el valor de h en el manómetro? ¿Es esto independiente del fluido en movimiento y el fluido en el manómetro?.

85. Si la lectura de presión de su tubo de pitot es de 15.0 mmHg a una velocidad de 200 km / h, ¿cuál será a 700 km / h a la misma altitud?.

86. Los vientos en Boulder, Colorado, alcanzan velocidades sostenidas de 45.0 m / s (aproximadamente 100 mph) cuando la corriente en chorro desciende a principios de la primavera. Aproximadamente, ¿cuál es la fuerza debida a la ecuación de Bernoulli en un techo con una superficie de 220 m²? La densidad de aire típica en Boulder es de 1,14 kg / m³, y la presión atmosférica correspondiente es de 8,89 × 10⁴ N / m². (El principio de Bernoulli como se indica en el texto asume un flujo laminar. El uso del principio aquí solo produce un resultado aproximado, porque hay una turbulencia significativa).

87. ¿Cuál es la caída de presión debida al efecto Bernoulli) cuando el agua ingresa en una boquilla de 3.00 cm de diámetro desde una manguera de incendio de 9.00 cm de diámetro mientras transporta un flujo de 40.0 L / s? (b) ¿A qué altura máxima sobre la boquilla puede subir esta agua? (La altura real será significativamente menor debido a la resistencia del aire).

88. (a) Usando la ecuación de Bernoulli, muestre que la velocidad v del fluido medida en un tubo de Pitot, como la de la Figura 4.32 , viene dada por
v = (2ρ′ghρ )^1/2, donde h es la altura del fluido del manómetro , ρ′ es la densidad del fluido del manómetro, ρ es la densidad del fluido en movimiento, y g es la aceleración debida a la gravedad. (Tenga en cuenta que v es de hecho proporcional a la raíz cuadrada de h, como se indica en el texto).(b) Calcule v para el aire en movimiento si la h de un manómetro de mercurio es 0.200 m..

89. Un contenedor de agua tiene un área de sección transversal de A = 0.1 m². Un pistón se asienta sobre el agua (consulte la siguiente figura). Hay un pico ubicado a 0.15 m del fondo del tanque, abierto a la atmósfera, y una corriente de agua sale del pico. El área de la sección transversal del pico es A_s = 7.0 × 10^-4m ². (a) ¿Cuál es la velocidad del agua cuando sale del pico? (b) Si la apertura de la el pico está ubicado a 1.5 m por encima del suelo, ¿a qué distancia del pico cae el agua al piso? Ignora todas las fuerzas de fricción y disipación.



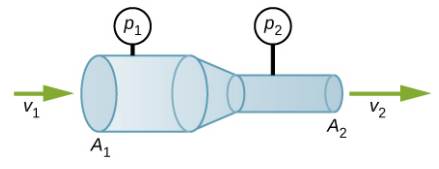
90. Un fluido de densidad constante fluye a través de una reducción en una tubería. Encuentre una ecuación para el cambio en la presión, en términos de v₁, A₁, A₂ y la densidad..

4.7. Viscosidad y turbulencia

91. (a) Calcule la fuerza de retardo debido a la viscosidad de la capa de aire entre un carro y una pista de aire nivelada dada la Información siguiente: la temperatura del aire es de 20°C, el carro se mueve a 0.400 m/s, su área de superficie es de 2.50 × 10^-2 m², y el espesor de la capa de aire es de 6.00 × 10^-5m. (b) ¿Cuál es la relación de esta fuerza con el peso del carro de 0.300 kg?.

92. Las arteriolas (arterias pequeñas) que conducen a un órgano se contraen para disminuir el flujo al órgano. Para llegar a un órgano, el flujo de sangre se reduce naturalmente al 1.00% de su valor original. ¿Por qué factor se contraen los radios de las arteriolas?.

93. Una partícula esférica que cae a una velocidad terminal en un líquido debe tener la fuerza gravitacional equilibrada por la fuerza de arrastre y la fuerza de flotación. La fuerza de flotación es igual al peso del fluido desplazado, mientras que se supone que la fuerza de arrastre viene dada por la Ley de Stokes, Fs = 6πrηv. Demuestre que la velocidad terminal viene dada por
v = 2R²g/9η( ρ₂−ρ₁),donde R es el radio de la esfera, ρs es su densidad y ρ₁ es la densidad del fluido, y η el coeficiente de viscosidad.

94. Usando la ecuación del problema anterior, encuentre la viscosidad del aceite de motor en el cual una bola de acero de radio de 0.8 mm cae con una velocidad terminal de 4.32 cm/s. Las densidades de la bola y el aceite son 7.86 y 0.88 g / mL, respectivamente..

95. Un paracaidista alcanzará una velocidad terminal cuando la resistencia del aire sea igual a su peso. Para un paracaidista con un cuerpo grande, la turbulencia es un factor a altas velocidades. La fuerza de arrastre es entonces aproximadamente proporcional al cuadrado de la velocidad. Tomando la fuerza de arrastre para ser F_D = 1/2ρAv², y configurando esto igual al peso del paracaidista, encuentre la velocidad terminal para que una persona caiga en "águila extendida".

96. (a) Verifique que una disminución del 19.0% en el flujo laminar a través de un tubo sea causada por una disminución del radio del 5.00%, asumiendo que todos los demás factores permanecen constantes. (b) ¿Qué aumento en el flujo se obtiene a partir de un aumento de 5.00% en el radio, asumiendo nuevamente que todos los demás factores permanecen constantes?.

97. Cuando los médicos diagnostican obstrucciones arteriales, citan la reducción en la tasa de flujo. Si la tasa de flujo en una arteria se redujo a 10.0% de su valor normal por un coágulo de sangre y la diferencia de presión promedio aumentó en 20.0%, ¿en qué factor el coágulo redujo el radio de la arteria?.

98. Una ráfaga de aceite dispara crudo a 25.0 m en el aire a través de una tubería con un diámetro de 0.100 m. Si se desprecia la resistencia del aire pero no la resistencia de la tubería y, suponiendo un flujo laminar, calcule la presión en la entrada de la tubería vertical de 50.0 m de longitud. Tome la densidad del aceite a ser 900 kg / m³ y su viscosidad será de 1.00 (N/m²) s (o 1.00 Pa s). Tenga en cuenta que debe tener en cuenta la presión debida a la columna de aceite de 50.0 m en la tubería.

99. El hormigón se bombea desde un mezclador de cemento al lugar donde se está colocando, en lugar de ser transportado en carretillas. El caudal es de 200 L / min a través de una manguera de 50.0 m de largo y 8.00 cm de diámetro, y la presión en la bomba es de 8.00 × 106 N / m². (a) Calcule la resistencia de la manguera. (b) ¿Cuál es la viscosidad del concreto, asumiendo que el flujo es laminar? (c) ¿Cuánta potencia se suministra, suponiendo que el punto de uso se encuentre al mismo nivel que la bomba? Puede descuidar la potencia suministrada para aumentar la velocidad del hormigón..

100. Verifique que el flujo de aceite sea laminar para un acumulador de aceite que dispara crudo a 25.0 m en el aire a través de una tubería con un diámetro de 0.100 m. El tubo vertical tiene una longitud de 50 m. Tome la densidad del aceite para que sea de 900 kg / m³ y su viscosidad sea de 1.00 (N / m²) s (o 1.00 Pa s).

101. Calcule los números de Reynolds para el flujo de agua a través de (a) una boquilla con un radio de 0.250 cm y (b) una manguera de jardín con un radio de 0.900 cm, cuando la boquilla está unida a la manguera. El caudal a través de la manguera y la boquilla es de 0.500 l/s. ¿El flujo puede ser laminar?.

102. Una manguera de incendios tiene un diámetro interior de 6,40 cm. Supongamos que una manguera de este tipo transporta un flujo de 40.0 L / s a partir de una presión manométrica de 1.62 × 10⁶ N/m². La manguera sube 10,0 m por una escalera hasta una boquilla con un diámetro interior de 3,00 cm. Calcule los números de Reynolds para el flujo en la manguera de incendios y la boquilla para mostrar que el flujo en cada uno debe ser turbulento..

103. ¿A qué velocidad de flujo podría comenzar a desarrollarse la turbulencia en una cañería de agua con un diámetro de 0.200 m? Supongamos una temperatura de 20°C..

PROBLEASM ADICIONALES

104. Antes de los dispositivos de almacenamiento digital, como la memoria de su teléfono celular, la música se almacenaba en discos de vinilo con ranuras con diferentes profundidades cortadas en el disco. Un fonógrafo usaba una aguja, que se movía sobre las ranuras, midiendo la profundidad de las ranuras. La presión ejercida por una aguja de fonógrafo en un registro es sorprendentemente grande. Si el equivalente de 1.00 g es soportado por una aguja, cuya punta es un círculo con un radio de 0.200 mm, qué presión se ejerce sobre el registro  ¿en Pa?.

105. Las torres de agua almacenan el agua por encima del nivel de los consumidores para tiempos de uso intensivo, eliminando la necesidad de bombas de alta velocidad. ¿Qué tan alto por encima del usuario debe ser el nivel del agua para crear una presión manométrica de 3.00 × 10⁵N/m²?.

106. El humor acuoso en el ojo de una persona ejerce una fuerza de 0.300 N en el área de 1.10 cm2 de la córnea. ¿Qué presión es esta en mm Hg?.

107. (a) Convierta las lecturas de presión arterial normal de 120 a 80 mm Hg en newtons por metro cuadrado utilizando la relación de presión debida al peso de un fluido (p = hρg) en lugar de un factor de conversión. (b) Explique por qué la presión arterial de un bebé probablemente sea menor que la de un adulto. Considere la altura más pequeña a la que se debe bombear la sangre.

108. Las ollas a presión han existido durante más de 300 años, aunque su uso ha disminuido considerablemente en los últimos años (los primeros modelos tenían la mala costumbre de explotar). ¿Cuánta fuerza deben soportar los pestillos que sostienen la tapa en una olla a presión si la tapa circular tiene un diámetro de 25.0 cm y la presión manométrica interior es de 300 atm? Ignorar el peso de la tapa..

109. Los huesos de los pájaros tienen bolsas de aire para reducir su peso: esto también les da una densidad promedio significativamente menor que la de los huesos de otros animales. Supongamos que un ornitólogo pesa un hueso de ave en el aire y en el agua y encuentra que su masa es de 45.0 gy su masa aparente cuando está sumergida es de 3.60 g (se supone que el hueso es impermeable). (a) ¿Qué masa de agua se desplaza? (b) ¿Cuál es el volumen del hueso? (c) ¿Cuál es su densidad media?.

110. En una medida de inmersión de la densidad de una mujer, se encuentra que tiene una masa de 62.0 kg en el aire y una masa aparente de 0.0850 kg cuando está completamente sumergida con los pulmones vacíos. (a) ¿A qué masa de agua desplaza? (b) ¿Cuál es su volumen? (c) Calcule su densidad. (d) Si su capacidad pulmonar es de 1.75 L, ¿puede flotar sin pisar el agua con los pulmones llenos de aire? .

111. Algunos peces tienen una densidad ligeramente menor que la del agua y deben ejercer una fuerza (nadar) para permanecer sumergidos. ¿Qué fuerza debe ejercer un mero de 85.0 kg para permanecer sumergido en agua salada si su densidad corporal es de 1015 kg/m³?.

112. El sistema de circulación humana tiene aproximadamente 1 × 109 vasos capilares. Cada recipiente tiene un diámetro de aproximadamente 8 µm. Suponiendo que el gasto cardíaco es de 5 l / min, determine la velocidad promedio del flujo sanguíneo a través de cada vaso capilar..

113. El caudal de sangre a través de un capilar de radio de 2.00 × 10^-6 m es de 3.80 × 10⁹ cm³/ s. (a) ¿Cuál es la velocidad del flujo sanguíneo? (b) Suponiendo que toda la sangre en el cuerpo pasa a través de los capilares, ¿cuántos de ellos deben haber para llevar un flujo total de 90.0 cm³ / s?.

114. El ventrículo izquierdo del corazón de un adulto en reposo bombea sangre a una velocidad de flujo de 83.0 cm³/s, aumentando su presión en 110 mm Hg, su velocidad de cero a 30.0 cm / s, y su altura en 5.00 cm. (Todos los números se promedian a lo largo de todo el latido del corazón). Calcule la potencia total de salida del ventrículo izquierdo. Tenga en cuenta que la mayor parte del poder se utiliza para aumentar la presión arterial.

115. Una bomba de sumidero (utilizada para drenar el agua del sótano de las casas construidas debajo del nivel freático) drena un sótano inundado a una velocidad de 0.750 L / s, con una presión de salida de 3.00 × 10⁵ N / m². (a) El agua entra en una manguera con un diámetro interior de 3,00 cm y se eleva 2,50 m por encima de la bomba. ¿Cuál es su presión en este punto? (b) La manguera recorre el muro de la cimentación, perdiendo 0.500 m de altura y se ensancha a 4.00 cm de diámetro. ¿Cuál es la presión ahora? Puede descuidar las pérdidas por fricción en ambas partes del problema.

116. Una solución de glucosa se administrada por vía intravenosa tiene un caudal de 4,00 cm³/min. ¿Cuál será la nueva tasa de flujo si la glucosa es reemplazada por sangre entera con la misma densidad pero con una viscosidad 2,50 veces mayor que la de la glucosa? Todos los demás factores permanecen constantes.

117. Una arteria pequeña tiene una longitud de 1,1 × 10^-3m y un radio de 2,5 × 10^-5m. Si la caída de presión a través de la arteria es de 1,3 kPa, ¿cuál es la tasa de flujo a través de la arteria? (Supongamos que la temperatura es de 37 °C .)

118. La angioplastia es una técnica en la que las arterias parcialmente bloqueadas con placa se dilatan para aumentar el flujo sanguíneo. ¿Por qué factor debe aumentarse el radio de una arteria para aumentar el flujo sanguíneo en un factor de 10?.

119. Supongamos que el radio de un vaso sanguíneo se reduce a 90.0% de su valor original por depósitos de placa y el cuerpo lo compensa aumentando la diferencia de presión a lo largo del vaso para mantener constante la tasa de flujo. ¿Por qué factor debe aumentar la diferencia de presión? b) Si la obstrucción crea turbulencia, ¿qué efecto adicional tendría en el caudal?.

Problemas de Desafío

120. La presión sobre la presa mostrada al principio de la sección de problemas aumenta con la profundidad. Por lo tanto, hay un torque neto en la presa. Encuentra el par torque.

121. La temperatura de la atmósfera no siempre es constante y puede aumentar o disminuir con la altura. En una atmósfera neutra, donde no hay una cantidad significativa de mezcla vertical, la temperatura disminuye a una velocidad de aproximadamente 6,5 K por km. La magnitud de la disminución de la temperatura a medida que aumenta la altura se conoce como la tasa de caducidad (Γ). (El símbolo es la letra griega mayúscula gamma.) Supongamos que la presión superficial es p₀ = 1,013 × 10⁵ Pa donde T = 293 K y la tasa de caducidad es (-Γ = 6.5 K/km),estimación de la presión a 3,0 km por encima del nivel del mar la superficie de la Tierra.

122. Un submarino queda varado en el fondo del océano con su escotilla a 25,0 m por debajo de la superficie. Calcular la fuerza necesaria para abrir la escotilla desde el interior, ya que es circular y tiene un diámetro de 0,450 m. La presión del aire dentro del submarino es de 1.00 atm.

123.Los troncos a veces flotan verticalmente en un lago porque un extremo se ha vuelto acuoso y más denso que el otro. ¿Cuál es la densidad promedio de un tronco de diámetro uniforme que flota con 20.0% de su longitud sobre el agua?.

124. Se sabe que los estafadores malintencionados representan lingotes de tungsteno bañados en oro como oro puro y los venden a precios muy por debajo del valor del oro pero muy por encima del costo del tungsteno. ¿Con qué precisión debe poder medir la masa de un lingote dentro y fuera del agua para indicar que se trata de tungsteno casi puro en lugar de oro puro?.

125. El volumen interior de una casa es equivalente al de un sólido rectangular de 13.0 m de ancho por 20.0 m de largo por 2.75 m de alto. La casa se calienta por un calentador de gas de aire forzado. El principal conducto de aire de captación del calentador es de 0.300 m de diámetro. ¿Cuál es la velocidad promedio del aire en el ducto si lleva un volumen igual al del interior de la casa cada 15 minutos?.

126. Una manguera de jardín con un diámetro de 2,0 cm se utiliza para llenar un cubo, que tiene un volumen de 0,10 metros cúbicos. Se tarda 1,2 minutos en llenarse. Una boquilla ajustable está conectada a la manguera para disminuir el diámetro de la abertura, lo que aumenta la velocidad del agua. La manguera se mantiene nivelada hasta el suelo a una altura de 1,0 metros y el diámetro es de disminuye hasta que se alcanza un parterre a 3,0 metros de distancia. (a) ¿Cuál es la tasa de flujo volumétrico del agua a través del cuando el diámetro es de 2,0 cm? b) ¿Cuál es la velocidad? del agua que sale de la manguera? c) ¿Qué es lo que hace que la la velocidad del agua que sale de la manguera tiene que ser llegar al parterre a 3,0 metros de distancia? d) ¿Qué es el diámetro de la boquilla necesaria para llegar al lecho de flores?.

127. Una regla empírica que se cita con frecuencia en el diseño de aviones es que las alas deben producir alrededor de 1000 N de elevación por cuadrado metro de ala. (El hecho de que un ala tenga una parte superior e inferior la superficie no duplica su área.) a) En el momento del despegue, una aeronave se desplaza a 60,0 m/s, de modo que la velocidad del aire relativa a la la parte inferior del ala es de 60,0 m/s. Dada la densidad del nivel del mar de aire como 1,29 kg/m³ qué tan rápido debe moverse sobre el superficie superior para crear la elevación ideal? b) La rapidez con la que deben el aire se mueve sobre la superficie superior a una velocidad de crucero de 245 m/s y a una altitud donde la densidad del aire es de un cuarto que a nivel del mar? (Tenga en cuenta que esto no es todo lo que la aeronave el ascensor - algunos vienen del cuerpo del avión, otros de el empuje del motor, y así sucesivamente. Además, el principio de Bernoulli da una respuesta aproximada porque el flujo sobre el ala crea turbulencia).

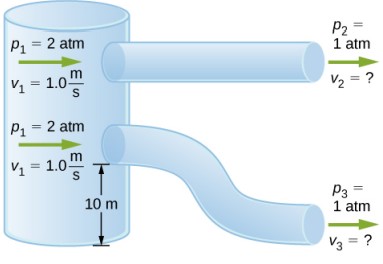
128. Dos tubos de diámetro igual y constante salen de una estación de bombeo de agua y vierten el agua por un extremo abierto y abierto a la atmósfera (véase la figura siguiente). El agua entra a una presión de dos atmósferas y una velocidad de (v₁ = 1,0 m/s). Un tubo cae a una altura de 10 m. ¿Cuál es la velocidad del agua cuando el agua sale de cada tubo?.



129. El fluido fluye originalmente a través de un tubo a una velocidad de 100 cm³/s . Para ilustrar la sensibilidad del caudal a varios factores, calcule el nuevo caudal para el los siguientes cambios, con todos los demás factores permaneciendo iguales como en las condiciones originales. a) Diferencia de presión aumenta en un factor de 1,50. (b) Un nuevo fluido con 3.00 veces la mayor viscosidad es sustituida. c) El tubo es reemplazado por uno que tiene 4.00 veces la longitud. d) Otro se utiliza con un radio de 0,100 veces el original. e) Sin embargo otro tubo es sustituido por un radio de 0,100 veces el de original y la mitad de la longitud, y la diferencia de presión es incrementado por un factor de 1,50.

130. Durante una carrera de maratón, el flujo sanguíneo de una corredora aumenta a 10.0 veces su tasa de descanso. La viscosidad de su sangre ha caído al 95.0% de su valor normal, y la diferencia de presión arterial a través del sistema circulatorio ha aumentado en un 50.0%. ¿Por qué factor ha aumentado el radio promedio de sus vasos sanguíneos?.

131. El agua suministrada a una casa por una red de suministro de agua tiene un valor de presión de 3,00 × 10⁵ N/m² temprano en un día de verano cuando el uso en el vecindario es bajo. Esta presión produce una de 20,0 L/min a través de una manguera de jardín. Más tarde en el día, presión en la salida de la cañería principal de agua y en la entrada a la y se obtiene un caudal de sólo 8,00 L/min. a través de la misma manguera. a) La presión que se ejerce actualmente suministrado a la casa, asumiendo que la resistencia es constante? (b) ¿Por qué factor aumentó el caudal en la tubería principal de agua? para causar esta disminución en la presión de entrega? El la presión en la entrada de la tubería principal de agua es 5,00 × 10⁵ N/m^{2 y el caudal original era de 200 L/min. c) ¿Cuántos usuarios más hay, suponiendo que cada uno consumiría 20.0 L / min por la mañana?.}

132. La gasolina se conduce bajo tierra desde las refinerías hasta los principales usuarios. El caudal es de 3,00 × 10^-2 m ³3/s (aproximadamente 500 gal/min), la viscosidad de la gasolina es de 1,00 × 10^-3 (N/m²)s, y su densidad es de 680 kg/m³. (a) ¿Qué diámetro mínimo debe tener la tubería si el número de Reynolds va a ser inferior a 2000? b) ¿Qué diferencia de presión debe mantenerse a lo largo de cada kilómetro de la carretera? para mantener este caudal?.