Preguntas y problemas - Capítulo III

Preguntas conceptuales

3.1 Condiciones para el equilibrio estático

1. ¿Qué puedes decir acerca de la velocidad de un cuerpo en movimiento que está en equilibrio dinámico?

2. ¿Bajo qué condiciones puede un cuerpo en rotación estar en equilibrio? Dar un ejemplo.

3. ¿Cuáles tres factores afectan el torque creado por una fuerza relativa a un punto de pivote específico?

4. Los mecánicos a veces colocan una longitud de tubo sobre el mango de una llave cuando intentan quitar un perno muy apretado. ¿Cómo ayuda esto?

Para los siguientes cuatro problemas, evalúa la afirmación como verdadera o falsa y explique tu respuesta.

5. Si solo hay una fuerza externa (o torque) que actúa sobre un objeto, no puede estar en equilibrio.

6. Si un objeto está en equilibrio, debe haber un número par de fuerzas que actúen sobre él.

7. Si un número impar de fuerzas actúa sobre un objeto, el objeto no puede estar en equilibrio.

8. Un cuerpo que se mueve en un círculo con una velocidad constante está en equilibrio de rotación.

9. ¿Para qué sirve un poste largo y flexible que llevan los caminantes de alambre?

3.2 Ejemplos de equilibrio estático

10. ¿Es posible apoyar una escalera contra una pared áspera cuando el piso no tiene fricción?

11. Muestra cómo se puede usar una báscula de resorte y un punto de apoyo simple para pesar un objeto cuyo peso es mayor que la lectura máxima en la báscula.

12. Un pintor sube una escalera. ¿Es más probable que la escalera se resbale cuando el pintor está cerca del fondo o cerca de la parte superior?

3.3 Esfuerzo, deformación y módulo elástico

Nota: a menos que se indique lo contrario, se supone que los pesos de los alambres, varillas y otros elementos son despreciables. Los módulos elásticos de los materiales seleccionados se dan en la Tabla 3.1.

13. ¿Por qué puede una ardilla saltar de la rama de un árbol al suelo y huir sin daños, mientras que un humano podría romper un hueso en una caída de este tipo?

14. Cuando una botella de vidrio llena de vinagre se calienta, tanto el vinagre como el vaso se expanden, pero el vinagre se expande significativamente más con la temperatura que el vaso. La botella se romperá si se llena hasta su tapa muy apretada. Explica por qué y cómo una bolsa de aire sobre el vinagre evita que se rompa la botella.

15. Se utiliza un alambre delgado tendido entre dos clavos en la pared para sostener una imagen grande. ¿Es probable que el cable se rompa si está bien sujeto para que se hunda considerablemente?

16. Revisa la relación entre el esfuerzo y la deformación. ¿Puedes encontrar alguna similitud entre las dos cantidades?

17. ¿Qué tipo de esfuerzo estás aplicando cuando presionas los extremos de una barra de madera? Cuando tiras de sus extremos?

18. ¿Se puede aplicar tensión de compresión a una banda de goma?

19. ¿Puede el módulo de Young tener un valor negativo? ¿Qué pasa con el módulo de volumen?

20. Si un material hipotético tiene un módulo de volumen negativo, ¿qué sucede cuando aprietas un pedazo de él?

21. Discute cómo podrías medir el módulo de volumen de un líquido.

3.4 Elasticidad y platicidad

Nota: a menos que se indique lo contrario, se supone que los pesos de los alambres, varillas y otros elementos son despreciables. Los módulos elásticos de los materiales seleccionados se dan en la Tabla 3.1.

22. ¿Qué se entiende cuando una línea de pesca se designa como "una prueba de 10 libras?"

23. Las varillas de acero se colocan comúnmente en el concreto antes de que se asiente. ¿Cuál es el propósito de estas varillas?

Problemas

3.1 Condiciones para el equilibrio estático

24. Al apretar un perno, presiona perpendicularmente sobre una llave con una fuerza de 165 N a una distancia de 0.140 m desde el centro del perno. ¿Qué torque está ejerciendo en relación con el centro del tornillo?

25. Cuando abres una puerta, la empujas perpendicularmente con una fuerza de 55.0 N a una distancia de 0.850 m desde las bisagras. ¿Qué torque estás ejerciendo en relación con las bisagras?

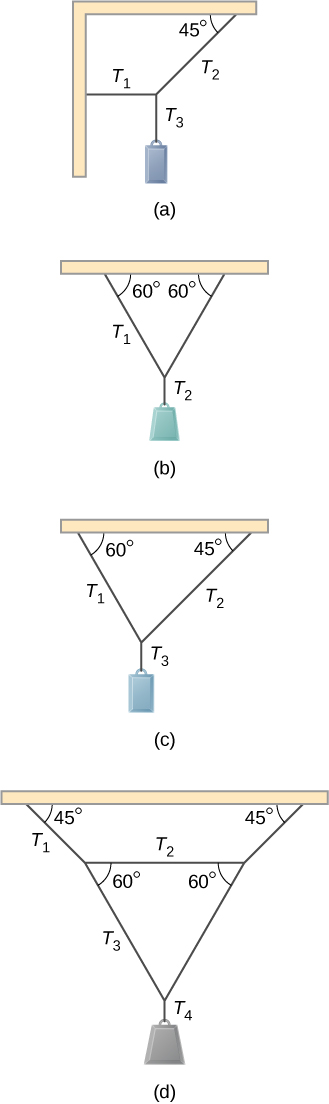
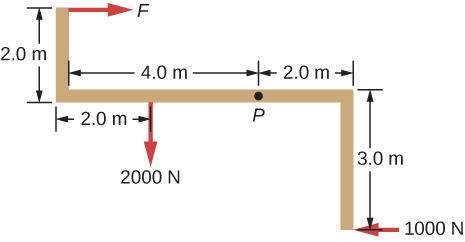
26. Encuentra la magnitud del esfuerzo en cada cable de soporte que se muestra a continuación. En cada caso, el peso del cuerpo suspendido es de 100.0 N y las masas de los cables son insignificantes.

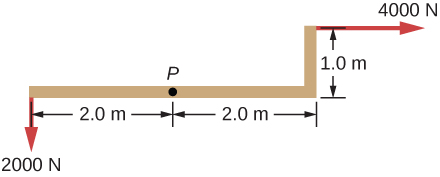
27. ¿Qué fuerza debe aplicarse en el punto P para mantener la estructura mostrada en equilibrio? El peso de la estructura es despreciable.

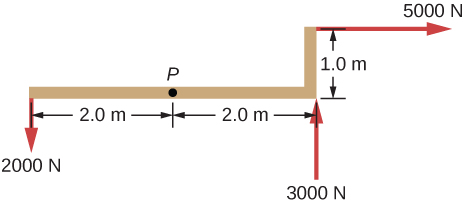
28. ¿Es posible aplicar una fuerza en P para mantener en equilibrio la estructura mostrada? El peso de la estructura es despreciable.

29. Dos niños empujan los lados opuestos de una puerta durante el juego. Ambos empujan horizontalmente y perpendicular a la puerta. Un niño empuja con una fuerza de 17.5 N a una distancia de 0.600 m desde las bisagras, y el segundo niño empuja a una distancia de 0.450 m. ¿Qué fuerza debe ejercer el segundo niño para evitar que la puerta se mueva? Supongamos que la fricción es despreciable.

30. Un pequeño SUV de 1000 kg tiene una distancia entre ejes de 3,0 m. Si el 60% de su peso descansa sobre las ruedas delanteras, ¿a qué distancia de las ruedas delanteras se encuentra el centro de masa del vagón?

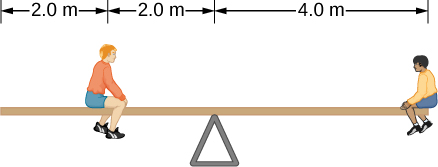
31. El balancín uniforme está equilibrado en su centro de masa, como se ve a continuación. El niño más pequeño a la derecha tiene una masa de 40.0 kg. ¿Cuál es la masa de su amigo?

3.2 Ejemplos de equilibrio estático

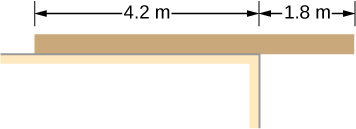
32. Una tabla uniforme descansa sobre una superficie nivelada como se muestra a continuación. La tabla tiene una masa de 30 kg y mide 6,0 m de largo. ¿Cuánta masa se puede colocar en su extremo derecho antes de que se incline? (Sugerencia: cuando el tablero está a punto de volcarse, hace contacto con la superficie solo a lo largo del borde que se convierte en un eje de rotación momentáneo).

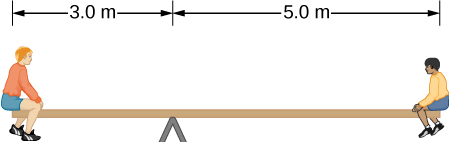
33. El balancín uniforme que se muestra a continuación está equilibrado en un punto de apoyo ubicado a 3.0 m del extremo izquierdo. El niño más pequeño a la derecha tiene una masa de 40 kg y el niño más grande a la izquierda tiene una masa de 80 kg. ¿Cuál es la masa del tablero?

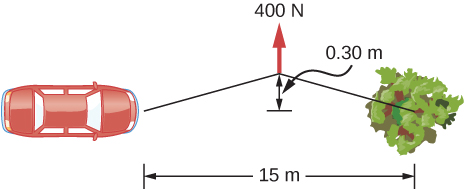
34. Para sacar su automóvil del barro, un hombre ata un extremo de una cuerda al parachoques delantero y el otro extremo a un árbol a 15 m de distancia, como se muestra a continuación. Luego tira del centro de la cuerda con una fuerza de 400 N, lo que hace que su centro se desplace a 0,30 m, como se muestra. ¿Cuál es la fuerza de la cuerda en el coche?

35. Un andamio uniforme de 40.0 kg de longitud de 6.0 m está soportado por dos cables de luz, como se muestra a continuación. Un pintor de 80.0 kg se para a 1.0 m del extremo izquierdo del andamio, y su equipo de pintura está a 1.5 m del extremo derecho. Si la tensión en el cable izquierdo es el doble que en el cable derecho, encuentre las tensiones en los cables y la masa del equipo.

36. Cuando la estructura que se muestra a continuación se apoya en el punto P, está en equilibrio. Encuentra la magnitud de la fuerza F y la fuerza aplicada en P. El peso de la estructura es despreciable.

37. Para levantarse sobre el techo, una persona (masa de 70.0 kg) coloca una escalera de aluminio de 6.00 m (masa de 10.0 kg) contra la casa en una plataforma de concreto con la base de la escalera a 2.00 m de la casa. La escalera descansa contra un canal de plástico para la lluvia, que podemos asumir sin fricción. El centro de masa de la escalera está a 2.00 m del fondo. La persona está parada a 3.00 m del fondo. Encuentra las fuerzas normales de reacción y fricción en la escalera en su base.

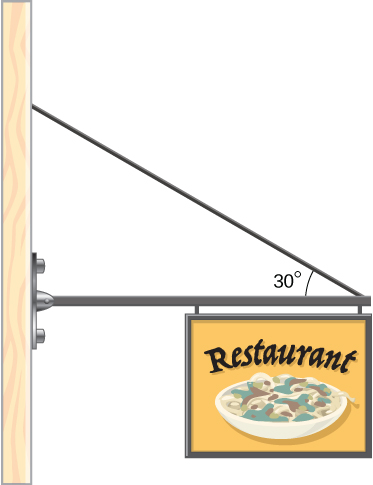
38. Un puntal horizontal uniforme pesa 400.0 N. Un extremo del puntal está unido a un soporte articulado en la pared, y el otro extremo del anclaje está unido a una señal que pesa 200.0 N. El puntal también se sujeta mediante un cable conectado entre El final del puntal y el muro. Suponiendo que todo el peso del letrero esté adherido al final del puntal, encuentra la tensión en el cable y la fuerza en la bisagra del puntal.

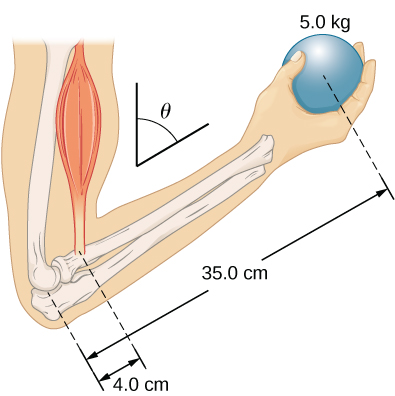
39. El antebrazo que se muestra a continuación se coloca en un ángulo con respecto al brazo superior, y sostiene una masa de 5.0 kg en la mano. La masa total del antebrazo y la mano es de 3.0 kg, y su centro de masa está a 15.0 cm del codo. (a) ¿Cuál es la magnitud de la fuerza que el músculo bíceps ejerce sobre el antebrazo para θ = 60°? (b) ¿Cuál es la magnitud de la fuerza en la articulación del codo para el mismo ángulo? (c) ¿Cómo dependen estas fuerzas del ángulo θ?

40. El brazo uniforme que se muestra a continuación pesa 3000 N. Está soportado por el cable de sujeción horizontal y por el soporte articulado en el punto A. ¿Cuáles son las fuerzas en el brazo debido al cable y debido al soporte en A? ¿La fuerza en A actúa a lo largo de la pluma?

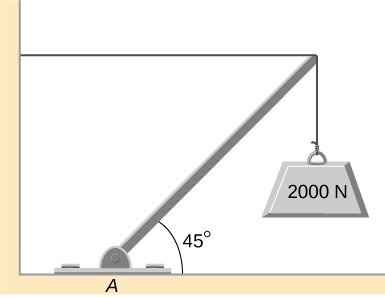
41. El brazo uniforme que se muestra a continuación pesa 700 N, y el objeto que cuelga de su extremo derecho pesa 400 N. El brazo está soportado por un cable de luz y por una bisagra en la pared. Calcula la tensión en el cable y la fuerza sobre la bisagra de la pluma. ¿La fuerza en la bisagra actúa a lo largo de la pluma?

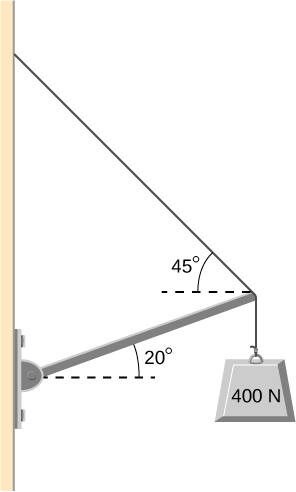
42. A continuación se muestra una pluma de 12.0 m, AB, de una grúa que levanta una carga de 3000 kg. El centro de masa de la pluma está en su centro geométrico, y la masa de la pluma es de 1000 kg. Para la posición que se muestra, calcula la tensión T en el cable y la fuerza en el eje A.

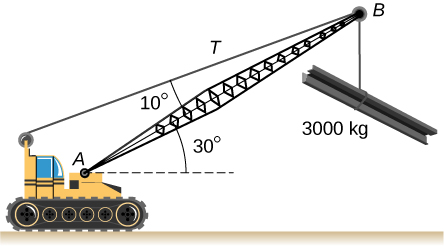
43. Una trampilla uniforme que se muestra a continuación mide 1,0 m por 1,5 m y pesa 300 N. Se apoya en una sola bisagra (H) y en una cuerda liviana atada entre el centro de la puerta y el piso. La puerta se mantiene en la posición que se muestra, donde la losa forma un ángulo de 30° con el suelo horizontal y la cuerda forma un ángulo de 20° con el suelo. Encuentra la tensión en la cuerda y la fuerza en la bisagra.

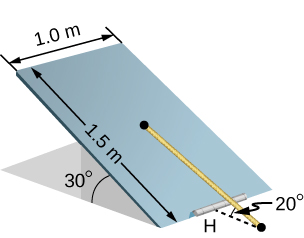
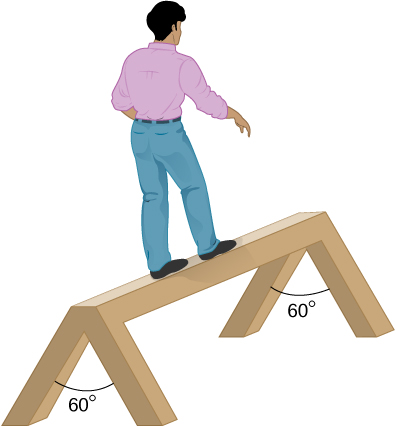
44. Un hombre de 90 kg camina sobre un caballete, como se muestra abajo. El caballete tiene una longitud de 2,0 m y una altura de 1,0 m, y su masa es de 25,0 kg. Calcula la fuerza de reacción normal en cada pierna en el punto de contacto con el piso cuando el hombre esté a 0.5 m del extremo más alejado del caballete (Sugerencia: en cada extremo, primero encuentra la fuerza de reacción total. Esta fuerza de reacción es la suma vectorial de dos fuerzas de reacción, cada una actuando a lo largo de una pierna. La fuerza de reacción normal en el punto de contacto con el piso es la normal, con respecto a el piso.

3.3 Esfuerzo, deformación y módulo elástico

45. El "plomo" en los lápices es una composición de grafito con un módulo de Young de aproximadamente 1.0 × 10⁹N/m². Calcula el cambio en la longitud del plomo en un lápiz automático si lo tocas directamente en el lápiz con una fuerza de 4.0 N. El plomo tiene un diámetro de 0.50 mm y una longitud de 60 mm.

46. Las antenas de televisión son las estructuras artificiales más altas de la Tierra. En 1987, un físico de 72.0 kg se colocó a sí mismo y 400 kg de equipo en la parte superior de una antena de 610 m de altura para realizar experimentos de gravedad. ¿Cuánto se comprimió la antena, si consideramos que es equivalente a un cilindro de acero de 0.150 m de radio?

47. ¿Cuánto cuesta una cuerda de nylon de 0.800 cm de diámetro para una escaladora de montaña de 65.0 kg cuando cuelga 35.0 m por debajo de un afloramiento de rocas? (Para nylon, Y = 1.35 × 10⁹ Pa).

48. Cuando el agua se congela, su volumen aumenta un 9,05%. ¿Qué fuerza por unidad de área es el agua capaz de ejercer sobre un recipiente cuando se congela?

49. Un granjero que hace jugo de uva llena una botella de vidrio hasta el borde y lo tapa herméticamente. El jugo se expande más que el vaso cuando se calienta, de tal manera que el volumen aumenta un 0.2%. Calcula la fuerza ejercida por el jugo por centímetro cuadrado si su módulo de volumen es 1.8 × 10⁹ N/m², suponiendo que la botella no se rompa.

50. Un disco entre las vértebras en la columna vertebral se somete a una fuerza de cizallamiento de 600.0 N. Encuentra su deformación de cizallamiento, utilizando el módulo de cizallamiento de 1.0 × 10⁹ N/m². El disco es equivalente a un cilindro sólido de 0.700 cm de alto y 4.00 cm de diámetro.

51. Una vértebra se somete a una fuerza de cizallamiento de 500.0 N. Encuentra la deformación de cizallamiento, tomando la vértebra como un cilindro de 3.00 cm de alto y 4.00 cm de diámetro. ¿Cómo se compara su resultado con el resultado obtenido en el problema anterior? ¿Son más comunes los problemas de la columna vertebral en los discos que en las vértebras?

52. Calcula la fuerza que aplica un afinador de piano para estirar un cable de piano de acero en 8,00 mm, si el cable originalmente tiene una longitud de 1,35 m y su diámetro es de 0,850 mm.

53. Un mástil de aluminio hueco de 20.0 m de altura es equivalente en resistencia a un cilindro sólido de 4.00 cm de diámetro. Un viento fuerte dobla el palo tanto como lo haría una fuerza horizontal de 900.0 N en la parte superior. ¿A qué distancia hacia el lado se flexiona la parte superior del palo?

54. Un cable de cobre de 1.0 cm de diámetro se estira 1.0% cuando se usa para levantar una carga hacia arriba con una aceleración de 2.0 m/s². ¿Cuál es el peso de la carga?

55. A medida que se perfora un pozo de petróleo, cada nueva sección de tubería de perforación soporta su propio peso y el peso de la tubería y la broca debajo de ella. Calcula el estiramiento en una nueva tubería de acero de 6.00 m de longitud que soporta una broca de 100 kg y una tubería de longitud de 3.00 km con una densidad de masa lineal de 20.0 kg/m. Trata el tubo como un cilindro sólido con un diámetro de 5,00 cm.

56. Una gran varilla de acero cilíndrica uniforme de densidad ρ = 7,8 g/cm³ tiene una longitud de 2,0 m y un diámetro de 5,0 cm. La varilla se sujeta a un piso de concreto con su eje largo vertical. ¿Cuál es el esfuerzo normal en la varilla en la sección transversal ubicada a (a) 1.0 m desde su extremo inferior? (b) 1.5 m desde el extremo inferior?

57. Un escalador de montaña de 90 kg cuelga de una cuerda de nylon y lo estira 25,0 cm. Si la cuerda originalmente tenía 30.0 m de largo y su diámetro es de 1.0 cm, ¿cuál es el módulo de Young para el nylon?

58. Una barra de suspensión de un puente colgante tiene una longitud de 25.0 m. Si la varilla está hecha de acero, ¿cuál debe ser su diámetro para que no se estire más de 1.0 cm cuando pasa un camión de 2.5 x 10⁴ kg? Supongamos que la barra soporta todo el peso del camión.

59. Un cable de cobre tiene una longitud de 1,0 m y su diámetro es de 1,0 mm. Si el cable cuelga verticalmente, ¿cuánto peso debe agregarse a su extremo libre para estirarlo 3.0 mm?

60. Un peso de 100 N está unido a un extremo libre de un cable metálico que cuelga del techo. Cuando se agrega un segundo peso de 100 N al cable, se estira 3.0 mm. El diámetro y la longitud del alambre son de 1,0 mm y 2,0 m, respectivamente. ¿Cuál es el módulo de Young del metal utilizado para fabricar el alambre?

61. El módulo de volumen de un material es 1.0 × 10¹¹ N/m². ¿A qué cambio fraccional de volumen se somete una parte de este material cuando se le somete a un aumento de tensión en masa de 10⁷ N/m²? Supongamos que la fuerza se aplica uniformemente sobre la superficie.

62. Las fuerzas normales de magnitud 1,0 × 10⁶ N se aplican uniformemente a una superficie esférica que encierra un volumen de un líquido. Esto hace que el radio de la superficie disminuya de 50.000 cm a 49.995 cm. ¿Cuál es el módulo de volumen del líquido?

63. Durante una caminata sobre una cuerda, un caminante de cuerda floja crea una tensión de 3.94 × 10³ N en un cable que se estira entre dos palos de soporte que están separados por 15.0 m. El alambre tiene un diámetro de 0,50 cm cuando no está estirado. Cuando el caminante está en el cable en el medio entre los palos, el cable forma un ángulo de 5.0° por debajo de la horizontal. ¿Cuánto estira esta tensión el cable de acero cuando el caminante está en esta posición?

64. Al utilizar un borrador de lápiz, ejerce una fuerza vertical de 6.00 N a una distancia de 2.00 cm desde la junta del borrador de madera dura. El lápiz tiene un diámetro de 6.00 mm y se mantiene en un ángulo de 20.0° con respecto a la horizontal. (a) ¿En qué medida la madera se flexiona perpendicular a su longitud? (b) ¿Cuánto se comprime longitudinalmente?

65. Las fuerzas normales se aplican uniformemente sobre la superficie de un volumen esférico de agua cuyo radio es de 20.0 cm. Si la presión en la superficie aumenta en 200 MPa, ¿cuánto disminuye el radio de la esfera?

3.4 Elasticidad y platicidad

66. Una cuerda uniforme de área de sección transversal de 0.50 cm² se rompe cuando la tensión de tracción en ella alcanza 6.00 × 10⁶ N/m². (a) ¿Cuál es la carga máxima que la cuerda puede elevar lentamente a una velocidad constante? (b) ¿Cuál es la carga máxima que puede levantar la cuerda con una aceleración de 4.00 m/s²?

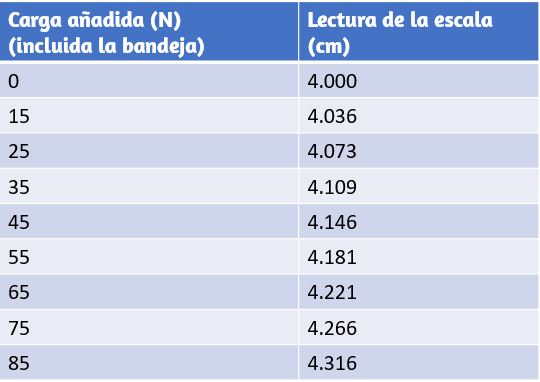
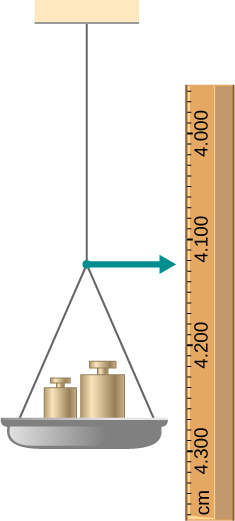
67. Un extremo de un cable metálico vertical de 2,0 m de diámetro y 1,0 mm de diámetro está unido a un techo, y el otro extremo está unido a una bandeja de peso de 5.0 N, como se muestra a continuación. La posición del puntero antes de la bandeja es de 4.000 cm. Luego se agregan diferentes pesos al área del platillo, y la posición del puntero se registra en la tabla que se muestra. Traza la tensión frente a la tensión para este cable, luego usa la curva resultante para determinar el módulo de Young y el límite de proporcionalidad del metal. ¿Qué metal es más probable que sea esto?

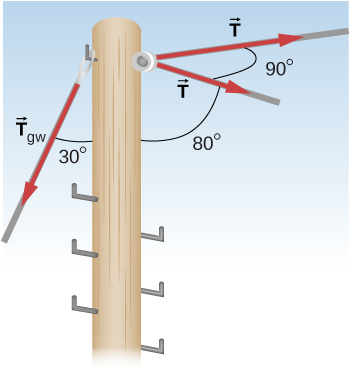
68. Un cable de aluminio (ρ = 2,7 g/cm³) se suspende del techo y se cuelga verticalmente. ¿Cuánto tiempo debe durar el cable antes de que la tensión en su extremo superior alcance el límite de proporcionalidad, que es de 8,0 × 10⁷ N/m²?

Problemas adicionales

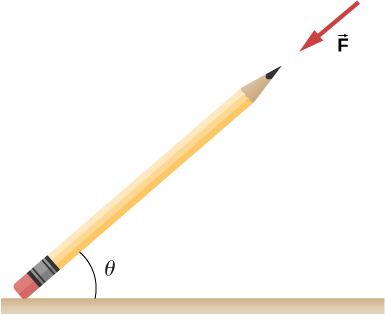
69. El coeficiente de fricción estática entre el borrador de goma del lápiz y la mesa es μ_s = 0.80. Si la fuerza F→ se aplica a lo largo del eje del lápiz, como se muestra a continuación, ¿cuál es el ángulo mínimo en el que el lápiz se puede colocar sin deslizarse? Ignora el peso del lápiz.

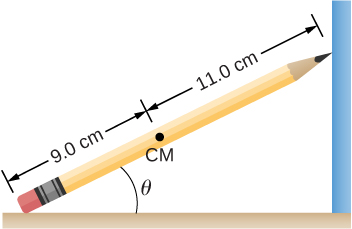
70. Un lápiz descansa contra una esquina, como se muestra a continuación. El extremo afilado del lápiz toca una superficie vertical lisa y el extremo del borrador toca un suelo áspero horizontal. El coeficiente de fricción estática entre el borrador y el piso es μ_s = 0.80. El centro de masa del lápiz se encuentra a 9.0 cm de la punta del borrador y a 11.0 cm de la punta del lápiz. Encuentra el ángulo mínimo θ para el cual el lápiz no se desliza.

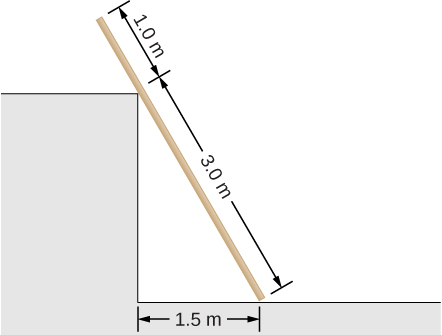
71. Una tabla uniforme de 4.0 m que pesa 200.0 N descansa contra la esquina de una pared, como se muestra a continuación. No hay fricción en el punto donde la tabla se encuentra con la esquina. (a) Encuentra las fuerzas que la esquina y el piso ejercen sobre la tabla. (b) ¿Cuál es el coeficiente mínimo de fricción estática entre el piso y la tabla para evitar que la tabla se resbale?

72. Un niño de 40 kg salta desde una altura de 3.0 m, aterriza en un pie y descansa en 0.10 s después de que toca el suelo. Supongamos que se detiene con una desaceleración constante. Si el área transversal total de los huesos en sus piernas justo por encima de los tobillos es de 3.0 cm², ¿cuál es el esfuerzo de compresión en estos huesos? Los huesos de las piernas se pueden fracturar cuando se someten a una tensión superior a 1.7 × 10⁸ Pa. ¿Está el niño en peligro de romperse la pierna?

73. Dos varillas finas, una hecha de acero y la otra de aluminio, se unen de extremo a extremo. Cada vástago tiene una longitud de 2,0 m y una sección transversal de 9,1 mm². Si se aplica una fuerza de tracción de 10,000 N en cada extremo de la combinación, encuentra: (a) tensión en cada barra; (b) esfuerzo en cada varilla; y, (c) alargamiento de cada varilla.

74. Dos varillas, una de cobre y otra de acero, tienen las mismas dimensiones. Si la barra de cobre se estira 0,15 mm bajo cierta tensión, ¿cuánto se estira la barra de acero bajo la misma tensión?

Problemas de Desafío

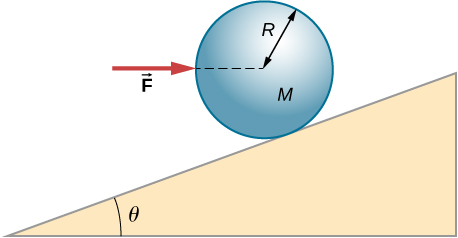
75. Una fuerza horizontal F→ se aplica a una esfera uniforme en la dirección exacta hacia el centro de la esfera, como se muestra a continuación. Encuentra la magnitud de esta fuerza para que la esfera permanezca en equilibrio estático. ¿Cuál es la fuerza de fricción de la inclinación sobre la esfera?

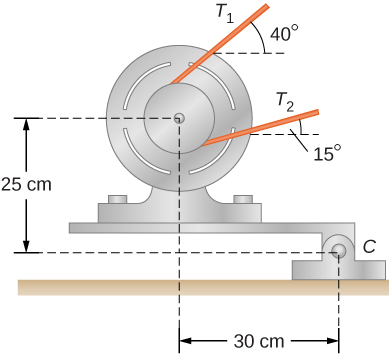
76. Cuando se coloca un motor en un soporte giratorio que se ve a continuación, se puede usar su peso para mantener la tensión en la correa de transmisión. Cuando el motor no está funcionando, las tensiones T₁ y T₂ son iguales. La masa total de la plataforma y el motor es de 100.0 kg, y el diámetro de la polea de la correa de transmisión es de 16.0 cm. cuando el motor está apagado, encuentra: (a) la tensión en la correa, y (b) la fuerza en el soporte de la plataforma articulada en el punto C. Supón que el centro de masa de la plataforma más el motor está en el centro del motor.

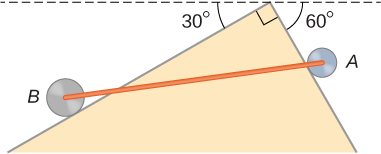
77. Dos ruedas A y B con pesos w y 2w, respectivamente, están conectadas por una barra uniforme con peso w/2, como se muestra a continuación. Las ruedas son libres de rodar sobre las superficies inclinadas. Determina el ángulo que forma la varilla con la horizontal cuando el sistema está en equilibrio. Sugerencia: Hay cinco fuerzas que actúan sobre la barra, que son dos pesos de las ruedas, dos fuerzas de reacción normales en los puntos donde las ruedas hacen contacto con la cuña y el peso de la barra.

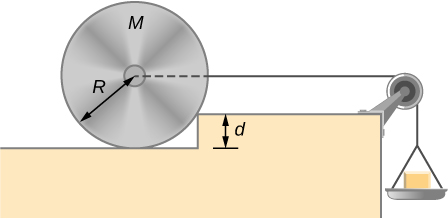
78. Los pesos se agregan gradualmente a una bandeja hasta que una rueda de masa M y el radio R se arrastra sobre un obstáculo de altura d, como se muestra a continuación. ¿Cuál es la masa mínima de los pesos más la bandeja necesaria para lograr esto?

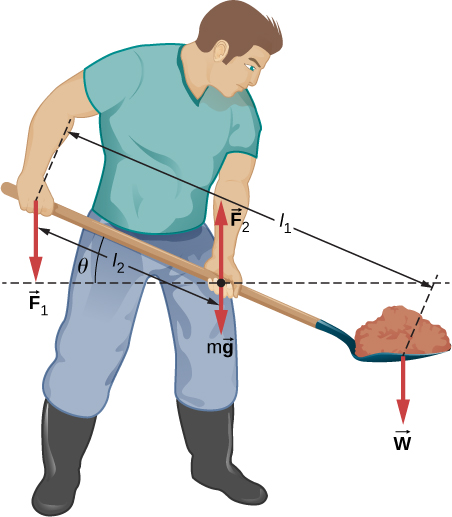
79. Para levantar una pala de tierra, un jardinero empuja hacia abajo en el extremo de la pala y tira hacia arriba a la distancia l₂ desde el extremo, como se muestra a continuación. El peso de la pala es mg→ y actúa en el punto de aplicación de F→₂. Calcula las magnitudes de las fuerzas F→₁ y F→₂ como funciones de l₁, l₂, mg y el peso W de la carga. ¿Por qué tus respuestas no dependen del ángulo θ que hace la pala con la horizontal?

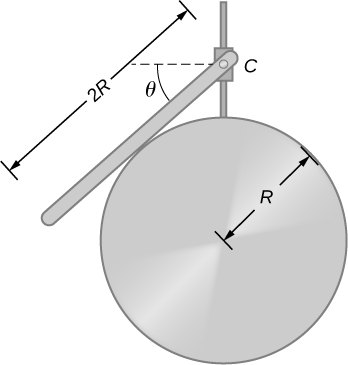
80. Una varilla uniforme de longitud 2R y masa M está unida a un pequeño collar C y descansa sobre una superficie cilíndrica de radio R, como se muestra a continuación. Si el collar se puede deslizar sin fricción a lo largo de la guía vertical, encuentra el ángulo para el cual la varilla está en equilibrio estático.

81. El palo que se muestra a continuación está en una curva de 90.0° en una línea eléctrica y, por lo tanto, está sujeto a una mayor fuerza de corte que los palos en las partes rectas de la línea. La tensión en cada línea es 4.00 × 10 N, en los ángulos mostrados. El palo tiene una altura de 15,0 m, tiene un diámetro de 18,0 cm y puede considerarse que tiene la mitad de la resistencia de la madera dura. (a) Calcula la compresión del palo. (b) Encuentra cuánto se dobla y en qué dirección. (c) Encuentra la tensión en un cable de retención usado para mantener el palo recto si está unido a la parte superior del poste en un ángulo de 30.0° con la vertical. El cable de retención está en la dirección opuesta a la curva.