Preguntas y problemas - Capítulo II

Preguntas conceptuales

2.1 Movimiento de rodadura

1. ¿Puede un objeto redondo liberado del reposo en la parte superior de una pendiente sin fricción someterse a un movimiento de rodadura?

2. Una lata cilíndrica de radio R está rodando sobre una superficie horizontal sin resbalar. (a) Después de una revolución completa de la lata, ¿cuál es la distancia que ha recorrido su centro de masa? (b) ¿Esta distancia sería mayor o menor si ocurriera deslizamiento?

3. Una rueda se suelta desde la parte superior en una pendiente. ¿Es más probable que se resbale la rueda si la inclinación es empinada o ligeramente inclinada?

4. ¿Cuál rueda más rápido en un plano inclinado, un cilindro hueco o una esfera sólida? Ambos tienen la misma masa y radio.

5. Una esfera hueca y un cilindro hueco del mismo radio y masa ruedan en una pendiente sin deslizarse y tienen el mismo centro inicial de velocidad de masa. ¿Qué objeto alcanza una mayor altura antes de detenerse?

2.2 Momento Angular

6. ¿Puedes asignar un momento angular a una partícula sin definir primero un punto de referencia?

7. Para una partícula que viaja en línea recta, ¿hay algún punto sobre el cual el momento angular sea cero? Supón que la línea se cruza con el origen.

8. ¿En qué condiciones un cuerpo rígido tiene un momento angular pero no un momento lineal?

9. Si una partícula se está moviendo con respecto a un origen elegido, tiene un momento lineal. ¿Qué condiciones deben existir para que el momento angular de esta partícula sea cero sobre el origen elegido?

10. Si conoces la velocidad de una partícula, ¿puedes decir algo sobre el momento angular de la partícula?

2.3 Conservación del momento angular

11. ¿Cuál es el propósito de la pequeña hélice en la parte posterior de un helicóptero que gira en el plano perpendicular a la gran hélice?

12. Supongamos que un niño camina desde el borde exterior de un carrusel giratorio hacia el interior. ¿La velocidad angular del tiovivo aumenta, disminuye o permanece igual? Explica tu respuesta. Supongamos que el carrusel gira sin fricción.

13. Cuando la cuerda de una pelota atada gira alrededor de un poste, ¿qué ocurre con la velocidad angular de la pelota?

14. Supón que las capas de hielo polar se liberaron y flotaron hacia el ecuador de la Tierra sin fundirse. ¿Qué pasaría con la velocidad angular de la Tierra?

15. Explica por qué las estrellas giran más rápido cuando colapsan.

16. Los buceadores competitivos tiran de sus extremidades y acurrucan sus cuerpos cuando lo hacen. Justo antes de entrar al agua, extienden completamente sus extremidades para entrar directamente hacia abajo (ver imagen). Explica el efecto de ambas acciones en sus velocidades angulares. También explica el efecto en su momento angular.

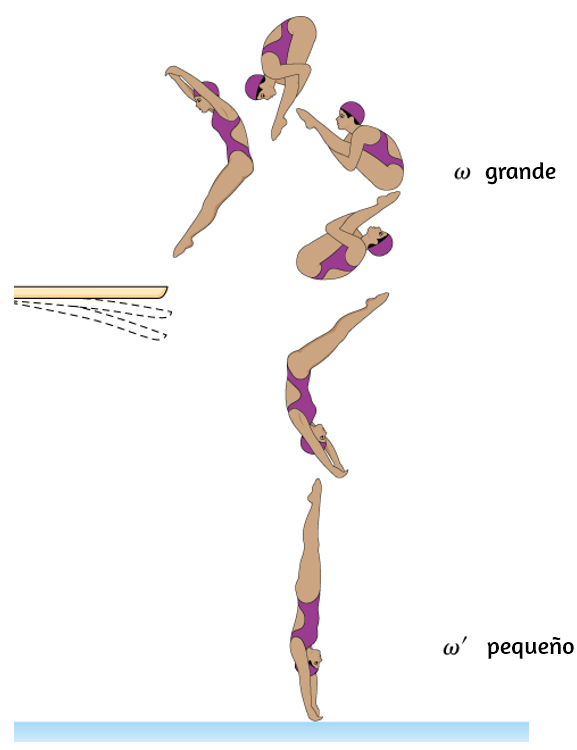
2.4 Precesión de un giroscopio

17. Los giroscopios utilizados en los sistemas de guía para indicar las direcciones en el espacio deben tener un momento angular que no cambie en la dirección. Cuando se colocan en el vehículo, se colocan en un compartimiento que está separado del fuselaje principal, de modo que los cambios en la orientación del fuselaje no afectan la orientación del giroscopio. Si el vehículo espacial está sometido a grandes fuerzas y aceleraciones, ¿cómo puede la dirección de los giroscopios el momento angular ser constante en todo momento?

18. La tierra tiene un precedente sobre su eje vertical con un período de 26,000 años. Discute si la ecuación 2.12 puede usarse para calcular la velocidad angular de precesión de la Tierra.

Problemas

19. ¿Cuál es la velocidad angular de un neumático de 75.0 cm de diámetro en un automóvil que viaja a 90.0 km/h?

20. Un niño monta su bicicleta 2.00 km. Las ruedas tienen un radio de 30.0 cm. ¿Cuál es el ángulo total por el que giran los neumáticos durante su viaje?

21. Si el niño en la bicicleta en el problema anterior acelera desde el reposo a una velocidad de 10.0 m/s en 10.0 s, ¿cuál es la aceleración angular de los neumáticos?

22. Los autos de carreras de Fórmula Uno tienen neumáticos de 66 cm de diámetro. Si un Fórmula Uno promedia una velocidad de 300 km/h durante una carrera, ¿cuál es el desplazamiento angular en revoluciones de las ruedas si el auto de carreras mantiene esta velocidad durante 1,5 horas?

23. Una canica rueda por una pendiente a 30° del reposo. (a) ¿Cuál es su aceleración? (b) ¿Qué tan lejos llega en 3.0 s?

24. Repite el problema anterior reemplazando la canica con un cilindro sólido. Explica el nuevo resultado.

25. Un cuerpo rígido con una sección transversal cilíndrica se libera desde la parte superior de una inclinación de 30°. Rueda 10.0 m hacia abajo en 2.60 s. Encuentra el momento de inercia del cuerpo en términos de su masa m y radio r.

26. Se puede pensar en un yo-yo de un cilindro sólido de masa m y radio r que tiene una cuerda ligera envuelta alrededor de su circunferencia (ver imagen). Un extremo de la cuerda se mantiene fijo en el espacio. Si el cilindro cae mientras la cuerda se desenrolla sin deslizarse, ¿cuál es la aceleración del cilindro?



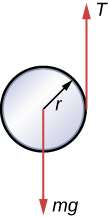
27. Un cilindro sólido de radio 10.0 cm rueda hacia abajo por una inclinación con deslizamiento. El ángulo de la inclinación es de 30°. El coeficiente de fricción cinética en la superficie es 0.400. ¿Cuál es la aceleración angular del cilindro sólido? ¿Cuál es la aceleración lineal?

28. Una bola de boliche rueda por una rampa de 0.5 m de alto sin resbalar al almacenamiento. Tiene una velocidad inicial de su centro de masa de 3.0 m/s. (a) ¿Cuál es su velocidad en la parte superior de la rampa? (b) Si la rampa tiene 1 m de altura, ¿llega a la cima?

29. Un cilindro sólido de 40.0 kg está rodando sobre una superficie horizontal a una velocidad de 6.0 m/s. ¿Cuánto trabajo se requiere para detenerlo?

30. Una esfera sólida de 40.0 kg está rodando sobre una superficie horizontal con una velocidad de 6.0 m/s. ¿Cuánto trabajo se requiere para detenerlo? Compara los resultados con el problema anterior.

31. Un cilindro sólido rueda una inclinación en un ángulo de 20°. Si comienza en la parte inferior con una velocidad de 10 m/s, ¿qué tan arriba de la pendiente viaja?

32. Una rueda cilíndrica sólida de masa M y radio R es tirada por una fuerza F→ aplicada al centro de la rueda a 37° con respecto a la horizontal (ver la siguiente figura). Si la rueda debe rodar sin deslizarse, ¿cuál es el valor máximo de |F→|? Los coeficientes de fricción estática y cinética son μ_s = 0.40 y μ_k = 0.30.



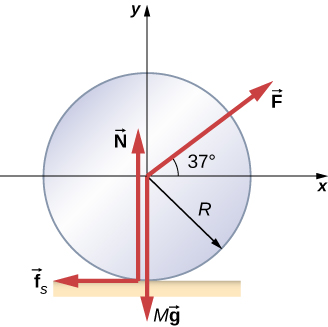
33. Un cilindro hueco que rueda sin deslizarse recibe una velocidad de 5.0 m/s y rueda en una pendiente hasta una altura vertical de 1.0 m. Si se le da a una esfera hueca de la misma masa y radio la misma velocidad inicial, ¿cuán verticalmente sube la pendiente?

2.2 Momento Angular

34. Una partícula de 0.2 kg viaja a lo largo de la línea y = 2.0 m con una velocidad de 5.0 m/s. ¿Cuál es el momento angular de la partícula sobre el origen?

35. Un pájaro vuela desde lo alto desde donde te encuentras a una altitud de 300.0 m y a una velocidad horizontal al suelo de 20.0 m/s. El pájaro tiene una masa de 2.0 kg. El vector de radio al ave forma un ángulo θ con respecto al suelo. El vector de radio para el ave y su vector de momento se encuentran en el plano xy. ¿Cuál es el momento angular del pájaro sobre el punto donde estás parado?

36. Un auto de Fórmula Uno con una masa de 750.0 kg corre a toda velocidad por un recorrido en Mónaco y entra en un giro circular a 220.0 km/h en el sentido contrario a las agujas del reloj sobre el origen del círculo. En otra parte del recorrido, el automóvil entra en un segundo giro circular a 180 km/h también en el sentido contrario a las agujas del reloj. Si el radio de curvatura del primer giro es de 130.0 m y el del segundo es de 100.0 m, compara los momentos angulares del auto de carrera en cada vuelta tomada sobre el origen del giro circular.

37. Una partícula de masa 5.0 kg tiene el vector de posición r→ = (2.0i^ - 3.0j^) m en un instante particular de tiempo cuando su velocidad es v→ = (3.0i^) m/s con respecto al origen. (a) ¿Cuál es el momento angular de la partícula? (b) Si una fuerza F→ = 5.0j^ N actúa sobre la partícula en este instante, ¿cuál es el torque sobre el origen?

38. Usa la regla de la mano derecha para determinar las direcciones de los momentos angulares sobre el origen de las partículas como se muestra a continuación. El eje z está fuera de la página.



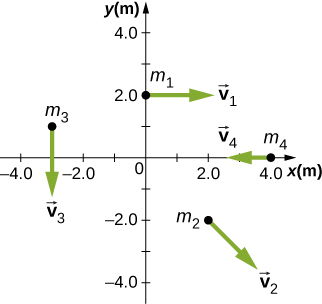
39. Supón que las partículas en el problema anterior tienen masas m₁ = 0.10 kg, m₂ = 0.20 kg, m₃ = 0.30 kg, m₄ = 0.40 kg. Las velocidades de las partículas son v₁ = 2.0i^ m/s, v₂ = (3.0i^ - 3.0j^) m/s, v₃ = -1.5j^ m/s, v₄ = -4.0i^ m/s. (a) Calcula el momento angular de cada partícula sobre el origen. (b) ¿Cuál es el momento angular total del sistema de cuatro partículas sobre el origen?

40. Dos partículas de igual masa viajan con la misma velocidad en direcciones opuestas a lo largo de líneas paralelas separadas por una distancia d. Demuestra que el momento angular de este sistema de dos partículas es el mismo, sin importar el punto que se use como referencia para calcular el momento angular.

41. Un avión de masa 4,0 × 10⁴ kg vuela horizontalmente a una altitud de 10 km con una velocidad constante de 250 m/s relativa a la Tierra. (a) ¿Cuál es la magnitud del momento angular del avión en relación con un observador del suelo directamente debajo del plano? (b) ¿El momento angular cambia cuando el avión vuela a una altitud constante?

42. En un instante particular, la posición de una partícula de 1.0 kg es r→ = (2.0i^ - 4.0j^ + 6.0k^) m, su velocidad es v→ = (- 1.0i^ + 4.0j^ + 1.0k^) m/s, y la la fuerza sobre ella es F→ = (10.0i^ + 15.0j^) N. (a) ¿Cuál es el momento angular de la partícula sobre el origen? (b) ¿Cuál es el torque en la partícula sobre el origen? (c) ¿Cuál es la tasa de cambio de tiempo del momento angular de la partícula en este instante?

43. Una partícula de masa m cae en el punto (-d, 0) y cae verticalmente en el campo gravitacional de la Tierra -gj^. (a) ¿Cuál es la expresión del momento angular de la partícula alrededor del eje z, que apunta directamente fuera de la página como se muestra a continuación? (b) Calcula el torque en la partícula alrededor del eje z. (c) ¿Es el torque igual a la tasa de cambio de tiempo del momento angular?



44. (a) Calcula el momento angular de la Tierra en su órbita alrededor del Sol. (b) Compara este momento angular con el momento angular de la Tierra sobre su eje.

45. Una roca de 20 kg de masa y un radio de 20 cm baja por una colina a 15 m de altura del reposo. ¿Cuál es su momento angular cuando está en la mitad de la cuesta? (b) En la parte inferior?

46. ​​Un satélite está girando a 6.0 rev/s. El satélite consiste en un cuerpo principal en forma de una esfera de radio de 2,0 m y una masa de 10,000 kg, y dos antenas que sobresalen del centro de masa del cuerpo principal y que se pueden aproximar con varillas de 3,0 m de longitud cada una y masa 10 kg. La antena se encuentra en el plano de rotación. ¿Cuál es el momento angular del satélite?

47. Una hélice consta de dos cuchillas de 3,0 m de longitud y 120 kg de masa cada una. La hélice se puede aproximar con una sola barra girando alrededor de su centro de masa. La hélice comienza desde el reposo y gira hasta 1200 rpm en 30 segundos a velocidad constante. (a) ¿Cuál es el momento angular de la hélice en t = 10 s; t = 20 s? (b) ¿Cuál es el torque en la hélice?

48. Un pulsar es una estrella de neutrones que gira rápidamente. El pulsar de la nebulosa Cangrejo en la constelación de Tauro tiene un período de 33,5 × 10^-3 s, un radio de 10,0 km y una masa de 2,8 × 10³⁰ kg. El período de rotación del pulsar aumentará con el tiempo debido a la liberación de radiación electromagnética, que no cambia su radio sino que reduce su energía de rotación. (a) ¿Cuál es el momento angular del pulsar? (b) Supón que la velocidad angular disminuye a una velocidad de 10^-14 rad/s². ¿Cuál es el torque en el pulsar?

49. Las palas de una turbina eólica son de 30 m de longitud y giran a una velocidad de rotación máxima de 20 rev/min. (a) Si las cuchillas son de 6000 kg cada una y el conjunto del rotor tiene tres cuchillas, calcula el momento angular de la turbina a esta velocidad de rotación. (b) ¿Cuál es el par requerido para rotar las cuchillas hasta la tasa máxima de rotación en 5 minutos?

50. Una montaña rusa tiene una masa de 3000.0 kg y necesita hacerlo de forma segura a través de un circuito circular vertical de radio de 50.0 m. ¿Cuál es el momento angular mínimo de la montaña rusa en la parte inferior del lazo para que pase de manera segura? Desprecia la fricción en la pista. Toma la montaña rusa como una partícula puntual.

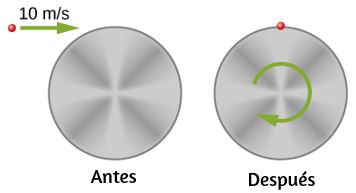
51. Un ciclista de montaña da un salto en una carrera y sale volando. La bicicleta de montaña viaja a 10.0 m/s antes de que salga volando. Si la masa de la rueda delantera de la bicicleta es de 750 g y tiene un radio de 35 cm, ¿cuál es el momento angular de la rueca en el aire en el momento en que la bicicleta deja el suelo?

2.3 Conservación del momento angular

52. Un disco de masa 2.0 kg y radio de 60 cm con una pequeña masa de 0.05 kg unida en el borde gira a 2.0 rev/s. La pequeña masa se separa repentinamente del disco. ¿Cuál es la tasa de rotación final del disco?

53. La masa del Sol es de 2.0 × 10³⁰ kg, su radio es de 7.0 × 10⁵ km y tiene un período de rotación de aproximadamente 28 días. Si el Sol se colapsase en una enana blanca de radio de 3,5 × 10³ km, ¿cuál sería su período si no se expulsara la masa y una esfera de densidad uniforme pudiera modelar el Sol antes y después?

54. Un cilindro con inercia rotacional I₁ = 2.0 kg • m² gira en sentido horario alrededor de un eje vertical a través de su centro con velocidad angular ω₁ = 5.0 rad/s. Un segundo cilindro con inercia rotacional I₂ = 1.0 kg • m² gira en sentido antihorario sobre el mismo eje con velocidad angular ω₂ = 8.0 rad/s. Si los cilindros se acoplan para que tengan el mismo eje de rotación, ¿cuál es la velocidad angular de la combinación? ¿Qué porcentaje de la energía cinética original se pierde por la fricción?

55. Un buzo fuera de la tabla alta imparte una rotación inicial con su cuerpo totalmente extendido antes de entrar en una operación de enrrollamiento y ejecutar tres saltos mortales con la espalda antes de golpear el agua. Si su momento de inercia antes del pliegue es de 16.9 kg • m² y después del pliegue durante los saltos mortales es 4.2 kg • m², qué velocidad de rotación debe impartir a su cuerpo directamente desde el tablero y antes de la curvatura si tarda 1.4 s en ejecutarse los saltos mortales antes de golpear el agua?

56. Un satélite de la Tierra tiene su apogeo a 2500 km sobre la superficie de la Tierra y perigeo a 500 km sobre la superficie de la Tierra. En el apogeo su velocidad es de 730 m s. ¿Cuál es su velocidad en el perigeo? El radio de la Tierra es 6370 km (ver imagen).



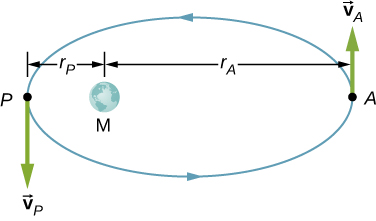
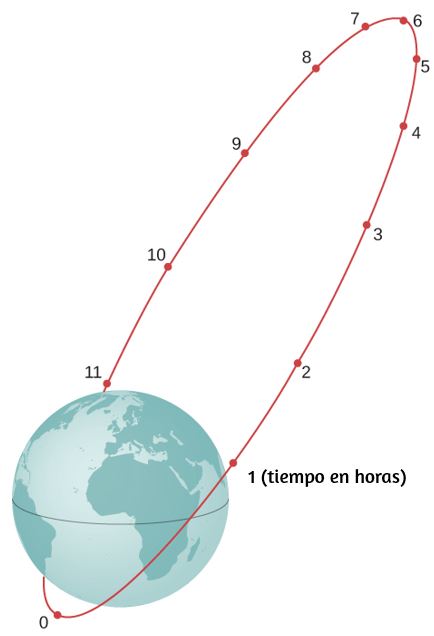
57. Una órbita de Molniya es una órbita altamente excéntrica de un satélite de comunicaciones a fin de proporcionar una cobertura de comunicaciones continua para los países escandinavos y la Rusia adyacente. La órbita se coloca de modo que estos países tengan el satélite a la vista durante largos períodos de tiempo (ver imagen). Si un satélite en esa órbita tiene un apogeo a 40,000.0 km medidos desde el centro de la Tierra y una velocidad de 3.0 km/s, ¿cuál sería su velocidad en el perigeo medido a 200.0 km de altitud?



58. A continuación se muestra una pequeña partícula de masa de 20 g que se mueve a una velocidad de 10,0 m/s cuando colisiona y se adhiere al borde de un cilindro sólido uniforme. El cilindro puede rotar libremente sobre su eje a través de su centro y es perpendicular a la página. El cilindro tiene una masa de 0.5 kg y un radio de 10 cm, y está inicialmente en reposo. (a) ¿Cuál es la velocidad angular del sistema después de la colisión? (b) ¿Cuánta energía cinética se pierde en la colisión?



59. Un bicho de masa de 0.020 kg está en reposo en el borde de un disco cilíndrico sólido (M = 0.10 kg, R = 0.10m) girando en un plano horizontal alrededor del eje vertical a través de su centro. El disco está girando a 10.0 rad/s. El bicho se arrastra al centro del disco. (a) ¿Cuál es la nueva velocidad angular del disco? (b) ¿Cuál es el cambio en la energía cinética del sistema? (c) Si el bicho se arrastra nuevamente al borde externo del disco, ¿cuál es la velocidad angular del disco? (d) ¿Cuál es la nueva energía cinética del sistema? (e) ¿Cuál es la causa del aumento y la disminución de la energía cinética?

60. Una vara uniforme de 200 g de masa y 100 cm de longitud puede girar libremente en un plano horizontal alrededor de un eje vertical fijo a través de su centro, perpendicular a su longitud. Dos pequeñas cuentas, cada una de masa de 20 g, están montadas en ranuras a lo largo de la barra. Inicialmente, las dos cuentas se sujetan mediante enganches en lados opuestos del centro de la barra, a 10 cm del eje de rotación. Con las cuentas en esta posición, la barra está girando con una velocidad angular de 10.0 rad/s. Cuando se liberan las capturas, las cuentas se deslizan hacia afuera a lo largo de la barra. (a) ¿Cuál es la velocidad angular de la varilla cuando las cuentas alcanzan los extremos de la varilla? (b) ¿Cuál es la velocidad angular de la barra si las cuentas salen volando de la barra?

61. Un tiovivo tiene un radio de 2,0 my un momento de inercia de 300 kg • m². Un niño de 50 kg de masa corre tangente a la rueda a una velocidad de 4.0 m/s y salta. Si el tiovivo está inicialmente en reposo, ¿cuál es la velocidad angular después de que el niño salta?

62. Un carrusel de patio de recreo tiene una masa de 120 kg y un radio de 1,80 m y está girando con una velocidad angular de 0,500 rev/s. ¿Cuál es su velocidad angular después de que un niño de 22.0 kg lo agarra agarrándose de su borde exterior? El niño está inicialmente en reposo.

63. Tres niños viajan al borde de un tiovivo de 100 kg, tiene un radio de 1.60 m y gira a 20.0 rpm. Los niños tienen masas de 22.0, 28.0 y 33.0 kg. Si el niño que tiene una masa de 28.0 kg se mueve al centro del tiovivo, ¿cuál es la nueva velocidad angular en rpm?

64. (a) Calcula el momento angular de un patinador de hielo girando a 6.00 rev/s dado que su momento de inercia es de 0.400 kg • m². (b) Reduce su velocidad de giro (su velocidad angular) al extender sus brazos y aumentar su momento de inercia. Encuentra el valor de su momento de inercia si su velocidad angular disminuye a 1.25 rev/s. (c) Supongamos que en lugar de eso mantiene sus brazos adentro y permite que la fricción del hielo lo desacelere a 3.00 rev/s. ¿Qué torque promedio se ejerció si esto toma 15.0 s?

65. Los patinadores gemelos se aproximan entre sí como se muestra a continuación y se dan la mano. (a) Calcula su velocidad angular final, dado que cada uno tenía una velocidad inicial de 2.50 m/s con respecto al hielo. Cada uno tiene una masa de 70.0 kg, y cada uno tiene un centro de masa ubicado a 0.800 m de sus manos bloqueadas. Puedes aproximar sus momentos de inercia para que sean los puntos de masas en este radio. (b) Compara la energía cinética inicial y la energía cinética final.



66. Un receptor de béisbol extiende su brazo hacia arriba para atrapar una bola rápida con una velocidad de 40 m/s. La pelota de béisbol es de 0.145 kg y la longitud del brazo del receptor es de 0.5 m y una masa de 4.0 kg. (a) ¿Cuál es la velocidad angular del brazo inmediatamente después de atrapar la bola medida desde el socket del brazo? (b) ¿Cuál es el torque aplicado si el receptor detiene la rotación de su brazo 0.3 s después de atrapar la pelota?

67. En 2015, en Varsovia, Polonia, Olivia Oliver, de Nueva Escocia, batió el récord mundial por ser la más rápida en patines de hielo. Logró un récord de 342 rev/min, superando el récord mundial Guinness existente en 34 rotaciones. Si un patinador de hielo extiende sus brazos a esa tasa de rotación, ¿cuál sería su nueva velocidad de rotación? Supongamos que puede aproximarse con una varilla de 45 kg que tiene 1,7 m de altura con un radio de 15 cm en el giro de grabación. Con sus brazos estirados, toma la aproximación de una vara de 130 cm de largo con el 10% de su masa corporal alineado perpendicularmente al eje de giro. Desprecia las fuerzas de fricción.

68. Un satélite en una órbita circular geosincrónica se encuentra a 42,164.0 km del centro de la Tierra. Un pequeño asteroide colisiona con el satélite y lo envía a una órbita elíptica de apogeo de 45,000.0 km. ¿Cuál es la velocidad del satélite en el apogeo? Supón que su momento angular se conserva.

69. Una gimnasta hace volteretas a lo largo del piso y luego se lanza al aire y ejecuta varios volteos mientras está en el aire. Si su momento de inercia al ejecutar las ruedas de carro es 13.5 kg • m² y su velocidad de giro es de 0.5 rev/s, ¿cuántas revoluciones hará en el aire si su momento de inercia en el pliegue es 3.4 kg • m² y tiene 2.0 s para hacer los saltos en el aire?

70. La centrífuga en el Centro de Investigación Ames de la NASA tiene un radio de 8.8 m y puede producir fuerzas en su carga útil de 20 g o 20 veces la fuerza de la gravedad en la Tierra. (a) ¿Cuál es el momento angular de una carga útil de 20 kg que experimenta 10 g en la centrífuga? (b) Si el motor del conductor se apagó en (a) y la carga útil perdió 10 kg, ¿cuál sería su nueva velocidad de giro, teniendo en cuenta que no hay fuerzas de fricción presentes?

71. Una atracción en un carnaval tiene cuatro radios a los que se adjuntan cápsulas que pueden contener a dos personas. Los radios son cada uno de 15 m de largo y están unidos a un eje central. Cada radio tiene una masa de 200.0 kg, y las vainas tienen una masa de 100.0 kg cada una. Si la atracción gira a 0.2 rev/s con cada cápsula que contiene dos niños de 50.0 kg, ¿cuál es la nueva velocidad de rotación si todos los niños saltan del camino?

72. Un patinador sobre hielo se está preparando para un salto con giros y tiene los brazos extendidos. Su momento de inercia es de 1.8 kg • m² mientras sus brazos están extendidos, y él está girando a 0.5 rev/s. Si se lanza al aire a 9.0 m/s en un ángulo de 45° con respecto al hielo, ¿cuántas revoluciones puede ejecutar mientras está en el aire si su momento de inercia en el aire es de 0.5 kg • m²?

73. Una estación espacial consiste en un cilindro hueco giratorio gigante de 106 kg de masa que incluye personas en la estación y un radio de 100.00 m. Está girando en el espacio a 3.30 rev/min para producir gravedad artificial. Si 100 personas de una masa promedio de 65.00 kg caminan por el espacio hasta una nave espacial en espera, ¿cuál es la nueva tasa de rotación cuando todas las personas están fuera de la estación?

74. Neptuno tiene una masa de 1.0 × 10²⁶ kg y se encuentra a 4.5 × 10⁹ km del Sol con un período orbital de 165 años. Los planetesimales del sistema solar primordial externo hace 4.500 millones de años se fusionaron en Neptuno durante cientos de millones de años. Si el disco primordial que se desarrolló en nuestro sistema solar actual tiene un radio de 10¹¹ km y si la materia que compone estos planetesimales que más tarde se convirtieron en Neptuno se extendieron uniformemente en los bordes de la misma, ¿cuál fue el período orbital de los bordes externos? del disco primordial?

2.4 Precesión de un giroscopio

75. Un giroscopio tiene un disco de 0.5 kg que gira a 40 rev/s. El centro de masa del disco está a 10 cm de un pivote que también es el radio del disco. ¿Cuál es la velocidad angular de precesión?

76. La velocidad angular de precesión de un giroscopio es de 1.0 rad/s. Si la masa del disco giratorio es de 0,4 kg y su radio es de 30 cm, así como la distancia desde el centro de masa al pivote, ¿cuál es la velocidad de rotación en rev/s del disco?

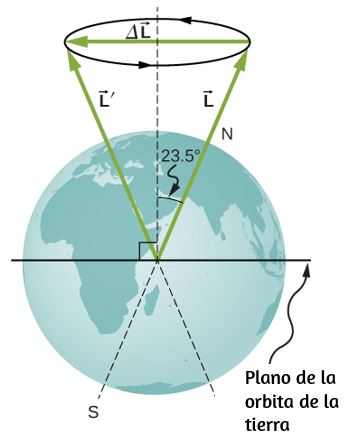
77. El eje de la Tierra forma un ángulo de 23.5° con una dirección perpendicular al plano de la órbita de la Tierra. Como se muestra a continuación, este eje se adelanta, haciendo una rotación completa en 25,780 y. (a) Calcula el cambio en el momento angular por la mitad esta vez. (b) ¿Cuál es el torque promedio que produce este cambio en el momento angular? (c) Si este torque fue creado por un par de fuerzas que actúan en el punto más efectivo del ecuador, ¿cuál sería la magnitud de cada fuerza?

Problemas adicionales

78. Una canica está rodando por el suelo a una velocidad de 7,0 m/s cuando arranca un plano inclinado a 30° con respecto a la horizontal. (a) ¿Qué tan lejos a lo largo del avión viaja la canica antes de llegar a un descanso? (b) ¿Cuánto tiempo transcurre mientras la canica sube por el avión?

79. Repite el problema anterior reemplazando la canica con una esfera hueca. Explica los nuevos resultados

80. La masa de un aro de radio 1.0 m es 6.0 kg. Rueda sobre una superficie horizontal con una velocidad de 10.0 m/s. (a) ¿Cuánto trabajo se requiere para detener el aro? (b) Si el aro comienza una superficie a 30° con respecto a la horizontal con una velocidad de 10.0 m/s, ¿qué tan lejos a lo largo de la pendiente se desplazará antes de detenerse y retroceder?

81. Repite el problema anterior para una esfera hueca del mismo radio y masa y velocidad inicial. Explica las diferencias en los resultados.

82. Una partícula tiene una masa de 0.5 kg y está viajando a lo largo de la línea x = 5.0 m a 2.0 m/s en la dirección y positiva. ¿Cuál es el momento angular de la partícula sobre el origen?

83. Una partícula de 4.0 kg se mueve en un círculo de radio de 2.0 m. El momento angular de la partícula varía en el tiempo según l = 5.0t². (a) ¿Cuál es el torque en la partícula sobre el centro del círculo en t = 3.4 s? (b) ¿Cuál es la velocidad angular de la partícula en t = 3.4 s?

84. Un protón se acelera en un ciclotrón a 5,0 × 10⁶ m/s en 0,01 s. El protón sigue un camino circular. Si el radio del ciclotrón es de 0.5 km, (a) ¿Cuál es el momento angular del protón alrededor del centro a su velocidad máxima? (b) ¿Cuál es el torque en el protón sobre el centro a medida que acelera a la velocidad máxima?

85. (a) ¿Cuál es el momento angular de la Luna en su órbita alrededor de la Tierra? (b) ¿Cómo se compara este momento angular con el momento angular de la Luna en su eje? Recuerda que la Luna mantiene un lado hacia la Tierra en todo momento.

86. Un DVD está girando a 500 rpm. ¿Cuál es el momento angular del DVD si tiene un radio de 6.0 cm y una masa de 20.0 g?

87. El disco de un alfarero gira desde el reposo hasta 10 rev/s en 15 s. El disco tiene una masa de 3.0 kg y un radio de 30.0 cm. ¿Cuál es el momento angular del disco en t = 5 s, t = 10 s?

88. Supoón que arrancas un automóvil antiguo ejerciendo una fuerza de 300 N en su manivela durante 0.250 s. ¿Cuál es el momento angular dado al motor si la manivela está a 0.300 m del pivote y se ejerce la fuerza para crear el torque máximo todo el tiempo?

89. Un cilindro sólido de masa de 2,0 kg y un radio de 20 cm gira en sentido antihorario alrededor de un eje vertical a través de su centro a 600 rev/min. Un segundo cilindro sólido de la misma masa y radio gira en el sentido de las agujas del reloj alrededor del mismo eje vertical a 900 rev/min. Si los cilindros se acoplan para que giren sobre el mismo eje vertical, ¿cuál es la velocidad angular de la combinación?

90. Un niño se encuentra en el centro de una plataforma que está girando sin fricción a 1.0 rev/s. El niño sostiene pesas lo más lejos posible de su cuerpo. En esta posición, el momento total de inercia del niño, la plataforma y los pesos es de 5.0 kg • m². El niño dibuja los pesos cerca de su cuerpo, disminuyendo así el momento total de inercia a 1.5 kg • m². (a) ¿Cuál es la velocidad angular final de la plataforma? (b) ¿Cuánto aumenta la energía cinética de rotación?

91. Ocho niños, cada uno con una masa de 40 kg, suben a un pequeño tiovivo. Se posicionan de manera uniforme en el borde exterior y unen sus manos. El tiovivo tiene un radio de 4.0 m y un momento de inercia de 1000.0 kg • m². Después de que al carrusel se le da una velocidad angular de 6.0 rev/min, los niños caminan hacia adentro y se detienen cuando están a 0.75 m del eje de rotación. ¿Cuál es la nueva velocidad angular del tiovivo? Supón que hay un par de fricción insignificante en la estructura.

92. Un palo delgado de 150 g de masa gira alrededor de un eje perpendicular al eje largo del palo a una velocidad angular de 240 rev/min. ¿Cuál es el momento angular de la palanca si el eje de rotación (a) pasa por el centro de la palanca? (b) Pasa a través de un extremo del palo?

93. Un satélite en forma de esfera de masa 20,000 kg y radio 5,0 m gira alrededor de un eje a través de su centro de masa. Tiene una velocidad de rotación de 8.0 rev/s. Dos antenas se despliegan en el plano de rotación que se extiende desde el centro de masa del satélite. Cada antena se puede aproximar ya que una varilla tiene una masa de 200.0 kg y una longitud de 7.0 m. ¿Cuál es la nueva velocidad de rotación del satélite?

94. Un principal tiene un momento de inercia de 3.2 × 10^-4 kg • m² y un radio de 4.0 cm desde el centro de masa hasta el punto de pivote. Si gira a 20.0 rev/s y está en proceso de precesión, ¿cuántas revoluciones precede en 10.0 s?

Problemas de Desafío

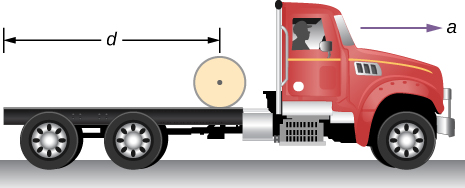
95. El camión que se muestra a continuación está inicialmente en reposo con un sólido rollo de papel cilíndrico en su camabaja. Si el camión avanza con una aceleración uniforme a, ¿a qué distancia se mueve antes de que el papel ruede hacia atrás? (Sugerencia: si el rollo acelera hacia adelante con a', entonces se acelera hacia atrás con respecto al camión con una aceleración a - a'. Además, Rα = a - a').



96. Una bola de bolos de radio 8.5 cm es lanzada a una pista de bolos con una velocidad de 9.0 m/s. La dirección del lanzamiento es hacia la izquierda, según lo ve el observador, por lo que la bola de boliche comienza a girar hacia la izquierda cuando está en contacto con el piso. El coeficiente de fricción cinética en el carril es 0.3. (a) ¿Cuál es el tiempo requerido para que la pelota llegue al punto en que no se deslice? ¿Cuál es la distancia d hasta el punto donde la bola rueda sin deslizarse?

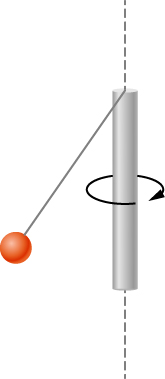
97. Una pequeña bola de masa de 0,50 kg está unida por una cuerda sin masa a una varilla vertical que gira como se muestra a continuación. Cuando la varilla tiene una velocidad angular de 6.0 rad/s, la cuerda forma un ángulo de 30° con respecto a la vertical. (a) Si la velocidad angular se incrementa a 10.0 rad/s, ¿cuál es el nuevo ángulo de la cuerda? (b) Calcula los momentos angulares iniciales y finales de la pelota. (c) ¿Puede la barra girar lo suficientemente rápido para que la bola quede horizontal?



98. Un insecto que vuela horizontalmente a 1.0 m/s colisiona y se pega al extremo de una vara uniforme que cuelga verticalmente. Después del impacto, la palanca se balancea a un ángulo máximo de 5.0° desde la vertical antes de girar hacia atrás. Si la masa del palo es 10 veces mayor que la del error, calcule la longitud del palo.