11.1 Difracción de una sola rendija
1. A medida que se reduce el ancho de la rendija que produce un patrón de difracción de una sola rendija, ¿cómo cambiará el patrón de difracción producido?
2. Compara interferencias y difracción.
3. Si tu y un amigo están en lados opuestos de una colina, puedes comunicarte con walkie-talkies pero no con linternas. Explica.
4. ¿Qué sucede con el patrón de difracción de una rendija única cuando todo el aparato óptico está sumergido en el agua?
5. En nuestro estudio de la difracción por una sola rendija, asumimos que la longitud de la rendija es mucho mayor que el ancho. ¿Qué sucede con el patrón de difracción si estas dos dimensiones fueran comparables?
6. Una rendija rectangular es dos veces más ancha que alta. ¿Es el pico de difracción central más ancho en la dirección vertical o en la dirección horizontal?
11.2 Intensidad en la difracción de una sola rendija
7. En la ecuación 11.4, el parámetro β parece un ángulo, pero no es un ángulo que se pueda medir con un transportador en el mundo físico. Explica qué representa β.
11.3 Difracción de doble rendija
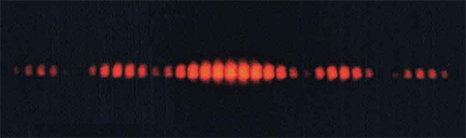
8. A continuación se muestra la parte central del patrón de interferencia para una longitud de onda pura de luz roja proyectada en una doble rendija. El patrón es en realidad una combinación de interferencia de una y dos rendijas. Observa que los puntos brillantes están espaciados uniformemente. ¿Es esta una característica de doble o de una sola rendija? Ten en cuenta que algunos de los puntos brillantes son tenues a ambos lados del centro. ¿Es esta una característica de una o doble rendija? ¿Cuál es más pequeño, el ancho de la rendija o la separación entre rendijas? Explica tus respuestas.

11.5 Aperturas circulares y resolución
9. ¿Se obtiene una resolución más alta en un microscopio con luz roja o azul? Explica tu respuesta.
10. La potencia de resolución del telescopio refractor aumenta con el tamaño de su lente objetivo. ¿Qué otra ventaja se gana con una lente más grande?
11. La distancia entre los átomos en una molécula es de aproximadamente 10-8 cm. ¿Se puede usar la luz visible para "ver" las moléculas?
12. Un haz de luz siempre se extiende. ¿Por qué no se puede crear un haz con rayos paralelos para evitar la propagación? ¿Por qué no se pueden usar lentes, espejos o aberturas para corregir la propagación?
11.6 Difracción de rayos X
13. Las redes cristalinas se pueden examinar con rayos X pero no con rayos UV. ¿Por qué?
11.7 Holografía
14. ¿Cómo se puede decir que un holograma es una verdadera imagen tridimensional y que las películas tridimensionales no lo son?
15. Si se graba un holograma utilizando luz monocromática en una longitud de onda, pero su imagen se ve en otra longitud de onda, digamos 10% más corta, ¿qué verás? ¿Qué pasa si se ve con luz de exactamente la mitad de la longitud de onda original?
16. ¿Qué imagen se verá si un holograma se graba con luz monocromática pero su imagen se ve en luz blanca? Explica.
11.1 Difracción de una sola rendija
17. (a) ¿En qué ángulo se encuentra el primer mínimo para que la luz de 550 nm caiga en una sola rendija de ancho 1,00 μm? (b) ¿Habrá un segundo mínimo?
18. (a) Calcula el ángulo en el que una rendija de 2.00 μm de ancho produce su primer mínimo para luz violeta de 410 nm. (b) ¿Dónde está el primer mínimo para luz roja de 700 nm?
19. (a) ¿Qué ancho tiene una rendija que produce su primer mínimo para luz de 633 nm en un ángulo de 28.0°? (b) ¿En qué ángulo será el segundo mínimo?
20. (a) ¿Cuál es el ancho de una rendija única que produce su primer mínimo a 60.0° para luz de 600 nm? (b) Encuentre la longitud de onda de la luz que tiene su primer mínimo en 62.0°.
21. Encuentra la longitud de onda de la luz que tiene su tercer mínimo en un ángulo de 48.6° cuando cae en una sola rendija de ancho 3.00μm.
22. (a) La luz de vapor de sodio con un promedio de 589 nm en longitud de onda cae en una sola rendija de ancho 7.50μm. ¿En qué ángulo produce su segundo mínimo? (b) ¿Cuál es el mínimo de mayor orden producido?
23. Considera un patrón de difracción de una sola rendija para λ = 589 nm, proyectado en una pantalla que está a 1.00 m desde una rendija de ancho de 0.25 mm. ¿A qué distancia del centro del patrón están los centros de la primera y la segunda franjas oscuras?
24. (a) Encuentra el ángulo entre los primeros mínimos para las dos líneas de vapor de sodio, que tienen longitudes de onda de 589.1 y 589.6 nm, cuando caen sobre una sola rendija de ancho de 2.00μm. (b) ¿Cuál es la distancia entre estos mínimos si el patrón de difracción cae en una pantalla a 1.00 m de la rendija? (c) Discute la facilidad o dificultad de medir tal distancia.
25. (a) ¿Cuál es el ancho mínimo de una sola rendija (en múltiplos de λ) que producirá un primer mínimo para una longitud de onda λ? (b) ¿Cuál es su ancho mínimo si produce 50 mínimos? (c) 1000 minimos?
26. (a) Si una sola rendija produce un primer mínimo a 14.5°, ¿en qué ángulo es el mínimo de segundo orden? (b) ¿Cuál es el ángulo del mínimo de tercer orden? (c) ¿Hay un mínimo de cuarto orden? (d) Usa tus respuestas para ilustrar cómo el ancho angular del máximo central es aproximadamente el doble del ancho angular del siguiente máximo (cuál es el ángulo entre el primer y el segundo mínimo).
27. Si la separación entre el primer y el segundo mínimo de un patrón de difracción de una sola rendija es de 6,0 mm, ¿cuál es la distancia entre la pantalla y la rendija? La longitud de onda de la luz es de 500 nm y el ancho de la rendija es de 0.16 mm.
28. Un rompe olas en la entrada a un puerto consiste en una barrera de roca con una abertura de 50.0 m de ancho. Las olas del océano de 20.0 m de longitud de onda se aproximan a la abertura en línea recta. ¿En qué ángulos de la dirección incidente están los botes dentro del puerto más protegidos contra la acción de las olas?
29. Un técnico de mantenimiento de aeronaves pasa por una puerta alta del hangar que actúa como una sola rendija para el sonido que entra al hangar. Fuera de la puerta, en una línea perpendicular a la abertura de la puerta, un motor a reacción produce un sonido de 600 Hz. ¿En qué ángulo con la puerta el técnico observará el primer mínimo en intensidad de sonido si la apertura vertical es de 0,800 m de ancho y la velocidad del sonido es de 340 m/s?
11.2 Intensidad en la difracción de una sola rendija
30. Una luz de sodio amarillo de longitud de onda de 589 nm ilumina una única rendija de 3.0 μm de ancho. Encuentra la intensidad en un ángulo de 15° con respecto al eje en términos de la intensidad del máximo central.
31. Una luz de mercurio con una longitud de onda de 576 nm ilumina una sola rendija de 0,1 mm de ancho. Encuentre la intensidad en un ángulo de 10° con respecto al eje en términos de la intensidad del máximo central.
32. El ancho del pico central en un patrón de difracción de una sola rendija es de 5.0 mm. La longitud de onda de la luz es de 600 nm y la pantalla está a 2.0 m de la rendija. (a) ¿Cuál es el ancho de la rendija? (b) Determina la relación de la intensidad a 4.5 mm desde el centro del patrón a la intensidad en el centro.
33. Considere el patrón de difracción de una rendija para λ = 600 nm, D = 0.025 mm y x = 2.0 m. Encuentra la intensidad en términos de Io en θ = 0.5°, 1.0°, 1.5°, 3.0° y 10.0°.
11.3 Difracción de doble rendija
34. Dos rendijas de ancho 2 μm, cada una en un material opaco, están separadas por una distancia de centro a centro de 6 μm. Una luz monocromática de 450 nm de longitud de onda incide en la doble rendija. Encuentra un patrón combinado de interferencia y difracción en la pantalla.
(a) ¿Cuántos picos de la interferencia se observarán en el máximo central del patrón de difracción?
(b) ¿Cuántos picos de la interferencia se observarán si el ancho de la rendija se duplica manteniendo la misma distancia entre las rendijas?
(c) ¿Cuántos picos de interferencia se observarán si las rendijas están separadas por el doble de la distancia, es decir, 12 μm, al mismo tiempo que se mantienen los anchos de las rendijas?
(d) ¿Qué ocurrirá en (a) si en lugar de la luz de 450 nm se usa otra luz de longitud de onda de 680 nm?
(e) ¿Cuál es el valor de la relación entre la intensidad del pico central y la intensidad del próximo pico brillante en (a)?
(f) ¿Esta relación depende de la longitud de onda de la luz?
(g) ¿Esta relación depende del ancho o la separación de las rendijas?.
35. Una doble rendija produce un patrón de difracción que es una combinación de interferencia de una y dos rendijas. Encuentra la relación entre el ancho de las rendijas y la separación entre ellas, si el primer mínimo del patrón de una sola rendija cae en el quinto máximo del patrón de la doble rendija (Esto reducirá en gran medida la intensidad del quinto máximo).
36. Para una configuración de doble rendija donde la separación de la rendija es cuatro veces el ancho de la rendija, ¿cuántas franjas de interferencia se encuentran en el pico central del patrón de difracción?.
37. La luz de 500 nm de longitud de onda cae normalmente en 50 rendijas con un ancho de 2.5 × 10−3 mm y espaciadas de 5.0 × 10−3 mm. ¿Cuántas franjas de interferencia se encuentran en el pico central del patrón de difracción?.
38. Una luz monocromática de longitud de onda de 589 nm que incide en una doble rendija con un ancho de rendija de 2,5 μm y una separación desconocida da como resultado un patrón de difracción que contiene nueve picos de interferencia dentro del máximo central. Encuentra la separación de las rendijas.
39. Cuando una luz monocromática de longitud de onda de 430 nm incide en una doble rendija de separación de 5 μm, hay 11 franjas de interferencia en su máximo central. ¿Cuántas franjas de interferencia habrá en el máximo central de una luz de longitud de onda de 632.8 nm para la misma doble rendija?.
40. Determina las intensidades de dos picos de interferencia distintos al pico central en el máximo central de la difracción, si es posible, cuando una luz de longitud de onda de 628 nm incide en una doble rendija de ancho de 500 nm y separación de 1500 nm. Usa la intensidad del punto central para ser 1mW/cm2.
11.4 Rejillas de difracción
41. Una rejilla de difracción tiene 2000 líneas por centímetro. ¿En qué ángulo será el máximo de primer orden para luz verde de longitud de onda de 520 nm?
42. Encuentra el ángulo para el máximo de tercer orden para la luz amarilla de longitud de onda de 580 nm que cae en una rejilla de difracción que tiene 1500 líneas por centímetro.
43. ¿Cuántas líneas por centímetro hay en una rejilla de difracción que proporciona un máximo de primer orden para luz azul de 470 nm en un ángulo de 25.0°?
44. ¿Cuál es la distancia entre líneas en una rejilla de difracción que produce un máximo de segundo orden para luz roja de 760 nm en un ángulo de 60.0°?
45. Calcule la longitud de onda de la luz que tiene su máximo de segundo orden a 45.0° cuando cae en una rejilla de difracción que tiene 5000 líneas por centímetro.
46. Una corriente eléctrica a través de gas de hidrógeno produce varias longitudes de onda distintas de luz visible. ¿Cuáles son las longitudes de onda del espectro de hidrógeno, si forman máximos de primer orden en los ángulos 24.2°, 25.7°, 29.1° y 41.0° cuando se proyectan en una rejilla de difracción con 10,000 líneas por centímetro?
47. (a) ¿En qué se convierten los cuatro ángulos del problema anterior si se usa una rejilla de difracción de 5000 líneas por centímetro? (b) Usando esta rejilla, ¿cuáles serían los ángulos para los máximos de segundo orden? (c) Discute la relación entre las reducciones integrales en líneas por centímetro y los nuevos ángulos de varios máximos de orden.
48. ¿Cuál es el espacio entre las estructuras en una pluma que actúa como una rejilla de reflexión, dado que producen un máximo de primer orden para luz de 525 nm en un ángulo de 30.0°?
49. Un ópalo como el que se muestra en la Figura 11.15 actúa como una rejilla de reflexión con filas separadas por aproximadamente 8 μm. Si el ópalo se ilumina normalmente, (a) ¿en qué ángulo se verá la luz roja y (b) en qué ángulo se verá la luz azul?
50. ¿En qué ángulo una rejilla de difracción produce un máximo de segundo orden para la luz que tiene un máximo de primer orden de 20.0°?
51. (a) Encuentra el número máximo de líneas por centímetro que puede tener una rejilla de difracción y produzca un máximo para la longitud de onda más pequeña de la luz visible. (b) ¿Sería útil tal rejilla para los espectros ultravioleta? (c) Para espectros infrarrojos?
52. (a) Demuestra que una rejilla de 30,000 líneas por centímetro no producirá un máximo de luz visible. (b) ¿Cuál es la longitud de onda más larga para la cual produce un máximo de primer orden? (c) ¿Cuál es el mayor número de líneas por centímetro que puede tener una rejilla de difracción y produce un espectro completo de segundo orden para la luz visible?
53. El análisis que se muestra a continuación también se aplica a las redes de difracción con líneas separadas por una distancia d. ¿Cuál es la distancia entre las franjas producidas por una rejilla de difracción que tiene 125 líneas por centímetro para luz de 600 nm, si la pantalla está a 1,50 m de distancia? (Sugerencia: la distancia entre las franjas adyacentes es Δy = xλ/d, suponiendo que la separación d de la rendija es comparable a λ).

11.5 Aperturas circulares y resolución
54. El radiotelescopio Arecibo de 305 m de diámetro que se muestra en la figura 11.20 detecta ondas de radio con una longitud de onda promedio de 4.00 cm. (a) ¿Cuál es el ángulo entre dos fuentes puntuales que solo se pueden resolver para este telescopio? (b) ¿Qué tan cerca podrían estar estas fuentes puntuales a la distancia de 2 millones de años luz de la Galaxia de Andrómeda?
55. Suponiendo la resolución angular encontrada para el Telescopio Hubble en el Ejemplo 11.6, ¿cuál es el detalle más pequeño que se pudo observar en la Luna?
56. La difusión de difracción para una linterna es insignificante en comparación con otras limitaciones en su óptica, como las aberraciones esféricas en su espejo. Para mostrar esto, calcula la dispersión angular mínima de un haz de linterna que originalmente tiene un diámetro de 5.00 cm con una longitud de onda promedio de 600 nm.
57. (a) ¿Cuál es la dispersión angular mínima de un rayo láser de He-Ne de longitud de onda de 633 nm que originalmente tiene un diámetro de 1.00 mm? (b) Si este láser apunta a un acantilado de montaña a 15.0 km de distancia, ¿qué tan grande será el lugar iluminado? (c) ¿Qué tan grande sería un punto iluminado en la luna, despreciando los efectos atmosféricos? (Esto podría hacerse para golpear un reflector de esquina para medir el tiempo de ida y vuelta y, por lo tanto, la distancia).
58. Se puede usar un telescopio para ampliar el diámetro de un rayo láser y limitar la difusión de difracción. El rayo láser se envía a través del telescopio en dirección opuesta a la normal y luego se puede proyectar en un satélite o la luna. (a) Si esto se hace con el telescopio Mount Wilson, que produce un haz de 2,54 m de diámetro de luz de 633 nm, ¿cuál es la dispersión angular mínima del haz? (b) Dejando de lado los efectos atmosféricos, ¿cuál es el tamaño del punto que este rayo haría en la luna, asumiendo una distancia lunar de 3.84 × 108m?
59. El límite a la agudeza del ojo está realmente relacionado con la difracción por parte de la pupila. (a) ¿Cuál es el ángulo entre dos puntos de luz justamente resolubles para una pupila de 3,00 mm de diámetro, suponiendo una longitud de onda promedio de 550 nm? (b) Toma tu resultado como el límite práctico para el ojo. ¿Cuál es la distancia más grande que puede tener un auto si puede resolver sus dos faros, dado que están a 1,30 m de distancia? (c) ¿Cuál es la distancia entre dos puntos que se pueden resolver y que se mantienen a la distancia de un brazo (0,800 m) desde tu ojo? (d) ¿Cómo se compara su respuesta con (c) con los detalles que normalmente observas en las circunstancias cotidianas?
60. ¿Cuál es el espejo de diámetro mínimo en un telescopio que le permitiría ver detalles tan pequeños como 5,00 km en la Luna a unos 384,000 km de distancia? Supón una longitud de onda promedio de 550 nm para la luz recibida.
61. Encuentra el radio de la imagen de una estrella en la retina de un ojo si su pupila está abierta a 0,65 cm y la distancia de la pupila a la retina es de 2,8 cm. Supongamos que λ = 550 nm.
62. (a) El planeta enano Plutón y su luna, Caronte, están separados por 19,600 km. Dejando de lado los efectos atmosféricos, ¿el telescopio Palomar Mountain de 5.08 m de diámetro podrá resolver estos cuerpos cuando se encuentren a 4,50 × 109 km de la Tierra? Supongamos una longitud de onda promedio de 550 nm. (b) En realidad, es apenas posible discernir que Plutón y Caronte son cuerpos separados usando un telescopio terrestre. ¿Cúales son las razones para esto?
63. Un satélite espía orbita la Tierra a una altura de 180 km. ¿Cuál es el diámetro mínimo de la lente del objetivo en un telescopio que se debe usar para resolver columnas de tropas que se alejan marchando con 2,0 m de distancia? Supongamos que λ = 550 nm.
64. ¿Cuál es la separación angular mínima de dos estrellas que solo pueden resolverse con el telescopio Gemini Sur de 8.1 m, si los efectos atmosféricos no limitan la resolución? Usa 550 nm para la longitud de onda de la luz de las estrellas.
65. Los faros de un coche están separados por 1,3 m. ¿Cuál es la distancia máxima a la que el ojo puede resolver estos dos faros? Tomar el diámetro de la pupila a 0,40 cm.
66. Cuando se colocan puntos en una página desde una impresora láser, deben estar lo suficientemente cerca para que no se vean los puntos individuales de tinta. Para hacer esto, la separación de los puntos debe ser menor que el criterio de Raleigh. Toma la pupila del ojo de 3.0 mm y la distancia desde el papel hasta el ojo de 35 cm; encuentra la separación mínima de dos puntos de manera que no puedan resolverse. ¿A cuántos puntos por pulgada (ppp) corresponde esto?
67. Supongamos que estás mirando hacia abajo en una carretera desde un avión que vuela a una altitud de 6.0 km. ¿A qué distancia deben estar dos coches si puedes distinguirlos? Supón que λ = 550 nm y que el diámetro de tus pupilas es de 4.0 mm.
68. ¿Puede un astronauta que orbita la Tierra en un satélite a una distancia de 180 km de la superficie distinguir dos rascacielos que están separados por 20 m? Supongamos que las pupilas de los ojos del astronauta tienen un diámetro de 5.0 mm y que la mayor parte de la luz está centrada alrededor de 500 nm.
69. Los caracteres de una pantalla de un estadio se forman con bombillas muy separadas que irradian principalmente luz amarilla (Usa λ = 600 nm). ¿Qué tan cerca deben estar las bombillas separadas para que un observador a 80 m de distancia vea una pantalla de líneas continuas en lugar de las bombillas individuales? Supongamos que la pupila del ojo del observador tiene un diámetro de 5.0 mm.
70. Si un microscopio puede aceptar la luz de objetos en ángulos tan grandes como α = 70°, ¿cuál es la estructura más pequeña que puede resolverse cuando se ilumina con luz de 500 nm de longitud de onda y (a) la muestra está en el aire? (b) ¿Cuando el espécimen se sumerge en aceite, con un índice de refracción de 1.52?
71. Una cámara usa una lente con apertura de 2.0 cm. ¿Cuál es la resolución angular de una fotografía tomada a una longitud de onda de 700 nm? ¿Puedes hallar las marcas milimétricas de una regla colocada a 35 m de distancia?
11.6 Difracción de rayos X
72. Los rayos X de longitud de onda de 0.103 nm se reflejan en un cristal y se registra un máximo de segundo orden en un ángulo de Bragg de 25.5°. ¿Cuál es el espacio entre los planos de dispersión en este cristal?
73. Se observa un máximo de reflexión de Bragg de primer orden cuando una radiografía monocromática cae sobre un cristal en un ángulo de 32.3° con respecto al plano reflectante. ¿Cuál es la longitud de onda de esta radiografía?
74. Se realiza un experimento de dispersión de rayos X en un cristal cuyos átomos forman planos separados por 0.440 nm. Usando una fuente de rayos X de 0.548 nm de longitud de onda, ¿cuál es el ángulo (con respecto a los planos en cuestión) en el cual el experimentador necesita iluminar el cristal para observar un máximo de primer orden?
75. La estructura del cristal de NaCl forma planos que reflejan una separación de 0.541 nm. ¿Cuál es el ángulo más pequeño, medido desde estos planos, en el cual se puede observar la difracción de rayos X, si se usan rayos X de longitud de onda de 0.085 nm?
76. En un cristal determinado, se observa un máximo de difracción de rayos X de primer orden en un ángulo de 27,1° con respecto a su superficie, utilizando una fuente de rayos X de longitud de onda desconocida. Además, cuando se ilumina con un valor diferente, esta vez de longitud de onda conocida de 0.137 nm, se detecta un máximo de segundo orden a 37.3°. Determina (a) el espacio entre los planos reflectantes y (b) la longitud de onda desconocida.
77. Los cristales de calcita contienen planos de dispersión separados por 0.30 nm. ¿Cuál es la separación angular entre los máximos de difracción de primer orden y de segundo orden cuando se usan rayos X de longitud de onda de 0.130 nm?
78. El ángulo de Bragg de primer orden para un cristal determinado es 12.1°. ¿Cuál es el ángulo de segundo orden?
79. La luz blanca cae sobre dos rendijas estrechas separadas por 0.40 mm. El patrón de interferencia se observa en una pantalla a 3.0 m de distancia. (a) ¿Cuál es la separación entre los primeros máximos para la luz roja (λ = 700 nm) y la luz violeta (λ = 400 nm)? (b) ¿En qué punto más cercano al máximo central coincidirá un máximo para luz amarilla (λ = 600 nm) con un máximo para luz violeta? Identificar el orden de cada máximo.
80. Las microondas de 10.0 mm de longitud de onda caen normalmente sobre una placa metálica que contiene una rendija de 25 mm de ancho. (a) ¿Dónde están los primeros mínimos del patrón de difracción? (b) ¿Habría mínimos si la longitud de onda fuera de 30.0 mm?
81. Los cuásares, o fuentes de radio casi estelares, son objetos astronómicos descubiertos en 1960. Son emisores de ondas de radio distantes pero fuertes con un tamaño angular tan pequeño que originalmente no estaban resueltos, al igual que las estrellas. El quasar 3C405 es en realidad dos fuentes de radio discretas que subtienden un ángulo de 82 segundos de arco. Si este objeto se estudia utilizando emisiones de radio a una frecuencia de 410 MHz, ¿cuál es el diámetro mínimo de un radiotelescopio que puede resolver las dos fuentes?
82. Dos ondas, cada una con un ancho de 1800 nm y separadas por la distancia de centro a centro de 1200 nm están iluminadas por ondas planas de un láser de ión kriptón que emite un láser a una longitud de onda de 461.9 nm. Encuentre el número de picos de interferencia en el pico de difracción central.
83. Un microondas de una longitud de onda desconocida incide en una sola rendija de ancho 6 cm. El ancho angular del pico central es de 25°. Encuentra la longitud de onda.
84. La luz roja (longitud de onda de 632.8 nm en el aire) de un láser de helio-neón incide en una sola rendija de ancho de 0.05 mm. Todo el aparato se sumerge en agua de índice de refracción 1.333. Determina el ancho angular del pico central.
85. Un rayo de luz de longitud de onda de 461.9 nm emerge de una abertura circular de 2 mm de un láser de ión criptón. Debido a la difracción, el haz se expande a medida que se mueve hacia afuera. ¿Qué tan grande es el punto brillante central en (a) 1 m, (b) 1 km, (c) 1000 km y (d) en la superficie de la luna a una distancia de 400,000 km de la Tierra.
86. ¿A qué distancia deben estar dos objetos en la luna para poder distinguirlos a simple vista si los efectos de difracción de la pupila del ojo limitan la resolución? Asume 550 nm para la longitud de onda de la luz, el diámetro de la pupila de 5.0 mm y 400,000 km para la distancia a la luna.
87. ¿Qué tan separados deben estar los dos objetos en la luna para poder ser resueltos por el telescopio Gemini Norte de 8.1 m de diámetro en Mauna Kea, Hawai, si los efectos de difracción de la apertura del telescopio limitan la resolución? Supongamos 550 nm para la longitud de onda de la luz y 400,000 km para la distancia a la luna.
88. Se dice que un satélite espía puede resolver objetos a 10 cm de distancia mientras opera a 197 km por encima de la superficie de la Tierra. ¿Cuál es el diámetro de la apertura del telescopio si la resolución solo está limitada por los efectos de difracción? Utiliza 550 nm para la luz.
89. La luz monocromática de longitud de onda de 530 nm pasa a través de una rendija horizontal de 1,5 μm de ancho en una placa opaca. Una pantalla de dimensiones de 2,0 m × 2,0 m está a 1,2 m de la rendija. (a) ¿De qué manera se extiende el patrón de difracción en la pantalla? (b) ¿Cuáles son los ángulos de los mínimos con respecto al centro? (c) ¿Cuáles son los ángulos de los máximos? (d) ¿Qué ancho tiene la franja central brillante en la pantalla? (e) ¿Qué ancho tiene la próxima franja brillante en la pantalla?
90. Una luz monocromática de longitud de onda desconocida incide en una rendija de 20 μm de ancho. Se ve un patrón de difracción en una pantalla a 2,5 m de distancia, donde el máximo central se extiende sobre una distancia de 10,0 cm. Encuentra la longitud de onda.
91. Una fuente de luz que tiene dos longitudes de onda de 550 nm y 600 nm de igual intensidad incide en una rendija de ancho de 1,8 μm. Encuentra la separación de los puntos brillantes m = 1 de las dos longitudes de onda en una pantalla a 30.0 cm de distancia.
92. Una sola rendija de ancho 2100 nm se ilumina normalmente por una onda de longitud de onda 632.8 nm. Encuentra la diferencia de fase entre las ondas desde la parte superior y un tercio desde la parte inferior de la rendija hasta un punto en una pantalla a una distancia horizontal de 2.0 my una distancia vertical de 10.0 cm desde el centro.
93. Una luz de sodio amarillo de longitud de onda de 589 nm ilumina una sola rendija de 3.0 μm de ancho. Encuentra la intensidad en un ángulo de 15° con respecto al eje en términos de la intensidad del máximo central.
94. Una lámpara de mercurio con una longitud de onda de 576 nm ilumina una sola rendija de 0,10 mm de ancho. Encuentra la intensidad en un ángulo de 10° con respecto al eje en términos de la intensidad del máximo central.
95. Una rejilla de difracción produce un segundo máximo que está a 89.7 cm del máximo central en una pantalla a 2.0 m de distancia. Si la rejilla tiene 600 líneas por centímetro, ¿cuál es la longitud de onda de la luz que produce el patrón de difracción?
96. Se utiliza una rejilla con 4000 líneas por centímetro para difractar la luz que contiene todas las longitudes de onda entre 400 y 650 nm. ¿Qué tan ancho es el espectro de primer orden en una pantalla a 3.0 m de la rejilla?
97. Se utiliza una rejilla de difracción con 2000 líneas por centímetro para medir las longitudes de onda emitidas por un tubo de descarga de gas hidrógeno. (a) ¿En qué ángulos encontrarás el máximo de las dos líneas azules de primer orden de longitudes de onda de 410 y 434 nm? (b) Los máximos de otras dos líneas de primer orden se encuentran en 1 = 0.097 rad y θ2 = 0.132 rad. ¿Cuáles son las longitudes de onda de estas líneas?
98. Para luz blanca (400 nm < λ < 700nm) que cae normalmente en una rejilla de difracción, demuestra que los espectros de segundo y tercer orden se superponen sin importar cuál sea la constante de rejilla d.
99. ¿Cuántos órdenes completos del espectro visible (400 nm < λ < 700nm) se pueden producir con una rejilla de difracción que contiene 5000 líneas por centímetro?
100. Dos lámparas que producen una luz de longitud de onda de 589 nm se fijan a una distancia de 1,0 m en una tabla de madera. ¿Cuál es la distancia máxima que un observador puede tener y aún puede resolver las lámparas como dos fuentes de luz separadas, si la resolución se ve afectada únicamente por la difracción de la luz que entra en el ojo? Supongamos que la luz entra en el ojo a través de una pupila de 4,5 mm de diámetro.
101. En un día claro y luminoso, estás en la cima de una montaña y mirando a una ciudad a 12 km. Hay dos torres altas separadas por 20.0 m en la ciudad. ¿Puede tu ojo resolver las dos torres si el diámetro de la pupila es de 4.0 mm? Si no, ¿cuál debería ser la potencia de aumento mínima del telescopio necesaria para resolver las dos torres? En tus cálculos, usa 550 nm para la longitud de onda de la luz.
102. Los radiotelescopios son telescopios utilizados para la detección de emisiones de radio desde el espacio. Debido a que las ondas de radio tienen longitudes de onda mucho más largas que la luz visible, el diámetro de un radiotelescopio debe ser muy grande para proporcionar una buena resolución. Por ejemplo, el radiotelescopio en Penticton, BC en Canadá, tiene un diámetro de 26 m y puede operarse a frecuencias tan altas como 6.6 GHz. (a) ¿Cuál es la longitud de onda correspondiente a esta frecuencia? (b) ¿Cuál es la separación angular de dos fuentes de radio que puede resolver este telescopio? (c) Compara la resolución del telescopio con el tamaño angular de la luna.

103. Calcula la longitud de onda de la luz que produce su primer mínimo en un ángulo de 36.9° cuando cae en una sola rendija de ancho 1.00 μm.
104. (a) Encuentra el ángulo del tercer mínimo de difracción para que la luz de 633 nm caiga en una rendija de 20.0 μm de ancho. (b) ¿Qué ancho de hendidura colocaría este mínimo en 85.0°?
105. Como ejemplo de difracción por aberturas de dimensiones cotidianas, considera una puerta de ancho de 1,0 m. (a) ¿Cuál es la posición angular del primer mínimo en el patrón de difracción de la luz de 600 nm? (b) Repite este cálculo para una nota musical de frecuencia 440 Hz (A por encima de la mitad C). Toma la velocidad del sonido a 343 m/s.
106. ¿Cuáles son las posiciones angulares del primer y segundo mínimo en un patrón de difracción producido por una rendija de 0.20 mm de ancho que está iluminada por luz de 400 nm? ¿Cuál es el ancho angular del pico central?
107. ¿Qué tan lejos colocarías una pantalla de la rendija del problema anterior de modo que el segundo mínimo sea una distancia de 2.5 mm desde el centro del patrón de difracción?
108. ¿Qué tan estrecha es una rendija que produce un patrón de difracción en una pantalla a 1,8 m de distancia cuyo pico central tiene 1,0 m de ancho? Supongamos que λ = 589 nm.
109. Supón que el pico central de un patrón de difracción de una sola rendija es tan ancho que se puede suponer que los primeros mínimos se producen en posiciones angulares de ± 90°. Para este caso, ¿cuál es la relación entre el ancho de la ranura y la longitud de onda de la luz?
110. El pico de difracción central del patrón de interferencia de doble rendija contiene exactamente nueve franjas. ¿Cuál es la relación entre la separación de la ranura y el ancho de la ranura?
111. Determina las intensidades de tres picos de interferencia distintos al pico central en el máximo central de la difracción, si es posible, cuando una luz de 500 nm de longitud de onda incide normalmente en una doble rendija de 1000 nm de ancho y 1500 nm de separación. Usa la intensidad del punto central para ser 1 mW/cm2.
112. La luz amarilla de una lámpara de vapor de sodio parece ser de longitud de onda pura, pero produce dos máximos de primer orden a 36.093° y 36.129° cuando se proyecta en una rejilla de difracción de 10,000 líneas por centímetro. ¿Cuáles son las dos longitudes de onda con una precisión de 0.1 nm?
113. Las estructuras en una pluma de ave actúan como una rejilla de reflexión que tiene 8000 líneas por centímetro. ¿Cuál es el ángulo del máximo de primer orden para la luz de 600 nm?
114. Si una rejilla de difracción produce un máximo de primer orden para la longitud de onda más corta de la luz visible a 30.0°, ¿en qué ángulo será el máximo de primer orden para la mayor longitud de onda de la luz visible?
115. (a) ¿Qué longitud de onda visible tiene su máximo de cuarto orden en un ángulo de 25.0° cuando se proyecta en una rejilla de difracción de 25,000 líneas por centímetro? (b) ¿Qué es irrazonable acerca de este resultado? (c) ¿Qué suposiciones son irrazonables o inconsistentes?
116. Considera un espectrómetro basado en una rejilla de difracción. Crea un problema en el que calculas la distancia entre dos longitudes de onda de radiación electromagnética en su espectrómetro. Entre las cosas a considerar están las longitudes de onda que deseas poder distinguir, el número de líneas por metro en la rejilla de difracción y la distancia desde la rejilla a la pantalla o detector. Discute la practicidad del dispositivo en términos de poder discernir entre longitudes de onda de interés.
117. Un astrónomo aficionado quiere construir un telescopio con un límite de difracción que le permita ver si hay personas en las lunas de Júpiter. (a) ¿Qué diámetro de espejo se necesita para poder ver un detalle de 1.00 m en una luna joviana a una distancia de 7.50 × 108 km de la Tierra? La longitud de onda de la luz promedia 600 nm. (b) ¿Qué es irrazonable acerca de este resultado? (c) ¿Qué suposiciones son irrazonables o inconsistentes?
118. La luz azul de longitud de onda de 450 nm cae en una rendija de ancho de 0,25 mm. Una lente convergente de 20 cm de distancia focal se coloca detrás de la rendija y enfoca el patrón de difracción en una pantalla. (a) ¿A qué distancia está la pantalla de la lente? (b) ¿Cuál es la distancia entre el primer y el tercer mínimo del patrón de difracción?
119. (a) Supón que los máximos están a medio camino entre los mínimos de un patrón de difracción de una sola rendija. El uso del diámetro y la circunferencia del diagrama de fasores, como se describe en el apartado de la Intensidad en la difracción de una sola rendija, para determinar las intensidades de los máximos tercero y cuarto en términos de la intensidad del máximo central. (b) Haz el mismo cálculo, utilizando la ecuación 11.4.
120. (a) Al diferenciar la Ecuación 11.4, demuestra que los máximos de orden superior del patrón de difracción de rendija única ocurren a valores de β que satisfacen tanβ = β. (b) Grafica y = tanβ y y = β versus β y encuentra las intersecciones de estas dos curvas. ¿Qué información te dan sobre las ubicaciones de los máximos? (c) Convéncete a ti mismo de que estos puntos no aparecen exactamente en β = (n + 1/2)π, donde n = 0,1,2, ..., pero están muy cerca de estos valores.
121. ¿Cuál es el número máximo de líneas por centímetro que puede tener una rejilla de difracción y produce un espectro completo de primer orden para la luz visible?
122. Demuestre que una rejilla de difracción no puede producir un máximo de segundo orden para una longitud de onda de luz dada a menos que el máximo de primer orden esté en un ángulo menor a 30.0°.
123. Un rayo láser de He-Ne se refleja desde la superficie de un CD hacia una pared. El punto más brillante es el haz reflejado en un ángulo igual al ángulo de incidencia. Sin embargo, también se observan franjas. Si la pared está a 1,50 m del CD y la primera franja está a 0,600 m del máximo central, ¿cuál es el espaciado de las ranuras en el CD?
124. Los objetos vistos a través de un microscopio se colocan muy cerca del punto focal de la lente objetivo. Demuestra que la separación mínima x de dos objetos que se pueden resolver a través del microscopio viene dada por
x = 1.22λf0D, donde f0 es la distancia focal y D es el diámetro de la lente objetivo como se muestra a continuación.
