1.1 Variables rotacionales
1. Un reloj está montado en la pared. Cuando lo miras, ¿cuál es la dirección del vector de velocidad angular de la segunda mano?
2. ¿Cuál es el valor de la aceleración angular de la manecilla de segundos del reloj en la pared?
3. Se gira un bate de béisbol. ¿Todos los puntos en el bate tienen la misma velocidad angular? ¿La misma velocidad tangencial?
4. Las cuchillas de una licuadora en un mostrador giran en el sentido de las agujas del reloj, al mirarlas desde la parte superior. Si la licuadora se pone a una velocidad mayor, ¿en qué dirección es la aceleración angular de las cuchillas?
1.2 Rotación con aceleración angular constante
5. Si un cuerpo rígido tiene una aceleración angular constante, ¿cuál es la forma funcional de la velocidad angular en términos de la variable tiempo?
6. Si un cuerpo rígido tiene una aceleración angular constante, ¿cuál es la forma funcional de la posición angular?
7. Si la aceleración angular de un cuerpo rígido es cero, ¿cuál es la forma funcional de la velocidad angular?
8. Una atadura sin masa con una masa atada a ambos extremos gira alrededor de un eje fijo a través del centro. ¿Puede la aceleración total de la combinación curda/masa ser cero si la velocidad angular es constante?
1.1 Variables rotacionales
28. Calcula la velocidad angular de la Tierra.
29. Una estrella de la pista corre por una carrera de 400 m en una pista circular de 400 m en 45 s. ¿Cuál es su velocidad angular asumiendo que es constante?
30. Una rueda gira a una velocidad constante de 2.0 × 103 rev / min. (a) ¿Cuál es su velocidad angular en radianes por segundo? (b) ¿A través de qué ángulo gira en 10 s? Expresar la solución en radianes y grados.
31. Una partícula se mueve 3.0 m a lo largo de un círculo de radio de 1.5 m. (a) ¿A través de qué ángulo gira? (b) Si la partícula realiza este viaje en 1,0 s a una velocidad constante, ¿cuál es su velocidad angular? (c) ¿Cuál es su aceleración?
32. Un disco compacto gira a 500 rev / min. Si el diámetro del disco es de 120 mm, (a) ¿Cuál es la velocidad tangencial de un punto en el borde del disco? (b) ¿En un punto a medio camino del centro del disco?
33. Resultados irrazonables. La hélice de un avión gira a 10 rev / s cuando el piloto apaga el motor. La hélice reduce su velocidad angular a una constante de 2.0rad /s2 durante un período de tiempo de 40 s. ¿Cuál es la velocidad de rotación de la hélice en 40 s? ¿Es esta una situación razonable?
34. Un giroscopio disminuye su velocidad inicial de 32.0 rad / s a una velocidad de 0.700rad /s2. ¿Cuánto tiempo se tarda en detenerse?
35. En el despegue, las hélices en un UAV (vehículo aéreo no tripulado) aumentan su velocidad angular desde el reposo a una velocidad de ω = (25.0t) rad / s durante 3.0 s. (a) ¿Cuál es la velocidad angular instantánea de las hélices en t = 2.0s? (b) ¿Cuanto
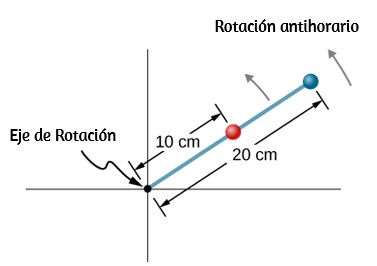
36. La posición angular de una varilla varía como 20.0t2 radianes desde t = 0. La varilla tiene dos canicas en ella, como se muestra en la siguiente figura, una a 10 cm del eje de rotación y la otra a 20 cm del eje de rotación. (a) ¿Cuál es la velocidad angular instantánea de la barra en t = 5 s? (b) ¿Cuál es la aceleración angular de la barra? (c) ¿Cuáles son las velocidades tangenciales de las canicas en t = 5 s? (d) ¿Cuáles son las aceleraciones tangenciales de las canicas en t = 5 s? (e) ¿Cuáles son las aceleraciones centrípetas de las canicas en t = 5 s?

1.2 Rotación con aceleración angular constante
37. Una rueda tiene una aceleración angular constante de 5.0rad /s2. A partir del reposo, y gira 300 rad. a) ¿Cuál es su velocidad angular final? (b) ¿Cuánto tiempo pasa mientras pasa a través de los 300 radianes?
38. Durante un intervalo de tiempo de 6.0 s, un volante con una aceleración angular constante gira a través de 500 radianes adquiriendo una velocidad angular de 100 rad / s. (a) ¿Cuál es la velocidad angular al comienzo de los 6.0 s? (b) ¿Cuál es la aceleración angular del volante?
39. La velocidad angular de un cuerpo rígido giratorio aumenta de 500 a 1500 rev / min en 120 s. (a) ¿Cuál es la aceleración angular del cuerpo? (b) ¿A través de qué ángulo gira en estos 120 s?
40. Un volante se desacelera de 600 a 400 rev / min mientras gira 40 revoluciones. (a) ¿Cuál es la aceleración angular del volante? (b) ¿Cuánto tiempo transcurre durante las 40 revoluciones?
41. Una rueda de 1,0 m de diámetro gira con una aceleración angular de 4.0rad /s2. (a) Si la velocidad angular inicial de la rueda es 2.0 rad / s, ¿cuál es su velocidad angular después de 10 s? (b) ¿A través de qué ángulo gira en el intervalo de 10 s? (c) ¿Cuáles son la velocidad tangencial y la aceleración de un punto en el borde de la rueda al final del intervalo de 10 s?
42. Una rueda vertical con un diámetro de 50 cm comienza desde el reposo y gira con una aceleración angular constante de 5.0rad / s2 alrededor de un eje fijo a través de su centro en sentido antihorario. (a) ¿Dónde está el punto que inicialmente está en la parte inferior de la rueda en t = 10s? (b) ¿Cuál es la aceleración lineal del punto en este instante?
43. Un disco circular de 10 cm de radio tiene una aceleración angular constante de 1.0rad /s2; en t = 0 su velocidad angular es de 2.0 rad / s. (a) Determine la velocidad angular del disco en t = 5.0s. (b) ¿Cuál es el ángulo por el que ha girado durante este tiempo? (c) ¿Cuál es la aceleración tangencial de un punto en el disco en t = 5.0s?
44. La velocidad angular en función del tiempo para un ventilador es como se muestra en la siguiente figura. (a) ¿Cuál es el ángulo a través del cual giran las aspas del ventilador en los primeros 8 segundos? (b) Verifique su resultado usando las ecuaciones cinemáticas.

45. Una varilla de 20 cm de longitud tiene dos canicas unidas a sus extremos. La varilla con las canicas comienza a girar desde el reposo. Si las canicas tienen una velocidad tangencial de 20 m / s en 7 s, ¿cuál es la aceleración angular de la barra para lograr esto?
1.3 Relación de las cantidades angulares y translacionales
46. En su punto máximo, un tornado tiene un diámetro de 60.0 m y lleva vientos de 500 km / h. ¿Cuál es su velocidad angular en revoluciones por segundo?
47. Un hombre se para en un tiovivo que gira a 2.5 rad / s. Si el coeficiente de fricción estática entre los zapatos del hombre y el tiovivo es μs = 0.5, ¿a qué distancia del eje de rotación puede pararse sin deslizarse?
48. Una ultracentrífuga acelera desde el reposo hasta las 100.000 rpm en 2.00 min. (a) ¿Cuál es la aceleración angular promedio en rad /s2? (b) ¿Cuál es la aceleración tangencial de un punto a 9.50 cm del eje de rotación? (c) ¿Cuál es la aceleración centrípeta en m /s2 y los múltiplos de g de este punto a rpm completas? (d) ¿Cuál es la distancia total recorrida por un punto a 9,5 cm del eje de rotación de la ultracentrífuga?
49. Una turbina eólica está girando en sentido contrario a las agujas del reloj a 0,5 rev /s y se desacelera hasta detenerse en 10 s. Sus cuchillas son de 20 m de longitud. (a) ¿Cuál es la aceleración angular de la turbina? (b) ¿Cuál es la aceleración centrípeta de la punta de las cuchillas en t = 0s? (c) ¿Cuál es la magnitud y la dirección de la aceleración lineal total de la punta de las cuchillas en t = 0s?
50. Cuál es (a) la velocidad angular y (b) la velocidad lineal de un punto en la superficie de la Tierra a una latitud de 30° N. Tome el radio de la Tierra en 6309 km. (c) ¿En qué latitud sería su velocidad lineal 10 m /s?
51. Un niño con una masa de 40 kg se sienta en el borde de un carrusel a una distancia de 3.0 m de su eje de rotación. El carrusel acelera desde el reposo hasta 0,4 rev / s en 10 s. Si el coeficiente de fricción estática entre el niño y la superficie del tiovivo es de 0,6, ¿se cae el niño antes de los 5 s?
52. Una rueda de bicicleta con un radio de 0,3 m gira desde el reposo hasta 3 rev / s en 5 s. ¿Cuál es la magnitud y la dirección del vector de aceleración total en el borde de la rueda a 1.0 s?
53. La velocidad angular de un volante con un radio de 1,0 m varía según ω (t) = 2.0t. Grafique ac(t) y at(t) de t = 0 a 3.0 s para r = 1.0m. Analice estos resultados para explicar cuándo ac >> at y ac << at para un punto en el volante de radio 1.0 m.
1.4 Momento de inercia y energía cinética rotacional
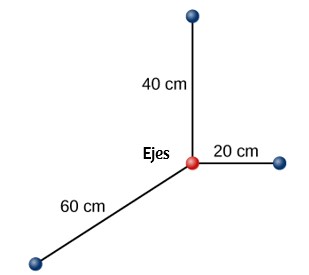
54. En la siguiente figura se muestra un sistema de partículas puntuales. Cada partícula tiene una masa de 0,3 kg y todas se encuentran en el mismo plano. (a) ¿Cuál es el momento de inercia del sistema sobre el eje dado? (b) Si el sistema gira a 5 rev / s, ¿cuál es su energía cinética rotacional?
55. (a) Calcule la energía cinética rotacional de la Tierra sobre su eje. (b) ¿Cuál es la energía cinética de rotación de la Tierra en su órbita alrededor del Sol?
56. Calcule la energía cinética rotacional de una rueda de motocicleta de 12 kg si su velocidad angular es de 120 rad /s. Su radio interior es de 0.280 m y el radio exterior de 0.330 m.
57. Un lanzador de béisbol lanza la pelota en un movimiento donde hay rotación del antebrazo alrededor de la articulación del codo, así como otros movimientos. Si la velocidad lineal de la bola con respecto a la articulación del codo es 20.0 m / s a una distancia de 0.480 m desde la articulación y el momento de inercia del antebrazo es 0.500kg m2, ¿cuál es la energía cinética rotacional del antebrazo?
58. Un buceador entra en un salto mortal durante una inmersión al meter sus extremidades. Si su energía cinética de rotación es de 100 J y su momento de inercia en el pliegue es de 9.0kg m2, ¿cuál es su tasa de rotación durante el salto mortal?
59. Cuando la hélice cae, desde un avión que va a 300 metros de altura y que vuela horizontalmente a 40.0 m / s . La hélice tiene una velocidad de rotación de 20 rev / s, un momento de inercia de 70.0kg m2 y una masa de 200 kg. Ignorar la resistencia del aire. (a) ¿Con qué velocidad de traslación golpea la hélice al suelo? (b) ¿Cuál es la velocidad de rotación de la hélice en el impacto?
60. Si la resistencia del aire está presente en el problema anterior y reduce la energía cinética rotacional de la hélice en el impacto en un 30%, ¿cuál es la tasa de rotación de la hélice en el impacto?
61. Una estrella de neutrones de masa de 2 × 1030 kg y un radio de 10 km gira con un período de 0,02 segundos. ¿Cuál es su energía cinética rotacional?
62. Una lijadora eléctrica que consiste en un disco giratorio de masa de 0,7 kg y un radio de 10 cm gira a 15 rev / seg. Cuando se aplica a una pared de madera rugosa, la tasa de rotación disminuye en un 20%. (a) ¿Cuál es la energía cinética rotacional final del disco giratorio? (b) ¿Cuánto ha disminuido su energía cinética rotacional?
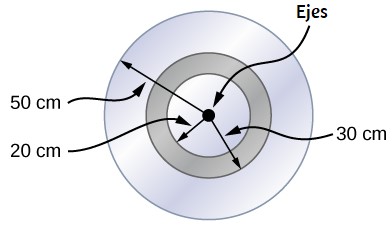
63. Un sistema consiste en un disco de masa de 2,0 kg y un radio de 50 cm sobre el cual se monta un cilindro anular de masa de 1,0 kg con un radio interior de 20 cm y un radio exterior de 30 cm (ver más abajo). El sistema gira alrededor de un eje a través del centro del disco y el cilindro anular a 10 rev / s. (a) ¿Cuál es el momento de inercia del sistema? (b) ¿Cuál es su energía cinética rotacional?
1.5 Cálculo de momentos de inercia
64. Mientras golpea un balón de fútbol, un pateador gira su pierna sobre la articulación de la cadera. El momento de inercia de la pierna es 3.75kgm2 y su energía cinética rotacional es de 175 J. (a) ¿Cuál es la velocidad angular de la pierna? (b) ¿Cuál es la velocidad de la punta del zapato del punter si está a 1.05 m de la articulación de la cadera?
65. Usando el teorema del eje paralelo, ¿cuál es el momento de inercia de la barra de masa m sobre el eje que se muestra a continuación?
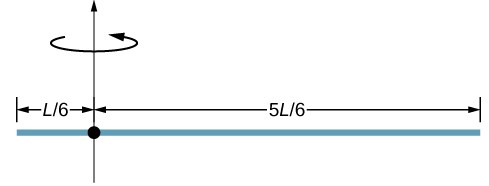
66. Encuentre el momento de inercia de la barra en el problema anterior mediante integración directa.
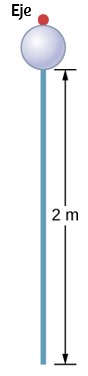
67. Una barra uniforme de masa de 1,0 kg y una longitud de 2,0 m puede girar libremente alrededor de un extremo (consulte la figura siguiente). Si la barra se suelta desde el reposo en un ángulo de 60° con respecto a la horizontal, ¿cuál es la velocidad de la punta de la barra cuando pasa la posición horizontal?
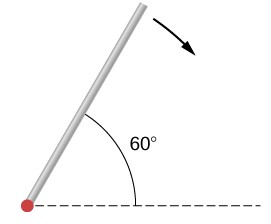
68. Un péndulo consiste en una barra de masa de 2 kg y una longitud de 1 m con una esfera sólida en un extremo con una masa de 0,3 kg y un radio de 20 cm (consulte la siguiente figura). Si el péndulo se libera del reposo en un ángulo de 30°, ¿cuál es la velocidad angular en el punto más bajo?
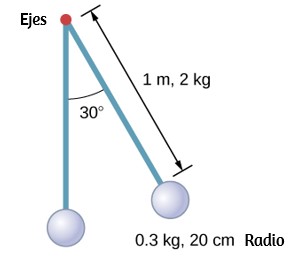
69. Se permite que una esfera sólida de radio 10 cm gire libremente alrededor de un eje. La esfera recibe un golpe brusco para que su centro de masa comience desde la posición que se muestra en la siguiente figura con una velocidad de 15 cm / s. ¿Cuál es el ángulo máximo que hace el diámetro con la vertical?
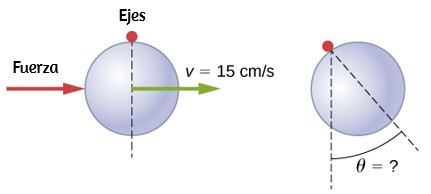
70. Calcule el momento de inercia mediante la integración directa de una barra delgada de masa M y longitud L alrededor de un eje a través de la barra en L/3, como se muestra a continuación. Comprueba tu respuesta con el teorema del eje paralelo

1.6 Torque
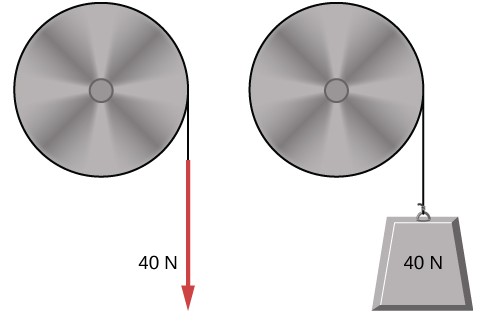
71. Dos volantes de masa despreciable y diferentes radios están unidos entre sí y giran alrededor de un eje común (ver más abajo). El volante más pequeño de 30 cm de radio tiene una cuerda que tiene una fuerza de tracción de 50 N. ¿Qué fuerza de tracción se debe aplicar al cable que conecta el volante de mayor tamaño con un radio de 50 cm para que la combinación no gire?

72. Los tornillos de cabeza cilíndrica de un automóvil deben apretarse con un par de torsión de 62.0Nm. Si un mecánico usa una llave de 20 cm de longitud, ¿qué fuerza perpendicular debe ejercer en el extremo de la llave para apretar un perno correctamente?
73. (a) Cuando abre una puerta, la empuja perpendicularmente con una fuerza de 55.0 N a una distancia de 0.850 m desde las bisagras. ¿Qué torque estás ejerciendo en relación con las bisagras? (b) ¿Importa si empuja a la misma altura que las bisagras? Solo hay un par de bisagras.
74. Al apretar un perno, presiona perpendicularmente sobre una llave con una fuerza de 165 N a una distancia de 0.140 m desde el centro del perno. ¿Cuánta torsión está ejerciendo en newton metros (en relación con el centro del tornillo)?
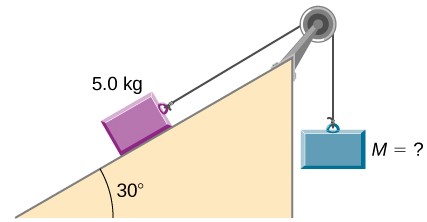
75. ¿Qué masa colgante debe colocarse en el cable para evitar que la polea gire (consulte la siguiente figura)? La masa en el plano sin fricción es de 5.0 kg. El radio interior de la polea es de 20 cm y el radio exterior es de 30 cm
76. Un péndulo simple consiste en una cuerda sin masa de 50 cm de longitud conectada a un pivote y una pequeña masa de 1.0 kg unida al otro extremo. ¿Cuál es el torque sobre el pivote cuando el péndulo forma un ángulo de 40° con respecto a la vertical?
77. Calcule el torque sobre el eje z que está fuera de la página en el origen en la siguiente figura, dado que F1 = 3N, F2 = 2N, F3 = 3N, F4= 1.8N

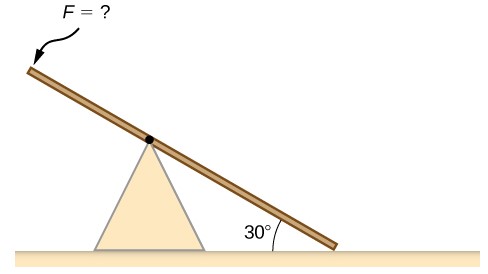
78. Un balancín tiene una longitud de 10.0 m y una masa uniforme de 10.0 kg,descansa en un ángulo de 30°con respecto al suelo (consulte la siguiente figura). El pivote se encuentra a 6,0 m. ¿Qué magnitud de fuerza debe aplicarse perpendicular al balancín en el extremo elevado para permitir que el balancín comience a girar apenas?
79. Un péndulo consiste en una barra de masa de 1 kg y una longitud de 1 m conectada a un pivote con una esfera sólida unida en el otro extremo con una masa de 0,5 kg y un radio de 30 cm. ¿Cuál es el torque sobre el pivote cuando el péndulo hace un ángulo de 30° con respecto a la vertical?
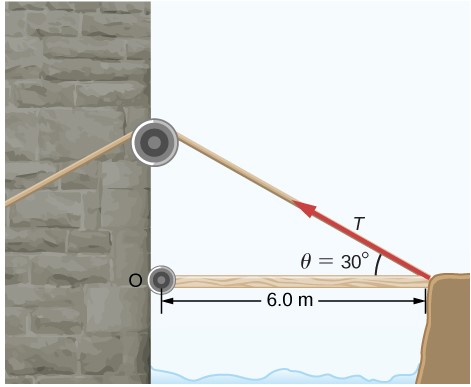
80. Se requiere un torque de 5.00 × 103Nm para elevar un puente levadizo (vea la siguiente figura). ¿Cuál es la tensión necesaria para producir este par? ¿Sería más fácil elevar el puente levadizo si el ángulo fuera mayor o menor?
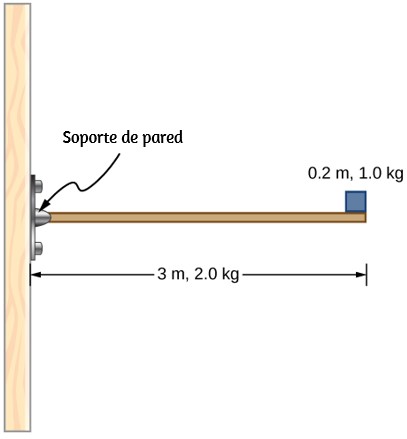
81. Una viga horizontal de 3 m de longitud y 2,0 kg de masa tiene una masa de 1,0 kg y una anchura de 0,2 m al final de la viga (consulte la figura siguiente). ¿Cuál es el par del sistema sobre el soporte en la pared?
82. ¿Qué fuerza debe aplicarse al extremo de una varilla a lo largo del eje x de 2.0 m de longitud para producir un par de torsión de 8.0 k^ Nm sobre la varilla en el origen?
83. ¿Cuál es el torque sobre el origen de la fuerza (5.0i^ − 2.0j^ + 1.0k^) N si se aplica en el punto cuya posición es: r→ = (- 2.0i^+ 4.0j^) m?
1.7 Segunda ley de Newton para movimiento rotacional
84. Una piedra de afilar (en forma de disco) de 90.0 kg, tiene un radio de 0.340 m, gira a 90.0 rpm y presiona un hacha de acero contra ella con una fuerza radial de 20.0 N. (a) Suponiendo el coeficiente cinético de fricción entre el acero y la piedra es 0.20, calcule la aceleración angular de la piedra. (b) ¿Cuántos giros hará la piedra antes de detenerse?
85. Supongamos que se ejerce una fuerza tangencial de 180 N a una piedra de 0.280 m y 75.0 kg . (a) ¿Qué par se ejerce? (b) ¿Cuál es la aceleración angular asumiendo una fricción opuesta y despreciable? (c) ¿Cuál es la aceleración angular si hay una fuerza de fricción opuesta de 20.0 N ejercida a 1.50 cm del eje?
86. Un volante (I = 50 kgm2) que comienza desde el reposo adquiere una velocidad angular de 200.0 rad / s mientras está sujeto a un par constante de un motor durante 5 s. (a) ¿Cuál es la aceleración angular del volante? (b) ¿Cuál es la magnitud del par?
87. Se aplica un par constante a un cuerpo rígido cuyo momento de inercia es de 4,0 kgm2 alrededor del eje de rotación. Si la rueda comienza desde el reposo y alcanza una velocidad angular de 20.0 rad / s en 10.0 s, ¿cuál es el par aplicado?
88. Se aplica un torque de 50.0 Nm a una piedra (I = 20.0 kg m2) durante 20 s. (a) Si comienza desde el reposo, ¿cuál es la velocidad angular de la piedra después de eliminar el par? (b) ¿A través de qué ángulo se mueve la rueda mientras se aplica el torque?
89. Un volante (I = 100.0 kg m2) que gira a 500.0 rev / min se detiene por fricción en 2.0 min. ¿Cuál es el par de la fricción con el volante?
90. Un motor eléctrico acciona una piedra cilíndrica uniforme de 50,0 kg de masa y un diámetro de 1,0 m. La fricción en los rodamientos es despreciable. (a) ¿Qué torque se debe aplicar a la rueda para llevarla del reposo a 120 rev / min en 20 revoluciones? (b) Una herramienta cuyo coeficiente de fricción cinética con la rueda es 0.60 se presiona perpendicularmente contra la rueda con una fuerza de 40.0 N. ¿Qué par debe ser suministrado por el motor para mantener la rueda girando a una velocidad angular constante?
91. Supongamos que cuando se creó la Tierra, no estaba girando. Sin embargo, después de la aplicación de un par de torsión uniforme después de 6 días, giraba a 1 rev / día. (a) ¿Cuál fue la aceleración angular durante los 6 días? (b) ¿Qué torque se aplicó a la Tierra durante este período? (c) ¿Qué fuerza tangente a la Tierra en su ecuador produciría este par?
92. Una polea con momento de inercia de 2.0kg m2 está montada en una pared como se muestra en la siguiente figura. Las cuerdas ligeras se envuelven alrededor de dos circunferencias de la polea y los pesos están unidos. ¿Cuáles son (a) la aceleración angular de la polea y (b) la aceleración lineal de los pesos? Supongamos los siguientes datos: r1 = 50 cm, r2 = 20 cm, m1 = 1.0 kg, m2 = 2.0 kg.

93. Un bloque de masa de 3 kg se desliza por un plano inclinado en un ángulo de 45° con una atadura sin masa unida a una polea con una masa de 1 kg y un radio de 0,5 m en la parte superior de la inclinación (consulte la figura siguiente). La polea se puede aproximar como un disco. El coeficiente de fricción cinética en el plano es 0.4. Cual es la aceleración del bloque?
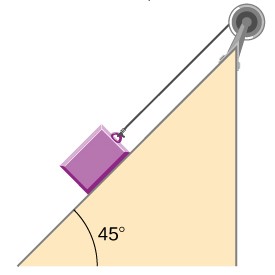
94. El carro que se muestra a continuación se mueve a través de la mesa al caer el bloque. ¿Cuál es la aceleración del carro? Ignore la fricción y asuma los siguientes datos: m1 = 2.0kg, m2 = 4.0kg, I = 0.4kg m2, r = 20cm
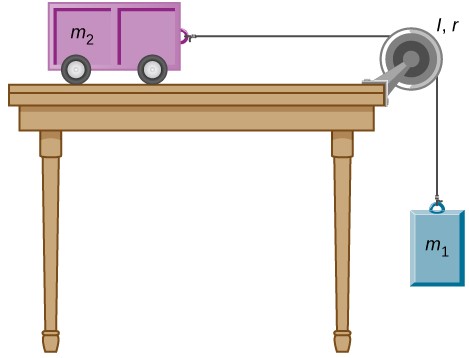
95. Una barra uniforme de masa y longitud se mantiene verticalmente mediante dos cuerdas de masa despreciable, como se muestra a continuación. (a) Inmediatamente después de cortar la cuerda, ¿cuál es la aceleración lineal del extremo libre del palo? (b) De la mitad del palo?
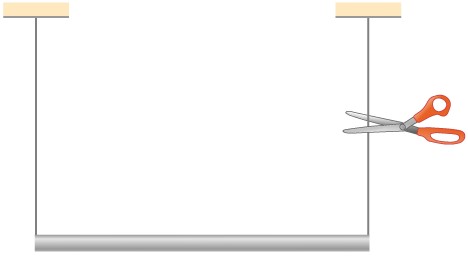
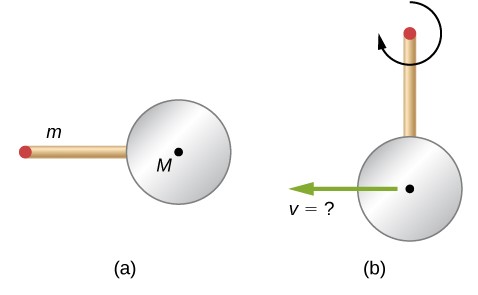
96. Una barra delgada de masa de 0,2 kg y longitud L = 0,5 m se une al borde de un disco metálico de masa M = 2,0 kg y radio R = 0,3 m. El palo puede girar libremente alrededor de un eje horizontal a través de su otro extremo (consulte la siguiente figura). (a) Si la combinación se libera con la palanca horizontal, ¿cuál es la velocidad del centro del disco cuando la palanca es vertical? (b) ¿Cuál es la aceleración del centro del disco en el momento en que se suelta el palo? (c) ¿En el instante en que el palo pasa por la vertical?
1.8 Trabajo y potencia para el movimiento de rotación
97. Una turbina eólica gira a 20 rev / min. Si su potencia de salida es de 2.0 MW, ¿cuál es el par producido en la turbina por el viento?
98.Un cilindro de arcilla de 20 cm de radio en una rueda de alfarero gira a una velocidad constante de 10 rev / s. El alfarero aplica una fuerza de 10 N a la arcilla con sus manos donde el coeficiente de fricción es 0.1 entre sus manos y la arcilla. ¿Cuál es la potencia que el alfarero tiene que entregar a la rueda para mantenerla girando a este ritmo constante?
99. Una piedra cilíndrica uniforme tiene una masa de 10 kg y un radio de 12 cm. (a) ¿Cuál es la energía cinética de rotación de la piedra afilar cuando está girando a 1.5 × 103rev / min? (b) Después de apagar el motor de piedra de afilar, una cuchilla se presiona contra el borde exterior de la piedra con una fuerza perpendicular de 5.0 N. El coeficiente de fricción cinética entre la piedra de afilar y la hoja es de 0.80. Usa el teorema de la energía de trabajo para determinar cuántas vueltas hace la piedra antes de detenerse.
100. Un disco uniforme de 500 kg de masa y un radio de 0.25 m está montado sobre cojinetes sin fricción para que pueda girar libremente alrededor de un eje vertical a través de su centro (consulte la siguiente figura). Se enrolla un cordón alrededor del borde del disco y se tira con una fuerza de 10 N. (a) ¿Cuánto trabajo se ha realizado en el momento en que el disco ha completado tres revoluciones, comenzando desde el reposo? (b) Determine el torque debido a la fuerza, luego calcule el trabajo realizado por este torque en el instante en que el disco ha completado tres revoluciones. (c) ¿Cuál es la velocidad angular en ese instante? (d) ¿Cuál es la potencia de salida de la fuerza en ese instante?

101. Una hélice se acelera desde el reposo hasta una velocidad angular de 1000 rev / min durante un período de 6,0 segundos con un par constante de 2,0 × 103 N m. (a) ¿Cuál es el momento de inercia de la hélice? (b) ¿Qué potencia se proporciona a la hélice 3.0 s después de que comience a girar?
102. Una esfera de masa de 1,0 kg y un radio de 0,5 m se une al extremo de una barra sin masa de 3,0 m de longitud. La barra gira alrededor de un eje que se encuentra en el extremo opuesto de la esfera (ver más abajo). El sistema gira horizontalmente alrededor del eje a una velocidad constante de 400 rev / min. Después de girar a esta velocidad angular en el vacío, se introduce resistencia al aire y proporciona una fuerza de 0.15N en la esfera opuesta a la dirección del movimiento. ¿Cuál es la potencia proporcionada por la resistencia del aire al sistema 100.0 s después de que se introduce la resistencia del aire?

103. Una barra uniforme de longitud L y masa M se sostiene verticalmente con un extremo apoyado en el piso como se muestra a continuación. Cuando se suelta la varilla, gira alrededor de su extremo inferior hasta que toca el suelo. Suponiendo que el extremo inferior de la varilla no se deslice, ¿cuál es la velocidad lineal del extremo superior cuando toca el suelo?
104. Un atleta en un gimnasio aplica una fuerza constante de 50 N a los pedales de una bicicleta para mantener la velocidad de rotación de la rueda a 10 rev / s. La longitud de los brazos del pedal es de 30 cm. ¿Cuál es la potencia entregada a la bicicleta por el atleta?
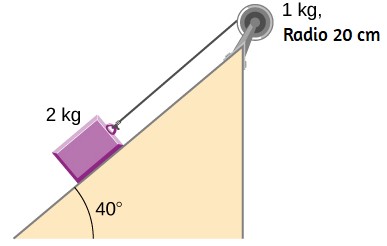
105. Un bloque de 2 kg en un plano inclinado sin fricción a 40° tiene una cuerda unida a una polea de 1 kg y un radio de 20 cm (consulte la figura siguiente). (a) ¿Cuál es la aceleración del bloque en el plano? (b) ¿Cuál es el trabajo realizado por la fuerza gravitacional para mover el bloque 50 cm?
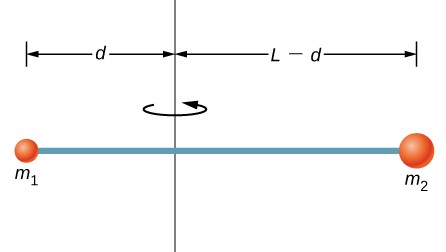
106. Los cuerpos pequeños de masa m1 y m2 están unidos a los extremos opuestos de una varilla delgada y rígida de longitud L y masa M. La varilla se monta de manera que pueda girar libremente en un plano horizontal alrededor de un eje vertical (ver más abajo). ¿Qué distancia d desde m1 debería ser el eje de rotación de modo que se requiera una cantidad mínima de trabajo para ajustar la varilla girando a una velocidad angular ω?
107.Un ciclista está montando de manera tal que las ruedas de la bicicleta tienen una velocidad de rotación de 3.0 rev / s. Si el ciclista frena de tal manera que la velocidad de rotación de las ruedas disminuya a una velocidad de 0,3 rev / s2, ¿cuánto tiempo tarda el ciclista en detenerse por completo?
108. Calcule la velocidad angular del movimiento orbital de la Tierra alrededor del Sol.
109. Un giradiscos de fonógrafo que gira a 33 1/3 rev / min empieza a lentificar y se detiene en 1.0 min. (a) ¿Cuál es la aceleración angular de la plataforma giratoria suponiendo que es constante? (b) ¿Cuántas revoluciones hace la plataforma giratoria mientras se detiene?
110.Con la ayuda de una cuerda, un giroscopio se acelera desde el reposo hasta 32 rad / s en 0,40 s bajo una aceleración angular constante. (a) ¿Cuál es su aceleración angular en rad / s2? (b) ¿Cuántas revoluciones pasa en el proceso?
111.Supongamos que una pieza de polvo ha caído en un CD. Si la velocidad de giro del CD es de 500 rpm y el polvo está a 4.3 cm del centro, ¿cuál es la distancia total recorrida por el polvo en 3 minutos? (Ignore las aceleraciones debido a que el CD gira).
112. Un sistema de partículas puntuales gira alrededor de un eje fijo a 4 rev / s. Las partículas se fijan unas respecto a otras. Las masas y las distancias al eje de las partículas puntuales son m1 = 0.1kg, r1 = 0.2m, m2 = 0.05kg, r2 = 0.4m, m3= 0.5kg, r3 = 0.01m. (a) ¿Cuál es el momento de inercia del sistema? (b) ¿Cuál es la energía cinética rotacional del sistema?
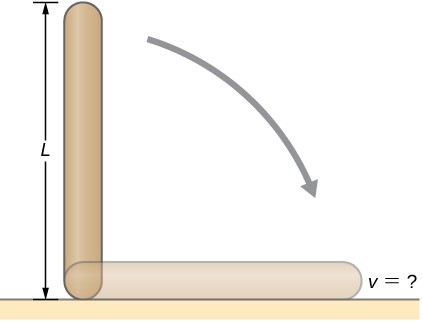
113.Calcula el momento de inercia de un patinador dada la siguiente información. (a) El patinador de 60.0 kg se aproxima como un cilindro que tiene un radio de 0.110 m. (b) El patinador con los brazos extendidos se aproxima por un cilindro de 52,5 kg, tiene un radio de 0,110 m, y tiene dos brazos de 0,900 m de longitud que son 3,75 kg cada uno y se extienden directamente desde el cilindro, como las varillas rotadas alrededor de sus extremos.
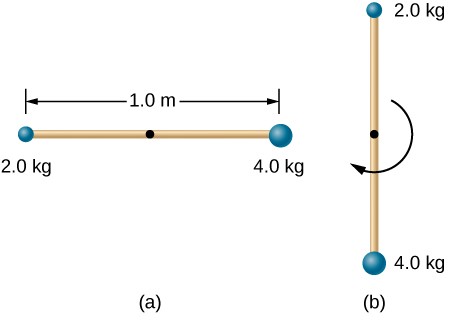
114.Una barra de longitud de 1,0 m y una masa de 6,0 kg puede girar libremente alrededor de un eje horizontal a través del centro. Pequeños cuerpos de masas de 4,0 y 2,0 kg están unidos a sus dos extremos (ver la siguiente figura). El palo se libera desde la posición horizontal. ¿Cuál es la velocidad angular del palo cuando se mueve a través de la vertical?
115. Un péndulo consiste en una barra de 2 m de longitud y 3 kg de masa con una esfera sólida de 1 kg y un radio de 0,3 m unidos por un extremo. El eje de rotación se muestra a continuación. ¿Cuál es la velocidad angular del péndulo en su punto más bajo si se libera desde el reposo en un ángulo de 30°?
116. Calcule el torque de la fuerza de 40 N alrededor del eje a través de O y perpendicular al plano de la página como se muestra a continuación.

117. Dos niños empujan los lados opuestos de una puerta durante el juego. Ambos empujan horizontalmente y perpendicular a la puerta. Un niño empuja con una fuerza de 17.5 N a una distancia de 0.600 m desde las bisagras, y el segundo niño empuja a una distancia de 0.450 m. ¿Qué fuerza debe ejercer el segundo niño para evitar que la puerta se mueva? Supongamos que la fricción es despreciable.
118. La fuerza de 20 j^N se aplica en r→ = (4.0 i^ − 2.0 j^) m. ¿Cuál es el par de esta fuerza sobre el origen?
119. Un motor de automóvil puede producir 200 N m de torque. Calcule la aceleración angular producida si el 95.0% de este par se aplica al eje de transmisión, el eje y las ruedas traseras de un automóvil, dada la siguiente información. El coche está suspendido para que las ruedas puedan girar libremente. Cada rueda actúa como un disco de 15,0 kg que tiene un radio de 0,180 m. Las paredes de cada neumático actúan como un anillo anular de 2.00 kg que tiene un radio interior de 0.180 m y un radio exterior de 0.320 m. La banda de rodadura de cada neumático actúa como un aro de 10.0 kg de radio de 0.330 m. El eje de 14.0 kg actúa como una barra que tiene un radio de 2.00 cm. El eje de transmisión de 30.0 kg actúa como una barra que tiene un radio de 3.20 cm.
120. Una piedra de afilar con una masa de 50 kg y un radio de 0,8 m mantiene una velocidad de rotación constante de 4,0 rev / s con un motor mientras se presiona una cuchilla contra el borde con una fuerza de 5,0 N. El coeficiente de fricción cinética entre la piedra y la cuchilla es 0,8. ¿Cuál es la potencia proporcionada por el motor para mantener la piedra con velocidad de rotación constante?
121. La aceleración angular de un cuerpo rígido giratorio viene dada por α = (2.0−3.0t) rad / s2. Si el cuerpo comienza a girar desde el reposo en t = 0, (a) ¿cuál es la velocidad angular? (b) Posición angular? (c) ¿En qué ángulo gira en 10 s? (d) ¿Dónde se encuentra el vector perpendicular al eje de rotación que indica 0° en t = 0 en t = 10s?
122. El día de la Tierra ha aumentado 0,002 s en el último siglo. Si este aumento en el período de la Tierra es constante, ¿cuánto tiempo tomará para que la Tierra se detenga?
123. Un disco de masa m, radio R y área A tiene una densidad de masa de superficie σ = mrAR (consulte la siguiente figura). ¿Cuál es el momento de inercia del disco sobre un eje que atraviesa el centro?
124. Zorch, un archienemigo del hombre de rotación, decide ralentizar la rotación de la Tierra una vez cada 28.0 h al ejercer una fuerza opuesta en y paralela al ecuador. El hombre rotación no se encuentra preocupado, porque sabe que Zorch solo puede ejercer una fuerza de 4.00 × 107N (un poco más grande que el empuje de un cohete Saturn V). ¿Cuánto tiempo debe Zorch empujar con esta fuerza para lograr su objetivo? (Este período le da tiempo al hombre de rotación para dedicarse a otros villanos.)
125.Se enrolla un cordón alrededor del borde de un cilindro sólido de radio de 0,25 m, y se ejerce una fuerza constante de 40 N sobre el cordón, como se muestra en la siguiente figura. El cilindro está montado sobre cojinetes sin fricción, y su momento de inercia es de 6,0 kg / m2. (a) Use el teorema de la energía de trabajo para calcular la velocidad angular del cilindro después de que se hayan quitado 5.0 m de cable. (b) Si la fuerza de 40 N se reemplaza por un peso de 40 N, ¿cuál es la velocidad angular del cilindro después de que se hayan desenrollado 5.0 m de cable?.